天津科技大学高等数学试题库(定积分)答案

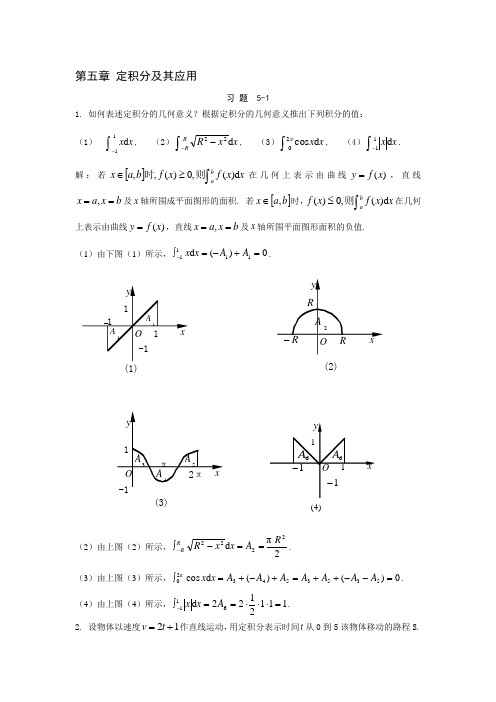
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义？根据定积分的几何意义推出下列积分的值： （1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11.解：若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时，⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围平面图形面积的负值. （1）由下图（1）所示，0)(d 1111=+-=⎰-A A x x .（2）由上图（2）所示，2πd 2222R A x x R R R==-⎰-.（3）由上图（3）所示，0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . （4）由上图（4）所示，1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动，用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解：=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解：任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =，小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式：∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解：上在]1,0[)(2x x f =连续函数，故可积，因此为方便计算，我们可以对[]0,1 n 等分，分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点，故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ（即时∞→n ），由定积分的定义得： 120d x x ⎰=31．5. 利用定积分的估值公式，估计定积分⎰-+-1134)524(x x x d 的值.解：先求524)(34+-=x x x f 在[]1,1-上的最值，由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小，知min max 5093,111024f f ==，由定积分的估值公式，得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ，哪个积分值较大？解：在[]0,1区间内：22xx x x e e ≥⇒≥ 由性质定理知道：⎰1d xe x≥⎰1d 2x e x7. 证明：⎰---<<2121212d 22x e ex 。

定积分试题及答案详解1. 计算定积分 \(\int_{0}^{1} x^2 dx\)。

答案：首先，我们需要找到被积函数 \(x^2\) 的原函数。

原函数为\(\frac{1}{3}x^3\)。

接下来，我们计算定积分：\[\int_{0}^{1} x^2 dx = \left[\frac{1}{3}x^3\right]_{0}^{1} = \frac{1}{3}(1)^3 - \frac{1}{3}(0)^3 = \frac{1}{3} - 0 =\frac{1}{3}\]所以，定积分的值为 \(\frac{1}{3}\)。

2. 求定积分 \(\int_{1}^{2} \frac{1}{x} dx\)。

答案：对于被积函数 \(\frac{1}{x}\)，其原函数为 \(\ln|x|\)。

计算定积分：\[\int_{1}^{2} \frac{1}{x} dx = [\ln|x|]_{1}^{2} = \ln(2) - \ln(1) = \ln(2)\]因此，定积分的值为 \(\ln(2)\)。

3. 计算定积分 \(\int_{0}^{\pi} \sin(x) dx\)。

答案：被积函数 \(\sin(x)\) 的原函数是 \(-\cos(x)\)。

计算定积分：\[\int_{0}^{\pi} \sin(x) dx = [-\cos(x)]_{0}^{\pi} = -\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2\]所以，定积分的值为 2。

4. 求定积分 \(\int_{0}^{1} (2x + 3) dx\)。

答案：被积函数 \(2x + 3\) 的原函数为 \(x^2 + 3x\)。

计算定积分：\[\int_{0}^{1} (2x + 3) dx = [x^2 + 3x]_{0}^{1} = (1^2 + 3\cdot 1) - (0^2 + 3 \cdot 0) = 1 + 3 - 0 = 4\]因此，定积分的值为 4。

定积分典型例题20例答案例1 求33322321lim(2)n n n n n →∞+++．分析 将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．解 将区间[0,1]n 等分，则每个小区间长为1i x n ∆=，然后把2111n n n=⋅的一个因子1n 乘入和式中各项．于是将所求极限转化为求定积分．即33322321lim(2)n n n n n →∞+++=333112lim ()n n n n nn →∞+++=13034xdx =⎰．例2 2202x x dx -⎰=_________．解法1 由定积分的几何意义知，2202x x dx -⎰等于上半圆周22(1)1x y -+= (0y ≥)与x 轴所围成的图形的面积．故2202x x dx -⎰=2π． 解法2 本题也可直接用换元法求解．令1x -=sin t （22t ππ-≤≤），则222x x dx -⎰=2221sin cos t tdt ππ--⎰=2221sin cos t tdt π-⎰=2202cos tdt π⎰=2π 例3 （1）若22()x t xf x e dt -=⎰，则()f x '=___；（2）若0()()xf x xf t dt =⎰，求()f x '=___．分析 这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ''=-⎰．解 （1）()f x '=422x x xe e ---；（2） 由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =⎰，则可得()f x '=0()()xf t dt xf x +⎰．例4 设()f x 连续，且31()x f t dt x -=⎰，则(26)f =_________．解 对等式310()x f t dt x -=⎰两边关于x 求导得32(1)31f x x -⋅=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =． 例5 函数11()(3)(0)x F x dt x t =->⎰的单调递减开区间为_________．解 1()3F x x'=-，令()0F x '<得13x >，解之得109x <<，即1(0,)9为所求． 例6 求0()(1)arctan xf x t tdt =-⎰的极值点．解 由题意先求驻点．于是()f x '=(1)arctan x x -．令()f x '=0，得1x =，0x =．列表如下：故1x =为()f x 的极大值点，0x =为极小值点．例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中2arcsin 0()xt g x e dt -=⎰，[1,1]x ∈-，试求该切线的方程并求极限3lim ()n nf n→∞．分析 两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ''=．解 由已知条件得2(0)(0)0t f g e dt -===⎰，且由两曲线在(0,0)处切线斜率相同知2(arcsin )2(0)(0)11x x e f g x -=''===-．故所求切线方程为y x =．而3()(0)3lim ()lim33(0)330n n f f n nf f n n→∞→∞-'=⋅==-． 例8 求 22000sin lim(sin )x x xtdtt t t dt→-⎰⎰；分析 该极限属于型未定式，可用洛必达法则． 解 22000sin lim (sin )x x xtdtt t t dt→-⎰⎰=2202(sin )lim (1)(sin )x x x x x x →-⋅⋅-=220()(2)lim sin x x x x →-⋅-=304(2)lim 1cos x x x→-⋅-x(,0)-∞0 (0,1)1 (1,)+∞()f x '-＋－=2012(2)lim sin x x x→-⋅=0．注 此处利用等价无穷小替换和多次应用洛必达法则．例9 试求正数a 与b ，使等式2201lim1sin x x t dt x b x a t→=-+⎰成立． 分析 易见该极限属于型的未定式，可用洛必达法则． 解 20201lim sin x x t dt x b x a t →-+⎰=220lim 1cos x x a x b x →+-=22001lim lim 1cos x x x b x a x→→⋅-+201lim 11cos x x b x a →==-，由此可知必有0lim(1cos )0x b x →-=，得1b =．又由2012lim 11cos x x x a a→==-， 得4a =．即4a =，1b =为所求． 例10 设sin 20()sin x f x t dt =⎰，34()g x x x =+，则当0x →时，()f x 是()g x 的（ ）．A ．等价无穷小．B ．同阶但非等价的无穷小．C ．高阶无穷小．D ．低阶无穷小．解法1 由于 22300()sin(sin )cos lim lim()34x x f x x xg x x x →→⋅=+ 2200cos sin(sin )lim lim34x x x x x x →→=⋅+ 22011lim 33x x x →==． 故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到sin 223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+⎰，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x x x→→→-+-+===++． 例11 计算21||x dx -⎰．分析 被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -⎰＝0210()x dx xdx --+⎰⎰＝220210[][]22x x --+＝52．注 在使用牛顿－莱布尼兹公式时,应保证被积函数在积分区间上满足可积条件．如 33222111[]6dx x x --=-=⎰，则是错误的．错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界.例12 设()f x 是连续函数，且10()3()f x x f t dt =+⎰，则()________f x =．分析 本题只需要注意到定积分()baf x dx ⎰是常数（,a b 为常数）．解 因()f x 连续，()f x 必可积，从而10()f t dt ⎰是常数，记1()f t dt a =⎰，则()3f x x a =+，且11(3)()x a dx f t dt a +==⎰⎰．所以2101[3]2x ax a+=，即132a a +=， 从而14a =-，所以 3()4f x x =-．例13 计算2112211x x dx x-++-⎰．分析 由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性． 解 2112211x x dx x-++-⎰=211112221111x x dx dx x x--++-+-⎰⎰．由于22211x x+-是偶函数，而211x x+-是奇函数，有112011xdx x-=+-⎰, 于是2112211x x dx x -++-⎰=2102411x dx x +-⎰=22120(11)4x x dx x--⎰=11200441dx x dx --⎰⎰ 由定积分的几何意义可知12014x dx π-=⎰, 故211122444411x x dx dx xππ-+=-⋅=-+-⎰⎰．例14 计算220()xd tf x t dt dx -⎰，其中()f x 连续． 分析 要求积分上限函数的导数，但被积函数中含有x ，因此不能直接求导，必须先换元使被积函数中不含x ，然后再求导．解 由于220()xtf x t dt -⎰=2221()2x f x t dt-⎰． 故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以220()x tf x t dt -⎰=201()()2x f u du -⎰=201()2x f u du ⎰， 故220()x d tf x t dt dx -⎰=201[()]2x d f u du dx ⎰=21()22f x x⋅=2()xf x ．错误解答220()x d tf x t dt dx -⎰22()(0)xf x x xf =-=． 错解分析 这里错误地使用了变限函数的求导公式，公式()()()xad x f t dt f x dx 'Φ==⎰中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．例15 计算30sin x xdx π⎰．分析 被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．解30s i n x x d x π⎰30(c o s )x d x π=-⎰33[(c o s )](c o s )x x x d x ππ=⋅---⎰ 30cos 6xdx ππ=-+⎰326π=-． 例16 计算120ln(1)(3)x dx x +-⎰．分析 被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-⎰=101ln(1)()3x d x +-⎰=1100111[ln(1)]3(3)(1)x dx x x x +-⋅--+⎰ =101111ln 2()2413dx x x-++-⎰11ln 2ln324=-． 例17 计算20sin x e xdx π⎰．分析 被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法．解 由于2sin xe xdx π⎰20sin xxde π=⎰220[sin ]cos xx e x e xdx ππ=-⎰220cos x e e xdx ππ=-⎰， （1）而20cos xe xdx π⎰20cos xxde π=⎰220[cos ](sin )xx e x e x dx ππ=-⋅-⎰20sin 1x e xdx π=-⎰， （2）将（2）式代入（1）式可得20sin xe xdx π⎰220[sin 1]x e e xdx ππ=--⎰,故20sin xe xdx π⎰21(1)2e π=+．例18 计算1arcsin x xdx ⎰．分析 被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．解 10arcsin x xdx ⎰210arcsin ()2x xd =⎰221100[arcsin ](arcsin )22x x x d x =⋅-⎰21021421x dx x π=--⎰． （1） 令sin x t =，则2121x dx x-⎰222sin sin 1sin td t tπ=-⎰220sin cos cos ttdt t π=⋅⎰220sin tdt π=⎰201cos22t dt π-==⎰20sin 2[]24t t π-4π=． （2）将（2）式代入（1）式中得1arcsin x xdx =⎰8π． 例19设()f x [0,]π上具有二阶连续导数，()3f π'=且0[()()]cos 2f x f x xdx π''+=⎰，求(0)f '．分析 被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解． 解 由于0[()()]cos f x f x xdx π''+⎰00()sin cos ()f x d x xdf x ππ'=+⎰⎰[]000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx ππππ'''=-++⎰⎰()(0)2f f π''=--=．故 (0)f '=2()235f π'--=--=-． 例20 计算243dxx x +∞++⎰． 分析 该积分是无穷限的的反常积分，用定义来计算． 解2043dx x x +∞++⎰=20lim 43t t dx x x →+∞++⎰=0111lim ()213t t dx x x →+∞-++⎰ =011lim [ln ]23t t x x →+∞++=111lim (ln ln )233t t t →+∞+-+ =ln 32．。

大学积分考试题及答案一、选择题（每题2分，共20分）1. 以下哪项不是积分的基本性质？A. 线性性质B. 微积分基本定理C. 区间可加性D. 反演性质答案：D2. 定积分∫[a,b] f(x) dx的几何意义表示什么？A. 曲线下的面积B. 曲线上的点C. 曲线的斜率D. 曲线的切线答案：A3. 如果函数f(x)在区间[a,b]上连续，那么∫[a,b] f(x) dx等于：A. 0B. f(a)C. f(b)D. f(a) + f(b)答案：A4. 以下哪个函数是奇函数？A. f(x) = x^2B. f(x) = |x|C. f(x) = sin(x)D. f(x) = cos(x)答案：C5. 根据牛顿-莱布尼茨公式，如果F(x)是f(x)的一个原函数，那么∫[a,b] f(x) dx等于：A. F(a) - F(b)B. F(b) - F(a)C. F(a) + F(b)D. 2F(b) - F(a)答案：B6. 以下哪个选项是正确的积分公式？A. ∫sin(nx) dx = cos(nx) / n + CB. ∫cos(nx) dx = sin(nx) / n + CC. ∫tan(nx) dx = -1/n cos(nx) + CD. ∫csc^2(nx) dx = -1/n cot(nx) + C答案：D7. 以下哪个积分是收敛的？A. ∫[1,∞) (1/x) dxB. ∫[1,∞) (x^2) dxC. ∫[1,∞) (1/x^2) dxD. ∫[1,∞) (sin(x)/x) dx答案：C8. 函数f(x) = e^x在区间[0,1]上的平均值为：A. (e - 1)/2B. e/2C. (1 + e)/2D. 1/e答案：A9. 如果f(x)在区间[a,b]上可积，那么以下哪个选项是正确的？A. f(x)在[a,b]上必定连续B. f(x)在[a,b]上必定有界C. f(x)在[a,b]上必定单调递增D. f(x)在[a,b]上必定有一个原函数答案：B10. 以下哪个积分可以通过换元积分法求解？A. ∫x^2 dxB. ∫1/x dxC. ∫sin(x)/x dxD. ∫x * e^x dx答案：D二、填空题（每题3分，共15分）11. 定积分∫[0,1] x dx的值为_________。

第六章 一元函数定积分的应用一、微元法（元素法）实际问题中可化为定积分来计算的待求量A ，一般总可按“分割、近似求和、取极限”这三个步骤导出它的积分表达式。

但为了简捷实用起见，常常采用微元法（又称元素法）。

微元法的关键就在于寻找待求量A 的微小增量（部分量）能近似表达为x ∆的线性形式，()x x f A ∆≈∆而且当0→∆x 时，()()x x x f A ∆=∆-∆0，亦即()dx x f dA =，其中()x f 为[]b a ,上的某一个连续函数。

量dA 称为待求量的微元素。

然后把()dx x f 在[]b a ,上积分，即待求量⎰=badx x f A )(。

这就是微元法。

在采用微元法时，必须注意如下几点：（1）选好坐标系，这关系到计算简繁问题。

（2）待求量A 具有以区间的可加性，即A =∑∆A ；（3）取好微元x x f d )(，经常应用“以匀代变”“以直代曲”的思想决定A ∆的线性主部，这关系到结果正确与否的问题。

定积分的几何应用一、平面图形的面积 1．直角坐标的情形求)(1x y ϕ=与)(2x y ϕ=与所围图形的面积方法（1）以x 为积分变量由)(1x ϕ)(2x ϕ=解出两个常数值a x =，b x =，面积元素dA =dx x x )]()([12ϕϕ-，面积A =x x x bad )]()([12ϕϕ-⎰，（b x a ≤≤）。

方法(2) 以y 为积分变量由)(1x y ϕ=、)(2x y ϕ=解出x 的两个表达式)(1y x ϕ=，)(2y x ϕ=，再根据)(1y ϕ)(2y ϕ=解出y 的两个常数值c y =，d y =，面积元素dA =dy y y )]()([12ϕϕ-，面积A =y y y dc d )]()([12ϕϕ-⎰，（d y c ≤≤）。

以x 还是y 为积分变量，要视具体情况分析，总之要让计算最简单。

（1）X — 型平面图形的面积 （2） Y — 型平面图形⎰-=badx x g x f S )()( ⎰-=dcdy y g y f S )()(2．参数方程情形求)(x f y =、a x =、b x =以及x 轴所围图形的面积（b a x f <≥,0)(），如果曲边)(x f y =的方程为参数方程为⎩⎨⎧==)()(t y t x φϕ，则其面积dx y A ba ⎰==dt t t )(')(ϕφβα⎰，其中)(),(βϕαϕ==b a3．极坐标情形设平面图形是由曲线 )(θϕ=r 及射线αθ=，βθ=围成的曲边扇形。

天津科技大学《高等数学》(一)检测题8-1答案一、填空题1. c b a 6142+-；2. )2,1,2(31-±；3. 3232313--，，，；4. 22；5.2020z y +，0z ； 6. )1,0,0(；7. )1(43222-=-+z z y x .二、选择题1.（B ）；2. (C)；3.（C ）.三、解答题1．解：c b-=-=+=，)2(31)(3131c b c b c +=-+=+=+=，)2(31)(3232c b c b c +=-+=+=+=.2. 解：由++=，++=，得)(21+=，而)1,2,4()3,6,0(-=--=、，于是)1,4,2(--=. 或由中点坐标公式，得N M 、点坐标为)2/5,5,1(M 、)2/3,1,3(N 于是)1,4,2(--=.3. 解：由49)3()2(62222=-+-+=AB ，49)6(3)2(2222=-++-=AC ， 98)3(5)8(2222=-++-=BC ，有AC AB =及222BC AC AB =+，所以，三角形ABC 是等腰直角三角形.天津科技大学《高等数学》(一)检测题8-2答案一、填空题1. 2， )13,4,7(--；2. 2，212arccos ；3. )2,1,1(-k （k 是任何实数）；4. 3.二、选择题1.（A ）；2.（B ）；3.（C ）；4. (D) .三、解答题1．解：22253)3()2(n n m m n m n m b a -⋅+=-⋅+=⋅08532cos 5322=-+=-⋅+=nn m mθ.2. 解：8=⋅b a ，8=⋅c a，于是k j b c b c a c b a 248)(8)()(--=-=⋅-⋅；k j kj i c a b a+=--=-⨯-=-⨯+111443)1,11()443()()(，，，；k j i kj i b a+--=--=⨯58311132， 2)(=⋅⨯c b a. 3. 解：(2=u +a +b ()⋅c +a +b )c14)(2222=⋅+⋅+⋅+++=c b c a b a c b a ，所以14=u.=⋅⋅=u a u a θcos 14141411===⋅⋅+⋅+⋅u u a c a b a a a. 4．)301(-=，，，)021(，，=A ，)236(021301，，-=-=⨯kj i，==S 27.天津科技大学《高等数学》(一)检测题8-3答案一、填空题1. 6)2()1()1(222=-+++-z y x ； 2. 2222)1(x z y +=+，221z x y ++=； 3. 122=-z x ，z ，单叶旋转双曲面； 4. 圆锥面； 5. 椭圆，椭圆柱面； 6.2x z =，抛物柱面.二、选择题1.（B ）；2.（B ）；3.（C ）；4. (D) .三、解答题1．解：配方得 14)3()2()1(222+=-+++-a z y x ， 当14->a 时，是球心在)3,2,1(0-M ，半径14+=a R 的球面；当14-=a 时，是一点)3,2,1(0-M ；当14-<a 时，不表示任何图形. 2. 解：将方程改写为2222)(y z x =+±，由此可见，它是由xOy 平面是直线x y ±=，或由yOz 平面是直线z y ±=绕y 轴旋转形成. 它是圆锥面，其特点是顶点在原点，半顶角为4/π，y 轴是中心轴，开口向y 轴两侧. 3. 解：（1） （2）天津科技大学《高等数学》(一)检测题8-4答案一、填空题1. 圆；2. 16322=-z y ； 3.⎩⎨⎧=-；022y x ,12=z4. ,cos 3θ=x ,sin 3θ=y θsin 3=z （πθ20<≤）；5. 0=-y x ；6. 62=+-z y x ；7. 0==C B ，0≠A .二、选择题1.（C ）；2.（C ）；3.（D ）.三、解答题1．解： 取法向量)4,3,1()2,3,1()12,2(3121=-⨯--=⨯=M M M M n， 平面方程为0)2(4)0(3)1(=-+-+-z y x ，即943=++z y x . 2. 解：取法向量)0,1,1(2)1,1,1()11,1(1-=⨯-=⨯=n n， 平面方程为0)1(0)1()1(=-+---z y x ，即0=-y x .3. 解：由平面过y 轴，于是设所求平面方程为0=+Cz Ax ，再由平面到B A 、两点的距离相等，有222232C A A C A C A +-=++，即132=+AC，得C A -=或C A 3-=，代入0=+Cz Ax 得所求平面方程为0=-z x 或03=-z x .4．解：设所求平面方程为132=++az a y a x ，由到原点的距离是6，有 2223121116⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=a a a ，即766a=，得7±=a ， 代入方程132=++aza y a x 并化简，得所求平面为42236±=++z y x .天津科技大学《高等数学》(一)检测题8-5答案一、填空题1. )5,3,1(--；2. 42132zy x =-+=-； 3. z y x ==； 4.232211-=--=-z y x ； 5. 0. 二、选择题1.（D ）；2.（D ）；3.（B ）.三、解答题1．解：取)1,1,3()1,2,1()2,1,1(21-=-⨯-=⨯=n n s，所求直线方程为111231-=--=+z y x . 2. 解：在直线上取一点)0,3,4(0-M ，并取所求平面的法向量为)22,9,8()2,4,1()1,2,5(0--=-⨯=⨯=MM s n，所求平面方程为0)2(22)1(9)3(8=+----z y x ，即592298=--z y x . 3. 解：设所求平面方程为012=+--+z z y x λ，将点M 代入有03=-λ，得3=λ，于是所求方程为122=++z y x .4．解：设所求直线方程为pz n y m x 321-=-=-，由与已知直线垂直，有0=++p n m ①；又设与z 轴交点为),0,0(0z ，有pz n m 3210-=-=-②，由①、②两式得m p m n 32-==、，所求直线方程是332211--=-=-z y x . 5．解：过点M 作平面垂直于所给直线，方程为0)2(2)1(=--+y x ，将直线改写为参数方程0221=--=+=z t y t x ，，并代入平面方程，有0510=+t ，得2-=t ，投影点为)0,2,1(0-M ，所以30==MM d .天津科技大学《高等数学》(一)检测题9-1答案一、填空题1．u u 22+，1-+y x ； 2．}0,1),{(22≥<+x y x y x ；3．{}x y y x ±=),(.二、选择题1．（B ）； 2．（C ）； 3．（D ）；三、解答题1．解：令y x u +=，x y v =.则v u x +=1，vuvy +=1.于是 vv u v uv v u y x x y y x f v u f +-=+-+=-=+=1)1()1()1(),(),(22222.所以yy x y x f +-=1)1(),(2.2．解：))((2)()(),(44ty tx ty tx ty tx f -+=2t =).,()2(244y x f t xy y x =-+3．解：由⎩⎨⎧≥->--,0)(,0122x y x y x 有⎪⎩⎪⎨⎧≥-≥<+；，，00122x y x y x 或⎪⎩⎪⎨⎧≤-≤<+.00122x y x y x ，，得⎩⎨⎧≥≥<+；0,122x y y x 或⎩⎨⎧≤≤<+.0,122x y y x于是，定义域为：)0,1(),{(22≥≥<+=x y y x y x D 或)}0,1(22≥≥<+x y y x .天津科技大学《高等数学》(一)检测题9-2答案一、填空题1．)1(22xy x y -； 2．z 2或yx 2； 3．1； 4．3.二、选择题1．（A ）； 2．（C ）；三、解答题1．解：；y x x z y e 2=∂∂ .)1(e )e e (2222yy x y y x y z y y y -=-⋅=∂∂ 2．解：x y x x y x y xx y x y x x y x x z cos sin 21)(cos sin 212-=-⋅+=∂∂； .cos 1)1(cos x y xx x y x y z =⋅=∂∂ 3．证明：由)ln(2122y x z +=，有2222)(22y x x y x x x z +=+=∂∂， 由变量y x ，的对称性，得22y x y y z +=∂∂，于是1=∂∂+∂∂yz y x z x . 4．证明：由于)2sin(21)21)](2sin()[2cos(2t x t x t x t z -=----=∂∂, )2cos(2122t x tz --=∂∂； )2c o s (22t x x t zt x z -=∂∂∂=∂∂∂. 所以, 0)2cos()2cos(2222=-+--=∂∂∂+∂∂t x t x t x ztz . 天津科技大学《高等数学》(一)检测题9-3答案一、填空题1．119.0-,125.0-；2．y yx x y y d )11(d )1(2-++；3．)1ln 2(sec 2++t t t ； 二、选择题1．（B ）； 2．（A ）；三、解答题1. 解：由 y y xyx y x y y y x y x x z 2csc2cossin 11tan sec 2==⋅=∂∂,22222c s c2c o ss i n )(t a n s e cy y xx yx y x y x y x y x y x y z -=-=-⋅=∂∂. 得)d d (2csc 2d 2csc 2d 2csc 2d 22y x x y y xyy y x y x x y x y z -=-=. 2. 解：2222212222)d 2d 2()(d )(d d 21yx y y x x y x y y y x yx y z ++⋅+⋅-+=+=-)d d ()(2/322y x x y y x x-+-=. 3. 解：由)ln(2122y x z u +=，有2222)(22y x xz y x x z x u +=+⋅=∂∂， 由变量y x ,的对称性,得22y x yz y u +=∂∂；又22ln y x zu +=∂∂. 所以，.d ln d d d 222222z y x y yx yz x y x xz u +++++=天津科技大学《高等数学》(一)检测题9-4答案一、填空题1．21e2f x f y xy'+'-； 2．31cos 12f yxy f x '+'； 3．2e -； 4．z x z+；)(2z x y z +； .二、选择题 1．（B ）； 2．（A ）； 3．（C ）. 三、解答题1．解：.222121f x f y x f y f xz'+'=⋅'+⋅'=∂∂ )2(22)2(22212121122f x f y x f f x f y y xz''+''+'+''+''=∂∂222212112244f f x f xy f y '+''+''+''=. =∂∂∂yx z2)2(2)2(222112111f y f x x f y f x y f ''-''+''-''+' 1221222114)(2f f xy f y x f xy '+''-''-+''=. 2．解：方程两边对y 求导，有)(12xz yxyzxyzyx+∂∂=+∂∂， 即xz y x yz xyz y x xyz+∂∂=+∂∂2. 解得.2yzxyz xyz xz y x --=∂∂ 3．解：方程0),(=++xzy y z x F 两边对x ，y 求导，有 0)11(221=-∂∂⋅'+∂∂+⋅'x zx zxF x z y F . （1） 0)11(221=∂∂+⋅'+-∂∂⋅'yz x F y zyz yF . （2） （1），（2）移项并相比，有yz x x z x zx y z yzy xzy ∂∂+-∂∂=-∂∂∂∂+11/)(/)(1122，化简得.xy z yz y x z x-=∂∂+∂∂天津科技大学《高等数学》(一)检测题9-5答案一、填空题1．314211-=-+=-z y x ；2．122=--z y x ； 3．101-； 4．⎪⎭⎫⎝⎛5354，. 二、选择题 1．(D)； 2．（C ）. 三、解答题1．解：以x 为参数，于是1)(24)(2-='='x z z x y y ，，在点)1,2,1(-M 处，2/1)1(1)1(='='z y ，. 取切线方向向量)1,2,2())1()1(1(2=''=z y T ，，，切线方程为：112221+=-=-z y x ； 法平面方程为：0)1()2(2)1(2=++-+-z y x ，即522=++z y x .2．解：设切点为),,(000z y x M ，442),,(222-++=z y x z y x F ， 取法向量),4,2()2,8,4(21),,(21000000z y x z y x F F F n M z y x =='''=， 由切平面与已知平面平行，有12422000z y x ==，即000022y z y x ==，， 代入椭球面方程，得2/10±=y ，100±==z x ，切平面方程为：0)1()2/1(2)1(2=±+±+±z y x ，即0422=±++z y x .3．解：设所求点为),,(000z y x M ，则法向量)1,,()1,,(00-=-''=x y z z nM y x，根据已知，有113100-==x y ，得31300000==-=-=y x z y x ，，， 切平面方程为：0)3()1(3)3(=-++++z y x ，即033=+++z y x ； 法线方程为：133113-=+=+z y x . 4．解：设曲面上任意一点为),,(000z y x M ，1),,(-=xyz z y x F ，则法向量),,(),,(000000y x z x z y F F F n Mz y x ='''=，于是切平面方程为：0)()()(000000000=-+-+-z z y x y y z x x x z y ， 化为截距式方程为：1333000=++z z y y x x ， 四面体体积292933361000000==⋅⋅⋅=z y x z y x V ， 所以，曲面1=xyz 上任一点处的切平面与三个坐标面围成的四面体体积为定值2/9.天津科技大学《高等数学》(一)检测题9-6答案一、填空题1．)2,2(-，8； 2．)1,1(-，0； 3．41)21,21(=z ； 二、选择题1．(A)； 2．（C ） 3．(C)； 4．(B)； 5．(D).三、解答题1．解：设两直角边分别为x 、y ，三角形面积为A ，则xy A 21=，条件222l y x =+. 设(),(λ+=xy y x L )222l y x -+，)0(l y x <<，，由⎪⎩⎪⎨⎧=+=+='=+=',,02,02222l y x y x L x y L y xλλ 得惟一可疑点2l y x ==，由实际意义，斜边一定时直角三角形面积为A 有最大值，于是在斜边长为l 的直角三角形中，以等边直角三角形面积最大，最大面积为42maxl A =. 2．解：设水箱的长、宽、高分别为z y x ,,.则表面积z y x xy A )(2++=， )0,0,0(>>>z y x .约束条件为V xyz =.设)()(2),,(V xyz z y x xy z y x L -+++=λ，由⎪⎪⎩⎪⎪⎨⎧==++='=++='=++=',,0)(2,02,02V xyz xy y x L xz z x L yz z y L z yxλλλ 得惟一可疑点32V y x==，3212V z =. 由实际意义，体积一定时，长方体表面积A 有最小值. 所以，当水箱的长、宽都为32V ，高为3212V时，最省材料.天津科技大学《高等数学》(一)检测题10-1答案一、填空题1．2； 2．3π； 3．y x ，，⎰⎰211d d y yx xy y ．二、选择题 1．（D ）； 2．（A ）； 3．（C ）． 三、解答题1．证：设 143),(22-+=y x y x f ，由⎩⎨⎧=='==',08),(,06),(y y x f x y x f yx在区域D 内得驻点)0,0(O ，1)0,0(-=f .又在D 的边界上，212212]143[),(2222y y x y x f y x y x +=-+==+=+，（11≤≤-y ）于是，在D 的边界上，),(y x f 的最小值21=m ，最大值31=M ． 在D 上，),(y x f 的最小值1-=m ，最大值3=M ，D 的面积πσ=． (或者：222213414()13x y x y -≤+-≤+-≤) 所以，⎰⎰≤-+≤-Dy x y xππ3d d )143(22．2．证：设22arctan()(,)x y f x y x y+=+，则(,)f x y 除原点之外连续. 由二重积分的中值定理，知2222arctan()arctan()d 1nD x y x y ξησξη++=⋅++⎰⎰ 又221lim0n ξη→∞=+，arctan()2πξη+<有界，故22arctan()lim d 0nn D x y x y σ→∞+=+⎰⎰. 3. 解：(1) 先对y 再对x：120d (,)d x I x f x y y -=⎰⎰；先对x 再对y ：212201d (,)d d (,)d y y I y f x y x y f x y x -=+⎰⎰⎰⎰.(2) 先对y 再对x ：110110d (,)d d (,)d d (,)d x xxI x f x y y x f x y y x f x y y ---==+⎰⎰⎰⎰⎰；先对x 再对y：101d (,)d (,)d y yI y f x y x y f x y x -=+⎰⎰⎰⎰.天津科技大学《高等数学》(一)检测题10-2答案一、填空题1．⎰⎰⎰⎰+2112102d ),(d d ),(d x x x y y x f x y y x f x ； 2．⎰⎰--1)1(212d ),(d y yx y x f y ；3．⎰⎰2cos 20d )(d πθρρρθa f 。

第五章定积分(A 层次)1．203cos sin xdx x ；2．a dx x ax222；3．31221xxdx ；4．1145x xdx ；5．411xdx ；6．14311xdx ；7．21ln 1e xx dx ；8．02222xxdx ；9．dx x 02cos 1；10．dx x x sin 4；11．dx x 224cos 4；12．55242312sin dx xxx x ；13．342sin dx xx ；14．41ln dx xx ；15．1xarctgxdx ；16．202cosxdx e x ；17．dx x x 02sin ；18．dx x e 1ln sin ；19．243cos cos dx x x ；20．40sin 1sin dx x x ；21．dx xxx 02cos 1sin ；22．2111lndx xx x ；23．dx xx 4211；24．20sin ln xdx ；25．211dx xxdx0。

(B 层次)1．求由0cos 0x y ttdtdte 所决定的隐函数y 对x 的导数dxdy 。

2．当x 为何值时，函数x tdt tex I 02有极值？3．x xdt t dxd cos sin 2cos 。

4．设1,211,12xx x x xf ，求20dx x f 。

5．1lim22xdtarctgt xx 。

6．设其它,00,sin 21xx xf ，求x dt t f x。

7．设时当时当0,110,11xex xxf x，求201dx xf 。

8．2221limnn nnn。

9．求nk nknknnen e 12lim 。

10．设x f 是连续函数，且12dt t f x x f ，求x f 。

11．若2ln 261xtedt ，求x 。

12．证明：212121222dxeex。

13．已知axxx dx ex axa x 224lim，求常数a 。

一、填空题1. ]4,2()2,1( ；2. 2 ；3. 2e 1-=-x y ；4. ]2,1[.二、选择题1. （D ）；2. （B ）；3. （D ）；4. (C) .三、解答题1. 解：==)e ()]([xf xg f ⎪⎪⎩⎪⎪⎨⎧>-=<,1e ,1,1e ,0,1e ,1x x x 即=)]([x g f ⎪⎩⎪⎨⎧>-=<.0,1,0,0,0,1x x x==)(e )]([x f x f g ⎪⎩⎪⎨⎧>=<-,1,e ,1,e ,1,e 101x x x 即=)]([xfg ⎪⎩⎪⎨⎧>=<-.1,e ,1,1,1,e 1x x x 2. 解：因为，x xf x f =+)1()(3， )0(≠x （1）所以，令tx 1=，则x t 1=，故有t t f t f 1)()1(3=+，即 xx f x f 1)1(3)(=+ （2） 联立方程（1）（2）解得xx x f 8183)(-=.3. 解：（1）21,,tan x v v u u y -===；（2） xx v v u u y 1,sin ,22-===； （3）x v u u y v-=+==1,e 1,ln ； （4）x t t v v u u y =-===,sin 1,arctan ,.一、填空题1. n n 1-；2. 112)1(---n n ； 3. n n )1(1-+； 4. （1）1； （2）0； （3）0； （4）不存在.二、选择题1. (A)；2. (C)；3. (A)；4. (D)；5. (D).天津科技大学《高等数学》(一)检测题答案1-3一、填空题1. 0xa ； 2.b ax +0； 3. 1； 4. 0； 5. 2-； 6.2π； 7. 不存在； 8. 0. 二、选择题1. (B)；2. (B)；3. (D)；4. (D)；5. (C) .天津科技大学《高等数学》(一)检测题答案1-4一、填空题1. 1、1-；2. 0、∞+、+-1； 3. 0； 4. 2-.二、选择题1. (D)；2. (C) 、(B)；3. (D) . 三、计算题1. 解：2112lim )1)(1()2)(1(lim 123lim 11221-=-+=-+++=-++-→-→-→x x x x x x x x x x x x . 2.解：222032203303)33(lim 33lim )(limx h xh x hh xh h x h x h x h h h =++=++=-+→→→. 3. 解：21111lim )11(lim 11lim000=++=++=-+→→→x x x x x x x x x . 4. 解：2111lim )1)(1(1lim 1211lim 1121=+=+--=⎪⎭⎫⎝⎛---→→→x x x x x x x x x .5. 解：110101cos 1sin lim cos sin lim -=-+=-+=-+∞→∞→xx x xx x x x x x . 6. 解：因为01lim 2=+∞→x x x ，而x arctan 有界，所以0arctan 1lim 2=+∞→x xx x .于是，2)02)(01(arctan 1211lim 2=-+=⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+∞→x x x x x . 7. 解:()11lim 12/)121(lim 112531lim2222=-=--+=--++++∞→∞→∞→n n n n n n n n n n . 8. 解:由21)1()(1lim )11(lim 22=-++-+-=---+∞→∞→xx a x a b b b ax x x x x ，有 ⎩⎨⎧=-=+,2,01b a a 得⎩⎨⎧-=-=.3,1b a天津科技大学《高等数学》(一)检测题答案1-5一、填空题1. 1；2.52； 3. 21； 4. e 1； 5. 4e1； 6. 2e .二、选择题1. (C)；2. (B)；3. (D)；4. (B).三、计算题1.解：212/)(lim cos 1lim 200==-++→→x x x x x x . 2.解：41)1)(1)(1(1lim 11lim 1)1sin(lim12121=++--=--=--→→→x x x x x x x x h h h . 3.解：e e 1221lim 1212lim 1122212==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-+--∞→∞→x x x x x x x x x .4.解： 2sin 221sin 10e )21(lim )21(lim =⎥⎦⎤⎢⎣⎡+=+→→xx xx xx x x .四、解答题1.解：因为33/)1(1lim )1)1(1(1lim 11lim )()(lim131311=---=--+--=--=→→→→x xx x x x x x x x x x βα，所以当1→x 时，x x -=1)(α与31)(x x -=β是同阶但不等价无穷小. 2.证明：设22212111nn n n x n ++++++=，则，≤n xn y nnn ==+++1111222； ≥n xn z nnn n nn nn nn =+=+=++++++/1111112222，因为1lim lim ==∞→∞→n n n n z y ，所以112111lim 222=⎪⎪⎭⎫⎝⎛++++++∞→n n n nn .天津科技大学《高等数学》（一）检测题1-6答案一、填空题1. ),2()2,1()1,(+∞---∞、、，1-=x ；2. π-，0；3. 1.二、选择题1.（D ）；2. （C ）；3. （B ）；4. （C ）.三、解答题1.解：原式2)45)(1()1(4lim)45)(1()45)(45(lim11=+---=+--+---=→→x x x x x x x x x x x x x .2.解：原式1e ln )11(lim ln )11ln(lim ==+=+=+∞→+∞→x x x x x x.3.解：原式22lim 2222ππ==→∞n nn .4.解：原式23)1cos sin 3(lim 211cossin 3lim 21020=+=+=→→x x x x xx x x x x .5.解：因为0)313(lim 1=+-+→x x x 故02])[(lim 1=+=++→B A B x B A x 即B A 2-=，代入)(x f 表达式有.2)1(2)313)(1(lim313)1(lim)(lim 111B x x x x B x x x B x f x x x -=-+++--=+-+--=→→→ 要使)(x f 在1=x 处连续，必需4)1()(lim 1==→f x f x ，故42=-B ，2-=B ，4=A .天津科技大学《高等数学》（一）检测题1-7答案一、选择题1.（D ）；2. （B ）.二、证明题1.证明：令1sin )(--=x x x f ，由于)(x f 是初等函数，所以在],0[π上连续且01)0(<-=f ，01)(>-=ππf .由零点定理得方程1sin +=x x 在),0(π内至少有一个实根.2.证明：设2/1ln )(-+=x x x f ，则函数)(x f 在闭区间]1,2/1[上连续，又02ln )21(<-=f ，021)1(>=f ，由零点定理知方程x x -=21ln 在)1,21(内至少有一个实根，从而至少有一个不超过1的正根.注：0)21(<f 也可以用0)(lim 0<-∞=+→x f x 替代. 3.证明：记)()()(x g x f x F -=，由题设知)(x F 在闭区间],[b a 上连续，且0)()()(≤-=a g a f a F ， 0)()()(≥-=b g b f b F .若)()(a g a f =或)()(b g b f =，则可取a =ξ或b =ξ，若)()(a g a f ≠，)()(b g b f ≠，则得0)(<a F ，0)(>b F .由闭区间上连续函数的零点定理，知至少存在一),(b a ∈ξ，使0)(=ξF 即)()(ξξg f =. 综上：至少存在一],[b a ∈ξ，使得)()(ξξg f =.4．证明：由函数)(x f 在闭区间],[1n x x 上连续，则)(x f 在闭区间],[1n x x 上有最小值m 与最大值M ，而M nx f x f x f m n ≤+++≤)()()(21 ，由介值定理推论有],[1n x x ∈ξ使得nx f x f x f f n )()()()(21+++=ξ.。

定积分习题及答案定积分习题及答案定积分是微积分中的重要概念之一，广泛应用于数学、物理、工程等领域。

掌握定积分的计算方法和应用是学习微积分的关键。

在本文中，我们将介绍一些常见的定积分习题，并给出详细的解答。

1. 计算定积分∫(0 to 1) x^2 dx。

解答：根据定积分的定义，我们可以先求出x^2的不定积分，然后再进行定积分的计算。

x^2的不定积分为(1/3)x^3，所以∫(0 to 1) x^2 dx = (1/3)x^3 |(0 to1) = (1/3)(1^3 - 0^3) = 1/3。

2. 计算定积分∫(1 to 2) (2x + 1) dx。

解答：根据定积分的性质，我们可以将定积分拆分为两个部分：∫(1 to 2) 2x dx + ∫(1 to 2) 1 dx。

第一个部分的不定积分为x^2，第二个部分的不定积分为x。

所以∫(1 to 2) (2x + 1) dx = (x^2) |(1 to 2) + (x) |(1 to 2) = (2^2 - 1^2) + (2 - 1)= 4 - 1 + 1 = 4。

3. 计算定积分∫(0 to π) sin(x) dx。

解答：sin(x)的不定积分为-cos(x)，所以∫(0 to π) sin(x) dx = (-cos(x)) |(0 to π) = -cos(π) - (-cos(0)) = 1 - (-1) = 2。

4. 计算定积分∫(0 to 1) e^x dx。

解答：e^x的不定积分为e^x，所以∫(0 to 1) e^x dx = (e^x) |(0 to 1) = e^1 -e^0 = e - 1。

5. 计算定积分∫(0 to 2π) cos(x) dx。

解答：cos(x)的不定积分为sin(x)，所以∫(0 to 2π) cos(x) dx = (sin(x)) |(0 to 2π)= sin(2π) - sin(0) = 0。

天津科技大学高等数学检测题（一.二）94天津科技大学《高等数学》(一)检测题8-1专业 学号姓名一、填空题1. 设向量cb a u+-=32，cb a v -+=3用cb a 、、表示向量=-v u 24 .2. 与向量)212(，，-=a平行的单位向量是 .3. 给定点)3,2,1(M 及)1,0,2(N ，则=MN ；MN 的方向余弦是=αcos ，=βcos ，=γcos .4. 若向量γ 的模是4，它与z 轴的夹角是4π，则=γ zj Pr .5．点),,(0z y x M 到x 轴的距离=xd ；到xOy面的距离=xoyd.6．z 轴上与两点)3,3,1(-A 及)2,3,2(B 距离相等的点是 . 7．一动点),,(z y x M 与定点)2,0,0(0M的距离是它到xOy 面距离的2倍，则z y x ,,所满足的关系式是 .95二、选择题1. 点),,(000z y x M 关于y轴的对称点是（ ）.(A)),,(000z y x -； (B) ),,(000z y x --；(C)),,(000z y x ---； (D)),,(000z y x --.2. 满足与三个坐标轴夹角都相等且模为3的向量是（ ）. (A) )1,1,1(； (B) )1,1,1(---； (C))1,1,1(±； (D))1,1,1(31±.3. 设点)7,1,2(-A ，已知5=AB ，且与向量)15,0,20(-=a平行，则B 点的坐标是（ ）.(A))3,0,4(B ； (B))7,5,5(-B ；(C))4,1,6(--B ； (D) )4,1,6(-B .三、计算或证明题1.四边形ABCD顶点坐标分别是)3,5,2(A、B、)2,5,0(C、)3,3,4(D，N,2(,1)0AC、M、分别是BD 之中点，求向量MN .2. 一单位向量e 与yx、轴的夹角相等，与z 轴夹角是前者的2倍，求向量e .96973. 给定三点)9,1,4(A 、)6,1,10(-B 、)3,4,2(C ，证明三角形ABC 是等腰直角三角形.天津科技大学《高等数学》(一)检测题8-2专业 学号姓名一、填空题1．设向量)1,2,3(=a，)2,3,2(-=b，则=⋅b a ，=⨯b a .2．设向量)4,1,2(=a，)1,2,2(-=b，则=a bj Pr ，向量ba 、的夹角=θ .3．与向量)2,1,3(=a，)0,1,1(-=b都垂直的所有向量是 .4. 平行四边形ABCD 两邻边是)2,1,2(-=、98)1,2,3(-=，则该平行四边形的面积=S .二、选择题1．两非零向量),,(),,(z y x z y x b b b b a a a a ==、，（ ）不是a与b平行的充分必要条件. (A)=⋅b a ； (B) 0=⨯b a ；(C)bk a=（k是非零常数）；(D)zzy y x x b a b a b a ==.2． 若非零向量a与b满足ba b a -=+，则必有（ ）.(A) a与b方向相同； (B)a与b方向相反；(C) a与b垂直； (D) 以上都不对. 3．设向量bc a a c b u)()(⋅-⋅=，则有（ ）.(A) u与a垂直； (B) u与b垂直； (C)u与c 垂直； (D) u 与c 平行.4．若向量a、b、c满足ca b a ⨯=⨯，则必有（ ）.99(A)=a ； (B) 当≠a 时，cb =； (C)b与c平行； (D) a与cb -平行.三、计算或证明题1. 若向量m 与n的夹角为3πθ=且21==n m 、，设nm a2+=，nm b -=3，求ba ⋅ .2. 设向量k j i a+-=32，kj i b 3+-=，ji c2-=，求bc a c b a )()(⋅-⋅，cb a ⨯⨯)(及cb a ⋅⨯)(.3. 设向量a 、b 、c两两垂直，且1=a 、2=b 、，令=u +a +b c ，求向量u 的模及u 与向量a c=3的夹角θ的余弦.4．用向量证明直径所对的圆周角是直角.天津科技大学《高等数学》(一)检测题8-3专业学号姓名100101一、填空题1．以点)2,1,1(-M 为球心，且过原点的球面方程是 .2．由xOy 面上抛物线21x y +=绕x 轴旋转所形成的旋转面方程是 ； 绕y轴旋转所形成的旋转面方程是 . 3．曲面1222=-+z y x 是由xOz面上曲线绕 轴旋转所形成的，曲面名称是 . 4．方程)(322y x z +=所表示的曲面名称是 .5．方程2222=+y x在平面解析几何中所表示的图形名称是 ；在空间解析几何中所表示的图形全称是 .6．以xOz 面上曲线2x z =为准线，母线平行于y轴的曲面方程是 ，它的全称是 .二、选择题1021．下列方程中，（ ）是旋转面方程. (A)22212y z x +=+； (B)2221y z x -=-；(C)22y xz -=； (D) 03222=++z y x .2．旋转面yz y x 42222=++的旋转轴是（ ）.(A) x 轴； (B) y 轴； (C) z轴； (D) 直线1=y . 3．柱面1)1(22=--y x 的母线平行于（ ）.(A) x 轴； (B) y 轴； (C) z轴； (D) 直线1-=x y .4. 下列方程中，（ ）是椭圆抛物面方程. (A) 0222=--z y x ； (B)1222=+-z y x ；(C)22y x z -=； (D)22y x z +=.三、解答题1.讨论方程az y x z y x=-+-++642222所表示的图形，并指出图形的主要特点.2.问旋转面22z2=是怎样形成的？它表yx-示什么图形？图形特点是什么？3.作出下列空间区域草图：（1）由圆锥面22y x z +=与上半 （2）由两圆柱面222R y x=+及球面222y x z --=围成.222R z x =+围成第一卦限部分.天津科技大学《高等数学》(一)检测题8-4专业 学号姓名一、填空题1．方程⎩⎨⎧=+++=1,22222z y x y x z 所表示的曲线名称是 . 2．平行于x 轴且过曲线⎩⎨⎧=+-=++0,162222222z y x z y x 的柱面方程是 . 3．曲线⎩⎨⎧=+xy y x 22,12=-z 在xOz面上的投影是 . 4．曲线⎩⎨⎧=+zy y x 222,92=+z 的参数方程可以表示为 . 5．过z轴及点)1,1,1(的平面方程是 .6．设)3,2,1(A 、)5,2,3(-B ，线段AB 的垂直平分面方程是 .7．当 时，平面=+++D Cz By Ax 平行于yOz 平面.二、选择题1．过原点且与平面3=-+z y x 平行的平面是（ ）. (A)2=++z y x ； (B)1=-+z y x ； (C) 0=+--z y x ； (D)=++z y x .2．平面922=--z y x 适合条件（ ）.(A) 经过点)2,3,1(-； (B) 与平面3342=++z y x 垂直；(C) 与原点的距离为3； (D) 与平面032=+-z y x 成4/π夹角. 3．在空间解析几何中，方程022=-y x 表示（ ）.(A) 双曲面； (B) 一张平面； (C) 两张平行平面； (D) 两张垂直平面.三、解答题1. 求过三点)2,0,1(1M 、)1,2,1(2-M、)4,3,2(3-M的平面方程.2. 求过两点)2,2,2()1,1,1(B A 、，且与平面=-+z y x 垂直的平面方程.3. 求过y轴且与两点)0,1,1(A、距离相B,7)3,2(等的平面方程.4．一平面与原点的距离是6，且在z，轴x，y上的截距之比是1∶2∶3，求该平面方程.天津科技大学《高等数学》(一)检测题8-5专业 学号姓名一、填空题1．直线⎩⎨⎧=+-=-+02,12z y x z y x 的方向向量=s .2．将直线t z t y t x 42132=--=+=，，改写为对称式方程是 .3．过原点且垂直于平面1=++z y x 的直线方程是 . 4．过两点)3,2,1(A 和)5,0,2(B 的直线方程是 .5．直线⎩⎨⎧=--=++0,03z y x z y x 与平面132=--z y x 的夹角=ϕ .二、选择题1．若直线λzy x =+=-10111与直线⎩⎨⎧=+-=++05,012z x y x λ垂直，则=λ（ ）.(A) 4； (B) 2； (C)2-； (D)2±.2．直线2zy x ==与直线⎩⎨⎧=+=-3,0z x y x 的位置关系是（ ）.(A) 平行但不重合； (B) 重合； (C) 垂直但不相交； (D) 垂直且相交.3． 直线431232--=+=-z y x 与平面3=++z y x 的位置关系是（ ）.(A) 平行但直线不在平面上； (B) 直线在平面上； (C) 垂直； (D) 斜交.三、解答题1.求过点)1,2,1(-M 且平行于直线⎩⎨⎧=+-+=--+012,012z y x z y x 的直线方程.2. 求过点)2,1,3(-M 及直线12354zy x =+=-的平面方程.3. 求过点)1,1,1(-M 及直线⎩⎨⎧=+02z y x ,1=-z 的平面方程.4．过点)3,2,1(M ，求垂直于直线z y x ==且与z 轴相交的直线方程.5．求点)3,2,1(-M 到直线02211zy x =-+=-的距离d .天津科技大学《高等数学》(一)检测题9-1专业 学号姓名一、填空题1．设函数)1(-+=y f x z ，且当1=x 时，y z =，则函数=)(u f ；函数=z . 2．函数yx y z arcsin 2+-=的定义域=D .3．函数221yx x z --=的定义域=D .4．函数22)sin(x y y x z -+=在点集=E上是间断的.二、单项选择题1．函数)ln(122y x z z u ---=的的定义域=D （ ）.（A ）{}1),,(22<<+z y xz y x ； （B ）{}1),,(22≤<+z y x z y x ；（C ）{}1),,(22<≤+z y xz y x ； （D ）{}1),,(22≤≤+z y xz y x .2．函数xy xz cos sin 2-=（ ）（A ） 只是x的偶函数；（B ）只是y 的偶函数；（C ） 即是x 的偶函数，又是y 的偶函数； （D ） 以上都不对. 3．函数xyy x y x f 22),(+=在（ ）处不连续.（A ） 点)0,0(； （B ） 0=x 且0≠y ； （C ）=y 且0≠x ； （D ）0=x 或=y .4．极限=-→2)1,0(),(sin limxy xy x （ ）.（A ） 不存在； （B ） 0； （C ）1-； （D ）1.三、解答题1． 设函数22),(y xx yy x f -=+，求),(y x f .2． 若函数xyy x y x f 2),(44-+=，证明),(),(2y x f t ty tx f =.3． 求函数)()1ln(22x y x y x z -+--=的定义域，并作定义域草图.4．求极限xy xy y x 42lim)0,0(),(+-→.天津科技大学《高等数学》(一)检测题9-2专业 学号姓名一、填空题1．设函数)arcsin(x y z =，则=∂∂xz. 2．设函数zxy u /12)(=，则=∂∂zu. 3．设函数yx z =，则=∂∂+∂∂yzx x z y xln 1 . 4．设函数yx y x y x f arcsin)1(),(-+=，则=')1,(x f x . 5．设函数)ln(xy x z =，则=∂∂∂23yx z.6．设函数yx y x z z y x f 322)ln(),,(++=，则=-'')0,1,1(xyf .二、单项选择题1．设函数22),(y x y x f +=，在原点处)0,0(xf '及)0,0(y f '（ ）.（A ）都不存在； （B ） 都存在，但不相等；（C ）都存在，且都等于0； （D ）都存在，且都等于1. 2．设函数222zy x u ++=，则=∂∂+∂∂+∂∂222222zuy u x u （ ）.（A ）0； （B ）2222z y x ++；（C ）2222zy x ++； （D ）2222zy x ++-.3．曲线⎪⎩⎪⎨⎧=--=1922x y x z ，在点)2,2,1(处的切线（ ）.(A) 对于x 轴的倾角是4/π； (B) 对于x 轴的倾角是4/3π；(C) 对于y 轴的倾角是4/π； (D) 对于y 轴的倾角是4/3π. 三、解答题 1．设函数yx z ye 2=，求xz∂∂及y z ∂∂.2．设函数x yx z sin=，求xz∂∂及y z ∂∂.3．验证函数22ln y x z +=，满足方程1=∂∂+∂∂yzy x z x .4．设函数)2(cos 2tx z -=，证明2222=∂∂∂+∂∂t x z tz .天津科技大学《高等数学》(一)检测题9-3专业 学号姓名一、填空题1．设函数x yz =，当2=x ，1=y ，1.0=∆x ，2.0-=∆y 时，=∆z ；=z d .2．设函数zyxu 1)(=，则=)1,1,e (d u.3．函数yx xy z +=的全微分=z d .4．设函数t y x z ln +=，而t x tan =，2t y =，则=tz d d .5．设函数1)(e 2+-=a z y u ax ，x z x a y cos sin ==，，则=x u d d .二、单项选择题1．函数),(y x f z =在点),(0y x P 处两个偏导数),(00y x f x '及),(0y x f y'存在，是函数),(y x f z =在点),(000y x P 可微的（ ）条件.（A ）充分； （B ）必要； （C ）充分且必要； （D ） 即非充分又非必要. 2．函数),(y x f z =的两个偏导数)(y x f x ，'及)(y x f y ，'在点),(0y x P 处连续，是函数),(y x f z =在点),(0y x P 可微的（ ）条件. （A ）充分； （B ）必要； （C ）充分且必要； （D ） 即非充分又非必要.3．设vu z =，而xu e =，x v ln =，则=x zd d （ ）. （A ）)1(ln ln e 2x x xx +； （B ）)1(ln ln e 2x x xx -；（C ）xx xeln 1+； （D ）xx x e ln 1-.三、解答题1．求函数y x z tan ln =的全微分z d .2．求函数22yx y z +=的全微分z d .3．求函数22ln y x z u +=的全微分u d .4． 设y x z arctan =，而v u x +=，v u y -=，求vzu z ∂∂∂∂，.天津科技大学《高等数学》(一)检测题9-4专业 学号姓名一、填空题1．若函数),(v u f 可微，)e ,(22xy y xf z -=，则=∂∂yz .2．若函数),,(w v u f 可微，)sin ,,(22yxy xf z =，则=∂∂xz .3．设函数),,(v u x f z =，而),(y x u u =，),(y x v v =，若函数),,(v u x f ，),(y x u ，),(y x v 都可微，则=∂∂xz. 4．若函数)(x y y =由方程1ln =+y xy 确定，则==0d d x xy. 5．若函数),(y x z z =由方程yzz x ln =确定，则=∂∂x z；=∂∂yz. 6．若函数),(y x z z =由方程zz y x ln 222=++确定，则=z d .二、单项选择题1．设)(u xF xy z +=，而x yu =，其中)(u F 可导，则=∂∂xz （ ）.（A ）xy x y F y -+)(； （B ）)()(xyF x y x y F y '-+；（C ）)()(xyF x y x y F y x '-+； （D ）)()(xyF x y x y F y y '-+.2．若函数),(y x z z =由方程xyzz=e 确定，则=∂∂yz （ ）.（A ）)1(-z y z ； （B ）)1(-z x z ； （C ）xyxz -1 （D ）y z xz -.3．设函数),(y x z z =由方程)(nz y mz x -=-ϕ确定，其中)(u ϕ可微，则=∂∂+∂∂yzn x z m （ ）. （A ）nm +； （B ）0；（C ）1； （D ）2. 三、解答题1．设函数)(22y x f y z -=，其中)(u f 可微，证明.112yzy z y x z x =∂∂+∂∂2．若函数),(v u f 有二阶连续偏导数，设),(22y x xy f z -=，求22x z ∂∂及yx z ∂∂∂2.3．设函数),(z y x x =由方程xyzz y x 22=++确定，求.yx ∂∂4．若函数),(v u F 可微，而函数),(y x z z =由方程0),(=++xzy y z x F 确定，证明.xy z yzy x z x -=∂∂+∂∂天津科技大学《高等数学》(一)检测题9-5专业 学号姓名一、填空题1．曲线322t z t y t x =-==，，在点)1,2,1(-M 处的切线方程为 . 2．抛物面221y x z ++=在点)3,1,1(-M 处的切平面方程为 .3．圆⎩⎨⎧=++=++0222z y x z y x ,6在点)2,1,1(-M 处的切线方向向量=T .4．函数)e eln(yxz +=在原点O 处沿l =（其中P点的坐标是)4,3(-）方向上的方向导数=∂∂lz. 5．设函数22),(y x y x f +=，则grad =)3,4(f .二、单项选择题1．球面4222=++z y x在点)2,1,1(-M 处指向内侧的单位法向量=n（ ）.（A ）)22,21,21(； （B ）)22,21,21(-； （C ）)22,21,21(-；（D ）)22,21,21(--.2．函数zy xu -+=22在点)2,1,1(M 处沿抛物面22y x z +=在点M 处的法向量n 上的方向导数=∂∂nz（ ）. （A ）3； （B ）3-； （C ）3±； （D ）9±. 三、解答题 1． 求曲线xz x y-==2422，在点)1,2,1(-M 处的切线及法平面方程.2．求椭球面442222=++z y x上平行于平面122=++z y x 的切平面方程.3．在曲面xy z =上求一点，使得该点处的法线垂直于平面0x，并写出该点处+zy3=+的切平面及法线方程.4．证明曲面1=xyz上任一点处的切平面与三个坐标面围成的四面体体积为定值.天津科技大学《高等数学》(一)检测题9-6专业 学号姓名一、填空题1．函数22)(4),(y x y x y x f ---=的极大值点是 ；极大值是 .2．函数1),(22+-+++=y x y xy x y x f 的极小值点是 ；极小值是 . 3．函数222)2(x y xz -+=在圆域D ：xy x222≤+上的最小值=m ；最大值=M . 4．函数xy z =在附加条件1=+y x 下的极大值为 .二、单项选择题1．点)0,0(O 是函数xy z =的（ ）. （A ）驻点； （B ）极小值点； （C ）极大值点； （D ）不可微点. 2．函数)4)(6(),(22y y x x y x f --=在驻点)0,0(O 处（ ）.（A ）取极小值； （B ）取极大值； （C ）不取极值； （D ）无法判定. 3．函数22)1()1(-+-=y x z 在点)1,1(P 处（ ）.（A ） 有偏导数且取极小值； （B ） 有偏导数但不取极值；（C ） 无偏导数且取极小值； （D ） 无偏导数也不取极值.4．可微函数),(y x f z =在点),(0y x P 取极值是),(),(0000='='y x f y x f y x 是的（ ）条件.（A ）充分必要； （B ）充分； （C ）必要； （D ）无关.5．若函数),(y x f z =在点),(0y x P 有二阶连续偏导数，记),(0y x f A xx''=，),(),(0000y x f C y x f B yy xy''=''=，，则02>-BAC 是函数),(y x f z 在),(0y x P 取极值的（ ）条件.（A ）充分； （B ）必要； （C ）充分必要； （D ）即不充分，也不必要. 三、解答题1． 在斜边长为l 的直角三角形中，求面积最大的三角形及其面积.2．要造一容积为定值V 的长方体无盖水箱，为最省材料应如何设计水箱的尺寸？3．某商家通过报纸及电视两种媒体做某商品广告。

第六章定积分的应用习题6-2 (A) 1．求下列函数与x 轴所围部分的面积：(1) y x 2 6x 8, [0, 3]( 2) y 2x x2 , [ 0, 3]2．求下列各图中阴影部分的面积：1.图 6-13．求由下列各曲线围成的图形的面积：(1) y e x , y e x与x1;( 2) y ln x 与 x 0, y ln a, y ln b (b a 0) ;(3) y 2x x2与 y x , y 0 ;( 4) y 2 2 x , y 2 (x 1) ;(5) y 2 4(1 x) 与 y 2 x , y 0 ;(6) y x2 与 y x , y 2x ;(7) y 2 sin x , y sin 2x (0 x ) ;(8) y x 2,x 2 y 2 （两部分都要计算）;2 84．求由曲线y ln x 与直线 y 0, x e 1 , x e 所围成的图形的面积。

5．求抛物线y x 2 4 x 3 及其在点 (0, 3) 和 (3, 0) 处的切线所围成的图形的面积。

6．求抛物线y 2 2 px 及其在点 ( p, p) 处的法线所围成的图形的面积。

27．求曲线x y a 与两坐标轴所围成的图形的面积。

x 2 y 21 所围图形的面积。

8．求椭圆2 b 2a9．求由摆线x a(t sin t), y a(1 cost ) 的一拱（0 t 2 ) 与横轴所围图形的面积。

10．求位于曲线y e x下方与由该曲线过原点的切线的左方及x 轴之间的图形的面积。

11．求由下列各方程表示的曲线围成的图形的面积：(1) 2a sin (a 0) ;( 2) 2a (2 cos ) (a 0);(3) 2 2 cos 2 （双纽线） ;12. 把抛物线y2 4ax 及直线 x x( x 0 0) 所围成的图形绕x 轴旋转，计算所得旋转抛物体的体积。

13. 由 y x 3 , x 2 , y 0 所围成的图形，分别绕x 轴及 y 轴旋转，计算所得两个旋转体的体积。