完全二叉树总结点数与叶结点数关系分析讲义

完全二叉树节点和叶子节点关系完全二叉树是一种特殊的二叉树，它的每一层都是满的，除了最后一层，最后一层的节点从左到右排列。

在完全二叉树中，节点和叶子节点之间有着特殊的关系，本文将从定义、性质和应用三个方面来探讨完全二叉树节点和叶子节点的关系。

一、定义完全二叉树是一种特殊的二叉树，它的每一层都是满的，除了最后一层，最后一层的节点从左到右排列。

完全二叉树的定义可以用递归的方式来描述：如果一棵二叉树为空，则它是一棵完全二叉树；如果一棵二叉树的左子树是一棵满二叉树，右子树是一棵完全二叉树，并且左子树的高度等于右子树的高度或者右子树的高度比左子树的高度少1，则这棵二叉树是一棵完全二叉树。

二、性质完全二叉树的节点和叶子节点之间有着特殊的关系，具体来说，完全二叉树的节点数为2^h-1，其中h为完全二叉树的高度。

叶子节点的数量为2^(h-1)，也就是说，完全二叉树的叶子节点占据了整个树的一半以上。

完全二叉树的节点和叶子节点之间还有一个重要的性质，就是叶子节点的编号从1到2^(h-1)连续排列，而非叶子节点的编号从2^(h-1)+1到2^h-1连续排列。

这个性质在完全二叉树的应用中非常重要，可以用来快速定位节点和叶子节点的位置。

三、应用完全二叉树的节点和叶子节点关系在算法和数据结构中有着广泛的应用。

其中最常见的应用是堆，堆是一种特殊的完全二叉树，它有两种形式：最大堆和最小堆。

最大堆的每个节点都大于等于它的子节点，最小堆的每个节点都小于等于它的子节点。

堆的应用非常广泛，比如在排序算法中，堆排序是一种高效的排序算法，它的时间复杂度为O(nlogn)。

除了堆之外，完全二叉树的节点和叶子节点关系还可以用来实现哈夫曼树，哈夫曼树是一种用于数据压缩的树形结构，它的叶子节点代表着数据中的字符，而非叶子节点代表着字符出现的频率。

哈夫曼树的构建过程中需要用到完全二叉树的节点和叶子节点关系，可以快速定位叶子节点的位置，从而实现高效的数据压缩。

数据结构之⼆叉树（BinaryTree）⽬录导读 ⼆叉树是⼀种很常见的数据结构，但要注意的是，⼆叉树并不是树的特殊情况，⼆叉树与树是两种不⼀样的数据结构。

⽬录 ⼀、⼆叉树的定义 ⼆、⼆叉树为何不是特殊的树 三、⼆叉树的五种基本形态 四、⼆叉树相关术语 五、⼆叉树的主要性质（6个） 六、⼆叉树的存储结构（2种） 七、⼆叉树的遍历算法（4种） ⼋、⼆叉树的基本应⽤：⼆叉排序树、平衡⼆叉树、赫夫曼树及赫夫曼编码⼀、⼆叉树的定义 如果你知道树的定义（有限个结点组成的具有层次关系的集合），那么就很好理解⼆叉树了。

定义：⼆叉树是n(n≥0)个结点的有限集，⼆叉树是每个结点最多有两个⼦树的树结构，它由⼀个根结点及左⼦树和右⼦树组成。

（这⾥的左⼦树和右⼦树也是⼆叉树）。

值得注意的是，⼆叉树和“度⾄多为2的有序树”⼏乎⼀样，但，⼆叉树不是树的特殊情形。

具体分析如下⼆、⼆叉树为何不是特殊的树 1、⼆叉树与⽆序树不同 ⼆叉树的⼦树有左右之分，不能颠倒。

⽆序树的⼦树⽆左右之分。

2、⼆叉树与有序树也不同（关键） 当有序树有两个⼦树时，确实可以看做⼀颗⼆叉树，但当只有⼀个⼦树时，就没有了左右之分，如图所⽰：三、⼆叉树的五种基本状态四、⼆叉树相关术语是满⼆叉树；⽽国际定义为，不存在度为1的结点，即结点的度要么为2要么为0，这样的⼆叉树就称为满⼆叉树。

这两种概念完全不同，既然在国内，我们就默认第⼀种定义就好）。

完全⼆叉树：如果将⼀颗深度为K的⼆叉树按从上到下、从左到右的顺序进⾏编号，如果各结点的编号与深度为K的满⼆叉树相同位置的编号完全对应，那么这就是⼀颗完全⼆叉树。

如图所⽰：五、⼆叉树的主要性质 ⼆叉树的性质是基于它的结构⽽得来的，这些性质不必死记，使⽤到再查询或者⾃⼰根据⼆叉树结构进⾏推理即可。

性质1：⾮空⼆叉树的叶⼦结点数等于双分⽀结点数加1。

证明：设⼆叉树的叶⼦结点数为X，单分⽀结点数为Y，双分⽀结点数为Z。

公共基础专题探究——二叉树1．6 树与二叉树树是一种简单的非线性结构，所有元素之间具有明显的层次特性。

在树结构中，没有前件的结点只有一个，称为树的根结点，简称树的根。

每一个结点可以有多个后件，称为该结点的子结点。

没有后件的结点称为叶子结点。

在树结构中，一个结点所拥有的后件的个数称为该结点的度，所有结点中最大的度称为树的度。

为该结点的左子树与右子树。

二叉树的基本性质：必考的题目（1）在二叉树的第k层上，最多有2k-1(k≥1)个结点；（2）深度为m的二叉树最多有2m-1个结点；（3）度为0的结点（即叶子结点）总是比度为2的结点多一个；（4）二叉树中 n = n0 +n1 +n2k层上有2k-1个结点深度为m的满二叉树有2m-1个结点。

若干结点。

二叉树的遍历：（一般画个图要你把顺序写出来）后序遍历（访问根结点在访问左子树和访问右子树之后）重点题型：二叉树的遍历例1：某二叉树的前序序列为ABCD，中序序列为DCBA，则后序序列为（DCBA ）。

【解析】前序序列为ABCD，可知A为根结点。

根据中序序列为DCBA可知DCB是A的左子树。

根据前序序列可知B是CD的根结点。

再根据中序序列可知DC是结点B的左子树。

根据前序序列可知，C是D的根结点，故后序序列为DCBA例2：对下列二叉树进行前序遍历的结果为 ABDYECFXZ例3：设二叉树如下，则后序序列为 DGEBHFCA【解析】本题中前序遍历为ABDEGCFH，中序遍历为DBGEAFHC，后序遍历为DGEBHFCA完全二叉树指除最后一层外，每一层上的结点数均达到最大值，在最后堆排序问题：例1：已知前序序列与中序序列均为ABCDEFGH，求后序序列【解析】设根节点为D≠0，左子树为L，右子树为R，有遍历顺序为：前：D-L-R 已知ABCDEFGH中：L-D-R 已知ABCDEFGH后：L-R-D 待求由此可知，L=0，D-R= ABCDEFGH故R-D=HGFEDCBA，即后序序列= HGFEDCBA变式训练1：已知后序序列与中序序列均为ABCDEFGH，求前序序列答案：HGFEDCBA，（这次R=0）结论：若前序序列与中序序列均为某序列，则后序序列为该序列的倒序，且为折线；同样地，若后序序列与中序序列均为某序列，则前序序列为该序列的倒序，且为折线例2：已知前序序列=ABCD，中序序列=DCBA，求后序序列【解析】设根节点为D≠0，左子树为L，右子树为R，有遍历顺序为：前：D-L-R 已知ABCD中：L-D-R 已知DCBA后：L-R-D 待求因为ABCD与DCBA正好相反，由此可知，R=0所以D-L=ABCD，即L-D=DCBA所以后序序列= DCBA变式训练2-1：中序序列=BDCA，后序序列=DCBA，求前序序列【解析】设根节点为D≠0，左子树为L，右子树为R，有遍历顺序为：前：D-L-R 待求中：L-D-R 已知BDC,A后：L-R-D 已知DCB,A通过观察可知，R=0，L={B,D,C}，D=A中、后变换时，{B,D,C}发生了变化，说明左子树结构特殊，进一步令中’：L’-D’-R’已知B,DC后’：L’-R’-D’已知DC,B可知L’=0，即D’=B，R’= DC可以画出二叉树示意图为：Array所以前序序列= ABCD变式训练2-2：中序序列=ABC，后序序列=CBA，求前序序列【解析】设根节点为D≠0，左子树为L，右子树为R，有遍历顺序为：前：D-L-R 待求中：L-D-R 已知ABC后：L-R-D 已知通过观察可知，L=0，D-R=ABC，R-D=CBA所以前序序列=D-L-R= D-R=ABC变式训练2-3：前序序列=ABC，中序序列=CBA，求后序序列【解析】设根节点为D≠0，左子树为L，右子树为R，有遍历顺序为：前：D-L-R 已知A,BC中：L-D-R 已知CB,A后：L-R-D 待求通过观察可知，D=A ，L={B,C}，R=0所以后序序列=CBA (一边偏)题型二：求二叉树的深度。

树和二叉树的基本知识树是一种非线性的数据结构，用它能很好地描述有分支和层次特性的数据集合。

树型结构在现实世界中广泛存在，如把一个家族看作为一棵树，树中的结点为家族成员的姓名及相关信息，树中的关系为父子关系，即父亲是儿子的前驱，儿子是父亲的后继；把一个国家或一个地区的各级行政区划分看作为一棵树，树中的结点为行政区的名称及相关信息，树中的关系为上下级关系，如一个城市包含有若干个区，每个区又包含有若干个街道，每个街道又包含有若干个居委会；把一本书的结构看作是一棵树，树中的结点为书、章、节的名称及相关信息，树中的关系为包含关系。

树在计算机领域中也有广泛应用，如在编译系统中，用树表示源程序的语法结构；在数据库系统中，树型结构是数据库层次模型的基础，也是各种索引和目录的主要组织形式。

在许多算法中，常用树型结构描述问题的求解过程、所有解的状态和求解的对策等。

在树型结构中，二叉树是最常用的结构，它的分支个数确定，又可以为空，具有良好的递归特性，特别适宜于程序设计，因此我们常常将一般树型结构转换成二叉树进行处理。

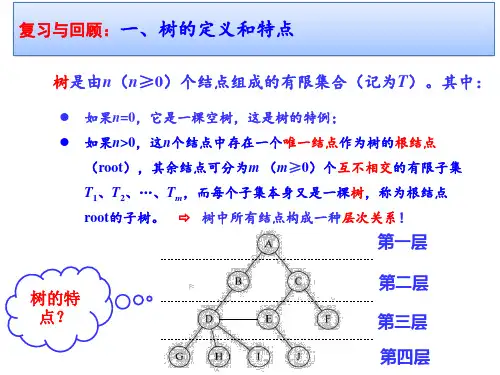
第一节树一、树的定义一棵树（tree）是由n（n>0）个元素组成的有限集合，其中：1．每个元素称为结点(node)；2．有一个特定的结点，称为根结点或树根（root）；3．除根结点外，其余结点被分成m（m>=0）个互不相交的有限集合T0,T1,T2,……T m-1，而每一个子集T i又都是一棵树（称为原树的子树subtree）。

图1图1就是一棵典型的树结构。

从树的定义可以看出：1．树是递归定义的，这就决定了树的操作和应用大都是采用递归思想来解决；2．一棵树中至少有1个结点，这个结点就是根结点，如上图中的结点1；3．只有根结点没有前趋结点，其余每个结点都有唯一的一个前趋结点；4．所有结点都可以有0或多个后继结点；二、树的基本概念下面以图1为例给出树结构中的一些基本概念：1．一个结点的子树个数，称为这个结点的度（degree），如结点1的度为3，结点3的度为0。

⼆叉树知识整理1.1.树的定义树是由结点或顶点和边组成的(可能是⾮线性的)且不存在着任何环的⼀种数据结构。

没有结点的树称为空(null或empty)树。

⼀棵⾮空的树包括⼀个根结点，还(很可能)有多个附加结点，所有结点构成⼀个多级分层结构。

特点：树状图是⼀种数据结构，它是由n（n>=0）个有限结点组成⼀个具有层次关系的集合。

把它叫做“树”是因为它看起来像⼀棵倒挂的树，也就是说它是根朝上，⽽叶朝下的。

它具有以下的特点：每个结点有零个或多个⼦结点；没有⽗结点的结点称为根结点；每⼀个⾮根结点有且只有⼀个⽗结点；除了根结点外，每个⼦结点可以分为多个不相交的⼦树；种类：⽆序树：树中任意节点的⼦结点之间没有顺序关系，这种树称为⽆序树,也称为⾃由树;有序树：树中任意节点的⼦结点之间有顺序关系，这种树称为有序树；⼆叉树：每个节点最多含有两个⼦树的树称为⼆叉树；完全⼆叉树：在⼀棵⼆叉树中，除最后⼀层外，若其余层都是满的，并且最后⼀层或者是满的，或者是在右边缺少连续若⼲节点，则此⼆叉树为完全⼆叉树。

满⼆叉树：⼀棵深度为i，且有2i-1个节点的⼆叉树，称为满⼆叉树。

霍夫曼树：带权路径最短的⼆叉树称为哈夫曼树或最优⼆叉树；1.2.⼆叉树相关术语1) 节点的度：⼀个节点含有的⼦树的个数称为该节点的度；2) 叶节点或终端节点：度为0的节点称为叶节点；3) ⾮终端节点或分⽀节点：度不为0的节点；4) 双亲节点或⽗节点：若⼀个节点含有⼦节点，则这个节点称为其⼦节点的⽗节点；5) 孩⼦节点或⼦节点：⼀个节点含有的⼦树的根节点称为该节点的⼦节点；6) 兄弟节点：具有相同⽗节点的节点互称为兄弟节点；7) 树的度：⼀棵树中，最⼤的节点的度称为树的度；8) 节点的层次：从根开始定义起，根为第1层，根的⼦节点为第2层，以此类推；9) 树的⾼度或深度：树中节点的最⼤层次；10) 堂兄弟节点：双亲在同⼀层的节点互为堂兄弟；11) 节点的祖先：从根到该节点所经分⽀上的所有节点；12) ⼦孙：以某节点为根的⼦树中任⼀节点都称为该节点的⼦孙。

树和二叉树知识考点整理●树的基本概念●树的定义●n个结点的有限集●n=0代表空树●满足条件●只有一个根的结点●其余结点是互不相交的有限集，每个集合本身是一棵树，是根的子树●树是一种递归的数据结构●树的根结点没有前驱，其余结点只有一个前驱●树中所有结点可以有零个或多个后驱●基本术语●双亲、兄弟、孩子、祖先●度：孩子个数●分支结点：度大于0●叶子结点：度为0●深度：从下往上；●高度：从上往下；●有序树：从左到右是有次序的●路径和路径长度：路径是从上往下的●森林：m棵互不相交的树的集合。

●树的基本性质●结点数=所有结点度数之和+1●度为m的树中第i层上至多有m的i-1次分个结点●高度为h的m叉树至多有（m^h-1）/（m-1）个结点●具有n个结点的m叉树的最小高度为「logm（n（m-1）+1）]●二叉树的概念●定义●一种树形结构，特点是每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点）并且二叉树的子树有左右之分，次序不可颠倒●二叉树与度为2的有序树区别●度为2的可以有三个结点，二叉树可以是空树●度为2的有序树的孩子左右之分是根据另一个孩子而言的；二叉树无论有没有，都要确定左右●特殊的二叉树●满二叉树●树中每一层都含有最多的结点●完全二叉树●高度为h，有n个结点的二叉树，当且仅当，每个结点都与高度为h的满二叉树中的编号一一对应●二叉排序树●用途：可用于元素的排序、搜索●左子树上所有结点的关键字均小于根结点的关键字；右子树上所有结点的关键字均大于根结点的关键字；左子树和右子树又是一棵二叉排序树●二叉树的性质●非空二叉树上的叶子结点数等于度为2的结点树加1，即n0=n2+1●非空二叉树上第k层至多有2^（k-1）个结点●高度为h的二叉树至多有2^h-1个结点●具有n个结点的完全二叉树的高度为log2（n+1）取顶或者log2n取底+1●二叉树的存储结构●顺序存储结构●只适合存储完全二叉树，数组从0开始●链式存储结构●顺序存储的空间利用率太低●至少三个指针域：数据域、左指针域、右指针域●增加了指向父结点后，变为三叉链表的存储结构●在含有n个结点的二叉链表中，含有n+1个空链域●二叉树的遍历和线索二叉树●二叉树的遍历●先序遍历●根左右●应用：求树的深度●中序遍历●左根右●后序遍历●左右根●应用：求根到某结点的路径、求两个结点的最近公共祖先等●三个遍历时间复杂度都是O(n)●递归算法和非递归算法的转换●层次遍历●需要借助队列●步骤●二叉树根结点入队，然后出队，访问出队结点，若有左子树，左子树根结点入队●遍历右子树，有右子树，右子树根结点入队。

实验5：树（二叉树）（采用二叉链表存储）一、实验项目名称二叉树及其应用二、实验目的熟悉二叉树的存储结构的特性以及二叉树的基本操作。

三、实验基本原理之前我们都是学习的线性结构，这次我们就开始学习非线性结构——树。

线性结构中结点间具有唯一前驱、唯一后继关系，而非线性结构中结点的前驱、后继的关系并不具有唯一性。

在树结构中，节点间关系是前驱唯一而后继不唯一，即结点之间是一对多的关系。

直观地看，树结构是具有分支关系的结构（其分叉、分层的特征类似于自然界中的树）。

四、主要仪器设备及耗材Window 11、Dev-C++5.11五、实验步骤1.导入库和预定义2.创建二叉树3.前序遍历4.中序遍历5.后序遍历6.总结点数7.叶子节点数8.树的深度9.树根到叶子的最长路径10.交换所有节点的左右子女11.顺序存储12.显示顺序存储13.测试函数和主函数对二叉树的每一个操作写测试函数，然后在主函数用while+switch-case的方式实现一个带菜单的简易测试程序，代码见“实验完整代码”。

实验完整代码：#include <bits/stdc++.h>using namespace std;#define MAX_TREE_SIZE 100typedef char ElemType;ElemType SqBiTree[MAX_TREE_SIZE];struct BiTNode{ElemType data;BiTNode *l,*r;}*T;void createBiTree(BiTNode *&T){ElemType e;e = getchar();if(e == '\n')return;else if(e == ' ')T = NULL;else{if(!(T = (BiTNode *)malloc(sizeof (BiTNode)))){cout << "内存分配错误!" << endl;exit(0);}T->data = e;createBiTree(T->l);createBiTree(T->r);}}void createBiTree2(BiTNode *T,int u) {if(T){SqBiTree[u] = T->data;createBiTree2(T->l,2 * u + 1);createBiTree2(T->r,2 * u + 2); }}void outputBiTree2(int n){int cnt = 0;for(int i = 0;cnt <= n;i++){cout << SqBiTree[i];if(SqBiTree[i] != ' ')cnt ++;}cout << endl;}void preOrderTraverse(BiTNode *T) {if(T){cout << T->data;preOrderTraverse(T->l);preOrderTraverse(T->r);}}void inOrderTraverse(BiTNode *T) {if(T){inOrderTraverse(T->l);cout << T->data;inOrderTraverse(T->r);}}void beOrderTraverse(BiTNode *T){if(T){beOrderTraverse(T->l);beOrderTraverse(T->r);cout << T->data;}}int sumOfVer(BiTNode *T){if(!T)return 0;return sumOfVer(T->l) + sumOfVer(T->r) + 1;}int sumOfLeaf(BiTNode *T){if(!T)return 0;if(T->l == NULL && T->r == NULL)return 1;return sumOfLeaf(T->l) + sumOfLeaf(T->r);}int depth(BiTNode *T){if(!T)return 0;return max(depth(T->l),depth(T->r)) + 1;}bool LongestPath(int dist,int dist2,vector<ElemType> &ne,BiTNode *T) {if(!T)return false;if(dist2 == dist)return true;if(LongestPath(dist,dist2 + 1,ne,T->l)){ne.push_back(T->l->data);return true;}else if(LongestPath(dist,dist2 + 1,ne,T->r)){ne.push_back(T->r->data);return true;}return false;}void swapVer(BiTNode *&T){if(T){swapVer(T->l);swapVer(T->r);BiTNode *tmp = T->l;T->l = T->r;T->r = tmp;}}//以下是测试程序void test1(){getchar();cout << "请以先序次序输入二叉树结点的值，空结点用空格表示:" << endl; createBiTree(T);cout << "二叉树创建成功!" << endl;}void test2(){cout << "二叉树的前序遍历为:" << endl;preOrderTraverse(T);cout << endl;}void test3(){cout << "二叉树的中序遍历为:" << endl;inOrderTraverse(T);cout << endl;}void test4(){cout << "二叉树的后序遍历为:" << endl;beOrderTraverse(T);cout << endl;}void test5(){cout << "二叉树的总结点数为：" << sumOfVer(T) << endl;}void test6(){cout << "二叉树的叶子结点数为：" << sumOfLeaf(T) << endl; }void test7(){cout << "二叉树的深度为：" << depth(T) << endl;}void test8(){int dist = depth(T);vector<ElemType> ne;cout << "树根到叶子的最长路径:" << endl;LongestPath(dist,1,ne,T);ne.push_back(T->data);reverse(ne.begin(),ne.end());cout << ne[0];for(int i = 1;i < ne.size();i++)cout << "->" << ne[i];cout << endl;}void test9(){swapVer(T);cout << "操作成功!" << endl;}void test10(){memset(SqBiTree,' ',sizeof SqBiTree);createBiTree2(T,0);cout << "操作成功!" << endl;}void test11(){int n = sumOfVer(T);outputBiTree2(n);}int main(){int op = 0;while(op != 12){cout << "-----------------menu--------------------" << endl;cout << "--------------1：创建二叉树--------------" << endl;cout << "--------------2：前序遍历----------------" << endl;cout << "--------------3：中序遍历----------------" << endl;cout << "--------------4：后序遍历----------------" << endl;cout << "--------------5：总结点数----------------" << endl;cout << "--------------6：叶子节点数--------------" << endl;cout << "--------------7：树的深度----------------" << endl;cout << "--------------8：树根到叶子的最长路径----" << endl;cout << "--------------9：交换所有节点左右子女----" << endl;cout << "--------------10：顺序存储---------------" << endl;cout << "--------------11：显示顺序存储-----------" << endl;cout << "--------------12：退出测试程序-----------" << endl;cout << "请输入指令编号:" << endl;if(!(cin >> op)){cin.clear();cin.ignore(INT_MAX,'\n');cout << "请输入整数!" << endl;continue;}switch(op){case 1:test1();break;case 2:test2();break;case 3:test3();break;case 4:test4();break;case 5:test5();break;case 6:test6();break;case 7:test7();break;case 8:test8();break;case 9:test9();break;case 10:test10();break;case 11:test11();break;case 12:cout << "测试结束!" << endl;break;default:cout << "请输入正确的指令编号!" << endl;}}return 0;}六、实验数据及处理结果测试用例：1.创建二叉树（二叉链表形式）2.前序遍历3.中序遍历4.后序遍历5.总结点数6.叶子结点数7.树的深度8.树根到叶子的最长路径9.交换所有左右子女10.顺序存储七、思考讨论题或体会或对改进实验的建议通过这次实验，我掌握了二叉树的顺序存储和链式存储，体会了二叉树的存储结构的特性，掌握了二叉树的树上相关操作。

NOIP普及组（初赛）试题精选一、计算机系统1.在以下各项中，（）不是CPU的组成部分。

（NOIP2007）A．控制器 B．运算器 C．寄存器 D．主板【答案】D。

CPU由控制器、运算器和寄存器组成。

2.在下列各项中，只有（）不是计算机存储容量的常用单位。

（NOIP2007）A．Byte B．KB C．UB D．TB【答案】C。

存储容量：Byte=8 bit（位）、1KB=1024B、1MB=1024KB、1GB=1024MB、1TB=1024G B。

3.与十进制数1770对应的八进制数是（）。

（NOIP2007）A．3350 B．3351 C．3352 D．3540【答案】C。

考查进制转换，掌握十进制、二进制、八进制和十六进制互换，以及多个不同进制数的运算（转换为同一进制数进行计算）。

4.与十进制数28.5625相等的四进制数是（）。

（NOIP2008）A．123.21 B．131.22 C．130.22 D．130.21【答案】D。

熟练掌握进制转换的知识。

5.计算机在工作过程中，若突然停电，（）中的信息不会丢失。

（NOIP2008）A．ROM 和 RAM B．CPU C．ROM D．RAM【答案】C。

ROM（只读存储器）断电后信息不丢失，RAM（随机存储器，内存）断电后信息全部丢失。

6.在32*32点阵的“字库”中，汉字“北”与“京”的字模占用字节数之和是（）。

（NOIP2008）A．512 B．256 C．384 D．128【答案】B。

32*32点阵的字库，每个字占字节数为32*32/8=128字节（1个字节等于8个二进制位，1Byte=8bits，而1位对应点阵中的1个点）。

所以2个汉字共要256个字节。

7.在下面各世界顶级的奖项中，为计算机科学与技术领域做出杰出贡献的科学家设立的奖项是（）。

（NOIP2006）A. 沃尔夫奖B. 诺贝尔奖C. 菲尔兹奖D. 图灵奖【答案】D。

沃尔夫奖主要是奖励对推动人类科学与艺术文明做出杰出贡献的人士；诺贝尔奖有生理或医学奖、文学奖、物理学奖、化学奖、经济学奖和和平奖；菲尔兹奖－数学界的诺贝尔奖；图灵奖－计算机界的诺贝尔奖，2000年姚期智获得“图灵奖”，也是迄今为止获得此项殊荣的唯一华裔计算机科学家。

树、⼆叉树、满⼆叉树、完全⼆叉树概念分清⾃由树⾃由树是⼀个连通的，⽆回路的⽆向图。

令G=(V，E)为⼀个⽆向图。

下⾯的表述是等价的。

1) G是⾃由树。

2) G中任意两个顶点由唯⼀⼀条简单路径得到。

3) G是连通的，但从E中去掉任何边后得到的图都是⾮连通的。

4) G是⽆回路的，且|E|=|V|-1。

5) G是连通的，且|E|=|V|-1。

6) G是⽆回路的，但添加任何边到E中得到的图包含回路。

⼆叉树在计算机科学中，⼆叉树是每个节点最多有两个⼦树的树结构。

通常⼦树被称作“左⼦树”（left subtree）和“右⼦树”（right subtree）。

⼆叉树的每个结点⾄多只有⼆棵⼦树(不存在度⼤于2的结点)，⼆叉树的⼦树有左右之分，次序不能颠倒。

⼆叉树的第i层⾄多有2^(i-1)个结点；深度为k的⼆叉树⾄多有2^k-1个结点；（等⽐数列1+2+4+…+2^(k-1) = 2^k-1）。

对任何⼀棵⼆叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0 = n2 + 1。

树和⼆叉树的三个主要差别：1) 树的结点个数⾄少为1，⽽⼆叉树的结点个数可以为0；2) 树中结点的最⼤度数没有限制，⽽⼆叉树结点的最⼤度数为2；3) 树的结点⽆左、右之分，⽽⼆叉树的结点有左、右之分。

满⼆叉树⼀棵深度为k，且有2^k-1个节点的树是满⼆叉树。

另⼀种定义：除了叶结点外每⼀个结点都有左右⼦叶且叶⼦结点都处在最底层的⼆叉树。

这两种定义是等价的。

从树的外形来看，满⼆叉树是严格三⾓形的，⼤家记住下⾯的图，它就是满⼆叉树的标准形态：所有内部节点都有两个⼦节点，最底⼀层是叶⼦节点。

性质：1) 如果⼀颗树深度为h，最⼤层数为k，且深度与最⼤层数相同，即k=h;2) 它的叶⼦数是： 2^(h-1)3) 第k层的结点数是： 2^(k-1)4) 总结点数是： 2^k-1 (2的k次⽅减⼀)5) 总节点数⼀定是奇数。

6) 树⾼：h=log2(n+1)。

完全二叉树总结点数与叶结点数关系分析作者：刘松蓝鹰来源：《电脑知识与技术》2008年第34期摘要：该文从两个角度分析了完全二叉树的总结点数与叶结点数之间的关系。

其一，通过归纳找到总结点数的奇偶性与度为1的结点个数之间的关系，进而导出总结点数与叶结点数的关系；其二，由最后一个结点的父结点为倒数第一个分支结点的事实，找到总结点数与叶结点数的关系。

这种多角度的分析有利于学生对此数据结构的深入理解。

关键词：数据结构；树；二叉树；完全二叉树中图分类号：TP311文献标识码：A文章编号：1009-3044(2008)34-1569-02Complete Binary Tree Nodes and Leaves Number RelationLIU Song, LAN Ying(College of Computer Science and Technology, Jilin Normal University, Siping 136000, China)Abstract: This paper analyzed the relation between the complete binary tree nodes and the leaves number by two ways. First, it induced the relation between the odevity of complete binary tree nodes and the number of one degree nodes, then come to the conclusion. Second, through the fact that the parent of the last node is the last branch node, the paper got the same conclusion. Analyzing by two ways is helpful for students to understand complete binary tree.Key words: Data Structure; Tree; Binary Tree; Complete Binary Tree1 引言1.1 树的定义及几个基本术语[1]树（tree）是n（n≥0）个结点的有限集合T，如果T为空，则它是一棵空树（null tree），否则：1) T中有一个特别标出的称为根（root）的结点；2) 除根结点之外，T中其余结点被分成m个（m≥0）互不相交的非空集合T1，T2，…，Tm，其中每个集合本身又都是树。