12.2.2单项式与多项式相乘 课件

4
3
练一练：
下列各题的解法是否正确，如果错了，指 出错在什么地方，并改正过来。
①
-2a2b
×
-
1 4
ab2c
=
1 2
a3b3
1 2
a
3
b3c×
② 3a2b 1 - ab2c = -3a3b3 3a2b - 3a3b3c ×
③ -3a2 a2 + 2a -1 = -3a4 + 6a3 -3a2 ×
解法(一):先求三家连锁店的总销量,再求总收入,即 总收入(单位:元)为:
m(a+b+c) ①
解法(二):先分别求三家连锁店的收入,再求它们的和, 即总收入(单位:元)为:
ma+mb+mc ②
由于①和②表示同一个量,所以:
m(a+b+c)=ma+mb+mc
m(a+b＋c) = ma+mb＋mc
观察这个式子有什么特征? 思考：
你能说出单项式与多项式相乘的法则吗？
单项式乘以多项式法则：
单项式与多项式相乘,就是用单项 式去乘多项式的每一项,再把所得 的积相加.
m(a+b+c) =ma+mb+mc
例1计算：（- 4x）·(2x2+3x-1)
思路： 单×多 转 化 单×单
分配律
例2计算： ( 3 ab2 3ab) 1 ab
-3a4 - 6a3 + 3a2
练一练：
1.口答：(1) a(m+n) = am+an (2) a(m-n) = am-an (3) - a(m-n) = -am+an (4)m(a+b-c) = ma+mb-mc (5)m(-a+b-c) = -ma+mb-mc

-
5
解：(1)(－2a)·
1a3－1 4
＝(－2a)1·12a.23.2＋单(－项式2a与)多·(－项式1)相乘＝－1a4＋2a.
4
2
(2)(2x2－3x＋5)·(－3x)
＝2x2·(－3x)＋(－3x)·(－3x)＋5·(－3x)
＝－6x3＋9x2－15x.
(3)
－1ab 2
·
2ab2－2ab＋4b
图 12－2－3
大长方形法的则：面单积项式等与于多三项式个相小乘，长将方单项形式的分面别乘积以之多项和．
式的m字_(母a表＋达式b：_＋m_，(a再＋c将b)＋所-＝c得)＝的_m___a_＋m_b．＋__.mc. 7
变式训练 12.2.2 单项式与多项式相乘 例 2 [课本练习第 2 题变式题] 先化简，再求值： x2(3－x)＋x(x2－2x)＋1，其中 x＝2.
问题：如图所示，图把1一2－块2－边2长为a米的正方
形场问地题 的1：长如扩图大12b－米2－，2宽所不示变，把，一则块扩边大长后为 的a 米长的方正方
形形场场地地的长的扩长大是b_米_(_，a＋__宽b)_不_米变，，则宽扩是大_后_a_的_米长方，形面场积地是的长
是_a__(_a_＋__b_) ___米平，方宽米是；__原__米场，地面的积面是积__是__a__2 __平_平方方米米；原，场 地此扩的可大以面部得积到是分一_的_个_面_等平积式方是，米这_，_a个b扩__等大平式部方是分米_的_ ．面积由是此_可___以平得方到米__．．一由
最终结果中，有同类项时要合并同类项得出最简
结果．
-
12
多做多练
课本P27 练习：1、2
课本P30 习题：3、4

6a410 a2b
单项式与多项式相乘时，分两个阶段：
①按分配律把乘积写成单项式与单项式乘 积的代数和的形式；
②单项式的乘法运算.
单项式乘以多项式法则：
单项式与多项式相乘，就是用 单项式去乘多项式的每一项，再把 所得的积相加。（利用乘法分配律）
计算：(2ab2 2ab)1ab
3
2
解:原式 2ab2 1ab(2ab) 1ab
a 3 4
2
b

a 1 b 3
3xy2x3y33x4 y5
这节课我们学习了单项式乘单项式， 单项式乘多项式的运算法则，你有何 新的收获和体会？
七嘴八舌说一说
小结
1、单项式与多项式相乘的依据是乘 法对加法的分配律 2、单项式与多项式相乘，其积仍是 多项式，项数与原多项式的项数相 同，注意不要漏乘项 3、积的每一项的符号由原多项式各 项符号和单项式的符号来决定
（3）其余字母连同它的指数不变，作为积的因式
计算： (1) (-5a2b)(-3a)；
(2) (2x)3(-5xy2).
注 (1)先做乘方，再做单项式相乘 意 (2)系数相乘要注意符号 点 (3)单项式乘以单项式的结果仍是单项式
解：
1 5 a 2 b 3 a 22x35x2 y
5 3 a 2 a b 23x35x2y
作业
1a3b2 23ab2aa
15a3b
8x35x2y
8 5 x 3xy 2
40x4y2
下面的计算对不对？如果不对，怎样改正？
⑴5a22a31a 06 ×
10 a5
2 3 s 2 s7 6 s7 ×
6s8
(3) 3x2+4x2=7x4
×
7x2

乘法分配律的运用
乘法分配律是数学中的一个基本定律，它指出一个数乘以 两个数的和等于这个数分别乘以这两个数再求和。在单项 式与多项式相乘时，乘法分配律是非常重要的。
例如，单项式$a^3$与多项式$b + c$相乘时，可以运用 乘法分配律进行计算：$(a^3)(b+c) = a^3b + a^3c$。 这样可以简化计算过程，提高计算效率。
单项式与多项式相乘公开课课件
contents
目录
• 单项式与多项式简介 • 单项式与多项式相乘的法则 • 单项式与多项式相乘的运算实例 • 单项式与多项式相乘的注意事项 • 习题与解答
01
单项式与多项式简介
单项式的定义与性质
定义
单项式是只包含一个项的代数式 ，通常表示为数字、字母的积。
性质
单项式具有加法封闭性、乘法交 换律和结合律等基本性质。
单项式的几何意义
在数轴上，单项式可以表示一个点或一个单位长度。例如，$3x$表示在x轴上， 每移动一个单位长度，坐标增加3。
多项式的几何意义
多项式可以表示一条曲线或曲面。例如，$y = x^2$表示一个开口向上的抛物线 。
02
单项式与多项式相乘的法则
单项式乘以多项式的法则
单项式乘以多项式的运算法则，是将单项式中的每一个因子 与多项式中的每一个项分别相乘，然后将所得的积相加。
多项式的定义与性质
定义
多项式是由有限个单项式通过加法运 算组成的代数式，表示为$P(x) = a_n x^n + a_{n-1} x^{n-1} + cdots + a_1换律 和结合律等基本性质，还具有分配律 和幂的运算法则等特殊性质。
单项式与多项式的几何意义

实质上是转化为同底数幂的运算
单项式× 多项式
实质上是转化为单项式×单项式
四点 注意
（1）计算时,要注意符号问题,多项式中每一项都 包括它前面的符号,单项式分别与多项式的每一项 相乘时，同号相乘得正，异号相乘得负 （2）不要出现漏乘现象 （3）运算要有顺序：先乘方，再乘除，最后加减 （4）对于混合运算，注意最后应合并同类项
6.计算：－2x2·(xy+y2)-5x(x2y-xy2). 解：原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2 =-7x3 y+3x2y2.
注意 （1）将2x2与5x前面的“-”看成性质符号； （2）单项式与多项式相乘的结果中， 应将同类项合并.
（1）利用乘法交换律和结合律有： (3×105)×(5×102)=(3×5)×(105×102)=15×107. 这种书写规范吗？ 不规范，应为1.5×108. （2） ac5 ·bc2=（a ·b) ·(c5·c2) (乘法交换律、结合律）
=abc5+2 (同底数幂的乘法） =abc7.
初中数学课件 知识要点
单项式与单项式的乘法法则 单项式与单项式相乘，把它们的系数、同底数幂分
别相乘，对于只在一个单项式里含有的字母，则连同它 的指数作为积的一个因式.
注意 （1）系数相乘； （2）相同字母的幂相乘； （3）其余字母1 计算： (1) (-5a2b)(-3a)；
a
b
c
p
p
p
如果把它看成三个小长方形，那么它们的面积可分别表示为 __p_a__、__p_b__、___p_c_.

练习：
1. (-2ab)3(5a2b–2b3) 2.(3x2y-xy2)·(-3xy)
3.(3x2y1x2y5y3)(4x2y ) 4 26
4.-2a2·(ab+b2)-5a(a2b-ab2)
单项式与多项式相乘
深入探索----算一算
先化简再求值:
x2(x2x1 )x(x3x2x5)，x 其 1.中 25
m(a+b+c)= ma + mb + mc
类似的:
单项式与多项式相乘的法则:
2a2(3单a项2-5式b与)=多2项a2式.3a相2乘+2,只a2要.(-将5单b)项=6式a分4-1别0a2b (-2a2乘)(以3a多b2项-5式b的)=各(-项2a,再2)将.3a所b得2 +的(积-2相a2加)..(-5b)
单项式与多项式相乘
深入探索----解一解
解不等式: 2x(x1)2x25
解：去括号得：
2x2 2x＞ 2x2 5
移项合并得：2x＞-5
解得：x＞ 5 2
单项式与多项式相乘
知识运用----试一试
小李家住房的结构如图所示,小李打算把客
厅和卧室铺上木地板,请你帮他算一算,他至少
需买多少平方米木地板?
p 3 5 p p 3 5 p 2 5 p 2 5 p
⑷ 2p310 p210 p ( 3 x 2 )3 7 x 3 [x 3 x (4 x 2 1 )]
2x6 7 7x3(x34x3x)2x7 67x3(3x3x)
2x7 62x6 17x448x67x4
单项式与多项式相乘
辩一辩
下列各题的解法是否正确，如果错了，指
单项式与多项式相乘
小结& 思考 ☞

解：(6)不能.(1)、（3）、（5）为正确， （2）、（4）是错误的。
正确的命题称为 真命题
错误的命题称为 假命题
这样可以 判断它是 正确的或 是错误的 句子叫做 命题.
看下面的句子，哪些是真命题，哪些是假命题？
(1)对顶角相等
（真）
(2)内错角相等
（假）
(3)如果两直线被第三直线所截,那么同位角相等 （真）
一地,能明确指出概念含义或特征的句子,称 为定义.
请给它们下定义
直角三角形: 有一个角为直角的三角形叫直 角三角形.
锐 角:
大于00且小于900的 角叫锐角.
圆周 角:
顶点在圆上,两边与圆相交 的角叫圆周角.
你能举出一些老师在教学上重点提 示的一些不确切的定义吗?
注意！
定义的严密性
看下面的句子: (1)对顶角相等 (2)内错角相等 (3)如果两直线被第三直线所截,那么同位角相等 (4)3＜2 (5)三角形的内角和等于1800 (6)x＞2 能判断真假吗?哪能是正确的?哪些是错误的?
.
2.例题讲解.
例1 计算 :
(1)0.5ab( 2 ab2 2ab); 3
(2)x(x2 xy y2 ) y(x2 xy y2 );
(3)4ab[2a2b (ab ab2 ) 3b].
解:
(1)0.5ab(2 ab2 2ab) 3
1 a b(2 a b2 2a b) 23
1 2
a
b(
2 3
a
b2
)
1 2
a
b(
2a
b
)
1 3
a
2b3
a
2b2
;
(2)x(x2 xy y2 ) y(x2 xy y2 )

12.2.2单项式与多项式相乘学习目标1、理解单项式乘以多项式的意义；2、理解并掌握单项式乘以多项式的乘法法则，会进行单项式乘以多项式的乘法运算。

重占单项式与多项式的乘法运算。

难点推测单项式与多项式的乘法法则。

教学过程一、创设情境，导入新知1、教师引导学生复习单项式乘以单项式法则.整式的乘法实际上就是单项式X单项式单项式义多项式多项式X多项式(点评：培养学生前后知识的连续性.)前面我们已经学过单项式X单项式，今天我们来学习单项式与多项式相乘。

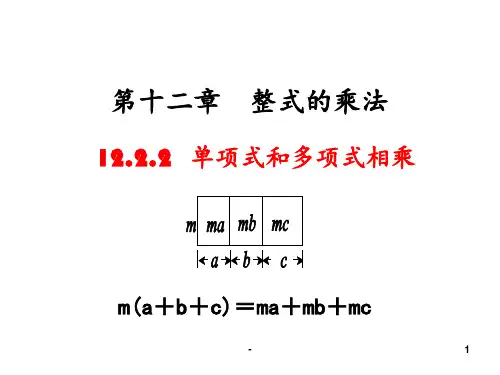
2、教师演示长方形的面积问题.学生通过讨论，有的学生列出式子：m(a+b+c)；有的学生列出式子：ma+mb+mc那么这两个式子一样吗？你知道为什么吗？(1)大长方形的长是a÷b÷c,宽是m(2)①、②、③三个小长方形的面积分别是ma、mb、me(3)由(1)(2)得出等式m(a+b+c)=ma+mb+mc二、合作交流，探究新知1、方案1：学生独立思考并回答问题.方案2：分组讨论、交流.2、在学生发言的基础上，教师总结单项式X多项式的乘法法则.单项式与多项式相乘，将单项式分别乘以多项式的各项，再将所得的积相加.(根据所得法则，验证画面面积问题.)［点评］让学生体会法则的理论依据：利用乘法的分配律.得出法则后，将所学知识用于解决生活中的实际问题.三、运用新知，深化理解例1 (―24)•(3"—5")；［点评］强调法则的运用特点，学生刚接触，故要求学生按步骤解题，且提醒学生不能漏项.例2计算：-2ab∙(a'—3a+1).错解：原式=—2ab∙a?—2ab•(―3a)+1=—2a,b+6a2b+1错解分析：错解漏乘了多项式中的常数项。

正解：原式=-2ab∙a3—2ab•(―3a)—2ab•1=-2a'b+6a⅞—2ab四、课堂练习，巩固提高1.判断题：(1)3a3∙5a3=15a3( )(2)6^∙7ab=42ab( )(3)3√∙(2a2-2a3)=6a3-6a12( )⑷一义(2”一孙)=—2产，一力( )2.计算：(1)—3x(—y—xyz) (2)2a(-2ab÷3ab2)3、化简：x（x2-1）+2X2（X+1）-3X（2χ-5）五、反思小结，梳理新知1.指导学生总结本节课的知识点、学习过程.2.单项式X多项式的积的项数、符号（结合去括号法则）及不能漏乘等注意事项给予强调.3.要善于在图形变化中发现规律，能熟练地对整式加减及单项式与多项式相乘进行运算.六、布置作业1.教材P30习题12.2第3、4题.七、板书设计（一）情境导入（二）合作交流，探究新知（三）运用新知，深化理解例1例2（四）课堂练习，巩固提高1、判断题2、计算3、拓展（五）小结（六）作业布置八、教学反思。

八年级 八年级 数学 数学
第十四章 第十二章 整式的乘法 整式的乘除
情景 & 导入
某街道为美化环境,对街道进行了大整治。其中 一项就是把一块矩形的空地补上了彩色地砖(如下 图),成为市民休闲健身的场所。 你能够表示出这块矩形空地的面积吗?
m
ma
mb
mc
c a b m(a b c) = ma mb mc
2
18x 6 x 4x
2
八年级 数学
第十四章 整式的乘法
2
(3) (x - 3y) (-6x )
解 : 原式
x (-6x2 ) 3y (-6x2 )
3
-6x 3 2 -6x 18x y
(18x2 y )
运算时要注意哪些问题？
1、不能漏乘: 即单项式要乘以多项式的每一项. 2、计算时，要注意符号问题，多项式的每一项 都包括它前面的符号，单项式分别与多项式的每 一项相乘时，同号相乘得正，异号相乘得负。 3、单项式与多项式的结果仍是多项式，积的项 数与原多项式的项数相同。
例3
八年级 数学
计算 3(5a2b–2b3) ： (-2ab)
=(-8a3b3)·5a2b+(-8a3b3)·(-2b3） =-40a5b4+16a3b6
第十四章 整式的乘法
解:原式=(-8a3b3)(5a2b–2b3)
说明：先进行乘方运算，再进行 单项式与多项式的乘法运算。
八年级 数学
第十四章 整式的乘法
6x -3xy
2 4.-3x（2x-5y+6z)=___________________ -6x +15xy-18xz 5-8a4b+4a4c -4a 2 2 5.(-2a ) （-a-2b+c)=__________________

= 15a3b
=[8×(-5)](x3•x)y2
=-40x4y2
第11页/共28页
判断下面的计算是否正确？如果 不对，怎样改正？
⑴5a2 2a3 1100aa65 ⑵2x 3x4 56x55
？
⑶ 3s 2s7 66ss78
⑷ 2 a3 a26a3 ⑸ 28 2a3 29 a3
路程=速度×时间
(3×105 ) ×(5×102)
第6页/共28页
一、单项式乘单项式
(3×105
)
×(5×102)
利用乘法的交换律和 结合律，把各个因式
和因数分类，具有相
=(3×5)×(105×102)同 常
字 数
母 项
的 归
分 为
为 一
一类 类
，
=15×107
=1.5×108
第7页/共28页
一、单项式乘单项式
-3a4 - 6a3 + 3a2
第23页/共28页
先化简再求值:
x2 (x2 x 1) x(x3 x2 x 5)，其中x 1 . 25
解：原式 x4 x3 x2 x4 x3 x2 5x
5x
当x 1 时 25
原式 5 1 1 25 5
第24页/共28页
解方程
7x-(x–3)x–3x(2–x)=(2x+1)x+6
事实上，多项式乘单项式=单项式乘多项式 （乘法交换律）
第21页/共28页
⑴ 2x(x 1) 3x
2x x 2x (1) 3x
⑵a(a 1) a2
a a a (1) a2
2x2 2x 3x
a2 a a2
2x2 5x
a
⑶p( p2 5) p2 ( p 5) 5 p( p 1)

m(a+b+c)=ma+mb+ mc
例1 计算：
(1)(-4x)·(2x2+3x-1)；
解： (-4x)·(2x2+3x-1)
＝ (-4x)·(2x2) + (-4x)·3x + (-4x)·(-1
＝-8x3-12x2+4x
注意：（-1）这项不要漏乘，也不要当成是1。
例1 计算：
(2)2ab22ab•1ab
=(-2a)•2a2+(-2a)•(-3a)+(-2a)•
（乘法分配律）
=-4a3+6a2-2a （单项式与单项式相乘法则）
怎样叙述单项式与多项式相乘的法则?
m(a+b+c)=ma+mb+ mc
(m、a、b、c都是单项式)
单项式与多项式相乘法则
单项式与多项式相乘，就 是用单项式去乘多项式的每 一项，再把所得的积相加。
其中y=-3,n=2. 解:yn(yn + 9y-12)–3(3yn+1-4yn)
=y2n+9yn+1-12yn–9yn+1+12yn =y2n
当y=-3，n=2时， 原式=(-3)2×2=(-3)4=81
课堂小结
你 来 总 结
本题课你有 什么收获或 感想？你还 有什么疑问？
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月3日星期四2022/3/32022/3/32022/3/3 •2、科学的灵感，决不是坐等可以等来的。如果说，科学上的发现有什么偶然的机遇的话，那么这种‘偶然的机遇’只能给那些学有素养的人，给那些善于独 立思考的人，给那些具有锲而不舍的人。2022年3月2022/3/32022/3/32022/3/33/3/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/32022/3/3March 3, 2022 •4、享受阅读快乐，提高生活质量。2022/3/32022/3/32022/3/32022/3/3

2
2
2
×)
(-2)•（ + -3)=-22-2 − (
2
1
2
3.计算： (1) ( 3 ab 2ab) 2 ab ；
2
4
(2) (2 x x ) (9 x)；
3
9
2
(3) (x-3y) (-6x ).
2 2 1
解:（1）原式 ab ab 2ab 1 ab
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
注意 （1）将22与5前面的“-”看成性质符号；
（2）单项式与多项式相乘的结果中， 应将同类项合并.
随堂训练
1.下列计算错误的是( D)
(A)5(22-)=103-5
(B)-3+ •4-=-
连同它的指数一起作为积的一个因式.
3.完成下列各题：
3
-8x
y
（1）
2 x （ - 4 xy）=
2
3
（2）（ - 2 x ）
（ - 3 xy）= 6x y
2
1
2 2 - 1 a 2b 3
（3） - ab ab =
3
2
3

2 3 5
（4）
12 - = 9
＝-7 + .
5.如果(－3x)2(x2－2nx＋2)的展开式中不含x3 项，
求n的值．
解：
(－3x)2(x2－2nx＋2)
＝9x2(x2－2nx＋2)
＝9x4－18nx3＋18x2.
∵展开式中不含x3项，∴n＝0.
课堂小结
单项式×

教师课堂用语在学科专业方面重在进行“引”与“导”，通过点拨、搭桥等方式让学生豁然开朗，得出结论，而不是和盘托 出，灌输告知。一般可分为：启发类、赏识类、表扬类、提醒类、劝诫类、鼓励类、反思类。
一、启发类
1. 集体力量是强大的，你们小组合作了吗?你能将这个原理应用于生活吗?你的探究目标制定好了吗? 2. 自学结束，请带着疑问与同伴交流。 3. 学习要善于观察，你从这道题中获取了哪些信息? 4. 请把你的想法与同伴交流一下，好吗? 5. 你说的办法很好，还有其他办法吗?看谁想出的解法多? 二、赏识类
基础巩固练
9．当 m5＝－12，n＝－1 时，3m2－m(2m－5n)－n(5m－n)等于 ___4_____．
基础巩固练
10．一个长方体的长、宽、高分别是 3x－4，2x 和 x，则它的体 积等于_6_x_3_－__8_x_2____．
基础巩固练
11．计算： (1)12x2y－2xy＋y2·(－4xy)；
能力提升练
15．如图，从边长为(a＋4)cm 的正方形纸片中剪去一个边长为 (a＋1)cm 的正方形(a>0)，剩余部分沿虚线又剪拼成一个长 方形(不重叠无缝隙)，则长方形的面积为_(6_a_＋__1_5_)_cm2.
能力提升练 16．【教材改编题】设 n 为自然数，试说明 n(2n＋1)－2n(n－1)
能力提升练
19．解下列方程和不等式． (1)x(x2＋5x－6)－x(5x＋6)＝x(x2－5)－5(x－1)； 解：x(x2＋5x－6)－x(5x＋6)＝x(x2－5)－5(x－1)，
x3＋5x2－6x－5x2－6x＝ x3－5x－5x＋5， －2x＝ 5， x＝－52.
能力提升练
(2)3x(1－x)＜16－(3x－1)x. 解：3x(1－x)＜16－(3x－1)x，

这个长方形可分割为宽为m，长分别为a、b、c 的三个小长方形，它们的面积之和为ma+mb+mc
∴ m(a+b+c)=ma+mb+mc
m ma a
mb
mc
b
c
m(a+b＋c) = ma+mb＋mc
观察这个式子有什么特征? 思考：
你能说出单项式与多项式相乘的法则吗？
如何进行单项式与多项式相乘的 运算？
①按乘法分配律把乘积写成单项式与单项 式乘积的代数和的形式；
②单项式的乘法运算。
几点注意：
1.单项式乘多项式的结果是多项式， 积的项数与原多项式的项数相同。
2.单项式分别与多项式的每一项相乘时， 要注意积的各项符号的确定： 同号相乘得正，异号相乘得负
3.不要出现漏乘现象，运算要有顺序。
一:计算：
用单项式分别去乘多项式的 每一项，再把所得的积相加。
你能用字母表示这一结论吗？
m(a+b＋c) = ma+mb＋mc
思路：单×多
转化 分配律
单×单
例题: 计算： （1）(- 2a) • (2a 2 - 3a + 1)
= (- 2a) • 2a 2 +(- 2a) •( - 3a)+(- 2a) • 1
2.
12×
2 3
-
3 4
+
5 6
=
12×2 3
+
12×
-
3 4
+
12×5 6
=9
小明读<哈利·波特与火焰杯>这 本书，第一天读了2x页，第二天 读了y页,第三天读的页数是前两 天读的总页数的a倍，小明第三