湍流强度计算公式

FLUENT边界条件（2）—湍流设置（fluent教材—fluent入门与进阶教程于勇第九章）Fluent：湍流指定方法（Turbulence Specification Method）2009-09-16 20:50使用Fluent时，对于velocity inlet边界，涉及到湍流指定方法（Turbulence Specification Method），其中一项是Intensity and Hydraulic Diameter （强度和水利直径），本文对其进行论述。

其下参数共两项，（1）是Turbulence Intensity，确定方法如下：I=0.16/Re_DH^0.125 (1)其中Re_DH是Hydraulic Diameter（水力直径）的意思，即式(1)中的雷诺数是以水力直径为特征长度求出的。

雷诺数Re_DH=u×DH/υ(2)u为流速，DH为水利直径，υ为运动粘度。

水利直径见（2）。

（2）水利直径水力直径是水力半径的二倍，水力半径是总流过流断面面积与湿周之比。

水力半径R＝A/X (3)其中，A为截面积（管子的截面积）＝流量/流速X为湿周(字面理解水流过各种形状管子外圈湿一周的周长)例如：方形管的水利半径R=ab/2(a+b)水利直径DH=2×R (4)举例如下：如果水流速度u=10m/s，圆形管路直径2cm，水的运动粘度为1×10-6 m2/s。

则DH=2×3.14*r^2/(2*3.14*r)=2*3.14*0.01^2/(3.14*0.02)=0.01 r为圆管半径Re_DH=u×DH/υ=10*0.02/10e-6=20000I=0.16/Re_DH^0.125=0.16/20000^0.125=0.0463971424017634≈5%水力半径：润湿周长横截面积=h r ， 水力直径：h h r 4D =对圆管而言，管道直径和水力直径是一回事。

Fluent 笔记在选择网格的时候，你应该考虑下列问题：● 初始化的时间● 计算花费● 数值耗散网格质量对计算精度和稳定性有很大的影响。

网格质量包括：节点分布，光滑性，以及歪斜的角度（skewness ）。

体积为负值表示一个或多个单元有不正确的连接。

通常说来我们可以用Iso-Value Adaption 确定负体积单元，并在图形窗口中察看它们。

进行下一步之前这些负体积必须消除。

对于轴对称算例，在x 轴下方的节点数将被列出。

对于轴对称算例来说x 轴下方是不需有节点的，这是因为轴对称单元的体积是通过旋转二维单元体积得到的，如果x 轴下方有节点，就会出现负体积。

修改网格网格被读入之后有几种方法可以修改它。

你可以标度和平移网格，可以合并和分离区域，创建或切开周期性边界。

除此之外，你可以在区域内记录单元以减少带宽。

还可以对网格进行光滑和交换处理。

并行处理时还可以分割网格。

注意：不论你何时修改网格，你都应该保存一个新的case 文件和数据文件（如果有的话）。

如果你还想读入旧的data 文件，也要把旧的case 保留，因为旧的数据无法在新的case 中使用。

湍流强度I 定义为相对于平均速度u_avg 的脉动速度u^'的均方根。

小于或等于1%的湍流强度通常被认为低强度湍流，大于10%被认为是高强度湍流。

完全发展的管流的核心的湍流强度可以用下面的经验公式计算：()81Re 16.0-≅'≡H D avg u u I对于压力入口边界条件你需要输入如下信息● 驻点总压● 驻点总温● 流动方向● 静压● 湍流参数（对于湍流计算）● 辐射参数(对于使用P-1模型、DTRM 模型或者DO 模型的计算)● 化学组分质量百分比(对于组分计算)● 混合分数和变化(对于PDF 燃烧计算)● 程序变量(对于预混和燃烧计算)● 离散相边界条件(对于离散相的计算)● 次要相的体积分数(对于多相计算)速度入口边界条件需要输入下列信息● 速度大小与方向或者速度分量。

FLUENT边界条件使用范围速度入口边界条件：用于定义流动入口边界的速度和标量。

压力入口边界条件：用来定义流动入口边界的总压和其它标量。

质量流动入口边界条件：用于已知入口质量流速的可压缩流动。

在不可压缩流动中不必指定入口的质量流，因为当密度是常数时，速度入口边界条件就确定了质量流条件。

压力出口边界条件：用于定义流动出口的静压（在回流中还包括其它的标量）。

当出现回流时，使用压力出口边界条件来代替质量出口条件常常有更好的收敛速度。

压力远场边界条件：用于模拟无穷远处的自由可压缩流动，该流动的自由流马赫数以及静态条件已知。

这一边界类型只用于可压缩流。

质量出口边界条件：用于在解决流动问题之前，所模拟的流动出口的流速和压力的详细情况还未知的情况。

在流动出口是完全发展的时候这一条件是适合的，这是因为质量出口边界条件假定出了压力之外的所有流动变量正法向梯度为零。

不适合于可压缩流动。

进风口边界条件：用于模拟具有指定的损失系数、流动方向以及周围（入口）环境总压和总温的进风口。

进气扇边界条件：用于模拟外部进气扇，它具有指定的压力跳跃、流动方向以及周围（进口）总压和总温。

通风口边界条件：用于模拟通风口，它具有指定的损失系数以及周围环境（排放处）的静压和静温。

排气扇边界条件：用于模拟外部排气扇，它具有指定的压力跳跃以及周围环境（排放处）的静压。

速度入口边界条件速度入口边界条件用于定义流动速度以及流动入口的流动属性相关标量。

这一边界条件适用于不可压缩流，如果用于可压缩流它会导致非物理结果，这是因为它允许驻点条件浮动。

应该注意不要让速度入口靠近固体妨碍物，因为这会导致流动入口驻点属性具有太高的非一致性。

压力入口边界条件压力入口边界条件用于定义流动入口的压力以及其它标量属性。

它即可以适用于可压缩流，也可以用于不可压缩流。

压力入口边界条件可用于压力已知但是流动速度和/或速率未知的情况。

这一情况可用于很多实际问题，比如浮力驱动的流动。

流体阻力计算公式流体阻力计算公式是用来计算物体在流体中受到的阻力的数学公式。

阻力是物体运动过程中对物体运动的削减和消耗力的一种表现。

在流体力学中，流体阻力的计算公式可以分为不同情况，包括层流阻力和湍流阻力的计算。

下面将分别介绍这两种情况下的流体阻力计算公式。

1.层流阻力计算公式：在层流条件下，当物体在流体中运动时，流体与物体之间存在着黏滞性，因此会产生黏滞阻力。

黏滞阻力的大小与流体的粘度、物体的速度、物体的形状以及液体的密度等有关。

对于小球在粘性流体中的运动，斯托克斯提出了斯托克斯定律，该定律描述了小球在稳态下受到的阻力与速度和粘度之间的关系。

根据斯托克斯定律，小球的阻力F可表示为：F = 6πηrv其中，η为流体的粘度，r为物体的半径，v为物体在流体中的速度。

对于平板在层流条件下的运动，平板的阻力F与速度v的关系可表示为：F=0.664ηLv其中，η为流体的粘度，L为平板的特征长度，v为平板在流体中的速度。

2.湍流阻力计算公式：在湍流条件下，流体运动的速度会发生不规则变化，流体的粘度无法抗拒流动，因此湍流阻力的计算比层流阻力要复杂一些。

湍流阻力的大小与流体的密度、流体运动的速度、物体的形状以及流体的运动状态等因素有关。

根据韦伯引理，湍流阻力F与速度v的关系可以表示为：F=0.5ρC_dAv^2其中，ρ为流体的密度，C_d为流体阻力系数，A为物体的横截面积，v为物体在流体中的速度。

需要注意的是，湍流阻力系数C_d是个与物体形状和流体运动状态等有关的无量纲常数，对于不同的物体和不同的流体运动状态，在计算时需要通过实验测量或者经验公式来确定其数值。

总结：流体阻力计算公式根据流体的运动状态以及物体的形状和特性的不同可分为层流阻力和湍流阻力计算公式。

层流阻力在小球和平板的情况下可以通过斯托克斯定律来计算，而湍流阻力则需要引入流体阻力系数来计算。

流体阻力的计算对于设计物体运动、流体流动和工程应用等领域非常重要，而实际的计算涉及到更复杂的情况，需要通过数值模拟、实验与经验公式结合来完成。

湍流方程及其解法湍流是大自然中常见的一种流动方式。

在许多工业和实际应用中，湍流的存在和发展是无法避免的。

因此，对湍流的研究一直是科学家们关注的焦点。

湍流方程是描述湍流流动的一组偏微分方程，其解法对于理解湍流现象有着重要意义。

一、湍流方程湍流方程可以分为两类：一类是基于平均场的运动方程，另一类是直接模拟湍流流动的Navier-Stokes方程。

对于前者，一般采用雷诺平均方法（RANS）来进行模拟。

RANS假设湍流流动可以用时间平均值表示，这样可以把湍流流动分解成平均流动和湍流脉动两部分。

根据这个假设，可以得到雷诺平均Navier-Stokes方程和湍流模型。

其中，湍流模型根据不同的湍流流动特性和物理机制，采用不同的假设和公式来描述湍流脉动。

对于后者，Navier-Stokes方程是描述流体运动基本规律的方程之一。

它由连续性方程和动量方程组成。

其中，连续性方程描述了连续体的质量守恒定律，动量方程描述了连续体的动量守恒定律。

由于这两个方程的非线性和耦合性，Navier-Stokes方程的解析解一直未能得到，只能采用数值方法对其进行求解。

二、湍流模拟方法对于湍流方程的求解，可以采用直接数值模拟（DNS）、大涡模拟（LES）和雷诺平均模拟（RANS）等方法。

DNS是直接模拟湍流流动的方法，它对Navier-Stokes方程进行数值求解，没有对湍流进行平均处理。

由于DNS需要对所有长度尺度的湍流涡进行精细模拟，所以计算量非常大。

目前，DNS主要用于理论研究和小规模问题的模拟。

LES是基于湍流能量分布的假设，将大尺度涡流动进行模拟，小尺度涡流动则采用湍流模型进行预测。

这样可以降低计算量，同时也能够保留一定的湍流结构。

LES主要用于工程实践问题的模拟。

RANS则是利用时间平均方法对流场进行模拟。

RANS基于湍流统计平均，采用不同的湍流模型来描述湍流脉动。

RANS计算量比DNS和LES小得多，但精度也相对较低，主要用于工程大规模问题的模拟。

光伏与风资源评估中几个重要参数及其定义风速：空气相对于地球某一固定地点的运动速率，风速的常用单位是m/s 。

平均风速：一定时段内，数次观测的风速的平均值。

一般表达方式为[m/s]。

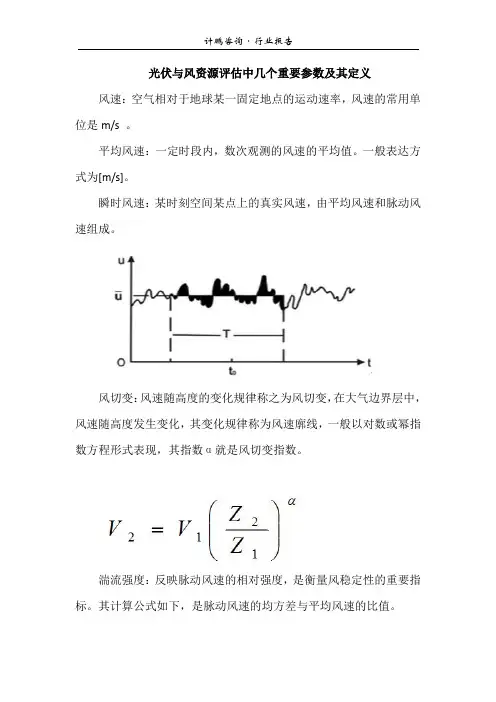
瞬时风速：某时刻空间某点上的真实风速，由平均风速和脉动风速组成。

风切变：风速随高度的变化规律称之为风切变，在大气边界层中，风速随高度发生变化，其变化规律称为风速廓线，一般以对数或幂指数方程形式表现，其指数α就是风切变指数。

湍流强度：反映脉动风速的相对强度，是衡量风稳定性的重要指标。

其计算公式如下，是脉动风速的均方差与平均风速的比值。

风能：空气运动的动能
风功率密度：单位面积时，风能具有的功率（W/m2），计算公式如下：
风向：指风的方向，通常用16个方位来表示风向。

按照月或者年统计风向变化的平均值，可以绘制出风向玫瑰图。

50年一遇最大风速：风电场在设计时，从安全性和经济性综合考虑，要合理确定一个设计最大风速，这个值是要间隔相当时期才会出现的（间隔的时期为重现期），根据全国风能资源评价技术规定，风电场设计的重现期为50年，即50年一遇最大风速。

代表年风资源数据：根据风电场附近气象站等长期测站观测数据，用相关分析的方法将验证后的风电场测风数据订正为一套反映风电场长期平均水平的代表性数据，即风电场代表年的逐小时风速风向数据。

湍流量的指定方法湍流强度I定义为相对于平均速度u_avg的脉动速度u^'的均方根。

小于或等于1%的湍流强度通常被认为低强度湍流，大于10%被认为是高强度湍流。

从外界，测量数据的入口边界，你可以很好的估计湍流强度。

例如：如果你模拟风洞试验，自由流的湍流强度通常可以从风洞指标中得到。

在现代低湍流风洞中自由流湍流强度通常低到0.05%。

.对于内部流动，入口的湍流强度完全依赖于上游流动的历史，如果上游流动没有完全发展或者没有被扰动，你就可以使用低湍流强度。

如果流动完全发展，湍流强度可能就达到了百分之几。

完全发展的管流的核心的湍流强度可以用下面的经验公式计算：例如，在雷诺数为50000是湍流强度为4%湍流尺度l是和携带湍流能量的大涡的尺度有关的物理量。

在完全发展的管流中，l被管道的尺寸所限制，因为大涡不能大于管道的尺寸。

L和管的物理尺寸之间的计算关系如下：l07L=.0其中L为管道的相关尺寸。

因子0.07是基于完全发展湍流流动混合长度的最大值的，对于非圆形截面的管道，你可以用水力学直径取代L。

如果湍流的产生是由于管道中的障碍物等特征，你最好用该特征长度作为湍流长度L而不是用管道尺寸。

注意：公式Ll07=并不是适用于所有的情况。

它只是在大多.0数情况下得很好的近似。

对于特定流动，选择L和l的原则如下：对于完全发展的内部流动，选择强度和水力学直径指定方法，并在水力学直径流场中指定L=D_H。

对于旋转叶片的下游流动，穿孔圆盘等，选择强度和水力学直径指定方法，并在水力学直径流场中指定流动的特征长度为L 对于壁面限制的流动，入口流动包含了湍流边界层。

选择湍流强度和长度尺度方法并使用边界层厚度d_99来计算湍流长度尺度l，在湍流长度尺度流场中输入l=0.4d_99这个值湍流粘性比m_t/m直接与湍流雷诺数成比例(Re_t?k^2/(e n))。

Re_t在高湍流数的边界层，剪切层和完全发展的管流中是较大的(100到1000)。

湍流强度计算公式湍流强度是流体中湍流运动的强度的量度，它描述了流场中速度的变化情况。

湍流强度计算公式根据不同的流动情况和流体性质会有所不同。

首先，湍流强度可以通过湍流能量来计算。

湍流能量是指湍流流场中速度的涨落所具有的能量，可以通过速度的方差来表示。

设流体速度的涨落值为u’，则湍流能量的方差即为：(E)=<(u’)^2>其中，<>表示概率平均。

这个计算公式可以用于流体中的湍流强度的计算。

其次，湍流强度可以利用雷诺应力来计算。

雷诺应力是湍流流场中涡旋产生的应力。

在湍流中，涡旋的产生是由于流体速度的涨落造成的。

涡旋与速度的关系可以通过雷诺应力的定义来描述：(τ)=〈(u’v’)〉其中，(u’v’)表示涡旋速度的涨落值。

利用雷诺应力的计算公式可以求得湍流流场中的湍流强度。

此外，湍流强度还可以利用湍流耗散率来计算。

湍流耗散率描述了湍流运动中能量的损耗情况。

在湍流中，能量的损耗是由于速度梯度引起的。

(ε)=〈(∂u/∂x)²+(∂v/∂y)²+(∂w/∂z)²〉其中，∂/∂x、∂/∂y和∂/∂z分别表示速度在x、y和z方向上的梯度。

湍流耗散率的计算公式可以用来计算流场中的湍流强度。

最后，湍流强度还可以通过湍流流场中湍流的特征尺度来计算。

湍流的特征尺度描述了湍流流体运动的空间或时间特征。

湍流的特征尺度可以通过湍流流场中的能量谱密度函数来获得。

从能量谱密度函数中可以计算出湍流流场中的湍流强度。

综上所述，湍流强度的计算公式可以根据不同的流动情况和流体性质采用不同的方法来求解。

这些方法包括利用湍流能量、雷诺应力、湍流耗散率和湍流的特征尺度等。

通过计算湍流强度，可以更好地了解流体中湍流运动的特性和行为。

在流场的入口、出口和远场边界上，用户需要定义流场的湍流参数。

在FLUENT 中可以使用的湍流模型有很多种。

在使用各种湍流模型时，哪些变量需要设定，哪些不需要设定以及如何给定这些变量的具体数值，都是经常困扰用户的问题。

本小节只讨论在边界上设置均匀湍流参数的方法，湍流参数在边界上不是均匀分布的情况可以用型函数和UDF（用户自定义函数）来定义，具体方法请参见相关章节的叙述。

在大多数情况下，湍流是在入口后面一段距离经过转捩形成的，因此在边界上设置均匀湍流条件是一种可以接受的选择。

特别是在不知道湍流参量的分布规律时，在边界上采用均匀湍流条件可以简化模型的设置。

在设置边界条件时，首先应该定性地对流动进行分析，以便边界条件的设置不违背物理规律。

违背物理规律的参数设置往往导致错误的计算结果，甚至使计算发散而无法进行下去。

在Turbulence Specification Method （湍流定义方法）下拉列表中，可以简单地用一个常数来定义湍流参数，即通过给定湍流强度、湍流粘度比、水力直径或湍流特征长在边界上的值来定义流场边界上的湍流。

下面具体讨论这些湍流参数的含义，以保证在设置模型时不出现违背流动规律的错误设置：（1）湍流强度（Turbulence Intensity）湍流强度I的定义为：I=Sqrt(u’*u’+v’*v’+w’*w’)/u_avg(8-1)上式中u',v' 和w' 是速度脉动量，u_avg是平均速度。

湍流强度小于1％时，可以认为湍流强度是比较低的，而在湍流强度大于10％时，则可以认为湍流强度是比较高的。

在来流为层流时，湍流强度可以用绕流物体的几何特征粗略地估算出来。

比如在模拟风洞试验的计算中，自由流的湍流强度可以用风洞的特征长度估计出来。

在现代的低湍流度风洞中，自由流的湍流强度通常低于0.05%。

内流问题进口处的湍流强度取决于上游流动状态。

如果上游是没有充分发展的未受扰流动，则进口处可以使用低湍流强度。

基于fluent的兴波阻力计算本文主要研究内容本文的工作主要涉及小型航行器在近水面航行时的绕流场及兴波模拟和阻力的数值模拟两个方面。

在阅读大量文献资料的基础上，通过分析、比较上述领域所采用的理论和方法，针对目前需要解决的问题，选择合理的方法加以有机地综合运用。

具体工作体现在以下几个方面：1．本人利用FLUENT软件的前处理软件GAMBIT自主建立简单回转体潜器模型，利用FLUENT求解器进行计算，得出在不同潜深下潜器直线航行的绕流场、自由面形状及阻力系数的变化情况。

2．通过对比潜器在不同潜深情况下的阻力系数，论证了增加近水面小型航行器的深度可以有效降低阻力。

通过对模型型线的改动，为近水面小型航行器的型线设计提供了一定的参考。

通过改变附体形状和位置计算了附体对阻力的影响程度，为附体的优化设计提供了一定的依据。

计算模型航行器粘性流场的数值计算理论水动力计算数学模型的建立根据流体运动时所遵循的物理定律，基于合理假设（连续介质假设）用定量的数学关系式表达其运动规律，这些表达式成为流体运动的数学模型，它们是对流体运动的一种定量模型化，称为流体运动控制方程组。

根据控制方程组，结合预先给定的初始条件和边界条件，就可以求解反映流体运动的变量值，从而实现对流体运动的数值模拟预报，形成分析报告。

基于连续介质假设的流体力学中流体运动必须满足要遵循的物理定律:1) 质量守恒定律2）动量守恒定律3）能量守恒定律4）组分质量守恒方程针对具体研究的问题，有选择的满足上述四个定律。

船体的粘性不可压缩绕流运动，如果不考虑水温对水物理性质的影响，水的密度和分子粘性系数都是常数，同时没有能量的转换，就仅仅需要满足质量守恒定律、动量守恒定律。

在满足这些定律下所建立的数学模型称为Navier-Stokes方程。

另外，自由液面的存在也需要建立合适的数学模型。

本文是利用FLUENT 进行数值模拟，而软件里面关于自由液面模拟是用界面追踪方法的一种－流体体积法（VOF）,基于该方法所建立的数学模型称为流体体积分数方程。

尾流衰减常数和湍流强度的比值是气象和环境科学领域中一个重要的参数，它对于风能利用、大气扩散和空气污染传输等方面具有重要的影响。

在这篇文章中，我们将探讨尾流衰减常数和湍流强度的比值的意义、计算方法以及其在实际应用中的意义。

1. 尾流衰减常数和湍流强度的定义尾流衰减常数是指风场中各个高度处风速的衰减速率，它描述了风速在空间中的递减情况。

湍流强度是指风场中湍流的强度，它描述了风场中湍流的程度。

2. 尾流衰减常数和湍流强度的计算尾流衰减常数和湍流强度的计算通常需要通过实地观测或数值模拟来获取。

在实地观测中，可以通过使用测风塔或风能利用装置来获取风速和湍流强度的数据，然后利用相关的统计方法来计算尾流衰减常数和湍流强度的比值。

3. 尾流衰减常数和湍流强度的比值的物理意义尾流衰减常数和湍流强度的比值反映了风场中风速的变化与湍流程度的关系，它对于风能利用和大气扩散等方面具有重要的影响。

较小的尾流衰减常数和湍流强度的比值意味着风速在空间中递减缓慢且湍流程度较小，适合用于风能利用；而较大的尾流衰减常数和湍流强度的比值则意味着风速在空间中递减较快且湍流程度较大，适合用于大气扩散。

4. 尾流衰减常数和湍流强度的比值在实际应用中的意义尾流衰减常数和湍流强度的比值在风能利用、大气扩散和空气污染传输等方面具有重要的应用价值。

在风能利用中，合理选择尾流衰减常数和湍流强度的比值可以提高风能利用装置的效率；在大气扩散和空气污染传输中，可以通过尾流衰减常数和湍流强度的比值来评估大气扩散的情况和空气污染的传输程度。

尾流衰减常数和湍流强度的比值是一个重要的参数，它对于风能利用、大气扩散和空气污染传输等方面具有重要的意义。

通过对尾流衰减常数和湍流强度的比值的计算和分析，可以为相关领域的研究和实际应用提供重要的参考依据。

在气象和环境科学领域中，尾流衰减常数和湍流强度的比值对于风能利用、大气扩散和空气污染传输等方面具有重要的影响。

在风能利用方面，理解尾流衰减常数和湍流强度的比值可以帮助优化风力发电场的布局，提高风能利用效率。

湍流强度如何计算1、湍流强度定义：速度波动的均⽅根与平均速度的⽐值⼩于1%为低湍流强度，⾼于10%为⾼湍流强度。

计算公式：I=0.16*(re)^(-1/8)式中：I—湍流强度，re—雷诺数2、湍流尺度及⽔⼒直径湍流尺度（turbulence length)：a physical quantity related to the size of the large eddies that contain the energy in turbulent flows。

通常计算⽅式：l=0.07LL为特征尺度，可认为是⽔⼒直径，因数0.07是基于充分发展的湍流管流中的混合长度的最⼤值。

湍流参数的选取：（1）充分发展的内部流动，选取湍流强度(intensity)和⽔⼒直径(hydraulic diameter)（2）导流叶⽚流动、穿孔板等流动，选取强度(intensity)和长度尺度(length scale)。

（3）四周为壁⾯引起湍流边界层的流动，选取强度（intensity)和长度尺度(length scale)，使⽤边界层厚度，特征长度等于0.4倍边界层，输⼊此值到turbulence length scale中。

3、湍动能（Kinetic energy)湍流模型中最常见的物理量（k）。

利⽤湍流强度估算湍动能：k=3/2*(u*I)^2其中：u—平均速度，I—湍流强度4、湍流耗散率(turbulent disspipation rate)湍流耗散率即传说中的ε。

通常利⽤k和湍流尺度l估算ε计算公式为：cu通常取0.09，k为湍动能，l为湍流尺度5、⽐耗散率ω计算公式为：ω=k^0.5/(l*c^0.25)式中：k为湍动能，l为湍流尺度，c为经验常数，常取0.09。

湍流长度尺度计算
湍流长度尺度是描述湍流中涡旋大小的一个重要参数，通常用L来表示。

计算湍流长度尺度的方法有多种，其中一种常用的方法是利用湍流能谱函数来计算。

具体计算方法如下：
1. 首先需要获取湍流能谱函数E(k)，其中k为波数。

2. 然后计算湍流能量的积分值，即E_total = ∫E(k)dk，其中积分范围为0到无穷大。

3. 计算湍流能量的积分值的一半，即E_half = E_total / 2。

4. 找到能谱函数E(k)中满足E(k) = E_half的波数k值。

5. 计算湍流长度尺度L = 2π/ k。

需要注意的是，湍流长度尺度的计算结果可能会受到实验条件、流场特性等因素的影响，因此在实际应用中需要进行适当的修正和调整。