材料力学 孙训方 习题答案

材料力学第五版课后答案[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa m kNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(lxr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=，2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+-du d d ldx 122-=，)()(22)(221212udu d d l du u d d l x A dx -⋅-=⋅-=ππ 因此，)()(2)()(202100udu d d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214dEd Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。

材料力学第五版课后答案[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F kF l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa m kNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(l xr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=，2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+-du d d ldx 122-=，)()(22)(221212udu d d l du u d d l x A dx -⋅-=⋅-=ππ 因此，)()(2)()(202100udu d d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214dEd Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。

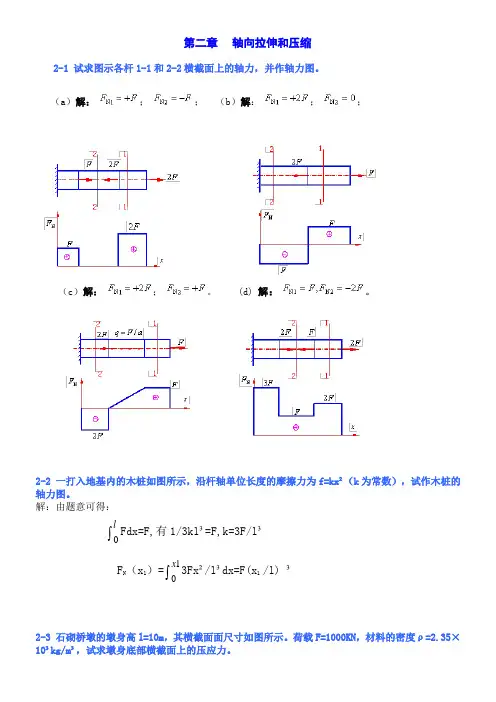
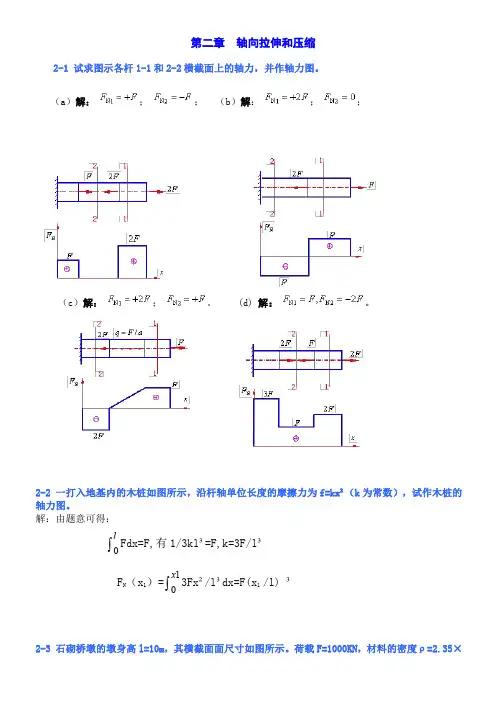
第二章 轴向拉伸和压缩2-1 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a ）解：；； （b ）解：；；（c ）解： ； 。

(d) 解： 。

2-2 一打入地基内的木桩如图所示，沿杆轴单位长度的摩擦力为f=kx ²（k 为常数），试作木桩的轴力图。

解：由题意可得：⎰0lFdx=F,有1/3kl ³=F,k=3F/l ³F N （x 1）=⎰1x 3Fx ²/l ³dx=F(x 1 /l) ³2-3 石砌桥墩的墩身高l=10m ，其横截面面尺寸如图所示。

荷载F=1000KN ，材料的密度ρ=2.35×10³kg/m ³，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa mkN A N 34.071.33914.9942.31042-≈-=-==σ2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm ×8mm 的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE 和EG 横截面上的应力。

解：=1） 求内力 取I-I 分离体得（拉）取节点E 为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

孙训方材料力学第五版课后习题目答案第二章 轴向拉伸和压缩2-1 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a ）解：；； （b ）解：；；（c ）解： ； 。

(d) 解： 。

[习题2-3] 石砌桥墩的墩身高m l 10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：gAl F G F N ρ--=+-=)( 2-3图)(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa m kN A N 34.071.33914.9942.31042-≈-=-==σ2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm ×8mm 的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE 和EG 横截面上的应力。

解：=1） 求内力 取I-I 分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdxl d =∆，⎰=∆lx EA F l 0)(lxr r r r =--121，22112112dx l d d r x l r rr +-=+⋅-=，2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx ld d du d x l d dd 2)22(12112-==+-dud d ldx 122-=，)()(22)(221212udu d d l du u dd l x Adx -⋅-=⋅-=ππ因此，)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π2-10 受轴向拉力F 作用的箱形薄壁杆如图所示。

材料力学（I）第五版(孙训芳编)甘肃建筑职业技术学院长安大学土木工程材料力学温习材料材料力学第五版课后答案(孙训芳编)4-1试求图示各梁中指定截面上的剪力和弯矩 a （5）=h （4）001100110002222200022132241111223121140,222233RA RB S S q F F a q a q F q a a q aa M q a q a q aF M q a a q a a q a ----==⨯==-⨯==-⨯⨯⨯===⨯-⨯⨯⨯=b （5）=f （4）4-2试写出以下各梁的剪力方程和弯矩方程，并作剪力图和弯矩图 a （5）=a （4）b（5）=b（4）f（5）=f（4）4-3试利用载荷集度，剪力和弯矩间的微分关系做以下各梁的弯矩图和剪力e和f题）（e）（f）（h）4-4试做以下具有中间铰的梁的剪力图和弯矩图。

4-4 （b） 4-5 （b）4-5．依照弯矩、剪力与荷载集度之间的关系指出以下玩具和剪力图的错误的地方，并更正。

4-6．已知简支梁的剪力图如下图，试做梁的弯矩图和荷载图，梁上五集中力偶作用。

4-6（a） 4-7（a）4-7．依照图示梁的弯矩图做出剪力图和荷载图。

4-8用叠加法做梁的弯矩图。

4-8（b） 4-8（c）4-9．选择适合的方式，做弯矩图和剪力图。

4-9（b） 4-9（c）4-104-14．长度l=2m的均匀圆木，欲锯做Fa=的一段，为使锯口处两头面开裂最小，硬是锯口处弯矩为零，现将圆木放在两只锯木架上，一只锯木架放在圆木一段，试求另一只锯木架应放位置。

x=4-184-19M=30KN 4-214-234-254-284-294-334-364-355-25-35-75-155-225-23 选22a工字钢5-246-4 6/((233))A l Fl EA ∆=+6-127-3-55mpa 。

-55mpa7-4[习题7-3] 一拉杆由两段沿n m -面胶合而成。

材料力学（I）第五版(孙训芳编)甘肃建筑职业技术学院长安大学土木工程材料力学复习材料材料力学第五版课后答案(孙训芳编)4-1试求图示各梁中指定截面上的剪力和弯矩 a （5）=h （4）001100110002222200022132241111223121140,222233RA RB S S q F F a q a q F q a a q aa M q a q a q aF M q a a q a a q a ----==⨯==-⨯==-⨯⨯⨯===⨯-⨯⨯⨯=b （5）=f （4）4-2试写出下列各梁的剪力方程和弯矩方程，并作剪力图和弯矩图 a （5）=a （4）b（5）=b（4）f（5）=f（4）4-3试利用载荷集度，剪力和弯矩间的微分关系做下列各梁的弯矩图和剪力e和f题）（e）（f）（h）4-4试做下列具有中间铰的梁的剪力图和弯矩图。

4-4 （b） 4-5 （b）4-5．根据弯矩、剪力与荷载集度之间的关系指出下列玩具和剪力图的错误之处，并改正。

4-6．已知简支梁的剪力图如图所示，试做梁的弯矩图和荷载图，梁上五集中力偶作用。

4-6（a） 4-7（a）4-7．根据图示梁的弯矩图做出剪力图和荷载图。

4-8用叠加法做梁的弯矩图。

4-8（b） 4-8（c）4-9．选择合适的方法，做弯矩图和剪力图。

4-9（b） 4-9（c）4-104-14．长度l=2m的均匀圆木，欲锯做Fa=0.6m的一段，为使锯口处两端面开裂最小，硬是锯口处弯矩为零，现将圆木放在两只锯木架上，一只锯木架放在圆木一段，试求另一只锯木架应放位置。

x=0.4615m4-184-19M=30KN 4-214-234-254-284-294-334-364-355-25-35-75-155-225-246-4 6/((233))A l Fl EA ∆=+6-127-3-55mpa 。

-55mpa7-4[习题7-3] 一拉杆由两段沿n m -面胶合而成。

Microsoft Corporation孙训方材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：；；（b）解：；；（c）解：；。

(d)解：。

返回2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：返回2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：返回2-4 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EG横截面上的应力。

解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。

解：2-6(2-8) 一木桩柱受力如图所示。

柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。

如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。

解：（压）（压）返回2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。

试求杆横截面上的应力与材料的弹性模量E。

解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。

已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。

解：横截面上的线应变相同因此返回2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。

材料力学课后习题答案（孙训方版）1. 弹簧的力学性质1.1 弹簧的刚度计算弹簧的刚度（k）是描述弹簧力学性质的重要指标，它代表了单位位移产生的恢复力大小。

弹簧的刚度可以通过以下公式计算：k = (F - F₀) / Δx其中，k为弹簧的刚度，F为施加在弹簧上的力，F₀为弹簧未受力时的长度恢复力，Δx为弹簧的位移。

1.2 弹簧势能的计算当弹簧发生位移时，由于其具有弹性而储存了一定的势能。

弹簧势能可以通过以下公式计算：Ep = (1/2) * k * Δx²其中，Ep为弹簧的势能，k为弹簧的刚度，Δx为弹簧的位移。

2. 常见材料的力学性质2.1 钢材的力学性质钢材是一种常见的工程材料，具有优良的力学性质。

以下是一些钢材的力学性质参数：钢材种类弹性模量（E）屈服强度（σy）抗拉强度（σu）延伸率（ε）铁石炭钢200 GPa250 MPa400 MPa20%不锈钢190 GPa210 MPa400 MPa15%高速钢235 GPa250 MPa500 MPa10%钢材的弹性模量决定了其在受力时的变形程度，屈服强度代表着材料开始发生可见整体变形的临界点，抗拉强度则反映了材料能够承受的最大应力。

延伸率则描述了材料可以在破坏之前发生高强度塑性变形的能力。

2.2 铝材的力学性质铝材是一种轻质金属材料，在航空航天、交通运输等领域有着广泛的应用。

以下是一些铝材的力学性质参数：铝材种类弹性模量（E）屈服强度（σy）抗拉强度（σu）延伸率（ε）6061-T669 GPa240 MPa260 MPa12%7075-T671 GPa470 MPa510 MPa9%2024-T673 GPa450 MPa500 MPa10%铝材相较于钢材，具有更轻的密度和较好的耐腐蚀性能。

弹性模量较低导致了铝材的刚度较小，而抗拉强度较高则提供了较好的耐久性能。

3. 弯曲应变的计算当受力物体发生弯曲时，会导致内部产生应变。

弯曲应变的计算可以使用公式：ε = (M * h) / (E * I)其中，ε为弯曲应变，M为弯矩，h为截面到受力轴的距离，E为弹性模量，I为截面的惯性矩。

材料力学第五版孙训方版课后习题答案[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(l xr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=，2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+- du d d l dx 122-=，)()(22)(221212udud d l du u d d lx A dx -⋅-=⋅-=ππ因此，)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。

材料力学课后习题答案（孙训方版）第一题题目一个长方形木框架，水平放置在水平地面上。

长框架的外尺寸为$30cm \\times 50cm$，它的截面尺寸为$3cm \\times 5cm$。

假设木框架的密度为0.8g/gg3。

求木框架的质量和总体积。

解答1.首先计算木框架的质量。

木框架的质量可以通过密度和体积来计算，即$质量 = 密度 \\times 体积$。

–密度：0.8g/gg3–体积：$30cm \\times 50cm \\times （3cm \\times 5cm）$2.接下来计算木框架的总体积。

木框架的总体积可以通过长方体的体积公式来计算，即$总体积 = 长 \\times 宽\\times 高$。

–长：30gg–宽：50gg–高：$3cm \\times 5cm$第二题题目一根长度为g的不可拉伸绳子的一端固定在墙上，另一端悬挂着一个长度为g的细杆。

绳子与杆之间的接触点到杆的一端的距离为g。

当绳子受到的拉力为g时，细杆的上升高度为多少？解答1.首先计算杆的上升高度。

当绳子受到拉力g时，杆会上升一定的高度。

杆的上升高度可以通过应变和材料的形变关系来计算，即$上升高度 = \\frac{F}{EA}$。

–F：绳子受到的拉力–E：材料的弹性模量–A：杆的截面积2.接下来计算杆的截面积。

杆的截面积可以通过杆的形状和尺寸计算，即$截面积 = \\pi r^2$。

–r：杆的半径–杆的形状为圆柱体，半径可以通过细杆的长度g和绳子与杆之间的距离g计算，即$r = \\sqrt{l^2 -a^2}$。

第三题题目一根长为g的不可拉伸绳子的一端固定，另一端挂着一个重物。

当重物受到的重力为g g时，绳子的张力为多少？解答1.首先计算绳子的张力。

绳子的张力可以通过平衡条件来计算，即g g=g g。

–F_t：绳子的张力–F_g：重物受到的重力第四题题目一根长为g的绳子悬挂在两个固定点之间，中间有一个重物。

当重物悬挂在中间位置时，绳子受到的张力为g。

材料力学I第五版孙训方版课后习题答案2-2 解由题意可得2-3 解墩身底面的轴力为2-3图墩身底面积因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

2-7图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解取长度为截离体（微元体）。

则微元体的伸长量为，，，，，因此，2-10 受轴向拉力F作用的箱形薄壁杆如图所示。

已知该材料的弹性常数为，试求C与D两点间的距离改变量。

解式中，，故，，2-11 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量，已知，，，。

试求C点的水平位移和铅垂位移。

变形协调图受力图2-11图解（1）求各杆的轴力以AB杆为研究对象，其受力图如图所示。

因为AB平衡，所以，，由对称性可知，，（2）求C 点的水平位移与铅垂位移。

A点的铅垂位移B点的铅垂位移1、2、3杆的变形协（谐）调的情况如图所示。

由1、2、3杆的变形协（谐）调条件，并且考虑到AB为刚性杆，可以得到C点的水平位移C点的铅垂位移2-12 图示实心圆杆AB和AC在A点以铰相连接，在A点作用有铅垂向下的力。

已知杆AB和AC的直径分别为和，钢的弹性模量。

试求A点在铅垂方向的位移。

解（1）求AB、AC杆的轴力以节点A为研究对象，其受力图如图所示。

由平衡条件得出 a b a b联立解得；（2）由变形能原理求A点的铅垂方向的位移式中，；；故2-13 图示A 和B两点之间原有水平方向的一根直径的钢丝，在钢丝的中点C加一竖向荷载F。

已知钢丝产生的线应变为，其材料的弹性模量，钢丝的自重不计。

试求（1）钢丝横截面上的应力（假设钢丝经过冷拉，在断裂前可认为符合胡克定律）；（2）钢丝在C点下降的距离；（3）荷载F的值。

解（1）求钢丝横截面上的应力（2）求钢丝在C点下降的距离。

其中，AC和BC各。

（3）求荷载F的值以C结点为研究对象，由其平稀衡条件可得2-15水平刚性杆AB由三根BC,BD和ED支撑，如图，在杆的A端承受铅垂荷载F20KN,三根钢杆的横截面积分别为A112平方毫米，A26平方毫米，A,39平方毫米，杆的弹性模量E210Gpa，求（1）端点A的水平和铅垂位移。

2-2解：由题意可得： 2-3 解：墩身底面的轴力为：g Al F G F N ρ--=+-=)(2-3图墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

2-7图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdxl d =∆，⎰⎰==∆l lx A dxE F dx x EA F l 00)()( lxr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=，2211222)(u d x ld d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+- du d d ldx 122-=，)()(22)(221212udu d d l du u d d l x A dx -⋅-=⋅-=ππ因此，)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π 2-10 受轴向拉力F 作用的箱形薄壁杆如图所示。

已知该材料的弹性常数为ν,E ，试求C 与D 两点间的距离改变量CD ∆。

解：EAFE AF νννεε-=-=-=/'式中，δδδa a a A 4)()(22=--+=，故：δνεEa F 4'-=δνεEa F a a 4'-==∆， δνE F a a a 4'-=-=∆δνE F a a 4'-=，a a a CD 12145)()(243232=+=2-11 图示结构中，AB 为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量GPa E 210=，已知m l 1=，221100mm A A ==，23150mm A =，kN F 20=。

[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F kF l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l 10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa mkNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(lxr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=， 2211222)(u d x l d d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+- du d d l dx 122-=，)()(22)(221212udud d l du u d d lx A dx -⋅-=⋅-=ππ因此，)()(2)()(202100u dud d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π ⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214d Ed Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。