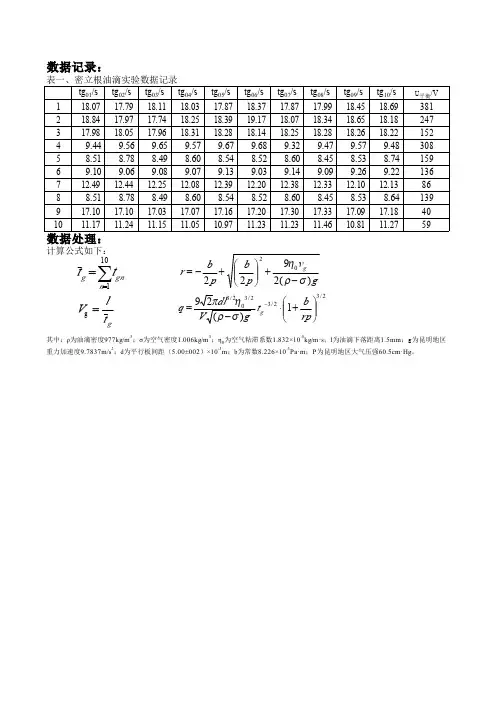
密立根油滴实验原始数据记录表

实验十九密立根油滴实验授课班级：教学课次：授课时间:授课地点：物理实验中心（3S311）授课形式：预习讲授和指导授课要点：理解密立根油滴实验的设计思想、实验方法，测定油滴的带电量，并推算基本电荷值e的大小时间分配：讲授25分钟，学生熟悉仪器等20分钟实验十九密立根油滴美国实验物理学家密立根于1909年设计并完成了密立根油滴实验，该实验证明了电荷的不连续性，任何带电体所带的电荷都是某一最小电荷的整数倍，精确测定了这一基本电荷的数值e=（1.60±0.002）×10-19c。

密立根油滴实验构思巧妙，实验方法简单，可得到精确和稳定的实验结果，是近代物理学史上一个十分重要的实验。

[实验目的]1、正确理解密立根油滴实验的设计思想、实验方法和实验技巧2、测定油滴的带电量，并推算基本电荷值e的大小。

[实验原理]密立根油滴实验主要是测定油滴的带电量，本实验采用平衡测量法来测定油滴所带的电量。

该法使带电油滴在电场中受到电场力的作用，正好与油滴的重力相抵消而达到平衡，据此可以测定该油滴所带的电量。

当油滴从喷雾器的喷嘴喷出时，极小的油滴由于摩擦均已带电。

油滴在平行极板间受重力mg 和静电力dU q作用。

若适当选择电压极性并调节两极板间电压U 的大小，可使两个力达到平衡，即d U q mg =（4-35-1） 由于U 、d 、g 均为已知量，只需测出油滴质量m ，便可求出油滴所带电量q 。

由于油滴质量m 很小，常规的方法难以测定，需用特殊方法来间接测定。

平行极板不加电压U 时，油滴受重力而加速下落，但空气黏滞所引起的阻力与速度成正比，经过一小段距离到达某一速度v 后，重力与阻力平衡，油滴将匀速下落。

由斯托克斯定律知：mg av f r ==πη6（4-35-2）式中，η为空气的黏度系数，a 为油滴半径，数量级为m 610-（由于表面张力的原因，油滴一般为小球形）。

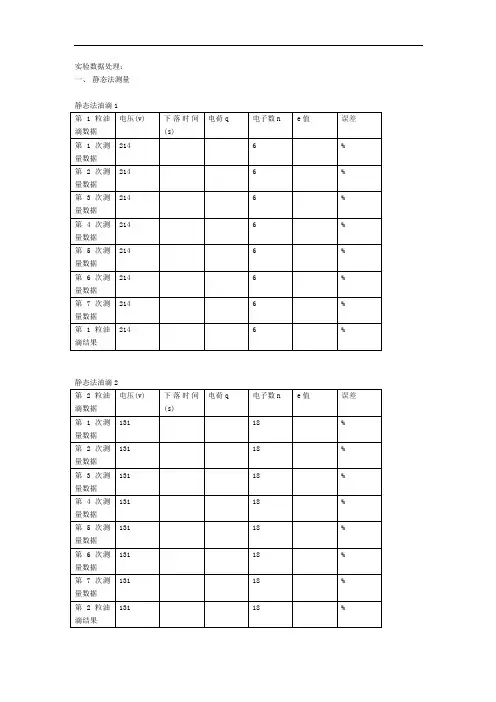
油滴质量为ρπ334a m =（4-35-3） 合并式（4-35-2）和式（4-35-3），得油滴半径为gv a ρη29=（4-35-4） 对于半径小到m 610-的小球，油滴半径接近于空气中气隙的大小，空气介质不能再认为是均匀、连续的，对斯氏定律予以修正，η修正为η'，即pa b+='1ηη（4-35-5）式中，常量cmHg m b ⋅⨯=-61017.6；p 为大气压强，单位为cmHg 。

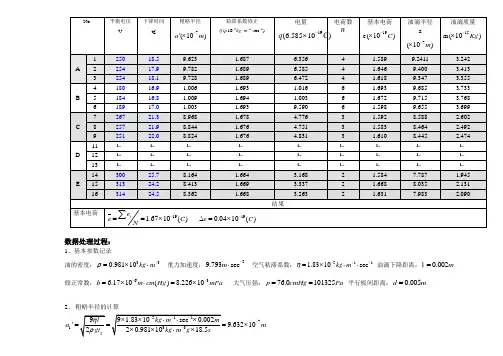
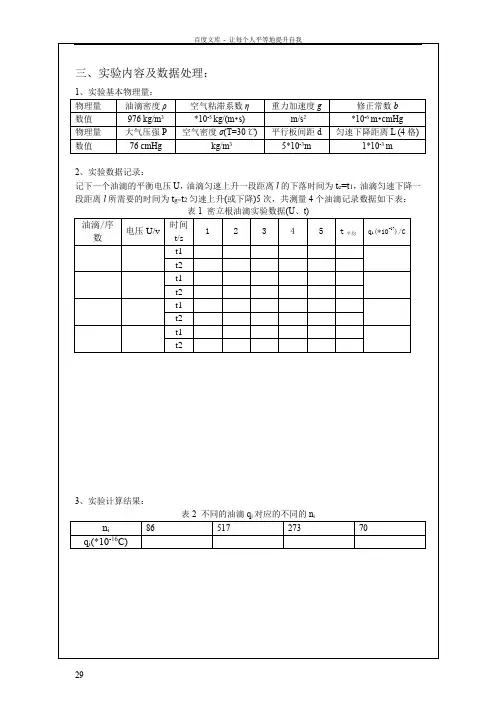
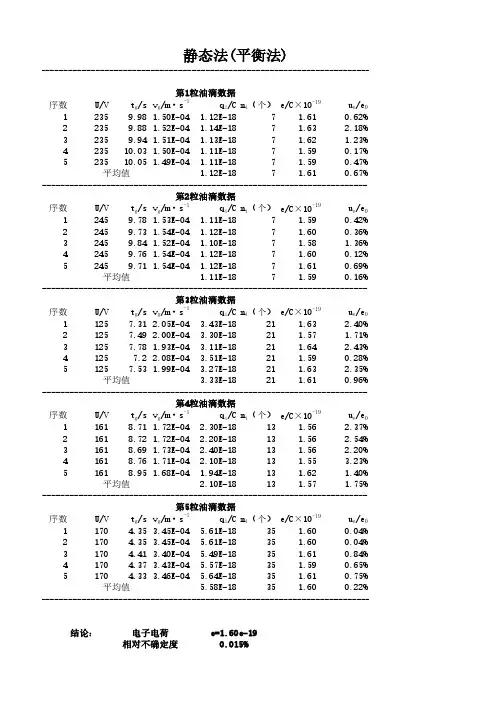
数据处理过程：1、基本参数记录油的密度：330.98110kg m ρ-=⨯⋅ 重力加速度：29.793secm -⋅ 空气粘滞系数：5111.8310sec kg m η---=⨯⋅⋅ 油滴下降距离：0.002m =修正常数：636.1710()8.22610b m cm H g m P a --=⨯⋅=⨯ 大气压强：76.0101325p cm H g P a == 平行板间距离：0.005d m =2、 粗略半径的计算71'9.63210a m -===⨯其他72'9.78210a m -=⨯,73'9.72810a m -=⨯,3、 粘滞系数修正511-5111371 1.8310sec' 1.68710sec8.2261011'1013259.63210kg mkg m b m P aP a P a mηη-------⨯⋅⋅===⨯⋅⋅⨯++⨯⨯其他-5112' 1.68910seckg mη--=⨯⋅⋅，-5113' 1.68910seckg mη--=⨯⋅⋅，4、 各次油滴电荷的电量计算3233''2219111110.0050.002 6.3561018.5250(1)g g ld l dm m q C b V t V t P a ηηη-⎡⎤⎡⎤⎢⎥⎡⎤⨯====⨯⎥⎥⎥⎥⎦⎦⎥+⎦ 其他192 6.58510q C -=⨯，192 6.47210q C -=⨯，5、 用倒算法计算各次电荷数以及基本电荷量（有能力的同学可以用作图法、最大公约数法） 倒算法即已知基本电荷数190 1.6010e -=⨯来验证，电荷的量子性电荷数：[]1911190 6.356101.6010q C n e --⎡⎤⎡⎤⨯==⎢⎥⎢⎥⨯⎣⎦⎣⎦取最近整数取最近整数取最近整数＝ 3.97＝4 基本电荷量：19191116.356101.589104q Ce C n --⨯===⨯其他19224, 1.64610n e C -=⨯＝；19334, 1.61810n e C -=⨯＝；19446, 1.69310n e C -=⨯＝；6、 求出基本电荷最佳值191.6710()iee C N-==⨯∑190.0410()e C -∆==⨯结果为：19(1.670.04)10e C -=±⨯； 2.3%e e E e∆==结果分析：（1） 与标准值的比较001.67 1.604%1.60e e E e --===，而仪器的电压精度，时间精度为1%与结果误差是同等级的，所以实验结果是比较理想的。

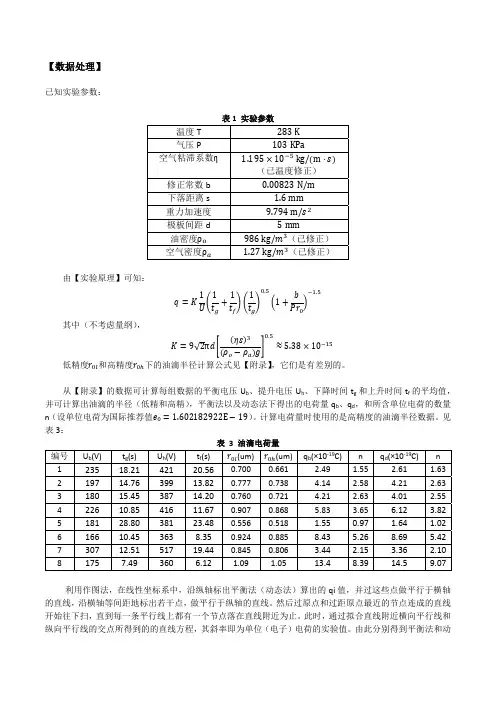
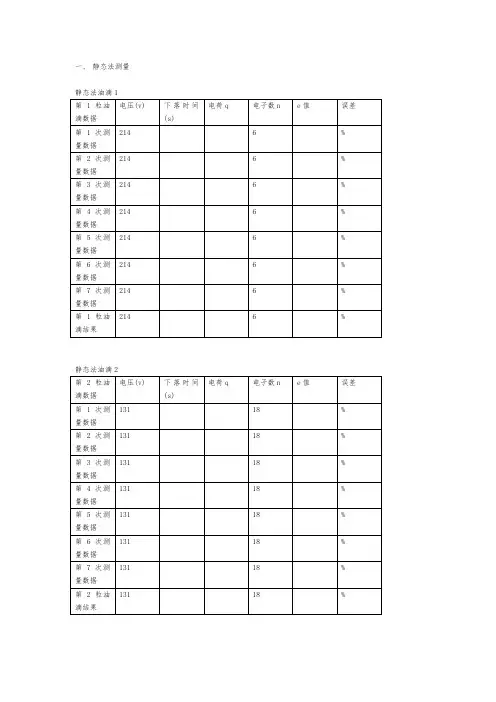
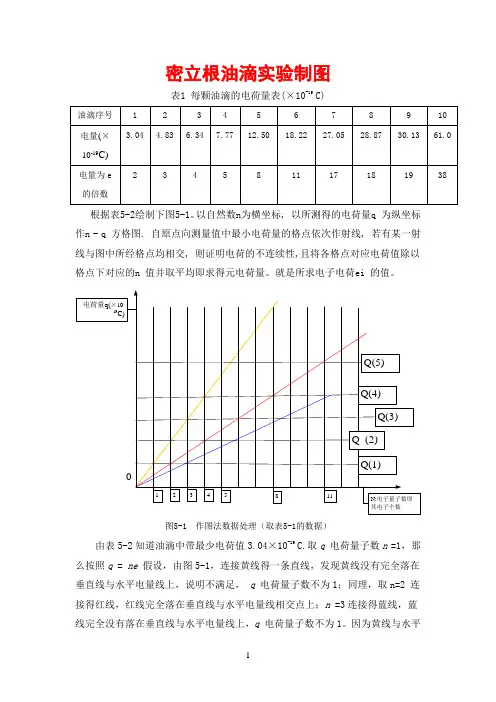
密立根油滴实验制图表1 每颗油滴的电荷量表(×10-19 C)根据表5-2绘制下图5-1。

以自然数n为横坐标, 以所测得的电荷量q 为纵坐标作n - q 方格图. 自原点向测量值中最小电荷量的格点依次作射线, 若有某一射线与图中所经格点均相交, 则证明电荷的不连续性,且将各格点对应电荷值除以格点下对应的n 值并取平均即求得元电荷量。

就是所求电子电荷ei 的值。

图5-1 作图法数据处理（取表5-1的数据）由表5-2知道油滴中带最少电荷值3.04×10-19 C.取q 电荷量子数n =1，那么按照q = ne 假设，由图5-1，连接黄线得一条直线，发现黄线没有完全落在垂直线与水平电量线上，说明不满足， q 电荷量子数不为1；同理，取n=2连接得红线，红线完全落在垂直线与水平电量线相交点上；n =3连接得蓝线，蓝线完全没有落在垂直线与水平电量线上，q 电荷量子数不为1。

因为黄线与水平线上各个相交点近似与各条垂直线重合，应该取的是红线，得出电荷值3.04×10-19 C的n=2，此方法证实了电子的量子化特性，但是估算值与整数的接近程度均不好，甚至相差太远，则此方法误差较大，甚至失效。

如n=4的估算值恰恰应取第3组。

假设根据已知用第3组估算值处理数据,所得的结果1.512 ×10-19 C，与元电荷的公认值e = 1. 602 ×10-19 C 的相对误差超过10%，误差是相当的大,可见无法处理该组实验数据。

5.3 对作图法的改进由上文可以看出, 作图法处理结果中，当q min =3.04×10-19 C 时,根据e的公认值判断可知误差较大，由此可见该方法确实有一定的局限性。

作图法局限性即要求qmin 要有足够的精确度。

若qmin误差较大,则得不到预想的结果。

由于上表选了最小的电荷作qmin，结果是有误差大于10%，针对以上出现的问题，因此取次最小的qi 为新的qmin去作相同的处理。

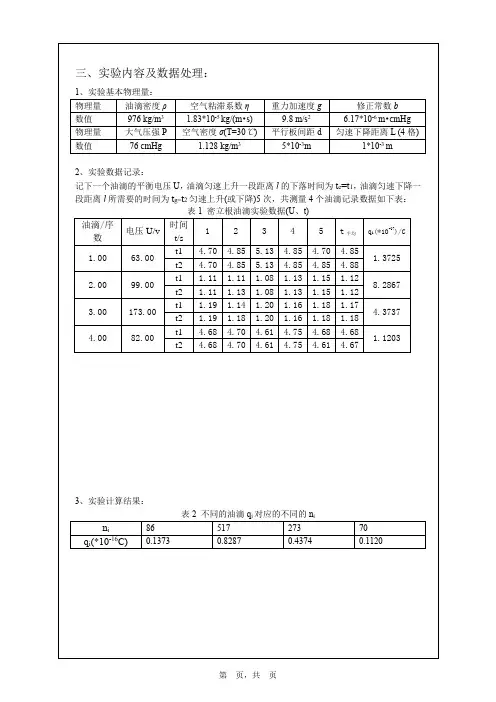
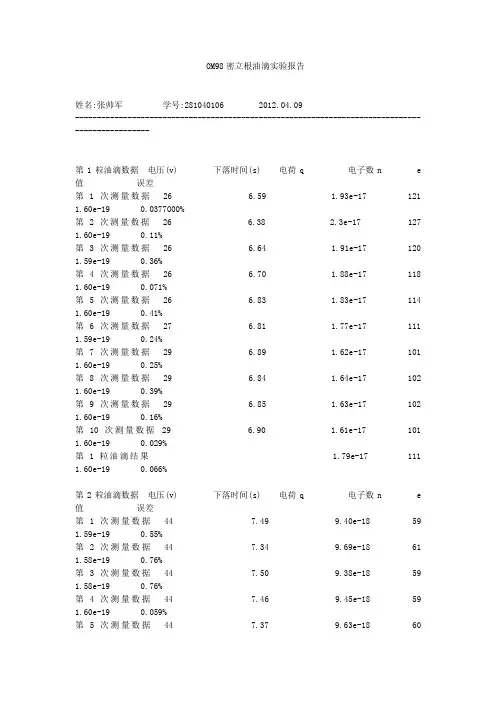
OM98密立根油滴实验报告姓名:张帅军学号:281040106 2012.04.09------------------------------------------------------------------------------------------------第1粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据26 6.59 1.93e-17 121 1.60e-19 0.0377O00%第2次测量数据26 6.38 2.3e-17 127 1.60e-19 0.11%第3次测量数据26 6.64 1.91e-17 120 1.59e-19 0.36%第4次测量数据26 6.70 1.88e-17 118 1.60e-19 0.071%第5次测量数据26 6.83 1.83e-17 114 1.60e-19 0.41%第6次测量数据27 6.81 1.77e-17 111 1.59e-19 0.24%第7次测量数据29 6.89 1.62e-17 101 1.60e-19 0.25%第8次测量数据29 6.84 1.64e-17 102 1.60e-19 0.39%第9次测量数据29 6.85 1.63e-17 102 1.60e-19 0.16%第10次测量数据29 6.90 1.61e-17 101 1.60e-19 0.029%第1粒油滴结果 1.79e-17 111 1.60e-19 0.066%第2粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据44 7.49 9.40e-18 59 1.59e-19 0.55%第2次测量数据44 7.34 9.69e-18 61 1.58e-19 0.76%第3次测量数据44 7.50 9.38e-18 59 1.58e-19 0.76%第4次测量数据44 7.46 9.45e-18 59 1.60e-19 0.059%第5次测量数据44 7.37 9.63e-18 60第6次测量数据44 7.48 9.41e-18 59 1.59e-19 0.35%第7次测量数据44 7.50 9.38e-18 59 1.58e-19 0.76%第8次测量数据44 7.44 9.49e-18 59 1.60e-19 0.47%第9次测量数据44 7.30 9.78e-18 61 1.60e-19 0.071%第10次测量数据44 7.39 9.59e-18 60 1.59e-19 0.16%第2粒油滴结果9.52e-18 59 1.59e-19 0.25%第3粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据29 3.55 4.49e-17 280 1.60e-19 0.14%第2次测量数据29 3.53 4.53e-17 283 1.60e-19 0.052%第3次测量数据29 3.56 4.47e-17 279 1.60e-19 0.075%第4次测量数据29 3.65 4.30e-17 269 1.60e-19 0.096%第5次测量数据29 3.60 4.39e-17 274 1.60e-19 0.17%第6次测量数据29 3.57 4.45e-17 278 1.60e-19 0.0051%第7次测量数据29 3.53 4.53e-17 283 1.60e-19 0.052%第8次测量数据29 3.65 4.30e-17 269 1.60e-19 0.096%第9次测量数据29 3.55 4.49e-17 280 1.60e-19 0.14%第10次测量数据29 3.58 4.43e-17 277 1.60e-19 0.062%第3粒油滴结果 4.44e-17 277 1.60e-19 0.018%第4粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据49 3.17 3.16e-17 197 1.60e-19 0.17%第2次测量数据49 3.20 3.11e-17 195第3次测量数据49 3.29 2.98e-17 186 1.60e-19 0.23%第4次测量数据49 3.24 3.5e-17 191 1.60e-19 0.072%第5次测量数据50 3.21 3.3e-17 190 1.59e-19 0.14%第6次测量数据50 3.25 2.98e-17 186 1.60e-19 0.088%第7次测量数据50 3.27 2.95e-17 184 1.60e-19 0.23%第8次测量数据49 3.25 3.4e-17 190 1.60e-19 0.018%第9次测量数据49 3.17 3.16e-17 197 1.60e-19 0.17%第10次测量数据49 3.28 3.鑖譲00e-17 187 1.60e-19 0.16%第4粒油滴结果 3.5e-17 190 1.60e-19 0.059%第5粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据52 5.81 1.17e-17 73 1.61e-19 0.58%第2次测量数据52 5.76 1.19e-17 74 1.61e-19 0.55%第3次测量数据52 5.75 1.19e-17 75 1.59e-19 0.51%第4次测量数据52 5.80 1.17e-17 74 1.59e-19 0.577O00%第5次测量数据52 5.79 1.18e-17 74 1.59e-19 0.24%第6次测量数据52 5.76 1.19e-17 74 1.61e-19 0.55%第7次测量数据52 5.72 1.20e-17 75 1.60e-19 0.28%第8次测量数据52 5.81 1.17e-17 73 1.61e-19 0.58%第9次测量数据52 5.83 1.17e-17 73 1.60e-19 0.058%第10次测量数据52 5.77 1.18e-17 74 1.60e-19 0.29%第5粒油滴结果 1.18e-17 73 1.60e-19 0.16%第6粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据160 5.05 4.74e-18 30 1.58e-19 1.31%第2次测量数据160 5.02 4.78e-18 30 1.59e-19 0.477O00%第3次测量数据160 4.98 4.84e-18 30 1.61e-19 0.82%第4次测量数据160 5.02 4.78e-18 30 1.59e-19 0.477O00%第5次测量数据160 5.03 4.77e-18 30 1.59e-19 0.71%第6次测量数据160 5.08 4.70e-18 29 1.62e-19 1.16%第7次测量数据160 5.02 4.78e-18 30 1.59e-19 0.477O00%第8次测量数据160 5.09 4.68e-18 29 1.61e-19 0.85%第9次测量数据160 5.14 4.61e-18 29 1.59e-19 0.64%第10次测量数据160 5.05 4.74e-18 30 1.58e-19 1.31%第6粒油滴结果 4.74e-18 29 1.59e-19 0.23%第7粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据27 5.33 2.58e-17 161 1.60e-19 0.29%第2次测量数据27 5.29 2.61e-17 163 1.60e-19 0.21%第3次测量数据27 5.41 2.52e-17 158 1.60e-19 0.11%第4次测量数据27 5.45 2.50e-17 156 1.60e-19 0.027%第5次测量数据27 5.38 2.55e-17 159 1.60e-19 0.11%第6次测量数据27 5.50 2.46e-17 154 1.60e-19 0.086%第7次测量数据27 5.33 2.58e-17 161 1.60e-19 0.29%第8次测量数据27 5.36 2.56e-17 160 1.60e-19 0.056%1.60e-19 0.28%第10次测量数据27 5.42 2.52e-17 157 1.60e-19 0.23%第7粒油滴结果 2.53e-17 158 1.60e-19 0.13%第8粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据30 3.59 4.26e-17 266 1.60e-19 0.17%第2次测量数据30 3.62 4.21e-17 263 1.60e-19 0.032%第3次测量数据30 3.51 4.41e-17 276 1.60e-19 0.068%第4次测量数据30 3.70 4.7e-17 254 1.60e-19 0.16%第5次测量数据30 3.64 4.17e-17 261 1.60e-19 0.047%第6次测量数据30 3.61 4.23e-17 264 1.60e-19 0.076%第7次测量数据30 3.75 3.99e-17 249 1.60e-19 0.11900%第8次测量数据30 3.65 4.16e-17 260 1.60e-19 0.083%第9次测量数据30 3.64 4.17e-17 261 1.60e-19 0.047%第10次测量数据30 3.69 4.9e-17 255 1.60e-19 0.18%第8粒油滴结果 4.18e-17 260 1.60e-19 0.049%第9粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据22 6.02 2.63e-17 164 1.60e-19 0.277O00%第2次测量数据22 5.98 2.66e-17 166 1.60e-19 0.016%第3次测量数据22 5.78 2.80e-17 175 1.60e-19 0.028%第4次测量数据22 5.69 2.87e-17 179 1.60e-19 0.12%第5次测量数据22 5.74 2.83e-17 177 1.60e-19 0.096%1.59e-19 0.14%第7次测量数据22 5.90 2.71e-17 170 1.59e-19 0.29%第8次测量数据22 5.88 2.73e-17 170 1.60e-19 0.23%第9次测量数据22 5.85 2.75e-17 172 1.59e-19 0.15%第10次测量数据22 5.92 2.70e-17 169 1.59e-19 0.22%第9粒油滴结果 2.75e-17 172 1.60e-19 0.035%第10粒油滴数据电压(v) 下落时间(s) 电荷q 电子数n e值误差第1次测量数据90 2.99 1.88e-17 117 1.60e-19 0.41%第2次测量数据90 2.89 1.98e-17 124 1.59e-19 0.19%第3次测量数据90 3.07 1.80e-17 113 1.59e-19 0.14%第4次测量数据90 3.00 1.87e-17 117 1.60e-19 0.095%第5次测量数据90 3.05 1.82e-17 114 1.60e-19 0.023%第6次测量数据90 2.95 1.92e-17 120 1.60e-19 0.058%第7次测量数据90 2.98 1.89e-17 118 1.60e-19 0.076%第8次测量数据90 2.97 1.90e-17 119 1.59e-19 0.25%第9次测量数据90 3.08 1.79e-17 112 1.60e-19 0.25%第10次测量数据90 3.01 1.86e-17 116 1.60e-19 0.25%第10粒油滴结果 1.87e-17 117 1.60e-19 0.022%本次实验最终结果: e=1.60e-19 误差=0.0016%。