【中小学资料】广东省清远市佛冈县龙山镇八年级数学下册 6.3 三角形的中位线学案(无答案)(新版)北师大

北师大版八年级下册数学《6.3 三角形的中位线》说课稿一. 教材分析《6.3 三角形的中位线》这一节内容是北师大版八年级下册数学的重点内容。

在此之前，学生已经学习了三角形的性质、角的计算等基础知识。

本节内容主要介绍了三角形的中位线性质及其应用。

通过对中位线的性质的学习，为学生后续学习三角形相似、解直角三角形等知识打下基础。

二. 学情分析八年级的学生已经具备了一定的几何基础知识，对三角形的性质有一定的了解。

但是，对于三角形中位线的性质及其应用，学生可能还较为陌生。

因此，在教学过程中，需要引导学生通过观察、操作、思考、讨论等方式，逐步发现并理解三角形中位线的性质。

三. 说教学目标1.知识与技能目标：使学生掌握三角形的中位线性质，能够运用中位线性质解决一些简单问题。

2.过程与方法目标：通过观察、操作、思考、讨论等过程，培养学生的空间想象能力、逻辑思维能力和合作交流能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养学生的耐心和毅力，使学生感受到数学的美。

四. 说教学重难点1.教学重点：三角形的中位线性质及其应用。

2.教学难点：三角形中位线性质的证明及其在实际问题中的应用。

五. 说教学方法与手段1.教学方法：采用问题驱动法、合作学习法、引导发现法等。

2.教学手段：多媒体课件、几何画板、黑板、粉笔等。

六. 说教学过程1.导入新课：通过复习三角形的相关知识，引出三角形的中位线，激发学生的学习兴趣。

2.探究中位线性质：引导学生观察、操作、思考，发现三角形中位线的性质。

3.证明中位线性质：分组讨论，引导学生运用已知知识和三角形内角平分线的性质，证明中位线的性质。

4.应用中位线性质：通过例题和练习，让学生学会运用中位线性质解决实际问题。

5.总结与拓展：对本节课的内容进行总结，提出拓展问题，激发学生的学习兴趣。

七. 说板书设计板书设计如下：三角形的中位线性质：三角形的中位线平行于第三边，且等于第三边的一半。

1.求三角形面积2.证明线段平行或相等3.解决实际问题八. 说教学评价本节课结束后，将通过课堂表现、作业完成情况、练习题的正确率等对学生进行评价。

2024北师大版数学八年级下册6.3《三角形的中位线》教学设计一. 教材分析《三角形的中位线》是北师大版数学八年级下册第六章第三节的内容。

本节内容主要介绍三角形的中位线的性质，包括中位线的长度等于它所对的边的一半，以及中位线平行于第三边。

这一节内容是学生学习几何的重要基础，对于培养学生的空间想象能力和逻辑思维能力具有重要意义。

二. 学情分析学生在学习本节内容之前，已经学习了三角形的性质，包括三角形的内角和定理，三角形的边长关系等。

学生对于几何图形的性质有一定的了解，但对于证明过程可能还不够熟练。

此外，学生对于中位线的概念可能还不够熟悉，需要通过实例和练习来加深理解。

三. 教学目标1.知识与技能目标：学生能够理解三角形的中位线的概念，掌握中位线的性质，能够运用中位线的性质解决实际问题。

2.过程与方法目标：通过观察、操作、推理等过程，培养学生的空间想象能力和逻辑思维能力。

3.情感态度与价值观目标：学生能够积极参与课堂活动，克服困难，体验成功，培养对数学的兴趣和自信心。

四. 教学重难点1.教学重点：三角形的中位线的性质，中位线的长度等于它所对的边的一半，中位线平行于第三边。

2.教学难点：证明三角形的中位线平行于第三边，以及证明中位线的长度等于它所对的边的一半。

五. 教学方法1.引导发现法：教师通过提出问题，引导学生观察、思考，发现中位线的性质。

2.几何画板辅助教学：利用几何画板展示几何图形，直观地演示中位线的性质。

3.小组合作学习：学生分组讨论，共同完成练习题，培养学生的合作精神和沟通能力。

六. 教学准备1.教学课件：制作课件，展示三角形的中位线的性质。

2.练习题：准备一些有关三角形中位线的练习题，巩固所学知识。

3.几何画板：准备几何画板软件，用于展示几何图形。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾三角形的基本性质，为新课的学习做好铺垫。

2.呈现（10分钟）教师利用几何画板展示三角形的中位线，引导学生观察中位线的性质，并提出问题，让学生思考。

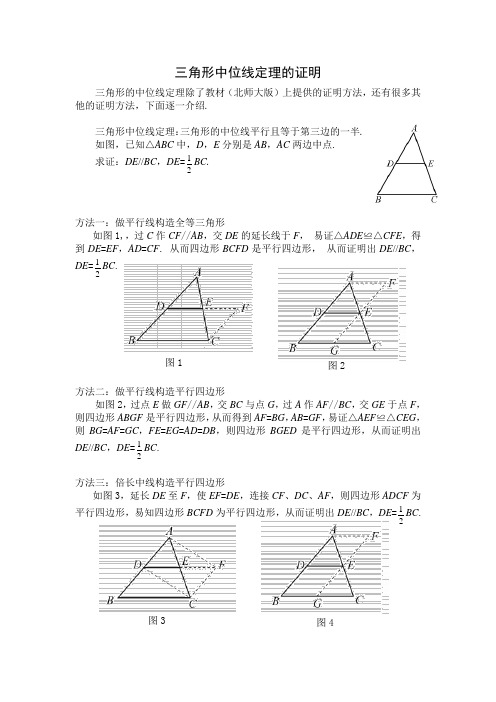
图3 图 4三角形中位线定理的证明三角形的中位线定理除了教材（北师大版）上提供的证明方法，还有很多其他的证明方法，下面逐一介绍.三角形中位线定理：三角形的中位线平行且等于第三边的一半.如图，已知△ABC 中，D ，E 分别是AB ，AC 两边中点.求证：DE //BC ，DE =21BC.方法一：做平行线构造全等三角形如图1,，过C 作CF //AB ，交DE 的延长线于F ， 易证△ADE ≌△CFE ，得到DE =EF ，AD =CF . 从而四边形BCFD 是平行四边形， 从而证明出DE //BC ，DE =21BC .方法二：做平行线构造平行四边形如图2，过点E 做GF //AB ，交BC 与点G ，过A 作AF //BC ，交GE 于点F ，则四边形ABGF 是平行四边形，从而得到AF =BG ，AB =GF ，易证△AEF ≌△CEG ，则BG =AF =GC ，FE =EG =AD =DB ，则四边形BGED 是平行四边形，从而证明出DE //BC ，DE =21BC .方法三：倍长中线构造平行四边形如图3，延长DE 至F ，使EF =DE ，连接CF 、DC 、AF ，则四边形ADCF 为平行四边形，易知四边形BCFD 为平行四边形，从而证明出DE //BC ，DE =21BC .图1 图2B C E D A y xO (0,a)(b,0)(c,0)图5-1 图5-2 图6图7 方法四：取中点截长线如图4，取BC 的中点G ，连接GE 并延长，使得FE =EG ，连接AF .易证△AEF ≌△CEG ，从而得到AF ∥GC ，AF =GC .所以AF ∥BG ，AF =BG ，易知四边形ABGF 和四边形DBFE 是平行四边形，从而证明出DE //BC ，DE =21BC .方法五:作垂线如图5-1，分别过点A ，B ，C 向DE 作垂线，垂足分别为F ，M ，N.易证△ADF ≌△BDM ，△AEF ≌△CEN ，从而MD =DF ，NE =EF ，则MN =2DE ，又由BM =AF =CN ，MB //NC ，得到四边形MBCN 为矩形，所以MN =BC ，从而证明出DE //BC ，DE =21BC . 如图5-2过点D 作DF ⊥BC 于F ，过点E 作EG ⊥BC 于G ，过A 作MN //BC ，分别与FD 、GE 的延长线交于M 、N.显而易见四边形MFGN 为矩形，于是MN =FG ,又可易证△MDA ≌△FDB ，△NEA ≌△GEC ，所以MD =DF =NE =EG ，AM =BF ，AN =CG 得到四边形DFGE 为矩形，FG =21BC .所以DE =FG .从而证明出DE //BC ，DE =21BC .方法六：面积法如图6：连接BE ，CD ，则CD 是△ABC 的中线，所以ABC BDC S S ∆∆=21，同理ABC BEC S S ∆∆=21，所以BEC BDC S S ∆∆=，故DE //BC (两三角形同底等高)，又因为DE 是△ABE 的中线，所以BEC ABE BDE S S S ∆∆∆==2121，故BC DE 21=（△BDE 和△BEC 等高）,从而证明出DE //BC ，DE =21BC . F N A B C D E M F N A B C D E MG方法七：建立平面直角坐标系如图7，建立平面直角坐标系，设A (0,a )，B (b ,0)，C (c ,0)则.2,2,2,2⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛a c E a b D 显然DE 平行于x 轴，即DE //BC .因为BC =c -a ，2-2a c DE = 所以BC DE 21=,从而证明出DE //BC ，DE =21BC . 证明三角形中位线定理的不同方法中有很多值得我们借鉴的地方:1.教材提供的证明是倍长中线做辅助线，本文方法一平行法做辅助线和本文方法五作垂直做辅助线，都能构造全等三角形，但它们都是利用了旋转变换，其本质思想一样.2.教材提供的证明中和方法三的倍长中线，方法四取中点截长线，是解决线段倍分问题的有效途径.3.方法七：建立平面直角坐标系是用代数方法解决几何问题，以后结合函数问题可以进一步探究.。

6．3 三角形的中位线1．掌握中位线的定义以及中位线定理；(重点)2．综合运用平行四边形的判定及中位线定理解决问题．(难点)一、情境导入如图所示，吴伯伯家有一块等边三角形的空地ABC ，已知点E ，F 分别是边AB ，AC 的中点，量得EF ＝5米，他想把四边形BCFE 用篱笆围成一圈放养小鸡，你能求出需要篱笆的长度吗？二、合作探究探究点：三角形的中位线【类型一】 利用三角形中位线定理求线段的长如图，在△ABC 中，D 、E 分别为AC 、BC 的中点，AF 平分∠CAB ，交DE 于点F .若DF ＝3，则AC 的长为( )A.32B ．3C ．6D ．9 解析：∵D 、E 分别为AC 、BC 的中点，∴DE ∥AB ，∴∠2＝∠3，又∵AF 平分∠CAB ，∠1＝∠3，∴∠1＝∠2，∴AD ＝DF ＝3，∴AC ＝2AD ＝6.故选C.方法总结：本题考查了三角形中位线定理，等腰三角形的判定与性质．解题的关键是熟记性质并熟练应用．【类型二】 利用三角形中位线定理求角如图，C 、D 分别为EA 、EB 的中点，∠E ＝30°，∠1＝110°，则∠2的度数为( )A ．80°B ．90°C ．100°D ．110°解析：∵C 、D 分别为EA 、EB 的中点，∴CD 是三角形EAB 的中位线，∴CD ∥AB ，∴∠2＝∠ECD .∵∠1＝110°，∠E ＝30°，∴∠ECD ＝80°，故选A.方法总结：中位线定理牵扯到平行线，所以利用中位线定理中的平行关系可以解决一些角度的计算问题．【类型三】 运用三角形的中位线性质进行证明如图，在△ABC 中，AB ＝5，AC ＝3，点N 为BC 的中点，AM 平分∠BAC ，CM⊥AM ，垂足为点M ，延长CM 交AB 于点D ，求MN 的长．解析：为证MN 为△BCD 的中位线，应根据三线合一，得到DM ＝MC ，即可解决问题． 解：∵AM 平分∠BAC ，CM ⊥AM ，∴AD ＝AC ＝3，DM ＝CM .∵BN ＝CN ，∴MN 为△BCD的中位线，∴MN ＝12(5－3)＝1. 方法总结：当已知三角形的一边的中点时，要注意分析问题中是否有隐含的中点．如已知一个三角形一边上的高又是这边所对的角平分线时，根据“三线合一”可知，这实际上是又告诉了我们一个中点．【类型四】 中位线定理的综合应用如图，E 为平行四边形ABCD 中DC 边的延长线上一点，且CE ＝DC ，连接AE ，分别交BC 、BD 于点F 、G ，连接AC 交BD 于O ，连接OF ，判断AB 与OF 的位置关系和大小关系，并证明你的结论．解析：本题可先证明△ABF ≌△ECF ，从而得出BF ＝CF ，这样就得出了OF 是△ABC的中位线，从而利用中位线定理即可得出线段OF 与线段AB 的关系．解：AB ＝2OF .证明如下：∵四边形ABCD 是平行四边形，∴AB ＝CD ，OA ＝OC .∴∠BAF ＝∠CEF ，∠ABF ＝∠ECF .∵CE ＝DC ，在平行四边形ABCD 中，CD ＝AB ，∴AB ＝CE .∴在△ABF 和△ECF 中，⎩⎪⎨⎪⎧∠BAF ＝∠CEF ，AB ＝CE ，∠ABF ＝∠BCE ，∴△ABF ≌△ECF (ASA)，∴BF ＝CF .∵OA ＝OC ，∴OF 是△ABC 的中位线，∴AB ＝2OF ，AB ∥OF .方法总结：本题综合的知识点比较多，解答本题的关键是判断出OF 是△ABC 的中位线．三、板书设计1．三角形的中位线连接三角形的两边中点的线段叫做三角形的中位线．2．三角形中位线定理三角形的中位线平行于第三边，且等于第三边的一半．本节课，通过实际生活中的例子引出三角形的中位线，又从理论上进行了验证．在学习的过程中，体会到了三角形中位线定理的应用时机．对整个课堂的学习过程进行反思，能够促进理解，提高认识水平，从而促进数学观点的形成和发展，更好地进行知识建构，实现良性循环.。

《三角形的中位线》学习要点
学习目标：
1．掌握三角形的中位线概念和性质．
2．能利用三角形的中位线解决简单的问题．
学习要点：
1．三角形中位线的概念
连结三角形两边中点的线段叫做三角形的中位线。

如下图中，若D、E分别是AB、AC的中点，则DE是△ABC的中位线。

2．与三角形中线的区别
三角形的中线的一个端点是三角形的顶点，另一个端点是对边的中点；而三角形的中位线的两个端点都是三角形的边的中点。

3．三角形中位线的性质
三角形的中位线平行于第三边，并且等于第三边的一半。

1/ 1。

八年级数学下册6.3 三角形的中位线三角形的中位线性质是什么素材（新版）北师大版
编辑整理：
尊敬的读者朋友们：
这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学下册6.3 三角形的中位线三角形的中位线性质是什么素材（新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学下册6.3 三角形的中位线三角形的中位线性质是什么素材（新版）北师大版的全部内容。

三角形的中位线性质是什么
难易度：★★★★
关键词：平行四边形的性质
答案：
三角形的中位线性质:三角形的中位线平行且等于第三边的一半。

【举一反三】
典例：以三角形的三个顶点及三边中点为顶点的平行四边形共有( ）
A、1个
B、2个
C、3个
D、4个
思路引导：根据中位线定理和平行四边形的判定，可知图中有3个平行四边形．
如下图所示，E、F、G分别是△ABC的边AB、边BC、边CA的中点,根据三角形的中位线性质：三角形的中位线平行且等于第三边的一半，可知图中四边形AEFG、BEGF、CFEG都是平行四边形．故选C．
标准答案:C。