四年级下册数学思维拓展训练巧数图形

第 4 讲巧数长（正）方形的个数数图形时要有次序、有条理，才能不遗漏、不重复，一般步骤应是：仔细观察，发现规律，应用规律。

长方形是用“点”或者“线”来数的，而正方形是用“块”来数的。

数长方形的公式：长边上的线段和×宽边上的线段和数正方形的公式：1、一个被划分成m×n 的小正方形的长方形中共可以数出的正方形的个数是：m×n＋（m-1）×（n-1）＋（m-2）×（n-2 ）＋⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯＋1×【n-（m-1）】（其中m<n）2 、当m=n时，即一个划分成n×n=n2个小正方形的正方形中，共可以数出正方形的个数是：n2＋（n-1）2＋⋯⋯⋯⋯⋯⋯⋯⋯＋22＋12典型例题：1、长方形的构成必须有长和宽，下图中有许多长方形，你能数出它们有多少个？分析与解答:因为长方形的构成与长的线段数有关，也与宽的线段数有关，所以数长方形的个数必须要看长与宽两个因素上图上长有6 条线段，即3＋2＋1=6（个）宽边上有3 条线段，即2＋1=3（个）因此，根据数长方形公式：6×3=18（个）答：上图中共有18 个长方形。

2、下图中共有多少个长方形？分析与解答：这道题比例1 横竖都多了一条线，那么长方形的个数明显增多了，利用公式仍然要数出长边上的线段数和宽边上的线段数即长边上的线段和：4＋3＋2＋1＝10 个宽边上的线段和：3+2+1=6个因此根据数长方形公式：10×6=60 个答：上图中共有60 个长方形。

3、下图中共有多少个正方形？分析与解答：我们先来数一数：只含一个正方形的有9个（即3×3=9）；含有4个正方形的有4个（即2×2=4）；含有9 个正方形的有1个通过刚才的数，我们发现图中正方形的个数为1× 1+2× 2+3×3=1+4+9=14 个，以后我们碰到类似的题目可以用这种方法数出正方形的个数。

四年级数学思维训练练习题库作者：王肖峰文章来源：本站原创点击数：4701 更新时间：2009-12-29一、数图形专题简析：我们已经认识了线段、角、三角形、长方形等基本图形，当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。

要想准确地计数这类图形中所包含的某一种基本图形的个数，就需要仔细地观察，灵活地运用有关的知识和思考方法，掌握数图形的规律，才能获得正确的结果。

教学方法：①数图形常用的方法有列举法和分类法，列举时要遵循一定的顺序，前后要统一，否则很可能重复或遗漏；分类时要注意选择恰当的分类标准。

②总的思考方式是关键从基本图形入手，首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新图形，并求出它们的和。

③一般常见的几何平面图形的计数可以根据“线段总条数=点数×（点数-1）÷2”来计算。

④正确、有序、合理、迅速地数出几何图形。

例1：数出下面图中有多少条线段。

思路导航：要正确解答这类问题，需要我们按照一定的顺序来数，做到不重复，不遗漏。

方法一：从图中可以看出，从A点出发的不同线段有3条：AB、AC、AD；从B点出发的不同线段有2条：B C、BD；从C点出发的不同线段有1条：CD。

因此，图中共有3+2+1=6条线段。

方法二：由线段总条数=点数×（点数-1）÷2计算。

因为线段AD间有4个点，所以线段总条数=4×（4－1）÷2例2：数一数下图中有多少个锐角。

思路导航：数角的方法和数线段的方法类似，图中的五条射线相当于线段上的五个点，因此，要求图中有多少个锐角，可根据公式1+2+3……（总射线数－1）求得：1+2+3+4=10（个）例3：数出下面图中共有多少个三角形。

二、巧求周长专题简析：一个图形的周长是指围成它的所有线段的长度和。

我们已经学会了求长方形、正方形这些标准图形的周长，那么怎样运用长方形、正方形的周长计算公式，巧妙地求一些复杂图形的周长呢？对于一些不规则的比较复杂的几何图形，要求它们的周长，我们可以运用平移的方法，把它转化为标准的长方形或正方形，然后再利用周长公式进行计算。

巧数图形（一） (2020-09-14 11:27:12)
分类：课程资源
巧数图形（一）
指点迷津
巧数图形，关键是要仔细观察，发现规律，掌握有次序、有条理地数或计算图形的方法。

巧数图形一般采用逐个计数法或分类计数法；较复杂的组合图形，可采用分步计数法，把图形分成若干组成部分，先数各部分图形的个数，再把结果相加；若能发现规律，也可直接计算图形的个数。

经典例题
数一数，下面图中有多少条线段？
思路导航
方法一，要正确解答这类问题，关键要按一定的顺序数，做到不重、不漏。

从图中可以看出，从A点出发的线段有4条：AB、AC、AD、AE；从B点出发的线段有3条，BC、BD、BE；从C点出发的线段有2条CD、CE；从D点出发的线段只有1条DE。

因此图中共有4 3 2 1=10（条）线段。

4 3 2 1=10（条）
方法二，把图中AB、BC 、CD、DE第四条线段看作基本线段，由两条基本线段组成的线段有AB、BD、CE3条，有三条基本线段组成的有AD、BE2条，由四条线段基本线段组成的只有AE1条。

从而算出线段的总数。

4 3 2 1=10（条）
答：图中有10条线段。

经进一步观察、分析不难发现：采用两种不同的分类计数法却列出了同一道加法算式，且算式中最大的加数等于线段上的总点数减1，线段的总数等于从1开始的若干个连续自然数的和，即线段总数=1 2 3 … （总点数-1）。

这个规律也适用于其他一些图形。

举一反三
数一数，下列图形中各有多少条线段？。

陈淑玲前沿教育中心四年级奥数 姓名： 动漫数学 11级第5讲 巧数图形

1、数出下图中共有多少条线段。

2、 下列各图形中，三角形的个数各是多少？

图(1)中有三角形 (个)。 图(2)中有三角形________(个)。 图(3)中有三角形_________(个)。 图(4)中有三角形_______________(个)。 图(5)中有三角形______________(个)。 3、下列图形中各有多少个三角形？

（1）共有三角形___________________(个)（填算式）。 所以，共有三角形 (个)。 (2)由1个小块组成的三角形有 个；由2个小块组成的三角形有____个； 由3个小块组成的三角形有________个； 由4个小块组成的三角形有_______个； 由6个小块组成的三角形有________个。 所以，共有三角形___________________(个)。 陈淑玲前沿教育中心四年级奥数 姓名： 4、右图中有多少个三角形？

解：假设每一个最小三角形的边长为1。按边的长度来分类计算三角形的个数。边长为1的三角形，从上到下一层一层地数，有 (个)； 边长为2的三角形有______个小三角形组成； 边长为3的三角形有_______(个)；边长为4的三角形有__________ 个。 所以，共有三角形 (个)。 5、数出下页左上图中锐角的个数。

6、在下图中，包含“*”号的长方形和正方形共有多少个 解：包含1小块的有 个；包含2小块的有___个； 包含3小块的有 个；包含4小块的有____个；包含5小块的有 个；包含6小块的有___个；包含8小块的有 个；包含9小块的有____个； 陈淑玲前沿教育中心四年级奥数 姓名： 包含10小块的有____个；包含12小块的有 个；

包含15小块的有___个。 所以共有______(个)。 练习 1.下列图形中各有多少条线段？

2.下列图形中各有多少个三角形？ 3.下列图形中，各有多少个小于180°的角？ 陈淑玲前沿教育中心四年级奥数 姓名： 5.下列图形中各有多少个长方形？

【四年级数学思维拓展】趣味入门—神奇的森林王国（三）------森林生活几何计数1、熟悉几何计数的特点。

2、会按规律解题。

学习各种基本图形的数法。

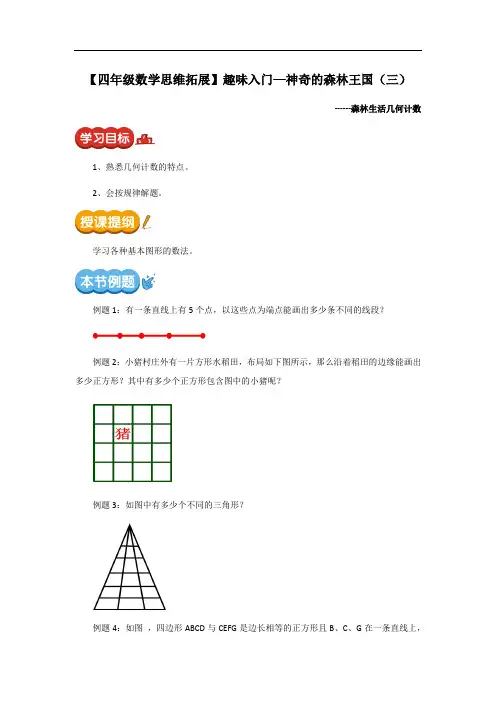
例题1：有一条直线上有5个点，以这些点为端点能画出多少条不同的线段？例题2：小猪村庄外有一片方形水稻田，布局如下图所示，那么沿着稻田的边缘能画出多少正方形？其中有多少个正方形包含图中的小猪呢？例题3：如图中有多少个不同的三角形？例题4：如图，四边形ABCD与CEFG是边长相等的正方形且B、C、G在一条直线上，则图中共有多少个正方形？有多少个等腰直角三角形？（即是该课程的课后测试）1、如图，以点A，B，C，D，E，F，G，H为端点的线段有多少条？2、按图里呈现的规律，第10个图由多少个○组成？3、将一个长5厘米、宽4厘米、高3厘米的长方体的表面刷上红漆，然后将这个长方体切割成棱长为1厘米的小正方体，则任何一面都没有被刷漆的小正方体有多少个？4、图中共有多少个三角形？5、图中有多少条对称轴？1、答案：28条。

由1小段组成的线段有7条；由2小段组成的线段有6条；由3小段组成的线段有5条；由4小段组成的线段有4条；由5小段组成的线段有3条；由6小段组成的线段有2条；由7小段组成的线段有1条。

所以一共有7+6+5+4+3+2+1=28条。

2、答案：27个。

根据规律第10个图每边有10个圆，每个角重复一个，那么三边共有10×3-3=27个圆。

3、答案：6个。

原来是5×4×3的长方体，如果把最外面一层去掉，则剩下3×2×1的长方体，体积为6立方厘米，所以有6个没有刷漆的小正方体。

4、答案：32个。

按规律数。

最小的三角形有16个，其次由两个最小三角形组成的大一些的三角形有8个，由四个最小三角形组成的再大一些的三角形有4个，由八个最小三角形组成的最大的三角形有4个。

则一共有16+8+4+4=32个。

5、答案：6条对称轴。

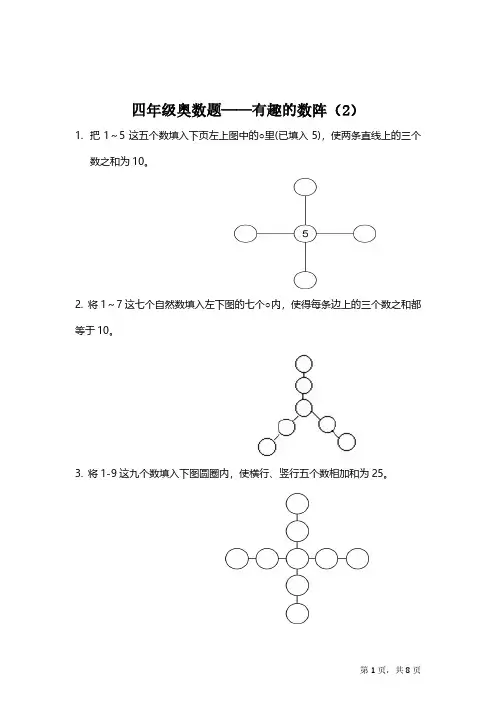
四年级奥数题——有趣的数阵（2）1.把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和为10。

2. 将1～7这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都等于10。

3. 将1-9这九个数填入下图圆圈内，使横行、竖行五个数相加和为25。

4. 将1-9这九个数填入下图圆圈内，使每条线上三个数字相加之和为12。

5. 将1、2、3、4、5、6填在下图中，使每条边上三个数之和等于9。

6. 2～9填入左下图的八个○中，使得每条边上的三个数之和都等于18。

7. 把1～7分别填入左下图中的七个空块里，使每个圆圈里的四个数之和都等于13。

8. 把2～7这六个数填入右上图的○里，使每个圆圈上的四个数之和都等于18。

参考答案1.解：1, 2，3，4，5还剩1，2，3，4这四个数，1+4=2+32. 三条数之和：3×10=301-9数之和：1+2+3+4+5+6+7=28A：（30-28）÷2=1134567八个数分为两组，使每组中两个数字之和：10-1=9则2+7=3+6=4+53. 横行、竖行五数和：25+25=501-9数之和：1+2+3+4+5+6+7+8+9=45 50-45=5 12346789八个数分为两组，使每组中四个数字之和：25-5=20 则1+4+6+9=2+3+7+84. 四条线数之和：12×4=481-9数之和：1+2+3+4+5+6+7+8+9=45A：（48-45）÷3=1剩下的数字平均分成四组，每组数字之和12-1=11所以应为：2+9、3+8、4+7、5+6。

5. 三条边数字总和：3×9=271-6六数之和：1+2+3+4+5+6=21A+B+C=27-21=6故只能选1，2，36. 四条边数字总和：4×18=722-9九数之和：2+3+4+5+6+7+8+9=44 A+B+C+D=72-44=28故只能选,4+9+8+7=287.8.。