小升初数学知识点精选：立体图形

北京小升初数学知识点：立体图形(一)长方体1特征六个面都是长方形(有时有两个相对的面是正方形)。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度区分叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或许正方体6个面的总面积，叫做它的外表积。

2计算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1特征六个面都是正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体可以看作特殊的长方体S表=6a2v=a3(三)圆柱1圆柱的看法圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做正面。

圆柱两个底面之间的距离叫做高。

进一法：实践中，运用的资料都要比计算的结果多一些，因此，要保管数的时分，省略的位上的是4或许比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2计算公式s侧=chs表=s侧+s底×2v=sh/3(四)圆锥1圆锥的看法圆锥的底面是个圆，圆锥的正面是个曲面。

从圆锥的顶点究竟面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点下面，竖直地量出平板和底面之间的距离。

把圆锥的正面展开失掉一个扇形。

v=sh/3(五)球1看法球的外表是一个曲面，这个曲面叫做球面。

球和圆相似，也有一个球心，用O表示。

从球心到球面上恣意一点的线段叫做球的半径，用r表示，每条半径都相等。

经过球心并且两端都在球面上的线段，叫做球的直径，用d表示，每条直径都相等，直径的长度等于半径的2倍，即d=2r。

2计算公式d=2r (编辑：郝梦恬)。

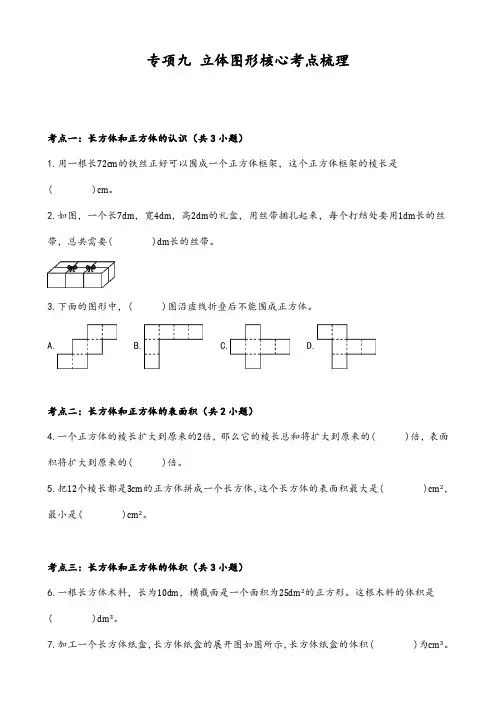
专项九立体图形核心考点梳理考点一：长方体和正方体的认识（共3小题）1.用一根长72cm的铁丝正好可以围成一个正方体框架，这个正方体框架的棱长是( )cm。

2.如图，一个长7dm，宽4dm，高2dm的礼盒，用丝带捆扎起来，每个打结处要用1dm长的丝带，总共需要( )dm长的丝带。

3.下面的图形中，( )图沿虚线折叠后不能围成正方体。

A. B. C. D.考点二：长方体和正方体的表面积（共2小题）4.一个正方体的棱长扩大到原来的2倍，那么它的棱长总和将扩大到原来的( )倍，表面积将扩大到原来的( )倍。

5.把12个棱长都是3cm的正方体拼成一个长方体，这个长方体的表面积最大是( )cm2，最小是( )cm2。

考点三：长方体和正方体的体积（共3小题）6.一根长方体木料，长为10dm，横截面是一个面积为25dm2的正方形。

这根木料的体积是( )dm3。

7.加工一个长方体纸盒，长方体纸盒的展开图如图所示，长方体纸盒的体积( )为cm3。

8.一块长方体木料，当它的高减少2dm后，表面积减少72dm2，刚好成为一个正方体。

这个正方体的表面积是( )dm2，体积是( )dm3。

考点四：体积和体积单位、容积和容积单位、体积（容积）单位间的进率及单位换算（共2小题）9.在下面的( )里填上适当的单位。

(1)集装箱的体积大约是80( )。

(2)中国的陆地面积约是960万( )。

(3)游泳池的占地面积约为1500( )，最多可盛水4500( )。

10.在下面的括号里填上合适的数。

0.16dm3=( )mL4080dm3=( )m3400mL=( )L1.08L=( )mL考点五：求不规则物体的体积和观察物体（共3小题）11.根据下图信息，可知黑球的体积是( )立方厘米。

12.一个长方体容器的底面是正方形，容器中水的高度是1dm，如果放入3个体积一样的鸡蛋后（鸡蛋完全浸没在水中），水面高度上升了1cm且无水溢出，要求一个鸡蛋的体积，只需要再知道( )即可。

小升初备考：数学知识点之立体图形立体图形(一)长方体1特征六个面都是长方形(有时有两个相对的面是正方形)。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6个面的总面积，叫做它的表面积。

2计算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1特征六个面都是正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体可以看作特殊的长方体2计算公式S表=6a2v=a3(三)圆柱1圆柱的认识圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比计算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2计算公式s侧=chs表=s侧+s底×2v=sh/3(四)圆锥1圆锥的认识圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

2计算公式v=sh/3(五)球1认识球的表面是一个曲面，这个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心并且两端都在球面上的线段，叫做球的直径，用d 表示,每条直径都相等,直径的长度等于半径的2倍，即d=2r。

2计算公式d=2r小升初二轮复习全攻略 | 小学期末考试（上册）试卷汇编小学1—6年级语数英知识要点归纳 |中外名著读后感大全。

第三节 立体图形小学梳理小学阶．段，我们主要学习的立体图形有长方体、正方体、圆柱、圆锥。

研究了各个立体图形的特征和表面积、体积的计算方法。

通过对物体的实际观察，使我们了解到从不同方向观察物体，所看到一、立体图形的特征 1、 长方体长方体有6个面，6个面一般都是长方形(也有可能相对的2个面是正方形)，长方体每一组相对的2个面形状相同、大小相等。

长方体有8个顶点、12条棱，每一组互相平行的4 条棱(相对的棱)的长度相等。

我们把相交于一个顶点的三条棱分别叫作这个长方体的长、宽、高。

2. 正方体正方体有6个面，6个面都是正方形，且面积相等。

正方体有8个顶点、l2条棱，12 条棱的长度相等。

有时我们也把正方体看成是长、宽、高都相等的长方体。

3、 圆柱圆柱由两个底面和一个曲面组成。

上、下两个底面是相等的两个圆，两个底面之间的距离叫作高，圆柱有无数条高。

把圆柱的侧面沿高展开后得到一个长方形(或正方形)，长方形的长相当于圆柱的底面周长，长方形的宽相当于圆柱的高。

4、 圆锥圆锥有一个顶点、一个曲面和一个圆形的底面。

从顶点到底面圆心的距离就是圆锥的高，圆锥只有一条高。

二、立体图形的表面积 1. 表面积的意义一个立体图形所有面的面积的和叫作这个立体图形的表面积。

2. 表面积的计算方法(1) 长方体的表面积：长方体6个面的面积的和就是这个长方体的表面积。

长方体的表面积计算公式：:S=(ab+ah+b)×2(2) 正方体的表面积：正方体6个面的面积的和就是这个正方体的表面积。

正方体的表面积计算公式： S =6a²(3)圆柱的表面积：两个底面的面积与一个侧面面积的和就是这个圆柱的表面积。

圆柱的表面积计算公式： S 底=S N +S 底×2(其中 S N =Cℎ)进一法：在实际生产中，使用的材料都要比计算的结果多一些，因此，在保留得数的时候，即使被省略的尾数的最高位上的数是4或者比4小，都要向前一位进1。

书山有路勤为径，学海无涯苦作舟
小升初数学立体图形知识点归纳
(一)长方体
1 特征
六个面都是长方形(有时有两个相对的面是正方形)。

相对的面面积相等，12 条棱相对的4 条棱长度相等。

有8 个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6 个面的总面积，叫做它的表面积。

2 计算公式
s=2(ab+ah+bh)
V=sh
V=abh
(二)正方体
1 特征
六个面都是正方形
六个面的面积相等
12 条棱，棱长都相等
有8 个顶点
正方体可以看作特殊的长方体
2 计算公式
S 表=6a2
v=a3。

小升初数学复习重点大全：立体图形（一）长方体1特点六个面差不多上长方形（有时有两个相对的面是正方形）。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6个面的总面积，叫做它的表面积。

2运算公式s=2（ab+ah+bh）V=shV=abh（二）正方体1特点六个面差不多上正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体能够看作专门的长方体2运算公式S表=6a2v=a3（三）圆柱1圆柱的认识圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比运算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2运算公式s侧=chs表=s侧+s底×2v=sh/3（四）圆锥1圆锥的认识圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

2运算公式v=sh/3（五）球1认识球的表面是一个曲面，那个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心同时两端都在球面上的线段，叫做球的直径，用d表示，每条直径都相等，直径的长度等于半径的2倍，即d=2r。

与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。

金代元好问《示侄孙伯安》诗云：“伯安入小学，颖悟专门貌，属句有夙性，说字惊老师。

”因此看，宋元时期小学教师被称为“老师”有案可稽。

清代称主考官也为“老师”，而一样学堂里的先生则称为“教师”或“教习”。

2019小升初数学立体图形知识点详解小升初数学是学习生涯的关键阶段，为了能够使同学们在数学方面有所建树，下面为大家分享小升初数学立体图形知识点，供大家参考!（一）立体图形【认识、表面积、体积】一、长方体、正方体都有6个面，12条棱，8个顶点。

正方体是特殊的长方体。

二、圆柱的特征：一个侧面、两个底面、无数条高。

三、圆锥的特征：一个侧面、一个底面、一个顶点、一条高。

四、表面积：立体图形所有面的面积的和，叫做这个立体图形的表面积。

五、体积：物体所占空间的大小叫做物体的体积。

容器所能容纳其它物体的体积叫做容器的容积。

六、圆柱和圆锥三种关系：①等底等高：体积1︰3②等底等体积：高1︰3③等高等体积：底面积1︰3七、等底等高的圆柱和圆锥：①圆锥体积是圆柱的1/3，②圆柱体积是圆锥的3倍，③圆锥体积比圆柱少2/3，④圆柱体积比圆锥多2倍。

八、等底等高的圆柱和圆锥：锥1、差2、柱3、和4。

九、立体图形公式推导：【1】圆柱的侧面展开后得到一个什么图形?这个图形的各部分与圆柱有何关系?(圆柱侧面积公式的推导过程)①圆柱的侧面展开后一般得到一个长方形。

②长方形的长相当于圆柱的底面周长，长方形的宽相当于圆柱的高。

③因为：长方形面积=长×宽，所以：圆柱侧面积=底面周长×高。

④圆柱的侧面展开后还可能得到一个正方形。

⑤正方形的边长=圆柱的底面周长=圆柱的高。

【2】我们在学习圆柱体积的计算公式时，是把圆柱转化成以前学过的一种立体图形(近似的)进行推导的，请你说出这种立体图形的名称以及它与圆柱体有关部分之间的关系?①把圆柱分成若干等份，切开后拼成了一个近似的长方体。

②长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高。

③因为：长方体体积=底面积×高，所以：圆柱体积=底面积×高。

即：V=Sh。

【3】请画图说明圆锥体积公式的推导过程?①找来等底等高的空圆锥和空圆柱各一只。

②将圆锥装满沙子，倒入圆柱中，发现三次正好装满，将圆柱里的沙子倒入圆锥中，发现三次正好倒完。

必备小升初数学知识点之立体图形为了能帮助广大小学生朋友们提高数学成绩和提升数学思维能力，下面为大家分享小升初数学知识点之立体图形，希望对大家有所帮助!立体图形(一)长方体1特征六个面都是长方形(有时有两个相对的面是正方形)。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6个面的总面积，叫做它的表面积。

2计算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1特征六个面都是正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体可以看作特殊的长方体2计算公式S表=6a2v=a3(三)圆柱1圆柱的认识圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比计算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2计算公式s侧=chs表=s侧+s底×2v=sh/3(四)圆锥1圆锥的认识圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

2计算公式v=sh/3(五)球1认识球的表面是一个曲面，这个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心并且两端都在球面上的线段，叫做球的直径，用d 表示，每条直径都相等，直径的长度等于半径的2倍，即d=2r。

2计算公式d=2r以上是为大家分享的小升初数学知识点之立体图形，希望大家认真学习哦！。

26.立体图形的体积知识要点梳理一、体积和容积1．体积：物体所占空间的大小叫做物体的体积。

2．容积：容器所能容纳物体的体积叫做容积。

容积单位一般用体积单位。

当容器所容纳的物体是液体时，常用升、毫升作单位。

（注：容积的计算方法跟体积的计算方法相同，但要从容器的里面量。

）二、立体图形的体积计算公式考点精讲分析典例精讲考点1方体和正方体的体积【例1】在一个长、宽、高分别是30厘米、25厘米、60厘米的长方体的箱子里，最多能装进棱长为1分米的立方体（）个。

A．45 B．30 C．36 D．72【精析】把这个长方体箱子的长、宽、高分别换算成分米是3分米、2.5分米、6分米，这个箱子一层长可以装进3个，宽只能装进2个棱长1分米的立方体，高可以装进6个，因此只能装进（3×2×6）＝36个。

【答案】 C【归纳总结】注意，此题容易出现的错误是不考虑实际，用这个箱子的容积除以每个立方体的体积。

考点2圆柱的体积【例2】下图是一根空心钢管，求它所用钢材的体积。

【精析】此题考查空心圆柱体积的求法。

根据空心圆柱的体积＝大圆柱的体积－小圆柱的体积计算即可。

【答案】 3.14×［（1.22）2－（0.62）2］×2.5＝2.1195（立方米）答：它所用钢材的体积是2．1195立方米。

【例3】有一种饮料瓶的瓶身呈圆柱形（不包括瓶颈），容积是20升。

瓶中装有一些饮料，正放时饮料高度为20cm，倒放时空余部分高度为5cm，问瓶中现有饮料（）升。

【精析】正放和倒放时，瓶中液体的体积不变，即空余部分体积相等。

【答案】20×［20÷（20＋5）］＝16（升）答：瓶中现有饮料16升。

【归纳总结】无论是正放还是倒放瓶子的饮料和瓶子的体积不变，所以它们的空余部分总是不变的。

考点2 圆锥的体积【例4】一个圆锥形沙堆，底面积是8平方米，高是1．5米。

用这堆沙在5米宽的路上铺2厘米厚，能铺多少米？【精析】沙子都铺在路面上后的形状，是一个宽5米、厚2厘米的近似长方体。

北京小升初数学知识点复习：立体图形北京小升初数学知识点复习：立体图形（一）长方体1特点六个面差不多上长方形（有时有两个相对的面是正方形）。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6个面的总面积，叫做它的表面积。

2运算公式s=2（ab+ah+bh）V=shV=abh（二）正方体1特点六个面差不多上正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体能够看作专门的长方体2运算公式S表=6a2v=a3（三）圆柱1圆柱的认识圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比运算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2运算公式s侧=chs表=s侧+s底×2v=sh/3（四）圆锥1圆锥的认识圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

2运算公式v=sh/3（五）球1认识球的表面是一个曲面，那个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心同时两端都在球面上的线段，叫做球的直径，用d表示，每条直径都相等，直径的长度等于半径的2倍，即d=2r。

2运算公式家庭是幼儿语言活动的重要环境，为了与家长配合做好幼儿阅读训练工作，小孩一入园就召开家长会，给家长提出早期抓好幼儿阅读的要求。

我把幼儿在园里的阅读活动及阅读情形及时传递给家长，要求小孩回家向家长朗诵儿歌，表演故事。

小升初考试数学立体图形知识点
1特征
六个面都是正方形
六个面的面积相等
12条棱，棱长都相等
有8个顶点
正方体可以看作特殊的长方体
2计算公式
S表=6a2
v=a3
(三)圆柱
1圆柱的认识
圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比计算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2计算公式
s侧=ch
s表=s侧+s底2
v=sh/3
(四)圆锥
1圆锥的认识
圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

2计算公式
v=sh/3
(五)球
1认识
球的表面是一个曲面，这个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心并且两端都在球面上的线段，叫做球的直径，用d 表示，每条直径都相等，直径的长度等于半径的2倍，即d=2r。

2计算公式
d=2r
希望我们准备的数学立体图形知识点符合小学生的实际需求，能在你们复习备考过程中起到实际的作用，愿大家都以
优异的成绩考入理想的重点初中院校!。

小升初数学知识要点：立体图形【编者按】查字典数学网小升初为大家收集整理了小升初数学知识要点：立体图形供大家参考，希望对大家有所帮助!小升初数学知识中，有很多的备考要点需要我们认真去分析和掌握。

抓住小升初数学知识中的这些重点内容，我们才能得到更好的发挥。

下面，我们就必须认真来了解了。

小升初数学知识：立体图形(一)长方体1特征六个面都是长方形(有时有两个相对的面是正方形)。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6个面的总面积，叫做它的表面积。

2计算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1特征六个面都是正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体可以看作特殊的长方体2计算公式S表=6a2v=a3(三)圆柱1圆柱的认识圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比计算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2计算公式s侧=chs表=s侧+s底2v=sh/3(四)圆锥1圆锥的认识圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

2计算公式v=sh/3(五)球1认识球的表面是一个曲面，这个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心并且两端都在球面上的线段，叫做球的直径，用d 表示，每条直径都相等，直径的长度等于半径的2倍，即d=2r。

备考小升初数学知识点之立体图形备考小升初数学知识点之立体图形这篇关于《小升初数学知识点之立体图形》，是特地为大家整理的，希望对大家有所帮助!小升初数学备考小升初数学知识点之立体图形立体图形(一)长方体1特征六个面都是长方形(有时有两个相对的面是正方形)。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6个面的总面积，叫做它的表面积。

2计算公式s=2(ab+ah+bh)V=shV=abh(二)正方体1特征六个面都是正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体可以看作特殊的长方体2计算公式S表=6a2v=a3(三)圆柱1圆柱的认识圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比计算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2计算公式s侧=chs表=s侧+s底2v=sh/3(四)圆锥1圆锥的认识圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

2计算公式v=sh/3(五)球1认识球的表面是一个曲面，这个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心并且两端都在球面上的线段，叫做球的直径，用d 表示,每条直径都相等,直径的长度等于半径的2倍，即d=2r。

2计算公式d=2r以上就是小升初数学知识点之立体图形，更多精彩请进入小升初频道。

小升初数学立体图形知识点详解八、等底等高的圆柱和圆锥：锥1、差2、柱3、和4。

九、立体图形公式推导：【1】圆柱的侧面展开后得到一个什么图形?这个图形的各部分与圆柱有何关系?(圆柱侧面积公式的推导过程)①圆柱的侧面展开后一般得到一个长方形。

②长方形的长相当于圆柱的底面周长，长方形的宽相当于圆柱的高。

③因为：长方形面积=长×宽，所以：圆柱侧面积=底面周长×高。

④圆柱的侧面展开后还可能得到一个正方形。

⑤正方形的边长=圆柱的底面周长=圆柱的高。

【2】我们在学习圆柱体积的计算公式时，是把圆柱转化成以前学过的一种立体图形(近似的)进行推导的，请你说出这种立体图形的名称以及它与圆柱体有关部分之间的关系?①把圆柱分成若干等份，切开后拼成了一个近似的长方体。

②长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高。

③因为：长方体体积=底面积×高，所以：圆柱体积=底面积×高。

即：V=Sh。

【3】请画图说明圆锥体积公式的推导过程?①找来等底等高的空圆锥和空圆柱各一只。

②将圆锥装满沙子，倒入圆柱中，发现三次正好装满，将圆柱里的沙子倒入圆锥中，发现三次正好倒完。

③通过实验发现：圆锥的体积等于和它等底等高的圆柱体积的三分之一;圆柱的体积等于和它等底等高的圆锥体积的三倍。

即：V=1/3Sh。

十、立体图形的棱长总和、表面积、体积计算公式：（二）图形与变换一、变换图形位置的方法有平移、旋转等，在变换位置时，每个图形的相应顶点、线段、曲线应同步平移，旋转相同的角度。

二、不改变图形的形状，只改变它的大小时，通常要使每个图形的要素，如长方形的长与宽，三角形的底与高等同时按相同比例放大或缩小。

三、对称图形是对称轴两边的图形经对折后能够完全重合，而不是完全相同。

(三)图形与位置一、当我们处在实际生活及情景中，面对教短距离时，通常用上、下、前、后来描述具体位置。

二、当我们面对地图、方位图时，通常用东、西、南、北，南偏东、北偏东……来描述方向。