牛顿第二定律的应用临界问题[上学期]--新课标人教版

牛顿运动定律的应用（要点四）------------临界问题姓名：班级：（）班学号：一．临界问题概述（P34页要点二）临界状态：物体由某种物理状态变化为另一种物理状态时，中间发生质的飞跃的转折状态，通常称之为临界状态。

二．解决临界问题的基本思路：（1）认真审题，仔细分析研究对象所经历的变化的物理过程，找出临界状态。

（2）寻找变化过程中相应物理量的变化规律，找出临界条件。

（3）以临界条件为突破口，列临界方程，求解问题。

三．典型例题：AB F例1：如图所示，m A=2kg，m B=1kg，A、B间动摩擦因素为0.3，水平面光滑。

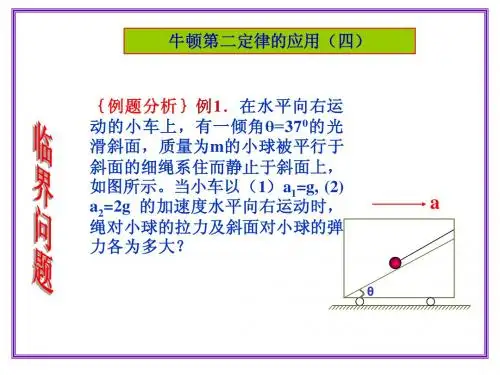
用水平力F拉A，使两物体一起沿水平面做匀加速直线运动，（g=10m/s2）（1）要使两物块保持相对静止，则水平力F不能超过多大？（2）若水平力改为作用在B上，要保持两物块一起匀加速直线运动，则水平力F不能超过多大？（3）要将物块B从A下面拉出，则水平F应满足什么条件？例2．如图所示，质量为m的物体放在质量为M的倾角为α的斜面上，如果物体与斜面间、斜面体与地面间摩擦均不计，问（1）作用于斜面体上的水平力多大时，物体与斜面体刚好不发生相对运动?（2）此时m对M的压力多大?(3)此时地面对斜面体的支持力多大?例题3．一个质量为0．1千克的小球，用细线吊在倾角a为37°的斜面顶端，如图所示。

系统静止时绳与斜面平行，不计一切摩擦。

求下列情况下，绳子受到的拉力为多少?(1)系统以6米／秒2的加速度向左加速运动；(2)系统以l0米／秒2的加速度向右加速运动；(3)系统以15米／秒2的加速度向右加速运动。

练习1。

P34页【典题演示2】例题4．如图所示，两光滑的梯形木块A和B，紧靠放在光滑水平面上，已知θ=60°，m A=2kg，m B=lkg，现水平推力F，使两木块使向右加速运动，要使两木块在运动过程中无相对滑动，则F的最大值多大?物理思想与规律总结：P41页【临界与极值问题】例题5．如图所示，传送带与地面的倾角为θ=370，从A到B的长度16m,传送带以10m/s的速率逆时针方向转动，在传送带上端无初速地放一个质量为m=0.5kg的物体，它与传送带之间的动摩擦因数为0.5，求物体从A到B 所需的时间是多少？（sin370=0.6 cos370=0.8 g=10m/s2）B★例题6．如图，在劲度系数为K的弹簧的下端挂一质量为m的物体，物体下端有一托盘，用托盘托着物体使弹簧恰好处于原长，然后使托盘以加速度a竖直向下做匀加速直线运动（a＜g）试求托盘向下运动多长时间能与物体脱离四．巩固练习1．如图所示，物体A放在物体B上，物体B放在光滑的水平面上，已知m A=6kg，m B=2kg，A、B间动摩擦因数=0.2.A物上系一细线，细线能承受的最大拉力是20N，水平向右拉细线，假设A、B之间最大静摩擦力等于滑动摩擦力.在细线不被拉断的情况下，下述中正确的是（g=10m/s2）A.当拉力F＜12N时，A静止不动B.当拉力F＞12N时，A相对B滑动C.当拉力F=16N时，B受A摩擦力等于4ND.无论拉力F多大，A相对B始终静止2．质量，m＝lkg的物块放在倾角为θ的斜面上，斜面体质量M=2kg，斜面与物块的动摩擦因数μ＝0.2，地面光滑，θ=37°，现对斜面体施一水平推力F，要使物体m相对斜面静止，力F应为多大?(设物体与斜面的最大静摩擦力等于滑动摩擦力，g取10m／s2)3．小车在水平路面上加速向右运动，一质量为m的小球用一条水平线和一条斜线（与竖直方向成30度角）把小球系于车上，求下列情况下，两绳的拉力：(1)加速度a1=g/3 (2)加速度a2=2g/3。

牛顿第二定律的应用临界问题和极值 问题
1、 舟 遥 遥 以 轻飏， 风飘飘 而吹衣 。 2、 秋 菊 有 佳 色，裛 露掇其 英。 3、 日 月 掷 人 去，有 志不获 骋。 4、 未 言 心 相 醉，不 再接杯 酒。 5、 黄 发 垂 整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华

第 1 页 共 2 页牛顿第二定律专题—临界问题与极值 1．临界问题和极值问题涉及临界状态的问题叫临界问题。

临界状态常指某种物理现象由量变到质变过渡到另一种物理现象的连接状态，常伴有极值问题出现。

临界问题常伴有特征字眼出现，如“恰好”、“刚刚”等1.如图所示，质量M=4kg 的小车放在水平光滑的平面上，在小车左端加一水平推力F=6N ，当小车向右运动的速度达到2m/s 时，在小车前端轻轻地放上一个大小不计，质量为m=1kg 的小物块，物块与小车间的动摩擦因数μ=0.2，小车足够长．（g 取10m/s2），求（1）放小物块后，小物块及小车的加速度各为多（2）经多长时间两者达到相同的速度？（3）从小物块放上小车开始，经过t=3s 小物块通过的位移大小为多少？ 有一质量M=4kg 的小车置于光滑水平桌面上，在小车上放一质量m=6kg µ=0.2,现对物块施加F=25N 的水平拉力,如图所示，（设车与物块之间的最大静摩擦力等于滑动摩擦力且g 10m/s2)第 2 页 共 2 页3托盘A 托着质量为m 的重物B ，B 挂在劲度系数为k 的弹簧下端，弹簧的上端悬挂于O 点，开始时弹簧竖直且为原长，今让托盘A 竖直向下做初速为零的匀加速运动，其加速度为a ，求经过多长时间，A 与B 开始分离（a g ）． 4.如图所示， m =4kg 的小球挂在小车后壁上，细线与竖直方向成37°角。

求：（1）小车以a=g 向右加速；（2）小车以a=g 向右减速时，细线对小球的拉力F1和后壁对小球的压力F2各多大？5．如图所示，一质量为0.2kg 的小球系着静止在光滑的倾角为53°的斜面上，斜面静止时，球紧靠在斜面上，绳与斜面平行，当斜面以10m/s2加速度水平向右作匀加速直线运动时，求线对小球的拉力和斜面对小球的弹力。

（g=10m/s2）6.传送带与水平面夹角37°，皮带以10m/s 的速率运动，皮带轮沿顺时针方向运动，如图所示.今在传送带上端A 处无初速度地放上一个质量为m=0.5kg 的小物体，它与传送带间的动摩擦因数为0.5，若传送带A 到B 的长度为16m ，g 取10m/s 2，则物体从A 运动到B 的时间为多少？（g 取为10m/s 2）。

国内最大的体育直播平台 此外，这部影片，我还看到普通老百姓的辛酸。贫穷限制了人们的想象，贫穷也拴住了人们的脚步，如果李义与马文这两个男人本事都大一点，任有一方有能力买套房搬出去，何至于三人同行这么
些日子呢？如果李义与杨欣婚后不和马文住在同一屋檐下，他们的婚后生活是不是会简单一点，幸福一点？?
当最后马文和杨欣重新站到一起时，李芹说了句：你们本来就是夫妻。是啊，夫妻本来就该如此才对。可是，人为什么总要在失去以后才懂得珍惜呢？杨欣一顿作，终于让自己的心灵安定，看清楚 了自己的内心，女人的心难道是要借助男人才能看清的吗？或者说是要经历过不同的感情才会成熟的吗？答案不是唯一，但感情经历的确让人迅速成长。
李义以为自己终于熬到头了，身边，他却毫无察觉。生意场上有句话：维护好老客户，总比开发一个新客户更加高效省力。还有这样 一句话，不要放弃过去的，说不定什么时候就会再次牵手。马文就是这两句话最好的鉴证者。?
贫贱夫妻百事哀，但平凡的生活能活出真情所在。
四
?下面来说说段先生推荐的另外一部影片《野山》。
《野山》是根据贾平凹的小说《鸡洼村的人家》改编的。讲述了改革春风吹到秦岭深处一个偏僻的小山村，两户人家“换老婆”的故事。

实验目的
实验器材
验证牛顿第二定律，即物体的加速度与作 用在物体上的力成正比，与物体的质量成 反比。
打点计时器、纸带、重物、弹簧测力计、 气垫导轨等。
实验步骤
实验结论
将重物置于气垫导轨上，用弹簧测力计拉 动重物，使其做匀加速直线运动，通过打 点计时器和纸带记录重物的运动情况。
通过测量重物的质量和加速度，验证了 F=ma关系。
惯性概念
物体保持原有运动状态的 性质称为惯性，惯性的大 小与物体的质量有关。
惯性现象
汽车启动时乘客向后仰， 刹车时向前倾；旋转的物 体停下来后会继续旋转一 段时间等。
第二定律：F=ma
定律表述
物体的加速度与作用在物体上的 合外力成正比，与物体的质量成 反比，加速度的方向与合外力的
方向相同。
公式解读
超重现象
电梯上升时，人体感受到 的向上加速度导致体重计 示数增大。
失重现象
电梯下降时，人体感受到 的向下加速度导致体重计 示数减小。
牛顿第二定律解释
加速度方向与合外力方向 相同，合外力大小等于质 量与加速度的乘积。
行走、跑步与摩擦力关系分析
行走时的摩擦力
静摩擦力使人与地面保持相对静止，实现行走动作。
牛顿第二定律解释
篮球运动过程中的加速度与合外力成正比，合外 力包括重力和空气阻力。
03
牛顿运动定律在工程 技术中的应用
桥梁设计中的力学原理
桥梁静力学
01
应用牛顿第二定律计算桥梁结构内力，确保桥梁在不同荷载下
的安全稳定。
桥梁动力学
02
利用牛顿运动定律分析桥梁在车辆、风、地震等动荷载作用下
的动力响应，避免共振和过度变形。
万有引力定律

a
将 a3=g 代入 得 F1=1.4mg FN1=-0.2mg -
拓展：上述问题中， 拓展：上述问题中，若小车向左加速运动 ，试求加 时的绳中张力。 速度a 时的绳中张力 速度 3=g时的绳中张力。
简析： 简析：
a F=0
FN y F x θ G
绳即将松弛时
此时a=gtan θ=3g/4 此时 故绳已松弛， 而a3 =g ，故绳已松弛， 绳上拉力为零
支持力F 随加速度a 易见 ：支持力 N 随加速度 的增大而减小 支持力F 当a=gcotθ= 4g/3 时，支持力 N =0 小球即将脱离斜面
当小车加速度a> 当小车加速度 4g/3时，小球已飘离斜面，如图所示 时 小球已飘离斜面， a 得 F=m a + g
2 2
将a2=2g 代入得 F2=
F ma θG
5 mg
[小结 相互接触的两个物体将要脱离的临界条件是 小结] 小结 相互作用的弹力刚好为零。 相互作用的弹力刚好为零。
拓展：上述问题中， 拓展：上述问题中，若小车向左加速运动 ，试求加 时的绳中张力。 速度a 时的绳中张力 速度 3=g时的绳中张力。
简析： 简析： 则沿x轴方向 则沿 轴方向 FNsinθ - Fcosθ =ma 沿y轴方向 轴方向 FNcosθ + Fsinθ=mg θ FN y F x G
F
14.34 N ≤ F ≤ 33.6 N
a
θ
取小球为研究对象并受力分析 解： 建立正交坐标系 则沿x轴方向 则沿 轴方向 沿y轴方向 轴方向 Fcosθ-FNsinθ=ma
a
Fsinθ+FNcosθ=mg FN F
将 a1=g 、a2=2g 分别代入 得 F1=7mg/5 FN1=mg/5 F2= 11mg/5 FN2=-2mg/5

F－mg＝ma，对 A：kx－mg＝ma。
即 F＝kx 时，A、B 分离，此时弹簧仍处于压缩状态，
由 F＝mg，设用恒力 F 拉 B 前弹簧压缩量为 x0，
则 2mg＝kx0，h＝x0－x，
mg
解以上各式得 k＝ h ，综上所述，只有 C 项正确。
[答案]
C
类型二
相对滑动的临界
在力F作用下A、B是否一起运动？
(A C )
A.当t=3 s时，A、B开始分离
B.当t=4.5 s时，A、B开始分离
C.A、B分离之前整体做加速度相同的匀加速直线运动
D.A、B分离之后A、B各做加速度不同的匀加速直线运动
A、B两物体由接触到脱离的临界条件: A、B间弹力FN=0
解析

当A、B分离时两者间作用力为零，且a相同，所以
竖直方向有
Ncosθ=mg+fsinθ，
联立以上各式，代入数据解得F=310N.
故F的大小范围为0≤F≤310N.
[练习3]
如图所示，质量为M的木楔倾角为θ，在水平面上保
持静止，当将一质量为m的木块放在木楔斜面上时，它正好匀速下
滑。如果用与木楔斜面成α角的力F拉着木块，木块能匀速上升，
已知木楔在整个过程中始终静止。当α为多大时，F有最小值，求
误;F=7 N<F0时,物块和长木板一起加速运动,长木板的加速度a=
F
7
=m/s 2 ,
M m 3
C错误;F=9 N>F0时,物块和长木板相对运动,长木板受到的摩擦力大小为μmg=
5 N,D正确。
类型三 动力学中的极值问题
例3 如图所示，一块质量m=2kg的木块放置在质量M=6kg、
倾角=37°的粗糙斜面体上，木块与斜面体间的动摩擦因数

牛顿第二定律的应用（四）
｛例题分析｝例1．在水平向右运 动的小车上，有一倾角θ=37 0 的光 滑斜面，质量为m的小球被平行于 斜面的细绳系住而静止于斜面上， 如图所示。当小车以（1）a1=g, (2) a2=2g 的加速度水平向右运动时， 绳对小球的拉力及斜面对小球的弹 力各为多大？
θ
a
牛顿第二定律的应用（四） 当小车加速度a＞4g/3时， 小球已飘离斜面，如图所 示
得 F=m
√a2＋g2
a
T ma
θ
Hale Waihona Puke 将a2=2g 代入得F2=√5 mg [小结] 相互接触的两个物 体将要脱离的临界条件是相 互作用的弹力为零。
mg
牛顿第二定律的应用（四） 拓展：上述问题中，若小车向左匀加速运动时 ，
试求加速度a3=
时的绳中张力为0。
取小球为研究对象，并进行受力分析，如图所示
a
FN T
m
M
F M
fm
牛顿第二定律的应用（四） 练习：如图，在光滑的地面上有小车A，其质量为 mA=2千克，小车上放一物体B，质量mB=1千克，A、B 间有摩擦，若给B施加一水平推力F1（如图甲所示）， 当F1逐渐增大到稍大于3牛时B开始相对于A滑动；若撤 去F1，对A施加一个水平推力F2（如图乙所示），要使 B不相对于A滑动， F2的最大值是多少？
θ
mg
牛顿第二定律的应用（四）
解：设绳中的拉力为零时，小车的加速度为a ，此 时小球的受力如图
a
得 a=gtanθ=3g/4
而a3 =g ，故绳已松弛，绳上拉 力为零
FN ma
θ
mg
[小结] 绳子松弛的临界条件是：绳中拉力为 零。
牛顿第二定律的应用（四）

牛顿第二定律的临界 问题
目录
CONTENTS
• 牛顿第二定律概述 • 临界状态分析 • 牛顿第二定律在临界问题中的应用 • 牛顿第二定律临界问题的实例解析 • 牛顿第二定律临界问题的求解方法 • 牛顿第二定律临界问题的扩展与展望
01 牛顿第二定律概述
定义与公式
定义
牛顿第二定律描述了物体的加速度与 作用力之间的线性关系，即F=ma。
建立动力学方程
根据牛顿第二定律，建立物体运动的动力学方程，包括加速度、 速度和位移等变量。
求解动力学方程
通过代数运算、微积分等数学方法，求解动力学方程，得到物体 的运动轨迹和状态变化。
初始条件和边界条件
在求解动力学方程时，需要给出物体的初始状态和边界条件，以 确定物体的运动轨迹。
数值模拟方法
离散化
速度最大
在临界状态下，物体的速度达到最大值，此时加速度 为零。
加速度为零
在临界状态下，物体的加速度为零，此时速度达到最 大值。
运动方向改变
在临界状态下，物体的运动方向可能发生改变，此时 速度和加速度同时为零。
03 牛顿第二定律在临界问题 中的应用
动力学问题
刚体动力学
01
牛顿第二定律在刚体动力学中用于描述刚体的运动规律，特别
详细描述
当汽车刹车时，摩擦力使汽车逐渐减速，直至停止。在这个过程中，汽车的加速度与摩擦力的大小和方向有关， 而速度的变化则取决于加速度的大小和作用时间。在临界状态下，汽车的加速度可能接近于零，但仍然存在摩擦 力，导致汽车无法立即停止。
跳水运动员入水问题
总结词
跳水运动员入水问题涉及到水的阻力和人体 的加速度。
近似解的精度
近似解析法的精度取决于所采用的近似方法和物理模型的简化程度。

临界问题教学设计
教学目标：
（1）知道临界问题的概念；
（2）熟悉各种临界条件；
（3）掌握临界问题的求解方法。

教学重难点：
（1）临界状态的推演的难度较大；
（2）重点强化利用临界条件建立方程求解问题。

教学过程：
一、知识要点
1.临界状态：物体由某种物理状态变化为另一种物理状态时，中间发生质的飞跃的转折状态，通常称之为临界状态。

2.临界问题：涉及临界状态的问题叫做临界问题。

3. 解决临界问题的基本思路
（1）仔细分析研究对象所经历的变化的物理过程,找出临界状态。

（2）寻找变化过程中相应物理量的变化规律，找出临界条件。

（3）以临界条件为突破口，列临界方程，求解问题。

4.三类临界问题的临界条件
（1）相互接触的两个物体将要脱离的临界条件是：
相互作用的弹力为零
（2）绳子松弛的临界条件是：
绳中拉力为零
（3）存在静摩擦的连接系统,相对滑动与相对静止的临界条件是：
静摩擦力达最大值
二、典例分析
例：在水平向右运动的小车上，有一倾角θ=370的光滑斜面，质量为m的小球被平行于斜面的细绳系住而静止于斜面上，如图所示。

当小车以（1）a1=g, (2) a2=2g 的加速度水平向右运动时，绳对小球的拉力及斜面对小球的弹力各为多大？拓展：（1）分解加速度；（2）向左加速。

详解与讲解过程见视频！
教学反思：
依托牛顿定律推演物理量的变化过程是非常难的，学生往往不易掌握；教师可以多举实例讲解。

由于时长限制，临界问题的教学设计只突破了分离的临界问题。

例题讲解中的正交分解（分解力与分解加速度）值得同学反复推敲，简化运算过程。

水平面光滑，用水平力F拉B，当拉力大小分别为F1=10N和
F2=20N时，A 、B旳加速度各为多大？
解：假设拉力为F0时，A、B之间旳静摩擦力
mA
到达5N，它们刚好保持相对静止．对于整体
F
和物体A，分别应用牛顿第二定律
B
F0 (mA mB )a ① fm mAa ②
联立①②两式解出 F0 15N
x2
x1
mg cos2 k sin
a
θ θ
mg
牛顿定律利用中旳临界和极值问题
例题分析:1、小车在水平路面上加速向右运动，一 质量为m旳小球用一条水平线和一条斜线（与竖 直方向成30度角）把小球系于车上，求下列情况 下，两绳旳拉力：
(1)加速度a1=g/3 (2)加速度a2=2g/3
B θ
A
O
分析（1）平衡态（a=0）受力分析 。
300 图1
分析：讨论涉及静摩擦力旳临界问题旳一般措施
是：1、抓住静摩擦力方向旳可能性。2、物体即 将由相对 静止旳状态即将变为相对 滑动状态旳 条件是f=μN（最大静摩擦力）。本题有两个临界 状态，
当物体具有斜向上旳 运动趋势时，物体受到旳摩 擦力为最大静摩擦力；
当物体具有斜向下旳运动趋势时，物体受到旳摩 擦力为最大静摩擦力。
mg 关键是找出装置现状（绳旳位置）和临界条件， 而不能以为不论α多大，绳子旳倾斜程度不变．
例6．质量为m旳小物块，用轻弹簧固定
在光滑旳斜面体上，斜面旳倾角为θ，如
图所示。使斜面体由静止开始向右做加速
度逐渐缓慢增大旳变加速运动，已知轻弹
簧旳劲度系数为k。求：小物块在斜面体
θ
上相对于斜面体移动旳最大距离。
T1 F0

六牛顿第二定律应用之四——临界问题若题目中出现“最大”、“最小”、“刚好”等词语的，一般都有临界现象出现，都要求出临界条件．分析时，为了把这个临界现象尽快暴露，一般用极限分析法，特别是某些题目的文字比较隐蔽．物理现象过程又比较复杂时，用极限分析法往往使临界现象很快暴露出来．★极限分析法通常情况下，由于物理现象涉及的因素较多，过程变化复杂，人们往往难以洞察其变化规律并对其作出迅速判断．但如果用极限分析法，将问题推到极端状态或极端条件下进行分析，问题有时会顿时变得明朗而简单了物理解题中的极端假设分析法分为三种类型：定性分析、定量分析和综合分析．（1）定性分析利用极端假设法进行定性分析，可使问题迅速得到解答．（2）定量计算在物理解题，特别是解答选择题时，采用极端假设分析法，选择适当的极限值——最大值、最小值、零值、无限大值以及临界值等代人备选答案，会使解题收到意想不到的简化效果．（3）综合分析对于综合性较强的题目，由于其隐含条件较深，或者隐含条件是应该熟悉的临界条件或者是重要的规律和结论时，再用极端假设法分析，就必须将定性分析与定量分析有机结合起来，灵活地运用物理知识和数学知识，才能“准而快”地对问题作出回答．【例题1】一个物体沿动摩擦因数一定的斜面加速下滑，下列图像，哪一个比较准确的描述了加速度a与斜面倾角θ的关系( )【例题2】如图3—46，在光滑水平面上放着紧靠在一起的A、B两物体，B的质量是A的2倍，B受到水平向右的恒力F B=2N，A受到的水平力F A＝(9－2t)N(t的单位是s) ．从t＝0开始计时，则：A．A物体在3s末时刻的加速度是初始时刻的5／11倍；B．t>4s后，B物体做匀加速直线运动；C．t=4.5s时，A物体的速度为零；D．t>4.5s后，A、B的加速度方向相反．【例题3】如图3－47，质量，m＝lkg的物块放在倾角为θ的斜面上，斜面体质量M=2kg，斜面与物块的动摩擦因数μ＝0.2，地面光滑，θ=37°，现对斜面体施一水平推力F，要使物体m相对斜面静止，力F应为多大?(设物体与斜面的最大静摩擦力等于滑动摩擦力，g取10m／s2)【例题4】一个弹簧秤放在水平地面上，Q为与轻弹簧上端连在一起的秤盘，P为一重物，已知P的质最M=l0.5kg，Q的质量m=1.5kg，弹簧的质量不计，劲度系数k=800N／m，系统处于静止，如下图所示，现给P施加一个方向竖直向上的力F，使它从静止开始向+卜做匀加速运动，已知在前0.2s时间内，F为变力，0.2s以后，F为恒力．求力F的最大值与最小值．(取g=10m／s2)．【例题5】如图3—51所示，把长方体切成质量分别为m和M的两部分，切面与底面的夹角为θ长方体置于光滑的水平地面，设切面亦光滑，问至少用多大的水平力推m，m才相对M滑动?解析：【例题6】如图3—52，平行于斜面的绳把小球系在倾角为θ的斜面上，为使球在光滑斜面上不相对运动，求斜面体水平运动的加速度．解析：【例题7】如图3—53，斜面倾角为θ，劈形物P上表面与m的动摩擦因数为μ，P上表面水平，为使m随P一起运动，当P以加速度口沿斜面向上运动时，则μ不应小于多少?当P在光滑斜面上自由下滑时，μ不应小于多少?解析：【例题8】如图3—54，质量分别为m1、m2的A、B两木块叠放在光滑的水平面上，A与B的动摩擦因数为μ，若要保持A和B相对静止，则施于A的水平拉力F的最大值为多少?若要保持A和B相对静止，施于B的水平拉力F的最大值为多少?若把A从B的上表面拉出，则施于A的水平拉力最小值为多少?。