锥体展开计算方法

三维形的展开与折叠在日常生活中，我们常常与三维形状打交道，如立方体、圆锥体等。

这些三维形状在展开与折叠时，能够呈现出不同的形态和特点。

本文将探讨三维形状的展开与折叠，以及它们在不同领域的应用。

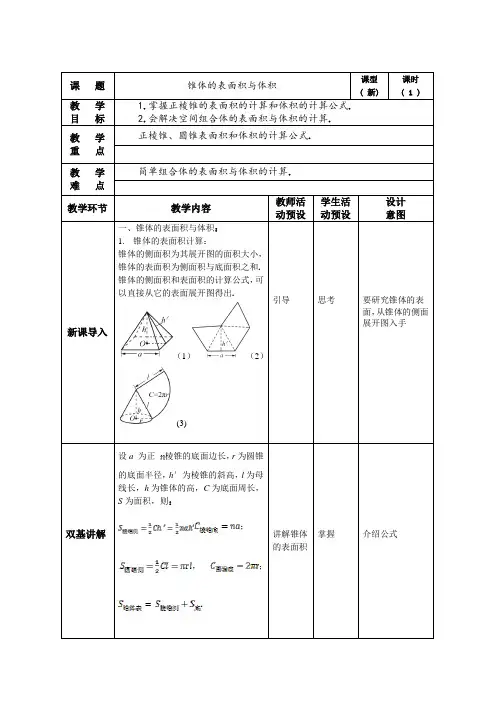
一、三维形状的展开三维形状的展开是指将其表面展平，形成二维的图形。

这样做的目的是为了更好地研究和理解三维形状的性质。

1. 展开方法展开三维形状的方法有很多种，常用的包括剪切法、折叠法和数学计算法。

剪切法是最常用的一种方法，它通过剪开三维形状的边缘，将其展开为一个连续的平面图形。

这种方法简单直观，适用于大多数三维形状的展开。

折叠法是一种比较独特的展开方法，它通过将三维形状按照特定的方式折叠起来，使之展开为一个平面图形。

这种方法在一些复杂的三维形状展开中较为常见，例如展开一个六面体。

数学计算法是一种利用数学模型和计算机算法来实现三维形状展开的方法。

这种方法适用于一些特殊的三维形状，如曲面或非欧几何形状。

2. 展开图形的特点展开后的二维图形保留了三维形状的一些重要特征，如面积、边长等。

同时，展开图形还能够展示出三维形状中的一些难以观察到的特点，如表面的缝隙、内部结构等。

展开图形还能够方便地进行测量和计算，如计算表面积、体积等。

这对于工程设计、制作模型等领域具有重要的意义。

二、三维形状的折叠与展开相反，三维形状的折叠是将其从二维状态重新折叠为三维形状。

折叠是一种常见的造型方法，它能够将平面图形变为立体造型，使之更具立体感和形态变化。

1. 折叠方法折叠方法主要包括手工折叠和机械折叠两种。

手工折叠是最常见的折叠方法，通常使用纸张或轻质材料，通过手工的方式将平面图形折叠成所需的立体形状。

这种方法简单易行，适用于各种规模的制作。

机械折叠是一种较为先进的折叠方法，它利用机械装置或机器人来完成折叠过程。

这种方法适用于大规模的制作，可以提高生产效率和准确度。

2. 折叠的应用三维形状的折叠在很多领域都有广泛应用。

在建筑领域，折叠技术可以用于建筑模型的制作，帮助设计师更好地理解和展示建筑形态。

圆锥体体积公式计算圆锥体是由一个圆形底面和一个顶点连接而成的几何体。

它是一种常见的几何形状，在数学、自然科学、建筑等领域经常被使用。

计算圆锥体的体积是一个基本的几何计算问题，下面将介绍圆锥体体积的计算公式及其推导过程。

圆锥体的体积公式可以通过对圆锥体进行切割并展开计算得到。

一种常用的方法是将圆锥体切割成薄圆环，并将所有的圆环展开成一条直线。

通过计算直线的长度和每个圆环的面积，可以推导出圆锥体的体积公式。

首先，假设圆锥体的底面半径为r，底面上的圆心角（圆心角是指圆上任意2点连线与圆心连线之间的夹角）为θ，圆锥体的高度为h。

可以将圆锥体切割成n个非常薄的圆环，每个圆环的半径为r_i，宽度为Δr_i，圆心角为θ_i，其中Δr_i是一个非常小的数值。

将每个圆环展开成直线后，直线的长度即为圆环的周长2πr_i，圆环的面积可以近似为一个长方形，宽度为Δr_i，高度为r_iθ_i（圆环的长度除以圆的周长，等于圆心角占据的比例），因此圆环的面积可以近似为ΔS_i=r_iθ_iΔr_i。

将所有的圆环的面积累加起来，即可得到整个圆锥体的面积S：S≈ΔS_1+ΔS_2+...+ΔS_n=r_1θ_1Δr_1+r_2θ_2Δr_2+...+r_nθ_nΔr_n当n趋向于无穷大时，所有圆环的面积的累加就可以等于整个圆锥体的面积。

因此，可以将上式改写为：S=∫(rθ)dA=∫(rθ)dπr^2= π∫r^3θdr其中，∫代表积分运算。

接下来，计算圆锥体的体积V。

将圆锥体切割成非常薄的圆环后，每个圆环的体积可以近似为一个圆柱体，高度为h，底面半径为r_i，体积可以近似为ΔV_i=πr_i^2h。

将所有圆环的体积累加起来，即可得到整个圆锥体的体积V：V≈ΔV_1+ΔV_2+...+ΔV_n=πr_1^2h+πr_2^2h+...+πr_n^2h=πh(r_1^2+r_2^2+...+r_n^2)当n趋向于无穷大时，所有圆环的体积的累加就可以等于整个圆锥体的体积。

钣金展开计算方法钣金展开计算是钣金工艺中的重要内容，也是完成钣金产品制作的关键步骤之一、钣金展开计算的目的是根据钣金产品的三维图纸，确定其展开长度和表面形状，以便进行钣金零件的切割和加工。

钣金展开计算主要包括平展面展开和曲面展开两种方法。

平展面展开是指将平面图形进行展开，形成展开图。

平展面展开计算方法主要适用于钣金产品的各种平面零件，如箱体、支架等。

（1）定积法展开计算方法：该方法适用于钣金产品的部分各种平面形状，如圆筒、弯管等。

定积法展开计算需要确定钣金材料的长度、重量、宽度等参数。

具体计算步骤如下：1）根据钣金产品的图纸，确定钣金的外径、内径、高度等参数。

2）计算钣金的周长和截面积，得到钣金的长度和重量。

3）根据钣金的长度和宽度，计算出钣金的展开图纸。

4）根据展开图纸进行钣金零件的切割和加工。

（2）图形展开计算方法：该方法适用于钣金产品的各种复杂平面形状，如弯曲的盖板、折弯的箱体等。

图形展开计算需要根据钣金产品的图纸，利用图形的几何关系和三角函数等知识进行计算。

具体计算步骤如下：1）根据钣金产品的图纸，将图纸投影到平面上。

2）根据图纸上的线段长度和角度，利用几何关系和三角函数等知识，推导出展开图形的边长和角度。

3）根据展开图形的边长和角度，计算出展开图纸。

4）根据展开图纸进行钣金零件的切割和加工。

曲面展开是指将曲面图形进行展开，形成展开图。

曲面展开计算方法主要适用于钣金产品的各种曲面零件，如球体、圆锥体等。

曲面展开计算方法较为复杂，需要借助计算机辅助设计和数学知识进行计算。

常用的曲面展开计算方法有拉伸展开法、分割展开法和均分展开法等。

具体计算步骤如下：1）根据钣金产品的图纸，将曲面投影到平面上。

2）根据曲面的曲率半径和展开的高度，进行拉伸和分割。

3）利用数学知识，计算出展开图形的边长和曲率。

4）根据展开图形进行钣金零件的切割和加工。

几何体的展开几何体是由各种几何形状组成的立体图形。

展开是指将立体图形按照一定规则展开成为平面上的二维图形。

本文将介绍几何体展开的概念、方法以及一些实际应用。

一、展开的概念展开是指将立体图形展开成为平面上的二维图形。

通过展开，我们可以清楚地看到几何体的各个面以及它们之间的结构关系。

相比于立体图形，展开后的二维图形更容易分析和计算。

二、展开的方法不同的几何体有不同的展开方法，下面将介绍几种常见的几何体展开方法。

1. 正方体展开正方体是最简单的立方体几何体，它有六个面。

展开时，我们可以将正方体的各个面按照一定的规则展开成为一个平面上的图形。

展开后的图形可以通过将各个面进行折叠来重新组合成一个正方体。

2. 圆柱展开圆柱是由一个圆面和一个矩形面组成的几何体。

展开时，我们可以将圆柱的圆面展开成为一个平面上的圆，矩形面展开成为一个长方形。

展开后的图形可以通过将圆形和矩形进行折叠来重新组合成一个圆柱体。

3. 锥体展开锥体是由一个圆锥面和一个底面组成的几何体。

展开时，我们可以将圆锥面展开成为一个平面上的扇形，底面展开成为一个多边形。

展开后的图形可以通过将扇形和多边形进行折叠来重新组合成一个锥体。

4. 球体展开球体是由无数个点组成的几何体，无法直接进行展开。

但是，在某些情况下，我们可以通过将球体上的一部分点进行投影，然后再将投影展开成为一个平面上的图形，来近似展开球体。

三、展开的应用几何体的展开在许多领域有着广泛的应用，下面将介绍一些常见的应用场景。

1. 建筑设计建筑设计师常常需要将三维建筑物的结构以及各个部位的尺寸等信息呈现给客户或者团队成员。

通过将建筑物的各个部分进行展开，可以清楚地展示建筑物的空间结构和各个部分之间的关系，帮助人们更好地理解和沟通。

2. 纸模型制作展开技术广泛应用于纸模型的设计和制作中。

通过将纸模型的各个部分进行展开，可以得到精确的切割和折叠模板，帮助制作者更方便地制作出精美的纸模型。

3. 机械工程在机械工程中，展开技术被广泛应用于钣金加工和制造过程中。

锥形油罐的重量计算公式
现实生活中，尽管储油罐的形状各式各样，仔细分析无非存在以下两种结构：卧式结构和立式结构。

无论卧式结构还是立式结构都是可能存在半椭圆圭寸头、平面圭寸头、半圆形圭寸头、圆锥形封头等。

本文主要介绍锥形油罐的重量计算公式：设锥体母线长为r，锥体底面园半径为r1,那么r1=rsin75度，锥体底面园周长l=2πr1，l就是锥体展开扇形的弧长，可以计算出展开扇形的中心角α=2×360×rsin75度,再计算出扇形面积（即为锥体展开面积）s=2πr2sin75度. 注：r后面2代表平方。

锥体下料的计算公式锥体是指由一个圆锥和一个底面与圆锥底面同心的圆台组成的几何图形，常用于建筑、机械制造、工艺加工等领域。

对于锥体下料，其计算公式可以帮助我们快速、准确地确定需要切割的材料大小和角度，实现精准加工。

一、锥台的基本概念锥台又称为圆锥台，是由一个底面半径为 R，顶部半径为 r，高度为 H 的圆锥和一个底面半径为 R，顶部半径为 r，高度为 h 的圆台组成的几何图形。

其中，R > r，H > h。

二、锥台的体积计算公式锥台的体积 V 可以用以下公式计算：V = 1/3 * πH(R^2 + Rr + r^2)其中，π 为圆周率，H 为圆锥的高度。

三、锥台的侧面积计算公式锥台的侧面积 S 可以用以下公式计算：S = πL(R + r)其中，L 为斜面长度，可以根据勾股定理计算得到：L = √(H^2 + (R-r)^2)四、锥台的下料计算公式在实际应用中，我们可能需要将一个锥台按照一定的尺寸和角度进行下料加工。

此时，我们可以使用以下公式计算出需要切割的材料尺寸和角度：1. 切割母线长度 L1：L1 = √(H^2 + (R-r)^2)2. 切割母线到底面的距离 L2：L2 = R - r3. 切割母线与底面的夹角α：α = arctan[(R-r)/H]切割母线的长度 L1，可以使锥台的表面展开成一个平面图形，方便进行下料加工；切割母线到底面的距离 L2，则是判断切割后材料尺寸的重要参数；切割母线与底面的夹角α，则可以帮助我们确定锥台的斜面角度和切割时的夹角。

总之，锥台下料的计算公式可以为我们提供重要的参考和指导，使加工过程更加精准、高效。

圆锥母线,弧长,⾯积计算公式
圆锥母线,弧长,⾯积计算公式
弧长计算公式
[编辑本段]弧长的定义
在圆上过2点的⼀段弧的长度叫做弧长。

[编辑本段]弧长的计算公式
弧长公式:弧长=θ*r ,θ是⾓度 r是半径
l＝nπr÷180
在半径是R的圆中，因为360°的圆⼼⾓所对的弧长就等于圆周长C＝2πR，所以n°圆⼼⾓所对的弧长为l＝nπR÷180。

例：半径为1cm，45°的圆⼼⾓所对的弧长为
l＝nπR÷180
＝45×派×1÷180
约等于0.785(cm)
如果已知他的沿圆锥体的⼀条母线和侧⾯与下底⾯圆的交线将圆锥体剪开铺平，就得到圆锥的平⾯展开图。

它是由⼀个半径为圆锥体的母线长，弧长等于圆锥体底⾯圆的周长的扇形和⼀个圆组成的，这个扇形⼜叫圆锥的侧⾯展开图。

补充公式：S扇=nπR^2/360
=πRnR/360
=2πRn/360×1/2R
=πRn/180×1/2R
所以：S扇=RL/2
[编辑本段]圆锥母线,弧长,⾯积计算公式
圆锥的表⾯积=圆锥的侧⾯积+底⾯圆的⾯积
其中：圆锥体的侧⾯积=πRL
圆锥体的全⾯积=πRl+πR2
π为圆周率＝3.14
R为圆锥体底⾯圆的半径。