当前位置：文档之家 › 统计学第七章假设检验

统计学第七章假设检验

  • 格式：doc
  • 大小：849.11 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

第七讲-假设检验

第七讲-假设检验
14
• 这里备择假设H1包含了 >0和 <0两方面。
13
H0： = 34.50 （该矿区新生儿的头围与当 地一般新生儿头围均数相同） H1： ≠ 34.50 （该矿区新生儿的头围与当 地一般新生儿头围均数不同）
2. 计算检验统计量
根据变量和资料类型、设计方案、 统计推断的目的、是否满足特定条件等 （如数据的分布类型）选择相应的检验统 计量。
2 1 2 2

2.9 5.2 1.9 / 32 2.7 2 / 40
2
4.23
两均数之差的标准误的估计值
由 于 u0.05/2=1.96 ， u0.01/2=2.58 ， |u|>u0.01/2, 得 P<0.01 ，按 α=0.05 水准，拒绝 H0 ，接受 H1 ，两 组间差别有统计学意义。可以认为试验组和对 照组退热天数的总体均数不相等，两组的疗效 不同。试验组的平均退热天数比对照组短。 例7-7已计算了的95%的可信区间： -3.3~-1.3 天， 给出了两总体均数差别的数量大小。
4
例 8-3(续例 7-7) 为比较某药治疗流行性出血热的疗效，
二、两样本比较的 u检验 (two-sample u-test) 适用于两样本含量较大 ( 如 n1>30 且 n2>30) 时。 检验统计量为
将 72 名流行性乙型脑炎患者随机分为试验组和对照组， 两组的例数、均数、标准差分别为： n1 32 ， X 1 2.9 ，
2
• 本例中一个总体均数已知，是特定的； • 另一个总体均数未知，只知道其中的一个样 本，属于单样本检验。 • 建立以下假设： H0： =0, 即 H1：≠0。 H0: =34.50， H1: ≠34.50。

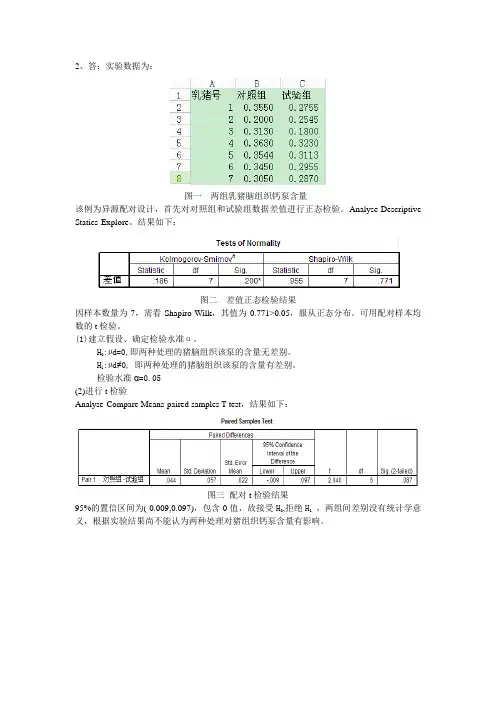
医学统计学第七章两样本均数比较的假设检验

医学统计学第七章两样本均数比较的假设检验

图一两组乳猪脑组织钙泵含量该例为异源配对设计，首先对对照组和试验组数据差值进行正态检验。

Analyse-Descriptive Statics-Explore。

结果如下：图二差值正态检验结果因样本数量为7，需看Shapiro-Wilk，其值为0.771>0.05，服从正态分布。

可用配对样本均数的t检验。

(1)建立假设、确定检验水准α。

H0:µd=0,即两种处理的猪脑组织该泵的含量无差别。

H1:µd≠0, 即两种处理的猪脑组织该泵的含量有差别。

检验水准α=0.05(2)进行t检验Analyse-Compare Means-paired samples T test，结果如下：图三配对t检验结果95%的置信区间为(-0.009,0.097)，包含0值，故接受H0,拒绝H1，两组间差别没有统计学意义，根据实验结果尚不能认为两种处理对猪组织钙泵含量有影响。

图四A、B鼠肝中铁的含量该例为完全随机设计。

首先对A、B两组进行正态性检验。

Analyse-Descriptive Statics-Explore。

结果如下：图五A、B两组鼠肝中铁含量的正态检验因样本数量为10，需看Shapiro-Wilk，A组值为0.319>0.05，服从正态分布。

B组值为0.269>0.05，服从正态分布。

对两组进行两样本方差齐性检验，Analyse-Compare Means-Independent samples T test结果为：图六A、B两组的方差齐性检验和t检验由上图得该两组样本方差齐性检验不满足方差齐性(F=8.246，P<0.05)。

可用均数比较的t`检验。

(1)建立假设、确定检验水准α。

H0:µ1=µ2,即不同饲料对鼠肝中铁的含量无影响。

H1:µ1≠µ2,即不同饲料对鼠肝中铁的含量有影响。

检验水准α=0.05(2)进行t检验如上述图六所示，两组样本方差齐性检验不满足方差齐性时，其95%的置信区间为(-0.1674,1.64674),包含0值。

《卫生统计学》第七章 假设检验基础二

《卫生统计学》第七章 假设检验基础二

24.06.2021
.
正态性检验
• 图示法:P-P图法；Q-Q图法。 • 矩法：分别对偏度和峰度系数进行检验。
（见公式7-19；公式7-21） 例2-2数据分析如下：
24.06.2021
.
24.06.2021
.
24.06.2021
.
24.06.2021
.
小结
➢ 两个大样本率的Ζ检验 ➢ 假设检验的两类错误 ➢ 假设检验的功效 ➢ 正态性检验 ➢ 讨论：思考与练习5.6.7.
计算检验统计量：
p0 0(10)/n
查标准正态分布表，得P值 若P＞α则接受 H0，反之，则拒绝 H0。
24.0体概率相等，即π1=π2 H1 ：π1≠π2
p1p2
p1p2
sp1p2
pc(1pc)(n11n12)
式中p1、p2分别为两个样本率，n1、n2分别为两样本含量， 为两个样本率之差的标准误，pc为合并阳性率。
X1 X2 X1 X2
（2）当两样本观察单位数不等时（见例7-10）
X1X2 X1/n1X2 /n2
24.06.2021
.
假设检验与区间估计的关系
➢ 置信区间具有假设检验的功能（例1）； ➢ 置信区间可以提供假设检验没有的信息：
是否有实际意义（图7-4）； ➢ 假设检验可以报告确切的概率大小，但置
.
假设检验的功效
➢ 1-β称为假设检验的功效； ➢ 意义：当所研究的总体间确有差别时，按检验水准α
能够发现它（拒绝H0）的概率。 ➢ 应用假设检验需要注意的问题： 1.应用检验方法必须符合其应用条件； 2.要权衡两类错误的危害来确定α的大小（如新药与常
规药物疗效比较时，α宜取小一些）； 3.正确理解p值的含义。

卫生统计学：第7-8章 假设检验与t检验

卫生统计学：第7-8章 假设检验与t检验
8
反证法
当一件事情的发生只有A、B两种可能的时候，为了肯 定其中的一种情况A，但又不能直接证实A，这时否定 了另一种情况B，则间接肯定了A。 证明A还是证明B？ 抗氧化剂 • 在H0成立的条件下，均数之间的差异是由抽样误差
引起的，有规律可循； • 在H1成立的条件下，均数间的不同包含种种未知情
形，无规律可循。 • 故从H0成立的角度出发，寻求其成立的概率。
分布。
数理统计的中心极限定理表明：从正态总体N ( , ) 中抽取例数均为n 的样 本，样本均 数也服从正态分布N( , X )。
Gosset 将此时的 u 转换：
X
定义为t 转换： t sX
u X X
并将t 值的分布命名为t 分布。
t 分布的图形及特征
• 单峰分布，以0为中心，左右对称 • t分布是一簇曲线，其形状与自由度υ(υ=n-1)
基本原则——小概率事件在一次试验中是不可能发生的。
建立检验假设，确定检验水准
假 设 检 验 步 骤
P≤α
计算检验统计量
确定P值
作推断结论
P>α
拒绝H0，接受H1
不拒绝H0
为了解某地1岁婴儿的血红蛋白浓度，某医 生从该地随机抽取了1岁婴儿25名，测得其血红 蛋白浓度的平均数为123.5g/L,标准差为11.6 g/L， 而一般正常小儿的平均血红蛋白浓度为125 g/L， 故认为该地1岁婴儿的平均血红蛋白浓度低于一 般正常小儿的平均血红蛋白浓度。
│t│值越大，则 P 值越小；反之，│t│值 越小，P 值越大。根据上述的意义，在同 一自由度下，│t│≥ tα ，则P≤ α ； 反之， │t│＜tα，则P＞α。
t 检验的应用条件：
单样本t 检验中，σ未知且样本含量较小 (n<50)时，要求样本来自正态分布总体；

统计学课件讲义 第7章 假设检验

统计学课件讲义 第7章 假设检验

第7章假设检验一、假设检验概述1.概念：假设检验是利用样本的实际资料来检验事先对总体某些数量特征所作的假设是否可信的一种统计分析方法。

2.主要目的：在于判决原假设的总体和当前抽样所取自的总体是否发生了显著的差异。

3.假设检验的检验法则假设检验过程就是比较样本观察结果与总体假设的差异。

差异显著，超过了临界点，拒绝H0；反之，差异不显著，接受H0。

4.假设检验中的两类错误：“弃真”、“取伪”在假设检验中，在一定样本容量下，不能同时做到犯这两类错误的概率都很小。

因为减少α会引起β增大，减少β会引起α增大。

5.基本思想：反证法思想、小概率原理6.假设检验的步骤：根据题意合理地建立原假设和备择假设→选择适当的检验统计量，并确定其分布形式→选定显著性水平，并根据相应统计量的统计分布表查出临界值→根据样本观察值计算检验统计量的观察值→根据检验规则作出接受或拒绝原假设的判断二、单个正态总体的假设检验（显著水平为α）三、两个正态总体的假设检（显著水平为α）注：2221212222212121211s s n n f s s n n n n ⎛⎫+ ⎪⎝⎭=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭+-- 四、总体比率的假设检验1、根据中心极限定理，在大样本条件下，若np 和nq 都大于5时，样本比率的抽样分布近似服从正态分布，因此，我们可用Z =作为检验统计量2、对于两总体比率之差的概率分布，可证明其近似地服从正态分布。

若总体比率未知，且1111,(1)n p n p -和 2222,(1)n p n p -都大于5时，我们可用样本比率1p 和2p 来替代。

因此，我们可用Z =五、假设检验中的其他问题1、区间估计与假设检验的关系：两者推断的角度不同、两者立足点不同、两者的主要决策参考点不同。

两者都属于统计推断方法，根据样本统计量对总体参数进行推断 对相同条件的推断问题，其推断的理论依据——抽样分布理论相同都是建立在概率基础上的推断，推断结果都具有一定的可靠程度或风险 利用置信区间可以进行假设检验2、假设检验中的p -值假设检验的p -值就是拒绝原假设的最小显著性水平。

医学统计学第七、八章 假设检验的基本概念和t检验

医学统计学第七、八章 假设检验的基本概念和t检验

S x 1 − x 2 为两样本均数差值的标准误
Sx −x
1
2
⎛1 1⎞ ⎟ = S ⎜ + ⎜n n ⎟ 2 ⎠ ⎝ 1
2 c
在两总体方差相等的条件下，可将两方差合并， 求合并方差(pooled variance) S c2
2 ⎡ ( Σ x1 ) ⎤ 2 ⎢ Σ x1 − ⎥ + n1 ⎦ ⎣ = n1 − 1 + 2 ⎡ ( Σx2 ) ⎤ 2 ⎢Σ x2 − ⎥ n2 ⎦ ⎣ n2 − 1
t 检验的应用条件:
① 单样本t检验中，σ 未知且n 较小，样本取自 正态总体； ② 两小样本均数比较时，两样本均来自正态分 布总体，两样本的总体方差相等；若两总体 方差不齐可用t’检验； ③ 两大样本均数比较时，可用Z检验。
1、样本均数与总体均数比较的 t 检验
• 使用范围：用于样本均数与已知总体均数（一 般为理论值、标准值或经过大量观察所得的稳 定值等）的比较。 • 分析目的：推断样本所代表的未知总体均数 μ 与已知总体均数 μ0有无差别。 • 若 n 较大，则 tα .ν ≈ tα .∞ , 可按算得的 t 值用 v = ∞ 查 t 界值表( t 即为 Z )得P值。
回到例子:
2.计算统计量
已知μ0＝ 3min，n＝50, X=4min
4−3 t= = 4 .7140 1 .5 / 50
υ = 50 − 1 = 49
3、确定 P 值，作出统计推断 根据算出的检验统计量如 t、z 值，查 相应的界值表，即可得到概率 P。 P值是在H0成立前提下，抽得比现有样 本统计量更极端的统计量值的概率。 P值越小只能说明：作出拒绝H0 ，接受 H1的统计学证据越充分。
X −μ X −μ 用公式：t = 或z = σX SX

应用统计学第7章 假设检验

应用统计学第7章 假设检验

•
μp
(1 )
σp
n
7.3 几种常见的假设检验
• p的抽样分布接近于 正态分布，所以检
验统计量是ZSTAT 值：
p的假设检验
Z STAT
pπ
nπ 5和 n(1-π) 5
π(1 π)
n
nπ < 5或 n(1-π) < 5
本章不讨论
7.3 几种常见的假设检验
关于总体比例，可建立如下假设：
提出原假设和备择假设 选择显著性水平 确定检验统计量 建立决策准则 做出决策
7.2 假设检验的五个步骤
7.2.1提出原假设和备择假设 原假设，H0
检验的声称或断言
例：在美国每个家庭平均有3台电视机
（H0 : μ 3）
是总体参数，不是样本统计量
H0 : μ 3
H0 : X 3
7.2 假设检验的五个步骤
的假设检验
σK已n知own (Z 检验)
检验统计量是：
σ Un未kn知own (t 检验)
7.3 几种常见的假设检验
根据抽样分布原理，当总体服从正态分布N(μ,2)时，那
么从中抽取（重复抽样）容量为n 的样本，其样本均值
服从正态分布
N , 2 / n ，而统计量
Z
x
服从标
准正态分布。
n
对于双侧检验，对给定的显著性水平α，当
解：由题意知，这是左单侧检验问题，可建立如下假设：
H0 : 0.9
H1 : 0.9
样本比例
p 82 0.82 ，检验统计量的值为:
100
Z
p
= 0.82 0.9 2.67
(1 )
0.9 0.1
n
100

应用统计学 经管类 第7章 假设检验

应用统计学 经管类 第7章 假设检验
5-5
• • • • • •
二、假设检验的步骤 （一）提出原假设与备择假设 （二）构造检验统计量 （三）确定拒绝域 （四）计算检验统计量的样本观测值 （五）做出结论
1、提出原假设与备择假设
• 消费者协会实际要进行的是一项统计检验 H0 工作。检验总体平均 =250是否成立。这 就是一个原假设(null hypothesis)，通常用 表示，即： H0 ： =250
第三节 自由分布检验
一、自由分布检验概述 自由分布检验与限定分布检验不同， 它是指在假设检验时不对总体分布的形状和参数加 以限制的检验。与参数检验相对应，自由分布检验又称为非参数检验，但这里的非参数只是 指未对检验统计量服从的分布及其参数做出限制， 并不意味着在检验中 “不涉及参数” “不 或 对参数进行检验” 。
• 解：通过统计软件进行计算。
（二）配对样本的均值检验 设配对观察值为(x,y)，其差值是 d = x-y。设 d 为差值的总体均值，要检验的是：
H 0 : d 0 ， H1 : d 0
记d
d ，则其方差是： n
2
2 d d / n Sd n(n 1) n
t
X 1000 S/ n
第三步：确定显著性水平，确定拒绝域。 α=0.05，查 t-分布表(自由度为 8)，得临界值是 t / 2, n 1 t0.025,8 =2.306， 拒绝域是(-,-2.306]∪[2.306,+)。在 Excel 中，可以使用函数 TINV(0.05,8) 得到临界值 t0.025,8 。 第四步：计算检验统计量的样本观测值。 将 X 986 ，n=9，S=24，代入 t 统计量得：
H1 • 与原假设对立的是备选假设(alternative hypothesis) ，备选假设是在原假设被否 定时另一种可能成立的结论。备选假设比 原假设还重要，这要由实际问题来确定， 一般把期望出现的结论作为备选假设。

社会统计学(卢淑华),第七章

社会统计学(卢淑华),第七章



3、给出小概率 4、用样本统计量的观测值进行判断
例：某地收入水平调查状况如下：x 870 s 21 n 50 问：该地上报的平均收入为880元是否 可信？（显著性水平为 0.05）


（二）两类错误 1、弃真错误： 把一次观测中出现在拒绝域的小概率事件 当作对原假设的拒绝，此时会发生。犯错 误的大小为 2、纳伪错误：
在接受原假设时犯的错误，犯错误的概率 为 。 0 越小， 数值越大
2
拒绝 H 0 ；反之接受 2）单边检验

H
0
右侧：只有当样本计算统计量的值过大：
z z 才会落入拒绝域；如果 z z 接受。

左侧： pz z
三、假设检验的步骤不两类错误
其分布
0



3、假设检验的基本原理： 小概率原理： 1）小概率事件是在一次观察中是不可能出现的事 件。 2）如果在一次观察中出现了小概率事件，那么， 合理的想法是否定原有事件具有小概率的说法。 假设检验思想在统计学中的描述：经过抽样获得 一组数据（即样本）：根据样本计算的统计量， 如果：原假设成立的条件下几乎不可能发生的， 就拒绝或否定原假设；如果在原假设成立的条件 下，根据样本计算的统计量发生的可能性不是 小，则接受。
第七章 假设检验的基本概念
一、统计假设 1、统计假设：

收集资料的范围仅是全体的一部分，是一 个随机样本，那么，这种和抽样手段联系 在一起，并且依靠抽样数据进行验证的假 设，即统计假设。
2、原假设和备择假设
1）原假设（虚无假设或解消假设）H 0 ： 根据已有资料周密考虑后确定 2）备择假设（研究假设）H 1 ： 原假设的逻辑对立假设 三种形式：单边（左、右） 双边

统计学,刘照德07-1第七章 假设检验

统计学,刘照德07-1第七章 假设检验

一、假设检验的概念
称为 t检验。 • 3. 显著性水平，即指原假设为真时拒绝原假 设的概率，通常很小，而1-就很大。若总体没 有发生显著性变化，则样本统计量应该落在以总 体待估参数为中心的概率为1-的区域内。该区域 称为抽样分布的接受域；否则，总体就发生了显 著性变化，样本统计量应该落在概率 为1-的区域 外，该区域被称为抽样分布的拒绝域。因此，被 称为显著性水平。常用的值有0.01, 0.05, 0.10。而 接受域和拒绝域的分界点的数值就称为临界值。
1.建立假设 H0：μ=μ0=5 H1：μ≠μ0= 5，
一、假设检验的概念
1. 假设是指对总体参数的数值所作的一种 陈述。总体参数包括总体均值、总体比例（成 数）、总体方差等。 原假设是指待检验的假设，研究者想收集 证据予以反对的假设，表示为H0 。通常有 , 或三种形式。【例7-1】中H0：μ=5。 备择假设是指与原假设对立的假设，研究 者想收集证据予以支持的假设，表示为H1 。 其通常对应原假设也有三种形式：,或三种 。【例7-1】中H1：μ≠5。
一、假设检验的概念
• 根据不同的显著性水平值，可得到不同的统 计量临界值。这些临界值可通过查表得到。【例 7-1】=0.05，查表得拒绝域：t t / 2 2.064
4. 检验规则，第一种是根据拒绝域，将检验统计量 的值与水平的临界值进行比较，得出拒绝或不拒绝原 假设H0的结论，称为临界值规则，【例7-1】解答用了 临界值规则。第二种是将检验统计量值对应的概率p与 显著性水平进行比较，若P＜α，则检验统计量落入拒 绝域，拒绝H0；否则，不能拒绝H0，称这种检验规则为 P-值规则，计算机软件中通常用P-值规则。
一、假设检验的概念
• 而那些“不明确的陈述”是指新的、可能的、猜 测的，处于备择假设的位置。例如某公司，以前 生产的产品的废品率不低于18%，是明确的陈述 18 % ；该公司对生产设备进行 ，因此， H 0： 改造后，生产的产品的废品率下降是不明确的陈 述，因此，H1：π＜18%。 • 假设检验是指利用样本统计量的取值，来检 验事先对总体参数或总体分布所作的假设是否成 立的一种统计推断方法。

假设检验课件

假设检验课件

z
0
0.916
25
0
• 3 . 拟定p值，作出推断结论 • 当z=0.916时相应旳单侧P=0.1788，P>0.05，按
α=0.05 • 水准，不拒绝H0，能够以为2023年该市无菌化脓17发
二、两独立样本资料旳z检验
当总体均数λ≥20时， Possion分布近似正态分布。
H0 λ1=λ2 H1 λ1≠λ2 α=0.05
2
1 n1
1 n2
样本估计值为 ：
S X1X2
Sc2
1 n1
1 n2
S
2 c
n1 n1
n2 n2
S
2 c
X
2 1
(X 1 )2
/
n1
X
2 2
n1 n2 2
(X 2 )2
/ n2
6
已知S1和S2时：
Sc2
(n1
1)S12
(n2
1)
S
2 2
n1 n2 2
若n1=n2时：
S X1X 2
降低II型错误旳主要措施：提升检验效能。 提升检验效能旳最有效措施：增长样本量。 怎样选择合适旳样本量：试验设计。
33
假设检验应该注意旳问题
34

正态性检验 和两样本方差比较旳F检验
35
➢ t 检验旳应用条件是正态总体且方差齐性；配对 t 检验则要求每对数据差值旳总体为正态总体。
➢ 进行两小样本t检验时，一般应对资料进行方差
15
Possion分布资料旳z检验
•当总体均数λ≥20时， Possion分布近似正态分布。
x
z
0
0
•一、单样本资料旳z检验

第7章思考与练习

第7章思考与练习

第七章 假设检验【思考与练习】一、思考题1．解释零假设与备择假设的含义。

2．简述假设检验的基本步骤。

3．举例说明单侧检验与双侧检验的选择。

4．解释I 型错误、II 型错误和检验效能，并说明它们之间的关系。

5．简述假设检验与置信区间估计的联系。

二、案例辨析题为了比较非洛地平与常规药物治疗高血压的疗效差异，某医生随机抽取100名原发性高血压患者，分别测量患者接受非洛地平治疗前后的血压差值，计算得其21.5X =mmHg ，8.0S =mmHg 。

现已知常规药能使高血压患者的血压平均下降20mmHg 。

该医生对其进行了t 检验，零假设是μμ0=，备择假设是μμ0≠，检验水准0.05α=。

计算得 1.875t =，按100ν查t 界值表，得0.10P 0.05<<，故接受0H ，认为非洛地平与常规药物治疗高血压的疗效无差别。

你认为该结论正确吗？请说明理由。

三、最佳选择题1．比较两药疗效时，下列可作单侧检验的情形是A ．已知A 药与B 药均有效 B ．已知A 药与B 药均无效C ．已知A 药不会优于B 药D ．已知A 药与B 药差不多好E ．不知A 药好还是B 药好 2．假设检验的基本步骤是A ．计算检验统计量、确定P 值、做出推断结论B ．建立无效假设、建立备择假设、确定检验水准C ．建立无效假设、计算检验统计量、确定P 值D ．确定单侧检验或双侧检验、选择t 检验或Z 检验、估计I 型错误概率和II 型错误概率E．建立检验假设和确定检验水准、计算检验统计量、确定P值并做出统计推断3．假设检验时，若检验水准α=0.05，则下列关于检验结果的说法正确的是A．若P<0.05，则不拒绝H，此时可能犯II型错误B．若P<0.05，则拒绝H，此时可能犯II型错误C．若P<0.05，则不拒绝H，此时可能犯I型错误D．若P>0.05，则拒绝H，此时可能犯I型错误E．若P>0.05，则不拒绝H，此时可能犯II型错误4．假设检验时，所犯II型错误概率最小的检验水准α为A．0.01 B．0.025 C．0.05D．0.10 E．0.205．有关两样本均数的比较，检验统计量t越大A．说明总体参数差别越大B．说明总体参数差别越小C．说明样本统计量差别越大D．说明样本统计量差别越小E．越有理由认为两总体参数不等6．在样本均数与已知总体均数比较的t检验中，结果 3.24t=，0.05/2,2.086tν=，0.01/2,2.845tν=，按检验水准0.05α=，可认为此样本均数A．与该已知总体均数不同B．与该已知总体均数差异很大C．所对应的总体均数与已知总体均数差异很大D．所对应的总体均数与已知总体均数相同E．所对应的总体均数与已知总体均数不同7．下列关于单侧检验和双侧检验的说法正确的是A．采用单侧检验更好B．采用双侧检验更好C．采用单、双侧检验都无所谓D．根据专业知识确定采用单侧检验还是双侧检验E．根据检验统计量的计算结果确定采用单侧检验还是双侧检验8．样本均数与已知总体均数比较的t检验时，P值越小说明A．样本均数与已知总体均数差别越小B．样本均数与已知总体均数差别越大C．样本所对应的总体均数与已知总体均数差别越大D．越有理由认为样本均数与已知总体均数不同E．越有理由认为样本所对应的总体均数与已知总体均数不同9．下列关于I型错误概率α和II型错误概率β的说法不正确的是A．当样本量确定时，α越小，β越大B．当样本量确定时，α越大，β越小C．欲减小犯I型错误的概率，可取较小αD．欲减小犯II型错误的概率，可取较大αE．若样本含量足够大，可同时避免犯这两型错误四、综合分析题1．已知服用某种营养素一个疗程后，受试者某项生化指标平均增加52个单位。

心理统计学 第七章假设检验

心理统计学 第七章假设检验
α和β 的关系就像翘翘板， 的关系就像翘翘板， 就大， α小β 就大， α大β 就小
β
α
四、单侧与双侧检验
• 1.双侧检验：只强调差异 1.双侧检验： 双侧检验 而不强调方向性的检验。 而不强调方向性的检验。
H 0 : µ = µ0
• 2.单侧检验：既强调差异 2.单侧检验： 单侧检验 又强调方向性的检验。 又强调方向性的检验。
• （二）两类错误的关系
• • • • • 1. α+β不等于1 不等于1 是在两个不同前提下的概率。 α和β是在两个不同前提下的概率。 2. α和β不可能同时增大或减小 增大样本容量n 可同时减小两类错误。 增大样本容量n，可同时减小两类错误。 3.统计检验力 统计检验力1 3.统计检验力1-β。
解： 提出假设：用μ1表示受过早期教育的儿童的平均智商。单侧检验，提出假设： ⑴提出假设 Ho： H1： Ho：μ1≤μo=100 H1：μ1＞μo=100 选择并计算统计量： ⑵选择并计算统计量：由于总体方差已知，样本平均数服从正态分布。
⑶查表确定临界值：Z0.05=1.645 查表确定临界值： 统计决断： p<0.05。 ⑷统计决断：Z=1.84> Z0.05=1.645 ，p<0.05。 p<0.05 落在拒绝区域，所以拒绝零假设，接受备择假设。 即应该认为受过良好早期教育的儿童智力高于一般水平。 即应该认为受过良好早期教育的儿童智力高于一般水平。
Ⅰ型错误：也称α型错误或弃真错误，即H0为真拒绝H0（拒 为真拒绝H 型错误：也称α型错误或弃真错误， 绝了一个本应接受的假设）； 绝了一个本应接受的假设）； 型错误：也称β型错误或取伪错误， 为假接受H Ⅱ型错误：也称β型错误或取伪错误，即H0为假接受H0（接 受了一个本应拒绝的假设）。 受了一个本应拒绝的假设）。 负责任的态度是无论做出什么决策， 负责任的态度是无论做出什么决策， 都应该给出该决策可能犯错误的概率。 都应该给出该决策可能犯错误的概率。

《应用统计学》第章：单个总体的假设检验

《应用统计学》第章：单个总体的假设检验

《应用统计学》第7章：单个总体的假设检验第7章单个总体的假设检验本章教学目标了解和掌握统计推断中的另一个基本问题：参假设检验及其在经济管理中的应用；掌握运用 Excel 的“数据分析”及其统计函数功能求解假设检验问题。

本章主要内容：§71>.1 案例介绍§7.2 假设检验的基本原理§7.3 单个正态总体均值的检验§7.4 单个正态总体方差的检验本章重点：假设检验中不可避免的两类错误及其应用 Excel“数据分析”功能的使用及其运行输出结果分析。

难点：假设检验中不可避免的两类错误及其应用。

§7.1 案例介绍【案例1】新工艺是否有效？某厂生产的一种钢丝的平均抗拉强度为 10560 (kg/cm2)。

现采用新工艺生产了一种新钢丝，随机抽取 10 根，测得抗拉强度为： 10512, 10623, 10668, 10554, 1077610707, 10557, 10581, 10666, 10670求得新钢丝的平均抗拉强度为 10631.4(kg/cm2)。

是否就可以作出新钢丝的平均抗拉强度高于原钢丝，即新工艺有效的结论?某台加工缸套外径的机床，正常状态下所加工缸套外径的标准差应不超过0.02 mm。

检验人员从加工的缸套中随机抽取 9 个，测得外径的样本标准差为 S = 0.03 mm。

问：该机床的加工精度是否符合要求?【案例2】机床加工精度是否符合要求?§7.2 假设检验的原理一、实际推断原理假设检验的理论是小概率原理，又称为实际推断原理，其具体内容是：小概率事件在一次试验中是几乎不可能发生的。

二、假设检验推理的思想方法假设检验推理的思想方法是某种带有概率性质的反证法。

三、基本原理和步骤例1：统计资料表明，某电子元件的寿命 X～N(??0 , ?? 2 )，其中 ??0已知，?? 2 未知。

现采用了新工艺生产，测得新工艺生产的 n 个元件寿命为 x1, x2, ···, xn。

统计学第七章假设检验和非参数统计

统计学第七章假设检验和非参数统计

4、计算T值：根据裁判的观察确定球的 反弹角度为X
5、统计判断：当一名球员使用上肢之外 的身体部分触球时，球的反弹角度为X的概率 为0.03。由于0.03＜0.05，拒绝原假设，即认 为球员A存在上肢触球。
在本例中，有3％的可能性发生弃真错误， 即球员A没有上肢触球，但裁判作出了错误判 断。
显著性水平α在这里决定了某一个结论能 否被接受。
例题：
对24名儿童依次进行一项测试活动，获得 下列分数序列：
31，23，36，43，41，44，12，26，43， 75，2，3，15，13，78，24，13，27，86，61， 13，7，6，8
转化成上下游程，为：－，＋，＋，－， ＋，－，＋，＋，＋，－，＋，＋，－，＋， －，－，＋，＋，－，－，－，－，＋
二、确定适当的检验统计量T
检验统计量T是用于检验原假设是否成立 的标准，在原假设成立的前提下，统计量T满 足某种特征。
四、计算检验统计量T的值
根据检验中获得的数据，计算统计量T的 值。
五、作出统计决策
根据T的取值特征，计算取该值的概率， 如果此概率小于a，则拒绝原假设。
第一节 检验原理
一、提出原假设（Null Hypothesis）和 备择假设（Alternative Hypothesis）
建立原假设H0：P＋＝P－
计算两种符号的数量S＋和S－，利用二 项分布计算S＋或S－出现的概率是否处于接受 域。
在n>20的情况下，二项分布可以用正态 分布进行近似：
符号检验中仍然没有利用总体的分布特 征。
四、游程检验
游程检验又称连贯检验或串检验，用于考 察一个序列中两种符号的出现次序是否随机。
本例，如果α变为0.15，这时当一名球员 使用上肢之外的身体部分触球时，球的反弹 角度为X的概率为0.10，就可以拒绝原假设， 即认为球员A存在上肢触球。但如果α为0.05， 在反弹角度为X的概率为0.10时，就要接受原 假设。

社会统计学第7章假设检验的基本概念

社会统计学第7章假设检验的基本概念
即直接检验H0,间接检验H1。
•小概率 原理：
如果对总体的某种假设是真实的，那么不利于 或不能支持这一假设的事件A（小概率事件）在 一次试验中几乎不可能发生的；要是在一次试 验中A竟然发生了，就有理由怀疑该假设的真实 性，拒绝这一假设。
总体
抽样
（某种假设）
检验
（接受）
小概率事件 未发生
样本 （观察结果）
H0：μ≤μ0，H1：μ＞μ0（右端检验）
右端检验与左端检验
右端检验：临界值和显
著性水平有如下的关系式：
P(Z>Z)= 左端检验：临界值和显著
性水平有如下关系式：
P(Z<-Z)=
注意：相同的情况下，
接受域
否定域
Z
一端检验比二端检验功效高些，
也就是说二端检验更难否定研
接受域
究假设。
否定域-Z
四、假设检验的检验规则
第七章
假设检验的基本概念
一、什么是假设检验
所谓假设检验，就是先成立一个关于 总体情况的假设，然后抽取一个随机样本， 以样本的统计值来验证对总体的假设。
假设检验的意义：由于我们难以完全 知道所关心的总体的数量特征与变化情况， 因此常常需要对其进行假设，而假设是否 成立，需要进行检验。
假设在社会科学中可以用于不同的层次。最高 层次是理论假设，而理论层次的假设一般是无法加 以直接验证的。为了能从理论上证实这些假设，必 须概念操作化，把理论假设转变为可操作的经验性 假设。再通过社会调查证明原有的假设是否合理。
显著性水平
显著性水平，一般是指在原假设成立
条件下，统计检验中所规定的小概率的标
准，即规定小概率的数量界线，常用的标
准有=0.10，=0.05或=0.01(即否定

统计学第四版第7章假设检验(简)总结

统计学第四版第7章假设检验(简)总结
02
~ 2 n 1
2 n 1 s 当H 为真时，统计量 2
2 n 1 s 20 10.0042 2 统计量的值 31.92
2
0.0025
2 0.10， 查 2分布表得 02.05 （ 19） 30.14， 0 19 10.12 .95

假设检验分为两类：参数检验、非参数检验/自
由分布检验
2
例1

消费者协会接到消费者投诉，指控品牌纸包装饮
料存在容量不足，有欺骗消费者之嫌。包装上标 明的容量为250毫升。消费者协会从市场上随机抽 取50盒该品牌纸包装饮品，测试发现平均含量为 248毫升，小于250毫升。这是生产中正常的波动， 还是厂商的有意行为？消费者协会能否根据该样 本数据，判定饮料厂商欺骗了消费者呢？

提出原假设和备择假设→根据抽样分布，计算样本统 计量→选择显著性水平α ，查表确定临界值→判断并 得出结论。
8
第一步：确定原假设与备择假设
： =255；

：

≠250
原假设H0：通常是研究者 想收集证据予以反对的假 设，也称为零假设
备择假设H1：通常是研究 者想收集证据予以支持的 假设，也称为研究假设。
3
例2

一种罐装饮料采用自动生产线生产，每罐
的容量是255ml，标准差为5ml。为检验每罐
容量是否符合要求，质检人员在某天生产
的饮料中随意抽取了40罐进行检验，测得每
罐平均容量为255.8ml。检验该天生产的饮
料容量是否符合标准要求。
4
例3

根据过去大量资料，某厂生产的产品的使
用寿命服从正态分布N（1020，1002）。现

第七章假设检验

第七章假设检验

第三节
u检验
u检验（u test ），亦称z检验（z test） 大样本均数（率）与总体均数（率）比较的u检 验、 两个大样本均数（率）比较的u检验 一、大样本均数比较的u检验 二、大样本率的u检验
一、大样本均数比较的u检验
假定样本数据服从正态分布 ，当总体标准差 未知时，可用样本标准差作为估计值 这里的总体均数一般是指已知的理论值、标准 值或经过大量观察所得到的稳定值，记作µ 0 （或记为 ）
两个样本率p1、p2的差值服从正态分布
u p1 p2
1 2
p p
2 2 p p p p 1 (1 1 ) / n1 2 (1 2 ) / n2
1 2 1 2
样本率p介于0.1～0.9之间，每组例数大于60 例
n1 p1 n2 p2 ˆ0 n1 n2
两样本均数比较的u检验
该检验方法适用于完全随机设计中两组 计量资料差别的比较 两样本均数差值服从正态分布
u Leabharlann 1 X 2X1X2
X
1X2
2 2 2 2 X / n 1 1 2 / n2 X2 1

当总体标准差未知，两组例数均超过30
ˆX
1X2
亦称样本率与总体率的比较的u检验，这里的 总体率一般是指已知的理论值、标准值或经大 量观察所获得的稳定值。
例7–3 全国调查的调查结果，学龄前儿童营 养性贫血患病率为23.5%。某医院为了解当
地学龄前儿童能够营养性贫血患病情况，对
当地1396例学龄前儿童进行了抽样调查，查
出营养性贫血患儿363例，患病率为26.0%。
ˆp p
1
2
1 1 ˆ0 (1 ˆ0 )( ) n1 n2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七章 假设检验Ⅰ．学习目的假设检验包括参数检验与非参数检验，是一种最能体现统计推断思想和特点的方法。

通过本章学习，要求：1.掌握统计检验的基本原理，理解该检验的规则及犯两类错误的性质；2.熟练掌握总体均值、总体成数及总体方差指标的各种检验方法，包括：z 检验、t 检验和p 值检验；3.掌握2 检验、符号检验、秩和检验及游程检验四种基本的非参数检验方法。

Ⅱ．课程内容要点 第一节 假设检验的基本原理一、假设检验的基本原理 “小概率原理”：小概率事件在一次试验中几乎是不会发生的。

事先所做的假设，是假设检验中关键的一项工作。

它包括原假设和备选假设两部分。

原假设是建立在假定原来总体参数没有发生变化的基础之上的。

备选假设是原假设的对立，是在否认原假设之后所要接受的，通常这是我们真正感兴趣的一个判断。

二、假设检验的规则与两类错误 1、假设检验的规则 假设检验的步骤：（1）首先根据实际应用问题确定合适的原假设0H 和备选假设1H ； （2）确定检验统计量，通过数理统计分析确定该统计量的抽样分布；（3）给定检验的显著性水平α。

在原假设成立的条件下，结合备选假设的定义，由检验统计量的抽样分布情况求出相应的临界值，该临界值为原假设的接受域与拒绝域的分界值；（4）从样本资料计算检验的样本统计量，并将其与临界值进行比较，判断是否接受或拒绝原假设。

从检验程序我们可以看出，统计量的取值范围可以分为接受域和拒绝域两个区域。

拒绝域正是统计量取值的小概率区域。

按照我们将这个拒绝域安排在所检验统计量的抽样分布的某一侧还是两端，可以将检验分为单侧检验或双侧检验。

双侧检验中，又可以根据拒绝域，是在左侧还是在右侧而分为左侧检验和右侧检验。

对于这些双侧、左、右单侧检验，我们要结合备选假设来考虑。

在检验规则中，我们经常碰到两种重要的检验方法：z检验与t检验。

p值检验的原理：给出原假设后，在假定原假设正确的情况下，参照备选假设，可以计算出检验统计量超过或者小于（还要依照分布的不同、单侧检验、双侧检验的差异而定）由样本所计算的检验统计量的数值的概率，这便是p值；而后将此概率值跟事先给出的显著性水平值α进行比较。

如果该值小于α，否定原假设，取对应的备选假设。

如果该值大于α，我们不就能否定原假设。

2、两类错误H实际为真，但我们却依据样本信息，做出拒绝的错误结论当原假设时，称为“弃真”错误；当原假设实际为假，而我们却错误接受时，称为“纳伪”错误。

通常记显著性水平α为犯“弃真”错误的可能性大小，β为犯“纳伪”错误的可能性大小。

由于两类错误是一对矛盾，在其他条件不变得情况下，减少犯“弃真”错误的可能性大小（α），势必增大犯“纳伪”错误的可能性大小（β），也就是说，β的大小和显著性水平α的大小成相反方向变化。

三、检验功效-可以用来表明所做假设检验工作好坏的一个指标，我们称之为检1β验功效。

它的数值表明我们做出正确决策的概率为1β-。

解决增强检验功效的唯一办法只有增大样本容量，这样既能保证满足取得较小的α，又能取得较小的β值。

第二节 总体参数假设检验一、总体均值的假设检验 1、总体方差2σ已知对于双侧检验，建立的假设为：0010:,:H H μμμμ=≠对于左（右）单侧检验来说，建立的假设为：0010:,:(H H μμμμ=<或>)检验统计量X z =～(0,1)N原假设的拒绝域为：样本统计量的值z 满足：12z zα->（双侧检验）；1z z α-<-（左单侧检验）；1z z α->（右单侧检验）。

当z 值处于拒绝域中时，我们就可拒绝原假设，否则不能拒绝原假设。

2、总体方差2σ未知对于双侧检验，建立的假设为：0010:,:H H μμμμ=≠ 对于左（右）单侧检验来说，建立的假设为：0010:,:(H H μμμμ=<或>)检验统计量X t =～(1)t n -，其中221()1ni i X X s n =-=-∑为样本标准差。

原假设的拒绝域为：样本统计量的值t 满足12(1)t tn α->-（双侧检验）；1(1)t t n α-<--（左单侧检验）；1(1)t t n α->-（右单侧检验）。

当t 值落入拒绝域，就拒绝原假设，否则不能拒绝原假设。

二、两个总体均值之差的检验1、两总体方差22X Yσσ、已知 ⑴ 双侧检验原假设为：0:X Y H μμ=，备选假设为1:X Y H μμ≠检验统计量：X Yz =～(0,1)N 。

该检验的否定域：12z zα->。

反之不能拒绝原假设。

⑵ 左单侧检验原假设与双侧一样，备选假设为1:X Y H μμ< 检验的否定域为：计算的样本统计量满足：1z z α-<- (3) 右单侧检验原假设与双侧一样，备选假设为1:X Y H μμ> 检验的否定域为：计算的样本统计量满足：1z z α->2、两总体方差22X Yσσ、未知但相等 双、单侧检验的原假设都相同，均为0:X Y H μμ=。

只是在双侧检验时，备选假设1:X Y H μμ≠；在左单侧检验时，备选假设为1:X Y H μμ<；在右单侧检验时，备选假设为1:X Y H μμ>。

检验统计量：X Yt =12(2)t n n +-。

对于双侧检验，原假设的拒绝域为：12t tα->。

反之就不能拒绝原假设。

对于左、右单侧检验，左单侧检验拒绝原假设的范围是：112(2)t t n n α-<-+-。

右单侧检验拒绝原假设的范围为：112(2)t t n n α->+-。

三、总体成数的假设检验1、单样本成数检验建立假设：0010:,:H P H P ρρ=≠检验统计量z =～(0,1)N 。

将样本统计量与临界值进行比较，若12z z α->，则否定原假设；反之则不能拒绝原假设。

当然，如果对应的原假设是单边的，即为00:()H P ρ≥≤或。

对应的临界值应该是1z α-，其余的计算和判断规则如上面所述。

2、两个样本总体成数差的检验检验统计量(0,1)z N =。

若建立的原假设为：012:H ρρ=，相应的临界值为12zα-；而如果建立的原假设为：012:()H ρρ≥≤或，相应的临界值为1z α-。

能否拒绝原假设的判断规则如前面所述。

四、正态总体方差的假设检验原假设为2200H σσ=：，备选假设：2210()H σσ≠≥≤：或者检验统计量 22212(1)n n s χχσ--=五、两个正态总体方差比的检验 1、两总体均值X Y μμ、已知检验统计量2122(,)X Ys F F n n s = ，其中122111()n X i X i s X n μ==-∑ ；222121()n Yi Y i s Y n μ==-∑。

原假设为：220X Y H σσ=：。

对于双侧检验，备选假设为：221X Y H σσ≠：，若()()1212122,,F F n n F Fn n αα-<>或则拒绝原假设，反之，则不能拒绝原假设。

对于左单侧检验： 备选假设：221X Y H σσ≥：，拒绝域为样本统计量()12,F F n n α<。

对于右单侧检验：备选假设：221X Y H σσ≤：，拒绝域为样本统计量()112,F F n n α->。

2、两样本均值X Y μμ、未知建立的原假设为：220X Y H σσ=：，检验统计量2122(1,1)XYS F F n n S =-- ，其中122111()1n Xi i S X X n ==--∑和222121()1n Yi i S Y Y n ==--∑。

对于双侧检验：备选假设：221X YH σσ≠：，当样本统计量122(1,1)F F n n α<--或1212(1,1)F Fn n α->--时，我们就拒绝原假设，反之不能拒绝原假设。

对于左单侧检验：建立的备选假设：221X YH σσ≥：，供判断的临界值为12(1,1)F n n α--，拒绝域为样本统计量()121,1F F n n α<--。

对于右单侧检验：建立的备选假设：221X YH σσ≤：，供判断的临界值为112(1,1)F n n α---，拒绝域为样本统计量()1121,1F F n n α->--。

第三节 非参数检验一、非参数检验概述实际问题中，可能无法获知或者是不一定很了解总体的分布类型，而只是通过样本来检验关于总体分布的假设。

这种检验方法称为非参数检验。

非参数检验与传统的参数检验比较有一些优缺点；对检验的限制更少，更加避免先见偏差，具有较好的稳健性；可以在更少样本资料要求的情况下进行，在一定程度上弥补有些实际中样本资料不足等的缺陷；可以弥补上述参数检验中碰到的无法运用的属性资料问题，然而，同时也就可能损失了其中所包含的另外信息。

二、2χ检验2χ检验是利用2χ分布的原理，通过对样本数据进行分析来对样本所属的总体情况进行判断的一种检验方法。

1．分布拟合检验原假设为：0010:()(),:()()H F X F X H F X F X =≠。

其中()F X 为总体的分布函数，0()F X 是某个事先假定的总体分布函数。

检验统计量：221()mi i i i f np np χ=-=∑～2(1)m k χ--。

其中i f 为各个样本区间内的实际频数，11()()()i i i i i p P X x X F X F X --=<<=-为落在各个区间的理论概率值，k 为待估计的参数个数。

拒绝原假设的值域：22(1)m k αχχ>--，如果样本统计量2χ大于2(1)m k αχ--，那么就可以拒绝原假设，否则不能拒绝原假设。

2．独立性检验该检验主要是考察多个变量之间是否有关联，如果变量之间没有关联性，那么就说变量之间是相互独立的。

我们这里的变量主要是定类、定序的资料。

为了分析变量之间的关联性，我们需要将资料整理成列联表的形式。

列联表是多行多列纵横交错所形成的一个表体。

三、符号检验1．单样本的符合检验在单样本的情况下，符号检验适用于检验总体中位数是否在某一指定的位置。

中位数检验的基本原理是，假设总体中位数的真值e M A =，然后在实际抽取的容量为n 的样本中，将每个观测值(1)i x i n ≤≤均减去A ，并只记录其差值的符合，即为()i i i x Asign x A x A +>⎧-=⎨-<⎩当当。

若i x A =，就略去不计。

接着分别计算“+”的个数（用n +表示）和“-”的个数（用n -表示）。

理论上，当中位数e M A =为真时，得到的正负号个数应该接近相等，即n n +-≈。

若从样本中得到的n +和n -相差较远，那么就有理由拒绝e M A =。