材料织构三维取向分析的数学基础
- 格式:pdf
- 大小:466.52 KB
- 文档页数:8

三维编织复合材料细观结构的几何学分析
三维编织复合材料细观结构的几何学分析,是指对三维编织复合材料细观结构进行几何学分析,以求解物理性能。
三维编织复合材料细观结构是指在三维编织中,由各种原料(如玻璃纤维、碳纤维、聚酯纤维、陶瓷纤维等)和基体材料(如聚氨酯树脂、环氧树脂等)组成的复合结构。
通过几何学分析,可以了解复合材料细观结构中纤维的布置方式、纤维的形状特征以及纤维与基体材料之间的相互作用关系等,为复合材料的性能预测提供重要信息。
它可以用来估算三维编织复合材料的力学性能,如拉伸强度、抗弯强度、抗压强度、拉伸模量、抗弯模量和抗压模量等。
此外,几何学分析还可以用来对复合材料的热物理性能进行预测,如热膨胀系数、热导率、热容量、热阻和热损失等。
以上信息有助于研究人员了解复合材料在多种环境条件下的行为和性能,为设计更先进和更高性能的复合材料提供参考。


三维编织复合材料细观结构与力学性能分析三维编织结构复合材料作为一种新型高级的复合材料,在国外得到迅速的发展,而国内对于这种结构复合材料的研究相对较少。
本文采用控制体积单元法与试验观察相结合的方法研究了三维编织复合材料的细观结构,并采用数值计算方法分析了三维编织复合材料的弹性性能,具有一定的理论价值和实际工程意义。
三维编织结构复合材料是完全整体、连续、多向的纺线(纤维束)的网络,充填以延性材料,这类新材料已失去通常复合材料的层合板概念,由此,层合板复合材料层间脆弱的致命弱点在编织结构复合材料中得到克服,所以编织结构复合材料具有高的强度和刚度(包括在厚度方向),接近实际形状的制造,高的冲击韧性、高的损伤阻抗,和按实际设计要求的特定的航空航天方面的使用功能,因而广泛地受到工业界和学术界的关注。
文中从三维编织物的编织工艺入手,得到编织复合材料的几何结构,建立了织物纱线构造模型(FAM-Fabric Architecture Model),进而分析其力学性能;另外,通过试验研究了这种复合材料的力学性能。
主要的研究内容包括以下几个方面:系统地研究了采用四步法1×1方型编织工艺编织的预成形件及其增强的复合材料的细观结构。
提出了纱线椭圆形横截面假设,考虑了编织纱线的细度和编织纱线填充因子的影响。
根据编织过程中携纱器的运动轨迹特点,将预成形件划分为三个不同的区域,分别定义了不同的控制体积单元,识别了预成形件的两种局部单胞模型,分析了预成形件的纱线构造,并导出了编织结构参数之间的关系,同时给出三维编织复合材料的设计方法。
主要的编织结构参数包括试件的外形尺寸、主体纱行数和列数,三个区域各自所占的体积百分比、编织纱线的细度、纱线填充因子、纤维体积含量、编织角以及编织花节长度。
以精确的复合材料单胞模型为基础,从最小的可重复的单胞入手,对单胞的结构进行简化分析,认为纤维是平直的,将单胞中的四个不同方向的纤维束看成是空间四个不同方向的单向复合材料,纤维束的性能可以等价于单向复合材料的宏观性能。

三维编织复合材料数值计算方法我折腾了好久三维编织复合材料数值计算方法,总算找到点门道。
一开始的时候,我真的是瞎摸索。
我就知道些基础的数值计算原理,比如有限元法,但对于三维编织复合材料,那完全是两眼一抹黑。
我当时就想,这三维编织复合材料结构那么复杂,那些纤维编织来编织去的,得从哪儿下手呢。
我最先尝试的就是按照普通复合材料的有限元方法去做,把三维编织复合材料当作普通的一样来处理。
我就定义材料的属性,划分网格啥的。
但是结果一出来,就知道完全错了。
我就纳闷儿,怎么回事呢?后来我仔细一研究才明白,三维编织复合材料的内部结构特殊,纤维之间的相互作用和普通的不一样。
这就好比你把一堆杂乱无章的绳子看作是直直的木棍一样,那肯定不行啊。
后来我就专门去找关于三维编织复合材料结构分析的书和论文。
看到有些方法提到要先对其微观结构进行合理的简化假设。
我就根据这个开始重新做。
比如说,我把复杂的编织结构假设成一些简单的单元组合,像一根根小的纤维束组合在一起。
这个时候再建立有限元模型进行数值计算,感觉就有点那么个意思了。
不过,在定义纤维和基体之间的相互作用参数的时候,又把我给难住了。
我按照一些资料上的数据设置,但是算出来的结果总是和实际有点偏差。
我也不确定是我测量参数的方式有问题,还是那个数据本身就不太适合我研究的这种具体的三维编织复合材料。
我只能反复去调整参数,一点点试。
又试了几次之后,我发现多考虑一些编织过程中产生的残余应力对数值计算影响还挺大的。
就好比你织毛衣的时候,你拉扯毛线留下的一种内在的松紧度一样,这个在三维编织复合材料里可不能忽视。
这时候得到的结果就比较接近实际检测的值了。
我还尝试过用离散单元法来做数值计算。
这个方法就是把材料离散成一个个小的单元,每个单元可以有不同的特性。
但是这个方法对于三维编织复合材料来说,计算量太大了。
我的电脑跑了好几天都没算出个结果来。
我就想,这方法虽然理论上可行,但是在实际操作中,你没有个超级计算机根本玩不转啊。




织构概述第一节钢板的常见织构类型1.1织构的表达方法织构是多晶体取向分布状态明显偏离随机分布的取向分布结构,通常用晶体的某晶面晶向在参考坐标系中的排布方式来表达晶体的取向。
在立方晶体轧制样品坐标系中,常用(HKL)[UVW]来表达某一晶粒的取向。
这种晶粒的取向特征为(HKL)晶面平行于轧面,[UVW]晶向平行于轧向。
另外也可以用[RST]=[HKL]×[UVW]表示平行于轧板横向的晶向。
1.2织构的分析方法关于织构的分析方法渊源已久,早在1924年Wever就提出了极图法,1948年以后,Deker和Schulz发展了用衍射仪测定极图的方法,使极图法趋于完善。
1952年Harris为测定轧制铀棒的织构提出了反极图法,后经Mueller等发展而完善。
1965年,Roe和Bunge分别采用级数展开方法,从几张极图中推导出晶体的三维取向分布函数(ODF),使材料织构的细致、定量分析成为可能。
ODF分析法把晶体取向与试样外观的关系用三维取向空间表达出来,这一取向空间就是欧拉空间(Eulerianspace),欧拉空间的坐标用欧拉角表示,它与归一化后的晶体取向(hkl)[uvw]有着一一对应的换算关系。
ODF法己成为目前定量分析深冲钢板织构的最有力的工具。
钢板的构往往聚集在取向空间的某些取向线上,图1所示为钢板中常见的织构取向线在邦厄(Bunge)系统欧拉空间中的位置。
图1钢板中的织构取向线a取向线和γ取向线是深冲钢板中存在的两种主要织构取向线。
其中a取向线在ODF图中的位置为φ1=00,φ=0-900,φ2=450主要织构类型为{001}〈110,{112}110,{111}110。
γ取向线在ODF图中的位置为φ1=0-900,中=54.70,φ2=450,主要织构类型为{111}110和{111}112,对于IF钢还往往出现{554}225织构(φ1=0-900,φ=610,φ2=450,与{111}112非常接近)。

多晶材料织构的又一表示法——三维取向分布函数(odf)分析法
近年来,随着多晶材料的迅速发展,多晶织构的表示方法亦在不断完善。
目前,除了常用的晶体布朗定律及其经典的Fourier变换方法外,另一种描述多晶织构的表示法─三维取向分布函数(odf)分析法也逐渐成为研究多晶材料织构的重要参考
依据。
首先,odf分析法针对每一个取向拟合一个单独的参数,确定材料在每个方向
上的取向分布,而这些参数便是其三维取向分布函数,因此,这种方法经过拟合可比较准确地描述多晶材料的取向结构,可以在呈现更新的结构特征方面发挥作用。
此外,利用odf分析可以更好的获取非等向性的研究结果,从而可以更准确地
描述材料的织构特性,在预测材料力学行为时发挥重要作用。
而且,此外此种分析可以提供非常明确的结构信息,可以帮助解释化学与多晶织构之间的相互影响。
总而言之,odf分析是多晶织构表示法中重要的参考依据,它既可以准确描述
材料取向结构,又能提供易于理解的结构信息,从而帮助进一步研究多晶材料的力学特性。
因此,odf分析法的开发和应用具有重要的意义。

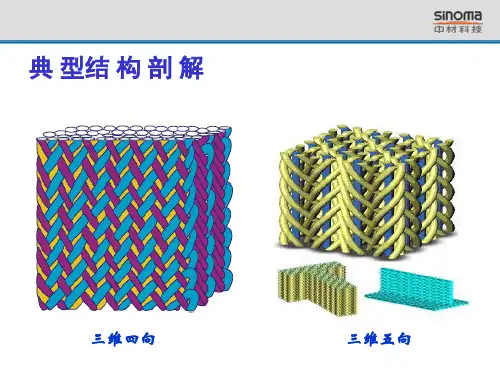
第16卷1999年 第3期8月复 合 材 料 学 报ACT A M AT ERIA E COM PO SIT A E SIN ICA V ol.16 No.3A ug ust 1999 收修改稿、初稿日期:1999-03-03,1998-06-24三维四向编织复合材料细观组织及分析模型庞宝君 杜善义 韩杰才(哈尔滨工业大学航天工程与力学系,哈尔滨150001)摘 要 以四向编织复合材料为对象,对所建立的单胞组织模型进行了细观组织的实验验证,所得结果与理论分析结果吻合较好。
证实了所建模型的正确性,成为三维多向编织复合材料性能分析与材料优化设计的基础。
关键词 编织复合材料,分析模型,细观组织,实验中图分类号 T B 330.1,T B 33 三维编织物结构上所具有的优点,使三维编织复合材料结构与性能具有显著的优势,整体性显著地提高了强度和刚度,具有优良的抗损坏性及良好的力学性能和耐烧蚀性能[1]。
三维编织复合材料已经在航天、航空等高科技行业得到了广泛的应用[2]。
编织复合材料具有显著的性能可设计性。
组分材料的性能、制造工艺决定了复合材料的性能。
同时,编织复合材料的材料单胞在力学上具有显著的结构特性,因此织物组织结构参数即编织参数也将影响编织复合材料的性能。
为了进行材料的优化设计,需要掌握编织复合材料内细观组织特性,即材料单胞内纤维束与基体在空间上的几何分布规律。
Cho u 等[3~4]将编织复合材料单胞看成由四个倾斜的单向复合材料层板组成,建立了倾斜板模型。
吴德隆等[5]研究了五向编织复合材料的分析模型,土方、福多等[6~9]对三维多向编织复合材料的材料模型在几何上作了探讨。
肖丽华与李嘉禄对三维编织工艺及编织复合材料进行了研究[10~11]。
柴雅凌对三维编织预制件中纱线结构进行了拓扑学研究[12]。
本文以矩形截面的碳/环氧四向编织复合材料试件为对象,为验证所建模型的正确性,进行了材料内部显微组织的观察实验,实验结果与所建立的四向编织复合材料单胞几何模型的理论分析结果吻合较好。
三维编织复合材料编织几何和力学性能的细观分析本文研究了三维编织复合材料的细观编织几何结构和细观力学数值模型,论文包括如下三个方面的工作:(1)从四步法编织工艺入手,分析了三维编织物中纱线的运动规律,模拟了横截面内任一纱线的空间运动轨迹,在此基础上提出了一种新的单胞划分方法;对实际的三维编织复合材料连续切片照相,并对细观照片进行图象处理,得到内部、表面和角点处纤维束横截面的形状和纤维束的空间走向,为细观力学建模提供了依据。
(2)在细观几何分析的基础上,建立了三维细观有限元单胞模型,讨论了不同区域纤维束填充因子的选取和单胞合理边界条件的施加方法,计算了内部、表面单胞的平均弹性常数。
研究了内胞、面胞的弹性常数随纤维体积含量的变化关系。
(3)在(2)的研究基础上,用三维有限元模型预测了三维编织复合材料试验件的弹性常数,并将结果同倾斜层板模型进行了对比分析,用试验验证了细观力学模型的可靠性。
对具有不同表面单胞体积含量三维编织复合材料进行了弹性常数的分析,得出表面编织尺寸效应对材料整体性能影响的规律。
三维编织复合材料细观结构的几何学分析三维编织复合材料是一种具有多种功能特性的新型材料,在航空航天、能源、交通等领域中有着广泛的应用。
本文旨在分析三维编织复合材料的细观结构的几何学特征,阐明它的特性与性能的关系。
首先,介绍三维编织复合材料的概念、分类和结构特征。
三维编织复合材料是一种由以针织方法制成的复合材料,其特点是由多种织物和粘合剂制成,织物的纤维结构可以指导复合材料的整体结构、宏尺寸和编织方式。
按照其织物材料的不同,三维编织复合材料可以分为碳纤维三维编织复合材料和针刺部件三维编织复合材料,按照织物的编织技术和流程,三维编织复合材料可以分为单层复合材料、双层复合材料和多层复合材料。
其次,介绍三维编织复合材料的细观结构的几何特征,以及其与材料性能的关系。
三维编织复合材料的细观结构可以由诸如结构面积、孔洞比例和孔径等几何特征来描述。
根据该结构的不同几何特征,三维编织复合材料可分为无孔材料、块状孔洞材料、管状孔洞材料和网状孔洞材料四类。
三维编织复合材料的细观结构特征影响着材料的性能,其中结构面积、孔洞比例和孔径的大小可以影响材料的强度、灵敏性和耐久性等特性。
最后,结合实例阐释三维编织复合材料的细观结构在各个领域的应用情况。
随着三维编织复合材料技术的进步,它已经被广泛应用于航空航天、能源、交通等领域中。
比如说,在航空航天领域中,三维编织复合材料的细观结构可以使其具有较强的抗拉强度和更高的抗拉延伸率,有利于提高飞行器的安全性、结构强度和体积效率等性能。
在能源领域,三维编织复合材料可用于太阳能电池片的制造,能够提高太阳能电池片的强度和耐久性,从而提高太阳能电池片的可靠性。
在交通运输领域,三维编织复合材料可用于车辆等交通工具的制造,可以提供良好的抗拉强度、抗疲劳性能和耐冲击性能,从而提高交通工具的安全性和耐用性。
综上所述,三维编织复合材料的细观结构的几何学特征对于材料的性能具有重要的影响。
不同的结构特征会带来不同的性能和特性,因此有必要了解三维编织复合材料的细观结构的几何学特征,以便正确开发新型材料,并且可以有效改善材料性能。
三维材质制作教学大纲三维材质制作教学大纲一、引言三维材质制作是计算机图形学中的重要组成部分,它能够为虚拟世界赋予真实感和细节。
本文将介绍三维材质制作的基本概念、技巧和流程,旨在帮助读者掌握三维材质制作的核心要点。
二、理论基础1. 材质的定义和分类介绍材质的概念,并根据其属性和用途进行分类,如金属材质、皮肤材质等。
2. 材质贴图的原理解释材质贴图的原理和作用,介绍纹理坐标、法线贴图、高光贴图等常用贴图技术。
三、材质制作流程1. 收集参考资料强调在制作材质之前,收集参考资料是至关重要的,可以从现实世界中的物体、照片或其他艺术作品中获取灵感和参考。
2. 创建基础材质介绍如何使用基础材质库创建简单的材质,并调整其颜色、光泽度和反射率等属性。
3. 制作纹理贴图详细介绍如何使用绘图软件(如Photoshop)制作纹理贴图,包括纹理绘制、图案设计和色彩调整等技巧。
4. 添加细节和效果讲解如何使用法线贴图、置换贴图和高光贴图等技术,为材质添加细节和特效,增强真实感和立体感。
5. 调整和优化强调在制作材质过程中,不断调整和优化是必要的,可以通过调整贴图参数、增加光源和调整材质属性等方式来达到理想效果。
四、案例分析通过几个实际案例,展示不同类型的材质制作过程和技巧,如金属材质、木质材质和布料材质等。
五、常见问题与解答整理学习过程中常见的问题,并给出解答和建议,帮助读者克服困难和提高学习效果。
六、结语总结全文内容,强调三维材质制作的重要性和学习的必要性,并鼓励读者在实践中不断探索和创新。
通过以上的教学大纲,读者可以系统地学习三维材质制作的基本知识和技巧。
掌握这些核心要点后,读者将能够创建出逼真、细腻的材质,为虚拟世界增添更多的真实感和美感。
希望本文能够帮助读者在三维材质制作领域取得更好的成果。
三维编织复合材料的群论分析三维编织复合材料的品种还比较少,用于描述编织几何结构的理论和系统的分类方法有待于深入研究,本文用对称群理论解决了这些问题。
编织几何结构的对称性可以用对称群加以描述。
用点群描述编织几何结构的点对称性,根据点对称性特征可将编织材料进行粗略分类,同时获得相应几何结构的单胞形式。
用空间群描述三维编织几何结构,可以将其进行详细分类,从而推导出系列全新的编织材料几何结构。
本文首先论述了与编织材料几何结构有关的对称群理论。
定义了与编织材料几何结构对称群有关的对称操作和对称元素等概念;阐述了编织几何结构的对称操作的类型和表达方法;通过编织几何结构的对称性定义了编织点群、编织点阵和编织空间(平面)群;用编织材料几何结构对称操作的矩阵表示推导了编织空间点群、空间群的矩阵表示;归纳了对应编织几何结构的平面点阵和空间点阵。
为了用平面点群研究二维编织几何结构的点对称性,本文定义了代表纱线段的点符号和基本对称单元等概念。
在此基础上,论述了对称单元的构建方法,从而将二维编织(包括平面机织)材料按几何结构合理分类。
用平面点对称操作构建相应的平面对称单元图案,得到对应不同几何结构的单胞。
在分析二维编织几何结构的简化方法及与平面点阵阵点对应关系的过程中,对编织平面点阵进行总结分类。
根据不同编织平面点阵的特点,归纳了二维编织几何结构惯用单胞的形状。
用编织平面群分析二维编织几何结构,将二维编织几何结构进行有效分类,系统推导了二维编织几何结构。
同时推导二维编织材料几何结构对应点群的矩阵表示,矩阵表示可用于编织复合材料的力学性能研究。
用空间点群将三维编织几何结构分类,并将其单胞的对称性用点群进行了描述。
推导了编织空间点群的矩阵表示,为将对称群变换应用到三维编织复合材料的力学性能研究打下基础。
通过验证得出编织空间点群不含有纯镜面对称群元素的结论。
将具有点对称性的纱线段组合用一个阵点表达,三维编织材料的几何结构就可以对应的不同空间点阵。