中考数学总复习专题训练二次根式4《二次根式》复习与巩固

中考数学总复习《二次根式》练习题附带答案一、单选题1．√123÷√213×√125值为（）A．1B．3C．√33D．√7 2．若√(a−b)2=b﹣a，则（）A．a＞b B．a＜b C．a≥b D．a≤b 3．与√a3b不是同类次根式的是（）A．1√abB．√baC．√ab2D．√ba34．下列运算正确的是（）A．√3+3=3√3B．4√2−√2=4C．√2+√3=√5D．3√3−√3=2√35．若代数式1x−1+√x有意义，则实数x的取值范围是（）A．x≠1B．x≥0C．x≠0D．x≥0且x≠1 6．a、b在数轴上的位置如图所示，那么化简√(b−a)2的结果是（）A．a-b B．a+b C．b-a D．-a-b7．设实数a，b在数轴上对应的位置如图所示，化简√a2+|a+b|的结果是（）A．-2a+b B．2a+b C．-b D．b8．若√3−m为二次根式，则m的取值为（）A．m≤3B．m＜3C．m≥3D．m＞39．下列运算正确的是（）A．(x−y)2=x2−y2B．|√3−2|=2−√3C．√8−√3=√5D．﹣（﹣a+1）=a+110．已知2<a<4，则化简√1−2a+a2+√a2−8a+16的结果是() A．2a﹣5B．5﹣2a C．﹣3D．311．下列运算中正确的是（）A．√2+√3=√5B．(−√5)2=5C．3√2−2√2=1D．√16=±4 12．下列计算正确的是（）A．(m−n)2=m2−n2B．(2ab3)2=2a2b6C．√8a3=2a√a D．2xy+3xy=5xy 二、填空题13．计算：√45﹣√25× √50=．14．若√12x是一个整数，则x可取的最小正整数是3．（判断对错）15．计算：√24−√12√3=．16．如果x2﹣3x+1=0，则√x2+1x2−2的值是．17．化简：√75=.18．已知实数a，b，c在数轴上的位置如图所示，化简代数式√a2−|a+c|+√(b−c)2−|−b|三、综合题19．完成下列问题：（1）若n（n≠0）是关于x的方程x2+mx+2n=0的根，求m+n的值；（2）已知x，y为实数，且y= √2x−5+√5−2x﹣3，求2xy的值．20．阅读材料，解答问题：（1）计算下列各式：①√4×9=，√4×√9=；②√16×25=，√16×√25=．通过计算，我们可以发现√a×b=（a>0，b>0）从上面的结果可以得到：√8=√2×√4=2√2，√12=√3×√4=2√3（2）根据上面的运算，完成下列问题①化简：√24②计算：√27+√48③化简：√a2b（a>0，b>0）21．在数学课外学习活动中，小明和他的同学遇到一道题：已知a=12+√3，求2a2−8a+1的值.他是这样解答的：∵a=2+√3=√3(2+√3)(2−√3)=2−√3，∴a−2=−√3∴(a−2)2=3，a2−4a+4=3∴a2−4a=−1∴2a2−8a+1=2(a2−4a)+1=2×(−1)+1=−1.请你根据小明的解析过程，解决如下问题：（1）1√3+√2=；（2）化简 √2+1+√3+√2√4+√3⋯+√256+√255 ； （3）若 a =√10−3，求 a 4−6a 3+a 2−12a +3 的值. 22．已知 x =√3+12 ， y =√3−12与 m =xy 和 n =x 2−y 2 . （1）求m ，n 的值；（2）若 √a −√b =m +72， √ab =n 2 求 √a +√b 的值. 23．计算： （1）√135•2 √3 •（﹣ 12 √10 ）； （2）√3a 2b •（ √b a ÷2 √1b）． 24．计算下列各题 （1）计算：（ 12 ）﹣2﹣6sin30°﹣（ √7−√5）0+ √2 +| √2 ﹣ √3 | （2）化简：（ x+2x 2−2x ﹣ x−1x 2−4x+4 ）÷ x−4x ，然后请自选一个你喜欢的x 值，再求原式的值．参考答案1．【答案】A2．【答案】D3．【答案】C4．【答案】D5．【答案】D6．【答案】A7．【答案】D8．【答案】A9．【答案】B10．【答案】D11．【答案】B12．【答案】D13．【答案】√514．【答案】对15．【答案】2√2−216．【答案】√517．【答案】5√318．【答案】019．【答案】（1）将x=n 代入方程x 2+mx+2n=0得n 2+mn+2n=0,则n(n+m+2)=0 因为n≠0,所以n+m+2=0即m+n=-2.（2）因为y=√2x −5+√5−2x -3有意义，则{2x −5≥05−2x ⩾0解得{x ⩾52x ≤52则x=52 所以y=0+0-3=-3即2xy=2×52×（-3）=-15. 20．【答案】（1）6；6；20；20；√a ×√b（2）解：①√24=√4×6=√4×√6=2√6；②√27+√48=√3×9+√3×16=√3×√9+√3×√16=3√3+4√3=7√3 ；③√a 2b =√a 2⋅√b =a √b （a >0，b >0）．21．【答案】（1）√3−√2（2）解：原式 =√2−1+√3−√2+√4−√3+⋯+√256−√255=−1+√2−√2+√3−√3+√4−⋯−√255+√256=√256−1=16−1=15 ；（3）解： ∵ a =√10−3 =√10+3 ∴a −3=√10∴(a −3)2=10即 a 2−6a +9=10 .∴a 2−6a =1 .∴a 4−6a 3=a 2∴a 4−6a 3+a 2−12a +3=2a 2−12a +3=2(a 2−6a)+3=2+3=5 .22．【答案】（1）解：由题意得， m =xy =√3+12×√3−12=12 n =(x +y)(x −y)=(√3+12+√3−12)(√3+12−√3−12)=√3 （2）解：由（1）得， √a −√b =4 √ab =3 ∴(√a +√b)2=(√a −√b)2+4√ab =42+4×3=28∵√a +√b >0∴√a +√b =2√723．【答案】（1）解： √135 •2 √3 •（﹣ 12 √10 ） =2×（﹣ 12 ） √135×3×10 =﹣ √16×3=﹣4 √3（2）解： √3a 2b •（ √b a ÷2 √1b）= √3a2b × √ba× 12× √b= √3424．【答案】（1）解：原式=4﹣6× 12﹣1+ √2+ √3﹣√2 = √3；（2）解：原式=[x+2x(x−2)﹣x−1(x−2)2]•xx−4= (x+2)(x−2)−x(x−1)x(x−2)2•xx−4=x−4x(x−2)2•xx−4=1 (x−2)2当x=10时，原式= 1 64．。

知识点01：二次根式的基本性质与化简【高频考点精讲】1．二次根式有意义的条件（1）二次根式中的被开方数必须是非负数；（2）如果所给式子中含有分母，那么除了保证被开方数为非负数外，还必须保证分母不为零。

2．二次根式的基本性质（1）≥0；a≥0（双重非负性）。

（2）（）2＝a（a≥0）（任何一个非负数都可以写成一个数的平方的形式）。

（3）＝a＝3．二次根式的化简（1）利用二次根式的基本性质进行化简。

（2）利用积的算术平方根的性质和商的算术平方根的性质进行化简。

＝•（a≥0，b≥0）＝（a≥0，b＞0）知识点02：同类二次根式及分母有理化【高频考点精讲】1．同类二次根式（1）一般地，把几个二次根式化为最简二次根式后，如果它们的被开方数相同，那么把这几个二次根式叫做同类二次根式。

（2）合并同类二次根式的方法：只合并根式外的因式，即系数相加减，被开方数和根指数不变。

2．分母有理化（1）分母有理化是指把分母中的根号化去，分母有理化是乘二次根式本身（分母只有一项）或与原分母组成平方差公式。

①＝＝；②＝＝．（2）两个含二次根式的代数式相乘时，它们的积不含二次根式，这样的两个代数式互为有理化因式。

知识点03：二次根式混合运算与化简求值【高频考点精讲】1．二次根式的混合运算顺序：先乘方再乘除，最后加减，有括号的先算括号里面的。

2．在运算中每个根式可以看做是一个“单项式”，多个不同类的二次根式的和可以看作“多项式”。

3．二次根式的运算结果要化为最简二次根式。

四、二次根式的应用【高频考点精讲】二次根式的应用主要是在解决实际问题的过程中用到有关二次根式的概念，性质和运算方法。

检测时间：90分钟试题满分：100分难度系数：0.61一．选择题（共10小题，满分20分，每小题2分）1．（2分）（2023•烟台）下列二次根式中，与是同类二次根式的是（）A．B．C．D．2．（2分）（2023•西宁）下列运算正确的是（）A．B．C．D．3．（2分）（2023•通辽）二次根式在实数范围内有意义，则实数x的取值范围在数轴上表示为（）A．B．C．D．4．（2分）（2023•巴中）下列运算正确的是（）A．x2+x3＝x5B．×＝C．（a﹣b）2＝a2﹣b2D．|m|＝m5．（2分）（2022•广州）代数式有意义时，x应满足的条件为（）A．x≠﹣1 B．x＞﹣1 C．x＜﹣1 D．x≤﹣16．（2分）（2023•济宁）若代数式有意义，则实数x的取值范围是（）A．x≠2 B．x≥0 C．x≥2 D．x≥0且x≠27．（2分）（2023•内蒙古）不等式x﹣1＜的正整数解的个数有（）A．3个B．4个C．5个D．6个8．（2分）（2023•内蒙古）下列运算正确的是（）A．+2＝2B．（﹣a2）3＝a6C．+＝D．÷＝9．（2分）（2021•荆门）下列运算正确的是（）A．（﹣x3）2＝x5B．＝xC．（﹣x）2+x＝x3D．（﹣1+x）2＝x2﹣2x+110．（2分）（2020•呼伦贝尔）已知实数a在数轴上的对应点位置如图所示，则化简|a﹣1|﹣的结果是（）A．3﹣2a B．﹣1 C．1 D．2a﹣3二．填空题（共10小题，满分20分，每小题2分）11．（2分）（2023•哈尔滨）计算的结果是．12．（2分）（2022•济宁）若二次根式有意义，则x的取值范围是．13．（2分）（2021•哈尔滨）计算﹣2的结果是．14．（2分）（2023•绥化模拟）古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式，称为海伦﹣秦九韶公式：如果一个三角形的三边长分别是a，b，c，记，那么三角形的面积为．如果在△ABC中，∠A，∠B，∠C所对的边分别记为a，b，c，若a＝5，b＝6，c＝7，则△ABC的面积为．15．（2分）（2023•池州模拟）要使式子有意义，则x的取值范围为．16．（2分）（2023•内蒙古）实数m在数轴上对应点的位置如图所示，化简：＝．17．（2分）（2023•潍坊）从﹣，，中任意选择两个数，分别填在算式（□+〇）2÷里面的“□”与“〇”中，计算该算式的结果是．（只需写出一种结果）18．（2分）（2023•临汾模拟）计算：＝．19．（2分）（2023•锦江区校级模拟）已知实数m＝﹣1，则代数式m2+2m+1的值为．20．（2分）（2023•大同模拟）计算（）（）的结果等于．三．解答题（共8小题，满分60分）21．（6分）（2023•陕西）计算：．22．（6分）（2023•金昌）计算：÷×2﹣6．23．（8分）（2023•龙岩模拟）（1）计算：；（2）解不等式组：．24．（8分）（2023•晋城模拟）高空抛物严重威胁着人们的“头顶安全”，即便是常见小物件，一旦高空落下，也威力惊人，而且用时很短，常常避让不及．据研究，高空抛物下落的时间t（单位：s）和高度h（单位：m）近似满足公式t＝（不考虑风速的影响，g≈10m/s2）．（1）求从60m高空抛物到落地的时间．（结果保留根号）（2）已知高空坠物动能（单位：J）＝10×物体质量（单位：kg）×高度（单位：m），某质量为0.2kg 的玩具被抛出后经过3s后落在地上，这个玩具产生的动能会伤害到楼下的行人吗？请说明理由．（注：伤害无防护人体只需要65J的动能）25．（8分）（2023•张家界）阅读下面材料：将边长分别为a，a+，a+2，a+3的正方形面积分别记为S1，S2，S3，S4．则S2﹣S1＝（a+）2﹣a2＝[（a+）+a]•[（a+）﹣a]＝（2a+）•＝b+2a例如：当a＝1，b＝3时，S2﹣S1＝3+2根据以上材料解答下列问题：（1）当a＝1，b＝3时，S3﹣S2＝，S4﹣S3＝；（2）当a＝1，b＝3时，把边长为a+n的正方形面积记作S n+1，其中n是正整数，从（1）中的计算结果，你能猜出S n+1﹣S n等于多少吗？并证明你的猜想；（3）当a＝1，b＝3时，令t1＝S2﹣S1，t2＝S3﹣S2，t3＝S4﹣S3，…，t n＝S n+1﹣S n，且T＝t1+t2+t3+…+t50，求T的值．26．（8分）（2023•晋城模拟）阅读与思考请仔细阅读下列材料，并完成相应的任务．＝，＝＝＝3+像上述解题过程中，与、﹣与+相乘，积不含有二次根式，我们可将这两个式子称为互为有理化因式，上述解题过程被称为分母有理化．任务：（1）的有理化因式；﹣2的有理化因式是．（2）写出下列式子分母有理化的结果：①＝；②＝．（3）计算：+……+．27．（8分）（2023•晋城模拟）问题：先化简，再求值：2a+，其中a＝3．小宇和小颖在解答该问题时产生了不同意见，具体如下．小宇的解答过程如下：解：2a+＝2a+……（第一步）＝2a+a﹣5……（第二步）＝3a﹣5．……（第三步）当a＝3时，原式＝3×3﹣5＝4．……（第四步）小颖为验证小宇的做法是否正确，她将a＝3直接代入原式中：2a+＝6+＝6+2＝8．由此，小颖认为小宇的解答有错误，你认为小宇的解答错在哪一步？并给出完整正确的解答过程．28．（8分）（2023•天山区校级模拟）计算：（1）；（2）．。

《二次根式》专题第四讲：《二次根式》全章复习与巩固一、 化简1、无条件的（所有字母取正数） 348m n ②2296x xy y ++③2(223)12-+-2、有附加条件的212a (0)a ＜ 25(03)x x -（2x+1）＜＜3、 有隐含条件的（有意义的字母的取值范围） ①22(1269x x x --+ ②31a a --4、 需要分类讨论的298m 22(1)(2)m m +-二、 因式分解（实数范围内）①44a a + ②232)6x x +③222215x x +-三、解方程（组） ①2253x x = ②236326x x ⎧-=⎪⎨+=⎪⎩四、填空1、20072008(23)32)=223-x ，小数部分为y ，则32x y +=3、①20(45(5132+=-②127(23)3-⎡⎤=⎣⎦41514 1413-5、∆ABC 的三边长为a 、b 、c 22()()a b c a b c --+-=6242x x =-成立的条件是2233x x x x--=--成立的条件是7)()()()())()a b a b a b a b a b a b a b a b a b a b a b a b ⎧-==-+-=⎨+⎪=+ 哪个对？五、计算技巧：1336=-2757575=-3、25552525=--4、化简b ab b a ab a -++5、化简(ab b ab a b a ab÷-+6、已知a+b=-3,ab=1,求ab b a 的值.7、如图所示，有一块边长为1的正方形铁片，将其每个角都剪下一个小等腰三角形，使其成为每条边都相等的八边形，求这个八边形的边长，你能将其结果写成没有分母或分母不带根号的形式吗？D CB A。

二次根式章节知识点题型及巩固习题(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（二次根式章节知识点题型及巩固习题(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为二次根式章节知识点题型及巩固习题(word版可编辑修改)的全部内容。

二次根式知识点一： 二次根式的概念定义：一般地，形如a （a≥0）的代数式叫做二次根式。

”“称为二次根号。

注意：在二次根式中,被开放数可以是数，也可以是单项式、多项式、分式等代数式，但必须注意：因为负数没有平方根,所以是为二次根式的前提条件，如，，等是二次根式,而，等都不是二次根式。

例1233x 1x x 〉0）0、422yx 1+、y x +(x ≥0，y•≥0)． 知识点二：取值范围1、 二次根式有意义的条件：由二次根式的意义可知，当a ≧0时,a 有意义，是二次根式，所以要使二次根式有意义,只要使被开方数大于或等于零即可。

2、 二次根式无意义的条件:因负数没有算术平方根，所以当a ﹤0时，a 没有意义。

例2．当x 是多少时，1x 3+在实数范围内有意义?例3．当x 是多少时，32x ++1x 1+在实数范围内有意义?知识点三:二次根式a(a≥0）的非负性a （a≥0）表示a 的算术平方根，也就是说，a （a≥0））是一个非负数，即a ≥(a≥0）.注：因为二次根式a （a≥0）表示a 的算术平方根,而正数的算术平方根是正数，0的算术平方根是0，所以非负数（a≥0)的算术平方根是非负数,即a ≥（a≥0），这个性质也就是非负数的算术平方根的性质，和绝对值、偶次方类似。

专题1.12 二次根式（全章复习与巩固）（巩固篇）（专项练习）一、单选题1．若3x =时，2x a -当5x =时，2x a -则a 的值可能是（ ）A ．4B ．8C ．12D ．162．下列二次根式中，是最简二次根式的是（ ）A 2B 12C 8D 123．若0xy <，则2x y ） A ．xy B ．x y -C ．x y --D ．x y -42243 ）A ．4和5之间B ．5和6之间C ．6和7之间D ．7和8之间5371115，，，…，则311 ）A ．第23项B ．第24项C ．第19项D ．第25项625x -1x -+x 值是（ ）A ．3-B ．2C ．3-或2D ．不存在7．下列计算正确的是（ ）A ．3553=B 236=C 235=D 12348．已知a b 、为实数，m n 、分别表示574am bn +=，则37a -+=（ ） A ．1 B ．32 C ．52 D ．2 9．当12022x +=3420252022x x --的值为（ ） A ．3B ．3-C ．1D ．1-10．观察下列二次根式的化简（ ）1221111111212S =+++-； 2222211111111111112231223S ⎛⎫⎛⎫+++++-++- ⎪ ⎪⎝⎭⎝⎭； 3222222111111111111111111122334122334S ⎛⎫⎛⎫⎛⎫=+++++++-++-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭； 则20222022S =（ ） A ．20222021 B ．20242023 C ．12022 D ．12024二、填空题11．已知1()2f x x=+，那么(3)f ＝_____． 12．求值：()(202220232332⋅+=______.132b +152b --a b -=________． 14．已知a 10b 是它的小数部分，则210a b +=______．15．若两不等实数a ，b 满足38a b +=，38b a +=，a b ab _____． 16．已知整数x ，y 满足2022202220222022x y x x y xy ，7x y --的最小值为 _____．17．已知等腰ABC 的两边长分别为37，则等腰ABC 的周长是______．18．在平面直角坐标系中，若干个边长为1个单位长度的等边三角形，按下图中的规律摆放．点P 从原点O 出发，以每秒1个单位长度的速度沿着等边三角形的边“112233445OA A A A A A A A A →→→→……”的路线运动．设第n 秒运动到点n P （n 为正整数），则点2023P 的坐标是_______________．三、解答题19．当2022a =时，求221a a a -+(1) 的解法是错误的；(2) 错误的原因在于未能正确地运用二次根式的性质： ；(3) 当3a >2691a a a -+-的值．20．计算： (1)148318243 (2) 03(51)(51)(2)27+-21．计算及解方程组： (1)1324126-（） (2) )26221532+22．已知32x =32y =，求下列各式的值：(1) 22x y -： (2) 222x xy y ++．23．小明在解决问题：已知23a =+2281a a -+的值．他是这样分析与解的：∵()()2323232323a -=++- ∵23a -=-∵()2223,443a a a -=-+=，∵241a a -=-，∵()()222812412111a a a a -+=-+=⨯-+=-． 请你根据小明的分析过程，解决如下问题： (1) 1315375121119+++++ (2) 若121a ， ∵求2481a a -+的值；∵直接写出代数式的值3231a a a ++-=___________．24．探究题(1) 用“＝”、“＞”、“＜”填空： 4+3 243⨯1+16 2116⨯，5+5 255． (2) 由（1）中各式猜想m +n 与mn m ≥0，n ≥0）的大小，并说明理由．(3) 请利用上述结论解决下面问题：某园林设计师要对园林的一个区域进行设计改造，将该区域用篱笆围成矩形的花圃．如图所示，花圃恰好可以借用一段墙体，为了围成面积为200m 2的花圃，所用的篱笆至少需要 m ．参考答案1．B【分析】二次根式有意义的条件是被开方数是非负数，根据这个条件列不等式即可． 解：∵当3x =2x a -∵230a ⨯-<，解得6a >，∵当5x =2x a -∵250a ⨯-≥，解得10a ≤，∵610a <≤，∵a 的值可能是8，故选：B ．)0a a ≥叫二次根式．关键是掌握二次根式中的被开方数必须是非负数，否则二次根式无意义．2．A【分析】根据二次根式化简方法和最简二次根式的概念进行化简辨别即可．解：A 2B 12434323⨯=12不是最简二次根式，该选项不符合题意；C 8424222⨯8D 1122212不是最简二次根式，该选项不符合题意； 故选：A ．【点拨】本题考查二次根式的化简，对于最简二次根式要满足两个条件：被开方数不含开的尽方得因数，被开方数不含分母，准确理解最简二次根式的概念，并能对二次根式进行正确的化简是解决问题的关键．3．D【分析】根据0xy <2x y 0,0x y <>，进而即可求解．解：∵0xy <2x y∵0,0x y <>， 2x y y x y ==-故选：D ．【点拨】本题考查了二次根式有意义的条件，根据二次根式的性质化简，得出0,0x y <>是解题的关键．4．B【分析】利用二次根式的混合运算将原式化简，再进行无理数的估算即可． 2243263=433=33=∵252736<<，∵5276<，即5336<， 22435和6之间，故选：B【点拨】本题考查了二次根式的混合运算以及估算无理数的大小，27的范围是解此题的关键．5．D【分析】通过观察，得出第n 项为：41n -再根据31199得出方程4199n -=，解出即可得出答案．解：∵371115，，，…， ∵通过观察，可得：第n 41n - ∵31191191199⨯∵4199n -=，解得：25n =，∵31125项．故选：D【点拨】本题考查了数字规律问题、二次根式的乘法，解本题的关键在正确找出已知数列的规律．6．A【分析】根据同类最简二次根式的定义求解即可解：根据题意得：215x x --+250x -≥，10x -+≥， 215x x --+∵215x x --+=，解得：3x =-或2x =（舍），∵3x =-，故选：A【点拨】本题考查了同类最简二次根式的定义，掌握同类最简二次根式的定义是解决问题的关键7．B【分析】根据二次根式的加减乘除运算法则求解判断即可．解：A 、35525B 236=C 23D 12312342=÷=，计算错误，不符合题意，选项错误，故选B ．【点拨】本题考查二次根式的加减乘除运算，熟练掌握相关运算法则是解题关键．8．D7m n 、的值，再代入计算即可．解：∵72＜＜3，∵372-＜＜-，∵72＜5＜3，∵57-2m =，小数部分57237n ==∵4am bn +=，∵(2374a b +=，∵372a -=， 故选：D ．【点拨】本题考查估算无理数的大小，二次根式的混合运算，掌握算术平方根的定义是正确解答的前提．9．D【分析】根据12022x +=2442021x x -=，然后将多项式3420252022x x --转化为22(442021)(442022)x x x x x --+--，然后代入计算即可．解：12022x += 2(21)2022x ∴-=，24412022x x ∴-+=，2442021x x ∴-=，∴多项式3420252022x x --22(442021)(442022)x x x x x =--+--(20212021)20212022x =-+-020212022=+-1=-，故选：D ．【点拨】本题难度较大，需要对要求的式子进行变形，同学们要学会转化的思想，这是数学中一种很重要的思想．10．B【分析】根据题目中给定的计算方法求出2022S ，再进行求解即可． 解：221111111212++=+-221111112323++=+-221111113434++=+-，…∵221111112022202320222023++=+-， ∵1221111111212S =++=+-， 2222211111111111112231223S ⎛⎫⎛⎫=++++=+-++- ⎪ ⎪⎝⎭⎝⎭， 322222111111111111111111122334122334S ⎛⎫⎛⎫⎛⎫=+++++++-++-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， …∵20221111111111111111223342021202220222023S ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-++-++-+++-++- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 1202220221202220232023=+-=+， ∵则20222022202212024202312022202220232023S +==+=． 故选B ． 【点拨】本题考查二次根式化简中的简便运算．熟练掌握题目中给定的计算方法是解题的关键．11．23【分析】根据1()2f x x =+代入计算即可； 解：∵1()2f x x =+， ∵()()23(3)23232323f -==++- 故答案是：23．【点拨】本题主要考查了代数式求值和分母有理化，准确利用平方差公式计算是解题的关键．12．322+ 【分析】先根据积的乘方得到原式＝20222022322322322-++（）（）（），然后利用平方差公式计算． 解：原式＝20222023322322-+（）（）＝20222022322322322-++（）（）（）＝(202298322-⨯+（） ＝322+故答案为：322+【点拨】本题考查了二次根式的混合运算：熟练掌握二次根式的性质、二次根式的乘法法则和积的乘方与幂的乘方是解决问题的关键．13．2【分析】根据最简二次根式、同类二次根式的性质计算，即可得到a 和b 的值；再将a和b 的值代入到代数式，通过计算即可得到答案．解：根据题意得：12a -=∵3a =∵2b +152b --∵252b b +=-∵1b =∵312a b -=-=故答案为：2．【点拨】本题考查了二次根式的知识；解题的关键是熟练掌握最简二次根式、同类二次根式、代数式的性质，从而完成求解．14．3【分析】由于34a <<，则3a =，103b =，然后代入所求代数式进行计算即可． 解：3104<<，3a ∴=，103b =，2106103103a b ∴+=．故答案为：3．【点拨】本题考查了估算无理数的大小，二次根式的加减，解题的关键是利用完全平方数和算术平方根对无理数的大小进行估算．15．4【分析】3a b =1ab ，然后代入原式即可求出答案．解：∵38a b +，38b a +， ∴33a a b b ++1633a b b a ++， ∴330b a b a +-， ∴30a ba b a b =-， ∵a b ， 0a b ， 3a b =，∵1633a b b a =++，∴7a b +=， ∵22a b a b ab =++()212a b a b ab -+=∴原式＝314+=．故答案为：4． 【点拨】本题考查二次根式的混合运算，解题的关键是a b a b a b -=，本题属于基础题型．16．18 2()2022()202220220xy x y x y xy =，然后因式分解为(2022)(2022)0x y xy =，20220xy =，进而分析得出337x =，6y =，则答案可得． 解：2022202220222022x y y x x y xy =， 2()2022()202220220xy x y x y xy ， ∵(2022)(2022)0x y xy =， 20220xy =，∵202223337xy ==⨯⨯，∵x ，y 均为整数，70x y -->，7x y --337x =，6y =，7x y --3376732418--==．故答案为：18． 20220xy ． 17．1423+2314 【分析】分两种情况：当等腰ABC 的腰长为37时，当等腰ABC 的腰长为7，底边长为23解：分两种情况：当等腰ABC的腰长为237时，233437+，∴不能组成三角形；当等腰ABC的腰长为7，底边长为3∴等腰ABC的周长773143=++=+综上所述：等腰ABC的周长是1423+故答案为：143+【点拨】本题考查了等腰三角形的性质，三角形的三边关系，分两种情况进行计算是解题的关键．18．3⎛⎝⎭【分析】每630，30，3，0，点的横坐标规律：12，1，32，2，52，3，…，2n，即可求解．解：如图，过1A作1A H x⊥轴于H，则130OA H∠=︒，而11OA=，∵12OH=，2211312A H⎛⎫=-=⎪⎝⎭，∵每630，30，3，0，∵20236337÷=余1，∵点2023P3由题意可知动点P 每秒的横坐标规律：12，1，32，2， 52 ，3，…，2n ， ∵点2023P 的横坐标为1011.5， ∵点2023P 的坐标3⎛ ⎝⎭， 故答案为3⎛ ⎝⎭． 【点拨】本题考查点的规律；理解题意，根据所给图形的特点，结合平面直角坐标系中点的特点及正三角形边的特点，确定点的坐标规律是解题的关键．19．(1)小亮 2||a a (3)-2【分析】（1）根据二次根式的性质化简即可求出答案．（2）根据二次根式的性质化简即可求出答案．（3）根据a 的范围判断3a -与1a -的符号，然后根据二次根式的性质以及绝对值的性质进行化简即可求出答案． 解：（1）原式2(1)a a =-1a a =+-，∵2022a =，∵10＜-a ，∵原式1212202214043a a a =+-=-=⨯-=，故小亮的解法错误，故答案为：小亮． （22a a ，2a a ．（3）∵3a >，30a ∴->，10a -<， ∵原式2(3)1a a =--，31a a =---()31a a =-+-31a a =-+-2=-．【点拨】本题考查二次根式的化简求值，解题的关键是熟练运用二次根式的性质，本题属于基础题型．20．(1)46 (2)2【分析】（1）直接利用二次根式的乘除运算法则、二次根式的性质化简，进而得出答案；（2）将原式用平方差公式化简，再求值即可（1148318243148318263=÷⨯16626=46=（2）03(51)(51)(2)27+-25113=-+-53=-2=【点拨】本题主要考查了二次根式的混合运算，解题的关键是熟练掌握二次根式的性质和混合运算法则． 21．(1)71210 (2)3107-【分析】（1）先计算括号，再计算除法，最后计算加减．（2）按照完全平方公式，二次根式的乘法计算即可． 解：（113242126-（） 63621（2 32156 3221==71210（2)26221532+ =331073-=3107-．【点拨】本题考查了二次根式的乘法，除法，完全平方公式，绝对值的化简，熟练掌握二次根式的乘除运算是解题的关键．22．(1)6 (2)12【分析】（1）先计算出x y +和x y -，再利用乘法公式得到()()22x y x y x y -=+-；（2）利用乘法公式得到222)2(x xy y x y =+++，然后利用整体代入的方法计算． （1）解：32x =+32y =，23x y ∴+=22x y -=()()22232246x y x y x y -=+-==（2）由（1）知3x y +=∵22222()(23)12x xy y x y ++=+==．【点拨】本题考查了二次根式的运算，完全平方公式、平方差公式等知识点．题目难度不大，注意整体代入思想的运用．23．(1)5 (2)∵5，∵0【分析】（1）原式各项分母有理化，计算即可求出值；（2）∵先把a 分母有理化可得到21a ，从而得到221a a -=，再把式子进行整理，将221a a -=代入计算即可求出值；∵将式子整理成()2221a a a a a --++，再代入221a a -=，即可求解． （11315375121119++++++ 13153751211192=+- ()112112= 1102=⨯5=；（2）解：∵∵()()122122211a -+-，∵12a -= ∵()2212,212a a a --=+=，∵221a a -=，∵()224814214115a a a a -+=-+=⨯+=； ∵∵221a a -=，∵3231a a a -++()2221a a a a a =--++21a a a =-++()221a a =--+=11-+0=．故答案为：0【点拨】本题考查了分母有理化，二次根式的化简求值，正确读懂例题，对二次根式进行化简是关键．24．(1)＞，＞，＝， (2)m +n mn (3)40【分析】（1）分别进行计算，比较大小即可；（2）根据第（1）问填大于号或等于号，所以猜想m +n mn 比较大小，可以作差，m +n -mn（3）设花圃的长为a 米，宽为b 米，需要篱笆的长度为（a +2b ）米，利用第（2）问的公式即可求得最小值．（1）解：∵4+3=7，43⨯3∵2749=，2(43)48=，∵49＞48，∵4+3＞43⨯∵1+16=76＞1，116⨯61，∵1+16＞116⨯；∵5+5=10，55⨯，55⨯故答案为：＞，＞，=；（2）解：m+n mn m≥0，n≥0）．理由如下：当m≥0，n≥0时，∵2()0m n≥，∵22()2()0m m n n-≥，∵m-mn n≥0，∵m+n mn（3）解：设花圃的长为a米，宽为b米，则a＞0，b＞0，S=ab=200，根据（2）的结论可得：222222220022040a b a b ab+≥⋅==⨯⨯=，∵篱笆至少需要40米．故答案为：40．【点拨】本题主要考查了二次根式的应用，体现了由特殊到一般的思想方法，解题的关键是联想到完全平方公式，利用平方的非负性求证．。

《二次根式》全章复习与巩固一、 化简1、无条件的（所有字母取正数）①348m n ②2296x xy y ++③2(223)12-+-2、有附加条件的①212a (0)a ＜ ②25(03)x x --（2x+1）＜＜3、 有隐含条件的（有意义的字母的取值范围） ①22(12)69x x x -+-+ ②31aa a ---4、 需要分类讨论的298m 22(1)(2)m m +-二、因式分解（实数范围内）①44a a + ②2(32)6x x +③222215x x +-三、解方程（组）①2253x x -= ②2363226x y x y ⎧-=⎪⎨+=⎪⎩四、填空1、20072008(23)(32)+-=2、实数123-的整数部分为x ，小数部分为y ，则32x y +=3、①20211()45()5132-÷+=-②127(23)3-⎡⎤--÷=⎣⎦4、比大小：1514- 1413-5、∆ABC 的三边长为a 、b 、c ，则22()()a b c a b c ---+-=6、①242x x =-成立的条件是 2233x x x x--=--成立的条件是7、()()()()()()()()a b a b a b a b a b a b a b a b a b a b a b a b a b a b ⎧----==-⎪-+-⎪-⎪=⎨+⎪+-⎪=-⎪+⎩哪个对？五、计算技巧： 1、336=-2、757575-=-3、25552525+=--4、化简babb aaba -++5、化简()ab ab bab a b a ab--÷-+6、已知a+b=-3,ab=1,求abb a的值.7、如图所示，有一块边长为1的正方形铁片，将其每个角都剪下一个小等腰三角形，使其成为每条边都相等的八边形，求这个八边形的边长，你能将其结果写成没有分母或分母不带根号的形式吗？DCB A中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．将抛物线y＝2x2向左平移3个单位得到的抛物线的解析式是( )A．y＝2x2+3 B．y＝2x2﹣3C．y＝2(x+3)2D．y＝2(x﹣3)2【答案】C【解析】按照“左加右减，上加下减”的规律，从而选出答案.【详解】y＝2x2向左平移3个单位得到的抛物线的解析式是y＝2（x＋3）2，故答案选C.【点睛】本题主要考查了抛物线的平移以及抛物线解析式的变换规律，解本题的要点在于熟知“左加右减，上加下减”的变化规律.2．已知一组数据1、2、3、x、5，它们的平均数是3，则这一组数据的方差为（）A．1 B．2 C．3 D．4【答案】B【解析】先由平均数是3可得x的值，再结合方差公式计算．【详解】∵数据1、2、3、x、5的平均数是3，∴12355x++++=3，解得：x=4，则数据为1、2、3、4、5，∴方差为15×[（1-3）2+（2-3）2+（3-3）2+（4-3）2+（5-3）2]=2，故选B．【点睛】本题主要考查算术平均数和方差，解题的关键是熟练掌握平均数和方差的定义．3．如图，直线m∥n，直角三角板ABC的顶点A在直线m上，则∠α的余角等于（）A ．19°B ．38°C ．42°D ．52°【答案】D【解析】试题分析：过C 作CD ∥直线m ，∵m ∥n ，∴CD ∥m ∥n ，∴∠DCA=∠FAC=52°，∠α=∠DCB ，∵∠ACB=90°，∴∠α=90°﹣52°=38°，则∠a 的余角是52°．故选D ．考点：平行线的性质；余角和补角．4．抛物线y=ax 2﹣4ax+4a ﹣1与x 轴交于A ，B 两点，C （x 1，m ）和D （x 2，n ）也是抛物线上的点，且x 1＜2＜x 2，x 1+x 2＜4，则下列判断正确的是（ ） A ．m ＜n B ．m≤n C ．m ＞n D ．m≥n【答案】C【解析】分析：将一般式配方成顶点式，得出对称轴方程2x =，根据抛物线2441y ax ax a =-+-与x 轴交于,A B 两点，得出()()244410a a a =--⨯->，求得0a >，距离对称轴越远，函数的值越大，根据121224x x x x <<+<，，判断出它们与对称轴之间的关系即可判定.详解：∵()2244121y ax ax a a x =-+-=--，∴此抛物线对称轴为2x =，∵抛物线2441y ax ax a =-+-与x 轴交于,A B 两点，∴当24410ax ax a -+-=时，()()244410a a a =--⨯->，得0a >， ∵121224x x x x <<+<，， ∴1222x x ，->-∴m n >，故选C ．点睛：考查二次函数的图象以及性质，开口向上，距离对称轴越远的点，对应的函数值越大，5．某校在国学文化进校园活动中，随机统计50名学生一周的课外阅读时间如表所示，这组数据的众数和中位数分别是（）A．14，9 B．9，9 C．9，8 D．8，9【答案】C【解析】解:观察、分析表格中的数据可得：∵课外阅读时间为1小时的人数最多为11人，∴众数为1．∵将这组数据按照从小到大的顺序排列，第25个和第26个数据的均为2，∴中位数为2．故选C．【点睛】本题考查（1）众数是一组数据中出现次数最多的数；（2）中位数的确定要分两种情况：①当数据组中数据的总个数为奇数时，把所有数据按从小到大的顺序排列，中间的那个数就是中位数；②当数据组中数据的总个数为偶数时，把所有数据按从小到大的顺序排列，中间的两个数的平均数是这组数据的中位数. 6．某青年排球队12名队员年龄情况如下：则这12名队员年龄的众数、中位数分别是（）A．20，19 B．19，19 C．19，20.5 D．19，20【答案】D【解析】先计算出这个队共有1+4+3+2+2=12人，然后根据众数与中位数的定义求解．【详解】这个队共有1+4+3+2+2=12人，这个队队员年龄的众数为19，中位数为20202=1．故选D．【点睛】本题考查了众数：在一组数据中出现次数最多的数叫这组数据的众数．也考查了中位数的定义．7．已知二次函数y＝ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④4a﹣2b+c ＜0；⑤c ﹣a ＞1，其中所有正确结论的序号是（ ）A ．①②B ．①③④C ．①②③⑤D ．①②③④⑤【答案】C【解析】根据二次函数的性质逐项分析可得解.【详解】解：由函数图象可得各系数的关系：a ＜0，b ＜0，c ＞0， 则①当x=1时，y=a+b+c ＜0，正确； ②当x=-1时，y=a-b+c ＞1，正确； ③abc ＞0，正确；④对称轴x=-1，则x=-2和x=0时取值相同，则4a-2b+c=1＞0，错误； ⑤对称轴x=-2ba=-1，b=2a ，又x=-1时，y=a-b+c ＞1，代入b=2a ，则c-a ＞1，正确． 故所有正确结论的序号是①②③⑤． 故选C8．如图,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB=2m,则树高为（ ）米A ．5B 3C 5D ．3【答案】C【解析】由题意可知，AC=1，AB=2，∠CAB=90° 据勾股定理则2222125AC AB ++=；∴AC+BC=（5m. 答：树高为（5 故选C.9．下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）A．甲和乙B．乙和丙C．甲和丙D．只有丙【答案】B【解析】分析：根据三角形全等的判定方法得出乙和丙与△ABC全等，甲与△ABC不全等．详解：乙和△ABC全等；理由如下：在△ABC和图乙的三角形中，满足三角形全等的判定方法：SAS，所以乙和△ABC全等；在△ABC和图丙的三角形中，满足三角形全等的判定方法：AAS，所以丙和△ABC全等；不能判定甲与△ABC全等；故选B．点睛：本题考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．10．如图所示是小孔成像原理的示意图，根据图中所标注的尺寸，求出这支蜡烛在暗盒中所成像CD的长（）A．16cm B．13cm C．12cm D．1cm【答案】D【解析】过O作直线OE⊥AB，交CD于F，由CD//AB可得△OAB∽△OCD，根据相似三角形对应边的比等于对应高的比列方程求出CD的值即可.【详解】过O作直线OE⊥AB，交CD于F，∵AB//CD，∴OF⊥CD，OE=12，OF=2，∴△OAB∽△OCD，∵OE、OF分别是△OAB和△OCD的高，∴OF CDOE AB=，即2126CD=，解得：CD=1.故选D.【点睛】本题考查相似三角形的应用，解题的关键在于理解小孔成像原理给我们带来的已知条件，熟记相似三角形对应边的比等于对应高的比是解题关键.二、填空题（本题包括8个小题）11．如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠3=40°，则∠4等于________．【答案】70°【解析】试题分析：由平角的定义可知，∠1+∠2+∠3=180°，又∠1=∠2，∠3=40°，所以∠1=（180°-40°）÷2=70°，因为ａ∥b，所以∠4=∠1=70°.故答案为70°.考点：角的计算；平行线的性质.12．如图，矩形ABCD中，AB＝1，BC＝2，点P从点B出发，沿B－C－D向终点D匀速运动，设点P 走过的路程为x，△ABP的面积为S，能正确反映S与x之间函数关系的图象是( )A ．B ．C ．D ．【答案】C【解析】分出情况当P 点在BC 上运动，与P 点在CD 上运动，得到关系，选出图象即可 【详解】由题意可知，P 从B 开始出发，沿B —C —D 向终点D 匀速运动，则 当0＜x≤2，s=12x 当2＜x≤3，s=1所以刚开始的时候为正比例函数s=12x 图像，后面为水平直线，故选C 【点睛】本题主要考查实际问题与函数图像，关键在于读懂题意，弄清楚P 的运动状态 13．已知关于x 方程x 2﹣3x+a=0有一个根为1，则方程的另一个根为_____． 【答案】1【解析】分析：设方程的另一个根为m ，根据两根之和等于-ba，即可得出关于m 的一元一次方程，解之即可得出结论．详解：设方程的另一个根为m ， 根据题意得：1+m=3， 解得：m=1． 故答案为1．点睛：本题考查了根与系数的关系，牢记两根之和等于-ba是解题的关键． 14．如图，在ABC 中A 60∠=︒，BM AC ⊥于点M ，CN AB ⊥于点N ，P 为BC 边的中点，连接PM,PN ，则下列结论：①PM PN =，②MN AB BC AC ⋅=⋅，③PMN 为等边三角形，④当ABC 45∠=︒时，CN 2PM =.请将正确结论的序号填在横线上__.【答案】①③④【解析】①根据直角三角形斜边上的中线等于斜边的一半可判断①；②先证明△ABM∽△ACN，再根据相似三角形的对应边成比例可判断②；③先根据直角三角形两锐角互余的性质求出∠ABM=∠ACN=30°，再根据三角形的内角和定理求出∠BCN+∠CBM=60°，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPN+∠CPM=120°，从而得到∠MPN=60°，又由①得PM=PN，根据有一个角是60°的等腰三角形是等边三角形可判断③；④当∠ABC=45°时，∠BCN=45°，进而判断④．【详解】①∵BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，∴PM=12BC，PN=12BC，∴PM=PN，正确；②在△ABM与△ACN中，∵∠A=∠A，∠AMB=∠ANC=90°，∴△ABM∽△ACN，∴AM ANAB AC，错误；③∵∠A=60°，BM⊥AC于点M，CN⊥AB于点N，∴∠ABM=∠ACN=30°，在△ABC中，∠BCN+∠CBM=180°-60°-30°×2=60°，∵点P是BC的中点，BM⊥AC，CN⊥AB，∴PM=PN=PB=PC，∴∠BPN=2∠BCN，∠CPM=2∠CBM，∴∠BPN+∠CPM=2（∠BCN+∠CBM）=2×60°=120°，∴∠MPN=60°，∴△PMN是等边三角形，正确；④当∠ABC=45°时，∵CN⊥AB于点N，∴∠BNC=90°，∠BCN=45°，∵P为BC中点，可得，故④正确．所以正确的选项有：①③④故答案为①③④【点睛】本题主要考查了直角三角形斜边的中线等于斜边的一半的性质，相似三角形、等边三角形、等腰直角三角形的判定与性质，等腰三角形三线合一的性质，仔细分析图形并熟练掌握性质是解题的关键． 15．因式分解：x 2y-4y 3=________. 【答案】y （x++2y ）（x-2y ）【解析】首先提公因式y ，再利用平方差进行分解即可．【详解】原式()224(2)(2)y x y y x y x y =-=-+．故答案是：y （x+2y ）（x-2y ）． 【点睛】考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．16．一次函数1y kx b =+与2y x a =+的图象如图，则()0kx b x a +-+>的解集是__．【答案】1x <-【解析】不等式kx+b-（x+a ）＞0的解集是一次函数y 1=kx+b 在y 2=x+a 的图象上方的部分对应的x 的取值范围，据此即可解答．【详解】解：不等式()0kx b x a +-+>的解集是1x <-． 故答案为：1x <-． 【点睛】本题考查了一次函数的图象与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=kx+b 的值大于（或小于）0的自变量x 的取值范围；从函数图象的角度看，就是确定直线y=kx+b 在x 轴上（或下）方部分所有的点的横坐标所构成的集合．17．若关于x 的一元二次方程230x x m -+=有实数根，则m 的取值范围是________． 【答案】94m ≤【解析】由题意可得，△=9-4m≥0，由此求得m的范围．【详解】∵关于x的一元二次方程x2-3x+m=0有实数根，∴△=9-4m≥0，求得m≤.故答案为：94 m≤【点睛】本题考核知识点：一元二次方程根判别式. 解题关键点：理解一元二次方程根判别式的意义.18．关于x的方程1101axx+-=-有增根，则a=______.【答案】-1【解析】根据分式方程11axx+-－1＝0有增根，可知x-1=0，解得x=1，然后把分式方程化为整式方程为：ax+1-（x-1）=0，代入x=1可求得a=-1.故答案为-1.点睛：此题主要考查了分式方程的增根问题，解题关键是明确增根出现的原因，把增根代入最简公分母即可求得增根，然后把它代入所化为的整式方程即可求出未知系数.三、解答题（本题包括8个小题）19．如图，已知正方形ABCD，E是AB延长线上一点，F是DC延长线上一点，且满足BF＝EF，将线段EF绕点F顺时针旋转90°得FG，过点B作FG的平行线，交DA的延长线于点N，连接NG．求证：BE＝2CF；试猜想四边形BFGN是什么特殊的四边形，并对你的猜想加以证明．【答案】（1）见解析；（2）四边形BFGN是菱形，理由见解析.【解析】（1）过F作FH⊥BE于点H，可证明四边形BCFH为矩形，可得到BH＝CF，且H为BE中点，可得BE＝2CF；（2）由条件可证明△ABN≌△HFE，可得BN＝EF，可得到BN＝GF，且BN∥FG，可证得四边形BFGN 为菱形．【详解】（1）证明：过F作FH⊥BE于H点，在四边形BHFC中，∠BHF＝∠CBH＝∠BCF＝90°，所以四边形BHFC为矩形，∴CF＝BH，∵BF＝EF，FH⊥BE，∴H为BE中点，∴BE＝2BH，∴BE＝2CF；（2）四边形BFGN是菱形．证明：∵将线段EF绕点F顺时针旋转90°得FG，∴EF＝GF，∠GFE＝90°，∴∠EFH＋∠BFH＋∠GFB＝90°∵BN∥FG，∴∠NBF＋∠GFB＝180°，∴∠NBA＋∠ABC＋∠CBF＋∠GFB＝180°，∵∠ABC＝90°，∴∠NBA＋∠CBF＋∠GFB＝180°−90°＝90°，由BHFC是矩形可得BC∥HF，∴∠BFH＝∠CBF，∴∠EFH＝90°−∠GFB−∠BFH＝90°−∠GFB−∠CBF＝∠NBA，由BHFC是矩形可得HF＝BC，∵BC＝AB，∴HF＝AB，在△ABN和△HFE中，NAB EHF90AB HFNBA EFH∠∠︒⎧⎪⎨⎪∠∠⎩＝＝＝＝，∴△ABN≌△HFE，∴NB＝EF，∵EF＝GF，∴NB＝GF，又∵NB∥GF，∴NBFG是平行四边形，∵EF＝BF，∴NB＝BF，∴平行四边NBFG是菱形．点睛：本题主要考查正方形的性质及全等三角形的判定和性质，矩形的判定与性质，菱形的判定等，作出辅助线是解决（1）的关键．在（2）中证得△ABN≌△HFE是解题的关键．20．我市正在开展“食品安全城市”创建活动，为了解学生对食品安全知识的了解情况，学校随机抽取了部分学生进行问卷调查，将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计，并绘制了下列两幅统计图（不完整）．请根据图中信息，解答下列问题：此次共调查了名学生；扇形统计图中D所在扇形的圆心角为；将上面的条形统计图补充完整；若该校共有800名学生，请你估计对食品安全知识“非常了解”的学生的人数．【答案】（1）120；（2）54°；（3）详见解析（4）1．【解析】（1）根据B的人数除以占的百分比即可得到总人数；（2）先根据题意列出算式，再求出即可；（3）先求出对应的人数，再画出即可；（4）先列出算式，再求出即可．【详解】（1）（25+23）÷40%=120（名），即此次共调查了120名学生，故答案为120；（2）360°×10+8120=54°， 即扇形统计图中D 所在扇形的圆心角为54°， 故答案为54°； （3）如图所示：；（4）800×30120=1（人）， 答：估计对食品安全知识“非常了解”的学生的人数是1人． 【点睛】本题考查了条形统计图、扇形统计图，总体、个体、样本、样本容量，用样本估计总体等知识点，两图结合是解题的关键．21．列方程解应用题:某地2016年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2018年在2016年的基础上增加投入资金1600万元.从2016年到2018年，该地投入异地安置资金的年平均增长率为多少?【答案】从2015年到2017年，该地投入异地安置资金的年平均增长率为50%.【解析】设年平均增长率为x ，根据：2016年投入资金×（1+增长率）2=2018年投入资金，列出方程求解可得.【详解】解:设该地投入异地安置资金的年平均增长率为x. 根据题意得:1280(1+x)2=1280+1600. 解得x 1=0.5=50%，x 2=-2.5(舍去)，答:从2016年到2018年，该地投入异地安置资金的年平均增长率为50%. 【点睛】本题考查了一元二次方程的应用，由题意准确找出相等关系并据此列出方程是解题的关键． 22．如图，直线y=kx+2与x 轴，y 轴分别交于点A （﹣1，0）和点B ，与反比例函数y=mx的图象在第一象限内交于点C （1，n ）．求一次函数y=kx+2与反比例函数y=mx 的表达式；过x 轴上的点D （a ，0）作平行于y 轴的直线l （a ＞1），分别与直线y=kx+2和双曲线y=mx交于P 、Q 两点，且PQ=2QD ，求点D的坐标．【答案】()1一次函数解析式为22y x =+；反比例函数解析式为4y x=；()()22,0D ． 【解析】(1)根据A （-1,0）代入y=kx+2，即可得到k 的值； （2）把C （1，n ）代入y=2x+2，可得C （1,4），代入反比例函数my x=得到m 的值； （3）先根据D （a,0），PD ∥y 轴，即可得出P （a,2a+2）,Q(a ，4a),再根据PQ=2QD ，即可得44222a a a+-=⨯，进而求得D 点的坐标.【详解】（1）把A （﹣1，0）代入y=kx+2得﹣k+2=0，解得k=2， ∴一次函数解析式为y=2x+2； 把C （1，n ）代入y=2x+2得n=4， ∴C （1，4），把C （1，4）代入y=mx得m=1×4=4， ∴反比例函数解析式为y=4x；（2）∵PD ∥y 轴， 而D （a ，0），∴P （a ，2a+2），Q （a ，4a）， ∵PQ=2QD ， ∴2a+2﹣4a =2×4a， 整理得a 2+a ﹣6=0，解得a 1=2，a 2=﹣3（舍去）， ∴D （2，0）． 【点睛】本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点.也考查了待定系数法求函数的解析式.23．已知：如图，在平行四边形ABCD 中，BAD ∠的平分线交BC 于点E ，过点D 作AE 的垂线交AE 于点G ，交AB 延长线于点F ，连接EF ，ED .求证：EF ED =；若60ABC ∠=︒，6AD =， 2CE =， 求EF 的长.【答案】（1）详见解析；（2）27EF =【解析】（1）根据题意AB 平分BAD ∠可得90AGF AGD ∠=∠=︒，从而证明()FAG DAG ASA ∆≅∆即可解答（2）由（1）可知6AF AD ==，再根据四边形ABCD 是平行四边形可得642BF AF AB =-=-=，过点F 作FH EB ⊥延长线于点H ，再根据勾股定理即可解答 【详解】（1）证明：AB 平分BAD ∠FAG DAG ∴∠=∠ DG AE ⊥90AGF AGD ∴∠=∠=︒又AG AG =()FAG DAG ASA ∴∆≅∆GF GD ∴=又DF AE ⊥EF ED ∴=（2）FAG DAG ∆≅∆6AF AD ∴==四边形ABCD 是平行四边形//AD BC ∴，6BC AD ==180********BAD ABC ∴∠=︒-∠=︒-︒=︒1602FAE BAD ∴∠=∠=︒ 60FAE B ∴∠=∠=︒ ABE ∴∆为等边三角形624AB AE BE BC CE ∴===-=-= 642BF AF AB =-=-=过点F 作FH EB ⊥延长线于点H .在Rt BFH ∆中，60HBF ABC ∠=∠=︒30HFB ∴∠=︒112BH BF ∴== 2222213HF BF BH =-=-=415EH BE BH =+=+=()22223527EF FH EH =+=+=【点睛】此题考查三角形全等的判定与性质，勾股定理，平行四边形的性质，解题关键在于作好辅助线24．如图所示，抛物线y ＝x 2+bx+c 经过A 、B 两点，A 、B 两点的坐标分别为（﹣1，0）、（0，﹣3）．求抛物线的函数解析式；点E 为抛物线的顶点，点C 为抛物线与x 轴的另一交点，点D 为y 轴上一点，且DC ＝DE ，求出点D 的坐标；在第二问的条件下，在直线DE 上存在点P ，使得以C 、D 、P 为顶点的三角形与△DOC 相似，请你直接写出所有满足条件的点P 的坐标．【答案】（1）y=x 2﹣2x ﹣3；（2）D （0，﹣1）；（3）P 点坐标（﹣13，0）、（13，﹣2）、（﹣3，8）、（3，﹣10）．【解析】(1)将A,B两点坐标代入解析式，求出b,c值，即可得到抛物线解析式；(2)先根据解析式求出C点坐标，及顶点E的坐标，设点D的坐标为（0，m），作EF⊥y轴于点F，利用勾股定理表示出DC,DE的长．再建立相等关系式求出m值，进而求出D点坐标；(3)先根据边角边证明△COD≌△DFE，得出∠CDE=90°，即CD⊥DE，然后当以C、D、P为顶点的三角形与△DOC相似时，根据对应边不同进行分类讨论：①当OC与CD是对应边时，有比例式OC ODDC DP=，能求出DP的值，又因为DE=DC,所以过点P作PG⊥y轴于点G，利用平行线分线段成比例定理即可求出DG,PG的长度，根据点P在点D的左边和右边，得到符合条件的两个P点坐标；②当OC与DP是对应边时，有比例式OC ODDP DC=，易求出DP，仍过点P作PG⊥y轴于点G，利用比例式DG PG DPDF EF DE==求出DG,PG的长度，然后根据点P在点D的左边和右边，得到符合条件的两个P点坐标；这样，直线DE上根据对应边不同，点P所在位置不同，就得到了符合条件的4个P点坐标. 【详解】解：（1）∵抛物线y=x2+bx+c经过A（﹣1，0）、B（0，﹣3），∴10{3b cc-+==-，解得2{3bc=-=-，故抛物线的函数解析式为y=x2﹣2x﹣3；（2）令x2﹣2x﹣3=0，解得x1=﹣1，x2=3，则点C的坐标为（3，0），∵y=x2﹣2x﹣3=（x﹣1）2﹣4，∴点E坐标为（1，﹣4），设点D的坐标为（0，m），作EF⊥y轴于点F（如下图），∵DC2=OD2+OC2=m2+32，DE2=DF2+EF2=（m+4）2+12，∵DC=DE，∴m2+9=m2+8m+16+1，解得m=﹣1，∴点D的坐标为（0，﹣1）；（3）∵点C（3，0），D（0，﹣1），E（1，﹣4），∴CO=DF=3，DO=EF=1，根据勾股定理，，在△COD和△DFE中，∵{90CO DFCOD DFE DO EF=∠=∠=︒=，∴△COD ≌△DFE （SAS ），∴∠EDF=∠DCO ，又∵∠DCO+∠CDO=90°，∴∠EDF+∠CDO=90°，∴∠CDE=180°﹣90°=90°，∴CD ⊥DE ，①当OC 与CD 是对应边时，∵△DOC ∽△PDC ， ∴OC OD DC DP=1DP ， 解得DP=3， 过点P 作PG ⊥y 轴于点G ， 则DG PG DP DF EF DE ==，即31DG PG ==, 解得DG=1，PG=13， 当点P 在点D 的左边时，OG=DG ﹣DO=1﹣1=0，所以点P （﹣13，0）， 当点P 在点D 的右边时，OG=DO+DG=1+1=2， 所以，点P （13，﹣2）； ②当OC 与DP 是对应边时，∵△DOC ∽△CDP ， ∴OC OD DP DC =，即3DP， 解得，过点P 作PG ⊥y 轴于点G ，则DG PG DPDF EF DE==，即3103110DG PG==，解得DG=9，PG=3，当点P在点D的左边时，OG=DG﹣OD=9﹣1=8，所以，点P的坐标是（﹣3，8），当点P在点D的右边时，OG=OD+DG=1+9=10，所以，点P的坐标是（3，﹣10），综上所述，在直线DE上存在点P，使得以C、D、P为顶点的三角形与△DOC相似，满足条件的点P共有4个，其坐标分别为（﹣13，0）、（13，﹣2）、（﹣3，8）、（3，﹣10）．考点：1.相似三角形的判定与性质；2.二次函数动点问题；3.一次函数与二次函数综合题.25．甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线OBCDA表示轿车离甲地距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：当轿车刚到乙地时，此时货车距离乙地千米；当轿车与货车相遇时，求此时x的值；在两车行驶过程中，当轿车与货车相距20千米时，求x的值．【答案】（1）30；（2）当x＝3.9时，轿车与货车相遇；（3）在两车行驶过程中，当轿车与货车相距20千米时，x 的值为3.5或4.3小时．【解析】（1）根据图象可知货车5小时行驶300千米，由此求出货车的速度为60千米/时，再根据图象得出货车出发后4.5小时轿车到达乙地，由此求出轿车到达乙地时，货车行驶的路程为270千米，而甲、乙两地相距300千米，则此时货车距乙地的路程为：300﹣270＝30千米；（2）先求出线段CD 对应的函数关系式，再根据两直线的交点即可解答；（3）分两种情形列出方程即可解决问题．【详解】解：（1）根据图象信息：货车的速度V 货＝300605=， ∵轿车到达乙地的时间为货车出发后4.5小时，∴轿车到达乙地时，货车行驶的路程为：4.5×60＝270（千米），此时，货车距乙地的路程为：300﹣270＝30（千米）．所以轿车到达乙地后，货车距乙地30千米．故答案为30；（2）设CD 段函数解析式为y ＝kx+b （k≠0）（2.5≤x≤4.5）．∵C （2.5，80），D （4.5，300）在其图象上， 2.5804.5300k b k b +=⎧⎨+=⎩，解得110195k b =⎧⎨=-⎩， ∴CD 段函数解析式：y ＝110x ﹣195（2.5≤x≤4.5）；易得OA ：y ＝60x ，11019560y x y x =-⎧⎨=⎩，解得 3.9234x y ==， ∴当x ＝3.9时，轿车与货车相遇；（3）当x ＝2.5时，y 货＝150，两车相距＝150﹣80＝70＞20，由题意60x ﹣（110x ﹣195）＝20或110x ﹣195﹣60x ＝20，解得x ＝3.5或4.3小时．答：在两车行驶过程中，当轿车与货车相距20千米时，x 的值为3.5或4.3小时．【点睛】本题考查了一次函数的应用，对一次函数图象的意义的理解，待定系数法求一次函数的解析式的运用，行程问题中路程＝速度×时间的运用，本题有一定难度，其中求出货车与轿车的速度是解题的关键．26．先化简(31a +－a ＋1)÷2441a a a -++，并从0，－1，2中选一个合适的数作为a 的值代入求值．【答案】1.【解析】试题分析：首先把括号的分式通分化简，后面的分式的分子分解因式，然后约分化简，接着计算分式的乘法，最后代入数值计算即可求解．试题解析：原式=223111(2)a aa a-++⨯+-=2(2)(2)11(2)a a aa a-+-+⨯+-=22aa+--；当a=0时，原式=1．考点：分式的化简求值．中考数学模拟试卷一、选择题（本题包括10个小题，每小题只有一个选项符合题意）1．如图，已知菱形ABCD 的对角线AC ．BD 的长分别为6cm 、8cm ，AE ⊥BC 于点E ，则AE 的长是（）A ．53cmB ．25cmC ．48cm 5D ．24cm 5【答案】D 【解析】根据菱形的性质得出BO 、CO 的长，在RT △BOC 中求出BC ，利用菱形面积等于对角线乘积的一半，也等于BC×AE ，可得出AE 的长度． 【详解】∵四边形ABCD 是菱形，∴CO=12AC=3，BO=12BD=，AO ⊥BO ， ∴2222BC CO BO 345=+=+=．∴ABCD 11S BD AC 682422=⋅=⨯⨯=菱形． 又∵ABCD S BC AE =⋅菱形，∴BC·AE=24，即()24AE cm 5=． 故选D ．点睛：此题考查了菱形的性质，也涉及了勾股定理，要求我们掌握菱形的面积的两种表示方法，及菱形的对角线互相垂直且平分．2．如图，四个有理数在数轴上的对应点M ，P ，N ，Q ，若点M ，N 表示的有理数互为相反数，则图中表示绝对值最小的数的点是（ ）A ．点MB ．点NC ．点PD ．点Q【答案】C【解析】试题分析：∵点M ，N 表示的有理数互为相反数，∴原点的位置大约在O 点，∴绝对值最小的数的点是P 点，故选C ．考点：有理数大小比较．3．如图，直线AB与半径为2的⊙O相切于点C，D是⊙O上一点，且∠EDC=30°，弦EF∥AB，则EF 的长度为（）A．2 B．23C．3D．22【答案】B【解析】本题考查的圆与直线的位置关系中的相切．连接OC,EC所以∠EOC=2∠D=60°，所以△ECO为等边三角形．又因为弦EF∥AB所以OC垂直EF故∠OEF=30°所以EF=3OE=23．4．已知关于x的一元二次方程mx2＋2x－1=0有两个不相等的实数根，则m的取值范围是（）. A．m＞－1且m≠0B．m＜1且m≠0C．m＜－1 D．m＞1【答案】A【解析】∵一元二次方程mx2＋2x－1=0有两个不相等的实数根，∴m≠0，且22－4×m×(﹣1)＞0，解得：m＞﹣1且m≠0.故选A.【点睛】本题考查一元二次方程ax2+bx+c=0(a≠0)根的判别式：（1）当△=b2﹣4ac＞0时，方程有两个不相等的实数根；（2）当△=b2﹣4ac=0时，方程有有两个相等的实数根；（3）当△=b2﹣4ac＜0时，方程没有实数根.5．如图，在△ABC中，点D在BC上，DE∥AC，DF∥AB，下列四个判断中不正确的是( )A．四边形AEDF是平行四边形B ．若∠BAC ＝90°，则四边形AEDF 是矩形C ．若AD 平分∠BAC ，则四边形AEDF 是矩形D ．若AD ⊥BC 且AB ＝AC ，则四边形AEDF 是菱形【答案】C【解析】A 选项，∵在△ABC 中，点D 在BC 上，DE ∥AC ，DF ∥AB ，∴DE ∥AF ，DF ∥AE ，∴四边形AEDF 是平行四边形；即A 正确；B 选项，∵四边形AEDF 是平行四边形，∠BAC=90°，∴四边形AEDF 是矩形；即B 正确；C 选项，因为添加条件“AD 平分∠BAC”结合四边形AEDF 是平行四边形只能证明四边形AEDF 是菱形，而不能证明四边形AEDF 是矩形；所以C 错误；D 选项，因为由添加的条件“AB=AC ，AD ⊥BC”可证明AD 平分∠BAC ，从而可通过证∠EAD=∠CAD=∠EDA 证得AE=DE ，结合四边形AEDF 是平行四边形即可得到四边形AEDF 是菱形，所以D 正确.故选C.6．如图，EF 过▱ABCD 对角线的交点O ，交AD 于E ，交BC 于F ，若▱ABCD 的周长为18， 1.5OE =，则四边形EFCD 的周长为( )A ．14B ．13C ．12D ．10【答案】C 【解析】∵平行四边形ABCD ，∴AD ∥BC ，AD=BC ，AO=CO ，∴∠EAO=∠FCO ，∵在△AEO 和△CFO 中，AEO CFO AO COAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AEO≌△CFO，∴AE=CF，EO=FO=1.5，∵C四边形ABCD=18，∴CD+AD=9，∴C四边形CDEF=CD+DE+EF+FC=CD+DE+EF+AE=CD+AD+EF=9+3=12.故选C.【点睛】本题关键在于利用三角形全等，解题关键是将四边形CDEF的周长进行转化.7．如图所示的几何体的俯视图是（）A．B．C．D．【答案】D【解析】找到从上面看所得到的图形即可，注意所有看到的棱都应表现在俯视图中．【详解】从上往下看，该几何体的俯视图与选项D所示视图一致．故选D．【点睛】本题考查了简单组合体三视图的知识，俯视图是从物体的上面看得到的视图．8．如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC于点N，则MN等于（）A．125B．95C．65D．165【答案】A【解析】连接AM，根据等腰三角形三线合一的性质得到AM⊥BC，根据勾股定理求得AM的长，再根据在直角三角形的面积公式即可求得MN的长．【详解】解：连接AM，∵AB=AC，点M为BC中点，∴AM⊥CM（三线合一），BM=CM，∵AB=AC=5，BC=6，∴BM=CM=3，在Rt△ABM中，AB=5，BM=3，∴根据勾股定理得：AM= 22AB BM-= 2253-=4，又S△AMC=12MN•AC=12AM•MC，∴MN=·AM CM AC= 125．故选A．【点睛】综合运用等腰三角形的三线合一，勾股定理．特别注意结论：直角三角形斜边上的高等于两条直角边的乘积除以斜边．9．苹果的单价为a元/千克，香蕉的单价为b元/千克，买2千克苹果和3千克香蕉共需（）A．（a+b）元B．（3a+2b）元C．（2a+3b）元D．5（a+b）元【答案】C【解析】用单价乘数量得出买2千克苹果和3千克香蕉的总价，再进一步相加即可．【详解】买单价为a元的苹果2千克用去2a元，买单价为b元的香蕉3千克用去3b元，共用去：(2a+3b)元.故选C.【点睛】本题主要考查列代数式，总价=单价乘数量.10．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值应是（）A ．110B ．158C ．168D ．178【答案】B【解析】根据排列规律，10下面的数是12，10右面的数是14， ∵8=2×4−0，22=4×6−2，44=6×8−4， ∴m=12×14−10=158. 故选C.二、填空题（本题包括8个小题）11．方程22310x x +-=的两个根为1x 、2x ，则1211+x x 的值等于______． 【答案】1．【解析】根据一元二次方程根与系数的关系求解即可. 【详解】解：根据题意得1232x x +=-，1212x x =-， 所以1211+x x =1212x x x x +=3212--=1． 故答案为1． 【点睛】本题考查了根与系数的关系：若1x 、2x 是一元二次方程20ax bx c ++=（a≠0）的两根时，12b x x a+=-，12c x x a=． 12．已知二次函数2y ax bx c =++的图象如图所示，若方程2ax bx c k ++=有两个不相等的实数根，则k 的取值范围是_____________．【答案】5k <【解析】分析：先移项，整理为一元二次方程，让根的判别式大于0求值即可．。

第4讲 二次根式☞【根底知识归纳】☜☞归纳1.二次根式的有关概念 ⑴式子)0(≥a a 叫做二次根式． 注意：被开方数a 只能是 ． a 0a ≥〕⑵最简二次根式被开方数所含因数是 ，因式是 ，不含能 的二次根式，叫做最简二次根式．(3)同类二次根式化成最简二次根式后，被开方数 几个二次根式，叫做同类二次根式．☞归纳2.二次根式的性质〔1〕a ≥0〔a ≥0〕〔2〕)0()(2≥=a a a〔32(0)(0)a a a a a a ≥⎧==⎨-<⎩〔4(0,0)ab a b a b =≥≥〔50,0)a a a b b b =≥>☞归纳3.二次根式的运算〔1〕二次根式的加减法 合并同类二次根式：在二次根式的加减运算中，把几个二次根式化为最简二次根式后，假设有同类二次根式，可把同类二次根式合并成一个二次根式．〔2〕二次根式的乘除法 ab ＝_______(0,0)a b ≥≥ 二次根式的除法：a b _________(0,0)a b ≥>☞【常考题型剖析】☜☺ 题型一 二次根式的意义及性质【例1】( 20221x -x 的取值范围是【举一反三】1. ( 2022威海〕函数2x y +=x 的取值范围是〔 〕 A. 2x ≥- B. 20x x ≥-≠且 C. 0x ≠ D. 02x x >≠-且2. ( 2022娄底〕函数x y =x 的取值范围是〔 〕 A. 02x x ≥≠且 B. 0x ≥ C. 2x ≠ D. 2x >3. ( 2022x x 的取值范围是☺ 题型二 最简二次根式与同类二次根式【例2】〔 2022白银〕以下根式中是最简二次根式的是〔 〕 233 9 12【例3】〔 20223 〕 18 13 24 0.3 【举一反三】4.〔 2022龙岩〕与5-是同类二次根式的是〔 〕 A. 10 B. 15 C. 20 D. 255.〔 2022自贡〕以下根式中，不是最简二次根式的是〔 〕 10 8 6 26.〔 2022锦州〕以下二次根式中属于最简二次根式的是〔 〕 2436a b 4a +☺ 题型三 二次根式的运算【例4】〔 2022218的结果是【例5】〔 20225(55) =【举一反三】7.〔 20223的结果是 ．8.〔 202282= ．9.〔 2022哈尔滨〕计算12182的结果是 ．10.〔 202227312的结果是 ．☞【稳固提升自我】☜1.〔 2022南充〕以下计算正确的选项是〔 〕 1223 332 3x x x -=- 2x x =2.〔 2022梅州〕二次根式x -2有意义，那么x 的取值范围是〔 〕A. 2>xB. 2<xC. 2≥xD. 2≤x3.〔 2022桂林〕计算355 〕 5535 D. 64.〔 202235的结果是〔 〕 81535 D. 535.〔 2022扬州〕以下二次根式中的最简二次根式是〔 〕 A. 30 B. 12 C. 8 D.21 6.〔 20223合并的是〔 〕 13323127.〔 2022潜江〕以下各式计算正确的选项是〔 〕 23543331= C. 363332=⨯27338.〔 2022武汉〕假设代数式2x -在实数范围内有意义，那么x 的取值范为是〔 〕A. 2x ≥-B. 2x >-C. 2x ≥D. 2x ≤ 9.〔 2022随州〕假设代数式11x x +-有意义，那么实数x 的取值范围是〔 〕 A. 1x ≠ B. 0x ≥ C. 0x ≠ D. 0x ≥且1x ≠10.〔 2022滨州〕如果式子26x +有意义，那么x 的取值范围在数轴上表示出来，正确的选项是〔 〕A.B. C.D.11.〔 2022朝阳〕估计18182⨯+的运算结果应在哪两个连续自然数之间〔 〕 A. 5和6 B. 6和7 C. 7和8 D. 8和912.〔 2022荆门〕当12a <<2(2)10a a --=的值是〔 〕A. 1-B. 1C. 23a -D. 32a -13.〔 2022呼伦贝尔〕假设12x <<，那么23(1)x x -- 〕A. 24x -B. ﹣2C. 42x -D. 214.〔 20229x -x 的取值范围是 ．15.〔 2022汕尾〕函数1y x =的自变量x 的取值范围是 .16.〔 2022泰州〕计算 21218-等于17.〔 2022南京〕计算5153 的结果是18.〔 2022哈尔滨〕计算22433-＝19.〔 2022包头〕计算 216(31)3-+＝20.〔 2022日照〕假设2(3)3x x -=-，那么实数x 的取值范围是【根底知识重温】1．二次根式的有关概念⑴ 式子)0(≥a a 叫做二次根式．注意被开方数a 只能是非负数．〔要使二次根式a 有意义，那么a ≥0.〕⑵ 最简二次根式被开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式， 叫做最简二次根式．(3) 同类二次根式化成最简二次根式后，被开方数相同的几个二次根式，叫做同类二次根式．2．二次根式的性质〔1〕a ≥ 0〔a ≥0〕；〔2〕)0()(2≥=a a a )0(≥a a〔3〕==a a 2)0(<-a a〔4〕)0,0(≥≥•=b a b a ab 〔5〕)0,0(≥≥=b a ba b a 3．二次根式的运算〔1〕．二次根式的加减法合并同类二次根式：在二次根式的加减运算中，把几个二次根式化为最简二次根式后，假设有同类二次根式，可把同类二次根式合并成一个二次根式．〔2〕．二次根式的乘除法二次根式的乘法：a ·b ＝ab (a ≥0，b ≥0)．二次根式的除法：a b ＝ba (a ≥0，b ＞0)．。

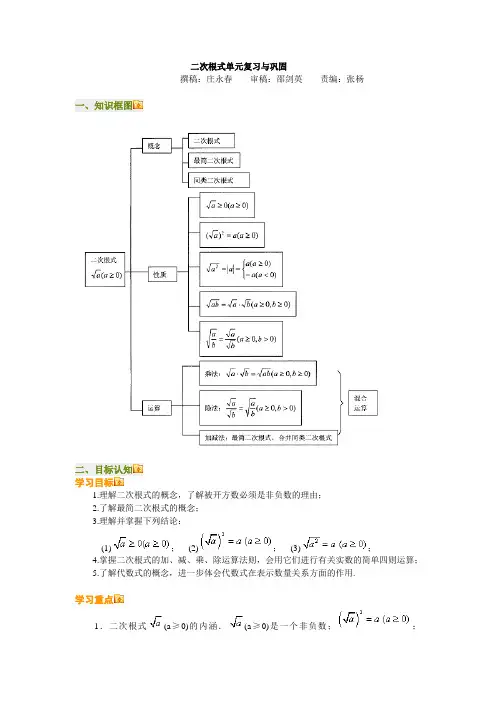
二次根式单元复习与巩固撰稿：庄永春审稿：邵剑英责编：张杨一、知识框图二、目标认知学习目标1.理解二次根式的概念，了解被开方数必须是非负数的理由；2.了解最简二次根式的概念；3.理解并掌握下列结论：(1)；(2)；(3)；4.掌握二次根式的加、减、乘、除运算法则，会用它们进行有关实数的简单四则运算；5.了解代数式的概念，进一步体会代数式在表示数量关系方面的作用.学习重点1．二次根式(a≥0)的内涵．(a≥0)是一个非负数；；及其运用；2．二次根式乘除法的规定及其运用；3．最简二次根式的概念；4．二次根式的加减运算．学习难点1．对(a≥0)是一个非负数的理解；对等式及的理解及应用；2．二次根式的乘法、除法的条件限制；3．利用最简二次根式的概念把一个二次根式化成最简二次根式．三、知识要点梳理知识点一、二次根式的主要性质：1.；2.；3.；4. 积的算术平方根的性质：；5. 商的算术平方根的性质：.6.若，则.知识点二、二次根式的运算1．二次根式的乘除运算(1) 运算结果应满足以下两个要求：①应为最简二次根式或有理式；②分母中不含根号.(2) 注意知道每一步运算的算理；(3) 乘法公式的推广：2．二次根式的加减运算先化为最简二次根式，再类比整式加减运算，明确二次根式加减运算的实质；3．二次根式的混合运算(1) 对二次根式的混合运算首先要明确运算的顺序，即先乘方、开方，再乘除，最后算加减，如有括号，应先算括号里面的；(2) 二次根式的混合运算与整式、分式的混合运算有很多相似之处，整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用.四、规律方法指导怎样快速准确地进行二次根式的混合运算.1.明确运算顺序，先算乘方，再算乘除，最后算加减，有括号先算括号里面的；2.在二次根式的混合运算中，原来学过的运算律、运算法则及乘法公式仍然适用；3.在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能收到事半功倍的效果.(1) 加法与乘法的混合运算，可分解为两个步骤完成，一是进行乘法运算，二是进行加法运算，使难点分散，易于理解和掌握.在运算过程中，对于各个根式不一定要先化简，可以先乘除，进行约分，达到化简的目的，但最后结果一定要化简.例如，没有必要先对进行化简，使计算繁琐，可以先根据乘法分配律进行乘法运算，，通过约分达到化简目的；(2) 多项式的乘法法则及乘法公式在二次根式的混合运算中同样适用.如：，利用了平方差公式.所以，在进行二次根式的混合运算时，借助乘法公式，会使运算简化.。

《二次根式》全章复习与巩固一、 化简1、无条件的(所有字母取正数） ①348m n ②2296x xy y ++③2(223)12-+-2、有附加条件的 ①212a (0)a ＜ ②25(03)x x --（2x+1）＜＜3、 有隐含条件的（有意义的字母的取值范围）①22(12)69x x x -+-+ ②31a a a ---4、 需要分类讨论的 298m 22(1)(2)m m +-二、 因式分解（实数范围内）①44a a + ②2(32)6x x +-③222215x x +-三、解方程(组） ①2253x x -= ②2363226x x =⎨=四、填空1、20072008(23)32)+=2、实数23-x ，小数部分为y ，则32x y +=3、①20(45(5132+=- ②127(23)3-⎡⎤=⎣⎦41514 14135、∆ABC 的三边长为a 、b 、c 22()()a b c a b c --+-6、①242x x =-成立的条件是 ②2233x x x x--=--成立的条件是7、()()()()()()()()a b a b a b a b a b a ba b a b a b a b a b a ba b ⎧----==-⎪-+-⎪⎪=⎨+⎪+-⎪=-⎪+⎩哪个对?五、计算技巧：1、336=-2、757575-=-3、25552525+=--4、化简b abb a ab a -++5、化简(ab bab a ab -+6、已知a+b=-3,ab=1，求a b b a 的值.7、如图所示，有一块边长为1的正方形铁片，将其每个角都剪下一个小等腰三角形，使其成为每条边都相等的八边形，求这个八边形的边长,你能将其结果写成没有分母或分母不带根号的形式吗？尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

儒洋教育学科教师辅导讲义
课题
二次根式复习与巩固
教学目标
1.知道二次根式与数的开平方运算之间的联系，理解 有意义的条件，理解 ；
2．能运用二次根式的性质进行计算，掌握二次根式混合运算的方法；
3．掌握二次根式的综合运用。
重点、难点
重点：1、理解 有意义的条件
2、掌握二次根式混合运算的方法
难点：1、掌握二次根式混合运算的方法
14．观察下列各式：……将你猜想到的规律用一个式子来表示：_____________________________________________。
15．化简：
(1)(2)
16．计算：
(1) 3(2)
(3) （4）
17．如图，在矩形ABCD中放两张面积分别为4和2的两张正方形纸片，问矩形ABCD至少有多大面积没有被盖住?
五、课堂反思：
课后练习:
一.选择题
1．下列式子一定是二次根式的是（）
A． B． C． D．
2．若 ，则（）
A．b>3 B．b<3C．b≥3 D．b≤3
3．若 有意义，则m能取的最小整数值是（）
A．m=0 B．m=1C．m=2 D．m=3
4．若x<0，则 的结果是（）
A．0 B．—2C．0或—2 D．2
（1） （2）
（3） （4）
22．化简(1)(2)(3)(
23．计算
(1) (2)
(3)
24.根据图形计算
已知：实数a，b在数轴上的位置如图所示，化简：-|a-b|
-3 -2 -1 0 1 2 3 4
a
b
x
25．化简计算
已知：
2、掌握二次根式的综合运用

专题12.11 二次根式（全章复习与巩固）（基础篇）（专项练习）一、单选题1. 下列各式中，一定是二次根式的是（ ）A. B. C. D. 2. 下列二次根式中，属于最简二次根式的是（ ）A. B. C. D.3. 是同类二次根式的是（ ）．A. B. C. 2 D. 4. 实数a 、b 在数轴上的位置如图所示，那么化简a -A. 2a b -B. bC. b -D. 2a b -+5. 的值应在（ ）A. 0和1之间 B. 1和2之间 C. 2和3之间 D. 3和4之间6. 下列计算中，正确的是（ ）A. =B. =C. 3= D. 2=7. 在下列各组线段中，能组成三角形的是（ ）A. 1cm ，2cm ，3cmB. 2221cm 2cm 3cm ，，C.cm cm D. cm ，cm ，5cm 8. 如图，从一个大正方形中截去面积为212cm 和218cm 的两个小正方形，则大正方形的边长是（ ）cm ．A.B. C. D.9. ，2，，…，，按下列方式进行排列：，2，；，4，…若2的位置记为()1,2，()2,1A. ()54， B. ()44， C. ()43， D. ()35，10. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为a ，b ，c ，记p ＝2a b c ++，则其面积S ．这个公式也被称为海伦﹣秦九韶公式．如果已知p ＝6，c ＝4，则此三角形面积的最大值为（ ）A.二、填空题11. =______．12. 有意义，那么x 的取值范围____________．13. _____ 1．14. 已知x ，y 都是实数，且4y =++，则y =__________．15. 已知实数m 、n 120n +-==______．16. 的整数部分为a 的小数部分为b ，求a b -=____．17. 已知x =，则221662x x x x-+--的值为________．18. 阅读理解：对于任意正整数a ，b ，有下面的不等式：2a b +≥，当且仅当a b =时，等号成立；结论：在a b +≥（a 、b 均为正实数）中，当且仅当a b =时，a b +有最小值0x >，式子23x x+有最小值为________．三、解答题19. 已知实数a 、b 在数轴上的对应点如图所示，化简a --．20. 计算：（1（2）(+-+21. 计算：（1⎛ ⎝（2）2+-22. （1）已知1x =+，1y =-，求22x xy y -+的值；（2）已知12x =+，12y =-，求y x x y +的值．23. 某居民小区有一块形状为长方形ABCD 的绿地，长方形绿地的长BC ，宽AB 为（即图中阴影部分），长方形花坛的长为)1m +，宽为)1m -，（1）长方形ABCD 的周长是多少？（结果化为最简二次根式）（2）除去修建花坛的地方．其他地方全修建成通道，通道上要铺上造价为50元每平方米的地砖，若铺完整个通道，则购买地砖需要花费多少元？24. 在数学小组探究学习中，张兵与他的小组成员遇到这样一道题：已知a =，求2281a a -+的值．他们是这样解答的：2==-∴2a -=∴()223a -=即2443a a -+=∴241a a -=-∴()()222812412111a a a a -+=-+=⨯-+=-．珇你根据张兵小组的解题方法和过程，解决以下问题：（1=______．（2+⋅⋅⋅；（3）若a =，求43443a a a --+的值．专题12.11 二次根式（全章复习与巩固）（基础篇）（专项练习）一、单选题【1题答案】【答案】C【解析】【分析】根据二次根式的定义即可得出正确选项．【详解】A是三次根式，不合题意；BCa＜时，不是二次根式，不合题意；D0故选C．【点睛】本题考查了二次根式的定义，掌握二次根式的定义是本题的关键．【2题答案】【答案】D【解析】【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式．是否同时满足，同时满足的就是最简二次根式，否则就不是．【详解】解：A=B=C11=，不属于最简二次根式，故本选项不符合题意；D属于最简二次根式，故本选项符合题意．故选：D【点睛】本题考查了最简二次根式，熟练掌握最简二次根式的概念是解答本题的关键．【3题答案】【答案】A【解析】【分析】根据二次根式的性质，把各个式子化成最简二次根式，根据同类二次根式的概念判断即可．【详解】解：A ==是同类二次根式，符合题意；B =C 、25=D ==故选:A ．【点睛】本题考查的是同类二次根式，二次根式的性质，熟记同类二次根式的概念是解题的关键．【4题答案】【答案】B【解析】【分析】根据差的绝对值是大数减小数，二次根式的性质，可化简代数式，根据整式的加减，可得答案．【详解】解：由数轴可知0a b ＜＜，∴0＜-a b ，∴a -()b a a =---b a a=-+b =．故选：B ．【点睛】本题考查了实数与数轴，利用差的绝对值是大数减小数、二次根式的性质化简整式是解题关键．【答案】C【解析】可．==<<，∴23<<，的值应在2到3之间，故选：C．的范围是解此题的关键．【6题答案】【答案】C【解析】【分析】根据二次根式的加减法对A、D进行判断；根据二次根式的乘法法则对B 进行判断；根据二次根式的除法法则对C进行判断．【详解】解：A、不是同类二次根式，不能合并，该选项不符合题意；B、=≠，该选项不符合题意；C3=，该选项符合题意；D、2-=，该选项不符合题意；故选：C．【点睛】本题考查了二次根式的运算，熟练掌握二次根式的运算法则是解题的关键．【7题答案】【解析】【分析】根据三角形的三边关系，即可求解．【详解】解：A . 123+=，不能组成三角形，故本选项不符合题意；B . 2221253+=<，不能组成三角形，故本选项不符合题意；C 1=>，能组成三角形，故本选项符合题意；D 5=< ，不能组成三角形，故本选项不符合题意；故选：C【点睛】本题主要考查了三角形的三边关系，熟练掌握三角形的两边之和大于第三边，两边之差小于第三边是解题的关键．【8题答案】【答案】B【解析】【分析】先根据正方形的面积公式计算出两小正方形的边长，再把两小正方形的边长相加即可得到大正方形的边长．=，=cm ，∴大正方形的边长为(+cm ．故选：B ．【点睛】本题考查二次根式的应用，解题关键是利用正方形面积公式求出小正方形的边长．【9题答案】【答案】C【解析】∵36218÷=，18533÷=4行，第3个数字．故选：C ．【点睛】此题考查的是数字的变化规律以及二次根式的化简，找出其中的规律是解题的关键．【10题答案】【答案】D【解析】【分析】根据公式算出a ＋b 的值，代入公式，根据完全平方公式的变形即可求出解．【详解】解：∵p ＝2a b c ++，p ＝6，c ＝4，∴6＝42a b ++，∴a ＋b ＝8，∴a ＝8−b ，∴S∴当b ＝4时，S 有最大值为故选：D ．【点睛】本题考查二次根式与完全平方公式的应用，解答本题的关键是明确题意，表示出相应的三角形的面积．二、填空题【11题答案】【答案】3π-##3π-+【解析】,0,0a aaa a≥⎧==⎨-<⎩由此即可求解．【详解】解：根据二次根式的性质得，∵3π<，∴30π-<，(3)3ππ=--=-，故答案为：3π-．【点睛】本题主要考查二次根式的性质，掌握二次根式开根的方法是解题的关键．【12题答案】【答案】23x≥【解析】有意义，可得320x-≥，再解不等式即可．【详解】解：∵有意义，∴320x-≥，解得：23x≥．故答案为：23x≥．【点睛】本题考查的是二次根式有意义的条件，掌握“被开方数为非负数”是解本题的关键．【13题答案】【答案】<【解析】【分析】与1-的倒数，再进行比较，然后根据倒数大的反而小，即可得出答案．【详解】解：-的倒数是：===，1-1==，又 1>+，∴1<-故答案为：<．【点睛】此题考查了实数的大小比较，分母有理化，掌握无理数的大小的比较方法是解题的关键．【14题答案】【答案】4【解析】【分析】利用二次根式被开方数的非负性求出x 值，再代入求出y 值，即可求解．【详解】解：∵4y =++，∴30x -≥，30x -≥，∴3x =，将3x =代入4y =，得：4y =，故答案为：4．【点睛】本题考查了二次根式被开方数的非负性，熟练掌握并灵活运用二次根式被开方数的非负性是解题的关键．【15题答案】【答案】【解析】【分析】根据绝对值和平方的非负性求出x 和y 的值，然后代入化简求值即可．【详解】120n +-=，∴30120m n -=⎧⎨-=⎩，解得312m n =⎧⎨=⎩，=+=+=，故答案为：【点睛】本题考查了绝对值和二次根式的非负性，二次根式的化简和加减运算，根据题意求出x 和y 的值是解题的关键．【16题答案】【答案】6【解析】的取值范围，从而求出a ，b 的值，然后代入计算即可．【详解】解：∵91116<<，<<，即34<<，∴3a =，3b =-，∴)336a b -+=--+=．故答案为：6．【点睛】本题主要考查了无理数的估算，解题关键是确定无理数的整数部分．【17题答案】【答案】4-【解析】【分析】根据题意可得3x =-，13x=+再把原式变形为()2213320x x ⎛⎫-+-- ⎪⎝⎭，再代入，即可求解．【详解】解：∵x =，∴3x =-，13x=+，∴221662x x x x-+--221669920x x x x =-++-+-()2213320x x ⎛⎫=-+-- ⎪⎝⎭()()22333320=-++--8820=+-4=-．故答案为：4-【点睛】本题主要考查了完全平方公式的应用，二次根式的混合运算，熟练掌握完全平方公式是解题的关键．【18题答案】【答案】【解析】【分析】根据题中所给方法可直接进行求解．【详解】解：由题意得：当0x >时，则23x x +≥=，当且仅当23x x =时，即x =时，23x x +取最小值为；故答案为【点睛】本题主要考查二次根式的性质，解题的关键是理解a b +≥．三、解答题【19题答案】【答案】3a-【解析】【分析】根据数轴可知0a b <<<，从而可知0a b +<>0a ，0b -<，再结合二次根式的性质、绝对值的性质进行化简计算即可．【详解】解：由数轴可知：0a b <<，∴0a b +<>0a -，0b -<，，(a a b a b =----+3a b b =--+-3a =-．【点睛】本题考查了二次根式的化简和性质、二次根式的加减运算，实数与数轴，解题的关键是注意开方结果是非负数、以及绝对值结果的非负性．【20题答案】【答案】（1）4（2）15【解析】【分析】（1）先开方，再乘除，再加减（2）先用平方差公式化简，并求出算术平方根，再加减【小问1详解】原式=+4=+【小问2详解】原式)2061=---141=+15=【点睛】本题考查二次根式的混合运算，掌握运算规则和方法技巧是本题关键．【21题答案】【答案】（1）-（2）10-+【解析】【分析】（1）直接利用二次根式的乘除运算法则化简，进而计算得出答案；（2）直接利用平方差公式以及完全平方公式化简结合二次根式的性质分别化简，进而计算得出答案．【小问1详解】⎛ ⎝122⎛⎫=⨯- ⎪⎝⎭==-【小问2详解】解：2-(53210=--+-5312=--+10=-+【点睛】此题主要考查了二次根式的混合运算以及乘法公式，正确化简各数是解题关键．【22题答案】【答案】（1）8；（2）8【解析】【分析】（1）先计算x y -与xy 的值，然后根据完全平方公式变形求值即可求解；（2）先计算x y +与xy 的值，然后根据分式的加法运算化简，再根据完全平方公式变形求值即可求解；【详解】（1）解：∵1x =，1y =，∴112x y -=+=，)114xy =+-=∴22x xy y -+＝()2x y xy -+224=+44=+8=；（2）解：∵12x =+，12y =-，∴111242x y xy +===-=∴y x x y +22x y xy+=()22x y xy xy+-=5112-=8=．【点睛】本题考查了二次根式的混合运算，完全平方公式变形求值，分式的化简求值，正确的计算是解题的关键．【23题答案】【答案】（1）（2）6600元【解析】【分析】（1）根据矩形周长公式列式计算即可；（2）用绿地面积减花坛面积差乘以50元，列式计算即可．【小问1详解】解：长方形ABCD的周长()=22m +==，答：长方形ABCD的周长是；【小问2详解】解：购买地砖需要花费)5011⎡⎤=+⎣⎦()50144131=-+50132=⨯6600=（元）答：购买地砖需要花费6600元．【点睛】本题考查二次根式的应用，根据题意列出版算式和掌握二次根式运用法则是解题的关键．【24题答案】【答案】（1）2（2）12（3）4【解析】【分析】(1)利用分母有理化计算；(2)先分母有理化，然后合并即可；(3)先利用=a 2+得到2a -=241a a -=，然后利用整体代入的方法计算．【小问1详解】=2=故答案为：2；【小问2详解】解：原式＝ 1+1-131=-12=；【小问3详解】2a ===+，∴ 2a -=∴2(2)5a -=，即2445a a -+=．∴241a a -=．∴43443a a a --+22443()a a a a =--+2143=⨯-+a a 243a a =-+13=+4=．【点睛】本题考查了二次根式的化简求值：二次根式的化简求值，一定要先化简再代入求值．二次根式运算的最后，注意结果要化到最简二次根式．。

【精品】2019年中考数学专题复习★★《二次根式》的巩固与提升分专题在数式相关的题型中，含二次根式的题是同学们感到比较头疼的，特别是其综合解答题的正确率也比较低；二次根式涵盖知识点多，解答的技巧性强；不但在代数中占据很重要的位置，而且有时在几何计算中也常能发挥很关键的作用，二次根式是很能考查同学们在初中阶段的数学素养的；下面我“分类”例举的一部分题型是对二次根式的巩固与提升，让我们来共同探究.一、善于挖掘隐含条件，准确的“移进”和“移出”例 ）A.-B.- D.分析隐含有a 0≤的条件.这是因为根据二次根式的定义可知3a 0-≥，所以a 0≤===-，故选C.例2.把(a 1-中的根号外面的因式“移入”根号内为 .分析：(a 1-隐含有101a>-的条件，所以1a 0->，可得a 1<，所以a 10-<；所以()a 11a -=--=(a 1-===. 点评：关于二次根式的根号内外的“移进”和“移出”，关键是要抓住二次根式的被开方数是变形化简；这类题在考试中常出现在考题的填空和选择题中，是正确率比较低的热点考题.二、利用二次根式中的算术平方根的双重非负数性[ )a 0≥有a 00≥≥]巧解题例1.x y 、6y =-，求1x y -的值？分析：根据式子有13x 03x 10-≥⎧⎨-≥⎩，从中可求得x 的值，进一步求得y 的值，使问题得以解决.略解：根据题意可知：13x 03x 10-≥⎧⎨-≥⎩ 解得：1x 3=；把1x 3=6y =-有：6y =-，解得：y 6= 所以111x y 636183--⎛⎫=⨯=⨯= ⎪⎝⎭.例2.的值？分析：本题显得比较抽象，似乎难以找到突破口，但题中有二次根式这一重要特点，所以抓23a 0-≥，可求得a 0=.略解：23a 0-≥，可得a 0≤ ；又∵a 0≥ ∴a 0=∴原式32106+-+=+=+++=.点评：二次根式的算术平方根的双重非负数性是属于考试中的高频考点，这个知识点容易与其它知识点联姻构成有一定含金量的综合题，而双重非负数性在其中扮演的往往是关键角色，上面的几道例题就是要抓住算术平方根及其被开方数都是非负数的破题；比如很多同学对于例2这类题不知从何入手，但只要抓住本题是二次根式构建的，从被开方数是非负数这点入手，就可以隐藏在其中的a 的值挖出来，从而使问题得以解决.三、逆用()2a a 0=≥即()2a a 0=≥化简例1.化简： 分析：根据题中式子可知,a 0b 0≥≥，∴,22a b ==∴22a b -=-=+,-等，即逆用()2a a 0=≥可以巧化简.略解 ： 原式==+=+-=a b ab +- 例2.分析：本题按常规可以把分母中根号化去，但若用()2a a 0=≥可以进行巧算，更简捷. 略解：原式===点评：逆用()2a a 0=≥即()2a a 0=≥来化简、计算或分解因式等往往能起到“四两破千斤”的作用.比如例2的计算化简（主要把分母中的根号化去，即分母有理化），按常规方法要分子和分母要同时乘以有理化因式，在计算中是容易出错的，但用()2a a 0=≥进行巧算，可以做到快速准确.。

专题16.8 《二次根式》全章复习与巩固（专项练习）一、单选题1．（2020·四川成都市·八年级期末）下列运算正确的是（）A2B3C＝0.5D=2．（2020·）A．2和3之间B．3和4之间C．4和5之间D．5和6之间3．（2020·达州市第一中学校八年级期中）下列根式中，最简二次根式是（）A B C D4．（2020·中，最简二次根式有（）A．1个B．2个C．3个D．4个5．（2020·上海市甘泉外国语中学八年级期中）下列各式中，（）A1B C D6．（2020·浙江杭州市·九年级）已知，在ABC中，D是BC边上一点，∠=∠=．若D是BC边的中点，则ACB30,45ABC ADC∠的度数为（）A．95°B．100°C．105°D．110°7．（2020·山东菏泽市·王浩屯镇中学八年级期中）实数a、b在数轴上对应点的位置如图所+的结果为（）a bA．b B．-2a+b C．2a+b D．2a-b8．（2020·温州育英国际实验学校八年级月考）下列四个式子中，与(a -的值相等的是（ ）AB ．CD ．二、填空题9．（2020·a 的取值范围是___________．10．（2020·河北邢台市·金华中学八年级期中）若实数x 、y |1|0y -=，则代数式x y +的值为________．11．（2019·鄄城县箕山镇箕山中学八年级期中）计算：=______．12．（2020·四川大学附属中学西区学校八年级期中）比较大小：______平方根是______．13．（2019·36==______．14．（2020·河南洛阳市·＝6﹣a ，则a 的取值范围是_____．15．（2020·上海普华教育信息咨询有限公司八年级期中）若最简二次根式2a 与4同类二次根式，则ab =_______．16．（2020·遵化市第三中学八年级月考）若b +6________．17．（2020·上海浦东新区·八年级期中）求值：()(2020202133⋅+＝_____．18．（2020·上海市第二工业大学附属龚路中学八年级期中）把(2-x 移到根号内得____________．19．（2020·上海浦东新区·上外浦东附中八年级期中）当0x >时，= _________________．20．（2019·的整数部分a =_______，小数部分b =_______．三、解答题21．（2019·浙江台州市·八年级期末）计算：（1）)031.4143--；（2 （3）()22633-÷xy x yz xy ；（4）()()()212141+---m m m m ．22．（2020·广东佛山市·平洲一中八年级月考）阅读下列运算过程，并完成各小题：3====．数学上把这种将分母中的根号去掉的过程称作“分母有理化”，如果分母不是一个无理数，而是两个无理数的和或差，此时也可以进1121===-；32===-模仿上例完成下列各小题：（1=______； （2=_______ （3n +++n 为正整数）． 23．（2020·上海市曹杨第二中学附属学校八年级期中）化简求值：当x =，y =时，（1）求222x xy y ++的值；（2的值．24．（2020·四川成都市·天府七中八年级期中）请计算下列各题．（1）已知x =，y =，若x 的小数部分为a ，y 的整数部分为b ，求ax by +的平方根．（2）已知a ，b ，c 数轴上对应的点如图所示，图中O 为原点，化简：2||b c +．参考答案1．D【分析】根据二次根式的性质进行化简．【详解】A，故原计算错误；BCD=故选：D．【点睛】本题考查二次根式的性质，熟练掌握相关知识是解题的关键，比较基础．2．D【分析】先计算原式的结果，再根据结果判断范围．【详解】原式===，2765<<，故选：D．【点睛】本题考查了无理数的估算问题，掌握计算规则并准确化简是解决问题的关键．3．D【分析】根据最简二次根式的概念进行辨析即可．【详解】A=，故错误；B=C=，故错误；D故选：D．【点睛】本题考查最简二次根式的辨析，掌握最简二次根式的概念是解决问题的关键．4．A【分析】利用最简二次根式的概念分析得出答案．【详解】解：==，不是最简二次根式；7最简二次根式有1个，故选：A．【点睛】本题考查了最简二次根式，正确理解二次根式的定义是解题的关键．5．D【分析】根据同类二次根式的定义逐项判断即可得．【详解】A1BC3=D=是同类二次根式，此项符合题意；故选：D．【点睛】本题考查了同类二次根式，熟记定义是解题关键．6．C【分析】过A 作AE ⊥BC 于E ，在AE 上取点F ，连接CF ，使得∠CFE=30°，设DE=x ，即可得出CE=DE -CD=(2x ，进而得到AE=(2+CE ，再根据CE ，CF=2CE ，得到AF=AE -EF=2CE=CF ，即可得到∠ACE 的度数，从而得到结果．【详解】解：如图所示，过A 作AE ⊥BC 于E ，在AE 上取点F ，连接CF ，使得∠CFE=30°， 设DE=x ，∵∠ABE=30°，∠ADE=45°，∴AE=x ，，BD=CD=)1x ，∴CE=x -)1x=(2x ，∴AE CE =2+AE=(2+CE ，又∵Rt △CEF 中，EF=CE ，CF=2CE ，∴AF=AE -EF=2CE=CF ，∴∠FAC=∠FCA=12∠CFE=15°， ∴∠ACE=∠ACF+∠ECF=15°+60°=75°，∴∠ACB=105°，故选C ．【点睛】本题主要考查了含30°角的直角三角形的性质以及等腰直角三角形的性质，在直角三角形中，30°角所对的直角边等于斜边的一半．7．A【分析】根据数轴上的位置可得a ＜0，|a |＞|b |，b ＞0，根据二次根式和绝对值的性质化简即可．解：根据题意可知，a ＜0，|a |＞|b |，b ＞0，|a +b |=（-a ）-（-a -b ）=-a +a +b =b ，故选：A ．【点睛】本题考查实数与数轴、二次根式和绝对值的性质，根据数轴上的位置得到a ＜0，|a |＞|b |，b ＞0是解题的关键．8．D【分析】根据二次根式有意义的条件可得出20210a ->，可得20210a -<，由此可将2021a -变形得出答案．【详解】由题意得：20210a ->，可得20210a -<，∴((2021a a ---== 故选：D ．【点睛】本题考查了二次根式的性质与化简，关键是由等式可确定出20210a ->． 9．1.4a ≥-【分析】二次根式有意义的条件：被开方数为非负数，再列不等式，解不等式即可得到答案．【详解】有意义， 410a ∴+≥41,a ∴≥-1,4a ∴≥- 故答案为：1.4a ≥-【点睛】本题考查的是二次根式有意义的条件，掌握“二次根式中，被开方数为非负数”是解题的关键．10．1根据二次根式与绝对值的非负性列式求解即可．【详解】根据非负性可知：10xy=⎧⎨-=⎩，解得1xy=⎧⎨=⎩，则1x y+=，故答案为：1．【点睛】本题考查了二次根式及绝对值的非负性，理解性质并准确求解是解题关键．11．2【分析】根据平方差公式和二次根式的性质计算即可【详解】解：7-5=2+=故答案为：2【点睛】本题考查了平方差公式和二次根式的性质，熟练掌握法则和性质是解题的关键12．<2±【分析】先求出==再比较即可；2±．【详解】解：∵==∵4575<，∴4=，∴4的平方根是2=±．故答案为：<；2±．【点睛】本题考查了二次根式的大小比较和平方根，掌握无理数的比较方法和平方根的定义是解题的关键．13．0.36利用无理数的除法运算法则即可计算出结果．【详解】360.36100==== 故答案为：0.36．【点睛】本题考查了无理数的除法运算法则，熟记法则是解决问题的核心．14．a ≤6．【分析】原式利用二次根式性质，以及绝对值的代数意义判断即可确定出a 的范围．【详解】＝|a ﹣6|＝6﹣a ，∴6﹣a ≥0，解得：a ≤6．故答案为：a ≤6．【点睛】本题考查了二次根式的性质，解题的关键是掌握二次根式的性质进行解题． 15．-4【分析】根据同类二次根式的根指数、被开方数相同可得出方程，解出即可得出答案． 【详解】解：∵最简二次根式2a 与4∴2a+b=4-a=2，3a=6解得：a=2，b=-2．∴()224=⨯-=-ab故答案为：-4．【点睛】此题考查了同类二次根式的知识，属于基础题，解答本题的关键是掌握同类二次根式的根指数、被开方数相同．16．【分析】由二次根式的性质，先求出a 、b 的值，然后代入计算，即可得到答案．【详解】解：根据题意，则∵30-≥a ，30a -≥，∴3a =，∴6b =，==故答案为：【点睛】本题考查了二次根式的性质，解题的关键是掌握二次根式的性质，正确的求出a 、b 的值．17．+3【分析】根据同底数幂的乘法和积的乘方逆运算法则解答即可．【详解】解：原式＝3)2020·2020·(+3)＝(﹣1)2020·+3)＝．故答案为：+3．【点睛】本题考查了同底数幂的乘法和积的乘方以及二次根式的运算等知识，属于常考题型，熟练掌握上述知识和解答的方法是关键．18．【分析】根据二次根式被开方数是非负数且分式分母不为零，将根号外的因式转化成正数形式，然后 解：102x >-， 20x ∴->；(2-x(x=--===故答案为：【点睛】本题考查二次根式的性质和二次根式计算，灵活运用二次根式的性质是解题关键．19．9 4【分析】先根据二次根式的定义和除法的性质可得0y>，再根据二次根式的性质化简，然后计算二次根式的除法即可得．由二次根式的定义得：250x yyx⎧≥⎪⎨≥⎪⎩，x，y∴≥，又除法运算的除数不能为0，0y∴≠，y∴>，35xy=3xy=，=49=，故答案为：94【点睛】本题考查了二次根式的定义与除法运算，熟练掌握二次根式的运算法则是解题关键．20．52【分析】先化简，然后用夹逼法求解即可．【详解】3==45<<23∴<<，536∴<<，3∴5，小数部分为352=，5a ∴=，2b =．故答案为：52．【点睛】本题考查了分母有理化，求无理数的整数部分和小数部分，熟练掌握分母有理化是解答本题的关键．21．（1）2627；（2）22+；（3）2y xz -；（4）41m - 【分析】（1）根据零指数幂和负整数指数幂的性质计算，即可得到答案；（2）根据二次根式的性质计算，即可得到答案；（3）根据整式混合运算的性质计算，即可得到答案；（4）根据平方差公式、整式乘法和加减法的性质计算，即可得到答案．【详解】（1）原式31261327=-=；（2）原式2222422=+⨯=+=+； （3）原式2263332=÷-÷=-xy xy x yz xy y xz ；（4）原式22414441=--+=-m m m m ．【点睛】本题考查了零指数幂、负整数指数幂、二次根式、整式混合运算、平方差公式的知识；解题的关键是熟练掌握零指数幂、负整数指数幂、二次根式、整式混合运算、平方差公式的性质，从而完成求解．22．（1；（2）2；（31．【分析】（1，然后约分即可；（2）把分子分母都乘以，然后利用平方差公式计算；（3）先分母有理化，然后合并即可．【详解】（1==；（22===；故答案为：2； （3n ++11n =+++1=．【点睛】本题考查了二次根式的混合运算：在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．23．（1）20；（2）2+【分析】（1）将x 、y 的值化简，计算出x+y 的值，然后代入原式=（x+y ）2计算可得；（2）先计算出x+y 、x -y 、xy 的值，再整体代入原式计算可得．【详解】解：∵x == 2=，y == 2=，∴2)2)x y +=+=2)2)4x y -=-=21)2xy ==，（1）()2222x xy y x y ++=+=2=20；（2+2=31+=2+【点睛】本题主要考查二次根式的化简求值，解题的关键是掌握二次根式的混合运算顺序和运算法则及二次根式分母有理化的能力．24．（1）±1；（2）2b -【分析】（1）先求出x ，y 的取值范围，再判断a ，b 的值，最后代入求解；（2）根据a ，b ，c 数轴上对应的点，判断a ，b ，c 的大小，根据然后根据绝对值及二次根式的性质进行化简即可．【详解】解：（1）2x ==，2y ==， x 的小数部分为a ，y 的整数部分为b ，242a ∴=-=，0b =，2)2)0ax by ∴+=+⨯542)0=-+⨯1=．1=±．（2）2||b c +||||a a b b c c =---+++()()a b a b c c =----++a b a b c c =--+--+2b =-．【点睛】本题考查了二次根式的化简，分母有理化及二次根式的计算，熟练的掌握二次根式的化简，分母有理化及二次根式的计算是解答本题的关键．。

《二次根式》全章复习与巩固
一、 化简
1、无条件的（所有字母取正数）
2、有附加条件的
①0)a ＜ ②
5(03)x x -＜＜
3、 有隐含条件的（有意义的字母的取值范围）
①2 ②
-
4、 需要分类讨论的
二、 因式分解（实数范围内）
①4a + ②2x x +-
③2215x +-
三、解方程（组）
①3x =
②=+=
四、填空
1
、20072008(22)
=
2、
x ，小数部分为y ，则32x y +=
3
、①20-÷=
②1(2-⎤=⎦
4
5、∆ABC 的三边长为a 、b 、c ，则
=
6
2x
=-成立的条件是
=成立的条件是
7
、
(a b
a b
⎧-
==
-
=⎨
=
哪个对？
五、计算技巧：
1
=
2
=
3
、+=
4、化简
b
ab
b
a
ab
a-
+
+
5
、化简
6、已知a+b=-3,ab=1,求
a b b a +的值.
7、如图所示，有一块边长为1的正方形铁片，将其每个角都剪下一个小等腰三角形，使其成为每条边都相等的八边形，求这个八边形的边长，你能将其结果写成没有分母或分母不带根号的形式吗？
D C B A。

二次根式（基础） 撰稿： 赵炜 审稿：杜少波 【巩固练习】一．选择题 1.若二次根式1x -有意义，则x 的取值范围是（ ）.A.1x ≠ B ．x ≥1 C.x<1 D.全体实数2. 若1a <,化简2(1)-1=a - ( ).A.2a -B.2a -C.aD.a -3.下列说法正确的是（ ）A ．4是一个无理数B ．函数11y x =-的自变量x 的取值范围是x ≥1 C ．8的立方根是2± D.若点(2,)-3)P a Q 和点（b ，关于x 轴对称，则a b +的值为5. 4. 若a 不等于0，a 、b 互为相反数，则下列各对数中互为相反数的一对数是( ).A.与B.与C.与D.与5.下列根式是最简二次根式的是（ ）.A ．8B ．24x y +C ．D ．6. 已知，化简二次根式的正确结果为（ ）.A. B. C. D.二. 填空题7.当x______时，式子x -在实数范围有意义；当x_______时，式子2x -在实数范围有意义.8.=____________. 若，则____________.9．（1）2)53(-=_____________.（2）9622++-a a a （a>0）=__________________________.10.22x x --2(1)x -11.当x ≤0时，化简21-x x 12.有如下判断：（1）11010x y xy x ⋅= (2)155=1 (3)55552424=+ (4)332363⨯=（5）222516541-=-=（6）a b a b ⋅=⋅成立的条件是,a b 同号.其中正确的有_____个.三 综合题13. 当x 为何值时，下列式子有意义？（1）21x + (2) 2x -（3）11y x =-； （4）11y x =-；14. 已知实数x ，y 满足，求代数式2013()x y +的值.15.若23324y x x x =---x y.【答案与解析】一、选择题1．【答案】B.2．【答案】D .【解析】因为1a < 原式=1111a a a --=--=-.3．【答案】 D.【解析】 4=2是有理数；11y x =-的x 的取值范围是x>1;8的立方根是2； 因为(2,)-3)P a Q 和点（b ，关于x 轴对称，所以3,2a b ==，及5a b +=,所以选D. 4．【答案】 C.5．【答案】 B.【解析】 根据最简二次根式的性质，A,D 选项都含有能开方的项，C 选项含有分母，所以选B.6．【答案】 D.【解析】 因为，2y x-是被开方数，所以y<0,x<0, 所以原式==x y x -=y --.二、填空题7.【答案】 x ≤0；x=0.8 【答案】2;7x m -=±. 9.【答案】(1) 45; (2) -3.10.【答案】 -1.【解析】因为22x x -+-=0，所以2-x ≥0，x-2≥0，所以x=2;则原式=2(12)112-=--. 11.【答案】 1.【解析】 原式=111x x x x --=-+=.12.【答案】 2个.【解析】只有（1），（3）正确.三、 解答题13.【解析】 （1）21x +≥0，即x 为任意实数； （2）2x -≥0，即2x ≤0，即x =0. （3）10,1x x ->∴> （4）0,10,0 1.x x x x ≥-≠∴≥≠且. 14.【解析】 因为. ，所以x=5，y=-4.则2013()x y +=2013(54)-=115.【解析】 因为23324y x x x ---2x-3≥0,3-2x ≥0，即x=32，10则xy36615225101010===.。

2024年中考数学专题练习：二次根式知识点回顾1、二次根式的定义a ≥0)的式子叫做二次根式。

2、二次根式的基本性质①2()a a =(a ≥0)；②2a a =(a ≥0)；③2a a =(a 取全体实数)。

3、二次根式的乘除(1)二次根式的乘法：①ab b a =⋅； ②b a ab ⋅= (a ≥0， b ≥0)。

(2)二次根式的除法：a a b b = a ab b= (a ≥0， b ＞0)。

4、最简二次根式最简二次根式满足的条件：①被开方数不含分母；②被开方数中不含能开得尽方的因数或因式。

5、二次根式的加减二次根式加减时，可以先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并。

专项练习一、选择题1．下列二次根式中，最简二次根式是（ ） A ．−√2B ．√12C ．√15D ．√22．下列各式中，正确的是（ ） A ．√(−3)2=−3B ．−√32=−3C ．√(−3)2=±3D ．√32=±33．下列计算正确的是（ ） A ．√2+√3=√5B ．2+√2=2√2C ．√8−√3=√5D ．3√2−√2=2√24．若代数式 √x +4 有意义，则 x 的取值范围是（ ） A ．x ≤−4B ．x ≥4C ．x ≠−4D ．x ≥−45．下列计算错误的是（ ） A ．√8−√2=√2B ．√8÷√2=4C ．√2×√3=√6D ．√32=36．若√3−x =3−x ，则x 的值是（ ） A ．0B ．2C ．3D ．2或37．一个长方体的体积是 √48cm 3 ，长是 √6cm ，宽是 √2cm ，则它的高是（ ）A．4cm B．√3cm C．2√2cm D．2cm 8．已知x=√5+2，y=√5−2，则√x2+y2+7的值为（）A．3 B．4 C．5 D．6 二、填空题9．化简：√32= .10．使√3x−1有意义的x的取值范围是．11．√(a−2)2=2−a，则a的取值范围是．12．已知y=√2x−5+√5−2x−3，则2xy的值为．13．已知x=√5−22，则x2+x+1=．三、解答题14．计算（1）√(−2)2+√2(1−√12)+|−√8|（2）√18−√8+(√3+1)×(√3−1)15．先化简，再求值（32m++m﹣2）÷2212m mm-++；其中m2+1.16．数a，b在数轴上的位置如图所示，化简．17．已知，．（1）试求的值；（2）试求的值．18．阅读理解材料：把分母中的根号化掉叫做分母有理化，例如：①√5=√5√5×√5=√55；②√2−1=√2+1)(√2−1)(√2+1)=√2+1(√2)2−12=√2+1等运算都是分母有理化．根据上述材料，（1）化简：；2√3（2）化简：；√5−√3)(√2023+1)．（3）计算：(√3+1√5+√3√7+√5√2023+√2021参考答案 1．A 2．B 3．D 4．D 5．B 6．D 7．D 8．C 9．√6210．x ≥13 11．a ≤2 12．-15 13．9−2√5414．（1）解： √(−2)2+√2(1−√12)+|−√8| =2+√2−√2×12+2√2=2+√2−1+2√2 =1+3√2 ；（2）解： √18−√8+(√3+1)×(√3−1) =3√2−2√2+(√3)2−12 =√2+2.15．解：原式＝（23422m m m -+++）÷2(1)2m m -+ ＝2(1)(1)22(1)m m m m m +-+⋅+-＝11m m +-， 当m 2+1时， 2211+-21．16．解：如图得，﹣2＜a＜﹣1，1＜b＜2，∴a﹣b＜0，b﹣1＞0，a+1＜0，∴．＝b﹣a+b﹣1﹣（﹣a﹣1），＝2b﹣a﹣1+a+1，＝2b．17．（1）解：∵，，∴x+y==4，xy==1∴；（2）解：∵，，∴x+y==4，x-y=，xy==1 ∴ .18．（1）解：2√3=√32√3×√3=√36；（2）解：√5−√3=√5+√3)(√5−√3)×(√5+√3)=√5+√35−3=√5+√32；（3）解：(√3+1√5+√3√7+√5+⋅⋅⋅√2023+√2021)(√2023+1)=[√3−1)(√3+1)×(√3−1)+√5−√3)(√5+√3)×(√5−√3)⋯√2023−√2021)(√2023+√2021)×(√2023−√2021)](√2023+1)=(√3−12+√5−√32+√7−√52+⋯⋯+√2023−√20212)(√2023+1)=(√3−1+√5−√3+√7−√5⋯⋯√2023−√20212)(√2023+1)=(√2023−1)(√2023+1)2=2023−12=1011．。