电机学序论及第1篇变压器
- 格式:doc
- 大小:317.00 KB
- 文档页数:28







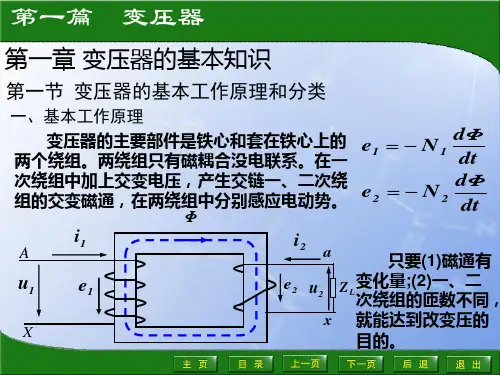
第一章 变压器基本工作原理和结构1-1从物理意义上说明变压器为什么能变压,而不能变频率?答:变压器原副绕组套在同一个铁芯上, 原边接上电源后,流过激磁电流I 0, 产生励磁磁动势F 0, 在铁芯中产生交变主磁通ф0, 其频率与电源电压的频率相同, 根据电磁感应定律,原副边因交链该磁通而分别产生同频率的感应电动势 e 1和e 2, 且有dt d N e 011φ-=, dt d N e 022φ-=, 显然,由于原副边匝数不等, 即N 1≠N 2,原副边的感应电动势也就不等, 即e 1≠e 2, 而绕组的电压近似等于绕组电动势,即U 1≈E 1,U 2≈E 2,故原副边电压不等,即U 1≠U 2, 但频率相等。
1-2 试从物理意义上分析,若减少变压器一次侧线圈匝数(二次线圈匝数不变)二次线圈的电压将如何变化?答:由dt d N e 011φ-=, dt d N e 022φ-=, 可知 , 2211N e N e =,所以变压器原、副两边每匝感应电动势相等。
又U 1≈ E 1, U 2≈E 2 , 因此,2211N U N U ≈, 当U 1 不变时,若N 1减少, 则每匝电压11N U 增大,所以1122N U N U =将增大。
或者根据m fN E U Φ=≈11144.4,若 N 1 减小,则m Φ增大, 又m fN U Φ=2244.4,故U 2增大。
1-3 变压器一次线圈若接在直流电源上,二次线圈会有稳定直流电压吗?为什么?答:不会。
因为接直流电源,稳定的直流电流在铁心中产生恒定不变的磁通,其变化率为零,不会在绕组中产生感应电动势。
1-4 变压器铁芯的作用是什么,为什么它要用0.35毫米厚、表面涂有绝缘漆的硅钢片迭成?答:变压器的铁心构成变压器的磁路,同时又起着器身的骨架作用。
为了铁心损耗,采用0.35mm 厚、表面涂的绝缘漆的硅钢片迭成。
1-5变压器有哪些主要部件,它们的主要作用是什么?答:铁心: 构成变压器的磁路,同时又起着器身的骨架作用。

《电机学》各章练习题与自测题参考答案第1章 思考题与习题参考答案1.1 变压器是怎样实现变压的?为什么能够改变电压,而不能改变频率?答:变压器是根据电磁感应原理实现变压的。
变压器的原、副绕组交链同一个主磁通,根据电磁感应定律dtd Ne φ=可知,原、副绕组的感应电动势(即电压)与匝数成正比,所以当原、副绕组匝数21N N ≠时,副边电压就不等于原边电压,从而实现了变压。
因为原、副绕组电动势的频率与主磁通的频率相同,而主磁通的频率又与原边电压的频率相同,因此副边电压的频率就与原边电压的频率相同,所以,变压器能够改变电压,不能改变频率。
1.2变压器一次绕组若接在直流电源上,二次侧会有稳定的直流电压吗,为什么?答:若一次绕组接直流电源,则铁心中将产生恒定的直流磁通,绕组中不会产生感应电动势,所以二次侧不会有稳定的直流电压。
1.3变压器铁心的作用是什么?为什么要用0.35mm 厚、表面涂有绝缘漆的硅钢片叠成?答:变压器铁心的主要作用是形成主磁路,同时也是绕组的机械骨架。
采用导磁性能好硅钢片材料是为了提高磁路的导磁性能和减小铁心中的磁滞损耗,而用薄的(0.35mm 厚)表面绝缘的硅钢片叠成是为了减小铁心中的涡流损耗(涡流损耗与硅钢片厚度成正比)。
1.4 变压器有哪些主要部件,其功能是什么?答:变压器的主要部件是器身,即铁心和绕组。
铁心构成变压器的主磁路,也是绕组的机械骨架;绕组构成变压器的电路,用来输入和输出电能。
除了器身外,变压器还有一些附属器件,如绝缘套管、变压器油、油箱及各种保护装置等。
1.5 变压器二次额定电压是怎样定义的?答:变压器一次绕组加额定电压,二次绕组空载时的端电压定义为变压器二次额定电压。
1.6 双绕组变压器一、二次侧的额定容量为什么按相等进行设计?答:变压器传递电能时,内部损耗很小,其效率很高(达95%以上),二次绕组容量几乎接近一次绕组容量,所以双绕组变压器的一次、二次额定容量按相等设计。
电机学绪论第一节概述一、电机在国民经济中的应用•什么是电机•电能•电机应用(1)发电机(2)变压器(3)电动机二、电机的分类形式很多,分类方式多样:•1.按功能*电动机电——>机*发电机机——>电*变压器电——>机*控制电机信号变换与传输•2.按速度*变压器n=0*同步电机n=同步速度n0*异步电机n≠n0 , 但接近同步速n0*直流电机n不定• 3.按电流性质•直流电机*直流发电机*直流电动机•交流电机*交流电动机*交流发电机*变压器第二节电机的电磁基本理论电机中的三大物理量:电、磁、机械(机电能量转换)*电:以“路”的形式出现,线圈(绕组)构成电路,较熟;*磁:以“场”的形式出现,本科阶段一般以磁路进行分析;*机:机械能,电机中与之相关的有转矩、转速等。
一、磁场、磁感应强度•磁场:•磁感应强度:描述磁场强弱的物理量•二、磁力线、磁通量(Φ)1.磁力线(1)定义(2)性质:–“符合右手螺旋定则”;–“永不相交,确定点的B方向确定、唯一”;–“闭合、无起点、终点”。
2.磁通(磁通量)➢垂直(正交)➢(S的法线与B方向之间夹角)➢任意曲面、不均匀磁场➢闭合曲面(高斯定理,磁通连续性原理)•三、磁场强度磁导率• 1 磁场强度(H)•2B与H的关系*磁导率、真空中的磁导率、相对磁导率• 3 没有磁绝缘的概念(电:>1010,磁:103~105)•四、全电流定律1.定义:(右手螺旋定则)2.磁压(磁位差):H沿路径的线积分称该路径上的磁压。
Um=∫Hdl3.磁势:磁场回路所匝链的电流F=∑I*磁势、磁压的单位均为:A*沿磁场中任一闭合回路,总磁压等于总磁势。
•五、磁路、磁路参数、全磁路欧姆定律• 1.磁路:导磁材料与非导磁材料、主磁通与漏磁通、磁路• 2.磁路欧姆定律*(1)部分磁路•电路:R=U/I•磁路:*(2)全磁路• 3.磁阻–比较电阻:•4.磁导•5.磁路第一定律(节点定律)•6.磁路第二定律(回路定律)•7 磁路与电路的异同•(1)同:绝大多数概念等价•(2)异:a 电流是电荷的移动磁通是假想的用于描述磁场的量b 直流电流通过电阻消耗能量恒定磁通通过磁阻不消耗能量•六、B-H曲线•1.磁化曲线•起始段:μ较小;•线性区:μ(较大)近似为直线•饱和区:μ很小,H增大,B基本不变•2.磁滞回线•磁滞现象•剩磁(剩余磁通密度、剩余磁感应强度)•矫玩力: Hc–软磁材料:Hc小,易被磁化,也易消失――电机中多用之–硬磁材料:Hc大,与上相反,做永磁材料,如永久磁铁• 3 基本磁化曲线•通不同电流形成不同的B-H曲线的各顶点的连线例:图(a)为硅钢片叠成的磁路(尺寸的单位:mm),图(b)所示为硅钢片的磁化曲线,励磁线圈有1000匝。
求当铁芯中磁通为1×10-3Wb时,励磁线圈中的电流为多少?解:• 1.铁芯部分:•设铁芯的叠片因数(叠片净厚度与总厚度之比)为0.94,则铁芯的净面积为•Ai =20×10-3×40×10-3×0.94=0.752×10-3(m2)•铁芯磁路的平均长度为•Li=2(100+80)-6=354(mm)=0.354(m)•铁芯中的平均磁通密度为:•由磁化曲线查得相应的铁芯磁场强度为Hi=560A/m。
•铁芯段磁路所需的磁动势为•198==iiiLHF(A)•2.气隙部分•不计气隙处磁通的扩散现象,则气隙磁通与铁芯中的磁通相同,•因为气隙部分的面积为•Ag =20×10-3×40×10-3=0.8×10-3(m2)•所以气隙部分的感应强度、磁场强度和气隙部分所需的磁势为 •3.总体 •所需的总磁势为 •F =FI + Fg = 6162(A) •线圈所需的励磁电流为 •I =Fi /N =6.162 (A) • 要点:气隙虽小,但所需的磁势却很大。
甚至可忽略铁芯的磁压降。
• 七、铁芯损耗• 交变的磁通在铁芯中产生损耗– (1)磁滞损耗(正比于频率)(2)涡流损耗(正比于频率的平方,正比于叠片厚度的平方,所以用很薄的硅钢片(0.3~0.5mm )而不用整块铁。
)• 八、磁场贮能1. 磁场能量(体)密度2. 总能量3.线性介质• 九、电感• (一)自感• 磁链:穿过线圈的磁通形成磁链• 磁链与穿过线圈的电流成正比:• 系数L 称电感,所以电感定义如下:• 一个线圈通过单位电流所形成的磁链叫该线圈的电感。
• (二)互感• 两个相邻回路:回路1中的电流I1产生的,与回路2交链(匝链)的磁链(注意下标顺序)• 定义:该磁链与产生该磁链的电流I1之比称回路1对回路2的互感M21。
• 同理:回路1对回路2的互感M12为:21212I M ψ= •问题:下标中第一个数代表?第二个数代表?• 同理,Λ==212121N N R N N M m• 其中:Rm 称两线圈间的磁阻,Λ为磁导。
• (三)漏磁通、漏磁链、漏电感• 1.漏磁通 21,σσΦΦ• 2.漏磁链 21,σσψψ• 3.漏电感 21,σσL L• (四)电抗 • 十、电磁感应定律•感应电势的两种形式•1.变压器电势–线圈中Φ变化–方向:楞茨定律•2.速度电势–导体运动产生–e = BLv–方向: 参考右手定则•十一、电磁力、电磁转矩•(1)电磁力•通电导体在B中受的力F=BIL(发电机的本质:外力F作用于导体,使其以v运动,则输入机械功率Fv;产生感应电势e,与外电路形成电流i, 则输出电功率ei。
不计损耗,功率平衡:)•(2)电磁转矩•十二、电机的可逆性•同一电机既可做发电机又可做电动机。
•发电机与电动机即有感应电势又有电磁力,只是形式不同,今后课程中注意体会。
•十三、磁路参量与电路参量的类比•电路I U E R G E j•磁路ΦUm F Rm ΛH B第一篇变压器序第二章变压器的基本作用原理与理论分析第三章三相变压器及分析第四章三相变压器不对称运行及瞬变过程第五章电力系统中的特种变压器序•本课程主要分析电力变压器•变压器的作用:改变电压等级•分类:*按电压升降†升压变压器;降压变压器*按相数:†单相变压器、†三相变压器、†多相变压器*按绕组个数:†双绕组变压器、†三绕组变压器、†单绕组变压器(自耦变压器)第二章变压器的基本作用原理与理论分析第一节变压器的基本结构和额定值第二节空载运行第三节负载运行第四节标么值第五节参数测定方法第六节运行性能第一节变压器的基本结构和额定值一、电力变压器的基本结构•五大部分:铁芯、绕组、变压器油、油箱、绝缘故套管。
• 1.铁芯*磁路部分*硅钢片叠成(减少涡流损耗),彼此绝缘*铁芯柱*铁轭*冲片2.绕组•电路部分•分类:按绕组在铁芯中的排列分两大类•铁芯式、铁壳式•电力变压器都用铁芯式•低压绕组靠近铁芯——为绝缘方便•绕组的基本形式:•同芯式:高低压绕组均做成圆筒形,同心地套在铁芯上•交叠式(饼式绕组):做成线饼,交错排列。
• 3. 变压器油•散热:将热量传递到变压器外壳表面•绝缘•4. 油箱及附件•隔离空气:减少氧化•油箱的散热 •油枕(储油器) •气体继电器 • 安全气道• 5. 绝缘套管• 油箱内的线圈与外电路连接 二、额定值 •额定容量:SN • 额定电压:线电压:U1N 、U2N •额定电流:线电流:I1N 、I2N • 单相:I1N =SN /U1N ; I2N =SN /U2N• 三相:N N N N N N U S I U S I 22113,3==• 定额频率:fN=50Hz• 相数 • 额定效率第二节 变压器的空载运行 • 预备知识• 分析方法:• 电磁关系• 平衡方程• 等值电路• 相量图• 述语:初级、次级;原方、副方•空载:原方接电源,副方空载• 下标约定:• 单相变压器† 单下标:原方:1 ;副方:2† 双下标:原方:AX ;副方:ax† 空载:下标加0• 三相变压器† 原方:首端A B C ,末端X Y Z ,零线N† 副方:首端a b c ,末端x y z ,零线n† 空载:下标加0一、电磁物理现象• 1.交变的:• 2.因为空载:0i i =• 所以:i0全部用于激磁: m i i =0• 3. 主磁通与漏磁通• 主磁通:( 同时交链N1 和N2),磁路磁阻小,易饱和• 漏磁通:( 只交链N1 或N2( 或其部分)) ,磁路磁阻大,不饱和• 4. i0 产生电阻压降:i0r1二、参考方向• u,i,e 等均交变,应规定参考正方向。
• 正方向任意假定,但一般约定俗成如下:• U1:参考方向,任意假定,• 注意:电压从高电压指向低电位。
• I1(I0):“ 负载惯例” ,由U1 决定• :由I1(I0)根据右手定则• 21,E E :与Φ 方向一致:手螺旋关系(课上画图讲解)• 注意:电势从低电压指向高电位。
+→-:E• U2:由E2 决定• I2:与E2 一致或“ 负载惯例”三、感应电势、电压变比• 空载:σ110,E r I 很小,所以:11E U -=• 变比:kN N E E ==2121• 方向:电势滞后磁通90度。
• 不计损耗:2211,E U E U =-= or: U1=E1,U2=E2,• 则:k=U1/U20四、励磁电流及其三个分量• 1. 磁路饱和的影响• 如不计饱和,磁通为正弦波,电流也为正弦波。
• 由于B-H 关系的非线性,当Φ为正弦波时,I 一定为尖顶波,反之当I 为正弦波则Φ为平顶波• 尖顶波分解为基波与若干谐波的叠加(主要是三次谐波)磁化电流:尖顶波与正弦波有等效的有效值的电流。
• 图:作图法求励磁电流(二)铁耗电流•2. 磁滞影响:励磁电流为不对称尖顶波。
•含磁滞损耗电流分量为 。
(简称:磁滞电流分量) •3.涡流影响 •涡流损耗电流分量为 (简称:涡流电流分量) •是有功分量与电势()同方向 • 称为磁化电流,不包括有功分量。
• 铁耗电流 h e Fe I I I += • 励磁电流 μI I I Fe m +=五、励磁电路模型• 分别为:激磁电阻、激磁电抗、激磁阻抗及对应的激磁电流压降。
• mm m m x I r I 22, 分别为变压器的铁耗、励磁无功功率。
• 激磁电阻并非实质电阻,是为计算铁耗引入的模拟电阻。
六、漏抗• 漏磁通产生漏电势,把漏电势也写成阻抗压降形式:• 分别为:初级绕组的漏电势、漏电抗、漏电感。
• 空载时:01I I I m== 七、电压平衡方程• 电磁关系中找所有与“电压量纲相同的量”。
• 注意方向• 原方:• 副方: 220E U= 八、等效电路与相量图• 等效电路• 相量图(课上演示相量图的画法)第三节、变压器负载运行• 负载运行:I2≠0一、负载运行时的物理现象•1 空载:I2=0 Φ由F1产生 Fm=F1,平衡; •2 负载 I2≠0 F2=N2I2≠0,打破原来平衡, 迫使I1发生变化。