光学教程第三章

3.1 证明反射定律符合费马原理。

证明：设两个均匀介质的分界面是平面，它们的折射率为n 1和n 2。

光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。

为了确定实际光线的路径，通过A,B 两点作平面垂直于界面，'OO 是它们的交线，则实际光线在界面上的反射点C 就可由费马原理来确定，如下图所示。

(1)反证法：如果有一点'C 位于线外，则对应于'C ，必可在'OO 线上找到它的垂足''C .由于''AC 'AC >,''BC 'BC >,故光线B AC'总是大于光程B ''AC 而非极小值，这就违背了费马原理，故入射面和反射面在同一平面内得证。

(2)在图中建立坐XOY 坐标系，则指定点A,B 的坐标分别为（x1，y1）和（x2，y2），未知点C 的坐标为（x ，0）。

C 点是在'A 、'B 之间的，光程必小于C 点在''B A 以外的相应光程，即21v x x <<，于是光程ACB 为y x x n y x x n CB n AC n ACB n 2211221221111)()(+-++-=+=根据费马原理，它应取极小值，即0)(1=n dxd0)sin (sin )()()()()()(21112222211212111=-='-'=+---+--=i i n B C C A n y x x x x n y x x x x n ACB n dx d 所以当11'i i =，取的是极值，符合费马原理。

3.2 根据费马原理可以导出在近轴条件下，从物点发出并会聚倒像点的所有光线的光程都相等。

由此导出薄透镜的物象公式。

解：略3.3 眼睛E 和物体PQ 之间有一块折射率为1.5的玻璃平板(见题3.3图),平板的厚度d 为30cm 。

1. 证：设两个均匀介质的分界面是平面，它们的折射率为n 1和n 2。

光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。

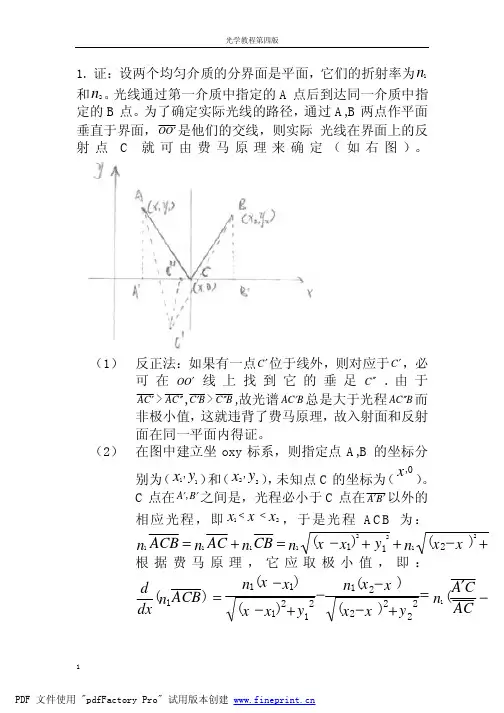
为了确定实际光线的路径，通过A,B 两点作平面垂直于界面，O O ′是他们的交线，则实际 光线在界面上的反射点C 就可由费马原理来确定（如右图）。

（1） 反正法：如果有一点C ′位于线外，则对应于C ′，必可在O O ′线上找到它的垂足C ′′.由于C A ′>C A ′′,B C ′>B C ′′,故光谱B C A ′总是大于光程B C A ′′而非极小值，这就违背了费马原理，故入射面和反射面在同一平面内得证。

（2） 在图中建立坐oxy 标系，则指定点A,B 的坐标分别为（y x 11,）和（yx 22,），未知点C 的坐标为（0,x ）。

C 点在B A ′′,之间是，光程必小于C 点在B A ′′以外的相应光程，即x xx 21<<，于是光程ACB 为：x x n y x x n CB n AC n ACB n 21121221111)()(+−++−=+=根据费马原理，它应取极小值，即：()()()()()(12222211212111−′=+−−−+−−=AC C A n y x x x x n y x x x x n ACB n dx dQ i i 11=′，∴0)(1=ACB n dx d取的是极值，符合费马原理。

故问题得证。

2.(1)证：如图所示，有位于主光轴上的一个物点S 发出的光束经薄透镜折射后成一个明亮的实象点S ′。

由于球面AC 是由S 点发出的光波的一个波面，而球面DB 是会聚于S ′的球面波的一个波面，固而SB SC =, B S D S ′=′.又Q光程FD EF n CE CEFD ++=，而光程AB n AB =。

根据费马原理，它们都应该取极值或恒定值，这些连续分布的实际光线，在近轴条件下其光程都取极大值或极小值是不可能的，唯一的可能性是取恒定值，即它们的光程却相等。

高等光学教程--第三章参考答案第三章光学薄膜的基本知识3.1 证明在TM 波入射的情况下单层膜的特征矩阵为=22sin cos sin cos j q jq ββββ⎛⎫- ⎪⎪⎪-⎝⎭M式中=2q 220cos /θμεn，其它参数及图示参考§3.1节中图3-2。

图p3-1解答: 模仿教材§3-1中推导TE 波入射情况下求特征矩阵所用的方法。

在界面I 处： 2II 2I 1I 1I I cos cos cos cos θθθθrt r i E E E E E '-=-= (p3.1-1) II I I I I rt r i H H H H H '+=+= (p3.1-2) 由非磁性介质中E 和的关系式H E s H ⨯=n 0με (p3.1-2)式化为 )()(II I 20I I 100I rt r i E E n E E n H '+=-=μεμε (p3.1-3) 在界面II 处： 3II 2II 2II II cos cos cos θθθt r i E E E E =-= (p3.1-4)II II II II t r i H H H H =+= (p3.1-5)由(p3.1-3)式，(p3.1-5)式化为II 30II II 200II )(t r i E n E E n H μεμε=+=(p3.1-6) 两个界面上的电矢量有关系式II tI II II j i j r r E E eE E eββ-⎧=⎪⎨'=⎪⎩ (p3.1-7)(p3.1-8)由(p3.1-7)和(p3.1-8)两式，(p3.1-4)、(p3.1-6)两式化为II tI 2I 2II2tI I cos cos (p3.1-9)(p3.1-10)()j j r j j r E E e E e H E e E e ββββθθ--'⎧=-⎪⎨'=+⎪⎩由(p3.1-9)和(p3.1-10)两式解出tI 2II 2II cos E E θ⎫=⎪⎪⎭H + (p3.1-11) 和 βθμεμεθj re n E n H E --='220II 20II 2II cos 2cos (p3.1-12)将(p3.1-11)、(p3.1-12)式代入(p3.1-1)式，并令有 II 2II 1sin cos H q j E E ββ-=(p3.1-13) 22q =用同样的方法得到II II 2I cos sin H E jq H ββ+-= (p3.1-14)由(p3.1-13)和(p3.1-14)式⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡II II 22I I cos sin sin cos H E jq q jH E ββββ ⎥⎥⎦⎤⎢⎢⎣⎡--=ββββcos sin sin cos 22I jq q j M∴式中 2202cos θμεn q =3.2 如图p3-2所示，有一单层介质膜，入射光由折射率为的介质经过界面I 、单层膜及界面II 后进入折射率为 的衬底，入射光在界面I 和界面II 一次反射的振幅反射率分别为和，一次透射的振幅透射率分别为和。

光学教程第三章第三章光学仪器基础3－1 一个年龄50岁的人，近点距离为－0.4m ，远点距离为无限远，试求他的眼睛的调节范围。

解：5.24.011=--∞=-=P R A D3－2 某人在其眼前2m 远的物看不清，问需要配怎样光焦度的眼镜才能使其眼恢复正常？另一个人对在其眼前0.5m 以内的物看不清，问需要配上怎样光焦度的眼镜才能使其眼恢复正常？解：第一个人是近视眼，所需眼镜的光焦度为：5.021-=- D 第二个人是远视眼，所需眼镜的光焦度为：25.0125.01=- D3－3 迎面而来的汽车的两个头灯其相距为1m ，问汽车在离多远时它们刚能为人眼所分辨？假定人眼瞳孔直径为3mm ，光在空气中的波长为0.5μm 。

解：眼睛的极限分辨角为：rad D e 336102033.0103105.022.122.1---?===λα 设汽车在离人眼l m 远时刚能被人眼所分辨，则两车灯对人眼所张的角度为：e l l αα=≈=222/1a r c t a n2 ∴8.49181==e l αm3－4 有一焦距为50mm ，口径为50mm 的放大镜，眼睛到它的距离为125mm ，求放大镜的视放大率和视场。

解：视放大率为：550250250=='=Γf 线视场为：2012552505005002=??=Γ=d h y mm ∴视场为：?=='='62.225010arctan 222arctan 22f y ω 3－5 要求分辨相距0.000375mm的二点，用55.0=λμm 的可见光斜照明，试求此显微镜的数值孔径。

若要求二点放大后的视角为2'，则显微镜的视放大率等于多少？解：数值孔径为：7333.0000375.000055.05.05.00=?==σλNA人眼放在明视距离处直接观察这两点时，其张角为：6105.1250000375.0tan -?==ω ∴视放大率为：7.386105.12tan tan tan 6=?'='=Γ-ωω 3－6 已知显微目镜152=Γ，物镜5.2=β，光学筒长180mm ，试求显微镜的总放大率和总焦距为多少？解：显微镜的总放大率为：5.37155.22=?=Γ=Γβ 目镜焦距：15 25025022=Γ='f mm 物镜焦距：725.21801=-=?-='βf mm ∴显微镜的总焦距为：67.6180152507221=?-=?''-='f f f mm 3－7 一个显微物镜被观察物体不发光，采用斜照明，NA ＝0.25，分别采用远紫外（2.0=λμm ）和D 光（5893.0=λμm ）照明物体，试分别求其最小分辨距。

1. 证：设两个均匀介质的分界面是平面，它们的折射率为n 1和n2。

光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。

为了确定实际光线的路径，通过A,B 两点作平面垂直于界面，O O '是他们的交线，则实际 光线在界面上的反射点C 就可由费马原理来确定（如右图）。

（1）反正法：如果有一点C '位于线外，则对应于C '，必可在O O '线上找到它的垂足C ''.由于C A >C A ,B C >B C ,故光谱B C A '总是大于光程B C A ''而非极小值，这就违背了费马原理，故入射面和反射面在同一平面内得证。

（2）在图中建立坐oxy 标系，则指定点A,B 的坐标分别为（y x 11,）和（y x22,），未知点C 的坐标为（0,x ）。

C 点在B A '',之间是，光程必小于C 点在B A ''以外的相应光程，即xx x 21<<，于是光程ACB为：y x x n y x x n n n n 2211221221111)()(+-++-=+=根据费马原理，它应取极小值，即：i i 11='，∴0)(1=ACB n dxd取的是极值，符合费马原理。

故问题得证。

0)sin (sin )()()()()()(21112222211212111=-='-'=+---+--=i i n CB B C AC C A n y x x x x n y x x x x n ACB n dx d2.(1)证：如图所示，有位于主光轴上的一个物点S 发出的光束 经薄透镜折射后成一个明亮的实象点S '。

由于球面AC 是由S 点 发出的光波的一个波面，而球面DB 是会聚于S '的球面波的一个 波面，固而SB SC =,BS D S '='.又光程FD EF n CE CEFD ++=，而光程AB n AB =。