伸长量计算方法

40mT梁预应力筋理论张拉伸长值计算
一、计算公式
ΔL=P p L/EA
Pp=Pq*[1-e-(kx+uθ)]/(kx+uθ)
Pz=Pq*e-(kx+uθ)
式中：
ΔL---预应力钢筋理论伸长值
L---预应力钢筋的长度
Pp---预应力筋的平均张拉力
x---从张拉端至计算截面孔道长度
A---预应力筋的截面积
E---预应力筋的弹性模量
P---预应力筋张拉端的张拉力
θ---从张拉端至计算截面曲线孔道部分切线的夹角之和
8索，张拉控制应力（按75%控制）F=140*8*1860*0.75=1562.4KN
9索，张拉控制应力（按75%控制）F=140*9*1860*0.75=1757.7KN
弹性模量E=1.95*105 ,管道摩擦系数u=0.2,管道偏差系数k=0.0025，钢绞线单位公称面积A=140mm2复核：计算：
以下为伸长量的计算：N1束：每束8根，p=1562.4KN
N2束：每束8根，p=1562.4KN
N3束：每束9根，p=1757.7KN
N4束：每束9根，p=1757.7KN
复核：计算：。

设计采用标准强度fpk=1860MPa的高强低松弛钢绞线，公称直径15.2mm，公称面积Ag=140mm2，弹性模量Eg=1.95×105MP。

为保证施工符合设计要求，施工中采用油压表读数和钢绞线拉伸量测定值双控。

理论伸长量计算采用《公路桥梁施工技术规范》JTJ041-2002附表G-8预应力钢绞线理论伸长量及平均张拉应力计算公式。

一、设计伸长量复核1.1计算公式及参数：1.1.1、预应力平均张拉力计算公式及参数Pp=P×（1-e- kx+μθ）/ kx+μθ式中：Pp-预应力平均张拉力（N）P—预应力筋张拉端的张拉力（N）X—从张拉端至计算截面的孔道长度（m）θ—从张拉端至计算截面的曲线孔道部分切线的夹角之和（rad）k—孔道每米局部偏差对摩檫的影响系数，取0.0015μ—预应力筋与孔道壁的摩檫系数，取0.151.1.2、预应力筋的理论伸长值计算公式及参数：ΔL= Pp×L/（Ap×Ep）式中：Pp—预应力筋平均张拉力（N）L—预应力筋的长度（mm）Ap—预应力筋的截面面积（mm2），取140 mm2Ep—预应力筋的弹性模量（N/ mm2），取1.95×105 N/ mm21.2伸长量计算N1束一端的伸长量：单根钢绞线张拉的张拉力P=0.75×1860×140=195300N1.2.1、X1=0.885mθ=0×π/180=0kx+μθ=0.0015×0.885+0.15×0=0.0013Pp=195300×（1-e-0.0013）/0.0013=195173.11 NΔL1= PpL/（Ap Ep）=195173.11×0.885/（140×1.95×105）=0.0063m1.2.2、X2=3.927mθ=5×π/180=0.0873 radkx+μθ=0.0015×3.927+0.15×0.0873=0.019Pp=195300×（1-e-0.0019）/0.0019=193456.35NΔL2= PpL/（Ap Ep）=193456.35×3.927/（140×1.95×105）=0.0278m1.2.3、X3=10.618mθ=0×π/180=0kx+μθ=0.0015×10.618+0.15×0=0.016Pp=195300×（1-e-0.0016）/0.0016=195143.84 NΔL3= PpL/（Ap Ep）=195143.84×10.618/（140×1.95×105）=0.0759m1.2.4、ΔL=ΔL1+ΔL2+ΔL3=0.0063m+0.0278m+0.0759m=0.110m设计值：104mm比较得：（110-104）/104=5.8%≦6%二、千斤顶张拉力与对应油表读数计算锚下控制应力：σk =0.75×1860=1395N/mm2二根钢绞线张拉控制应力：P=σk×Ap=1395×140×2=390.6KN 张拉顺序为：0→初应力（0.1σcon）→1.0σcon（持荷3分钟）→锚固1＃千斤顶（表170）：回归方程 X=0.0308Y+0.8042式中： X——油压表读数（MPa）Y——千斤顶拉力（KN）0.1σcon =0.1×390.6=39.06 KNX=0.0308Y+0.8042=0.0308×39.06 +0.8042=2.0073 MPa1.0σcon =1.0×390.6=390.6 KNX=0.0308Y+0.8042=0.0308×390.6 +0.8042=12.835 MPa2＃千斤顶（表171）：回归方程 X=0.0329Y+0.0456式中： X——油压表读数（MPa）Y——千斤顶拉力（KN）0.1σcon =0.1×390.6=39.06 KNX=0.0329Y+0.0456=0.0329×39.06 +0.0456=1.2378 MPa1.0σcon =1.0×390.6=390.6 KNX=0.0329Y+0.0456=0.0329×390.6+0.0456=12.835 MPa3＃千斤顶（表168）：回归方程 X=0.0312Y+0.2688式中： X——油压表读数（MPa）Y——千斤顶拉力（KN）0.1σcon =0.1×390.6=39.06 KNX=0.0312Y+0.2688=0.0312×39.06+0.2688=1.4875 MPa1.0σcon =1.0×390.6=390.6 KNX=0.0312Y+0.2688=0.0312×390.6+0.2688=12.4555 MPa4＃千斤顶（表5757）：回归方程 X=0.0338Y-0.3138式中： X——油压表读数（MPa）Y——千斤顶拉力（KN）0.1σcon =0.1×390.6=39.06 KNX=0.0338Y-0.3138=0.0338×39.06-0.3138=1.0064 MPa 1.0σcon =1.0×390.6=390.6 KNX=0.0338Y-0.3138=0.0338×390.6-0.3138=12.8885 MPa。

1、计算公式及说明：预应力钢绞线张拉理论伸长值计算公式(参照《公路桥涵施工技术规范》JTJ041-200 0)ΔL＝（PpL）/（ApEp）………………①①式中：Pp――预应力筋的平均张拉力（N），直线筋取张拉端的拉力，两端张拉的曲线筋，计算方法见公式②；L――预应力筋的长度（mm）Ap――预应力筋的截面面积（mm2）Ep――预应力筋的弹性模量（Mpa）Pp＝P（1－e-(kx+μθ)）／（kx＋μθ）……②②式中：Pp――预应力筋平均张拉力（N）P――预应力筋张拉端的张拉力（N）x――从张拉端至计算截面的孔道长度（m）θ――从张拉端至计算截面曲线孔道部分切线的夹角之和（rad）k――孔道每米局部偏差对摩擦的影响系数（1/m）μ――预应力筋与孔道壁的摩擦系数对公式的两点说明：（1）、因为预应力筋大多呈曲线布置，因此Pp的计算通常采用公式②进行，对于曲线筋还应根据不同的曲率半径进行分段，分别计算相应的Pp和ΔL。

（2）、对于②式中的θ，由它的符号解释可知，曲线孔道部分切线的夹角之和应等于曲线所对应的圆心角，根据几何关系得出：θ=L/R(rad),式中L是从张拉端至计算截面曲线孔道的长度（m），R是该段曲线孔道的曲率半径（m）。

2、基础数据选定由工程概况介绍及技术规范和钢绞线的规格选定下列数据：系数k及μ值表孔道成型方式k μ（钢绞线）预埋金属螺旋管道0.0015 0.20～0.25采用值0.0015 0.20钢绞线强度：钢绞线截面积：Ap＝140mm2钢绞线弹性模量：Ep=195000Mpa二、理论伸长值计算本例通过对中梁N1钢绞线的计算进行说明，钢绞线的设计见下图，由图可知，钢绞线成直线和曲线交错对称布置，因此选定半幅钢绞线分成AB，BC，CD三段分别计算伸长值，另外半幅伸长值与此相等。

对于中梁N1钢绞线：钢绞线股数：n＝7股1、张拉控制力计算钢绞线总的截面积：Ap＝7*140＝980mm2钢绞线弹性模量：Ep=195000Mpa钢绞线强度：单束钢绞线张拉控制应力σcon=0.75×1860=1395Mpa单束钢绞线张拉控制力：P1=1395*140=195300N超张拉张拉力：1.03P1×7＝1.03*195300*7＝1408113N2、分段起、终点力及平均张拉力计算，列表如下注：（rad）＝3.543/29＝0.1223、伸长量计算，将已知数据代人公式①，计算出△LAB=1397477.51*10124/(980*195000)=74.03mm△LBC=1366490.10*3543/(980*195000)=25.33mm△LCD=1345199.27*1074/(980*195000)=7.56mm△L/2=74.03+25.33+7.56＝106.92mm总伸长量：△L＝2*106.92＝214mm同理可知，初应力推算伸长值：△L2=(214/1.03)*0.1=21mm,式中张拉1.03时的伸长量为214，张拉至0.1时的应力为21mm。

钢绞线计算方法一、主要计算公式1.伸长量计算公式：△L=（P平×L）/（E×A）（1）△L：钢绞线伸长量，㎝P平：钢绞线平均张拉力，NL：钢绞线长度，㎝E：钢绞线弹性模量，MPa 一般图纸中有说明，但以试验室实测数据为准；A：钢绞线截面积，单根φ15.24钢绞线有效截面积为140㎜22.平均张拉力P平=P×｛1-e-(kL+μθ）｝/(KL+μθ) (2)P:张拉端张拉力，单根钢绞线张拉力P=1860×0.75×140=195.3KN K：孔道摩擦影响系数，图纸中有说明；μ：钢绞线与孔道的摩擦系数，图纸中有说明，θ：从张拉端至计算截面的孔道切线转角之和，当有平弯时同样参与计算, Rad(弧度)二、示例图中L1=5米，L2=8，L3=10；θ1=10.30，θ2=8.10，θ3=5.60钢绞线为15束，弹性模量E=2.0×105MPa,μ=0.15; k=0.001计算过程如下：1.θ=(10.3+8.1+5.6)/180×π=0.419(Rad);2.根据P平=P×｛1-e-(kL+μθ）｝/(KL+μθ)=195.3×15×｛1-e-(0.001×23+0.15×0.419）｝/(0.001×23+0.15×0.419)=2807.3KN3.根据△L=（P平×L）/（E×A）=（2807.3×23）/（2.0×105×140×15）=15.3㎝三、其它1.一般估计时每米钢绞线按伸长0.6㎝考虑，2.两端张拉时算出一半×2，3.根据校顶报告计算张拉力时采用内差法；4.有平弯时也要参与计算。

5.因为误差极小，所以，可用钢绞线的切线长可代替钢绞线长。

一、主要计算公式1.伸长量计算公式：△L=（P平×L）/（E×A）（1）△L：钢绞线伸长量，㎝P平：钢绞线平均张拉力，NL：钢绞线长度，㎝E：钢绞线弹性模量，MPa 一般图纸中有说明，但以试验室实测数据为准；A：钢绞线截面积，单根φ15.24钢绞线有效截面积为140㎜22.平均张拉力P平=P×｛1-e-(kL+μθ）｝/(KL+μθ) (2)P:张拉端张拉力，单根钢绞线张拉力P=1860×0.75×140=195.3KNK：孔道摩擦影响系数，图纸中有说明；μ：钢绞线与孔道的摩擦系数，图纸中有说明，θ：从张拉端至计算截面的孔道切线转角之和，当有平弯时同样参与计算, Rad(弧度)二、示例图中L1=5米，L2=8，L3=10；θ1=10.30，θ2=8.10，θ3=5.60 钢绞线为15束，弹性模量E=2.0×105MPa, μ=0.15; k=0.001 计算过程如下：1.θ=(10.3+8.1+5.6)/180×π=0.419(Rad);2.根据P平=P×｛1-e-(kL+μθ）｝/(KL+μθ)=195.3×15×｛1-e-(0.001×23+0.15×0.419）｝/(0.001×23+0.15×0.419)=2807.3KN3.根据△L=（P平×L）/（E×A）=（2807.3×23）/（2.0×105×140×15）=15.3㎝三、其它1.一般估计时每米钢绞线按伸长0.6㎝考虑，2.两端张拉时算出一半×2，3.根据校顶报告计算张拉力时采用内差法；4.有平弯时也要参与计算。

5.因为误差极小，所以，可用钢绞线的切线长可代替钢绞线长。

桥梁预应力张拉伸长量计算桥梁预应力张拉伸长量计算是指根据预应力张拉系统的参数和材料特性，计算出张拉后的杆件伸长量。

预应力张拉是在杆件上施加张拉力，以提高杆件的受力性能和抗裂性能。

张拉后的杆件伸长量是计算预应力张拉效果和工程设计的重要参数。

首先，需要了解一些基本概念和公式：1.应力（σ）：单位面积上的力，计算公式为σ=F/A，其中F为受力，A为面积。

2.应变（ε）：变形和原长度的比值，计算公式为ε=ΔL/L，其中ΔL为变形长度，L为原长度。

3.弹性模量（E）：材料的刚度指标，计算公式为E=σ/ε，其中σ为应力，ε为应变。

4.斯特藩公式：用于计算预应力杆件的伸长量，公式为ΔL=F/(E×A)×L，其中ΔL为伸长量，F为受力，E为弹性模量，A为杆件的横截面积，L为杆件的原长度。

通过斯特藩公式，我们可以计算出预应力张拉系统受力后的杆件伸长量。

以下是计算步骤：1.确定预应力系统参数和材料特性：需要知道杆件的原长度L，受力F，材料的弹性模量E，以及杆件的横截面积A。

2.计算伸长量：利用斯特藩公式，将上述参数代入公式计算伸长量，即ΔL=F/(E×A)×L。

3.根据实际情况调整计算结果：预应力杆件的伸长量会受到杆件的材料特性、外界温度、施力方式等因素的影响，因此在实际工程中，需要根据具体情况对计算结果进行调整。

需要注意的是，在实际工程设计中，还需要考虑其他因素，如杆件的变形和变形引起的应变，以及杆件与周围结构的相互作用等。

这些因素对预应力张拉伸长量的计算都会产生影响，需要在设计中进行全面考虑。

总之，预应力张拉伸长量的计算是桥梁设计中的重要环节，它直接关系到桥梁的安全性和工程质量。

通过合理的预应力张拉伸长量计算，可以保证桥梁的预应力设计效果，提高桥梁的承载能力和使用寿命。

0 钢绞线张拉伸长量计算示例汇总2010钢绞线张拉伸长量计算示例汇总[]2010-09-11A钢绞线伸长量计算方法 (4)计算说明: (4)计算中有关数据 (5)钢绞线长度 (5)Po,P的计算(б = 0.1бk) (5)钢绞线理论伸长值计算 (6)应力与伸长值及压力表读数之间的关系 (7)张拉过程及发现问题 (8)采取措施 (11)经验总结和体会 (13)B钢绞线伸长量计算 (15)一、主要计算公式 (15)1.伸长量计算公式： (15)2.平均张拉力 (15)二、示例 (15)三、其它 (16)C预应力钢绞线张拉伸长值的计算与施工操作 (17)1预应力伸长量的计算 (18)2 施工控制 (19)2.1钢绞线编穿束 (19)2.2张拉及实际伸长值测量 (20)结束语: (21)D设计伸长量复核 (22)一、计算公式及参数 (22)1、预应力平均张拉力计算公式及参数： (22)2、预应力筋的理论伸长值计算公式及参数： (22)二、伸长量计算： (22)1、N1束一端的伸长量： (22)2、N2束一端的伸长量： (23)E张拉时理论伸长量计算 (24)一、计算参数： (24)二、张拉时理论伸长量计算： (24)1、N1束一端的伸长量： (24)2、N2束一端的伸长量： (25)三、千斤顶张拉力与对应油表读数计算 (25)一、钢绞线的张拉控制应力： (25)二、1523号千斤顶张拉、0050号油表时： (25)三、1524号千斤顶张拉、0054号油表时： (26)四、1525号千斤顶张拉、0077号油表时： (26)五、1526号千斤顶张拉、0064号油表时： (27)F30m后张梁张拉计算书 (28)一、材料及性能 (28)二、张拉力计算 (28)三、施工控制应力与压力表的关系： (28)四、伸长量计算： (29)五、质量控制 (30)六、计算伸长量 (30)七、张拉顺序 (30)钢绞线张拉伸长量计算 (31)钢绞线张拉伸长量的计算 (31)一、直线布置的钢绞线伸长量计算 (31)二、曲线布置的钢绞线伸长量计算 (31)例：某盖梁钢绞线伸长量计算 (32)三、CASIO fx-4800P计算器的钢绞线伸长量计算程序 (33)四、千斤顶标定及计算中注意的问题 (34)高强度低松弛预应力热镀锌钢绞线 (35)前言 (35)1 范围 (35)2 引用标准 (35)3 定义 (36)4 几何尺寸及允许偏差 (36)5 技术要求 (37)6 试验方法 (39)7 检验规则 (39)8 包装、标志和质量证明书 (40)附录 A (41)(标准的附录) (41)屈服负荷试验 (41)附录 B (41)(标准的附录) (41)松弛试验 (41)附录 C (41)附录 D (43)(标准的附录) (43)脉动拉伸疲劳试验 (43)A钢绞线伸长量计算方法关数据的采用与理论伸长值的计算计算说明:预应力筋采用控制应力方法进行张拉时,应以伸长值进行校核.为控制预应力钢绞线张拉实际伸长值与理论伸长值的差值,应先计算出钢绞线的理论伸长值.根据《公路桥涵施工技术规范》(JTJ041-89)条文说明第11.5.7条,由直线与→曲线混合组成的预应力钢材,其伸长值应分段计算,然后叠加.钢绞线理论伸长值直线段采用公式:△L=P0×L/(Ay×Eg)式中:△L:钢绞线直线段理论伸长值(mm);P0:计算截面处钢绞线张拉力(N);L:预应力钢绞线长度(mm);Ay:预应力钢材截面面积(mm2);Eg:预应力钢材弹性模量(N/mm2).钢绞线理论伸长值曲线段采用公式:△L = P×L/(Ay×Eg)式中:△L:钢绞线曲线段理论伸长值(mm);P:预应力钢材平均张拉力(N);其余符号同直线段.关于P0,P的计算:P = P[1-e-(kx+uθ)]/(kx+uθ):P:张拉端钢绞线张拉力X:从张拉端至计算截面的孔道长度(m);θ:从张拉端至计算截面曲线孔道部分切线的切角之和(rad);K:孔道每m局部偏差对摩擦的影响系数;U:预应力钢材与孔道壁的摩擦系数;计算中有关数据Ay=140×6=840mm2(试验值)Rby=1860Mpaбk= 0.75Rby=1395MpaEg=1.96×105Mpa(试验值)K=0.015(规范取值)U=0.225(规范取值)θ = 0.0436rad钢绞线长度(1)考虑到实际施工中采用穿心式千斤顶,所以钢绞线长度应计入千斤顶长度,YCW150型千斤顶回程后的长度为450mm.(2)曲线段长:1.915m×2直线段长:15.771mPo,P的计算(б = 0.1бk)P =0.1бk×840 = 0.1×1395×840P=P[1-e-(kx+uθ)]/(kx+uθ)=117180×0.0126/0.0127=116439NPo=P[1-(-e-(kx+uθ))]=117180×(1-0.0126)=115704N钢绞线理论伸长值计算①当б = 0.1бk时千斤顶部分:△L = P×L/(Ay×Eg)=117180×450×2/(840×1.96×105) =0.64mm曲线部分:△L = 2×P×L/(Ay×Eg)=116439×1915×2/(840×1.96×105) =2.71mm直线部分:△L = Po×L/(Ay×Eg)=115704×15771/(840×1.96×105) =11.08mm∑△L = 0.64+2.71+11.08=14.43mm△L = 144.3mm③当б = 1.05бk时△L=144.3×1.05=151.51mm应力与伸长值及压力表读数之间的关系首先根据试验,按一元线性回归曲线标定出油表与相应的千斤顶之间的关系曲线方程,1562#压力表配套的千斤顶编号为022#,其关系曲线方程为y=-0.01+0.03601x;1557#压力表配套的千斤顶编号为023#,其关系曲线方程为y = -0.03+0.03606x;拉力单位KN,伸长值单位为mm,压力表单位为Mpa.其对应关系如下表:应力(Mpa)б=0.1бkб=0.2бkб=бkб=1.05бk张拉力(KN)117.18234.361171.801230.39伸长值(mm)28.96144.80152.04压力表读数(Mpa)1562#4.218.4342.1944.301557#4.208.4242.2244.34张拉过程及发现问题当一切准备工作就绪后,按照设计图纸要求的张拉程序进行施工(0→ 0.1бk → 0.2бk→1.05бk 持荷5分钟→бk),根据前面算出的各阶段的控制张拉力所对应的油表读数对张拉力进行控制,首先张拉到0.1бk,量出千斤顶相应的伸长值,再依次张拉到0.2бk,бk,1.05бk,并量出相应的伸长值.具体记录数据见下表:千斤顶编号记录项目0.1бk0.2бk1.0бk1.05бkN1022#油表读数(Mpa)4.218.4342.19 44.30伸长值(mm)19398586023#(Mpa)4.208.4242.2244.34伸长值(mm)14287683通过对记录数据的分析计算,0至0.1бk之间的伸长值,用相邻段伸长值代替(0.1бk到0.2бk),并扣除混凝土的压缩量(取C=4.5mm),其实际伸长值计算如下:△L实=85-19+(39-19)+76-14+(28-14)-C = 157.5mm△L实/△L=157.5/144.3=109%由以上数据可以看出,钢绞线实际伸长值超出理论伸长值达9%,超过规范允许的6%以内规定.为了保证施工质量,我们按照施工程序,下达了停止张拉指令.为了查明原因,我们进行了以下几个方面的检查工作:(1)检查计算过程符合规范要求,并且数据计算无误.(2)对油表与千斤顶等张拉设备进行重新标定,与原标定的结果在规范允许(3)重做钢绞线弹模试验,与上次试验相符.(4)检查张拉设备的安装情况,张拉过程,均符合要求.采取措施通过以上大量,细致的检查分析均未发现问题.为了使问题早点得到解决,指挥部和施工单位请来了许多专家和有经验的工程师来进行论证和探讨,分析了多种情况,也没有找到具体原因.最后本人通过对记录的数据进行分析,发现张拉过程中钢绞线的伸长值从0.1бk到0.2бk比从0到0.1бk的长度还要长,因此,分析可能是张拉时的初应力较小,计算的钢绞线的实际伸长值包括钢绞线松驰长度,从而造成钢绞线实际伸长值比理论值长.经过进一步的分析研究发现,当张拉力同步增长时,钢束的各阶段实测伸长量不相等,其实测伸长量增加值的平均值也不相等,其主要原因是各钢束受力不均匀,引起受力不均匀的主要因素包括钢绞线分布位置变动,锚具夹片滑移和部分钢绞线非弹性变形等,这些因素会使实测伸长量加大,有关文献将这部分加大的伸长量称做附加伸长量,而现行规范只考虑应变引起的伸长量,而未考虑非应变引起的附加伸长量.为了尽可能减少附加伸长量,我们将原张拉程序进行调整为:0→0.25бk →0.5бk→бk(持荷2分钟锚固),并且按照上述工序试张拉一片梁看情况如何.在施工过程中,严格按照《公路桥涵施工技术规范》(JT041-2000)的要求进行操作,张拉完成后,通过数据计算发现其实际伸长值与理论伸长值的差值在6%以内,符合规范要求.接着又按调整后的张拉程序张拉了几片梁,结果均符合要求.具体记录数据如下:千斤顶编号记录项目0.25бk0.5бk1.0бkN1022#油表读数(Mpa) 10.89 21.26 42.00伸长值(mm)274988023#油表读数(Mpa) 11.1942.20伸长值(mm)375393△L实= 88-27+(49-27)+93-37+(53-37)-C=150.5mm△L实/△L = 150.5/144.3=104%经验总结和体会为了准确控制钢绞线的伸长值,尽量减少实测伸长值与理论伸长值之间的差值,在后张法钢绞线张拉施工过程中,要认真做到以下几点:1,预留预应力筋管道的位置应准确,采用钢筋卡子定位,用铁丝绑扎固定,避免管道在浇筑混凝土过程中移位.合理确定钢绞线与管道之间的摩擦系数,及时调整k,u系数.2,钢绞线应符合《预应力混凝土用钢绞线》(GB/T5224-95)的要求,并应按规定抽样检查.每次到货的钢绞线都应重新测定其弹性模量,以确定出厂合格证书上的数值是否准确.3,千斤顶的精度应在使用前校准.使用超过6个月或200次,以及在使用过程中出现不正常现象时,应重新校准.任何时候在工地测出的预应力钢绞线伸长值有差异时,千斤顶应进行再校准.4,用于测力的千斤顶的压力表应同千斤顶视为一个单元同时校准,并在量程.5,应考虑锚具变形量和锚下混凝土的压缩量对实测伸长值的影响.6,施工过程中要根据实测伸长值和理论伸长值差值的大小,随时调整初应力的大小一、主要计算公式1.伸长量计算公式：△L=（P平×L）/（E×A）（1）△L：钢绞线伸长量，㎝P平：钢绞线平均张拉力，NL：钢绞线长度，㎝E：钢绞线弹性模量，MPa 一般图纸中有说明，但以试验室实测数据为准；A：钢绞线截面积，单根φ15.24钢绞线有效截面积为140㎜22.平均张拉力P平=P×｛1-e-(kL+μθ）｝/(KL+μθ)(2)P:张拉端张拉力，单根钢绞线张拉力P=1860×0.75×140=195.3KNK：孔道摩擦影响系数，图纸中有说明；μ：钢绞线与孔道的摩擦系数，图纸中有说明，θ：从张拉端至计算截面的孔道切线转角之和，当有平弯时同样参与计算, Rad(弧度)二、示例图中L1=5米，L2=8，L3=10；θ1=10.30，θ2=8.10，θ3=5.60计算过程如下：1.θ=(10.3+8.1+5.6)/180×π=0.419(Rad);2.根据P平=P×｛1-e-(kL+μθ）｝/(KL+μθ)=195.3×15×｛1-e-(0.001×23+0.15×0.419）｝/(0.001×23+0.15×0.419) =2807.3KN3.根据△L=（P平×L）/（E×A）=（2807.3×23）/（2.0×105×140×15）=15.3㎝三、其它1.一般估计时每米钢绞线按伸长0.6㎝考虑，2.两端张拉时算出一半×2，3.根据校顶报告计算张拉力时采用内差法；4.有平弯时也要参与计算。

工作段 1 2 3 4 5 6 合 计
55 52.4 418.9 313.05 0 12 0 0.001 0.059 0.005
781.200 781.200 780.586 736.126
781.200 780.586 736.126 732.678
781.200 780.893 758.139 734.401
4.00 3.81 29.58 21.42
839.35
58.8 118
2倍伸长量 锚固
直线分段1 曲线分段2 直线分段3
中量计算
工程名称： 庆景青公路滩坑库区景宁淹没段复建工程三标 张拉控制力 （KN） 781.2 分段长度L （cm） 钢绞线总截面 面积Ap（mm2) 曲线总切线 夹角θ（度） 560 梁号、束号： 中、边板N1# 钢绞线弹性模量 Ep(×105MPa) 分段起点拉力 Pq(KN) 1.917 分段终点拉力 Pz(KN) 局部偏差影响 系数K 平均拉力 Pp(KN) 0.0015 理论伸长量 （mm） 日期： 摩擦系数μ 2007年9月21日 0.25
分
段
kx+μθ
计算说明
1、计算公式： 分段理论伸长量Δ L=PpL/ApEp 分段平均张拉力 : Pp=Pq(1-e-(kx+μθ))/(kx+μθ) 分段终点拉力Pz=Pq×e-(kx+μθ) 2、分段起点拉力等于前段终点拉力。 3、锚固端外工作长度不需考虑孔道局部 偏差影响，作为直线单独计算。 4、计算时按直线-曲线-直线分段计算， 然后累加。两端张拉对称钢绞线时计算 1/2长钢绞线，全段伸长量乘以2倍。

张拉理论深长量计算4T＝Nsinα＋Fcosα=N(sinα＋μcosα)当角度α与摩阻系数μ都不变时，增大拉力T，N必然增大，因此，钢绞线必然与夹片沿T方法移动，以达到新的平衡。

因此，量测千斤顶活塞行程应进行修正。

2、直接量测钢绞线的伸长量的方法（简称“直接法”）。

即在工具锚外侧的钢绞线上做标记，做为量测的基准。

如图3所示。

使用这种方法有一个优点：不论经过几个行程，均以此来量测分级钢绞线的长度，累计的结果就是初应力与终应力之间的实测伸长值。

但也有两个缺点：一是量测不方便。

二是钢绞线在受力时，端头有发散现象，对钢绞线的伸长量有影响。

通过实践，采用自制的标尺，很好的解决了这个问题。

如图4所示，标尺为铝制的方条，长约10cm，宽高约为25mm，上留一直径约10mm的圆孔，圆孔上有固定螺丝。

张拉时，用铝条的圆孔套住钢绞线，并拧紧螺丝，做为标记。

既量测方便又解决了端头的发散现象。

注意标尺应尽量装在远离钢绞线端头的位置。

通过这个装置，量测的伸长量与理论值相符。

三、实际伸长量的测定（一）几个伸长量（回缩量）概念在说明实测伸长量的测定原则之前，说明一下几个伸长量与回缩量的概念。

1、工作长度的伸长量在钢绞线预应力张拉施工中，目前常用的千斤顶的工作锚位置分前夹式和后夹式，我们使用的是穿心式千斤顶，后夹式的，张拉时钢绞线在千斤顶中的工作长度较长，如图1 所示。

一梁端工作长度一般是指在张拉千斤顶装入钢绞线后，从工具锚锚板中心至工作锚锚板中心的距离。

即工作长度=千斤顶长度+锚厚度。

其伸长量可以通过计算得出：ΔL工作长度= PL/（Ap Ep）。

该值一般按理论计算取值。

2、工作锚具钢绞线回缩量该值理论上，一般取6mm，用来计算锚上的张拉控制应力及衡量实际测量回缩量精度的标准。

目前钢绞线预应力张拉施工以使用YCW型液压千斤顶为主，该千斤顶与工图4直接法量测装置图3 直接法量测方法5作锚接触处，设有一块限制工作锚夹片在张拉过程位移的限位板，钢绞线在张拉时工作锚夹片跟随钢绞线的拉伸，向后移动至限位板凹槽的底部，对钢绞线失去约束，当千斤顶将钢绞线张拉至设计控制张拉力，在回油放松钢绞线的瞬时，钢绞线弹性收缩，工作锚夹片跟随收缩向锚环孔内位移，随即将钢绞线锚固，这就是工作锚锚塞回缩的全过程。

伸长量计算公式范文
伸长量是指物体在受力作用下发生的变形。

在弹性变形范围内，可以使用胡克定律来计算伸长量，公式如下：
ΔL=(F*L)/(A*E)
其中
ΔL表示伸长量
F表示物体所受的拉力或挤压力
L表示物体的初始长度
A表示物体的横截面积
E表示物体的弹性模量
这个公式可以用于计算线弹性材料的伸长量，如金属丝、弹簧等。

对于线弹性材料，其弹性模量可以用胡克定律表示为：
E=(F/ΔL)/(A/L)
其中
E表示弹性模量
对于具体形状不规则的物体，可以将其分割成小块，然后分别计算每个小块的伸长量，再将伸长量相加得到整体的伸长量。

对于体弹性材料，可以使用下面的公式来计算伸长量：
ΔV=(F*V)/(A*E)
其中
ΔV表示体弹性材料的伸长量
F表示物体所受的拉力或挤压力
V表示物体的初始体积
A表示物体的截面积
E表示物体的弹性模量
需要注意的是，在使用上述公式计算伸长量时，一定要保持物体在弹
性变形范围内，避免超出该范围导致材料发生塑性变形或破坏。

另外，还可以使用庞加莱定律来计算伸长量，公式如下：
ΔL=α*L*ΔT
其中
ΔL表示伸长量
α表示物体的线膨胀系数
L表示物体的初始长度
ΔT表示物体的温度变化量
这个公式适用于计算温度变化引起的热胀冷缩或热应变造成的伸长量。

总结起来，伸长量的具体计算公式要根据物体的特性、形状以及所受
到的力的种类进行选择。

以上所提到的公式是常用的计算伸长量的方法，
可以根据具体情况选择合适的公式进行计算。

预应力伸长量计算公式1. 基本公式。

- 预应力筋的理论伸长值ΔL（mm）按下式计算：- Δ L = (PpL)/(ApEp)- 式中：- Pp：预应力筋的平均张拉力（N），直线筋取张拉端的拉力；对于曲线筋，按下式计算：- Pp=frac{P(1 - e^-(kx+μθ))}{kx+μθ}- 其中，P为预应力筋张拉端的张拉力（N），x为从张拉端至计算截面的孔道长度（m），θ为从张拉端至计算截面曲线孔道部分切线的夹角之和（rad），k为孔道每米局部偏差对摩擦的影响系数，μ为预应力筋与孔道壁的摩擦系数，e为自然对数的底，e = 2.71828。

- L：预应力筋的长度（mm）。

- Ap：预应力筋的截面面积（mm^2）。

- Ep：预应力筋的弹性模量（N/mm^2）。

2. 计算步骤示例。

- 假设我们有一预应力筋，张拉端张拉力P = 100000N，从张拉端至计算截面的孔道长度x = 10m，从张拉端至计算截面曲线孔道部分切线的夹角之和θ = 0.5rad，孔道每米局部偏差对摩擦的影响系数k = 0.0015，预应力筋与孔道壁的摩擦系数μ = 0.25，预应力筋的长度L = 10000mm，预应力筋的截面面积Ap = 100mm^2，预应力筋的弹性模量Ep = 200000N/mm^2。

- 首先计算曲线筋的平均张拉力Pp：- Pp=frac{P(1 - e^-(kx+μθ))}{kx+μθ}- 代入数值：kx+μθ=0.0015×10 + 0.25×0.5=0.14- Pp=frac{100000×(1 - e^-0.14)}{0.14}- 先计算e^-0.14≈0.8694- 则Pp=(100000×(1 - 0.8694))/(0.14)=(100000×0.1306)/(0.14)≈93285.71N - 然后计算理论伸长值Δ L：- Δ L=(PpL)/(ApEp)- 代入数值：Δ L=(93285.71×10000)/(100×200000)- Δ L=(932857100)/(20000000)≈46.64mm。

伸长量计算方法范文
伸长量是指材料在受力作用下发生的长度变化。

它是材料力学性能的
一项重要指标，可用于评估材料的延展性、柔韧性和抗拉强度等性能。

计
算伸长量的方法主要有两种：百分比伸长和标距法。

百分比伸长是指材料断裂前后的长度差与原始长度之比。

计算公式为：伸长率（%）=（断裂长度-原始长度）/原始长度×100%
百分比伸长法的优点是简单易懂，计算方法直观，适用于各种材料。

但它只能确定整体的伸长情况，无法提供局部伸长的数据。

因此，在一些
特殊情况下，需要使用标距法进行精确测量。

标距法是指在材料试验过程中，在标准距离上采用纵向放大系统测量
标距，然后计算出伸长量。

标距法需要通过测量初始标距和断裂时的标距
来计算伸长量。

计算公式为：
伸长量（mm）=（断裂标距 - 初始标距）/ 标距系数
在进行标距法伸长量的计算时，需要用到标距系数。

标距系数是通过
材料破断试验测量，以确保计算结果的准确性。

标距系数是由材料的应力
-应变曲线确定的，比如弹性标距系数、屈服标距系数和抗拉强度标距系
数等。

标距法的优点是可以测量材料的局部伸长情况，提供更准确的数据。

然而，它需要精确的仪器设备和复杂的测量过程，操作较为繁琐。

总之，无论使用百分比伸长还是标距法，都需要严格按照标准操作，
保证测量数据的准确性和可靠性。

此外，不同材料在受力作用下的伸长量
也会有所不同，因此需要针对具体材料和试验条件进行选择合适的计算方法，以得到准确的伸长量数据。

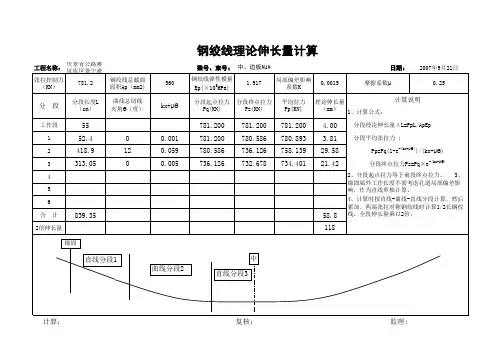
计算公式
1、预应力筋伸长值L ∆的计算按照以下公式：
p p p E A L
P L ⨯⨯=∆
L ∆——各分段预应力筋的理论伸长量；
P P ——各分段预应力筋的平均张拉力；
L ——预应力筋的分段长度，计算时同（2）中x 的值；
P A ——预应力筋的截面面积；
P E ——预应力筋的弹性模量。

2、《公路桥梁施工技术规范》（JTJ 041-2000）附录G-8中规定了P P 的计算公式：
μθ
μθ+-⨯=+-kx e P P kx P )1()( P ——预应力筋张拉端的张拉力，P =标准强度⨯0.75⨯预应力筋公称面积； θ——从张拉端至计算截面曲线孔道部分切线的夹角之和，对于圆曲线，为该段的圆心角，如果孔道在竖直面和水平面同时弯曲时，则θ为双向弯曲夹角的矢量和。

设水平角
为α，竖直角为β，则)cos arccos(cos
βαθ⨯=； x ——从张拉端至计算截面的孔道长度，分段后为每个分段长度； k ——孔道偏差系数，《公路桥涵通用图》中取0.0015；
μ——孔道摩阻系数，《公路桥涵通用图》中取0.17。

3、各曲线段长度计算
第一段：直线段，跨中至起弯点的长度，由《公路桥涵通用图》图纸可直接查得；
第二段：中间曲线段，半径R ⨯切线角β（弧度值）；
第三段：直线段，下料长度/2—第一段长度—第二段长度—工作长度。

伸长量计算公式范文
伸长量是指物体在受到外力作用下发生形变的程度，通常用伸长量计算公式来表示。

在弹性体力学中，常用的伸长量计算公式有胡克定律和应变能公式。

1.胡克定律：
胡克定律是描述线弹性体（如弹簧）受到外力时变形的规律。

根据胡克定律，当外力作用于线弹性体时，伸长量只与外力大小和材料的刚度有关，与具体几何形状无关。

其计算公式为：
F=k×ΔL
其中，F为外力的大小，k为弹簧的系数，ΔL为伸长量。

胡克定律适用于线弹性体，对于柔性材料如纤维、塑料等，伸长量的计算需要考虑应变。

2.应变能公式：
应变能公式是描述固体材料受到外力作用时发生变形的能量关系。

根据应变能公式，外力所做的功等于应变能的增量。

应变能的计算公式为：U=(1/2)×k×ΔL^2
其中，U为应变能，k为弹簧的系数，ΔL为伸长量。

应变能公式适用于一些具有较大伸长量的材料，如橡胶、金属等。

除了以上两种常用的伸长量计算公式外，还有其他针对不同情形的公式，如轴向应力计算公式和变形计算公式等。

这些公式的应用需要根据具体情况进行选择。

总之，伸长量的计算公式是根据材料特性和外力作用来确定的，不同材料、不同外力作用方式下的伸长量计算公式各有差异。

在实际应用中，需要根据具体情况选择合适的伸长量计算公式，以得到准确的结果。

伸长量计算公式范文伸长量是指物体在受到力的作用下发生的弹性形变。

在物理学中，伸长量可以通过应力和应变之间的关系来计算。

应力和应变的关系可以用胡克定律来描述。

胡克定律的数学表达式如下：σ=E·ε其中，σ表示应力，单位为帕斯卡（Pa）；E表示弹性模量，单位为帕斯卡（Pa）；ε表示应变，没有单位。

在弹性形变情况下，应力和应变成正比，即伸长量可以通过应力和弹性模量之间的比值来计算。

根据胡克定律，伸长量的计算公式为：ΔL=L·ε其中，ΔL表示伸长量，单位为米（m）；L表示原长度，单位为米（m）；ε表示应变。

应变可以分为线性应变和体积应变两种情况。

1.线性应变：当物体受到轴向力作用时，造成物体沿轴向伸长或缩短。

此时，伸长量计算公式为：ΔL=L·ε其中，ΔL表示伸长量，单位为米（m）；L表示原长度，单位为米（m）；ε表示线性应变。

2.体积应变：当物体受到均匀外压力作用时，物体发生体积变化。

此时，伸长量计算公式为：ΔV=V·ε其中，ΔV表示体积变化量，单位为立方米（m^3）；V表示原体积，单位为立方米（m^3）；ε表示体积应变。

应变的计算公式可以根据具体的情况进行推导和补充。

需要注意的是，伸长量的计算公式是基于弹性形变的情况，而非破坏性形变。

当物体超过了弹性限度，产生塑性变形或破坏时，伸长量的计算需要考虑更多的因素。

此外，胡克定律还可以应用于其他形式的应力和应变关系的计算，例如剪应力和剪应变、弯曲应力和弯曲应变等。

具体的计算公式可以根据不同情况来推导和补充。

总之，伸长量的计算公式可以根据胡克定律来描述，通过应力和应变之间的关系来计算。

具体的伸长量计算公式可以根据不同情况和应变类型进行推导和补充。

弹簧的伸长量公式弹簧是一种被广泛应用于机械工程中的一种非常实用的元件。

它可以抵抗力，使机械装置能够设计成更为轻便、灵活和可靠的结构。

学习和理解弹簧的物理特性对于在设计中正确应用弹簧十分重要。

为此，我们将讨论弹簧的伸长量公式，以及如何运用它来解决工程问题。

弹簧的伸长量公式是用来计算弹簧伸长量的数学公式，它是由德米斯特拉斯（Demosthenes）所提出的，经过多年的研究，最终得以完善。

弹簧的伸长量公式可以用来预测当某种力作用于弹簧时，弹簧包括连杆弹簧和卷簧等，会产生多大的伸长量。

其公式为：ε=F/K，其中ε表示弹簧伸长量，F表示外力的大小，K表示弹簧的刚度，其单位为牛顿/米（N/m）。

在实际的机械设计中，我们可以运用弹簧的伸长量公式来计算弹簧会在不同的条件下产生多少伸长量。

例如，当外力F施加在一个弹簧上，我们可以计算弹簧的伸长量，以及根据弹簧的特性，计算最终的伸长量是多少。

此外，我们还可以根据计算出的伸长量，计算外力F的大小，从而设计出适合弹簧的外力使其可以完成特定任务。

同时，弹簧的伸长量公式还可以用来检验已经安装在机械系统中的弹簧是否完好。

通过计算弹簧伸长量，我们可以根据其特性，检测弹簧是否出现了损坏或者变形的情况，以检验弹簧依然可以正常工作。

此外，在有些情况下，我们可以根据弹簧的伸长量公式计算出弹簧的负荷能力以及弹簧收缩的距离，以便更好地设计机械装置。

例如，在压缩弹簧中，我们可以根据伸长量公式计算出在某种负荷下，弹簧最大的负荷能力以及弹簧收缩的距离是多少，以便设计应用于机械系统的压缩弹簧的尺寸。

因此，我们可以说，弹簧的伸长量公式在机械工程中非常重要，可以用来预测和计算弹簧的特性。

综上所述，弹簧的伸长量公式是一种非常重要的数学公式，它可以用来计算弹簧会产生多少伸长量，从而帮助设计人员在设计机械装置时正确应用弹簧，更好地实现机械力学系统的设计以及检测机械系统中弹簧的完好状况，因此，弹簧的伸长量公式也可以说是机械工程中不可或缺的一部分。