三角形四心的向量性质

三角形四心与向量的关系三角形是几何学中的基本图形之一，它有许多重要的性质和特点。

在三角形中，有四个特殊的点，它们被称为三角形的四心，分别是重心、外心、垂心和内心。

本文将探讨这四个特殊点与向量之间的关系。

我们来介绍一下三角形的四心。

重心是三角形三条中线交于一点的点，它被定义为三角形三个顶点的坐标的平均值。

外心是三角形外接圆的圆心，它被定义为三角形三个顶点和三个外接圆弧的交点之一。

垂心是三角形三个高线交于一点的点，它被定义为三角形三个顶点和三个高线的交点之一。

内心是三角形的内切圆的圆心，它被定义为三角形三条边的垂直平分线的交点之一。

接下来，我们来研究这些四心与向量之间的关系。

首先，我们来看重心。

重心可以表示为三个顶点向量的平均值。

设三角形的三个顶点分别为A、B、C，对应的向量为a、b、c，则重心G可以表示为G=(a+b+c)/3。

这个公式说明了重心与向量之间的关系，即重心是三个顶点向量的平均值。

然后，我们来看外心。

外心可以表示为三个顶点向量的线性组合。

设三角形的三个顶点分别为A、B、C，对应的向量为a、b、c，则外心O可以表示为O=(a+b+c)/2。

这个公式说明了外心与向量之间的关系，即外心是三个顶点向量的线性组合。

接下来，我们来看垂心。

垂心可以表示为三个顶点向量的和的负数。

设三角形的三个顶点分别为A、B、C，对应的向量为a、b、c，则垂心H可以表示为H=-(a+b+c)。

这个公式说明了垂心与向量之间的关系，即垂心是三个顶点向量的和的负数。

我们来看内心。

内心可以表示为三条边的单位法向量的线性组合。

设三角形的三个顶点分别为A、B、C，对应的边向量为AB、BC、CA，单位法向量为n1、n2、n3，则内心I可以表示为I=(n1+n2+n3)/(|n1|+|n2|+|n3|)。

这个公式说明了内心与向量之间的关系，即内心是三条边的单位法向量的线性组合。

我们可以得出结论：三角形的四心与向量之间有着紧密的关系。

平面向量的应用——三角形四心的性质一 知识点精讲三角形四“心”向量形式的充要条件设O 为ABC ∆所在平面上一点，角,,A B C 所对边长分别为,,a b c ，则（1）O 为ABC ∆的外心222O A O B O C ⇔== . （2）O 为ABC ∆的重心0OA OB OC ⇔++= .证明： 证明： （3）O 为ABC ∆的垂心OA OB OB OC OC OA ⇔⋅=⋅=⋅.证明： （4）O 为ABC ∆的内心0aOA bOB cOC ⇔++=. 证明：二 典例解析一、重心1. 已知O 是平面上一定点，AB C ，，是平面上不共线的三个点，动点P 满足()OP OA AB AC λ=++，(0)λ∈+∞，，则P 的轨迹一定通过ABC △的（ ）． Ａ．外心 Ｂ．内心 Ｃ．重心 Ｄ．垂心2. 已知O 是平面上一定点，AB C ，，是平面上不共线的三个点，动点P 满足sin ||sin ||(CAC BAB ++=λ，(0)λ∈+∞，，则动点P 的轨迹一定通过ABC △的（ ）．Ａ．外心 Ｂ．内心 Ｃ．重心 Ｄ．垂心二、垂心3. O 是ABC △所在平面上一点，222222||||||||||||+=+=+，O 是ABC △___Ａ．外心 Ｂ．内心 Ｃ．重心 Ｄ．垂心4. 已知O 是平面上一定点，AB C ，，是平面上不共线的三个点，动点P 满足cos ||cos ||(CAC BAB ++=λ，(0)λ∈+∞，，则动点P 的轨迹一定通过ABC △的（ ）．Ａ．外心 Ｂ．内心 Ｃ．重心 Ｄ．垂心三、内心4.（2003江苏） 已知O 是平面上一定点，AB C ，，是平面上不共线的三个点，动点P 满足AB AC OP OA AB AC λ⎛⎫ ⎪=++ ⎪⎝⎭，(0)λ∈+∞，，则动点P 的轨迹一定通过ABC △的（ ）． Ａ．外心 Ｂ．内心 Ｃ．重心 Ｄ．垂心四、外心5. 已知O 是平面上的一定点，AB C ，，是平面上不共线的三个点，动点P 满足2cos cos OB OC AB AC OP AB B AC C λ⎛⎫+ ⎪=++ ⎪⎝⎭，(0)λ∈+∞，，则动点P 的轨迹一定通过ABC △的．Ａ．外心 Ｂ．内心 Ｃ．重心 Ｄ．垂心6. (2005湖南)．设P 是△ABC 内任意一点，S △ABC 表示△ABC 的面积，λ1＝ABcPBCS S ∆∆， λ2＝ABCPCAS S ∆∆， λ3＝ABCPAB S S ∆∆，定义),,()(321λλλ=p f ，若G 是△ABC 的重心，)61,31,21()(=Q f ，则（ ）A ．点Q 在△GAB 内 B ．点Q 在△GBC 内C ．点Q 在△GCA 内D ．点Q 与点G 重合定理：设P 是△ABC 内任意一点，S △ABC 表示△ABC 的面积，则有=++∆∆∆S S S PBC PAC PAB五 判断三角形的形状及求最值 7.在△ABC 中，已知向量210(==⋅+BC AC AB 满足与，则△ABC 为（ ）A ．三边均不相等的三角形B ．直角三角形C ．等腰非等边三角形D ．等边三角形8. 在ΔABC 中，O 为中线AM 上的一个动点，若AM=2，则)(+⋅的最小值为 .六 轨迹问题9．已知)0,1(),0,4(N M ，若动点(,)P x y 满足6||MN MP NP ⋅=，求动点P 的轨迹方程.三课堂检测：1若O 为ABC ∆的内心，且满足()(2)0OB OC OB OC OA -⋅+-=，则ABC ∆的形状为( ) A.等腰三角形 B.正三角形 C.直角三角形 D.钝角三角形2.已知ABC ∆的三个顶点,,A B C 及平面内一点P ，且PA PB PC AB ++=，则点P 与ABC ∆的位置关系是( ) A.P 在ABC ∆内部 B.P 在ABC ∆外部 C.P 在AB 边上或其延长线上 D.P 在AC 边上3.平面直角坐标坐标系中，O 为坐标原点，已知两点A(3，1)，B （－1，3），若点C 满足OC=αOA +βOB，若中α、β∈R ，且α+β=1，则点C 的轨迹方程为（ ）A 、（x －1）2+（y －2）2=5 B 、3x+2y －11=0 C 、2x －y=0 D 、x+2y －5=04.已积OB =（2，0），OC =（2，2），CA = （2cos α，2sin α），则OA 与OB 夹角的范围是（ ）A 、[0，π4]B 、[π4，5π12]C 、[π12，5π12] D、[5π12，π2] 5.平面向量a =（x ，y ），b =（x 2，y 2），c =（1，1），d =（2，2），若a ·c =b ·d =1，则这样的向量a有A 、1个B 、2个C 、多于2个D 、不存在6.设O 为ABC ∆所在平面上一定点, P 为平面上的动点,且满足()()0OP OA AB AC -⋅-=,则P 点的轨迹一定通过ABC ∆的 心.7. 已知ABC ∆的重心为G ，点O 为ABC ∆所在平面上任意一点，求证：1()3OG OA OB OC =++ .8.,,a b c 为△ABC 的内角A 、B 、C 的对边，(cos ,sin )22C C m = ，(cos ,sin )22C Cn =- ，且m 与n 的夹角为3π，求C ；9.已知A 、B 、C 是直线l 上的不同的三点，O 是外一点，向量,,OA OB OC满足23(1)[ln(23)]02OA x OB x y OC -+∙-+-∙=,记()y f x =.求函数()y f x =的解析式；。

龙源期刊网
三角形“四心”向量形式的充要条件
作者：祝兵
来源：《数理化学习·高一二版》2013年第06期
在高考中，往往将“向量作为载体”对三角形的“四心”进行考查.
一、三角形的“四心”定理
内心：三条角平分线的交点，也是三角形内切圆的圆心.
性质：到三边距离相等.
外心：三条中垂线的交点，也是三角形外接圆的圆心.
性质：到三个顶点距离相等.
重心：三条中线的交点.
性质：三条中线的三等分点，到顶点距离为到对边中点距离的2倍.
垂心：三条高所在直线的交点.
性质：此点分每条高线的两部分乘积相等.
二、第一组三角形的“四心” 定理的平面向量表达式及其证明
（证明方法同一法），证明参考外心充分性的证明.
[江西省九江一中（330399）]。

三角形“四心”向量形式的充要条件应用知识点总结1.0是的重心；若0是的重心，则故；为的重心.2.0是的垂心；若0是（非直角三角形）的垂心，则故3.0是的外心（或）若0是的外心则故4. 0是内心的充要条件是引进单位向量，使条件变得更简洁。

如果记的单位向量为，则刚才0是内心的充要条件可以写成，0是内心的充要条件也可以是。

若0是的内心，则故；是的内心；向量所在直线过的内心（是的角平分线所在直线）；xx 例（一）将平面向量与三角形内心结合考查例1. O是平面上的一定点，A,B,C是平面上不共线的三个点，动点P满足，则P 点的轨迹一定通过的（）（A）外心（B）内心（C）重心（D）垂心解析：因为是向量的单位向量设与方向上的单位向量分别为，又，则原式可化为，由菱形的基本性质知AP平分，那么在xx，AP平分，贝卩知选B.（二）将平面向量与三角形垂心结合考查“垂心定理”例2. H是厶ABC所在平面内任一点，点H是厶ABC的垂心.由,同理，.故H是厶ABC的垂心.（反之亦然（证略））例3.（xx）P 是厶ABC所在平面上一点，若，则P是厶ABCF（D ）A.外心B.内心C.重心D.垂心解析: 由. 即贝S所以P为的垂心.故选D.（三）将平面向量与三角形重心结合考查“重心定理”例4. G是厶ABC所在平面内一点，=0点G是厶ABC的重心.证明作图如右，图中连结BE和CE贝S CE=GB BE=GCBGCE平行四边形D是BC的中点，AD为BC边上的中线.将代入=0，得=0,故G是厶ABC的重心.（反之亦然（证略））例5. P是厶ABC所在平面内任一点.G是厶ABC的重心.证明••*是厶ABC的重心/• =0=0,即由此可得. （反之亦然（证略））例6 若为内一点, ,则是的（）A.内心B.外心C.垂心D.重心解析：由得，如图以OB OC为相邻两边构作平行四边形，贝卩，由平行四边形性质知,,同理可证其它两边上的这个性质,所以是重心,选D。

三角形四心的向量性质及证明符号说明：“AB”表示向量，“|AB|”表示向量的模【一些结论】：以下皆是向量1 若P是△ABC的重心PA+PB+PC=02 若P是△ABC的垂心PA*PB=PB*PC=PA*PC(内积）3 若P是△ABC的内心aPA+bPB+cPC=0(abc是三边）4 若P是△ABC的外心|PA|=|PB|=|PC|（AP就表示AP向量 |AP|就是它的模）5 AP=λ（AB/|AB|+AC/|AC|),λ∈[0,+∞) 则直线AP经过△ABC内心6 AP=λ（AB/|AB|cosB+AC/|AC|cosC),λ∈[0,+∞) 经过垂心7 AP=λ（AB/|AB|sinB+AC/|AC|sinC),λ∈[0,+∞）或AP=λ(AB+AC),λ∈[0,+∞) 经过重心8.若aOA=bOB+cOC,则0为∠A的旁心,∠A及∠B,∠C的外角平分线的交点【以下是一些结论的有关证明】1.O是三角形内心的充要条件是aOA向量+bOB向量+cOC向量=0向量充分性：已知aOA向量+bOB向量+cOC向量=0向量，延长CO交AB于D，根据向量加法得：OA=OD+DA,OB=OD+DB,代入已知得：a(OD+DA)+b(OD+DB)+cOC=0,因为OD与OC共线，所以可设OD=kOC,上式可化为(ka+kb+c) OC+(aDA+bDB)=0向量,向量DA与DB共线，向量OC与向量DA、DB不共线，所以只能有：ka+kb+c=0，aDA+bDB=0向量,由aDA+bDB=0向量可知：DA与DB的长度之比为b/a,所以CD为∠ACB的平分线，同理可证其它的两条也是角平分线。

必要性：已知O是三角形内心,设BO与AC相交于E，CO与AB相交于F，∵O是内心∴b/a=AF/BF，c/a=AE/CE过A作CO的平行线，与BO的延长线相交于N，过A作BO的平行线，与CO的延长线相交于M，所以四边形OMAN是平行四边形根据平行四边形法则，得向量OA=向量OM+向量ON=(OM/CO)*向量CO+(ON/BO)*向量BO=(AE/CE)*向量CO+(AF/BF)*向量BO=(c/a)*向量CO+(b/a)*向量BO∴a*向量OA=b*向量BO+c*向量CO∴a*向量OA+b*向量OB+c*向量OC=向量02.已知△ABC 为斜三角形,且O是△ABC所在平面上的一个定点,动点P满足向量OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)}, 求证P点轨迹过三角形的垂心OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},OP-OA=入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},AP=入{(AB /|AB|＾2*sin2B)+AC /(|AC|＾2*sin2C)},AP*BC=入{(AB*BC /|AB|＾2*sin2B)+AC*BC /(|AC|＾2*sin2C)}, AP*BC=入{|AB|*|BC|cos(180° -B) /(|AB|＾2*sin2B) +|AC|*|BC| cosC/(|AC|＾2*sin2C)},AP*BC=入{-|AB|*|BC| cos B/(|AB|＾2*2sinB cos B) +|AC|*|BC| cosC/(|AC|＾2*2sinC cosC)},AP*BC=入{-|BC|/ (|AB|*2sinB) +|BC|/(|AC|*2sinC )},根据正弦定理得：|AB|/sinC=|AC|/ sinB,所以|AB|*sinB=|AC|*sinC ∴-|BC|/ (|AB|*2sinB ) +|BC|/(|AC|*2sinC )=0，即AP*BC=0，P点轨迹过三角形的垂心3. OP=OA+λ(AB/(|AB|sinB)+AC/(|AC|sinC))OP-OA=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP与AB/|AB|sinB+AC/|AC|sinC共线根据正弦定理：|AB|/sinC=|AC|/sinB,所以|AB|sinB=|AC|sinC,所以AP与AB+AC共线 AB+AC过BC中点D，所以P点的轨迹也过中点D，∴点P过三角形重心。

三角形“四心”的向量性质及其应用三角形“四心”的概念介绍(1)重心—三条中线的交点：重心将中线长度分成2：1；(2)外心—三边中垂线的交点(外接圆的圆心)：外心到三角形各顶点的距离相等；(3)垂心—三条高线的交点：高线与对应边垂直；(4)内心—三条内角平分线的交点(内切圆的圆心)：角平分线上的任意点到角两边的距离相等．工具：O 为ABC △内一点，则有：0+⋅+⋅∆∆∆OC S OB S OA S O O CA O BC 证明：作：OA S OA OCB ⋅=∆'，OB S OB OCA ⋅=∆'，S OC OAB =∆'不难得知：AOB COA BOC OC B S S OC OC OB OB S S ∆∆∆∆⋅=⋅=''''即BO C AO B CO A O C B S S S S ∆∆∆∆⋅⋅=''；同理==∆∆''''O B A O A C S S ''O C B BO C AO B CO A S S S S ∆∆∆∆=⋅⋅ 从而：O 为'''C B A ∆的重心，则+'OA +'OB 0'=OC ， 得：0=⋅+⋅+⋅∆∆∆OC S OB S OA S O AB O CA O BC .一、三角形的重心的向量表示及应用知识：G 是ABC △的重心⇔)(31AC AB AG +=⇔0=++GC GB GA ⇔)(31OC OB OA OG ++= (O 为该平面上任意一点)变式：已知D E F ，，分别为ABC △的边BC AC AB ，，的中点．则0=++CF BE AD ． 二、三角形的外心的向量表示及应用知识：O 是ABC △的外心⇔222||||||OC OB OA OC OB OA ==⇔== 02sin 2sin 2sin =⋅+⋅+⋅⇔OC C OB B OA A略证：C B A S S S O AB O CA O BC 2sin :2sin :2sin ::=∆∆∆，得：02sin 2sin 2sin =⋅+⋅+⋅OC C OB B OA A ;常用结论：O 是ABC △的外心⇒.2|| ;2||22AC AO AC AB AO AB =⋅=⋅ 三、三角形的垂心的向量表示及应用知识：H 是ABC △的垂心⇔HA HC HC HB HB HA ⋅=⋅=⋅⇔222222||||||||||||AB HC CA HB BC HA +=+=+0tan tan tan =⋅+⋅+⋅⇔HC C HB B HA A略证：C B A S S S H AB H CA H BC tan :tan :tan ::=∆∆∆，得：0tan tan tan =⋅+⋅+⋅HC C HB B HA A ； 扩展：若O 是ABC △的外心，点H 满足：OC OB OA OH ++=，则H 是ABC △的垂心． 证明：如图：BE 为直径，H 为垂心，O 为外心，D 为BC 中点；'有：为平行四边形AHCE EA CH AB EA AB CH EC AH BC EC BC AH ⇒⎪⎪⎭⎪⎪⎬⎫⇒⎭⎬⎫⊥⊥⇒⎭⎬⎫⊥⊥////进而得到：,//EC AH 且EC AH =，即：EC AH =； 又易知：OC OB OD EC +==2；故：OA OH OC OB AH -=+=，即：OC OB OA OH ++=又：OG OC OB OA ⋅=++3（G 为重心），故：OG OH ⋅=3；故：得到欧拉线：ABC △的外心O ，重心G ，垂心H 三点共线(欧拉线)，且GH OG 21=．证毕． 四、三角形的内心的向量表示及应用知识：I 是ABC △的内心⇔⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎭⎫⎝⎛-⋅=⎭⎫⎝⎛-⋅=⎭⎫⎝⎛-⋅0||||0||||0||||CB CB CA CA CI BC BC BA BA BI AC AC AB AB AI ⇔⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎭⎫⎝⎛+⋅=⎭⎫⎝⎛+⋅=⎭⎫⎝⎛+⋅0||||0||||0||||CA CA BC BC CI BA BA CB CB BI AC AC BA BA AI 0=⋅+⋅+⋅⇔IC c IB b IA a c b a OCc OB b OA a OI ++⋅+⋅+⋅=⇔cb a ACc AB b AI ++⋅+⋅=⇔ 0sin sin sin =⋅+⋅+⋅⇔IC C IB B IA A 注：式子中|||,||,|AB c CA b BC a ===，O 为任一点．略证：C B A c b a S S S IAB ICA IBC sin :sin :sin ::::==∆∆∆，得之． 五．欧拉线：ABC △的外心O ，重心G ，垂心H 三点共线(欧拉线)，且GH OG 21=．（前已证） 测试题一．选择题1．O 是ABC ∆所在平面上一定点，动点P 满足)(AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心 解析：点P 的轨迹为BC 边的中线（射线），选C2．(03全国理4)O 是ABC ∆所在平面上一定点，动点P 满足AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心 解析：AC AB OA OP ++=λ⇔AC AB AP +=λAC AB +必平分BAC ∠，理由如下：ADACABACACABAB=+==1111,1==，故四边形11DCAB为菱形，对角线AD平分一组对角，ADACAB=+必定平分11ACB∠，即BAC∠，从而ACABAP+=λ也平分BAC∠.故知点P的轨迹为A∠的内角平分线（射线），选 B3．O是ABC∆所在平面上一定点，动点P满足ACABOAOP++=λ，R∈λ，则点P的轨迹一定通过ABC∆的( )A．外心B．内心C．重心D．垂心解析：ACABOAOP++=λ⇔ACABAP+=λ由BCACBCABBCACBCABBCAP+=+=⋅λλ得：0|)|||(=+-=⋅BCBCBCAPλ，得BCAP⊥点P的轨迹为BC边的高线所在直线. 选D4．O是ABC∆所在平面上一定点，动点P满足ACABOAOP+=λ，[)+∞∈,0λ，则点P的轨迹一定通过ABC∆的( )A．外心B．内心C．重心D．垂心解析：由于CACCbBcBAB sin||sinsinsin||=⋅=⋅=，知点P的轨迹为BC边的中线（射线）,选C5．O是ABC∆所在平面上一定点，动点P满足2cos cosOB OC AB ACOPAB B AC Cλ⎛⎫+ ⎪=++⎪⎝⎭，R∈λ，则点P的轨迹一定通过ABC△的( )．A．外心B．内心C．重心D．垂心解析：0||||=+-=+=⋅+BCBCBCACBCABBCACAB知点P的轨迹为BC边的中垂线, 选A6．O是ABC∆所在平面上一定点，动点P满足])21()1()1[(31OCOBOAOPλλλ++-+-=，*R∈λ，则点P的轨迹一定通过ABC△的( )．A．内心B．垂心C．重心D．AB边的中点解析：])21()1()1[(31OCOBOAOPλλλ++-+-=OCOD3)21(3)22(λλ++-=（D为AB边的中点）知CDP,,三点共线（因1321322=++-λλ），故知点P 的轨迹为AB 边的中线所在直线，但是0≠λ，故除去重心. 选D 7．已知O 是ABC ∆的重心，动点P 满足)22121(31OC OB OA OP ++=,则点P 一定为ABC △的( ) A ．AB 边中线的中点 B ．AB 边中线的三等分点(非重心)C ．重心D ．AB 边的中点解析：)22121(31OC OB OA OP ++=OC OD 3231+=（D 为AB 边的中点） 进而有：PC DP 2=，故为AB 边中线的三等分点(非重心), 选B8．在ABC △中，动点P 满足：CP AB CB CA ⋅-=222，则P 点轨迹一定通过△ABC 的( )Ａ．外心 Ｂ．内心 C ．重心 D ．垂心解析：CP AB CB CA ⋅-=222⇔02))((222=⋅-+-=⋅--CP AB CA CB CA CB CP AB CA CB 进而有：02=⋅PD AB （D 为AB 边的中点），故知点P 的轨迹为AB 边的中垂线, 选A9．已知ABC ∆三个顶点C B A 、、及平面内一点P ，满足0=++PC PB PA ，若实数λ满足：AP AC AB λ=+，则λ的值为( )A ．2B ．23C ．3D ．6 解析：P 为重心，得)(31AC AB AP +=，故AP AC AB ⋅=+3,选C10．设点P 是ABC ∆内一点，用ABC S ∆表示ABC ∆的面积，令ABC PBC S S ∆∆=1λ，ABCPCA S S∆∆=2λ，ABC PAB S S ∆∆=3λ．定义),,()(321λλλ=P f ，若)61,31,21()(),31,31,31()(==Q f G f 则( )A ．点Q 在ABG ∆内B ．点Q 在BCG ∆内C ．点Q 在CAG ∆内D ．以上皆不对 解析：G 为重心，画图得知, 选A11．若ABC ∆的外接圆的圆心为O ，半径为1，0=++OC OB OA ，则=⋅OB OA ( )A ．21 B ．0 C ．1 D ．21- 解析：由OC OB OA -=+，平方得知, 选D12．O 是平面上一定点，C B A 、、是平面上不共线的三个点，若222OB BC OA =+222AB OC CA +=+，则O 是ABC ∆的( )A ．外心B ．内心C ．重心D ．垂心 解析：由2222CA OB BC OA +=+⇔2222BC CA OB OA -=-BA BC CA OB OA BA BC CA BC CA OB OA OB OA ⋅-=+⋅⇔+-=+-⇔)()())(())(( 0)2()(=⋅=-++⋅⇔OC BA CA BC OB OA BA ，得AB OC ⊥；同理得：AC OB ⊥,BC OA ⊥，故为垂心, 选D 13．(06陕西)已知非零向量AB 与AC 满足0||||=⋅⎭⎫⎝⎛+BC AC AC AB AB 21||||=AC AC AB AB , 则ABC ∆为( ) A ．三边均不相等的三角形 B ．直角三角形 C ．等腰非等边三角形 D ．等边三角形解析：21||||=AC AC AB AB 0||||=⋅⎭⎫⎝⎛+BC AC AC AB AB ：表明A ∠的内平分线也垂直于BC （三线合一）， 知ABC ∆等腰；21||||=AC AC AB AB ：得到︒=∠60A ；两者结合得到ABC ∆为等边三角形. 选D 14．已知ABC ∆三个顶点C B A 、、，若CA BC CB AB AC AB AB ⋅+⋅+⋅=2，则ABC ∆为( )A ．等腰三角形B ．等腰直角三角形C ．直角三角形D ．既非等腰又非直角三角形 解析：CA BC CB AB AC AB AB ⋅+⋅+⋅=2CA BC AB CA BC CB AC AB ⋅+=⋅++⋅=2)( 得到：0=⋅CA BC ，得：︒=∠90C ,选C 二．填空题15．ABC ∆的外接圆的圆心为O ，两条边上的高的交点为H ，)(OC OB OA m OH ++=，则实数m = 1 ． 解析：直接用结论16．ABC ∆中，7,3,1===BC AC AB ，O 为重心，则=⋅AC AO27． 解析：)9(31)(31)(312+⋅=+⋅=+=⋅AC AB AC AC AB AC AC AB AC AO 利用：CB AC AB =-，两边平方得.23=⋅AC AB 故27)923(31=+=⋅AC AO17．点O 在ABC ∆内部且满足032=++OC OB OA ，则:ABC S ∆=∆AOC S 3 ．解析：法1：利用工具结论易知：AOB COA BOC S S S ∆∆∆=::3:2:1，得:ABC S ∆=∆AOC S 32:6= 法2：0422232=+=+++=++OD OE OC OB OC OA OC OB OA （E 为AC 的中点，D 为BC 的中点）易得：D O E ,,三点共线，且OD EO 2=，从而得到：ABC ADC AOC S S S ∆∆∆==3132. 法3：作：OA OA ='，OB OB 2'=，OC OC 3'=则+'OA +'OB 0'=OC ，则O 为'''C B A ∆的重心，则：''''''O B A O A C O C B S S S ∆∆∆==.设为S又⎪⎩⎪⎨⎧======∆∆∆∆∆∆SS SS S S S S S AOB OB A COA OA C BOC OC B 236'''''' 从而得：331:13:)236(:==++=∆∆S S S S S S COA ABC ． 18．点O 在ABC ∆内部且满足AC AB AO 5152+=，则:ABC S ∆=∆AOB S 5 ． 解析：法1：AC AB AO 5152+=，用O 拆开得：022=+⋅+⋅OC OB OA ， 'A 'B 'C O)(A BC利用工具结论易知：AO B CO A BO C S S S ∆∆∆=::1:2:2，则:ABC S ∆51:5==∆AO B S 法2：AC AD AC AB AO 51545152+=+=，（D 为AB 边的中点），得到：C O D ,,共线，且OD CO 4=， 则:ABC S ∆5:==∆OD CD S AO B . 法3：同上题中法3，此处略.19．已知ABC ∆中，6,5===BC AC AB ，I 为ABC ∆的内心，且BC AB AI μλ+=，则=+μλ1615. 解析：法1：由BC AB BC AB AB AC AB c b a AC c AB b AI ⋅+⋅=+⋅+⋅=++⋅+⋅=++⋅+⋅=165161016)(5555655法2：如图，线长易知，角平分线分线段成比例，得：3:5:=ID AI ， 故)21(8585BC AB AD AI ⋅+⋅=⋅=AB +⋅=1658520．已知ABC ∆中，1,1,2-=⋅==AC AB AC AB ，O 为ABC ∆的外心，且BC y AB x AO +=，则=+y x 27． 解析：法1：由BC y AB x AO +=AC y AB y x +-=)(，由AC AB y AB y x ABBC y AB y x AB AO AB ⋅+-=⇒+-⋅=⋅22)(2))((，得：y y x --=)(42；同理22)(2))((AC y AC AB y x ACBC y AB y x AC AO AC +⋅-=⇒+-⋅=⋅，得：y y x +--=)(21；易得：34,613==y x ，得27=+y x . 法2：以},{AC AB 为基底，表示：CO BO AO ,,，利用222CO BO AO ==，得之BC y AB x AO +=AC y AB y x +-=)(，y y x y y x AO )(2)(4222--+-=； AC y AB y x AB AO BO +--=-=)1(，y y x y y x BO )1(2)1(4222---+--=； AC y AB y x AC AO CO )1()(-+-=-=，)1)((2)1()(4222----+-=y y x y y x CO ；由22BO AO =0254=--⇒⇒y x 移项做差； 由22CO AO =0142=+-⇒⇒y x 移项做差； 联立方程解得：34,613==y x ，得27=+y x .BCA MNG21．已知O 为锐角ABC ∆的外心，︒=∠30A ，若AO m B C AC C B AB 2sin cos sin cos =⋅+⋅，则=m 21． 解析：由AO m AB B CAC C B AB AB 2)sin cos sin cos (⋅=⋅+⋅⋅ 得：22||sin cos cos ||||sin cos ||AB m B CA AC ABC B AB =⋅⋅⋅+⋅得：C m C A B mc BCA b c CB c sin cos cos cos sin cos cos sin cos 22⋅=+⇒=⋅⋅⋅+⋅得到：C A C A C A C A B C m sin sin cos cos )cos(cos cos cos sin =++-=+=⋅ 得：.2130sin sin =︒==A m 22．在ABC∆中，1,==⊥AD BC AB AD ，则⋅AD AC解析：.33)(2===⋅=⋅+=⋅AD AD AD BC AD BC AB AD AC 三．解答题23． 如图，已知点G 是ABC ∆的重心，过G 作直线与AC AB ,两边分别交于N M ,两点，且AM xAB = ，AN yAC = ，求证：113x y+=．解：由N G M ,,三点共线， 得：AN t AM t AG ⋅+⋅-=)1(AC ty AB x t ⋅+⋅-=)1(--------①又G 是ABC ∆的重心得：AC AB AG ⋅+⋅=3131 ---------② 由①②得：⎪⎪⎩⎪⎪⎨⎧==-3131)1(ty x t ，消去t 得：113x y +=.24．设O 在ABC ∆的内部，若有正实数321,,λλλ满足：0321=⋅+⋅+⋅OC OB OA λλλ， 求证：AO B CO A BO C S S S ∆∆∆=::::321λλλ．证明：作：OA OA ⋅=1'λ，OB OB ⋅=2'λ，OC OC ⋅=3'λ 则+'OA +'OB 0'=OC ，则O 为'''C B A ∆的重心，则：''''''O B A O A C O C B S S S ∆∆∆==.设为S又⎪⎩⎪⎨⎧=⋅==⋅==⋅=∆∆∆∆∆∆SS SS S S S S S AOB OB A COA OA C BOC OC B 2!''13''32''λλλλλλ 从而得：AOB COA BOC S S S SSS∆∆∆==::::::211332321λλλλλλλλλ25．已知向量1OP ，2OP ，3OP 满足条件1OP +2OP +3OP =0，|1OP |=|2OP |=|3OP |=1，求证：321P P P ∆为正三角形． 证明：由1OP +2OP +3OP =0⇒1OP +2OP =3OP -平方得：1212112121-=⋅⇒=⋅++OP OP OP OP'A 'B 'C OABC从而得：3||21====P P同理可得：3||||1332==P P P P ，即321P P P ∆为正三角形． 26．在ABC ∆中，︒===60,5,2A AC AB ，求从顶点B A ,出发的两条中线BE AD ,的夹角的余弦值．解：设b AB a AC ==,，则,560cos 25,4,2522=︒⨯⨯=⋅==b a b a且b a BE b a AD -=+=21),(21； 则,3)8525(41)2(41)21()(2122=--=-⋅-=-⋅+=⋅b b a a b a b a BE AD2394102521|)(|21||=++==+=b a AD22116202521|)2(|21||=+-==-=b a BE 故：.919149142212393||||,cos ==⋅=>=<BE AD BEAD BE AD27．已知H 是ABC △的垂心，且||||BC AH =，试求∠A 的度数．解：设ABC △的外接圆半径为R ，点O 是ABC △的外心。

三角形“四心”向量形式的结论及证明三角形的“四心”是指三角形的重心、外心、内心和垂心。

它们的位置可以用向量的形式来描述。

本文将分别介绍三角形“四心”的向量形式以及其证明。

1.重心:重心是指三角形三个顶点的中线交点所在的点，用G表示。

假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3)，则重心G的坐标可以通过以下公式得到：G=(A+B+C)/3其向量形式为：OG=(OA+OB+OC)/3其中O为坐标原点。

证明：由定义可知，重心是三角形三个顶点的中线交点所在的点。

而中线的坐标可以通过两个顶点的坐标的平均值得到。

因此，重心的坐标是三个顶点坐标的平均值。

根据向量加法的性质，可以得到上述结论。

2.外心:外心是指可以通过三角形的三个顶点作为圆心，找到一个圆使得三条边都是这个圆的切线。

用O表示外心。

假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3)，则外心O的坐标可以通过以下公式得到：O=(a^2*A+b^2*B+c^2*C)/(a^2+b^2+c^2)其中a、b、c分别表示三角形的边长BC、AC和AB的长度。

其向量形式为：OO=(a^2*OA+b^2*OB+c^2*OC)/(a^2+b^2+c^2)其中O为坐标原点。

证明：设外心为O，连接OA、OB、OC，并设AO的长度为R，BO的长度为R'，CO的长度为R''。

根据定义可知，OA，OB，OC都是截圆半径，可以得到以下关系：OA⊥BC，OB⊥AC，OC⊥AB由于OA、OB、OC是向量，因此上述关系可以写为：OA·BC=0，OB·AC=0，OC·AB=0其中“·”表示点乘。

根据向量的点乘性质可知：OA·(B-C)=0，OB·(C-A)=0，OC·(A-B)=0将向量差展开得：OA·B-OA·C=0，OB·C-OB·A=0，OC·A-OC·B=0进一步展开可得：R^2-R'^2=0，R'^2-R''^2=0，R''^2-R^2=0整理得：R^2-R'^2=R''^2-R^2移项得：2R^2=R'^2+R''^2根据圆的定义可知，外心到三角形的每个顶点的距离都相等，因此R=R'=R''。

三角形“四心”向量形式的充要条件应用知识点总结1．O是的重心;若O是的重心，则故;为的重心.2．O是的垂心;若O是(非直角三角形)的垂心，则故3．O是的外心(或)若O是的外心则故4．O是内心的充要条件是引进单位向量，使条件变得更简洁。

如果记的单位向量为，则刚才O是内心的充要条件可以写成，O是内心的充要条件也可以是。

若O是的内心，则故;是的内心;向量所在直线过的内心(是的角平分线所在直线)；xx 例(一)将平面向量与三角形内心结合考查例1．O是平面上的一定点，A,B,C是平面上不共线的三个点，动点P满足，则P点的轨迹一定通过的（）（A）外心（B）内心（C）重心（D）垂心解析：因为是向量的单位向量设与方向上的单位向量分别为，又，则原式可化为，由菱形的基本性质知AP平分，那么在xx，AP平分，则知选B.(二)将平面向量与三角形垂心结合考查“垂心定理”例2． H是△ABC所在平面内任一点，点H是△ABC的垂心.由,同理，.故H是△ABC的垂心. （反之亦然（证略））例3.(xx)P是△ABC所在平面上一点，若，则P是△ABC的（D ）A．外心B．内心C．重心D．垂心解析:由.即则所以P为的垂心. 故选D.(三)将平面向量与三角形重心结合考查“重心定理”例4． G是△ABC所在平面内一点，=0点G是△ABC的重心.证明作图如右，图中连结BE和CE，则CE=GB，BE=GCBGCE为平行四边形D是BC的中点，AD为BC边上的中线.将代入=0，得=0，故G是△ABC的重心.（反之亦然（证略））例5． P是△ABC所在平面内任一点.G是△ABC的重心.证明∵G是△ABC的重心∴=0=0，即由此可得.（反之亦然（证略））例6 若为内一点，，则是的（）A．内心B．外心C．垂心D．重心解析：由得，如图以OB、OC为相邻两边构作平行四边形，则，由平行四边形性质知，，同理可证其它两边上的这个性质，所以是重心，选D。

(四) 将平面向量与三角形外心结合考查例7若为内一点，，则是的（）A．内心B．外心C．垂心D．重心解析：由向量模的定义知到的三顶点距离相等。

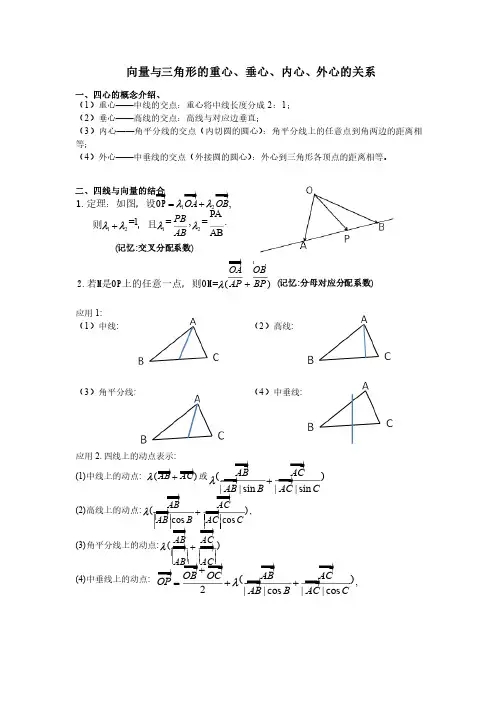
向量与三角形的重心、垂心、内心、外心的关系一、四心的概念介绍、（1）重心——中线的交点：重心将中线长度分成2：1； （2）垂心——高线的交点：高线与对应边垂直； （3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

二、四线与向量的结合121212,PA =1=,=.ABOA OB PB AB l l l l l l =++1.1.定理：如图，设定理：如图，设定理：如图，设OP OP 则则，且 (记忆:交叉分配系数) =()OA OBAP BP l +2.2.若若M 是OP OP上的任意一点，则上的任意一点，则上的任意一点，则OM OM (记忆:分母对应分配系数) 应用1: （1）中线: （2）高线: （3）角平分线: （4）中垂线: 应用2.四线上的动点表示: (1)中线上的动点: ()AB AC l +或()||sin ||sin AB AC AB B AC Cl +(2)高线上的动点:()cos cos AB AC AB BAC C l +, (3)角平分线上的动点:()AB ACABACl +(4)中垂线上的动点: ()2||cos ||cos OB OCAB AC OP AB B AC Cl +=++,O ABC OA S OB S OC D 定理：设是内任意一点，b a SAOBAOC：：：=D =1:1:1Û0OA OB OC ++=B tan A tan S AOB AOC ：：：=D 0OC OB OA 0aOA bOB cOC 1()3PO PA PB PC =++OA OB OB OC OC OA ×=×=× )))AB AC BC BA CA OC OB OA 已知O 是平面上一定点，||||AB AC AB AC l æö=++ç÷, l 题2：已知O 是平面上一定点，()OP OA AB AC l =++, l ÎO 是平面上的一定点，A ()||sin ||sin AB AC OP OA AB B AC Cl =++是平面上的一定点，A 、B ()||cos ||cos AB AC AB B AC Cl +题5：已知O 是平面上的一定点，A 、B 、C 是平面上不共线的三个点，动点()OB OCABAC++D. 内心,,OA OB OC 满足()||||AB CA OA AB CA ×+=(||BA OB BA ×+||CB CB ) ()||||BC CAOC BC CA ×+= 0内心 D. 外心OA OB OC ++= 0, 1()PO PA PB PC D. 垂心OA OB OB OC OC OA ×=×=×，则 D. 垂心 2222|||||||OA BC OB CA +=+=22|||OC AB +，则 D. 外心题11：已知O 是△ABC )OA OB AB +×()OB OC BC +×()OC OA CA +×= 0，则 D. 垂心aOA bOB cOC ++= = 00，则D. 垂心aPA bPB cPC =题14：△ABC 的外OH =()m OA OB OC ++，则实数二、与三角形形状相关的向量问题题15：已知||||ABACAB AC 12||||AB AC AB AC ×=，则△等边三角形|||2|OB OC OB OC OA -=+-，则等边三角形||BA tBC -≥||AC ，则△题18：已知a , b, c 分别为△GA b GB c GC ×+×+×= = 00, 则△内一点，23OA OB OC ++= 0, 则：题20：如图，已知点是△ABC 的重心，若PQ 过△ABC 的重心，记CA = a ,则11m n +=_____.|(sin AB OP OA C ABl =++sin )AC B ACG C P Q 。

与三角形四心相关的向量结论.doc
下面是一些与三角形的四个特殊点（重心、外心、内心和垂心）相关的向量结论：
1. 重心：三角形的重心是三条中线的交点，表示为G，并且满足以下向量等式：
AG + BG + CG = 0
2. 外心：三角形的外心是三角形外接圆的圆心，表示为O，并且满足以下向量等式：
AO = BO = CO = R（半径）
3. 内心：三角形的内心是三角形内切圆的圆心，表示为I，并
且满足以下向量等式：
AI = BI = CI = r（半径）
4. 垂心：三角形的垂心是三条高线（从顶点到对边垂直的线段）的交点，表示为H，并且满足以下向量等式：
AH + BH + CH = 0。

空间向量的四心公式空间向量的四心公式是空间解析几何中的一个重要定理，它描述了一个三角形的四个特殊点。

在本文中，我们将介绍四心公式的定义、性质和应用。

让我们来看一下四心公式的定义。

对于一个三角形ABC，它的四心分别是外心O、垂心H、重心G和内心I。

外心是三角形外接圆的圆心，垂心是三角形三条高的交点，重心是三角形三条中线的交点，内心是三角形内切圆的圆心。

四心公式给出了这四个点的坐标关系。

接下来，我们来看一下四心公式的性质。

首先，外心O是三角形三个顶点的中垂线的交点，即OA⊥BC，OB⊥AC，OC⊥AB。

其次，垂心H是三角形三个顶点的垂线的交点，即AH⊥BC，BH⊥AC，CH⊥AB。

再次，重心G是三角形三个顶点的中线的交点，即AG=2GM，BG=2GN，CG=2GL，其中M、N、L分别是BC、AC、AB的中点。

最后，内心I是三角形三条边的角平分线的交点，即∠BAI=∠CAI，∠ABI=∠CBI，∠BCI=∠ACI。

四心公式的应用非常广泛。

首先，它可以用于计算三角形的各种特征，如面积、周长、角度等。

例如，可以利用四心公式计算三角形的外接圆半径、内切圆半径和面积。

其次，四心公式还可以用于解决一些几何问题，如判断三角形的类型（锐角、直角、钝角）、判断四点是否共面等。

此外，四心公式还有一些拓展应用，如用于求解平面内的最小包围圆、最小包围球等。

在实际应用中，四心公式还可以与其他数学知识相结合，解决更复杂的问题。

例如，可以利用向量运算和线性代数的知识，推导出四心公式的几何解释和向量形式。

同时，四心公式也可以与三角函数、三角恒等式等知识相结合，推导出更深入的结论和定理。

空间向量的四心公式是空间解析几何中的一个重要定理，它描述了一个三角形的四个特殊点。

四心公式具有一些重要的性质和应用，可以用于计算三角形的各种特征和解决几何问题。

在实际应用中，四心公式还可以与其他数学知识相结合，解决更复杂的问题。

因此，掌握四心公式对于深入理解和应用空间解析几何非常重要。

用向量解决三角形“四心”问题外心，内心，重心，垂心是三角形的四个重要几何特征，这里简称为“四心”，而向量是一个具有代数和几何双重身份的数学工具。

因此，掌握有关结论，对于处理有关“心”的问题非常有益。

性质 设O 为ABC ∆所在平面内一点，,BC a CA b AB c ===，则（1）O 为ABC ∆的外心OA OB OC ⇔==；（2）O 为ABC ∆的内心aOA bOB cOC O ⇔++=；（3）O 为ABC ∆的重心OA OB OC O ⇔++=（4）O 为ABC ∆的垂心0OA BC OB CA OC AB ⇔⋅=⋅=⋅=这一组性质的应用在历年高考与竞赛中屡见不鲜，现例举如下： 1． 内心例题1（2003年全国卷）O 是平面上一定点，,,A B C 是平面上不共线的三点，且满足(),[0,)AB AC OP OA AB ACλλ=++∈+∞.则P 点的轨迹一定通过ABC ∆的（ ）.(A) 内心 (B) 外心 (C) 重心 (D) 垂心解析：由已知，(),AB AC AP OP OA AB AC λ=-=+ 而向量,AB ACAB AC λλ构成了菱形的两条邻边，点P 一定在和向量上，即BAC ∠的角平分线上，故选（A ）.2. 重心例题2.（2004年全国高中数学联赛试题）如图1，设O 为ABC ∆内一点，且满足230OA OB OC ++=，则ABC ∆的面积与AOC ∆的面积之比为（ ）.(A) 2 (B)32 (C) 3 (D) 53解析：如图2，延长OB 至1B ，使12OB OB =；延长OC 至1C ，使13OC OC =.则11230OA OB OC OA OB OC ++=++=， 故O 为11AB C ∆的重心.11111111111139112611618AOC AOC AB C AOB AOB AB C BOC B OC AB C S S S S S S S S S ======三式相加，得1113ABCAB C S S = .故应选 (C). 3.垂心例题3.（2003年山东省高中数学竞赛试题）设P 为ABC ∆内任一点，求证：AB 1B1CB CO 图2A BCO 图10AP BC BP CA CP AB ⋅+⋅+⋅=.解析：由欲证结论的特点，不难联想到三角形垂心的向量特征。

向量三角形四心重要推论1. 前言嗨，大家好！今天我们来聊聊一个听起来有点复杂，但其实超级有趣的几何话题——向量三角形的四个“心”。

不如就像拆解一块美味的蛋糕一样，逐步了解这些概念，顺便感受一下其中的奥妙吧！2. 向量三角形的基本概念2.1 向量是什么？首先，向量就是一种有方向和大小的量。

想象一下你从家里走到学校，这一路上的距离和方向就是一个向量。

它不仅告诉你多远，还告诉你去哪儿。

2.2 三角形的心是什么？三角形有四个特别的点，分别是：重心、外心、内心和垂心。

就像是三角形的四个小秘密，每个心都有自己特别的作用。

3. 四个心的详细解析3.1 重心——“重心”在哪儿？重心是三角形的平衡点。

你可以想象把一个三角形的纸板剪下来，然后用手指在重心上支撑，这样它会平衡得最好。

数学上，重心是三角形三个顶点的向量平均值。

就是简单的把三角形的“重心”找出来，让整个三角形“安静”下来。

3.2 外心——谁在三角形的外面呢？外心是三角形外接圆的圆心。

想象你在用一个圆圈把三角形包住，这个圆圈的中心就是外心。

外心的位置让我们知道了三角形的每个顶点都和外心保持相等的距离。

3.3 内心——三角形的“甜蜜点”内心是三角形内切圆的圆心。

你可以想象一下，把一个圆圈放在三角形的内部，这个圆圈刚好触及三角形的三条边。

内心的位置就像是三角形内切圆的“心脏”，它的作用是保持距离最短。

3.4 垂心——让三角形“站立”的点垂心是三角形的三条高线的交点。

高线就是从一个顶点垂直于对边的直线。

垂心就是这三条高线相交的地方。

想象一下一个三角形的三条“支撑柱”相交的地方，这就是垂心。

4. 四心的性质4.1 重心的特殊性重心具有一个非常有趣的性质，那就是不管三角形怎么变形，它的位置总是稳定的。

就像你玩弹珠游戏，重心就是那个弹珠能稳定停下来的地方。

4.2 外心和内心的关系外心和内心的位置关系可以告诉我们很多关于三角形的秘密。

比如，在某些特殊的三角形（如等边三角形），四个心的点实际上重合在一起，真的是特别的“奇妙”！4.3 垂心的奇妙之处垂心的位置会随三角形的形状变化而变化。