三相逆变器的建模
- 格式:doc
- 大小:1.94 MB
- 文档页数:10



三相SP WM 电压型逆变电源仿真建模和特性分析聂恩旺,谢志远,王 燕,郭忠涛(华北电力大学电子与通信工程系,河北保定071003)摘要:为了缩短对大功率电子装置(如逆变电源)的研制周期和减少研制费用,借助计算机仿真技术,利用Matlab 软件中Si m ulink 和Power Syste m B l ochset 建立了以I G BT (绝缘栅双极性晶体管)为开关器件具有数字P I 调压功能的SP WM 电压型逆变电源仿真模型,对其输出特性进行仿真,并利用傅里叶快速变换(FFT )分析工具对其仿真输出电压进行谐波分析。
仿真模型分别考虑了主电路和控制器模型,较为精确地反映了实际情况,验证了此模型和仿真方法的正确性,同样适用于其他电力电子线路。
关键词:电压型逆变电源;快速傅里叶变换;正弦脉宽调制中图分类号:T M91文献标识码:B 文章编号:1005-7641(2006)07-0020-03收稿日期:2006-01-16;修回日期:2006-02-150 引言近年来,随着大功率全控型电力电子器件(如GT O 、I G BT 、MOSFET 、I GCT 等)的开发成功和应用技术的不断成熟,电能变换技术出现了突破性进展,在一些领域中,已经开始应用各种新型逆变电源。
但是由于像逆变电源之类大功率电力电子装置的结构复杂,若直接对装置进行试验,不但经济代价高、且费时费力。
故在对它们的研制过程中,需要借助计算机仿真技术对装置的运行机理与特性、控制方法的有效性进行验证,以预测并解决潜在的问题,同时缩短了研制时间和减少了研制费用[1-3]。
Matlab 软件具有强大的数值计算功能,本文利用Matlab 软件中Si m ulink 和Power Syste m B l och 2set [4]为一个三相电压型SP WM 逆变电源[2]建立系统仿真模型,并对其输出特性进行仿真分析。
1 基本原理三相电压型SP WM 逆变电源系统的原理,如图1所示。


三相离网逆变器状态空间评价模型三相离网逆变器状态空间评价模型是用于评估离网逆变器系统性能和稳定性的数学模型。
它基于状态空间表示,用于描述系统的动态行为。
状态变量(StateVariables):离网逆变器状态空间评价模型中的状态变量可以包括逆变器的电压、电流、功率以及其他相关参数。
假设我们使用n个状态变量来描述离网逆变器的状态,可以将这些状态变量表示为一个n维向量,记为x。
输入变量(InputVariables):输入变量是指影响离网逆变器系统行为的外部输入信号,如太阳能电池板的输出功率、电网电压等。
假设我们使用m个输入变量来描述输入信号,可以将这些输入变量表示为一个m维向量,记为u。
输出变量(OutputVariables):输出变量是指从离网逆变器系统中获取的有用信息,如逆变器的输出电流、电压等。
假设我们使用p个输出变量来描述输出信号,可以将这些输出变量表示为一个p维向量,记为y。
状态空间方程(StateSpaceEquations):状态空间方程描述了离网逆变器系统状态变量随时间的变化规律。
一般形式的状态空间方程可以表示为:dx/dt=f(x,u),其中f是系统的状态方程。
离网逆变器状态空间评价模型中的状态方程可以根据具体系统的特点和设计来确定。
输出方程(OutputEquation):输出方程描述了离网逆变器系统输出变量与状态变量之间的关系。
一般形式的输出方程可以表示为:y=g(x,u),其中g是系统的输出方程。
离网逆变器状态空间评价模型中的输出方程可以根据具体系统的特点和设计来确定。
系统评价(SystemEvaluation):利用离网逆变器状态空间评价模型,可以对系统的性能和稳定性进行评估。
通过模型分析,可以得到系统的状态响应、频率响应、稳定性边界等信息,从而指导系统的设计和优化。

三相电压型半桥逆变器的数学模型研究半桥逆变器是一种常用的电力电子器件,广泛应用于交流驱动、太阳能逆变器和UPS等领域。
本文将围绕“三相电压型半桥逆变器的数学模型研究”展开讨论。
一、半桥逆变器简介半桥逆变器是一种常用的交流逆变器,由两个开关管组成,其中一个接通之后,另一个必须断开。
半桥逆变器可以将直流电源转换为交流电源,是工业控制和家庭电器中不可缺少的电力电子器件。
二、三相电压型半桥逆变器的数学模型1.电路图及符号说明三相电压型半桥逆变器的电路图如下所示:[图片]符号说明:· D1、D2、D3、D4:电势耦合二极管· Q1、Q2、Q3:IGBT管· L、C:滤波器· Ua、Ub、Uc:输出电压· Va、Vb、Vc:输入电压2.分析电路工作原理在控制信号的作用下,Q1、Q2、Q3依次开关,将Va、Vb、Vc的输入电压交替输出,形成三相电压信号。
电势耦合二极管D1、D4用于反响振荡,避免二极管反向势峰对IGBT的损坏。
L、C组成的滤波器则用于平滑输出波形。
3.建模建立三相半桥逆变器的数学模型,主要考虑控制信号、开关器件的状态与电路的等效原理,通过转换寻找电路的电压、电流相互关系。
通过控制信号与开关管的状态判断输出电压方向,即$$ U_{a}=+U_{dc},U_{b}=-U_{dc},U_{c}=0 $$其电压波形如下图所示:[图片]经过简单计算,可得出三相半桥逆变器的输出电流方程如下:$$ \left[\begin{matrix} I_{a}\\ I_{b}\\ I_{c}\end{matrix}\right]=\frac{2}{3}\left[\begin{matrix} I_{dc}\\ -\frac{1}{2}{I_{dc}}\\ -\frac{1}{2}{I_{dc}}\end{matrix}\right]+\frac{1}{3}\left[\begin{matrix} i_{a}\\ i_{b}\\ i_{c} \end{matrix}\right] $$其中,Ia、Ib、Ic为输出电流,Idc为直流侧电流,ia、ib、ic为三相负载电流。
![毕业设计建模教程 [三相电压型PWM逆变电路建模与仿真毕业设计]](https://uimg.taocdn.com/989d612bbb4cf7ec4bfed09b.webp)
毕业设计建模教程[三相电压型PWM逆变电路建模与仿真毕业设计]本科毕业设计题目:三相电压型PWM逆变电路建模与仿真姓名学院信息与电气工程学院专业电气工程及其自动化年级学号指导教师20XX年X月X目录1引言22三相PWM逆变电路的相关理论背景22.1逆变22.2PWM控制的基本原理32.3三相电压型PWM逆变电路控制原理53三相电压型PWM逆变电路模型的建立过程73.1三相电压型PWM逆变电路的建立步骤及相关说明73.1.1建立模型窗口73.1.2建立逆变器主电路模型并设置相关参数73.1.3PWM发生器的模型建立及其设置113.1.4LC滤波器的建立与参数设置123.1.5主回路负载建立及设置153.1.6直流电源设置163.1.7设置相应的测量和输入模块163.1.8对逆变系统各模块进行电气连接174对模型进行仿真设置及调整分析174.1对所搭建好的模型进行仿真174.2对仿真结果的分析及其调整195结束语21参考文献21致谢22三相电压型PWM 逆变电路的建模与仿真摘要:本文在以MATLAB软件中的Simulink为工具的基础上,对三相电压型PWM逆变电路进行了仿真研究。
根据三相电压型PWM逆变电路及MATLAB的相关理论背景,重点对逆变器系统模型的搭建进行详细说明,最后对模型进行了仿真研究。
本文首先详细分析了三相电压型PWM逆变器的电路结构、逆变的工作原理及PWM控制方法;在此基础上利用MATLAB这一仿真工具,对模型系统的每一个具体模块的建立及其相关参数进行了设置,并对主电路的模块进行了单独说明,同时也详细说明了LC滤波模块的设置及其封装;之后进行整体的连接搭建;最后设置仿真参数实现了对三相电压型PWM逆变电路的仿真研究,优化模型性能,获得了完美成果。
关键词:三相电压型PWM逆变器;调制法;MATLAB;仿真Three-phasevoltagetypePWMinvertercircuitmodelingandsimulation Abstract:Inthispaper,basedonSimulinkintheMATLABsoftware tools,three-phasePWMinvertercircuitissimulated.Thetheoreticalbackgr oundofthethree-phasevoltagesourcePWMinvertercircuitandMATLABfocusesont hestructuresoftheinvertersystemmodeldescribedindetail,thefinalmodel,asimulationstudy.Thisarticlefirstdetaileda nalysisofthecircuitstructureofthethree-phasevoltagesourcePWMinverter,theinverterworksandPWMcon trolmethod.Onthisbasis,usingMATLABsimulationtoolforeach specificmoduleofthemodelsystemtoestablishitsrelevantpar ametersset,andthemaincircuitmoduleseparateinstructions, aswellasdetaileddescriptionoftheLCfiltermodulesettingsa ndtheirpackaging.overallconnectionstructures.setthesimu lationparametersforthree-phasevoltagetypePWMinvertercircuitsimulationtooptimizem odelperformance,getperfectresults.Keywords:three-phasePWMinverter;modulationmethod;ofMATLAB;simulation1引言众所周知,当今控制技术高速迅猛发展,随之带来的是对于控制理论和相关电力电子器材及系统模型的性能的高效率、高稳定可靠性的要求。

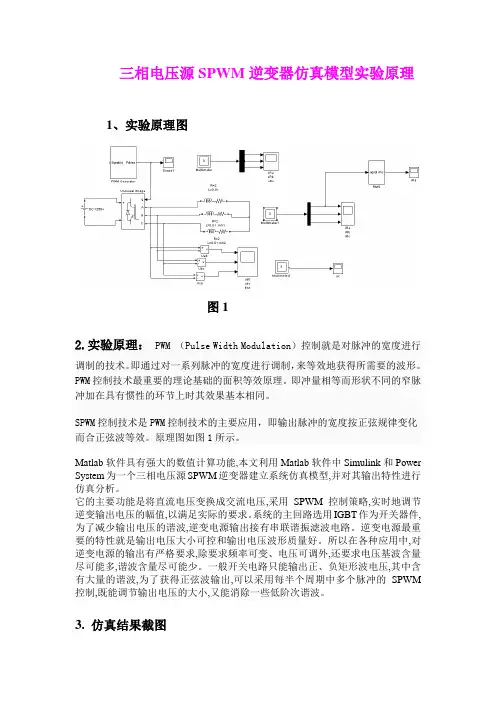
三相电压源SPWM逆变器仿真模型实验原理1、实验原理图图12.实验原理: PWM (Pulse Width Modulation)控制就是对脉冲的宽度进行调制的技术。
即通过对一系列脉冲的宽度进行调制,来等效地获得所需要的波形。
PWM控制技术最重要的理论基础的面积等效原理。
即冲量相等而形状不同的窄脉冲加在具有惯性的环节上时其效果基本相同。
SPWM控制技术是PWM控制技术的主要应用,即输出脉冲的宽度按正弦规律变化而合正弦波等效。
原理图如图1所示。
Matlab软件具有强大的数值计算功能,本文利用Matlab软件中Simulink和Power System为一个三相电压源SPWM逆变器建立系统仿真模型,并对其输出特性进行仿真分析。
它的主要功能是将直流电压变换成交流电压,采用SPWM控制策略,实时地调节逆变输出电压的幅值,以满足实际的要求。
系统的主回路选用IGBT作为开关器件,为了减少输出电压的谐波,逆变电源输出接有串联谐振滤波电路。
逆变电源最重要的特性就是输出电压大小可控和输出电压波形质量好。
所以在各种应用中,对逆变电源的输出有严格要求,除要求频率可变、电压可调外,还要求电压基波含量尽可能多,谐波含量尽可能少。
一般开关电路只能输出正、负矩形波电压,其中含有大量的谐波,为了获得正弦波输出,可以采用每半个周期中多个脉冲的SPWM 控制,既能调节输出电压的大小,又能消除一些低阶次谐波。
3.仿真结果截图(a)(b) 输出交流f=50HZ 调制度m=0时的仿真曲线(a)逆变器输出电压波形(b)逆变器输出电流波形(a)(b) 输出交流f=50HZ 调制度m=0.3时的仿真曲线(a)逆变器输出电压波形(b)逆变器输出电流波形(a)(b)输出交流f=50HZ 调制度m=0.6时的仿真曲线(a)逆变器输出电压波形(b)逆变器输出电流波形(a)(b)输出交流f=50HZ 调制度m=0.9时的仿真曲线(a)逆变器输出电压波形(b)逆变器输出电流波形。

T型三电平逆变器电驱动系统建模方法李敏裕;马晓军;闫之峰;张双喜【摘要】There are more areas in space vector diagram of three-level inverter than two-level inverter. Therefore the control algorithm will be very complex. The modeling method based on Simulink is not conducive for rapidly preparing,modifying and transplanting of control algorithm. A new method based on Simulink and S- function is proposed. The working principle of each module of the electric drive system is analyzed. The model is established by using Simulink or S- function according to the characteristics of different modules of the three-level speed regulating system.Finaly,all modules are connected to simulate.The simulation results verify the accuracy of the proposed modeling method.%与两电平逆变器相比,三电平逆变器空间矢量图分区数量大大增加,因此,控制算法的复杂性也大大增加,基于Simulink的建模方法不利于控制算法的快速编写、修改和移植.提出一种基于Simulink和S- 函数的复合建模方法,分析了三电平电驱动系统各个模块的原理,针对不同模块的特点,采用Simulink或者S- 函数方法建立MATLAB模型,最后将所有模块连接起来进行仿真,仿真结果验证了所提建模方法的准确性.【期刊名称】《火力与指挥控制》【年(卷),期】2017(042)010【总页数】5页(P44-48)【关键词】三电平逆变器;S函数;空间矢量【作者】李敏裕;马晓军;闫之峰;张双喜【作者单位】装甲兵工程学院,北京100072;装甲兵工程学院,北京100072;装甲兵工程学院,北京100072;北方自动控制技术研究所,太原030006【正文语种】中文【中图分类】TM743比起两电平逆变器,三电平逆变器能够有效提高逆变器输出电压等级、提高工作效率、改善输出谐波、降低电磁干扰,因此,具有很大的研究和应用价值[1]。

三相SSPWM 逆变电路的建模及应用仿真一、电路原理1、三相逆变电路原理图1 采用IGBT 作为开关器件的三相桥式电压型逆变电路。
图1 三相PWM 逆变电路当c rU U U >时,给V1导通信号,给V4关断信号,2/`'d UN U U =; 当c rU U U <时,给V4导通信号,给V1关断信号,2/`'d UN U U -=。
当给V1(V4)加导通信号时,可能是V1(V4)导通,也可能是VD1 ( VD4 )导通。
`'UN U 、`'VN U 和`'WN U 的PWM 波形只有2/d U+两种电平。
UV U 波形可由`'UN U 、`'VN U 得出,当1和6通时,UV U =Ud ,当3和4通时,UV U =Ud -,当1和3或4和6通时,UV U =0。
VW U 、WU U 的波形可同理得出。
2、正弦脉冲宽度调制SPWM 原理PWM (Pulse Width Modulation )控制就是对脉冲的宽度进行调制的技术,即通过对一系列脉冲的宽度进行调制,来等效地获得所需要的波形。
PWM 控制技术的重要理论基础是面积等效原理,即:冲量相等而形状不同的窄脉冲加在具有惯性的环节上时,其效果基本相同。
下面分析如何用一系列等幅不等宽的脉冲来代替一个正弦半波。
把正弦半波分成N 等分,就可以把正弦半波看成由N 个彼此相连的脉冲序列所组成的波形。
如果把这些脉冲序列用相同数量的等幅不等宽的矩形脉冲代替,使矩形脉冲的中点和相应正弦波部分的中点重合,且使矩形脉冲和相应的正弦波部分面积(冲量)相等,就可得到图2所示的脉冲序列,这就是PWM 波形。
像这种脉冲的宽度按正弦规律变化而和正弦波等效的PWM 波形,也称为SPWM 波。
如图2所示。
tV t v m ωsin )(1=0tω4θ5θππ21θ2θ3θ7θ8θ9θππ210πtωdV dV -)(t v ab (b))(t v 103π1245109876105π107π109π1θ=2θ=0(a)(b)SPWM 等效电压(a)正弦电压312345图2 SPWM 调制原理SPWM 调制方式根据载波三角波的不同,可以分为单极性和双极性两种,分别称为SSPWM 和BSPWM 。
学号:0121111360719课程设计题目三相逆变器仿真学院自动化学院专业自动化班级自动化1103班姓名黄诚指导教师吴勇2014 年 1 月9 日目录1概述及设计要求 (1)1.1概述 (1)1.2设计要求 (1)2方案比较及认证 (2)2.1升压电路模块方案选择 (2)2.2逆变电路方案选择 (2)2.3闭环反馈电路设计 (2)2.4总体电路方案设计 (2)3系统原理说明 (4)3.1升压斩波电路 (4)3.2三相电压型桥式逆变电路 (4)3.3SPWM逆变器的工作原理 (5)3.4S IMULINK仿真环境 (5)4 仿真建模 (7)4.1升压斩波电路仿真建模 (7)4.2三相桥式PWM逆变电路仿真建模 (8)4.3闭环反馈电路仿真建模 (8)4.4三相逆变电源总体电路仿真建模 (9)5仿真结果 (11)5.1直流升压斩波电路仿真结果 (11)5.2三相桥式PWM逆变电路仿真实现结果 (11)5.3闭环反馈电路仿真实现结果 (12)5.4三相逆变电源总体仿真实现结果 (13)6总结 (15)参考文献 (16)三相逆变器仿真1 概述及设计要求1.1 概述电力电子技术是一门新兴的应用于电力领域的电子技术,就是使用电力电子器件(如晶闸管,GTO,IGBT等)对电能进行变换和控制的技术。
电力电子技术的应用范围十分广泛,它不仅用于一般工业,也广泛用于交通运输、电力系统、通信系统、计算机系统、新能源系统等,在照明、空调等家用电器及其他领域中也有着广泛的应用。
PWM控制技术就是对脉冲的宽度进行调制的技术,即通过对一系列脉冲的宽度进行调制,来等效的获得所需要的波形(含形状和幅值);面积等效原理是PWM技术的重要基础理论。
本文主要通过对逆变电源的Matlab仿真,研究逆变电路的输入输出及其特性,以及一些参数的选择设置方法。
Simulink是MATLAB中的一种可视化仿真工具,是一种基于MATLAB的框图设计环境,是实现动态系统建模、仿真和分析的一个软件包,被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。
三相SPWM逆变器仿真一、原理分析1、基本原理按照输出交流电压半周期内的脉冲数,脉宽调制(PWM)可分为单脉冲调制和多脉冲调制;按照输出电压脉冲宽度变化规律,PWM可分为等脉宽调制和正弦脉宽调制(SPWM)。
等脉宽调制产生的电压波形中谐波含量仍然很高,为了使输出电压波形中基波含量增大,应选用正弦波作为调制信号u R。
这是因为等腰三角形的载波u T上、下宽度线性变化,任何一条光滑曲线与三角波相交时,都会得到一组脉冲宽度正比于该函数值的矩形脉冲。
而且在三角载波u T不变条件下,改变正弦调制波u R的周期就可以改变输出脉冲宽度变化的周期;改变正弦调制波u R的幅值,就可改变输出脉冲的宽度,进而改变u D中基波u D1的大小。
这就是正弦脉宽调制(sine pulse width modulated,SPWM)。
2、正弦脉宽调制方法(此处仅介绍了采样法)SPWM是以获得正弦电压输出为目标的一种脉宽调制方式。
这里就以应用最普遍的三相电压源型逆变电路来讨论SPWM具体实现方法。
下图就是三相电压源型PWM逆变器主电路结构图:图—1上图为一三相电压源型PWM逆变器,VT1~VT6为高频自关断器件,VD1~VD6为与之反并联的快速恢复二极管,为负载感性无功电流提供通路。
两个直流滤波电容C串联接地,中点O’可以认为与三相Y接负载中点O等电位。
逆变器输出A、B、C三相PWM电压波形取决于开关器件VT1~VT6上的驱动信号波行,即PWM的调制方式。
假设逆变电路采用双极性SPWM控制,三相公用一个三角形载波u T,三相正弦调制信号u RA、u RB、u RC互差120o,可用A相来说明功率开关器件的控制规律,正如下图中所示。
当u RA>u T时,在两电压的交点处,给A相上桥臂元件VT1导通信号、下桥臂元件VT4关断信号,则A相与电源中点O’间的电压u AO’=E/2。
当u RA<u T时,在两电压的交点处给VT4导通信号、VT1关断信号,则u AO’=-E/2。
三相逆变器的建模1.1逆变器主电路拓扑与数学模型三相全桥逆变器结构简单,采用器件少,并且容易实现控制,故选择三相三线两电平全桥逆变器作为主电路拓扑,如错误!未找到引用源。
所示。
图1三相三线两电平全桥逆变拓扑错误!未找到引用源。
中V dc为直流输入电压;C dc为直流侧输入电容;Q1-Q6为三个桥臂的开关管;L fj(j=a,b,c)为滤波电感;C fj(j=a,b,c)为滤波电容,三相滤波电容采用星形接法;N为滤波电容中点;L cj(j=a,b,c)是为确保逆变器输出呈感性阻抗而外接的连线电感;v oj(j=a,b,c)为逆变器的滤波电容端电压即输出电压;i Lj(j=a,b,c)为三相滤波电感电流,i oj(j=a,b,c)为逆变器的输出电流。
由分析可知,三相三线全桥逆变器在三相静止坐标系abc下,分析系统的任意状态量如输出电压v oj(j=a,b,c)都需要分别对abc三相的三个交流分量v oa、v ob、v oc进行分析。
但在三相对称系统中,三个交流分量只有两个是相互独立的。
为了减少变量的个数,引用电机控制中的Clark 变换到三相逆变器系统中,可以实现三相静止坐标系到两相静止坐标系的变换,即将abc坐标系下的三个交流分量转变成αβ坐标系下的两个交流分量。
由自动控制原理可以知道,当采用PI 控制器时,对交流量的控制始终是有静差的,但PI控制器对直流量的调节是没有静差的。
为了使逆变器获得无静差调节,引入电机控制中的Park变换,将两相静止坐标系转换成两相旋转坐标系,即将αβ坐标系下的两个交流分量转变成dq坐标系下的两个直流分量。
定义αβ坐标系下的α轴与abc三相静止坐标系下的A轴重合,可以得到Clark变换矩阵为:11122230ClarkT ⎡⎤--⎢⎥⎢=⎢⎢⎣ (1)两相静止坐标系αβ到两相旋转坐标系dq 的变换为Park 变换,矩阵为:cos()sin()sin()cos()Park t t T t t ωωωω⎡⎤=⎢⎥-⎣⎦(2)对三相全桥逆变器而言,设三相静止坐标系下的三个交流分量为:cos()cos(2/3)cos(2/3)a mb mc m u U t u U t u U t ωωπωπ==-=+ (3)经过Clark 和Park 后,可以得到:d m q u U u == (4)由式错误!未找到引用源。
和式错误!未找到引用源。
可以看出,三相对称的交流量经过上述Clark 和Park 变换后可以得到在 d 轴和 q 轴上的直流量,对此直流量进行 PI 控制,可以取得无静差的控制效果。
1.1.1 在abc 静止坐标系下的数学模型首先考虑并网情况下,微电网储能逆变器的模型。
选取滤波电感电流为状态变量,列写方程:000a a a la b f b b lb c c lc c di dt u u i di L u u r i dt u u i di dt ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(5)其中,f L 为滤波电感,r 为滤波电感寄生电阻,系统中三相滤波电感取值相同。
在abc 三相静止坐标系中,三个状态变量有两个变量独立变量,需要对两个个变量进行分析控制,但是其控制量为交流量,所以其控制较复杂。
1.1.2 在αβ两相静止坐标系下的数学模型由于在三相三线对称系统中,三个变量中只有两个变量是完全独立的,可以应用Clark 变换将三相静止坐标系中的变量变换到αβ两相静止坐标系下,如错误!未找到引用源。
所示。
A图 2 Clark 变换矢量图定义αβ坐标系中α轴与abc 坐标系中a 轴重合,根据等幅变换可以得到三相abc 坐标系到两相αβ坐标系的变换矩阵:12121203a b c u u u u u αβ⎡⎤--⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦(6)联立式(5)与式(6),可以得到微电网储能逆变器在αβ坐标系下的数学模型:00f di u u i dt L r u u i di dt ααααββββ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦(7)从式(7)可以看出,与三相静止坐标系下模型相比,减少了一个控制变量,而各变量仍然为交流量,控制器的设计依然比较复杂。
1.1.3 在dq 同步旋转坐标系下的数学模型根据终值定理,PI 控制器无法无静差跟踪正弦给定,所以为了获得正弦量的无静差跟踪,可以通过Clark 和Park 变换转换到dq 坐标系下进行控制。
dq 两相旋转坐标系相对于αβ两相静止坐标系以ω的角速度逆时针旋转,其坐标系间的夹角为θ,错误!未找到引用源。
给出了Park 变换矢量图。
图 3 Park 变换矢量图Park 变换矩阵方程为:cos sin sin cos d q u u t t u u tt αβωωωω⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦(8)联立式(7)和式(8)可得微电网储能逆变器在dq 坐标系下的数学模型:00df d d f q d qf q q f d q di L u u L i ri dtdi L u u L i ri dtωω⎧=-+-⎪⎪⎨⎪=---⎪⎩(9)在两相旋转坐标系下电路中控制变量为直流量,采用PI 控制能消除稳态误差,大大简化了系统控制器的设计。
但是,由于dq 轴变量之间存在耦合量,其控制需要采用解耦控制,解耦控制方法将在下节介绍。
1.1.4 解耦控制从式(9)可以看出,dq 轴之间存在耦合,需要加入解耦控制。
令逆变器电压控制矢量的d 轴和q 轴分量为:d gd q dqgq d q v u Li v v u Li v ωω=+-∆⎧⎪⎨=--∆⎪⎩ (10)其中d v ∆,q v ∆分别是d 轴和q 轴电流环的输出,当电流环采用PI 调节器,满足:**()()()()ii d ip d d ii q ip q q K v K i i sK v K i i s ⎧∆=+-⎪⎪⎨⎪∆=+-⎪⎩(11)ip K ,ii K 分别是电流PI 调节器的比例系数和积分系数,*d i ,*q i 分别为d 轴和q 轴的参考电流,d i ,q i 分别为d 轴和q 轴的实际电流采样。
把公式(10)代入公式(9)可得:dd d q q qdi L ri v dtdi L ri vdt⎧=-+∆⎪⎪⎨⎪=-+∆⎪⎩ (12)由式(12)可以看出,由于在控制矢量中引入了电流反馈,抵消了系统实际模型中的耦合电流量,两轴电流已经实现独立控制。
同时控制中引入电网电压前馈量gd u 和gq u ,提高了系统对电网电压的动态响应。
错误!未找到引用源。
是电流解耦控制框图。
解耦方法为在各轴电流PI 调节器输出中加入其他轴的解耦分量,解耦分量大小与本轴被控对象实际产生的耦合量大小一致,方向相反[1]。
图 4 电流解耦控制图对公式(12)进行拉普拉斯变换,同时把公式(11)代入公式(12)可得:()()()()()()ii d ip d dii q ip q qk Ls r i k i i s k Ls r i k i i s **⎧+=+-⎪⎪⎨⎪+=+-⎪⎩(13)在采用解耦控制之后,d 轴电流和q 轴电流分别控制。
错误!未找到引用源。
给出电流内环的结构框图。
*图 5 电流内环结构框图其中,s T 为电感电流采样周期,ip K 和ii K 对应电流环的PI 参数,1/(10.5)s T s +代表PWM 控制产生的惯性环节[2],1/(1)s T s +代表电流采样的延迟[3]。
PWM K 为调制比,由于本文空间矢量调制(Space Vector Pulse Width Modulation, SVPWM),调制过程中引入了直流电压的前馈环节,所以PWM K 可以表示为:1PWM K =(14)本系统开关频率和器件参数为:1/1/15kHz=66.7us s s T f ==, 1.5mH L =,0.1R =Ω,50uF C =。
由于d 轴和q 轴电流环完全对称,所以本文只分析d 轴电流环的设计过程。
由于合并小惯性环节并不会影响系统低频特性,可以将错误!未找到引用源。
化简,得到错误!未找到引用源。
图 6 d 轴电流环简化结构框图1.2 电压电流双环设计1.2.1 电流环设计由上述分析可知,在环路设计时可以对d 轴电流和q 轴电流分别进行控制[4],从而可以得到如错误!未找到引用源。
所示的电流环控制框图。
图 7 电流环控制框图其中, K ip 和K ii 对应电流环的PI 参数,T s 为电流内环采样周期,1/(1+T s s )和1/(1+分别代替电流环信号采样的延迟和PWM 控制的小惯性延时环节[5]。
本文设计的系统参数如下:L =,R =Ω,C =50μF ,T s =1/f s =1/15k Hz=μs 。
由于d 轴与q 轴的电流环类似,故以d 轴电流环为例进行分析。
补偿前电流环的开环传递函数为:0()(1.51)()PWMc s K G s T s R Ls =++(15)补偿网络的传递函数为:1()ip iiK s K H s s+=(16)直流增益20lg|G c 0(s)|=20dB ;幅频特性的转折频率为100Hz ,设定补偿后的穿越频率为1/10的开关频率,即1500Hz 。
则有:011(21500)(21500)c G j H j ππ⋅=⋅(17)若加入补偿网络后,系统回路的开环增益曲线以-20dB/dec 斜率通过0dB 线,变换器具有较好的相位裕量。
由于补偿前的传递函数在中频段的斜率已经为-20dB/dec ,因此补偿网络在1500Hz 时斜率为零。
将PI 调节器的零点设计在原传递函数的主导极点转折频率处,即100Hz 处。
令:ip iiK LK R= (18)联立式错误!未找到引用源。
及式错误!未找到引用源。
可得电流环的PI 参数:K ip =18,K ii =1200。
实际取值:K ip =10,K ii =1200。
频率/Hz图 8 电流环补偿前后的波特图错误!未找到引用源。
所示为电流环补偿前后的波特图。
可以看出,补偿前电流环的开环传递函数G c 0(s )在低频段的增益为20dB ,并且在100Hz 时穿越0dB 线,相位裕度为75°;加入补偿环节后,电流环的闭环传递函数G il (s )其幅频特性曲线在1000Hz 处以-20dB/dec 斜率通过0dB 线,相位裕度为60°。
补偿之后回路的开环传递函数为:()()(1.51)()PWM ip ii s K K s K G s s T s R Ls +=++ (19)因此,补偿之后电流环的闭环传递函数为:2()(1.51)()()1()() 1.51()11(1.51)()PWM ip ii s il PWM ip ii s ip PWM ip PWMs K K s K s T s R Ls G s G s K K s K LT LG s s s K K K K s T s R Ls +++===+++++++ (20)1.2.2 电压环设计电压外环主要是保证输出电压的稳态精度,动态响应相对较慢。