4.a 讲义 - 圆
- 格式:doc
- 大小:168.50 KB
- 文档页数:6

拓展三:与圆有关的轨迹问题知识点1 5种定义形式的圆1、“定义圆”:在平面内,到定点的距离等于定长的点的集合.数学语言描述为:在平面内,{|}M MA r =,其中M 为动点,A 为定点,0r >为定值.2、“斜率圆”:在平面内,与两定点斜率之积为-1的点的集合(除去定点所在垂直于x 轴的直线与曲线的交点).数学语言描述为∶在平面内,{|1}MA MB M k k ⋅=-,其中M 为动点,A ,B 为定点.且点M 的横坐标不等于A ,B 的横坐标.3、“平方圆”:在平面内,到两定点距离的平方和为定值的点的集合.数学语言描述为:在平面内,22{|}M MA MB λ+=,其中M 为动点,A ,B 为定点,λ为定值.注:若(,).(,)A a b B c d ,则点M 的轨迹方程为22221()()[()()]2224a cb d x y ac bd λ++-+-=--+-,此时221[()()]2a cb d λ>-+-.4、“向量圆”:在平面内,与两定点形成向量的数量积为定值的点的集合.数学语言描述为∶在平面内,{|}M MA MB λ⋅=,其中M 为动点,A ,B 为定点,λ为定值注:若(,).(,)A a b B c d ,则点M 的轨迹方程为22221()()[()()]224a cb d x y ac bd λ++-+-=+-+-,此时221[()()]4a cb d λ>--+-.特别地,若A ,B 为定点,且0MA MB ⋅=,则点M 的轨迹是以AB 为直径的圆拓展:“角度圆”:在平面内,与两定点所成角为定值的点的集合.(角度可用向量的夹角公式表示) 5、“比值圆”(阿波罗尼斯圆):在平面内,到两定点距离之比为定值的点的集合. 数学语言描述为:{|}MAM MBλ=,其中M 为动点,A ,B 为定点,λ为定值,λ>0且λ≠1. 注:当1λ=时,M 的轨迹是线段AB 的垂直平分线. 6、这些圆彼此之间的联系:(1)斜率圆可以看成向量圆的特例,即两向量互相垂直时可以转化为两直线斜率之积等于-1,需要注意斜率不存在的情形.也就是说数量积为零比斜率之积为-1更一般. (2)比值圆与平方圆是一样的,都是用两点间距离公式求解.知识点2 注意“轨迹”与“轨迹方程”的区别1、“轨迹”是图形,“轨迹方程”是方程.2、求轨迹方程后要检验求轨迹方程后一定要注意检验轨迹的纯粹性和完备性,在所得的方程中删去或补上相应的特殊点,以保证方程的解与曲线上的点具有一一对应关系.考点一 直接法求轨迹解题方略:直接法是指将动点满足的几何条件或者等量关系,直接坐标化,列出等式,然后化简而求出动点轨迹方程的一种方法.此法的一般步骤∶建系、设点、列式、化简、限制说明.注:(1)根据已知条件及一些基本公式(两点间距离公式、点到直线的距离公式、直线斜率公式等) (2)根据公式直接列出动点满足的等量关系式,从而得到轨迹方程。

一对一授课教案学员姓名:何锦莹年级:9 所授科目:数学一、圆的定义:1. 描述性定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,其中固定端点O叫做圆心,OA叫做半径.2 圆的表示方法:通常用符号⊙表示圆,定义中以O为圆心,OA为半径的圆记作“O⊙”,读作“圆O”.3 同圆、同心圆、等圆:圆心相同且半径相等的圆叫同圆;圆心相同,半径不相等的两个圆叫做同心圆;能够重合的两个圆叫做等圆.注意:同圆或等圆的半径相等.1. 弦:连结圆上任意两点的线段叫做弦.2. 直径:经过圆心的弦叫做圆的直径,直径等于半径的2倍.3. 弦心距:从圆心到弦的距离叫做弦心距.4. 弧:圆上任意两点间的部分叫做圆弧,简称弧.以A B、为端点的圆弧记作AB,读作弧AB.5. 等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.6. 半圆:圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.7. 优弧、劣弧:大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.1. 圆心角:顶点在圆心的角叫做圆心角.将整个圆分为360等份,每一份的弧对应1︒的圆心角,我们也称这样的弧为1︒的弧.圆心角的度数和它所对的弧的度数相等.2. 圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角.3. 圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧相等.推论2:半圆(或直径)所对的圆周角是直角,90︒的圆周角所对的弦是直径.推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.4. 圆心角、弧、弦、弦心距之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等.板块二:圆的对称性与垂径定理一、圆的对称性1. 圆的轴对称性:圆是轴对称图形,对称轴是经过圆心的任意一条直线.2. 圆的中心对称性:圆是中心对称图形,对称中心是圆心.3. 圆的旋转对称性:圆是旋转对称图形,无论绕圆心旋转多少角度,都能与其自身重合.二、垂径定理1. 垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.2. 推论1:⑴平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;⑵弦的垂直平分线经过圆心,并且平分弦所对的两条弧;⑶平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.3. 推论2:圆的两条平行弦所夹的弧相等.练习题;1.判断:(1)直径是弦,是圆中最长的弦。

圆的方程专题讲义一、知识梳理圆的定义与方程注意:1确定圆的方程主要方法是待定系数法,大致步骤:(1)根据题意,选择标准方程或一般方程.(2)根据条件列出关于a,b,r或D,E,F的方程组.(3)解出a,b,r或D,E,F代入标准方程或一般方程.2.点与圆的位置关系点和圆的位置关系有三种.已知圆的标准方程(x-a)2+(y-b)2=r2,点M(x0,y0)(1)点在圆上:(x0-a)2+(y0-b)2=r2;(2)点在圆外:(x0-a)2+(y0-b)2>r2;(3)点在圆内:(x0-a)2+(y0-b)2<r2.二、基础检测题组一:思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)确定圆的几何要素是圆心与半径.()(2)已知点A(x1,y1),B(x2,y2),则以AB为直径的圆的方程是(x-x1)(x-x2)+(y-y1)(y-y2)=0.()(3)方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是A=C≠0,B=0,D2+E2-4AF>0.( )(4)方程x2+2ax+y2=0一定表示圆.()(5)若点M(x0,y0)在圆x2+y2+Dx+Ey+F=0外,则x20+y20+Dx0+Ey0+F>0.()(6)方程(x+a)2+(y+b)2=t2(t∈R)表示圆心为(a,b),半径为t的圆.()题组二:教材改编2.以点(3,-1)为圆心,并且与直线3x+4y=0相切的圆的方程是()A .(x -3)2+(y +1)2=1B .(x -3)2+(y -1)2=1C .(x +3)2+(y -1)2=1D .(x +3)2+(y +1)2=13.圆C 的圆心在x 轴上,并且过点A (-1,1)和B (1,3),则圆C 的方程为_______.题组三:易错自纠4.若方程x 2+y 2+mx -2y +3=0表示圆,则m 的取值范围是( )A .(-∞,-2)∪(2,+∞)B .(-∞,-22)∪(22,+∞)C .(-∞,-3)∪(3,+∞)D .(-∞,-23)∪(23,+∞)5.若点(1,1)在圆(x -a )2+(y +a )2=4的内部,则实数a 的取值范围是( )A .-1<a <1B .0<a <1C .a >1或a <-1D .a =±46.若圆C 的半径为1,圆心在第一象限,且与直线4x -3y =0和x 轴都相切,则该圆的标准方程是( )A .(x -2)2+(y -1)2=1B .(x -2)2+(y +1)2=1C .(x +2)2+(y -1)2=1D .(x -3)2+(y -1)2=1三、典型例题题型一:圆的方典例 (1)过点A (4,1)的圆C 与直线x -y -1=0相切于点B (2,1),则圆C 的方程为__________.(2)已知圆C 经过P (-2,4),Q (3,-1)两点,且在x 轴上截得的弦长等于6,则圆C 的方程为______________. 思维升华:(1)直接法:直接求出圆心坐标和半径,写出方程.(2)待定系数法①若已知条件与圆心(a ,b )和半径r 有关,则设圆的标准方程,求出a ,b ,r 的值;②选择圆的一般方程,依据已知条件列出关于D ,E ,F 的方程组,进而求出D ,E ,F 的值.跟踪训练 一个圆与y 轴相切,圆心在直线x -3y =0上,且在直线y =x 上截得的弦长为27,则该圆的方程为______________________.题型二:与圆有关的最值问题典例 已知点(x ,y )在圆(x -2)2+(y +3)2=1上,求x +y 的最大值和最小值.引申探究1.在本例的条件下,求y x的最大值和最小值. 2.在本例的条件下,求x 2+y 2+2x -4y +5的最大值和最小值.思维升华:与圆有关的最值问题的常见类型及解题策略(1)与圆有关的长度或距离的最值问题的解法.一般根据长度或距离的几何意义,利用圆的几何性质数形结合求解.(2)与圆上点(x ,y )有关代数式的最值的常见类型及解法.①形如u =y -b x -a型的最值问题,可转化为过点(a ,b )和点(x ,y )的直线的斜率的最值问题;②形如t =ax +by 型的最值问题,可转化为动直线的截距的最值问题;③形如(x -a )2+(y -b )2型的最值问题,可转化为动点到定点(a ,b )的距离的平方的最值问题.跟踪训练:已知点P (x ,y )在圆C :x 2+y 2-6x -6y +14=0上.(1)求y x的最大值和最小值; (2)求x +y 的最大值与最小值.题型三:与圆有关的轨迹问题典例已知圆x 2+y 2=4上一定点A (2,0),B (1,1)为圆内一点,P ,Q 为圆上的动点.(1)求线段AP 中点的轨迹方程;(2)若∠PBQ =90°,求线段PQ 中点的轨迹方程.思维升华:求与圆有关的轨迹问题时,根据题设条件的不同常采用以下方法(1)直接法:直接根据题目提供的条件列出方程.(2)定义法:根据圆、直线等定义列方程.(3)几何法:利用圆的几何性质列方程.(4)代入法:找到要求点与已知点的关系,代入已知点满足的关系式等.跟踪训练 已知Rt △ABC 的斜边为AB ,且A (-1,0),B (3,0).求:(1)直角顶点C 的轨迹方程;(2)直角边BC 的中点M 的轨迹方程.注意:利用几何性质巧设方程求半径典例 在平面直角坐标系xOy 中,曲线y =x 2-6x +1与坐标轴的交点都在圆C 上,求圆C 的方程.四、反馈练习1.已知点A (-4,-5),B (6,-1),则以线段AB 为直径的圆的方程为( )A .(x +1)2+(y -3)2=29B .(x -1)2+(y +3)2=29C .(x +1)2+(y -3)2=116D .(x -1)2+(y +3)2=1162.圆心在y 轴上,且过点(3,1)的圆与x 轴相切,则该圆的方程是( )A .x 2+y 2+10y =0B .x 2+y 2-10y =0C .x 2+y 2+10x =0D .x 2+y 2-10x =0 3.圆(x -2)2+y 2=4关于直线y =33x 对称的圆的方程是( ) A .(x -3)2+(y -1)2=4B .(x -2)2+(y -2)2=4C .x 2+(y -2)2=4D .(x -1)2+(y -3)2=44.若a ∈}431,0,2{ ,则方程x 2+y 2+ax +2ay +2a 2+a -1=0表示的圆的个数为( )A .0B .1C .2D .3 5.圆x 2+y 2-2x -2y +1=0上的点到直线x -y =2的距离的最大值是( )A .1+ 2B .2C.1+22D.2+226.点P(4,-2)与圆x2+y2=4上任一点连线的中点的轨迹方程是()A.(x-2)2+(y+1)2=1 B.(x-2)2+(y+1)2=4C.(x+4)2+(y-2)2=4 D.(x+2)2+(y-1)2=17.已知a∈R,方程a2x2+(a+2)y2+4x+8y+5a=0表示圆,则圆心坐标是________,半径是________.8.若圆C经过坐标原点与点(4,0),且与直线y=1相切,则圆C的方程是__________________.9.已知圆C:x2+y2+kx+2y=-k2,当圆C的面积取最大值时,圆心C的坐标为__________.10.已知点M(1,0)是圆C:x2+y2-4x-2y=0内的一点,那么过点M的最短弦所在直线的方程是__________.11.在平面直角坐标系xOy中,已知圆P在x轴上截得的线段长为22,在y轴上截得的线段长为2 3. (1)求圆心P的轨迹方程;(2)若P点到直线y=x的距离为22,求圆P的方程.12.已知M为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).(1)求|MQ|的最大值和最小值;(2)若M(m,n),求n-3m+2的最大值和最小值.13.已知圆C:(x-3)2+(y-4)2=1,设点P是圆C上的动点.记d=|PB|2+|P A|2,其中A(0,1),B(0,-1),则d的最大值为________.14.已知圆C截y轴所得的弦长为2,圆心C到直线l:x-2y=0的距离为55,且圆C被x轴分成的两段弧长之比为3∶1,则圆C的方程为_________________.。

第3讲圆知识点1 圆周角定理1. 圆的有关概念(1)圆的定义:在一个个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径。
以点O 为圆心的圆记作“⊙O”,读作“圆O”.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴;圆是以圆心为对称中心的中心对称图形.(2)弦:连接圆上任意两点的线段叫做弦.(3)直径:经过圆心的弦叫做直径.(4)半圆:圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.(5)弧、优弧、劣弧圆上任意两点间的部分叫做圆弧,简称弧.弧用符号“⌒”表示,以A,B为端点的弧记作“”,读作“圆弧AB”或“弧AB”.大于半圆的弧叫做优弧(多用三个字母表示);小于半圆的弧叫做劣弧(多用两个字母表示).2. 圆心角、弧、弦的关系(1)定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”.3. 圆周角定理(1)圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.(2)圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.典例剖析例(1)如图,BC是⊙O的直径,A,D是⊙O上的两点,连接AB,AD,BD,若∠ADB=70°,则∠ABC的度数是()A.20°B.70°C.30°D.90°(例(1)图)(例(2)图)(2)如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD=度.跟踪训练1.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于()A.60°B.50°C.40°D.30°(第1题图)(第2题图)(第3题图)2.如图,A、B、C是⊙O上的三个点,若∠AOC=110°,则∠ABC=.3.如图,C、D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=.过关精练1.如图,△ABC是⊙O的内接三角形,若∠ABC=70°,则∠AOC的度数等于()A.140°B.130°C.120°D.110°(第1题图)(第2题图)(第3题图)(第4题图)2.如图,⊙O是△ABC的外接圆,AB是直径.若∠BOC=80°,则∠A等于()A.60°B.50°C.40°D.30°3.如图,AB是⊙O的直径,点C在⊙O上,则∠ACB的度数为()A.30°B.45°C.60°D.90°4.如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为()A.45°B.60°C.75°D.90°5.AB是⊙O的直径,点C在圆上,∠ABC=65°,那么∠OCA的度数是()A.25°B.35°C.15°D.20°(第5题图)(第6题图)(第7题图)(第8题图)6.如图,点A、B、C都在⊙O上,若∠AOC=140°,则∠B的度数是()A.70°B.80°C.110°D.140°7.如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是()A.40°B.50°C.70°D.80°8.如图,AB为⊙O的直径,点C、D在⊙O上,若∠CBA=70°,则∠D的度数是.9.如图,点A,B,C在⊙O上,点C在优弧上,若∠OBA=50°,则∠C的度数为.(第9题图)(第10题图)10.如图,点A、B、C为⊙O上的三个点,∠BOC=2∠AOB,∠BAC=40°,则∠ACB=度.知识点2 垂径定理(1)垂径定理垂直于弦的直径平分这条弦,并且平分所对的两条弧.(2)垂径定理的推论推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧.推论3:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.典例剖析例(1)如图⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为()A.8B.12C.16D.2(例(1)图)(例(2)图)(2)如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为.跟踪训练1.如图,在⊙O中,半径OC与弦AB垂直于点D,且AB=8,OC=5,则CD的长是()A.3B.2.5C.2D.1(第1题图)(第2题图)2.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为.3.已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是cm.1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=()A.8cm B.5cm C.3cm D.2cm(第1题图)(第2题图)(第3题图)2.如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是()A.B.2C.6D.83.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD =20°,则下列说法中正确的是()A.AD=2OB B.CE=EO C.∠OCE=40°D.∠BOC=2∠BAD 4.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是()A.2B.2C.2D.4(第4题图)(第5题图)(第6题图)(第7题图)5.如图,在直径为10cm的⊙O中,BC是弦,半径OA⊥BC于点D,AD=2cm,则BC的长为cm.6.如图所示,在⊙O中,直径CD⊥弦AB,垂足为E,已知AB=6,OE=4,则直径CD=.7.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为.知识点3 切线的性质(1)切线的性质①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.(2)切线性质的运用见切点,连半径,见垂直.例(1)如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD.若∠C=50°,则∠AOD的度数为()A.40°B.50°C.80°D.100°(例(1)图)(例(2)图)(2)如图,△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,AD=2,则线段CD的长是()A.2B.C.D.跟踪训练1.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD.若∠BAC=55°,则∠COD的大小为()A.70°B.60°C.55°D.35°(第1题图)(第2题图)2.如图,已知AB是⊙O的直径,点P在BA的延长线上,PD与⊙O相切于点D,过点B 作PD的垂线交PD的延长线于点C,若⊙O的半径为4,BC=6,则P A的长为()A.4B.2C.3D.2.5过关精练1.如图AB是⊙O的直径,AC是⊙O的切线,A为切点,若∠C=40°,则∠B的度数为()A.60°B.50°C.40°D.30°(第1题图)(第2题图)2.如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为()A.40°B.50°C.60°D.20°3.如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠OCB 的度数为()A.40°B.50°C.65°D.75°(第3题图)(第4题图)(第5题图)4.如图,CB为⊙O的切线,点B为切点,CO的延长线交⊙O于点A,若∠A=25°,则∠C的度数是()A.25°B.30°C.35°D.40°5.如图,AB为⊙O的切线,切点为A,连接AO、BO,BO与⊙O交于点C,延长BO与⊙O 交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为()A.54°B.36°C.32°D.27°6.如图,P是⊙O外一点,P A是⊙O的切线,PO=26cm,P A=24cm,则⊙O的周长为()A.18πcm B.16πcm C.20πcm D.24πcm(第6题图)(第7题图)7.如图,AB是⊙O的直径,P A切⊙O于点A,连结PO并延长交⊙O于点C,连结AC,AB=10,∠P=30°,则AC的长度是()A.B.C.5D.8.如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为()A.1B.2C.D.(第8题图)(第9题图)9.如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙O与AC相切于点D,BD平分∠ABC,AD=OD,AB=12,CD的长是()A.2B.2C.3D.410.如图,在△ABC中,D是边BC上的一点,以AD为直径的⊙O交AC于点E,连接DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为.(第10题图)(第11题图)(第12题图)11.如图,AB是⊙O的切线,点B为切点,若∠A=30°,则∠AOB=.12.如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为.13.如图,P A、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC =.(第13题图)(第14题图)(第15题图)14.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC.若∠A=36°,则∠C=度.15.如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠B=26°,则∠OCA=度.16.如图,C为⊙O外一点,CA与⊙O相切,切点为A,AB为⊙O的直径,连接CB.若⊙O的半径为2,∠ABC=60°,则BC=.(第16题图)(第17题图)17.已知:如图,CD是⊙O的直径,点A在CD的延长线上,AB切⊙O于点B,若∠A=30°,OA=10,则AB=.知识点4 扇形面积的计算(1)圆面积公式:S=πr2(2)扇形:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.(3)扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=πR2或S扇形=lR(其中l为扇形的弧长)(4)求阴影面积常用的方法:①直接用公式法;②和差法;③割补法.(5)求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.例(1)如图,四边形ABCD是矩形,AB=4,AD=2,以点A为圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部分的面积是.(2)如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为(结果保留π).跟踪训练1.如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE长为半径画弧,交BC于点F,则图中阴影部分的面积是()A.B.C.D.(第1题图)(第2题图)(第3题图)2.如图,在Rt△ABC中,∠BCA=90°,∠BAC=30°,BC=2,将Rt△ABC绕A点顺时针旋转90°得到Rt△ADE,则BC扫过的面积为()A.B.(2﹣)πC.πD.π3.如图,半圆的直径AB=6,点C在半圆上,∠BAC=30°,则阴影部分的面积为(结果保留π).1.如图,在矩形ABCD中,AB=4,AD=2,分别以点A、C为圆心,AD、CB为半径画弧,交AB于点E,交CD于点F,则图中阴影部分的面积是()A.4﹣2πB.8﹣C.8﹣2πD.8﹣4π(第1题图)(第2题图)(第3题图)2.如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=,则图中阴影部分的面积是()A.B.C.D.+3.如图,直角三角形ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为()A.2π﹣B.π+C.π+2D.2π﹣24.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是()A.π﹣1B.4﹣πC.D.2(第4题图)(第5题图)(第6题图)(第7题图)5.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA 的长为半径作半圆交AC于点D,则图中阴影部分的面积为()A.﹣B.+C.2﹣πD.4﹣6.如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π)()A.8﹣πB.16﹣2πC.8﹣2πD.8﹣π7.如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为()A.π﹣4B.C.π﹣2D.8.如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为()A.2π﹣4B.4π﹣8C.2π﹣8D.4π﹣4(第8题图)(第8 题图)(第10题图)9.如图,在Rt△ABC中,∠A=30°,BC=2,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是()A.﹣B.﹣C.﹣D.﹣10.如图,在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.(结果保留π)11.如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π).(第11题图)(第12题图)(第13题图)12.如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB 于点E,图中阴影部分的面积是(结果保留π).13.如图,在边长为4的正方形ABCD中,先以点A为圆心,AD的长为半径画弧,再以AB边的中点为圆心,AB长的一半为半径画弧,则两弧之间的阴影部分面积是(结果保留π).14.如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4.以A为圆心,AC长为第 11 页 共 12 页半径作弧,交AB 于点D ,则图中阴影部分的面积是 .(结果保留π)15.如图,在边长为4的正方形ABCD 中,以AB 为直径的半圆与对角线AC 交于点E ,则图中阴影部分的面积为 .(结果保留π)(第14题图) (第15题图)16.如图,一个圆心角为90°的扇形,半径OA =2,那么图中阴影部分的面积为 (结果保留π).(第16题图) (第17题图) (第18题图)17.如图在正方形ABCD 中,点E 是以AB 为直径的半圆与对角线AC 的交点,若圆的半径等于1,则图中阴影部分的面积为 .18.如图,在扇形OAB 中,∠AOB =90°.D ,E 分别是半径OA ,OB 上的点,以OD ,OE 为邻边的▱ODCE 的顶点C 在上.若OD =8,OE =6,则阴影部分图形的面积是 (结果保留π).19.如图,在Rt △ABC 中,∠ACB =90°,AC =BC =2,将Rt △ABC 绕点A 逆时针旋转30°后得到Rt △ADE ,点B 经过的路径为弧BD ,则图中阴影部分的面积为 .(第19题图) (第20题图)20.如图,在矩形ABCD 中,CD =2,以点C 为圆心,CD 长为半径画弧,交AB 边于点E ,且E 为AB 中点,则图中阴影部分的面积为 .21.如图,在▱ABCD 中,AD =2,AB =4,∠A =30°,以点A 为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π).22.如图,在直角三角形ABC中,∠ABC=90°,AC=2,BC=,以点A为圆心,AB.为半径画弧,交AC于点D,则阴影部分的面积是第12 页共12 页。

圆目录圆的定义及相关概念垂经定理及其推论圆周角与圆心角圆心角、弧、弦、弦心距关系定理圆内接四边形会用切线, 能证切线切线长定理三角形的内切圆了解弦切角与圆幂定理(选学)圆与圆的位置关系圆的有关计算一.圆的定义及相关概念【考点速览】考点1:圆的对称性:圆既是轴对称图形又是中心对称图形。
经过圆心的每一条直线都是它的对称轴。
圆心是它的对称中心。
考点2:确定圆的条件;圆心和半径①圆心确定圆的位置,半径确定圆的大小;②不在同一条直线上的三点确定一个圆;考点3:弦:连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
直径是圆中最大的弦。
弦心距:圆心到弦的距离叫做弦心距。
弧:圆上任意两点间的部分叫做弧。
弧分为半圆,优弧、劣弧三种。
(请务必注意区分等弧,等弦,等圆的概念)弓形:弦与它所对应的弧所构成的封闭图形。
弓高:弓形中弦的中点与弧的中点的连线段。
(请务必注意在圆中一条弦将圆分割为两个弓形,对应两个弓高)固定的已经不能再固定的方法:求弦心距,弦长,弓高,半径时通常要做弦心距,并连接圆心和弦的一个端点,得到直角三角形。
如下图:考点4:三角形的外接圆:锐角三角形的外心在 ,直角三角形的外心在 ,钝角三角形的外心在 。
考点5点和圆的位置关系 设圆的半径为r ,点到圆心的距离为d , 则点与圆的位置关系有三种。
①点在圆外⇔d >r ;②点在圆上⇔d=r ;③点在圆内⇔ d <r ;【典型例题】例1 在⊿ABC 中,∠ACB =90°,AC =2,BC =4,CM 是AB 边上的中线,以点C 为圆心,以5为半径作圆,试确定A,B,M 三点分别与⊙C 有怎样的位置关系,并说明你的理由。
例2.已知,如图,CD 是直径,︒=∠84EOD ,AE 交⊙O 于B ,且AB=OC ,求∠A 的度数。
M A B C DOEBC例3 ⊙O 平面内一点P 和⊙O 上一点的距离最小为3cm ,最大为8cm ,则这圆的半径是_________cm 。

同学们我们在初中的时候已经学习了圆的几何性质,今天开始我们从代数坐标系的角度再来学习圆的一些性质.1.圆的要素:在平面直角坐标系中,当圆心位置与半径大小确定后,圆就唯一确定了.因此,确定一个圆的基本要素是圆心与半径,即位置与大小.2.圆的定义:描述一:在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆.描述二:在同一平面内,到定点的距离等于定长的点的集合叫做圆. 如图所示:O 为定点(圆心),P 为动点()r b y a x =-+-⇒22)(根据点到点距离公式我们将上面这个方程平方也就得到了圆的标准方程.3.圆的标准方程: ()().11)0,0(),()0(22222称为单位圆的圆半径单位圆:我们把圆心为,半径圆心>=+==-+-y x r rb a r r b y a x理解:所说的标准方程其实也只是圆方程的一种书写形式,该方程的优势体现在能直观的看出圆心和半径长.其中标准方程的右边必须大于零才能表示圆,如果等于零,方程表示的只是一个点),(b a .现在我们将圆的标准方程括号去掉化简就可以得到圆的一般方程.※圆与方程4.圆的一般方程:24-2204-0222222F E D r ED FE DF Ey Dx y x +=--+=++++),圆心(>圆的判别式:一般方程:.022项,也没有的系数相同且与理解:xy y x ≠图像不存在<③表示点②表示圆>①一般方程:配方⇒+--⇒=+⇒++=+++−−→−=++++04-)2,2(04-04-44-)2()2(022*********2F E D ED FE DF E D FE D E y D xF Ey Dx y x圆的标准方程与一般方程在形式上存在区别,但又可以通过配方将二者相互转化.5.圆的参数方程:(一般用于求最值)()()[)πθθθθθθ2.0(sin cos sin cos 1)()()0(222222∈⎩⎨⎧+=+=⇒⎪⎪⎩⎪⎪⎨⎧=-=-⇒=-+-−−−−−−→−=-+-为参数,圆的参数方程>等号左右两边同除以b r y a r x rb y r a x rb y r a x r r b y a x r圆成立的条件很重要:0422>F E D -+例1:写出以下方程的圆心、半径、参数方程再作出图像,将标准方程化为一般方程,将一般方程化为标准方程.[)()⎩⎨⎧∈+====+-+=-+πθθθ2,02sin cos 1)2,0(0341)2(2222y x r y y x y x ,圆心一般方程:例:064)1(22=+-+y x y x 022)2(22=-++y x y x2)1()2)(3(22=-++y x 31)33()4(22=++y x2)1()1)(5(22=++-y x 0)6(22=++-y y x x例2:的取值范围是表示圆,则方程m m y mx y x 052422=+-++ .例3:写出下列圆的方程.2),1,2()1(半径长是圆心- .1),,0()2(半径长是圆心m -.),,()3(a b a 半径长是圆心- .1,)4(半径长是轴圆心在x.,012)5(轴相切的圆且与上圆心在直线y y x =+-)2,0(),3,2()6(为圆直径的两个端点分别.)4,3(),2,1(),5,0()7(三个点圆的方程求过---C B A.)5,2(),3,2(,032)8(的圆的标准方程且过点上求圆心在---=--B y x类型一:点与圆位置关系()()())(0)()3()(0)()2()(0)()1(),(002020********020********0202202000r d F Ey Dx y x r b y a x r d F Ey Dx y x r b y a x r d F Ey Dx y x r b y a x y x >>或>点在圆外<<或<点在圆内或点在圆上点++++-+-⇒++++-+-⇒==++++=-+-⇒.,011122的取值范围求始终存在公共点与圆:直线例a ay x y x kx y =+++++=例2:一束光线从点)1,1(-A 出发x 轴反射,到达圆1)3()2(:22=-+-y x C 上一点的最短距离是多少?:例3已知圆1)3()2(221=-+-y x C :,圆9)4()3(222=-+-y x C :,N M 、分别是圆21C C 、上的动点,P 是x 轴上的动点,则PN PM +的最小值为?:例4若点),15(a a M +在圆26)1(22=+-y x 的内部,则实数a 的取值范围是?1:图形表示与判断方法关系 相交 相切 相离图 像几 何 法r d <r d =r d >联立方程方程组两个解方程组一个解方程组无解直线与圆交点个数两个公共点一个公共点没有公共点判别式法0>∆0=∆0<∆:例1直线2+=kx y 与圆122=+y x 没有公共点,求k 的取值范围?:例2不论k 为何实数,直线1+=kx y 与圆0422222=--+-+a a ax y x 恒有交点,则实数a 的取值范围是?:例3若圆4)1(22=+-y x 关于直线022=+-+m y x 对称,则实数m 的值为?关系 外离外切相交内切内含图 像几 何 法d 为圆心距21r r d +>21r r d +=2121r r d r r +-<<21r r d -=210r r d -≤<公切线 四条三条两条一条无位置 关系几个结论(1)经过圆()()222r b y a x =-+-上一点),(00y x P 的切线方程为200))(())((r b y b y a x a x =--+--.(掌握)(2)已知圆222r y x =+的切线的斜率为k ,则圆的切线方程为12+±=k r kx y .(了解) (3)切点弦方程:过圆()()222r b y a x =-+-外一点),(00y x P 引圆的两条切线,切点分别为B A 、,则过B A 、的直线方程为200))(())((r b y b y a x a x =--+--(掌握)(4)圆与圆公共弦方程:()0)(00212121222222111221=-+-+-=++++=++++F F y E E x D D F y E x D y x O F y E x D y x O :公共弦,该直线方程为若两圆相交,则有一条:与圆:圆(5)弦长公式ak d r AB ∆⋅+=-=22212 )(为平方项的系数为斜率,其中a k(6)半圆、直线、射线、点29x y -= 0)2(22=-+y y x x ()042222=-++y x x241y x -=- ()04122=-+-+y x y x 22x y --=类型一:切线方程、切点弦方程、公共弦方程1.已知圆1)1(22=+-y x O :,求过点)2,2(P 与圆O 相切的切线方程.2.两圆0111221=++++F y E x D y x C :与0222222=++++F y E x D y x C :相交于A 、B 两点,求它们的公共弦AB 所在直线的方程.3.过圆122=+y x 外一点)3,2(M ,作这个圆的两条切线MA 、MB ,切点分别是A 、B ,求直线AB 的方程。

初中数学竞赛辅导讲义---圆与圆圆与圆的位置关系有外离、外切、相交、内切、内含五种情形,判定两圆的位置关系有如下三种方法:1.通过两圆交点的个数确定;2.通过两圆的半径与圆心距的大小量化确定;3.通过两圆的公切线的条数确定.为了沟通两圆,常常添加与两圆都有联系的一些线段,如公共弦、共切线、连心线,以及两圆公共部分相关的角和线段,这是解圆与圆位置关系问题的常用辅助线.熟悉以下基本图形、基本结论:【例题求解】【例1】如图,⊙O l与半径为4的⊙O2内切于点A,⊙O l经过圆心O2,作⊙O2的直径BC 交⊙O l于点D,EF为过点A的公切线,若O2D=22,那么∠BAF= 度.思路点拨直径、公切线、O2的特殊位置等,隐含丰富的信息,而连O2O l必过A点,先求出∠D O2A的度数.注:(1)两圆相切或相交时,公切线或公共弦是重要的类似于“桥梁”的辅助线,它可以使弦切角与圆周角、圆内接四边形的内角与外角得以沟通.同时,又是生成圆幂定理的重要因素.(2)涉及两圆位置关系的计算题,常作半径、连心线,结合切线性质等构造直角三角形,将分散的条件集中,通过解直角三角形求解.【例2】如图,⊙O l与⊙O2外切于点A,两圆的一条外公切线与⊙O1相切于点B,若AB 与两圆的另一条外公切线平行,则⊙O l 与⊙O2的半径之比为( )A.2:5 B.1:2 C.1:3 D.2:3思路点拨添加辅助线,要探求两半径之间的关系,必须求出∠CO l O2 (或∠DO2O l)的度数,为此需寻求∠CO1B、∠CO1A、∠BO1A的关系.【例3】如图,已知⊙O l与⊙O2相交于A、B两点,P是⊙O l上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O l于点N.(1)过点A作AE∥CN交⊙O l l于点E,求证:PA=PE;(2)连结PN,若PB=4,BC=2,求PN的长.思路点拨(1)连AB,充分运用与圆相关的角,证明∠PAE=∠PEA;(2)PB·PC=PD·PA,探寻PN、PD、PA对应三角形的联系.【例4】如图,两个同心圆的圆心是O,AB是大圆的直径,大圆的弦与小圆相切于点D,连结OD并延长交大圆于点E,连结BE交AC于点F,已知AC=24,大、小两圆半径差为2.(1)求大圆半径长;(2)求线段BF的长;(3)求证:EC与过B、F、C三点的圆相切.思路点拨(1)设大圆半径为R,则小圆半径为R-2,建立R的方程;(2)证明△EBC∽△ECF;(3)过B、F、C三点的圆的圆心O′,必在BF上,连OˊC,证明∠O′CE=90°.注:本例以同心圆为背景,综合了垂径定理、直径所对的圆周角为直角、切线的判定、勾股定理、相似三角形等丰富的知识.作出圆中基本辅助线、运用与圆相关的角是解本例的关键.【例5】 如图,AOB 是半径为1的单位圆的四分之一,半圆O 1的圆心O 1在OA 上,并与弧AB 内切于点A ,半圆O 2的圆心O 2在OB 上,并与弧AB 内切于点B ,半圆O 1与半圆O 2相切,设两半圆的半径之和为x ,面积之和为y . (1)试建立以x 为自变量的函数y 的解析式; (2)求函数y 的最小值.思路点拨 设两圆半径分别为R 、r ,对于(1),)(2122r R y +=π,通过变形把R 2+r 2用“x =R+r ”的代数式表示,作出基本辅助线;对于(2),因x =R+r ,故是在约束条件下求y 的最小值,解题的关键是求出R+r 的取值范围.注:如图,半径分别为r 、R 的⊙O l 、⊙O 2外切于C ,AB ,CM 分别为两圆的公切线,O l O 2与AB 交于P 点,则: (1)AB=2r R ;(2) ∠ACB=∠O l M O 2=90°; (3)PC 2=PA ·PB ; (4)sinP=rR rR +-; (5)设C 到AB 的距离为d ,则dR r 211=+.学力训练1.已知:⊙O l 和⊙O 2交于A 、B 两点,且⊙O l 经过点O 2,若∠AO l B=90°,则∠A O 2B 的度数是 .2.矩形ABCD 中,AB=5,BC=12,如果分别以A 、C 为圆心的两圆相切,点D 在圆C 内,点B 在圆C 外,那么圆A 的半径r 的取值范围 . (2003年上海市中考题)3.如图;⊙O l 、⊙O 2相交于点A 、B ,现给出4个命题:(1)若AC 是⊙O 2的切线且交⊙O l 于点C ,AD 是⊙O l 的切线且交⊙O 2于点D ,则AB 2=BC ·BD ;(2)连结AB 、O l O 2,若O l A=15cm ,O 2A=20cm ,AB=24cm ,则O l O 2=25cm ;(3)若CA 是⊙O l 的直径,DA 是⊙O 2 的一条非直径的弦,且点D 、B 不重合,则C 、B 、D 三点不在同一条直线上,(4)若过点A 作⊙O l 的切线交⊙O 2于点D ,直线DB 交⊙O l 于点C ,直线CA 交⊙O 2于点E ,连结DE ,则DE 2=DB ·DC ,则正确命题的序号是 (写出所有正确命题的序号) .4.如图,半圆O 的直径AB=4,与半圆O 内切的动圆O l 与AB 切于点M ,设⊙O l 的半径为y ,AM 的长为x ,则y 与x 的函数关系是 ,自变量x 的取值范围是 .5.如图,施工工地的水平地面上,有三根外径都是1米的水泥管两两相切摞在一起,则其最高点到地面的距离是( )A .2B .221+C .231+D .231+6.如图,已知⊙O l 、⊙O 2相交于A 、B 两点,且点O l 在⊙O 2上,过A 作⊙O l l 的切线AC交B O l 的延长线于点P ,交⊙O 2于点C ,BP 交⊙O l 于点D ,若PD=1,PA=5,则AC 的长为( )A .5B .52C .52+D .537.如图,⊙O l 和⊙O 2外切于A ,PA 是内公切线,BC 是外公切线,B 、C 是切点①PB=AB ;②∠PBA=∠PAB ;③△PAB ∽△O l AB ;④PB ·PC=O l A ·O 2A . 上述结论,正确结论的个数是( )A .1B .2C .3D .48.两圆的半径分别是和r (R>r),圆心距为d ,若关于x 的方程0)(222=-+-d R rx x 有两个相等的实数根,则两圆的位置关系是( )A.一定内切B.一定外切C.相交D.内切或外切9.如图,⊙O l和⊙O2内切于点P,过点P的直线交⊙O l于点D,交⊙O2于点E,DA与⊙O2相切,切点为C.(1)求证:PC平分∠APD;(2)求证:PD·PA=PC2+AC·DC;(3)若PE=3,PA=6,求PC的长.10.如图,已知⊙O l和⊙O2外切于A,BC是⊙O l和⊙O2的公切线,切点为B、C,连结BA并延长交⊙O l于D,过D点作CB的平行线交⊙O2于E、F,求证:(1)CD是⊙O l的直径;(2)试判断线段BC、BE、BF的大小关系,并证明你的结论.11.如图,已知A是⊙O l、⊙O2的一个交点,点M是O l O2的中点,过点A的直线BC垂直于MA,分别交⊙O l、⊙O2于B、C.(1)求证:AB=AC;(2)若O l A切⊙O2于点A,弦AB、AC的弦心距分别为d l、d2,求证:d l+d2=O1O2;(3)在(2)的条件下,若d l d2=1,设⊙O l、⊙O2的半径分别为R、r,求证:R2+r2= R2r2.12.已知半径分别为1和2的两个圆外切于点P,则点P到两圆外公切线的距离为.13.如图,7根圆形筷子的横截面圆半径为r,则捆扎这7根筷子一周的绳子的长度为.14.如图,⊙O l和⊙O2内切于点P,⊙O2的弦AB经过⊙O l的圆心O l,交⊙O l于C、D,若AC:CD:DB=3:4:2,则⊙O l与⊙O2的直径之比为( )A.2:7 B.2:5 C.2:3 D.1:315.如图,⊙O l与⊙O2相交,P是⊙O l上的一点,过P点作两圆的切线,则切线的条数可能是( )A.1,2 B.1,3 C.1,2,3 D.1,2,3,416.如图,相等两圆交于A、B两点,过B任作一直线交两圆于M、N,过M、N各引所在圆的切线相交于C,则四边形AMCN有下面关系成立( )A.有内切圆无外接圆B有外接圆无内切圆C.既有内切圆,也有外接圆D.以上情况都不对17.已知:如图,⊙O与相交于A,B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P P于点D,E,过点E作EF⊥CE交CB的延长线于F.(1)求证:BC是⊙P的切线;(2)若CD=2,CB=22,求EF的长;(3)若k=PE:CE,是否存在实数k,使△PBD恰好是等边三角形?若存在,求出是的值;若不存在,请说明理由.18.如图,⊙A和⊙B是外离两圆,⊙A的半径长为2,⊙B的半径长为1,AB=4,P为连接两圆圆心的线段AB上的一点,PC切⊙A于点C,PD切⊙B于点D.(1)若PC=PD,求PB的长;(2)试问线段AB上是否存在一点P,使PC2+PD2=4?,如果存在,问这样的P点有几个?并求出PB的值;如果不存在,说明理由;(3)当点F在线段AB上运动到某处,使PC⊥PD时,就有△APC∽△PBD.请问:除上述情况外,当点P在线段AB上运动到何处(说明PB的长为多少,或PC、PD 具有何种关系)时,这两个三角形仍相似;并判断此时直线CP与OB的位置关系,证明你的结论.19.如图,D、E是△ABC边BC上的两点,F是BA延长线上一点,∠DAE=∠CAF.(1)判断△ABD的外接圆与△AEC的外接圆的位置关系,并证明你的结论;(2)若△ABD的外接圆半径是△AEC的外接圆半径的2倍,BC=6,AB=4,求BE的长.20.问题:要将一块直径为2cm的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面.操作:方案一:在图甲中,设计一个使圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求,画示意图) .方案二;在图乙中,设计一个使圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);,探究:(1)求方案一中圆锥底面的半径;(2)求方案二中圆锥底面及圆柱底面的半径;(3)设方案二中半圆圆心为O,圆柱两个底面的圆心为O1、O2,圆锥底面的圆心为O3,试判断以O1、O2、O3、O为顶点的四边形是什么样的特殊四边形,并加以证明.参考答案。

第8讲圆及其基本性质知识定位讲解用时:3分钟A、适用范围:人教版初三,基础偏上B、知识点概述:本讲义主要用于人教版初三新课,本节课我们主要学习圆及其基本性质,重点掌握圆的有关概念,能够对相关概念进行辨析,其次理解与圆有关的性质、定理及其推论,着重学习圆心角与弧、弦的关系以及圆周角定理,能够利用相关定理及推论进行解题,本章是中考重点内容之一,也是历年常考难点知识点之一,希望同学们认真学习,为后面的学习奠定良好的基础。
知识梳理讲解用时:25分钟圆的相关概念(1)圆的定义①在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径,以O点为圆心的圆,记作“①O”,读作“圆O”;①圆可以看做是所有到定点O的距离等于定长r的点的集合.(2)半径:联结圆心和圆上任意一点的线段叫做圆的半径;(3)直径:经过圆心,并与圆两端相交的线段叫做圆的直径;(4)圆心角:以圆心为顶点并且两边都和圆相交的角叫做圆心角;(5)圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角;(6)弧:圆上任意两点之间的部分叫做圆弧,简称弧;(7)半圆:圆的任意一条直径的两个端点将圆分成两条弧,每一条弧都叫做半圆;(8)优弧:大于半圆的弧叫做优弧;课堂精讲精练【例题1】下列说法错误的是()。
A.直径是圆中最长的弦B.长度相等的两条弧是等弧C.面积相等的两个圆是等圆D.半径相等的两个半圆是等弧【答案】B【解析】本题考查了与圆有关的概念,A、直径是圆中最长的弦,所以A选项的说法正确;B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项的说法错误;C、面积相等的两个圆的半径相等,则它们是等圆,所以C选项的说法正确;D、半径相等的两个半圆是等弧,所以D选项的说法正确,故选:B.讲解用时:3分钟解题思路:根据直径的定义对A进行判断;根据等弧的定义对B进行判断;根据等圆的定义对C进行判断;根据半圆和等弧的定义对D进行判断。

圆__________________________________________________________________________________ __________________________________________________________________________________1.掌握与圆有关的概念、圆周角定理;2.掌握圆的有关概念、定理的应用.1.圆的定义:(1)线段OA 绕着它的一个端点O 旋转________,另一个端点A 所形成的封闭曲线,叫做圆.记作⊙O ,读作圆O.点O 叫做圆心,线段OA 叫做半径。
确定一个圆需要两个条件:第一是圆心,第二是半径。
(2)圆是到_______的距离等于_________的点的集合.2.弦和直径:(1)弦:连接圆上任意两点的线段叫做弦.(2)直径:经过圆心的弦叫做直径。
直径等于半径的两倍。
3.弧:(1) 弧:圆上任意两点间的部分叫做圆弧,简称弧,用符号⌒表示,以A,B 为端点的的弧记作AB ⌒,读作弧AB.(2)半圆、优弧、劣弧:圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
大于半圆的弧叫做优弧,优弧大于180º用三个字母表示,如ACB ⌒.小于半圆的弧叫做劣弧,如AB ⌒。
(3)等弧:在同圆或者等圆中能够相互重合的弧是等弧,度数或者长度相等的弧不一定是等弧。
(图一)(图二)4. 同心圆与等圆(1)同心圆:圆心相同,半径不相等的两个圆叫做同心圆。
如图一,半径为r1与半径为r2的⊙O叫做同心圆。
(2)等圆:圆心不同,半径相等的两个圆叫做等圆。
如图二中的⊙O 1与⊙O 2的半径都是r,它们是等圆。
同圆或者等圆的半径相同。
(3)同圆是指同一个圆;等圆、同心圆是指两个及两个以上的圆。
5.与圆有关的角(1)圆心角:顶点在__________的角叫圆心角.圆心角的性质:圆心角的度数等于它所对的_____________.(2)圆周角:顶点在__________,两边都和圆相交的角叫做圆周角.圆周角的性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;_________________,相等的圆周角所对的弧相等.③90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为_______.④如果三角形一边上的中线等于这边的一半,那么这个三角形是____________.⑤圆内接四边形的对角_______;外角等于它的内对角.(3)弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角叫弦切角.弦切角的性质:弦切角等于它夹的弧所对的圆周角.弦切角的度数等于它夹的弧的度数的一半.1.圆的基本概念【例1】下列说法中,不正确的是()A.过圆心的弦是圆的直径B. 等弧的长度一定相等C.周长相等的两个圆是等圆D. 同一条弦所对的两条弧一定是等弧【解析】A.过圆心的弦是圆的直径,说法正确;B. 等弧的长度一定相等,说法正确;C. 周长相等的两个圆是等圆,说法正确;D. 同一条弦所对的两条弧一定是等弧,说法错误,应是在同圆或等圆中,同一条弦所对的两条弧一定是等弧;【答案】D练习1.车轮要做成圆形,实际上就是根据圆的特征()A.同弧所对的圆周角相等B.直径是圆中最大的弦C.圆上各点到圆心的距离相等D.圆是中心对称图形练习2.下列说法:①直径是弦;②弦是直径;③过圆内一点有无数多条弦,这些弦都相等;④直径是圆中最长的弦.其中正确的有()A.1个B.2个C.3个D.4个2.圆周角定理【例2】(2014泉州中考)如图,点A,B,C都在⊙O上,若∠O=40°,则∠C=()A. 20°B. 40°C.50°D.80°【解析】根据圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半,得∠C=∠O=20°。
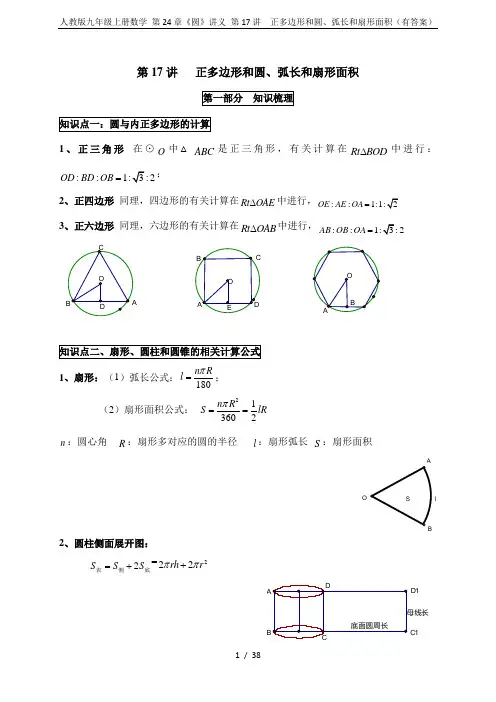
第17讲 正多边形和圆、弧长和扇形面积1、正三角形 在⊙O 中△ABC 是正三角形,有关计算在Rt BOD ∆中进行:::2OD BD OB=;2、正四边形 同理,四边形的有关计算在Rt OAE ∆中进行,::OE AE OA =3、正六边形 同理,六边形的有关计算在Rt OAB ∆中进行,::2AB OB OA =1、扇形:(1)弧长公式:180n Rl π=; (2)扇形面积公式: 213602n R S lR π== n :圆心角 R :扇形多对应的圆的半径l :扇形弧长 S :扇形面积lO2、圆柱侧面展开图:2S S S =+侧表底=222rh r ππ+C 1D 13、圆锥侧面展开图S S S =+侧表底=2Rr r ππ+考点1、正多边形和圆的求解例1、六边形的边长为10cm ,那么它的边心距等于( ) A .10cm B .5cm C .cmD .cm例2A .正三角形 B .正方形 C .正六边形 D .正十二边形例3、如图,在⊙O 内,AB 是内接正六边形的一边,AC 是内接正十边形的一边,BC 是内接正n 边形的一边,那么n= .例4、圆的内接正六边形边长为a ,这个圆的周长为 .例5、如图,已知边长为2cm 的正六边形ABCDEF ,点A 1,B 1,C 1,D 1,E 1,F 1分别为所在各边的中点,求图中阴影部分的总面积S .1、下列命题中的真命题是()A.三角形的内切圆半径和外接圆半径之比为2:1B.正六边形的边长等于其外接圆的半径C.圆外切正方形的边长等于其边A心距的倍D.各边相等的圆外切多边形是正方形2、已知正方形的边长为a,其内切圆的半径为r,外接圆的半径为R,则r:R:a=()A.1:1:B.1::2 C.1::1 D.:2:43、某工人师傅需要把一个半径为6cm的圆形铁片加工截出边长最大的正六边形的铁片,则此正六边形的边长为 cm.4、如图,正六边形与正十二边形内接于同一圆⊙O中,已知外接圆的半径为2,则阴影部分面积为.5、如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).(1)求证:四边形PEQB为平行四边形;(2)填空:①当t= s时,四边形PBQE为菱形;②当t= s时,四边形PBQE为矩形.考点2、弧长的计算例1、一条弧所对的圆心角是90°,半径是R,则这条弧长是()A.B.C.D.例2、一个滑轮起重装置如图所示,滑轮半径是10cm,当重物上升10cm时,滑轮的一条半径OA绕轴心O,绕逆时针方向旋转的角度约为(假设绳索与滑轮之间没有滑动,π取3.14,结果精确到1°)()A.115°B.160°C.57°D.29°例3、已知:如图,四边形ABCD内接于⊙O,若∠BOD=120°,OB=1,则∠BAD= 度,例4、如图,在Rt△ABC中,∠C=90°,∠A=60°,AC=cm,将△ABC绕点B旋转至△A′BC′的位置,且使点A、B、C′三点在一条直线上,则点A经过的最短路线的长度是.例5、如图,菱形ABCD的边长为6,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连接DC′.(1)求证:△ADC≌△ADC′;(2)求在旋转过程中点C扫过路径的长.(结果保留π)1、弧长为6π的弧所对的圆心角为60°,则弧所在的圆的半径为()A.6 B.6C.12D.182、如图,一块边长为10cm的正方形木板ABCD,在水平桌面上绕点D按顺时针方向旋转到A′B′C′D′的位置时,顶点B从开始到结束所经过的路径长为()A.20cm B.20cm C.10πcm D.5πcm3、一段铁路弯道成圆弧形,圆弧的半径是2km.一列火车以每小时28km的速度经过10秒通过弯道.那么弯道所对的圆心角的度数为度.(π取3.14,结果精确到0.1度).4、已知矩形ABCD的长AB=4,宽AD=3,按如图放置在直线AP上,然后不滑动地转动,当它转动一周时(A→A′),顶点A所经过的路线长等于.5、如图,在一个横截面为Rt△ABC的物体中,∠CAB=30°,BC=1米.工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在l上),最后沿BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).(1)请直接写出AB、AC的长;(2)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米).考点3、扇形面积的计算例1、已知五个半径为1的圆的位置如图所示,各圆心的连线构成一个五边形,那么阴影部分的面积是()A.B.2π C.D.3π例2、一个商标图案如图中阴影部分,在长方形ABCD中,AB=8cm,BC=4cm,以点A 为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积是()A.(4π+8)cm2 B.(4π+16)cm2C.(3π+8)cm2 D.(3π+16)cm2例3、如图,E是正方形ABCD内一点,连接EA、EB并将△BAE以B为中心顺时针旋转90°得到△BFC,若BA=4,BE=3,在△BAE旋转到△BCF的过程中AE扫过区域面积.例4、如图,有一直径为1米的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形,则剩下部分的(阴影部分)的面积是.例5、如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.(1)请说出旋转中心及旋转角度;(2)若连接PQ,试判断△PBQ的形状;(3)若∠BPA=135°,试说明点A,P,Q三点在同一直线上;(4)若∠BPA=135°,AP=3,PB=,求正方形的对角线长;(5)在(4)的条件下,求线段AP在旋转过程中所扫过的面积.1、若一个扇形的面积是相应圆的A.150°B.120°C.90°D.60°2、如图所示的4个的半径均为1,那么图中的阴影部分的面积为()A.π+1 B.2π C.4 D.63、如图,O为圆心,半径OA=OB=r,∠AOB=90°,点M在OB上,OM=2MB,用r 的式子表示阴影部分的面积是.4、如图,直角△ABC的直角顶点为C,且AC=5,BC=12,AB=13,将此三角形绕点A 顺时针旋转90°到直角△AB′C′的位置,在旋转过程中,直角△ABC扫过的面积是.(结果中可保留π)5、如图,四边形ABCD是长方形,AB=a,BC=b(a>b),以A为圆心AD长为半径的圆与CD交于D,与AB交于E,若∠CAB=30°,请你用a、b表示图中阴影部分的面积.考点4、圆锥侧面积计算例1、如果圆锥的高为3cm,母线长为5cm,则圆锥的侧面积是()A.16πcm2 B.20πcm2 C.28πcm2 D.36πcm2例2、新疆哈萨克族是一个游牧民族,喜爱居住毡房,毡房的顶部是圆锥形,如图所示,为防雨需要在毡房顶部铺上防雨布.已知圆锥的底面直径是5.7m,母线长是3.2m,铺满毡房顶部至少需要防雨布(精确到1m2)()A.58 m2 B.29 m2 C.26 m2 D.28 m2例3、扇形的圆心角为150°,半径为4cm,用它做一个圆锥,那么这个圆锥的表面积为 cm2.例4、在十年文革期间的“高帽子”.这种“高帽子”是用如图①所示的扇形硬纸板,做成如图②所示的无底圆锥体.已知接缝的重叠部分的圆心角为30°.(1)求重叠部分的面积.(结果保留π)(2)计算这顶“高帽子”有多高?(结果保留根号)例5、已知:一个圆锥的侧面展开图是半径为20cm,圆心角为120°的扇形,求这圆锥的底面圆的半径和高.1、若圆锥的侧面积为12πcm2,它的底面半径为3cm,则此圆锥的母线长为()A.4πcm B.4 cm C.2πcm D.2 cm2、圆锥的轴截面是一个等腰三角形,它的面积是10cm2,底边上的高线是5cm,则圆锥的侧面展开图的弧长等于()A.87πcm B.47πcm C.8 cm D.4 cm3、如图,扇形的半径为6,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得4、如图,有一边长为4的等边三角形纸片,要从中剪出三个面积相等的扇形,那么剪下的其中一个扇形ADE(阴影部分)的面积为;若用剪下的一个扇形围成一个圆锥,该圆锥的底面圆的半径r是.5(1)求图中阴影部分的面积;(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.1、如图,八边形ABCDEFGH中,∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=135°,AB=CD=EF=GH=1cm,BC=DE=FG=HA=cm,则这个八边形的面积等于()A.7cm2 B.8cm2 C.9cm2 D.14cm22、起重机的滑轮装置如图所示,已知滑轮半径是10cm,当物体向上提升3πcm时,滑轮的一条半径OA绕轴心旋转的角度为()A.108°B.60°C.54°D.27°3、如果一个圆锥的轴截面是等边三角形,它的边长为4cm,那么圆锥的全面积是()A.8πcm2 B.10πcm2 C.12πcm2 D.9πcm24、如图,OAB是以6cm为半径的扇形,AC切弧AB于点A交OB的延长线于点C,如果弧AB的长等于3cm,AC=4cm,则图中阴影部分的面积为()A.15cm2 B.6cm2 C.4cm2 D.3cm25、如图,⊙O1,⊙O2,⊙O3,⊙O4,⊙O的半径均为2cm,⊙O与⊙O1,⊙O3相外切,⊙O与⊙O2,⊙O4相外切,并且圆心分别位于两条互相垂直的直线L1,L2上,连接O1,O2,O3,O4得四边形O1O2O3O4,则图中阴影部分的面积为()平方厘米.A.32 B.32-8π C.16-4π D.8π6、如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,则AB的长为.7、将一块三角板和半圆形量角器按图中方式叠放,点A、O在三角板上所对应的刻度分别是8cm、2cm,重叠阴影部分的量角器弧所对的扇形圆心角∠AOB=120°,若用该扇形AOB 围成一个圆锥的侧面(接缝处不重叠),则该圆锥的底面半径为 cm.8、如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.9、如图,在正方形ABCD中有一点P,连接AP、BP,旋转△APB到△CEB的位置.(1)若正方形的边长是8,PB=4.求阴影部分面积;(2)若PB=4,PA=7,∠APB=135°,求PC的长.10、如图,有一直径为1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC (1)找到圆形铁皮的圆心O(要求尺规作图,保留作图痕迹);(2)求剪掉部分即阴影部分的面积(结果保留π);(3)用所留的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?11、如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(-1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O.(1)在旋转过程中,点B所经过的路径长是多少?(2)分别求出点A1,B1的坐标;(3)连接BB1交A1O于点M,求M的坐标.1、阅读下列材料,然后解答问题.经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆,圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形.如图,已知正四边形ABCD的外接圆⊙O,⊙O的面积为S1,正四边形ABCD的面积为S2,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON 分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H.设由OE、OF、及正四边形ABCD的边围成的图形(图中的阴影部分)的面积为S.①(1)当OM经过点A时(如图①),则S、S1、S2之间的关系为:S=______(用含S1、S2的代数式表示);(2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由;(3)当∠MON旋转到任意位置时(如图③),则(1)中的结论仍然成立吗?请说明理由.2、如图中有四个面积相同的圆,每个圆的面积都记为S,∠ABC的两边分别经过圆心O1、O2、O3和O4,四个圆盖的面积为5(S-1),∠ABC内部被圆盖住的面积为8,阴影部分的面积为S1、S2、S3满足关系式:.求S的值.3、铁匠王老五要制作一个圆锥体模型,操作规则是:在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)请你帮助他算一算可以吗?(1)请说明方案一不可行的理由;(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.1、如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是()A.72°B.60°C.54°D.36°2、如图中,正方形的边长都相等,其中阴影部分面积相等的有()A.(1)(2)(3)B.(2)(3)(4)C.(1)(3)(4)D.(1)(2)(3)(4)3、如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C接顺时针方向旋转到A′B′C′的位置.若BC=15cm,那么顶点A从开始到结束所经过的路径长为()A.10πcm B.30πcm C.15πcm D.20πcm4、圆锥的母线长5cm,底面半径长3cm,那么它的侧面展开图的圆心角是()A.180°B.200°C.225°D.216°5、如图,在半径为,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在上,则阴影部分的面积为(结果保留π)()A.B.C.D.6、将一个半径为8cm,面积为32πcm2的扇形铁皮围成一个圆锥形容器(不计接缝),那么这个圆锥形容器的高为()A.4cm B.4cm C.4cm D.2cm7、一元钱的硬币的直径约为24mm,则它完全覆盖住的正三角形的边长最大不能超过 mm(保留根号).8、如图,小明从半径为5cm的圆形纸片中剪下40%圆周的一个扇形,然后利用剩下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为 cm.9、如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm 的圆形,使之恰好围成图210、如图,以AD 为直径的半圆O 经过点E ,B ,点E 、B 是半圆弧的三等分点,弧BE长为 32,则图中阴影部分的面积为 .11、如图,正方形ABCD 的外接圆为⊙O ,点P 在劣弧CD 上(不与点C 重合). (1)求∠BPC 的度数;(2)若⊙O 的半径为4,求正方形ABCD 的边长.12、“五一”节,小雯和同学一起到游乐场玩大型摩天轮,摩天轮的半径为20m ,匀速转动一周需要12min ,小雯所坐最底部的车厢(离地面0.5m ).(1)经过2min 后小雯到达点Q ,如图所示,此时他离地面的高度是多少?(2)在摩天轮滚动的过程中,小雯将有多长时间连续保持在离地面不低于30.5m 的空中?13、如图,一个圆锥的高为3求:(1)圆锥的母线长与底面半径之比;(2)锥角的大小(锥角为过圆锥高的平面上两母线的夹角);(3)圆锥的侧面积.14、如图,已知△ABC,AC=BC=4,O是AB的中点,⊙O分别与AC、BC相切于点M、N,与AB交于E、F,连ME并延长交BD的延长线于D,∠1=∠2.(1)求证:∠C=90°;(2)设图中阴影部分的面积分别为S1、S2,求参考答案第17讲正多边形和圆、弧长和扇形面积考点1、正多边形和圆的求解例1、D例2、B例3、例4、例5、1、B2、B3、4、5、解答(1)证明:∵正六边形ABCDEF内接于⊙O,∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,∴AP=DQ=t,PF=QC=4-t,在△ABP和△DEQ中,∴△ABP≌△DEQ(SAS),∴BP=EQ,同理可证PE=QB,∴四边形PEQB是平行四边形.(2)解:①当PA=PF,QC=QD时,四边形PBEQ是菱形时,此时t=2s.②当t=0时,∠EPF=∠PEF=30°,∴∠BPE=120°-30°=90°,∴此时四边形PBQE是矩形.当t=4时,同法可知∠BPE=90°,此时四边形PBQE是矩形.综上所述,t=0s或4s时,四边形PBQE是矩形.故答案为2s,0s或4s.考点2、弧长的计算例1、C例2、C例3、例4、例5、1、D2、D3、4、5、考点3、扇形面积的计算例1、A例2、A例3、例4、例5、1、C2、C3、4、5、考点4、圆锥侧面积计算例1、B例2、B例3、例4、例5、1、B2、B3、4、5、1、A2、C3、C4、D5、B6、7、8、9、10、11、1、2、3、而制作这样的圆锥实际需要正方形纸片的对角线长为1、A2、C3、D4、D5、A6、B7、8、9、10、11、12、13、14、。
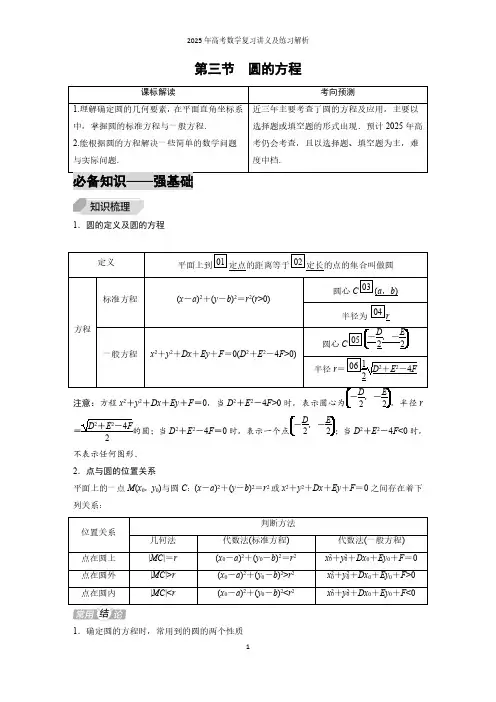
第三节圆的方程1.圆的定义及圆的方程=D 2+E 2-4F2的圆;当D 2+E 2-4F =0时,-D 2,D2+E 2-4F <0时,不表示任何图形.2.点与圆的位置关系平面上的一点M (x 0,y 0)与圆C :(x -a )2+(y -b )2=r 2或x 2+y 2+Dx +Ey +F =0之间存在着下列关系:位置关系判断方法几何法代数法(标准方程)代数法(一般方程)点在圆上|MC |=r (x 0-a )2+(y 0-b )2=r 2x 20+y 20+Dx 0+Ey 0+F =0点在圆外|MC |>r (x 0-a )2+(y 0-b )2>r 2x 20+y 20+Dx 0+Ey 0+F >0点在圆内|MC |<r(x 0-a )2+(y 0-b )2<r 2x 20+y 20+Dx 0+Ey 0+F <01.确定圆的方程时,常用到的圆的两个性质(1)圆心在过切点且与切线垂直的直线上.(2)圆心在任一弦的中垂线上.2.以A(x1,y1),B(x2,y2)为直径端点的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0.1.概念辨析(正确的打“√”,错误的打“×”)(1)圆x2+y2=a2的半径为a.()(2)方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是A=C≠0,B=0,D2+E2-4AF>0.()(3)若点M(x0,y0)在圆x2+y2+Dx+Ey+F=0外,则x20+y20+Dx0+Ey0+F>0.()答案(1)×(2)√(3)√2.小题热身(1)圆x2+y2-4x+6y=0的圆心坐标和半径分别是()A.(2,3),3B.(-2,3),3C.(-2,-3),13D.(2,-3),13答案D解析圆的方程可化为(x-2)2+(y+3)2=13,所以圆心坐标是(2,-3),半径r=13.故选D.(2)(人教A选择性必修第一册2.4.1练习T1改编)圆心为(1,1)且过原点的圆的标准方程是________________.答案(x-1)2+(y-1)2=2解析因为圆心为(1,1)且过原点,所以该圆的半径r=12+12=2,则该圆的标准方程为(x -1)2+(y-1)2=2.(3)(人教A选择性必修第一册复习参考题2T7改编)若圆C:x2+y2-2(m-1)x+2(m-1)y+2m2-6m+4=0过坐标原点,则实数m的值为________.答案2解析∵x2+y2-2(m-1)x+2(m-1)y+2m2-6m+4=0表示圆,∴[-2(m-1)]2+[2(m-1)]2-4(2m2-6m+4)>0,∴m>1.又圆C过原点,∴2m2-6m+4=0,∴m=2或m=1(舍去),∴m=2.(4)(人教A选择性必修第一册复习参考题2T6改编)圆心在直线x+y=0上,且过点(0,2),(-4,0)的圆的标准方程为________________.答案(x+3)2+(y-3)2=10解析点(0,2)与点(-4,0)确定直线的斜率为k=2-00-(-4)=12,其中点为(-2,1),所以线段的中垂线方程为y-1=-2(x+2),即2x+y+3=0,又圆心在直线x+y=0上,由x+y+3=0,+y=0,=-3,=3,所以圆心为(-3,3),r=(-3)2+(3-2)2=10,所以圆的标准方程为(x+3)2+(y-3)2=10.考点探究——提素养考点一求圆的方程例1(1)已知圆的圆心为(-2,1),其一条直径的两个端点恰好在两坐标轴上,则这个圆的一般方程是________________.答案x2+y2+4x-2y=0解析设直径的两个端点分别为A(a,0),B(0,b),圆心C为点(-2,1),由中点坐标公式,得a+02=-2,0+b2=1,解得a=-4,b=2.∴半径r=(-2+4)2+(1-0)2=5,∴圆的方程是(x+2)2+(y-1)2=5,即x2+y2+4x-2y=0.(2)(2024·江苏南京一中月考)已知△ABC的顶点A(0,0),B(0,2),C(-2,2),则其外接圆的标准方程为________________.答案(x+1)2+(y-1)2=2解析设△ABC的外接圆的方程为(x-a)2+(y-b)2=r2,因为△ABC的顶点A(0,0),B(0,2),C(-2,2),2+b2=r2,2+(2-b)2=r2,2-a)2+(2-b)2=r2,=-1,=1,=2,因此(x+1)2+(y-1)2=2即为所求圆的方程.【通性通法】(1)直接法:直接求出圆心坐标和半径,写出方程.(2)待定系数法①若已知条件与圆心(a,b)和半径r有关,则设圆的标准方程,求出a,b,r的值;②若已知条件没有明确给出圆心和半径,则选择圆的一般方程,依据已知条件列出关于D,E,F的方程组,进而求出D,E,F的值.【巩固迁移】1.(2024·河北邯郸模拟)已知三点A(3,2),B(5,-3),C(-1,3),以P(2,-1)为圆心作一个圆,使得A,B,C三点中的一个点在圆内,一个点在圆上,一个点在圆外,则这个圆的标准方程为________________.答案(x-2)2+(y+1)2=13解析由题设知,|PA|=10,|PB|=13,|PC|=5,∴|PA|<|PB|<|PC|,要使A,B,C三点中的一个点在圆内,一个点在圆上,一个点在圆外,则圆以|PB|为半径,故圆的标准方程为(x -2)2+(y+1)2=13.2.已知圆的圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5),则圆的一般方程为________________.答案x2+y2+2x+4y-5=0解析解法一:设所求圆的标准方程为(x-a)2+(y-b)2=r2,由题意,得2-a)2+(-3-b)2=r2,2-a)2+(-5-b)2=r2,-2b-3=0,=-1,=-2,2=10,故所求圆的方程为(x+1)2+(y+2)2=10,即x2+y2+2x+4y-5=0.解法二:线段AB的垂直平分线方程为2x+y+4=0,x+y+4=0,-2y-3=0,解得交点坐标C(-1,-2),又点C到点A的距离d=10,所以所求圆的方程为(x+1)2+(y+2)2=10,即x2+y2+2x+4y-5=0.考点二与圆有关的轨迹问题例2(2024·山东枣庄八中月考)已知Rt△ABC的斜边为AB,且A(-1,0),B(3,0).求:(1)直角顶点C的轨迹方程;(2)直角边BC的中点M的轨迹方程.解(1)解法一:设C(x,y),因为A,B,C三点不共线,所以y≠0.因为AC⊥BC,且直线AC,BC的斜率均存在,所以k AC k BC=-1,又k AC=yx+1,k BC=yx-3,所以yx+1·yx-3=-1,化简,得x2+y2-2x-3=0.因此直角顶点C的轨迹方程为x2+y2-2x-3=0(y≠0).解法二:设AB的中点为D,由中点坐标公式得D(1,0),由直角三角形的性质知|CD|=12|AB|=2.由圆的定义知,动点C的轨迹是以D(1,0)为圆心,2为半径的圆(由于A,B,C三点不共线,所以应除去与x轴的交点).所以直角顶点C的轨迹方程为(x-1)2+y2=4(y≠0).(2)设M (x ,y ),C (x 0,y 0),因为B (3,0),M 是线段BC 的中点,由中点坐标公式,得x =x 0+32,y =y 0+02,所以x 0=2x -3,y 0=2y .由(1),知点C 的轨迹方程为(x -1)2+y 2=4(y ≠0),将x 0=2x -3,y 0=2y 代入,得(2x -4)2+(2y )2=4,即(x -2)2+y 2=1(y ≠0).所以直角边BC 的中点M 的轨迹方程为(x -2)2+y 2=1(y ≠0).【通性通法】求与圆有关的轨迹问题的方法(1)直接法:直接根据题目提供的条件列出方程.(2)定义法:根据圆、直线等定义列方程.(3)几何法:利用圆的几何性质列方程.(4)相关点代入法:找到要求点与已知点的关系,代入已知点满足的关系式求解.【巩固迁移】3.已知两点A (-5,0),B (5,0),动点P 到点A 的距离是它到点B 的距离的3倍,则点P 的轨迹方程为________________.答案x 2+y 2-252x +25=0解析设P (x ,y ),由题意可知|PA |=3|PB |,由两点间距离公式,可得(x +5)2+y 2=3(x -5)2+y 2,化简,得x 2+y 2-252x +25=0.4.(2023·江苏淮安一模)已知点A (2,0)是圆x 2+y 2=4上一点,点B (1,1)是圆内一点,P ,Q 为圆上的动点.(1)求线段AP 的中点M 的轨迹方程;(2)若∠PBQ =90°,求线段PQ 的中点N 的轨迹方程.解(1)设AP 的中点为M (x ,y ),由中点坐标公式可知,点P 的坐标为(2x -2,2y ).因为点P在圆x 2+y 2=4上,所以(2x -2)2+(2y )2=4.故线段AP 的中点M 的轨迹方程为(x -1)2+y 2=1.(2)如图,设PQ 的中点N (x ,y ),在Rt △PBQ 中,|PN |=|BN |,设O 为坐标原点,则ON ⊥PQ ,所以|OP |2=|ON |2+|PN |2=|ON |2+|BN |2,所以x 2+y 2+(x -1)2+(y -1)2=4.故线段PQ 的中点N 的轨迹方程为x 2+y 2-x -y -1=0.考点三与圆有关的最值问题(多考向探究)考向1借助几何性质求最值例3已知M(x,y)为圆C:x2+y2-4x-14y+45=0上任意一点,且点Q(-2,3).(1)求|MQ|的最大值和最小值;(2)求y-3x+2的最大值和最小值;(3)求y-x的最大值和最小值.解(1)由圆C:x2+y2-4x-14y+45=0,可得(x-2)2+(y-7)2=8,所以圆心C的坐标为(2,7),半径r=2 2.又|QC|=(2+2)2+(7-3)2=42,所以|MQ|max=42+22=62,|MQ|min=42-22=22.(2)可知y-3x+2表示直线MQ的斜率k.设直线MQ的方程为y-3=k(x+2),即kx-y+2k+3=0.因为直线MQ与圆C有交点,所以|2k-7+2k+3|k2+1≤22,解得2-3≤k≤2+3,所以y-3x+2的最大值为2+3,最小值为2- 3.(3)设y-x=b,则x-y+b=0.当直线x-y+b=0与圆C相切时,截距b取到最值,所以|2-7+b|12+(-1)2=22,解得b=9或b=1,所以y-x的最大值为9,最小值为1.【通性通法】借助几何性质求最值的常见形式及求解方法(1)形如μ=y -bx -a形式的最值问题,可转化为动直线斜率的最值问题.(2)形如t =ax +by 形式的最值问题,可转化为动直线截距的最值问题.(3)形如(x -a )2+(y -b )2形式的最值问题,可转化为动点到定点的距离的平方的最值问题.【巩固迁移】5.已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为()A .4B .5C .6D .7答案A解析设圆心为C (x ,y ),则(x -3)2+(y -4)2=1,化简得(x -3)2+(y -4)2=1,所以圆心C 的轨迹是以M (3,4)为圆心,1为半径的圆,如图.所以|OC |+1≥|OM |=32+42=5,所以|OC |≥5-1=4,当且仅当C 在线段OM 上时取得等号.故选A.6.已知A (-2,0),B (2,0),点P 是圆C :(x -3)2+(y -7)2=1上的动点,则|AP |2+|BP |2的最大值为()A .40B .46C .48D .58答案D解析设O 为坐标原点,P (x ,y ),则|AP |2+|BP |2=(x +2)2+y 2+(x -2)2+y 2=2(x 2+y 2)+8=2|PO |2+8.圆C 的圆心为C (3,7),半径为r =1,|OC |=4,所以|PO |2的最大值为(|OC |+r )2=(4+1)2=25,所以|AP |2+|BP |2的最大值为58.考向2构建目标函数求最值例4(2023·湘潭质检)设点P (x ,y )是圆x 2+(y -3)2=1上的动点,定点A (2,0),B (-2,0),则PA →·PB →的最大值为________.答案12解析由题意,得PA →=(2-x ,-y ),PB →=(-2-x ,-y ),所以PA →·PB →=x 2+y 2-4,由于点P (x ,y )是圆上的点,故其坐标满足方程x 2+(y -3)2=1,故x 2=-(y -3)2+1,所以PA →·PB →=-(y -3)2+1+y 2-4=6y -12.易知2≤y ≤4,所以当y =4时,PA →·PB →的值最大,最大值为6×4-12=12.【通性通法】建立函数关系式求最值时,首先根据已知条件列出关于所求目标式子的函数关系式,然后根据关系式的特征选用配方法、判别式法、基本不等式法等求最值.【巩固迁移】7.等边三角形ABC 的面积为93,且△ABC 的内心为M ,若平面内的点N 满足|MN |=1,则NA →·NB →的最小值为()A .-5-23B .-5-43C .-6-23D .-6-43答案A解析设等边三角形ABC 的边长为a ,则面积S =34a 2=93,解得a =6.以AB 所在直线为x 轴,AB 的垂直平分线为y 轴建立如图所示的平面直角坐标系.由M 为△ABC 的内心,则M 在OC 上,且|OM |=13|OC |,则A (-3,0),B (3,0),C (0,33),M (0,3),由|MN |=1,则点N 在以M 为圆心,1为半径的圆上.设N (x ,y ),则x 2+(y -3)2=1,即x 2+y 2-23y +2=0,且3-1≤y ≤1+3,又NA →=(-3-x ,-y ),NB →=(3-x ,-y ),所以NA →·NB →=(x +3)(x -3)+y 2=x 2+y 2-9=23y -11≥23×(3-1)-11=-5-2 3.考向3利用对称性求最值例5一束光线,从点A (-2,2)出发,经x 轴反射到圆C :(x -3)2+(y -3)2=1上的最短路径的长度是()A .52-1B .52+1C .32+1D .32-1答案A解析如图,依题意知,圆C 的圆心C (3,3),半径r =1,点A (-2,2)关于x 轴的对称点为A ′(-2,-2),连接A ′C 交x 轴于点O ,交圆C 于点B ,圆外一点与圆上的点的距离的最小值是圆外这点到圆心的距离减去圆的半径,于是得点A ′与圆C 上的点的距离的最小值为|A ′B |=|A ′C |-r =(-2-3)2+(-2-3)2-1=52-1.在x 轴上任取点P ,连接AP ,A ′P ,PC ,PC交圆C于点B′,而|AO|=|A′O|,|AP|=|A′P|,|AO|+|OB|=|A′O|+|OB|=|A′B|=|A′C|-r≤|A′P|+|PC|-r=|AP|+|PB′|,当且仅当点P与点O重合时取“=”,所以最短路径的长度是52-1.故选A.【通性通法】求解形如|PA|+|PB|且与圆C有关的折线段的最值问题的基本思路:(1)“动化定”,把与圆上动点的距离转化为与圆心的距离;(2)“曲化直”,即将折线段之和转化为同一直线上的两线段之和,一般要通过对称性解决.【巩固迁移】8.(2024·浙江金华模拟)已知圆C:x2+(y-2)2=1上一动点A和定点B(6,2),点P为x轴上一动点,则|PA|+|PB|的最小值为________.答案213-1解析根据题意画出圆C:x2+(y-2)2=1,以及点B(6,2)的图象如图,作B关于x轴的对称点B′,连接B′C,则当A,P分别是B′C与圆和x轴的交点时,|PA|+|PB|最小,最小值|AB′|为点C(0,2)到点B′(6,-2)的距离减去圆的半径,即|AB′|=(6-0)2+(-2-2)2-1=213-1.课时作业一、单项选择题1.(2023·甘肃酒泉模拟)已知点(1,1)在圆x2+y2+ax+a=0外,则实数a的取值范围为() A.(-1,+∞)B.(-1,0)C.(-1,0)∪(4,+∞)D.(-∞,0)∪(4,+∞)答案C解析∵点(1,1)在圆x2+y2+ax+a=0外,∴a2-4a>0,且12+12+a+a>0,解得-1<a <0或a>4.∴实数a的取值范围为(-1,0)∪(4,+∞).故选C.2.(2023·重庆九龙坡期中)在平面直角坐标系xOy中,已知P(-2,4),Q(2,6)两点,若圆M 以PQ为直径,则圆M的标准方程为()A.x2+(y+5)2=5B.x2+(y-5)2=5C.x2+(y+5)2=25D.x2+(y-5)2=25答案B解析因为圆M以PQ为直径,所以圆心M的坐标为(0,5),半径为|MQ|=(0-2)2+(5-6)2=5,所以圆M的标准方程为x2+(y-5)2=5.故选B. 3.(2024·河南洛阳阶段考试)方程x2+y2+2x-m=0表示一个圆,则m的取值范围是() A.(-1,+∞)B.(-∞,-1)C.[-1,+∞)D.(-∞,-1]答案A解析由方程x2+y2+2x-m=0,可化为(x+1)2+y2=m+1,要使得方程x2+y2+2x-m=0表示一个圆,则满足m+1>0,解得m>-1,所以m的取值范围为(-1,+∞).故选A. 4.(2024·山东淄博淄川区期末)圆(x+2)2+(y-12)2=4关于直线x-y+6=0对称的圆的方程为()A.(x+6)2+(y+4)2=4B.(x-4)2+(y+6)2=4C.(x-4)2+(y-6)2=4D.(x-6)2+(y-4)2=4答案D解析由圆的方程(x+2)2+(y-12)2=4可得,圆心坐标为(-2,12),半径为2,由题意可得关于直线x-y+6=0对称的圆的圆心为(-2,12)关于直线对称的点,半径为2,设所求圆的圆心为(a,b),-b+122+6=0,1,解得a=6,b=4,故圆的方程为(x-6)2+(y-4)2=4.故选D.5.点A为圆(x-1)2+y2=1上的动点,PA是圆的切线,|PA|=1,则点P的轨迹方程是() A.(x-1)2+y2=4B.(x-1)2+y2=2C.y2=2x D.y2=-2x答案B解析∵|PA |=1,∴点P 和圆心的距离恒为2,又圆心坐标为(1,0),设P (x ,y ),∴由两点间的距离公式,得(x -1)2+y 2=2.故选B.6.已知圆C :(x -3)2+(y -4)2=1和两点A (-m ,0),B (m ,0)(m >0).若圆C 上存在点P ,使得∠APB =90°,则m 的最大值为()A .7B .6C .5D .4答案B解析∵在Rt △APB 中,原点O 为斜边中点,|AB |=2m (m >0),∴|OC |-r ≤m =|OP |≤|OC |+r ,又C (3,4),r =1,∴4≤|OP |≤6,即4≤m ≤6.故选B.7.若点P 为圆x 2+y 2=1上的一个动点,A (-1,0),B (1,0)为两个定点,则|PA |+|PB |的最大值为()A .2B .22C .42D .4答案B解析由已知,得线段AB 为圆的直径.所以|PA |2+|PB |2=4,由基本不等式,得≤|PA |2+|PB |22=2,所以|PA |+|PB |≤22,当且仅当|PA |=|PB |=2时,等号成立.故选B.8.(2023·内蒙古赤峰模拟)已知圆O :x 2+y 2=1,点P (x 0,y 0)是直线l :3x +2y -4=0上的动点,若在圆O 上总存在不同的两点A ,B ,使得直线AB 垂直平分OP ,则y 0的取值范围为()AB ,2413C-1013,D.-1013,答案C解析在圆O 上总存在不同的两点A ,B 使得AB 垂直平分OP .若P 为直线l 与y 轴的交点,得P (0,2),此时圆O 上不存在不同的两点A ,B 满足条件;若P为直线l 与x 轴的交点,得此时直线AB 的方程为x =23,满足条件,y 0=0;当直线AB 的斜率存在且不为0时,∵AB ⊥OP ,k OP =y 0x 0,∴k AB =-x 0y 0,∴直线AB 的方程为y -y 02=-化为2x 0x +2y 0y-x 20-y 20=0,由圆心到直线AB 的距离d =x 20+y 202<1,得x 20+y 20<4,又3x 0+2y 0-4=0,化为13y 20-16y 0-20<0,解得-1013<y 0<2,∴y 0-1013,故选C.二、多项选择题9.已知△ABC 的三个顶点为A (-1,2),B (2,1),C (3,4),则下列关于△ABC 的外接圆圆M 的说法正确的是()A .圆M 的圆心坐标为(1,3)B .圆M 的半径为5C .圆M 关于直线x +y =0对称D .点(2,3)在圆M 内答案ABD解析设△ABC 的外接圆圆M 的方程为x 2+y 2+Dx +Ey +F =0,+4-D +2E +F =0,+1+2D +E +F =0,+16+3D +4E +F =0,=-2,=-6,=5.所以△ABC 的外接圆圆M 的方程为x 2+y 2-2x -6y +5=0,即(x -1)2+(y -3)2=5.故圆M 的圆心坐标为(1,3),圆M 的半径为5,因为直线x +y =0不经过圆M 的圆心(1,3),所以圆M 不关于直线x +y =0对称.因为(2-1)2+(3-3)2=1<5,故点(2,3)在圆M 内.故选ABD.10.设有一组圆C k :(x -k )2+(y -k )2=4(k ∈R ),下列命题正确的是()A .不论k 如何变化,圆心C 始终在一条直线上B .所有圆C k 均不经过点(3,0)C .经过点(2,2)的圆C k 有且只有一个D .所有圆的面积均为4π答案ABD解析圆心C 的坐标为(k ,k ),在直线y =x 上,故A 正确;令(3-k )2+(0-k )2=4,化简,得2k 2-6k +5=0,∵Δ=36-40=-4<0,∴2k 2-6k +5=0无实数根,故B 正确;由(2-k )2+(2-k )2=4,化简,得k 2-4k +2=0,∵Δ=16-8=8>0,有两个不相等实根,∴经过点(2,2)的圆C k 有两个,故C 错误;由圆的半径为2,得圆的面积为4π,故D 正确.故选ABD.三、填空题11.(2024·安徽蚌埠模拟)已知定点A (4,0),P 是圆x 2+y 2=4上的一动点,Q 是AP 的中点,则点Q 的轨迹方程是________.答案(x -2)2+y 2=1解析如图所示,设P (x 0,y 0),Q (x ,y ),则x 20+y 20=4①,因为Q 为AP 的中点,所以x ,y 0=2x -4,0=2y②,所以由①②得,(2x -4)2+(2y )2=4,即(x -2)2+y 2=1,所以点Q 的轨迹方程为(x -2)2+y 2=1.12.(2023·广东湛江三模)已知圆C 过点A (-2,0),B (2,4),当圆心C 到原点O 的距离最小时,圆C 的标准方程为________.答案(x -1)2+(y -1)2=10解析由A (-2,0),B (2,4),可得线段AB 中点的坐标为(0,2),又k AB =4-02-(-2)=1,所以AB 垂直平分线的方程为y =-x +2,则圆心C 在线段AB 的垂直平分线y =-x +2上,当圆心C 到原点O 的距离最小时,则OC 垂直于直线y =-x +2,则OC ∥AB ,所以直线OC的方程为y =x ,=x ,=-x +2=1,=1,所以圆心C (1,1),又半径r 2=|AC |2=(-2-1)2+(0-1)2=10,所以圆C 的标准方程为(x -1)2+(y -1)2=10.13.(2024·福建泉州期中)已知点P (m ,n )在圆C :(x -2)2+(y -2)2=9上运动,则(m +2)2+(n +1)2的最大值为________.答案64解析由题意得,圆心C (2,2),半径r =3.(m +2)2+(n +1)2表示圆C 上的点P 到点M (-2,-1)的距离的平方,因为|CM |=5,所以|PM |max =5+3=8,即(m +2)2+(n +1)2的最大值为64.14.已知A (0,2),点P 在直线x +y +2=0上,点Q 在圆C :x 2+y 2-4x -2y =0上,则|PA |+|PQ |的最小值是________.答案25解析因为圆C :x 2+y 2-4x -2y =0,故圆C 是以C (2,1)为圆心,半径r =5的圆.设点A (0,2)关于直线x +y +2=0的对称点为A ′(m ,n ),+n +22+2=0,1,=-4,=-2,故A ′(-4,-2).由对称性可知|PA |+|PQ |=|A ′P |+|PQ |≥|A ′Q |≥|A ′C |-r =2 5.四、解答题15.(2023·广东佛山期中)已知圆C 过点A (4,0),B (0,4),且圆心C 在直线l :x +y -6=0上.(1)求圆C 的方程;(2)若从点M (4,1)发出的光线经过直线y =-x 反射,反射光线l 1恰好平分圆C 的圆周,求反射光线l 1的一般方程.解(1)由A (4,0),B (0,4),得直线AB 的斜率为k AB =0-44-0=-1,线段AB 的中点D (2,2),所以k CD =1,直线CD 的方程为y -2=x -2,即y =x ,+y -6=0,=x ,=3,=3,即C (3,3),所以半径r =|AC |=(4-3)2+(0-3)2=10,所以圆C 的方程为(x -3)2+(y -3)2=10.(2)由l 1恰好平分圆C 的圆周,得l1经过圆心C (3,3),设点M 关于直线y =-x 的对称点N (x ,y ),则直线MN 与直线y =-x 垂直,且线段MNy =-x 上,则有(-1)=-1,=-x +42,=-1,=-4,所以N (-1,-4),所以直线CN 即为直线l 1,且k l 1=k CN =3-(-4)3-(-1)=74,反射光线l 1的方程为y -3=74(x -3),即7x -4y -9=0.16.在平面直角坐标系xOy 中,曲线Γ:y =x 2-mx +2m (m ∈R )与x 轴交于不同的两点A ,B ,曲线Γ与y 轴交于点C .(1)是否存在以AB 为直径的圆过点C ?若存在,求出该圆的方程;若不存在,请说明理由;(2)求证:过A ,B ,C 三点的圆过定点.解由曲线Γ:y =x 2-mx +2m (m ∈R ),令y =0,得x 2-mx +2m =0.设A (x 1,0),B (x 2,0),由题意可得Δ=m 2-8m >0.则m <0或m >8,x 1+x 2=m ,x 1x 2=2m .令x =0,得y =2m ,即C (0,2m ).(1)若存在以AB 为直径的圆过点C ,则AC →·BC →=0,得x 1x 2+4m 2=0,即2m +4m 2=0,所以m =0(舍去)或m =-12.此时C (0,-1),AB 的中点M -14,,半径r =|CM |=174,+y 2=1716.(2)证明:设过A ,B 两点的圆的方程为x 2+y 2-mx +Ey +2m =0,将点C (0,2m )代入可得E =-1-2m ,所以过A ,B ,C 三点的圆的方程为x 2+y 2-mx -(1+2m )y +2m =0,整理,得x 2+y 2-y -m (x +2y -2)=0.2+y 2-y =0,+2y -2=0,=0,=1=25,=45.故过A ,B ,C 三点的圆过定点(0,1)17.(多选)已知圆C 过点M (1,-2)且与两坐标轴均相切,则下列叙述正确的是()A .满足条件的圆C 的圆心在一条直线上B .满足条件的圆C 有且只有一个C .点(2,-1)在满足条件的圆C 上D .满足条件的圆C 有且只有两个,它们的圆心距为42答案ACD解析因为圆C 和两个坐标轴都相切,且过点M (1,-2),所以设圆心坐标为(a ,-a )(a >0),故圆心在直线y =-x 上,故A 正确;圆C 的方程为(x -a )2+(y +a )2=a 2,把点M 的坐标代入可得a 2-6a +5=0,解得a =1或a =5,则圆心坐标为(1,-1)或(5,-5),所以满足条件的圆C 有且只有两个,故B 错误;圆C 的方程分别为(x -1)2+(y +1)2=1,(x -5)2+(y +5)2=25,将点(2,-1)代入这两个方程可知其在圆C 上,故C 正确;由C 项知,它们的圆心距为(5-1)2+(-5+1)2=42,D 正确.故选ACD.18.(多选)(2023·浙江温州期末)已知圆C :(x -2)2+(y -3)2=1,点M (4,2),点P 在圆C 上,O 为原点,则下列命题正确的是()A .M 在圆上B .线段MP 的长度的最大值为5+1C .当直线MP 与圆C 相切时,|MP |=2D .MO →·MP →的最大值为25+6答案BCD解析将M (4,2)代入圆的方程,(4-2)2+(2-3)2=5>1,所以M 在圆外,A 错误;线段MP的长度的最大值为|MC |+1=(4-2)2+(2-3)2+1=5+1,B 正确;当直线MP 与圆C 相切时,|MC |2=|MP |2+1=[(4-2)2+(2-3)2]2,∴|MP |=2,C 正确;设动点P (x ,y ),点P 的轨迹是圆心为(2,3),半径为1的圆,x =2+cos θ,y =3+sin θ,又M (4,2),所以MO →·MP →=(-4,-2)·(x -4,y -2)=-4(x -4)+(-2)·(y -2)=-4x -2y +20,因为x =2+cos θ,y =3+sin θ,所以MO →·MP →=-4cos θ-2sin θ+6=25sin(θ+φ)+6,θ∈[0,2π),且sin φ=-255,cos φ=-55,则MO →·MP →的最大值为25+6,D 正确.故选BCD.。
九年级上册圆专题讲义知识点一、圆的相关概念1、圆的定义在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径.2、圆的几何表示以点O为圆心的圆记作“⊙O”,读作“圆O”知识点二、弦、弧等与圆有关的定义(1)弦连接圆上任意两点的线段叫做弦.(如图中的AB)(2)直径经过圆心的弦叫做直径(如图中的CD),半径相等,直径等于半径的2倍.(3)弧、优弧、劣弧圆上任意两点间的部分叫做圆弧,简称弧.弧用符号“⌒”表示,以A,B为端点的弧记作“”,读作“圆弧AB”或“弧AB”.大于半圆的弧叫做优弧(多用三个字母表示);小于半圆的弧叫做劣弧(多用两个字母表示). (4)半圆圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆.(5)等圆能够重合的两个圆叫做等圆.(6)等弧在同圆或等圆中,能够互相重合的弧叫做等弧.1知识点三、垂径定理及其推论垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理及其推论可概括为:过圆心垂直于弦平分弦知二推三平分弦所对的优弧平分弦所对的劣弧例1.圆的半径为5cm,圆心到弦AB的距离为4cm,则AB=______cm练习1.如图1,CD为⊙O的直径,AB⊥CD于E,DE=8cm,CE=2cm,则AB=______cm(图1)(图2)(图3)练习2.如图2,⊙O的半径OC为6cm,弦AB垂直平分OC,则AB=______cm,∠AOB=______ 练习3.如图3,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP=______练习4.今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).此问题的实质就是解决下面的问题:“如图,OC是⊙O的半径,弦AB⊥OC于点D,CD=1,AB=10,求直径”23CC 中考链接:(2007昆明,13 ,3分)如图,AB 是⊙O 的弦,OC 是⊙O 的半径,OC ⊥AB 于点D ,AB=16cm ,OD=6cm ,那么⊙O 的半径是________cm(2009昆明,22节选 ,8分)如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 切⊙O 于点D ,过点D 作DF ⊥AB 于点E ,交⊙O 于点F ,已知OE =1cm ,DF =4cm .求⊙O 的半径知识点四、圆的对称性1、圆的轴对称性圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.2、圆的中心对称性圆是以圆心为对称中心的中心对称图形.知识点五、弧、弦、弦心距、圆心角之间的关系定理1、圆心角顶点在圆心的角叫做圆心角.2、弦心距从圆心到弦的距离叫做弦心距.3、弧、弦、弦心距、圆心角之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦想等,所对的弦的弦心距相等.推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.知识点六、圆周角定理及其推论1、圆周角顶点在圆上,并且两边都和圆相交的角叫做圆周角.2、圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等。
第3节圆的方程考试要求掌握确定圆的几何要素,掌握圆的标准方程与一般方程.1.圆的定义和圆的方程定义平面内到定点的距离等于定长的点的轨迹叫做圆方程标准(x-a)2+(y-b)2=r2(r>0)圆心C(a,b)半径为r一般x2+y2+Dx+Ey+F=0(D2+E2-4F>0)充要条件:D2+E2-4F>0圆心坐标:⎝⎛⎭⎪⎫-D2,-E2半径r=12D2+E2-4F2.点与圆的位置关系平面上的一点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2之间存在着下列关系:(1)|MC|>r⇔M在圆外,即(x0-a)2+(y0-b)2>r2⇔M在圆外;(2)|MC|=r⇔M在圆上,即(x0-a)2+(y0-b)2=r2⇔M在圆上;(3)|MC|<r⇔M在圆内,即(x0-a)2+(y0-b)2<r2⇔M在圆内.1.圆心在坐标原点,半径为r的圆的方程为x2+y2=r2.2.以A(x1,y1),B(x2,y2)为直径端点的圆的方程为(x-x1)·(x-x2)+(y-y1)(y-y2)=0.1.思考辨析(在括号内打“√”或“×”)(1)确定圆的几何要素是圆心与半径.()(2)方程x 2+y 2=a 2表示半径为a 的圆.( )(3)方程Ax 2+Bxy +Cy 2+Dx +Ey +F =0表示圆的充要条件是A =C ≠0,B =0,D 2+E 2-4AF >0.( )(4)若点M (x 0,y 0)在圆x 2+y 2+Dx +Ey +F =0外,则x 20+y 20+Dx 0+Ey 0+F >0.( )答案 (1)√ (2)× (3)√ (4)√解析 (2)当a =0时,x 2+y 2=a 2表示点(0,0);当a <0时,表示半径为|a |的圆. 2.圆x 2+y 2-4x +6y =0的圆心坐标和半径分别是( ) A.(2,3),3 B.(-2,3), 3 C.(-2,-3),13 D.(2,-3),13 答案 D解析 圆的方程可化为(x -2)2+(y +3)2=13,所以圆心坐标是(2,-3),半径r =13.3.(2021·合肥模拟)已知A (1,0),B (0,3)两点,则以AB 为直径的圆的方程是( ) A.⎝ ⎛⎭⎪⎫x -12 2+⎝ ⎛⎭⎪⎫y -322=104 B.⎝ ⎛⎭⎪⎫x +12 2+⎝ ⎛⎭⎪⎫y +322=104 C.⎝ ⎛⎭⎪⎫x +12 2+⎝ ⎛⎭⎪⎫y -322=104 D.⎝ ⎛⎭⎪⎫x -12 2+⎝ ⎛⎭⎪⎫y +322=104 答案 A 解析 |AB |=12+32=10,圆心为⎝ ⎛⎭⎪⎫12,32,半径r =102,∴圆的方程为⎝ ⎛⎭⎪⎫x -122+⎝ ⎛⎭⎪⎫y -322=104.4.(2022·银川模拟)若点(1,1)在圆(x -a )2+(y +a )2=4的内部,则实数a 的取值范围是( )A.(-1,1)B.(0,1)C.(-∞,-1)∪(1,+∞)D.{-4,4}答案 A解析因为点(1,1)在圆(x-a)2+(y+a)2=4的内部,所以表示点(1,1)到圆心(a,-a)的距离小于2,即(1-a)2+[1-(-a)]2<2,两边平方得:(1-a)2+(a+1)2<4,化简得a2<1,解得-1<a<1.5.(2020·北京卷)已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为()A.4B.5C.6D.7答案 A解析由平面几何知识知,当且仅当原点、圆心、点(3,4)共线时,圆心到原点的距离最小且最小值为d min=(3-0)2+(4-0)2-1=4.6.(易错题)若方程x2+y2+λxy+2kx+4y+5k+λ=0表示圆,则k的取值范围为________________.答案(-∞,1)∪(4,+∞)解析根据题意,若方程x2+y2+λxy+2kx+4y+5k+λ=0表示圆,则λ=0,方程为x2+y2+2kx+4y+5k=0,∴(2k)2+42-4×5k>0,即k2-5k+4>0,解得k<1或k>4,故k的取值范围为(-∞,1)∪(4,+∞).考点一圆的方程1.已知圆E 经过三点A (0,1),B (2,0),C (0,-1),则圆E 的标准方程为( ) A.⎝ ⎛⎭⎪⎫x -322+y 2=254 B.⎝ ⎛⎭⎪⎫x +342+y 2=2516 C.⎝ ⎛⎭⎪⎫x -342+y 2=2516 D.⎝ ⎛⎭⎪⎫x -342+y 2=254 答案 C解析 法一 (待定系数法)设圆E 的一般方程为x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0),则由题意得 ⎩⎪⎨⎪⎧1+E +F =0,4+2D +F =0,1-E +F =0,解得⎩⎪⎨⎪⎧D =-32,E =0,F =-1.所以圆E 的一般方程为x 2+y 2-32x -1=0,即⎝ ⎛⎭⎪⎫x -342+y 2=2516.法二 (几何法)因为圆E 经过点A (0,1),B (2,0),所以圆E 的圆心在线段AB 的垂直平分线y -12=2(x -1)上.又圆E 的圆心在x 轴的正半轴上, 所以圆E 的圆心坐标为⎝ ⎛⎭⎪⎫34,0.则圆E 的半径为 |EB |=⎝ ⎛⎭⎪⎫2-342+(0-0)2=54,所以圆E 的标准方程为⎝ ⎛⎭⎪⎫x -342+y 2=2516.2.在平面直角坐标系xOy 中,以点(0,1)为圆心且与直线x -by +2b +1=0相切的所有圆中,半径最大的圆的标准方程为( ) A.x 2+(y -1)2=4 B.x 2+(y -1)2=2 C.x 2+(y -1)2=8 D.x 2+(y -1)2=16答案 B解析 由直线x -by +2b +1=0可得该直线过定点A (-1,2),设圆心(0,1)为点B ,由题意可知要使所求圆的半径最大,则r max =|AB |=(-1-0)2+(2-1)2=2,所以半径最大的圆的标准方程为x 2+(y -1)2=2.3.已知圆C 的圆心在直线x +y =0上,圆C 与直线x -y =0相切,且截直线x -y -3=0所得的弦长为6,则圆C 的方程为________. 答案 (x -1)2+(y +1)2=2解析 法一 ∵所求圆的圆心在直线x +y =0上, ∴可设所求圆的圆心为(a ,-a ). ∵所求圆与直线x -y =0相切, ∴半径r =2|a |2=2|a |. 又所求圆截直线x -y -3=0所得的弦长为6,圆心(a ,-a )到直线x -y -3=0的距离d =|2a -3|2,∴d 2+⎝ ⎛⎭⎪⎫622=r 2,即(2a -3)22+32=2a 2,解得a =1,∴圆C 的方程为(x -1)2+(y +1)2=2.法二 设所求圆的方程为(x -a )2+(y -b )2=r 2(r >0), 则圆心(a ,b )到直线x -y -3=0的距离d =|a -b -3|2,∴r 2=(a -b -3)22+32,即2r 2=(a -b -3)2+3.① ∵所求圆与直线x -y =0相切, ∴|a -b |12+(-1)2=r .②又∵圆心在直线x +y =0上,∴a +b =0.③ 联立①②③,解得⎩⎪⎨⎪⎧a =1,b =-1,r =2,故圆C 的方程为(x -1)2+(y +1)2=2.感悟提升 求圆的方程时,应根据条件选用合适的圆的方程.一般来说,求圆的方程有两种方法:(1)几何法,通过研究圆的性质进而求出圆的基本量.确定圆的方程时,常用到的圆的三个性质:①圆心在过切点且垂直切线的直线上;②圆心在任一弦的中垂线上;③两圆内切或外切时,切点与两圆圆心三点共线; (2)代数法,即设出圆的方程,用待定系数法求解. 考点二 与圆有关的最值问题 角度1 利用几何意义求最值例1 已知实数x ,y 满足方程x 2+y 2-4x +1=0. (1)求yx 的最大值和最小值; (2)求y -x 的最大值和最小值; (3)求x 2+y 2的最大值和最小值.解 原方程可化为(x -2)2+y 2=3,表示以(2,0)为圆心,3为半径的圆. (1)y x 的几何意义是圆上一点与原点连线的斜率,所以设yx =k ,即y =kx . 当直线y =kx 与圆相切时,斜率k 取最大值或最小值,此时|2k -0|k 2+1=3,解得k=±3(如图1).所以yx的最大值为3,最小值为- 3.(2)y-x可看作是直线y=x+b在y轴上的截距,当直线y=x+b与圆相切时,纵截距b取得最大值或最小值,此时|2-0+b|2=3,解得b=-2±6(如图2).所以y-x的最大值为-2+6,最小值为-2- 6.(3)x2+y2表示圆上的一点与原点距离的平方,由平面几何知识知,在原点和圆心连线与圆的两个交点处取得最大值和最小值(如图3).又圆心到原点的距离为(2-0)2+(0-0)2=2,所以x2+y2的最大值是(2+3)2=7+43,x2+y2的最小值是(2-3)2=7-4 3. 感悟提升把有关式子进行转化或利用所给式子的几何意义解题,充分体现了数形结合以及转化的数学思想,其中以下几类转化较为常见:(1)形如m=y-bx-a的最值问题,可转化为动直线斜率的最值问题;(2)形如m=ax+by的最值问题,可转化为动直线截距的最值问题;(3)形如m=(x-a)2+(y-b)2的最值问题,可转化为两点间距离的平方的最值问题. 角度2利用对称性求最值例2 已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.52-4B.17-1C.6-2 2D.17答案 A解析 P 是x 轴上任意一点,则|PM |的最小值为|PC 1|-1,同理|PN |的最小值为|PC 2|-3,则|PM |+|PN |的最小值为|PC 1|+|PC 2|-4.作C 1关于x 轴的对称点C ′1(2,-3).所以|PC 1|+|PC 2|=|PC 1′|+|PC 2|≥|C 1′C 2|=52,即|PM |+|PN |=|PC 1|+|PC 2|-4≥52-4.感悟提升 求解形如|PM |+|PN |(其中M ,N 均为动点)且与圆C 有关的折线段的最值问题的基本思路:(1)“动化定”,把与圆上动点的距离转化为与圆心的距离;(2)“曲化直”,即将折线段之和转化为同一直线上的两线段之和,一般要通过对称性解决.角度3 建立函数关系求最值例3 (2022·衡水模拟)设点P (x ,y )是圆:x 2+(y -3)2=1上的动点,定点A (2,0),B (-2,0),则P A →·PB →的最大值为________. 答案 12解析 由题意,知P A →=(2-x ,-y ),PB →=(-2-x ,-y ),所以P A →·PB →=x 2+y 2-4,由于点P (x ,y )是圆上的点,故其坐标满足方程x 2+(y -3)2=1,故x 2=-(y -3)2+1,所以P A →·PB →=-(y -3)2+1+y 2-4=6y -12.由圆的方程x 2+(y -3)2=1,易知2≤y ≤4,所以,当y =4时,P A →·PB →的值最大,最大值为6×4-12=12. 感悟提升 根据题中条件列出相关的函数关系式,再根据函数知识或基本不等式求最值.训练1 已知M (x ,y )为圆C :x 2+y 2-4x -14y +45=0上任意一点,且点Q (-2,3).(1)求|MQ|的最大值和最小值;(2)求y-3x+2的最大值和最小值.解(1)由圆C:x2+y2-4x-14y+45=0,可得(x-2)2+(y-7)2=8,∴圆心C的坐标为(2,7),半径r=2 2. 又|QC|=(2+2)2+(7-3)2=42,∴|MQ|max=42+22=62,|MQ|min=42-22=2 2.(2)可知y-3x+2表示直线MQ的斜率k,设直线MQ的方程为y-3=k(x+2),即kx-y+2k+3=0.∵直线MQ与圆C有交点,∴|2k-7+2k+3|1+k2≤22,可得2-3≤k≤2+3,∴y-3x+2的最大值为2+3,最小值为2- 3. 考点三与圆有关的轨迹问题例4 已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.(1)求线段AP中点的轨迹方程;(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.解(1)设AP的中点为M(x,y),由中点坐标公式可知,P点坐标为(2x-2,2y).因为P 点在圆x 2+y 2=4上, 所以(2x -2)2+(2y )2=4.故线段AP 中点的轨迹方程为(x -1)2+y 2=1(x ≠2). (2)设PQ 的中点为N (x ,y ). 在Rt △PBQ 中,|PN |=|BN |.设O 为坐标原点,连接ON ,则ON ⊥PQ , 所以|OP |2=|ON |2+|PN |2=|ON |2+|BN |2, 所以x 2+y 2+(x -1)2+(y -1)2=4. 故线段PQ 中点的轨迹方程为 x 2+y 2-x -y -1=0.感悟提升 求与圆有关的轨迹问题时,根据题设条件的不同常采用以下方法: (1)直接法,直接根据题目提供的条件列出方程; (2)定义法,根据圆、直线等定义列方程; (3)几何法,利用圆的几何性质列方程;(4)代入法,找到要求点与已知点的关系,代入已知点满足的关系式等.训练2 设定点M (-3,4),动点N 在圆x 2+y 2=4上运动,以OM ,ON 为邻边作平行四边形MONP ,求点P 的轨迹方程. 解 如图,设P (x ,y ),N (x 0,y 0),则线段OP 的中点坐标为⎝ ⎛⎭⎪⎫x 2,y 2,线段MN 的中点坐标为⎝ ⎛⎭⎪⎫x 0-32,y 0+42. 因为平行四边形的对角线互相平分, 所以x 2=x 0-32,y 2=y 0+42, 整理得⎩⎪⎨⎪⎧x 0=x +3,y 0=y -4.又点N (x 0,y 0)在圆x 2+y 2=4上, 所以(x +3)2+(y -4)2=4,所以点P 的轨迹是以(-3,4)为圆心,2为半径的圆.直线OM 与轨迹相交于两点⎝ ⎛⎭⎪⎫-95,125和⎝ ⎛⎭⎪⎫-215,285,不符合题意,舍去,所以点P 的轨迹为(x +3)2+(y -4)2=4,除去两点⎝ ⎛⎭⎪⎫-95,125和⎝ ⎛⎭⎪⎫-215,285.1.圆x 2+y 2-6x +8y =0的圆心坐标和半径分别是( ) A.(3,4),5 B.(-3,4),5 C.(-3,-4),5 D.(3,-4),5答案 D解析 圆的方程可化为(x -3)2+(y +4)2=25,所以圆心坐标是(3,-4),半径r =5.2.过点A (1,-1),B (-1,1),且圆心在直线x +y -2=0上的圆的方程是( ) A.(x -3)2+(y +1)2=4 B.(x +3)2+(y -1)2=4 C.(x -1)2+(y -1)2=4 D.(x +1)2+(y +1)2=4 答案 C解析 设圆心C 的坐标为(a ,b ),半径为r . 因为圆心C 在直线x +y -2=0上, 所以b =2-a . 又|CA |2=|CB |2,所以(a -1)2+(2-a +1)2=(a +1)2+(2-a -1)2, 所以a =1,b =1,所以r =2, 所以方程为(x -1)2+(y -1)2=4.3.如果圆的方程为x 2+y 2+kx +2y +k 2=0,那么当圆面积最大时,圆心坐标为( ) A.(-1,1) B.(1,-1) C.(-1,0) D.(0,-1)答案 D 解析 r =12k 2+4-4k 2=124-3k 2,当k =0时,r 最大,此时圆心坐标为(0,-1). 4.(2022·太原期末)若k ∈⎩⎨⎧⎭⎬⎫-2,0,45,3,方程x 2+y 2+(k -1)x +2ky +k =0不表示圆,则k 的取值集合中元素的个数为( ) A.1 B.2 C.3 D.4 答案 A解析 方程x 2+y 2+(k -1)x +2ky +k =0表示圆的条件为(k -1)2+(2k )2-4k >0, 即5k 2-6k +1>0,解得k >1或k <15.又知该方程不表示圆,所以k 的取值范围为⎣⎢⎡⎦⎥⎤15,1.又因为k ∈⎩⎨⎧⎭⎬⎫-2,0,45,3,所以满足条件的k =45,即k 的取值集合为⎩⎨⎧⎭⎬⎫45. 5.(2022·昆明调研)已知圆C 经过P (-2,4),Q (3,-1)两点,且在x 轴上截得的弦长为6,则圆C 的方程为( )A.x 2+y 2-2x -4y -8=0B.x 2+y 2+2x -4y -8=0C.x 2+y 2-2x -4y -8=0或x 2+y 2-6x -8y =0D.x 2+y 2+2x -4y -8=0或x 2+y 2-6x -8y =0 答案 C解析 设圆的方程为x 2+y 2+Dx +Ey +F =0,D 2+E 2-4F >0, 将P ,Q 两点的坐标代入得 ⎩⎪⎨⎪⎧2D -4E -F =20, ①3D -E +F =-10. ②令y =0,得x 2+Dx +F =0, ③ 设x 1,x 2是方程③的两根, 由|x 1-x 2|=6得D 2-4F =36, ④ 由①②④得⎩⎪⎨⎪⎧D =-2,E =-4,F =-8或⎩⎪⎨⎪⎧D =-6,E =-8,F =0,故所求的圆的方程为x 2+y 2-2x -4y -8=0或x 2+y 2-6x -8y =0.6.已知两点A (-1,0),B (0,2),点P 是圆(x -1)2+y 2=1上任意一点,则△P AB 面积的最大值与最小值分别是( ) A.2,12(4-5) B.12(4+5),12(4-5) C.5,4- 5 D.12(5+2),12(5-2) 答案 B 解析 如图,圆心(1,0)到直线AB :2x -y +2=0的距离d =45,故圆上的点P 到直线AB 的距离的最大值是45+1,最小值是45-1.又|AB |=5,故△P AB 面积的最大值和最小值分别是2+52,2-52.7.(2021·郑州模拟)圆(x +2)2+(y -12)2=4关于直线x -y +8=0对称的圆的方程为________________. 答案 (x -4)2+(y -6)2=4 解析 设对称圆的圆心为(m ,n ), 则⎩⎪⎨⎪⎧n -12m +2=-1,m -22-n +122+8=0,解得⎩⎪⎨⎪⎧m =4,n =6,所以所求圆的圆心为(4,6), 故所求圆的方程为(x -4)2+(y -6)2=4.8.圆x 2+y 2-2x -2y +1=0上的点到直线x -y =2的距离的最大值是________. 答案2+1解析 将圆的方程化为(x -1)2+(y -1)2=1,圆心坐标为(1,1),半径为1,则圆心到直线x -y =2的距离d =|1-1-2|2=2,故圆上的点到直线x -y =2的距离的最大值为d +1=2+1.9.(2022·贵阳调研)已知A (0,2),点P 在直线x +y +2=0上,点Q 在圆C :x 2+y 2-4x -2y =0上,则|P A |+|PQ |的最小值是________. 答案 2 5解析 因为圆C :x 2+y 2-4x -2y =0,所以圆C 是以C (2,1)为圆心,半径r =5的圆.设点A (0,2)关于直线x +y +2=0的对称点为A ′(m ,n ),所以⎩⎪⎨⎪⎧m +02+n +22+2=0,n -2m -0=1,解得⎩⎪⎨⎪⎧m =-4,n =-2,故A ′(-4,-2).连接A ′C 交圆C 于Q (图略),此时,|P A |+|PQ |取得最小值,由对称性可知|P A |+|PQ |=|A ′P |+|PQ |≥|A ′Q |=|A ′C |-r =2 5.10.已知Rt △ABC 的斜边为AB ,且A (-1,0),B (3,0),求: (1)直角顶点C 的轨迹方程; (2)直角边BC 的中点M 的轨迹方程.解 (1)设AB 的中点为D ,由中点坐标公式得D (1,0),由直角三角形的性质知|CD |=12|AB |=2.由圆的定义知,动点C 的轨迹是以D (1,0)为圆心,2为半径的圆(由于A ,B ,C 三点不共线,所以应除去与x 轴的交点), 所以直角顶点C 的轨迹方程为(x -1)2+y 2=4(y ≠0).(2)设M (x ,y ),C (x 0,y 0),因为B (3,0),M 是线段BC 的中点,由中点坐标公式得x =x 0+32,y =y 0+02,所以x0=2x-3,y0=2y.由(1)知,点C的轨迹方程为(x-1)2+y2=4(y≠0),将x0=2x-3,y0=2y代入得(2x-4)2+(2y)2=4,即(x-2)2+y2=1.因此动点M的轨迹方程为(x-2)2+y2=1(y≠0). 11.已知点(x,y)在圆(x-2)2+(y+3)2=1上.(1)求yx的最大值和最小值;(2)求x+y的最大值和最小值;(3)求x2+y2+2x-4y+5的最大值和最小值.解(1)yx可视为点(x,y)与原点连线的斜率,yx的最大值和最小值就是与该圆有公共点的过原点的直线斜率的最大值和最小值,即直线与圆相切时的斜率.设过原点的直线的方程为y=kx,由直线与圆相切得圆心到直线的距离等于半径,即|2k+3|k2+1=1,解得k=-2+233或k=-2-233,∴yx的最大值为-2+233,最小值为-2-233.(2)设t=x+y,则y=-x+t,t可视为直线y=-x+t在y轴上的截距,∴x+y的最大值和最小值就是直线与圆有公共点时直线纵截距的最大值和最小值,即直线与圆相切时在y轴上的截距.由直线与圆相切得圆心到直线的距离等于半径,即|2+(-3)-t|2=1,解得t=2-1或t=-2-1.∴x+y的最大值为2-1,最小值为-2-1.(3)x2+y2+2x-4y+5=(x+1)2+(y-2)2,求它的最值可视为求点(x,y)到定点(-1,2)的距离的最值,可转化为求圆心(2,-3)到定点(-1,2)的距离与半径的和或差.又圆心到定点(-1,2)的距离为34, ∴x 2+y 2+2x -4y +5的最大值为34+1,最小值34-1.12.(2020·全国Ⅱ卷)若过点(2,1)的圆与两坐标轴都相切,则圆心到直线2x -y -3=0的距离为( ) A.55 B.255C.355D.455答案 B解析 设圆心为P (x 0,y 0),半径为r ,∵圆与x 轴,y 轴都相切, ∴|x 0|=|y 0|=r .又圆经过点(2,1),∴x 0=y 0=r 且(2-x 0)2+(1-y 0)2=r 2, ∴(r -2)2+(r -1)2=r 2,解得r =1或r =5.当r =1时,圆心坐标为(1,1),此时圆心到直线2x -y -3=0的距离 d =|2×1-1-3|22+(-1)2=255;当r =5时,圆心坐标为(5,5),此时圆心到直线2x -y -3=0的距离 d =|2×5-5-3|22+(-1)2=255.综上,圆心到直线2x -y -3=0的距离为255.13.(2022·郑州模拟)大约在2 000多年前,我国的墨子给出了圆的概念“一中同长也”,意思是说,圆有一个圆心,圆心到圆周上的点的长都相等.这个定义比古希腊数学家欧几里得给圆下定义要早100多年.现有动点P 满足|OP |=2,其中O 为坐标原点,若M ⎝ ⎛⎭⎪⎫12,-32,则|PM |的最小值为________.答案 1解析 由题意可得点P 在以O 为圆心,2为半径的圆上, 因为|OM |=⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫-322=1<2, 所以点M 在圆内,所以|PM |min =r -|OM |=2-1=1.14.设抛物线C :y 2=4x 的焦点为F ,过F 且斜率为k (k >0)的直线l 与C 交于A ,B 两点,|AB |=8. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程. 解 (1)由题意得F (1,0),l 的方程为 y =k (x -1)(k >0). 设A (x 1,y 1),B (x 2,y 2), 由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x得k 2x 2-(2k 2+4)x +k 2=0,Δ=16k 2+16>0,故x 1+x 2=2k 2+4k 2, 所以|AB |=|AF |+|BF | =(x 1+1)+(x 2+1)=4k 2+4k 2.由题设知4k 2+4k 2=8,解得k =-1(舍去),k =1, 因此l 的方程为y =x -1.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为y -2=-(x -3),即y =-x +5.设所求圆的圆心坐标为(x 0,y 0),则⎩⎪⎨⎪⎧y 0=-x 0+5,(x 0+1)2=(y 0-x 0+1)22+16, 解得⎩⎪⎨⎪⎧x 0=3,y 0=2或⎩⎪⎨⎪⎧x 0=11,y 0=-6.故圆的半径为x 0+p2=4或12,因此所求圆的方程为(x -3)2+(y -2)2=16或(x -11)2+(y +6)2=144.。
第5讲:圆的基本性质一、建构新知1.圆的定义:(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.(2)圆是到定点的距离等于定长的点的集合.2.圆的性质:(1)旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心.在同圆或等圆中,两个圆心角,两条弧,两条弦,两条弦心距,这四组量中的任意一组相等,那么它所对应的其他各组分别相等.(2)轴对称:圆是轴对称图形,经过圆心的任一直线都是它的对称轴.(3)垂径定理及推论:①垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.③弦的垂直平分线过圆心,且平分弦对的两条弧.④平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦.⑤平行弦夹的弧相等.3.两圆的性质:(1)两个圆是一个轴对称图形,对称轴是两圆连心线.(2)相交两圆的连心线垂直平分公共弦,相切两圆的连心线经过切点.4.与圆有关的角:(1)圆心角:顶点在圆心的角叫圆心角.圆心角的性质:圆心角的度数等于它所对的弧的度数.(2)圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角.圆周角的性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.③90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.⑤圆内接四边形的对角互补;外角等于它的内对角.二、经典例题例1.如图所示,△ABC的三个顶点的坐标分别为A(-1,3)、B (-2,-2)、C (4,-2),则△ABC外接圆半径的长度为.例2.如图所示,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,求CD的长.变式:如图,AB 、AC 都是圆O 的弦,OM ⊥AB ,ON ⊥AC , 垂足分别为M 、N ,如果MN =3,那么BC = .例3.如图,在⊙O 中,半径OC 垂直于弦AB ,垂足为点E .(1)若OC =5,AB =8,求tan ∠BAC ;(2)若∠DAC =∠BAC ,且点D 在⊙O 的外部,判断直线AD 与⊙O 的位置关系,并加以证明.例4. 如图,⊙O 是△ABC 的外接圆,FH 是⊙O 的切线,切点为F ,FH ∥BC ,连结AF 交BC 于E ,∠ABC 的平分线BD 交AF 于D ,连结BF .(1)证明:AF 平分∠BAC ; (2)证明:BF =FD .N MO C BA例5. 已知射线OF交⊙O于B,半径OA⊥OB,P是射线OF上的一个动点(不与O、B重合),直线AP交⊙O于D,过D作⊙O的切线交射线OF于E.(1)如图所示是点P在圆内移动时符合已知条件的图形,请你在图中画出点P在圆外移动时符合已知条件的图形.(2)观察图形,点P在移动过程中,△DPE的边、角或形状存在某些规律,请你通过观察、测量、比较写出一条与△DPE的边、角或形状有关的规律.(3)点P在移动过程中,设∠DEP的度数为x,∠OAP的度数为y,求y与x的函数关系式,并写出自变量x的取值范围.例6.如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,(1)求证:CB∥PD;(2)若BC=3,sin∠P=35,求⊙O的直径.三、基础演练1.如图所示,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于().A.70°B.64°C.62°D.51°2.在半径为27m的圆形广场中心点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图所示),则光源离地面的垂直高度SO为().A.54m B.m C.m D.m3.设计一个商标图案,如图所示,在矩形ABCD中,AB=2BC,且AB=8cm,以A为圆心、AD的长为半径作半圆,则商标图案(阴影部分)的面积等于().A. (4π+8)cm2B. (4π+16)cm2C. (3π+8)cm2D. (3π+16)cm24.如图,的半径为5,弦的长为8,点在线段(包括端点)上移动,则的取值范围是().A. B. C. D.5.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表示为:如图所示,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为() A.12.5寸B.13寸C.25寸D.26寸6.在平面直角坐标系中如图所示,两个圆的圆心坐标分别是(3,0)和(0,-4),半径分别是和,则这两个圆的公切线(和两圆都相切的直线)有()A. 1条B. 2条C. 3条D. 4条7.一条弦的两个端点把圆周分成4:5两部分,则该弦所对的圆周角为( ).A .80°B .100°C .80°或100°D .160°或200°8.如图所示,AB 、AC 与⊙O 分别相切于B 、C 两点,∠A =50°,点P 是圆上异于B 、C 的一动点,则∠BPC 的度数是( ).A .65°B .115°C .65°或115°D .130°或50° 9.如下左图,是的内接三角形,,点P 在上移动(点P 不与点A 、C 重合),则的变化范围是_____.10.如图所示,EB 、EC 是⊙O 是两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E =46°,∠DCF =32°,那么∠A 的度数是____________.11.已知⊙O 1与⊙O 2的半径、分别是方程的两实根,若⊙O 1与⊙O 2的圆心距=5.则⊙O 1与⊙O 2的位置关系是______________ .12.已知圆的直径为13 cm ,圆心到直线的距离为6cm ,那么直线和这个圆的公共点的个数是______.13. 两个圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径是______. 14. 已知正方形ABCD 外接圆的直径为,截去四个角成一正八边形,则这个正八边形EFGHIJLK 的边长为_______________,面积为_______________. 四、直击中考1.(2013年湖北)如,在Rt ABC 中,90ACB ∠=,3AC =,4BC =,以点C 为圆心,CA 为半径的圆与AB 交于点D ,则AD 的长为( ) A .95 B . 245 C . 185 D . 522.(2013黑龙江)如图,点A ,B ,C ,D 为⊙O 上的四个点,AC 平分∠BAD ,AC 交BD 于点E ,CE =4,CD =6,则AE 的长为( )CADBA .4B .5C .6D .73.(2013江苏)如图,已知AB 是⊙O 的直径,AD 切⊙O 于点A ,点C 是的中点,则下列结论不成立的是( ) A .OC ∥AE B .EC =BCC .∠DAE =∠ABED .AC ⊥OE4.(2013湖北)如图,DC 是⊙O 直径,弦AB ⊥CD 于F ,连接BC ,DB ,则下列结论错误的是( ) A .B . A F =BFC . O F =CFD . ∠DBC =90°5.(2013湖北)如图,M 是CD 的中点,EM ⊥CD ,若CD =4,EM =8,则所在圆的半径为 .6.(2013年广东)如图,在平面直角坐标系中,点O 为坐标原点,点P 在第一象限,P Θ与x 轴交于O ,A 两点,点A 的坐标为(6,0),P Θ的半径为13,则点P 的坐标为____________.7.(2013四川)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点G ,点F 是CD 上一点,且满足=31,连接AF 并延长交⊙O 于点E ,连接AD 、DE ,若CF =2,AF =3.给出下列结论:①△ADF ∽△AED ;②FG =2;③tan ∠E =;④S △DEF =4.其中正确的是(写出所有正确结论的序号).8.(2013浙江)如图,AE 是半圆O 的直径,弦AB =BC =4,弦CD =DE =4,连结OB ,OD ,则图中两个阴影部分的面积和为 . 9. (2013江苏)在平面直角坐标系xOy 中,已知点A (6,0),点B (0,6),动点C 在以半径为3的⊙O 上,连接OC ,过O 点作OD ⊥OC ,OD 与⊙O 相交于点D (其中点C 、O 、D 按逆时针方向排列),连接AB .(1)当OC ∥AB 时,∠BOC 的度数为 ; (2)连接AC ,BC ,当点C 在⊙O 上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值.(3)连接AD,当OC∥AD时:①求出点C的坐标;②直线BC是否为⊙O的切线?请作出判断,并说明理由.10.(2013四川)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.五、挑战竞赛1.如图所示,△ABC的三边满足关系BC=12(AB+AC),O,I分别为△ABC的外心和内心,∠BAC的外角平分线交⊙O于点E,AI的延长线交⊙O于点D,DE交BC于点H.求证:(1)AI=BD;(2)OI=12 AE.第22题图②OPCBA六、每周一练1.在△ABC 中,∠C 为锐角,分别以AB ,AC 为直径作半圆,过点B ,A ,C 作,如图所示.若AB =4,AC =2,S 1﹣S 2=,则S 3﹣S 4的值是( ) A .B .C .D .2.如图,在平面直角坐标系中,△ABC 是⊙O 的内接三角形, AB =AC ,点P 是⋂AB 的中点,连接P A ,PB ,PC . 如图②, 若2524sin =∠BPC ,则PAB ∠tan 的值为 . 3. 如图1,正方形ABCD 的边长为2,点M 是BC 的中点,P 是线段MC 上的一个动点(不与M 、C 重合),以AB 为直径作⊙O ,过点P 作⊙O 的切线,交AD 于点F ,切点为E . (1)求证:OF ∥BE ;(2)设BP =x ,AF =y ,求y 关于x 的函数解析式,并写出自变量x 的取值范围; (3)延长DC 、FP 交于点G ,连接OE 并延长交直线DC 与H (图2),问是否存在点P ,使△EFO ∽△EHG (E 、F 、O 与E 、H 、G 为对应点)?如果存在,试求(2)中x 和y 的值;如果不存在,请说明理由.。
初中数学竞赛辅导讲义---圆的基本性质到定点(圆心)等于定长(半径)的点的集合叫圆,圆常被人们看成是最完美的事物,圆的图形在人类进程中打下深深的烙印.圆的基本性质有:一是与圆相关的基本概念与关系,如弦、弧、弦心距、圆心角、圆周角等;二是圆的对称性,圆既是一个轴对称图形,又是一中心对称图形.用圆的基本性质解题应注意:1.熟练运用垂径定理及推论进行计算和证明;2.了解弧的特性及中介作用;3.善于促成同圆或等圆中不同名称等量关系的转化.熟悉如下基本图形、基本结论:【例题求解】【例1】在半径为1的⊙O 中,弦AB 、AC 的长分别为3和2,则∠BAC 度数为 .作出辅助线,解直角三角形,注意AB 与AC 有不同的位置关系.注: 由圆的对称性可引出许多重要定理,垂径定理是其中比较重要的一个,它沟通了线段、角与圆弧的关系,应用的一般方法是构造直角三角形,常与勾股定理和解直角三角形知识结 合起来.圆是一个对称图形,注意圆的对称性,可提高解与圆相关问题周密性.【例2】 如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为( )A .2B .25C .45D .16175思路点拨 所作最小圆圆心应在对称轴上,且最小圆应尽可能通过圆形的某些顶点,通过设未知数求解.【例3】 如图,已知点A 、B 、C 、D 顺次在⊙O 上,AB=BD ,BM ⊥AC 于M ,求证:AM=DC+CM .思路点拨 用截长(截AM)或补短(延长DC)证明,将问题转化为线段相等的证明,证题的关键是促使不同量的相互转换并突破它.【例4】 如图甲,⊙O 的直径为AB ,过半径OA 的中点G 作弦C E ⊥AB ,在CB 上取一点D ,分别作直线CD 、ED ,交直线AB 于点F ,M .(1)求∠COA 和∠FDM 的度数;(2)求证:△FDM ∽△COM ; (3)如图乙,若将垂足G 改取为半径OB 上任意一点,点D 改取在EB 上,仍作直线CD 、ED ,分别交直线AB 于点F 、M ,试判断:此时是否有△FDM ∽△COM? 证明你的结论.思路点拨 (1)在Rt △COG 中,利用OG=21OA=21OC ;(2)证明∠COM=∠FDM ,∠CMO= ∠FMD ;(3)利用图甲的启示思考.注:善于促成同圆或等圆中不同名称的相互转化是解决圆的问题的重要技巧,此处,要努力把圆与直线形相合起来,认识到圆可为解与直线形问题提供新的解题思路,而在解与圆相关问题时常用到直线形的知识与方法(主要是指全等与相似).【例5】 已知:在△ABC 中,AD 为∠BAC 的平分线,以C 为圆心,CD 为半径的半圆交BC 的延长线于点E ,交AD 于点F ,交AE 于点M ,且∠B=∠CAE ,EF :FD =4:3.(1)求证:AF =DF ;(2)求∠AED 的余弦值;(3)如果BD =10,求△ABC 的面积.思路点拨 (1)证明∠ADE =∠DAE ;(2)作AN ⊥BE 于N ,cos ∠AED =AEEN ,设FE=4x ,FD =3x ,利用有关知识把相关线段用x 的代数式表示;(3)寻找相似三角形,运用比例线段求出x 的值.⌒ ⌒ ⌒ ⌒注:本例的解答,需运用相似三角形、等腰三角形的判定、面积方法、代数化等知识方法思想,综合运用直线形相关知识方法思想是解与圆相关问题的关键.学历训练1.D是半径为5cm的⊙O内一点,且OD=3cm,则过点D的所有弦中,最小弦AB= .2.阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.对于平面图形A,如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖.例如:图甲中的三角形被一个圆所覆盖,图乙中的四边形被两个圆所覆盖.回答下列问题:(1)边长为lcm的正方形被一个半径为r的圆所覆盖,r的最小值是cm;(2)边长为lcm的等边三角形被一个半径为r的圆所覆盖,r的最小值是cm;(3)长为2cm,宽为lcm的矩形被两个半径都为r的圆所覆盖,r的最小值是cm.(2003年南京市中考题)3.世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆:它们看上去多么美丽与和谐,这正是因为圆具有轴对称和中心对称性.(1)请问以下三个图形中是轴对称图形的有,是中心对称图形的有(分别用下面三个图的代号a,b,c填空).(2)请你在下面的两个圆中,按要求分别画出与上面图案不重复的图案(草图) (用尺规画或徒手画均可,但要尽可能准确些,美观些).a .是轴对称图形但不是中心对称图形.b .既是轴对称图形又是中心对称图形.4.如图,AB 是⊙O 的直径,CD 是弦,若AB=10cm ,CD =8cm ,那么A 、B 两点到直线CD 的距离之和为( )A .12cmB .10cmC . 8cmD .6cm5.一种花边是由如图的弓形组成的,ACB 的半径为5,弦AB =8,则弓形的高CD 为( )A .2B .25C .3D .316 6.如图,在三个等圆上各自有一条劣弧AB 、CD 、EF ,如果AB+CD=EF ,那么AB+CD 与E 的大小关系是( )A .AB+CD =EFB .AB+CD=FC . AB+CD<EFD .不能确定7.电脑CPU 芯片由一种叫“单晶硅”的材料制成,未切割前的单晶硅材料是一种薄形圆片,叫“晶圆片”.现为了生产某种CPU 芯片,需要长、宽都是1cm 的正方形小硅片若干.如果晶圆片的直径为10.05cm ,问:一张这种晶圆片能否切割出所需尺寸的小硅片66张?请说明你的方法和理由(不计切割损耗).8.如图,已知⊙O 的两条半径OA 与OB 互相垂直,C 为AmB 上的一点,且AB 2+OB 2=BC 2,求∠OAC 的度数.9.不过圆心的直线l 交⊙O 于C 、D 两点,AB 是⊙O 的直径,AE ⊥l ,垂足为E ,BF ⊥l ,垂足为F .(1)在下面三个圆中分别补画出满足上述条件的具有不同位置关系的图形;(2)请你观察(1)中所画图形,写出一个各图都具有的两条线段相等的结论(不再标注其他字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程);(3)请你选择(1)中的一个图形,证明(2)所得出的结论.⌒ ⌒ ⌒ ⌒ ⌒ ⌒ ⌒10.以AB 为直径作一个半圆,圆心为O ,C 是半圆上一点,且OC 2=AC ×BC , 则∠CAB=.11.如图,把正三角形ABC 的外接圆对折,使点A 落在BC 的中点A ′上,若BC=5,则折痕在△ABC 内的部分DE 长为 .12.如图,已知AB 为⊙O 的弦,直径MN 与AB 相交于⊙O 内,MC ⊥AB 于C ,ND ⊥AB 于D ,若MN=20,AB=68,则MC —ND= .13.如图,已知⊙O 的半径为R ,C 、D 是直径AB 同侧圆周上的两点,AC 的度数为96°,BD 的度数为36°,动点P 在AB 上,则CP+PD 的最小值为 .14.如图1,在平面上,给定了半径为r 的圆O ,对于任意点P ,在射线OP 上取一点P ′,使得OP ×OP ′=r 2,这种把点P 变为点P ′的变换叫作反演变换,点P 与点P ′叫做互为反演点.(1)如图2,⊙O 内外各有一点A 和B ,它们的反演点分别为A ′和B ′,求证:∠A ′=∠B ;(2)如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形.①选择:如果不经过点O 的直线与⊙O 相交,那么它关于⊙O 的反演图形是( )A .一个圆B .一条直线C .一条线段D .两条射线②填空:如果直线l 与⊙O 相切,那么它关于⊙O 的反演图形是 ,该图形与圆O 的位置关系是 .15.如图,已知四边形ABCD 内接于直径为3的圆O ,对角线AC 是直径,对角线AC 和BD 的交点为P ,AB=BD ,且PC=0.6,求四边形ABCD 的周长.16.如图,已知圆内接△ABC 中,AB>AC ,D 为BAC 的中点,DE ⊥AB 于E ,求证:BD 2-AD 2=AB×AC .⌒ ⌒ ⌒17.将三块边长均为l0cm 的正方形煎饼不重叠地平放在圆碟内,则圆碟的直径至少是多少?(不考虑其他因素,精确到0.1cm)18.如图,直径为13的⊙O ′,经过原点O ,并且与x 轴、y 轴分别交于A 、B 两点,线段OA 、OB(OA>OB)的长分别是方程0602=++kx x 的两根.(1)求线段OA 、OB 的长; (2)已知点C 在劣弧OA 上,连结BC 交OA 于D ,当OC 2=CD ×CB 时,求C 点坐标;(3)在⊙O ,上是否存在点P ,使S △POD =S △ABD ?若存在,求出P 点坐标;若不存在,请说明理由.⌒参考答案。
一.圆的定义1.在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作⊙O,读作圆O.2.圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.3.确定圆的条件:⑴圆心;⑵半径,其中圆心确定圆的位置,半径长确定圆的大小.4.连结圆上任意两点的线段叫做弦.经过圆心的弦叫做直径,并且直径是同一圆中最长的弦,直径等于半径的2倍.、为端点的弧记作»AB,读作弧AB.5.圆上任意两点间的部分叫做圆弧,简称弧.以A B在同圆或等圆中,能够重合的弧叫做等弧.6.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.在一个圆中大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.9.如下图,(1)若点O为⊙O的圆心,则线段__________是圆O的半径;线段________是圆O的弦,其中最长的弦是______;______是劣弧;______是半圆.(2)若∠A=40°,则∠ABO=______,∠C=______,∠ABC=______.10.已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点.(1)求证:∠AOC=∠BOD;(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.11.已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°,求∠C及∠AOC的度数.12.已知:如图,△ABC,试用直尺和圆规画出过A,B,C三点的⊙O.点和圆的位置关系一、基础知识填空1.平面内,设⊙O的半径为r,点P到圆心的距离为d,则有d>r⇔点P在⊙O______;d=r⇔点P在⊙O______;d<r⇔点P在⊙O______.2.平面内,经过已知点A,且半径为R的圆的圆心P点在__________________________ 3.平面内,经过已知两点A,B的圆的圆心P点在______________________________________ 4.______________________________确定一个圆.5.在⊙O上任取三点A,B,C,分别连结AB,BC,CA,则△ABC叫做⊙O的______;⊙O 叫做△ABC的______;O点叫做△ABC的______,它是△ABC___________的交点.6.锐角三角形的外心在三角形的___________部,钝角三角形的外心在三角形的__________ ___部,直角三角形的外心在________________.7.若正△ABC外接圆的半径为R,则△ABC的面积为___________.8.若正△ABC的边长为a,则它的外接圆的面积为___________.9.若△ABC中,∠C=90°,AC=10cm,BC=24cm,则它的外接圆的直径为___________.10.若△ABC内接于⊙O,BC=12cm,O点到BC的距离为8cm,则⊙O的周长为___________.11.已知:如图,△ABC.作法:求件△ABC的外接圆O.12.已知:A,B,C,D,E五个点中无任何三点共线,无任何四点共圆,那么过其中的三点作圆,最多能作出( ).A.5个圆B.8个圆C.10个圆D.12个圆13.下列说法正确的是( ).A.三点确定一个圆B.三角形的外心是三角形的中心C.三角形的外心是它的三个角的角平分线的交点D.等腰三角形的外心在顶角的角平分线上14.下列说法不正确的是( ).A.任何一个三角形都有外接圆B.等边三角形的外心是这个三角形的中心C.直角三角形的外心是其斜边的中点D.一个三角形的外心不可能在三角形的外部15.正三角形的外接圆的半径和高的比为( ).A.1∶2 B.2∶3 C.3∶4 D.1∶316.已知⊙O 的半径为1,点P 到圆心O 的距离为d ,若关于x 的方程x 2-2x +d =0有实根,则点P ( ).A .在⊙O 的内部B .在⊙O 的外部C .在⊙O 上D .在⊙O 上或⊙O 的内部 17.在平面直角坐标系中,作以原点O 为圆心,半径为4的⊙O ,试确定点 A (-2,-3),B (4,-2),)2,32(-C 与⊙O 的位置关系.18.在直线123-=x y 上是否存在一点P ,使得以P 点为圆心的圆经过已知两点A (-3,2),B (1,2).若存在,求出P 点的坐标,并作图.弧长和扇形面积 一、基础知识填空1.在半径为R 的圆中,n °的圆心角所对的弧长l =_______. 2.____________和______所围成的图形叫做扇形.在半径为R 的圆中,圆心角为n °的扇形面积S 扇形=__________;若l 为扇形的弧长,则S 扇形=__________. 3.如图,在半径为R 的⊙O 中,弦AB 与所围成的图形叫做弓形. 当为劣弧时,S 弓形=S 扇形-______; 当为优弧时,S 弓形=______+S △OAB .3题图4.半径为8cm 的圆中,72°的圆心角所对的弧长为______;弧长为8cm 的圆心角约为______(精确到1′).5.半径为5cm 的圆中,若扇形面积为2cm 3π25,则它的圆心角为______.若扇形面积为15πcm 2,则它的圆心角为______.6.若半径为6cm 的圆中,扇形面积为9πcm 2,则它的弧长为______.7.如图,Rt △ABC 中,∠C =90°,AC =8,BC =6,两等圆⊙A ,⊙B 外切,那么图中两个扇形(即阴影部分)的面积之和为( ).7题图A .π425 B .π825 C .π1625D .π32258.如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 夹角为120°,AB 的长为30cm ,贴纸部分BD 的长为20cm ,则贴纸部分的面积为( ).8题图A .2πcm 100B .2πcm 3400C .2πcm 800D .2πcm 38009.如图,△ABC 中,BC =4,以点A 为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于E ,交AC 于F ,点P 是⊙A 上一点,且∠EPF =40°,则圆中阴影部分的面积是( ).A .9π4-B .9π84-C .94π8-D .98π8-10. 已知:如图,半圆O 的直径AB =12cm ,点C ,D 是这个半圆的三等分点.求∠CAD 的度数及弦AC ,AD 和围成的图形(图中阴影部分)的面积S .10.已知:如图,在边长为a 的正△ABC 中,分别以A ,B ,C 点为圆心,a 21长为半径作,,,求阴影部分的面积.11.已知:如图,Rt △ABC 中,∠C =90°,∠B =30°,,34 BC 以A 点为圆心,AC 长为半径作,求∠B 与围成的阴影部分的面积.12.已知:如图,以线段AB 为直径作半圆O 1,以线段AO 1为直径作半圆O 2,半径O 1C 交半圆O 2于D 点.试比较与的长.垂径定理一、垂径定理垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.符号语言:∵CD 为⊙O 的直径,AB 为⊙O 的弦,且CD ⊥AB ,垂足为E ,∴ AE=BE, = , = .推 论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.∵ CD 为⊙O 的直径,AB 为⊙O 的弦(不是直径),且AE=BE.∴ CD ⊥AB , = , = . 弦心距:圆心到弦的距离(垂线段OE )类型1. 垂径定理及推论概念例1.下面四个命题中正确的一个是( )A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必过这条弦所在圆的圆心D .在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心例2. 如图1-2,如果AB 为⊙O 直径,弦AB CD ⊥,垂足为E ,那么下列结论中错误的是( )A .DE CE =B .C .BAD BAC ∠=∠D .AD AC >类型2. 垂径定理的运用在垂径定理的运用中,通常的是要利用定理构建直角三角形,利用勾股定理进行运算.4.圆的半径为5cm ,圆心到弦AB 的距离为4cm ,则AB =______cm .5.1如图,CD 为⊙O 的直径,AB ⊥CD 于E ,DE =8cm ,CE =2cm ,则AB =______cm .5.2已知:如图1,AB 是⊙O 的弦,半径OC ⊥AB 于点D ,且AB=8cm,OC=5cm, 则DC 的长为: A 、3cm B 、2.5cm C 、2cm D 、1cmCDABO E5.3过⊙O外一点M到圆上最短距离是2cm,最远距离是10cm,则圆的半径是()cm5.4过⊙O内一点M的最长弦长为6cm,最短弦长为4cm,则OM的长为()A、cmB、cmC、2cmD、3cm5.5如图,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP=______.6.1如图,⊙O的弦AB垂直于CD,E为垂足,AE=3,BE=7,且AB=CD,则圆心O到CD的距离是______.O到AB的距离是______.6.2如图,⊙O的弦AB垂直于AC,AB=6cm,AC=4cm,则⊙O的半径等于______cm.7.1如图,⊙O的半径OC为6cm,弦AB垂直平分OC,则AB=_____cm,∠AOB=_____.7.2如图,AB为⊙O的弦,∠AOB=90°,AB=a,则OA=______,O点到AB的距离=______.7.3已知:如图,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,求CD的长.7.4如图3-3,在ABC Rt ∆中,∠C=900,AC=5cm ,BC=12cm ,以C 为圆心、AC 为半径的圆交斜边于D ,求AD 的长.7.4如图所示,在圆⊙O 内有折线OABC ,其中OA =8,AB =12,∠A =∠B =60°,则BC 的长为()A .19B .16C .18D .20类型3. 垂径定理分类讨论7.1已知:⊙O 的半径OA =1,弦AB 、AC 的长分别为2,3,求∠BAC 的度数.7.2已知:⊙O 的半径为25cm ,弦AB =40cm ,弦CD =48cm ,AB ∥CD .求这两条平行弦AB ,CD 之间的距离.7.3 已知:△ABC 内接于⊙O ,AB=AC ,半径OB=5cm ,圆心O 到BC 的距离为3cm ,求AB 的长.类型4. 垂径定理相关证明8.1.如图,F 是以O 为圆心,BC 为直径的半圆上任一点,A 是 弧BF 的中点,AD ⊥BC 于D. 求证:.21BF AD =8.2.已知,⊙O 的弦AB ,CD 相交于点P ,PO 是APC ∠的平分线,点M ,N 分别是,的中点,MN 分别交AB ,CD 于点E ,F .求证:PO MN ⊥.ACBDA B CD P O8.3. 如图6-2,AB 是⊙O 的直径,P 是AB 上一动点,C 、D 是⊙O 的两点,有∠CPB=∠DPB.求证:PC=PD.图6-28.4. 如图6-5,⊙O 的直径AB 和弦CD 相交于点M ,CD AE ⊥,CD BF ⊥,垂足分别是E ,F . (1)求证:DF CE =.(2)若26=AB ,24=CD ,求BF AE -的值.变式题2:如果弦CD 是动弦,与直径AB 不相交,AE ⊥CD 于E ,BF ⊥CD 于F ,此时是否有: CE=DF ;OE=OF.如果有请证明,如果不成立,请说明.类型5. 垂径定理的综合应用10.1一个圆弧形门拱的拱高为1米,跨度为4米,那么这个门拱的半径为 米.10.2如图,有一弧形拱桥,其跨度AB=10m ,拱高为1m 。
圆一.圆的定义及相关概念考点1:圆的定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径。
考点2:确定圆的条件:圆心和半径①圆心确定圆的位置,半径确定圆的大小;②不在同一条直线上的三点确定一个圆。
考点2:(圆的性质)圆的对称性:圆既是轴对称图形又是中心对称图形。
经过圆心的每一条直线都是它的对称轴。
圆心是它的对称中心。
考点3:弦:连结圆上任意两点的线段叫弦。
经过圆心的弦叫做直径。
直径是圆中最大的弦。
弦心距:圆心到弦的距离叫做弦心距。
弧:圆上任意两点间的部分叫做弧。
弧分为半圆,优弧、劣弧三种。
(请务必注意区分等弧,等弦,等圆的概念)弓形:弦与它所对应的弧所构成的封闭图形。
弓高:弓形中弦的中点与弧的中点的连线段。
(请务必注意在圆中一条弦将圆分割为两个弓形,对应两个弓高)考点4:三角形的外接圆:锐角三角形的外心在,直角三角形的外心在 ,钝角三角形的外心在。
考点5点和圆的位置关系设圆的半径为r,点到圆心的距离为d,则点与圆的位置关系有三种。
①点在圆外⇔d>r;②点在圆上⇔d=r;③点在圆内⇔ d<r;【典型例题】例1 在⊿ABC 中,∠ACB =90°,AC =2,BC =4,CM 是AB 边上的中线,以点C 为圆心,以5为半径作圆,试确定A,B,M 三点分别与⊙C 有怎样的位置关系,并说明你的理由。
例2.已知,如图,CD 是直径,︒=∠84EOD ,AE 交⊙O 于B ,且AB=OC ,求∠A 的度数。
例3 ⊙O 平面内一点P 和⊙O 上一点的距离最小为3cm ,最大为8cm ,则这圆的半径是_________cm 。
例4 在半径为5cm 的圆中,弦AB ∥CD ,AB=6cm ,CD=8cm ,则AB 和CD 的距离是多少?例5 如图,⊙O 的直径AB 和弦CD 相交于点E ,已知AE=6cm ,EB=2cm,ο30=∠CEA , 求CD 的长.例6.已知:⊙O 的半径0A=1,弦AB 、AC 的长分别为3,2,求BAC ∠的度数.AB DCO· E二.垂径定理及其推论考点1垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.推论1:①平分弦(不是直径)的直径重直于弦,并且平分弦所对的两条弧.②弦的垂直平分线经过圆心,并且平分弦所对的两条弧.③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.推论2.圆的两条平行弦所夹的弧相等.垂径定理及推论1中的三条可概括为:①经过圆心;②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧.以上五点已知其中的任意两点,都可以推得其它两点固定的已经不能再固定的方法:求弦心距,弦长,弓高,半径时通常要做弦心距,并连接圆心和弦的一个端点,得到直角三角形。