实验四_香农编码

信息论与编码课程考核大纲一、适应对象修读完本课程规定内容的通信工程专业的学生。

二、考核目的考核学生对信息论的基本理论以及编码理论与实现原理的理解和掌握程度；并通过实验教学加深学生对基本概念的理解，巩固基础理论知识，提升学生参与课堂的积极性，充分发挥其主观能动性。

最后通过分析考核成绩，检查本门课程的教学效果，不断改进和提高课程教学水平，促进课程建设和学科建设。

三、考核形式与方法开卷考试、实验成绩和平时成绩均为百分制。

1、平时成绩考核方法如下：1) 作业：50%按交作业的次数、每次作业质量和态度确定。

2) 考勤：50%2、实验成绩考核方法如下：实验成绩为单次实验成绩的平均值。

单次实验成绩考核方法及所占比例如下：单次实验成绩＝实验方案×40%+实验操作×20%+实验结果×40%1) 实验方案：40%实验方案主要考察方案设计的合理性和可靠性；实验数据的整理归纳能力；实验报告完成的质量等。

不做实验预习报告的、不能回答教师问题的，扣除当次实验方案成绩的40%；不按时交实验报告的，扣除当次实验方案成绩的20%；书写不合格的重写，扣除当次实验方案成绩的40%；未交试验报告的，扣除当次实验方案成绩的100%。

2) 实际操作: 20%着重考察学生实际操作的科学性、主动性、认真性、熟练性。

实验课程缺勤的，扣除当次实验成绩的100%。

3) 实验结果：40%实验结果着重考查其与实验方案、实验要求、实验操作的一致性。

4) 实验课堂纪律：凡违反学生实验守则或安全规则的扣除实验总成绩的60%，损坏物品要赔偿。

5) 考勤：实验课程缺勤的，扣除当次实验成绩的100%。

3、期末考核采用开卷笔试形式。

四、课程考核成绩构成本门课程考核成绩按百分计。

课程考核成绩=平时成绩×20%+实验成绩×20%+期末考核成绩×60%五、考核内容与要求第1章概论【考核内容】信息论的形成和发展，信息、信号、消息的区别，香农信息的定义，通信系统的模型。

《信息论与编码》-曹雪虹-课后习题答案 第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ，转移概率为：()11|1/2p u u =，()21|1/2p uu =，()31|0p u u =，()12|1/3p u u =，()22|0p u u =，()32|2/3p u u =，()13|1/3p u u =，()23|2/3p u u =，()33|0p u u =，画出状态图并求出各符号稳态概率。

解：状态图如下状态转移矩阵为：1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1，u 2，u 3稳定后的概率分别为W 1，W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0，1}组成的二阶马尔可夫链，其转移概率为：(0|00)p =0.8，(0|11)p =0.2，(1|00)p =0.2，(1|11)p =0.8，(0|01)p =0.5，(0|10)p =0.5，(1|01)p =0.5，(1|10)p =0.5。

画出状态图，并计算各状态的稳态概率。

解：(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵：0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为：设各状态00，01，10，11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子，也就是各面呈现的概率都为1/6，求：(1) “3和5同时出现”这事件的自信息； (2) “两个1同时出现”这事件的自信息； (3) 两个点数的各种组合（无序）对的熵和平均信息量；(4) 两个点数之和（即2, 3, … , 12构成的子集）的熵；(5) 两个点数中至少有一个是1的自信息量。

逼近香农极限的新型光调制技术光传输技术经历了多代的技术演进发展，频谱效率得到了显著改善，业界开始探讨香农通信理论在光纤传输系统上的最基本线性和非线性信号通道容限是多少，从而使下一代的新技术超越当前100G相干系统的传输性能，进一步提升谱效率和总容量，以接近香农的理论极限。

新技术包括了更复杂的调制码型和信道编解码方式、预滤波和其相结合的多符号同时检测算法、光正交频分复用(OFDM和奈奎斯特波分复用(Nyquist WDM)的多载波技术以及抵抗非线性的补偿方案。

新技术进一步优化后，很可能应用在超100G的光传输系统中，从而满足不断增长的带宽需求。

频谱效率；香农极限；高斯噪声；光信噪比；调制；非线性补偿Optical transmission technologies have gone through several generations of development. Spectral efficiency has significantly improved ，and industry has begun to seek the answer to a basic question ：What are the fundamental linear and nonlinear signal channel limitations of Shannon theory when there is no compensation in optical fiber transmission systems ？Next-generation technologies should exceed the 100G transmission capability of coherent systems in order to approach the Shannon limit. Spectral efficiency first needs to be improved before overall transmission capability can be improved. The means to improve spectral efficiency include more complex modulation formats and channel encoding/decoding algorithms ，pre-filtering with multisymbol detection ，optical OFDM and NyquistWDM multicarrier technologies ，and nonlinearity compensation. With further optimization ，these technologies will most likely be incorporated into beyond-100G optical transport systems to meet bandwidth demand.spectral efficiency ；Shannon limit ；Gaussian noise ；optical signal noise ratio ；modulation ；nonlinearity compensation1 业务和光传输容量需求随着海量视频、大规模云计算和移动互联网的迅猛发展，电信网络的业务量将继续保持高速增长态势。

第二章习题：补充题：掷色子，（1）若各面出现概率相同（2）若各面出现概率与点数成正比试求该信源的数学模型 解： （1）根据61()1ii p a ==∑，且16()()p a p a ==，得161()()6p a p a ===，所以信源概率空间为123456111111666666⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P （2）根据61()1i i p a ==∑，且126(),()2,()6p a k p a k p a k ===，得121k =。

123456123456212121212121⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P 2-2 由符号集{}0,1组成的二阶马尔可夫链，其转移概率为P(0/00)=0.8，P(0/11)=0.2，P(1/00)=0.2， P(1/11)=0.8，P(0/01)=0.5，P(0/10)=0.5，P(1/01)=0.5，P(1/10)=0.5。

画出状态图，并计算各状态的稳态概率。

解：由二阶马氏链的符号转移概率可得二阶马氏链的状态转移概率为： P(00/00)=0.8 P(10/11)=0.2 P(01/00)=0.2 P(11/11)=0.8 P(10/01)=0.5 P(00/10)=0.5 P(11/01)=0.5 P(01/10)=0.5二进制二阶马氏链的状态集S={,1S 432,,S S S }={00，01，10，11}0.80.20.50.50.50.50.20.8⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦P 状态转移图各状态稳定概率计算：⎪⎪⎩⎪⎪⎨⎧==∑∑==41411i jij i j j WP W W 即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=++++++=+++=+++=+++=143214443432421414434333232131342432322212124143132121111W W W W P W P W P W P W W P W P W P W P W W P W P W P W P W w P W P W P W P W W0.8得：14541==W W 14232==W W 即：P(00)=P(11)=145 P(01)=P(10)=1422-6掷两粒骰子，当其向上的面的小圆点数之和是3时，该消息所包含的信息量是多少？当小圆点数之和是7时，该消息所包含的信息量又是多少？ 解：2211111(3)(1)(2)(2)(1)666618(3)log (3)log 18()P P P P P I p ⎧=⋅+⋅=⨯+⨯=⎪⎨⎪=-=⎩比特 226(7)(1)(6)(2)(5)(3)(4)(4)(3)(5)(2)(6)(1)36(7)log (7)log 6()P P P P P P P P P P P P P I p ⎧=⋅+⋅+⋅+⋅+⋅+⋅=⎪⎨⎪=-=⎩比特2-72-7设有一离散无记忆信源,其概率空间为⎥⎥⎦⎤⎢⎢⎣⎡=====⎥⎦⎤⎢⎣⎡81,41,41,833,2,1,04321x x x x P X该信源发出的消息符号序列为(202 120 130 213 001 203 210 110 321 010 021 032 011 223 210),求此消息的自信息量是多少及平均每个符号携带的信息量?解:消息序列中,“0”个数为1n =14,“1”个数为2n =13,“2”个数为3n =12,“3”个数为4n =6. 消息序列总长为N =1n +2n +3n +4n =45(个符号)(1) 消息序列的自信息量: =I ∑==41)(i iix I n -)(log 412i i ix p n∑== 比特81.87)3(log 6)2(log 12)1(log 13)0(log 142222=----p p p p(2) 平均每个符号携带的信息量为:)/(95.14571.87符号比特==N I 2-14 在一个二进制信道中，信息源消息集X={0，1}，且P(1)=P(0),信宿的消息集Y={0，1}，信道传输概率P（1/0）=1/4，P （0/1）=1/8。

信息论之父—香农20世纪中叶，信息论、控制论、系统论等标新立异的新理论相继问世，有力地“晃动”着传统的科学框架。

克劳德·香农是一位美国数学工程师，作为信息论的创始人，人们认为他是20世纪最伟大的科学家之一。

他在通信技术与工程方面的创造性工作，为计算机与远程通信奠定了坚实的理论基础。

人们尊崇香农为信息论及数字通信时代的奠基之父。

确实，他对人类的贡献超过了一般的诺贝尔获奖者。

回顾20世纪的信息革命风暴，经他阐明的信息概念、连同“比特”这个单位已经深入人心，成为今天日常生活都离不开的词汇。

家庭背景克劳德·香农(Claude Elwood Shannon，1916-2001)1916年4月30日诞生于美国密西根州的Petoskey。

在Gaylord小镇长大，当时镇里只有三千居民。

父亲是该镇的法官，他们父子的姓名完全相同，都是Claude Elwood Shannon。

母亲是镇里的中学校长，姓名是Mabel Wolf Shannon。

他生长在一个有良好教育的环境，不过父母给他的科学影响好像还不如祖父的影响大。

香农的祖父是一位农场主兼发明家，发明过洗衣机和许多农业机械，这对香农的影响比较直接。

此外，香农的家庭与大发明家爱迪生(Thomas Alva Edison，1847-1931)还有远亲关系。

香农的大部分时间是在贝尔实验室和MIT(麻省理工学院)度过的。

在“功成名就”后，香农与玛丽(Mary Elizabeth Moore)1949年3月27日结婚，他们是在贝尔实验室相识的，玛丽当时是数据分析员。

他们共有四个孩子：三个儿子Robert、James、Andrew Moore和一个女儿Margarita Catherine。

后来身边还有两个可爱的孙女。

年2月24日，香农在马萨诸塞州Medford辞世，享年85岁。

贝尔实验室和MIT发表的讣告都尊崇香农为信息论及数字通信时代的奠基之父。

攻读学位年香农在密西根大学获得数学与电气工程学士学位，然后进入MIT念研究生。

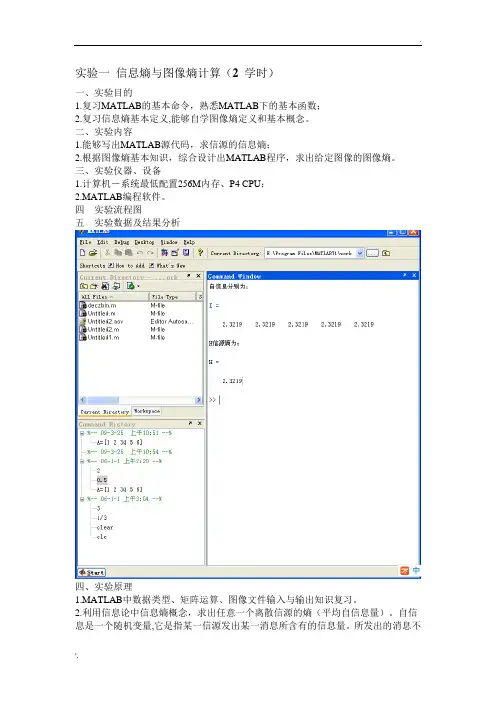
实验一信息熵与图像熵计算（2 学时）一、实验目的1.复习MATLAB的基本命令，熟悉MATLAB下的基本函数；2.复习信息熵基本定义,能够自学图像熵定义和基本概念。

二、实验内容1.能够写出MATLAB源代码，求信源的信息熵；2.根据图像熵基本知识，综合设计出MATLAB程序，求出给定图像的图像熵。

三、实验仪器、设备1.计算机－系统最低配置256M内存、P4 CPU；2.MATLAB编程软件。

四实验流程图五实验数据及结果分析四、实验原理1.MATLAB中数据类型、矩阵运算、图像文件输入与输出知识复习。

2.利用信息论中信息熵概念，求出任意一个离散信源的熵（平均自信息量）。

自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。

所发出的消息不同，它们所含有的信息量也就不同。

任何一个消息的自信息量都代表不了信源所包含的平均自信息量。

不能作为整个信源的信息测度，因此定义自信息量的数学期望为信源的平均自信息量：1( ) 1 ( ) [log ] ( ) log ( ) i n i i p a i H E p a p a X 信息熵的意义：信源的信息熵H是从整个信源的统计特性来考虑的。

它是从平均意义上来表征信源的总体特性的。

对于某特定的信源，其信息熵只有一个。

不同的信源因统计特性不同，其熵也不同。

3.学习图像熵基本概念，能够求出图像一维熵和二维熵。

图像熵是一种特征的统计形式，它反映了图像中平均信息量的多少。

图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量，令Pi表示图像中灰度值为i的像素所占的比例，则定义灰度图像的一元灰度熵为：2550 log i i i p p H图像的一维熵可以表示图像灰度分布的聚集特征，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。

选择图像的邻域灰度均值作为灰度2分布的空间特征量，与图像的像素灰度组成特征二元组，记为(i,j)，其中i表示像素的灰度值(0<=i<=255)，j表示邻域灰度(0<=j<=255),2 ( , ) / ij p f i j N上式能反应某像素位置上的灰度值与其周围像素灰度分布的综合特征，其中f(i,j)为特征二元组(i,j)出现的频数，N为图像的尺度，定义离散的图像二维熵为:2550 log ij ij i p p H构造的图像二维熵可以在图像所包含信息量的前提下，突出反映图像中像素位置的灰度信息和像素邻域内灰度分布的综合特征。

《信息论与编码》-曹雪虹-课后习题答案 第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ，转移概率为：()11|1/2p u u =，()21|1/2p uu =，()31|0p u u =，()12|1/3p u u =，()22|0p u u =，()32|2/3p u u =，()13|1/3p u u =，()23|2/3p u u =，()33|0p u u =，画出状态图并求出各符号稳态概率。

解：状态图如下状态转移矩阵为：1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1，u 2，u 3稳定后的概率分别为W 1，W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0，1}组成的二阶马尔可夫链，其转移概率为：(0|00)p =0.8，(0|11)p =0.2，(1|00)p =0.2，(1|11)p =0.8，(0|01)p =0.5，(0|10)p =0.5，(1|01)p =0.5，(1|10)p =0.5。

画出状态图，并计算各状态的稳态概率。

解：(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵：0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为：设各状态00，01，10，11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子，也就是各面呈现的概率都为1/6，求：(1) “3和5同时出现”这事件的自信息； (2) “两个1同时出现”这事件的自信息； (3) 两个点数的各种组合（无序）对的熵和平均信息量；(4) 两个点数之和（即2, 3, … , 12构成的子集）的熵；(5) 两个点数中至少有一个是1的自信息量。

《信息论基础》参考答案一、填空题1、信源编码的主要目的是提高有效性,信道编码的主要目的是提高可靠性。

2、信源的剩余度主要来自两个方面，一是信源符号间的相关性,二是信源符号的统计不均匀性。

3、三进制信源的最小熵为0，最大熵为bit/符号。

4、无失真信源编码的平均码长最小理论极限制为信源熵（或H(S)/logr= H r （S））。

5、当R=C或（信道剩余度为0）时，信源与信道达到匹配.6、根据信道特性是否随时间变化,信道可以分为恒参信道和随参信道。

7、根据是否允许失真，信源编码可分为无失真信源编码和限失真信源编码。

8、若连续信源输出信号的平均功率为，则输出信号幅度的概率密度是高斯分布或正态分布或时，信源具有最大熵，其值为值。

9、在下面空格中选择填入数学符号“”或“"（1）当X和Y相互独立时，H（XY)=H(X）+H（X/Y）=H（Y)+H（X）。

（2)（3）假设信道输入用X表示，信道输出用Y表示.在无噪有损信道中，H(X/Y)〉 0, H（Y/X)=0,I(X；Y）<H(X)。

二、若连续信源输出的幅度被限定在【2，6】区域内，当输出信号的概率密度是均匀分布时，计算该信源的相对熵，并说明该信源的绝对熵为多少.=2bit/自由度该信源的绝对熵为无穷大.三、已知信源(1）用霍夫曼编码法编成二进制变长码;（6分)（2）计算平均码长;（4分）（3）计算编码信息率；（2分）（4）计算编码后信息传输率；（2分）（5)计算编码效率。

(2分）(1)编码结果为：（2）（3）（4）其中，（5)四、某信源输出A、B、C、D、E五种符号，每一个符号独立出现,出现概率分别为1/8、1/8、1/8、1/2、1/8。

如果符号的码元宽度为0。

5。

计算:（1）信息传输速率。

（2）将这些数据通过一个带宽为B=2000kHz的加性白高斯噪声信道传输，噪声的单边功率谱密度为。

试计算正确传输这些数据最少需要的发送功率P。

解：（1）（2）五、一个一阶马尔可夫信源，转移概率为.（1) 画出状态转移图。

Polar SCL（Successive Cancellation List）是一种用于极化码译码的算法，它在译码性能和计算复杂度之间取得了很好的平衡。

极化码是一种能够接近香农极限的编码方式，因此在通信领域有着广泛的应用。

在极化码的译码过程中，Polar SCL算法能够有效地提高译码性能，并且相对于传统的译码算法来说，其计算复杂度更低。

本文将从以下几个方面对Polar SCL译码算法进行详细介绍：一、极化码的背景知识极化码是由Erdal Arikan教授在2009年提出的一种新型的编码方式，通过递归地应用变换矩阵，将输入比特逐步转化为输出比特，从而实现了输入比特的极化。

极化码因其低误码率和低译码复杂度而备受关注，在5G通信、卫星通信等领域有着广泛的应用。

二、Polar SCL算法的基本原理Polar SCL算法是一种基于列表译码的算法，它通过维护一个候选路径列表来实现译码。

在译码过程中，Polar SCL算法会不断地根据候选路径列表中的信息进行剪枝和合并，以保证译码性能的提高。

与传统的译码算法相比，Polar SCL算法在保证译码性能的能够显著降低计算复杂度。

三、Polar SCL算法的性能分析通过理论分析和实验验证，可以得出Polar SCL算法在误码性能和计算复杂度方面取得了良好的平衡。

在高信噪比条件下，Polar SCL算法能够接近香农极限，并且在低信噪比条件下，其性能优于传统的译码算法。

Polar SCL算法在实际应用中具有很大的优势。

四、Polar SCL算法的改进和应用针对Polar SCL算法在长块长度情况下存在的计算复杂度较高的问题，学术界提出了许多改进算法，例如Fast-SSC算法、List-Truncated算法等，这些算法在一定程度上降低了Polar SCL算法的计算复杂度，并且在保证译码性能的提高了译码的速度。

Polar SCL算法在5G通信、卫星通信、光通信等领域有着广泛的应用。

选题二
LDPC码在无线通信中的应用研究。探讨LDPC码在无线通信系统中的 编译码算法及性能优化方法。
选题三
极化码原理及性能分析。研究极化码的编译码原理，分析其在不同信 道条件下的性能表现，并与传统信道编码方案进行比较。
选题四
5G/6G通信中的信道编码技术。调研5G/6G通信系统中采用的信道编 码技术，分析其优缺点，并提出改进方案。
Polar码应用
探讨Polar码在5G通信、物联网等领域的应用，并分 析其性能表现。
22
06 实验环节与课程 设计
2024/1/25
23
实验环节介绍
实验一
信道容量与编码定理验证。 通过搭建简单的通信系统， 验证不同信道条件下的信道 容量及编码定理的有效性。
实验二
线性分组码编译码实验。利 用计算机软件实现线性分组 码的编译码过程，并分析其 纠错性能。
LDPC码基本原理
介绍LDPC码的编码结构、译码原理以及性 能分析。
LDPC码应用
探讨LDPC码在光纤通信、数据存储等领域 的应用，并分析其性能表现。
21
Polar码原理及应用
2024/1/25
Polar码基本原理
介绍Polar码的编码结构、信道极化原理以及性能分 析。
Polar码编译码算法
详细阐述Polar码的编码算法、译码算法以及关键技 术的实现。
2024/1/25
预测编码
利用信源符号间的相关 性进行预测，并对预测 误差进行编码，如差分 脉冲编码调制（DPCM ）。
变换编码
将信源信号通过某种变 换转换为另一域的信号 ，再对变换系数进行编 码，如离散余弦变换（ DCT）编码。
14
04 信道编码
2024/1/25

《信息论与编码》-曹雪虹-课后习题答案第二章错误!未定义书签。

2.1一个马尔可夫信源有3个符号{}1,23,uu u ，转移概率为：()11|1/2p u u =，()21|1/2p u u =，()31|0p u u =，()12|1/3p u u =，()22|0p u u =，()32|2/3p u u =，()13|1/3p u u =，()23|2/3p u u =，()33|0p u u =，画出状态图并求出各符号稳态概率。

W 2、W 31231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 2.2(0|p (0|01)p =0.5，(0|10)p 解：(0|00)(00|00)0.8p p ==(0|01)(10|01)0.5p p ==于是可以列出转移概率矩阵：0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ 状态图为：设各状态00，01，10，11的稳态分布概率为W1,W2,W3,W4有411iiWP WW==⎧⎪⎨=⎪⎩∑得13113224324412340.80.50.20.50.50.20.50.81W W WW W WW W WW W WW W W W+=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩计算得到12345141717514WWWW⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.31/6，求：(1)“3和5(2)“两个1(3)1的自信息量。

11 12 13 14 15 1621 22 23 24 25 2631 32 33 34 35 3641 42 43 44 45 4651 52 53 54 55 5661 62 63 64 65 66共有21种组合：其中11，22，33，44，55，66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯ (4)x p x p X H X P X i i i 1212181log 1812361log 3612 )(log )()(1211091936586173656915121418133612)( ⎝⎛⨯+⨯+⨯-=-=⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑2.575%是身高160厘米以上的占总数的厘米以上的某女孩是大学生”的设随机变量X 代表女孩子学历X x 1（是大学生） x 2（不是大学生）P(X) 0.25 0.75设随机变量Y 代表女孩子身高Y y1（身高>160cm）y2（身高<160cm）P(Y) 0.5 0.5已知：在女大学生中有75%是身高160厘米以上的即：bitxyp75.0)/(11=求：身高160即：ypxypxpyxpyxI5.075.025.0log)()/()(log)/(log)/(11111111⨯-=-=-=2.6掷两颗骰子，1()(1,2)(2,1)18p x p p=+=log()log18 4.170p x bit=-==7的概率log()log6 2.585p x bit=-==341231/41/8x x===⎫⎪⎭（1）求每个符号的自信息量（2）信源发出一消息符号序列为{202120130213001203210110321010021032011223210}，求该序列的自信息量和平均每个符号携带的信息量解：122118()log log 1.415()3I x bit p x === 同理可以求得233()2,()2,()3I x bit I x bit I x bit === 因为信源无记忆，所以此消息序列的信息量就等于该序列中各个符号的信息量之和就有：123414()13()12()6()87.81I I x I x I x I x bit =+++= 平均每个符号携带的信息量为87.81 1.9545=bit/符号 2.8试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍？解：四进制脉冲可以表示4个不同的消息，例如：{0,1,2,3}八进制脉冲可以表示8个不同的消息，例如：{0,1,2,3,4,5,6,7}二进制脉冲可以表示2个不同的消息，例如：{0,1}假设每个消息的发出都是等概率的，则：四进制脉冲的平均信息量symbol bit n X H / 24log log )(1=== 八进制脉冲的平均信息量symbol bit n XH / 38log log )(2=== 二进制脉冲的平均信息量symbol bit n X H / 12log log )(0===所以：四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。

[word格式]《量子力学导论》习题答案（曾谨言版，北京大学）
[pdf格式]《理论力学》习题答案（动力学和静力学）
[word格式]《大学物理》完整习题答案
[ppt格式]流体输配管网习题详解（重点）
[pdf格式]《结构化学基础》习题答案（周公度，北大版）
[pdf格式]《物理化学》习题答案与课件集合（南大）
三、课程内容改革
教学内容改革是课程改革的核心。根据我校相关专业的实际教学情况和效果，对信息论与编码教学内容改革有如下的考虑。
（一）注重教学内容的承上启下
教师在该课程教学中，要强调已学专业基础课中的信号与系统、数字信号处理和通信原理，分别解决点对点通信系统中关于信源和信道的一些具体问题，而信息论与编码将从更抽象的层面看待整个通信系统，为通信学科的发展指明了方向。正如著名通信理论家viterbi所说，如果把现代通信技术比喻成飞船，则晶体管是它的引擎，而信息论是它的方向盘[4]。注重该课程与已学课程融合的同时，还要突出该课程在后续课程学习中的作用，指出该课程是数据压缩技术、语音信号处理、图像处理等课程的理论基础。另外，教学过程中，还要适当介绍信息论的最新进展和研究热点，以激发学生的学习兴趣。
四、教学方式改革
教学方式改革的目的就是要激发学生的学习热情和学习兴趣，让学生成为教学的主体，信息论与编码的教学方式的改革包含以下几个方面。
（一）传统板书与多媒体结合
信息论与编码这一课程的内容多、理论性强，许多结论需严格的推理证明。因此，课程教学中需要把多媒体教学信息量大和传统板书易于展示复杂理论推导、表现力强、便于师生交流的优点相结合。这样，生动形象的多媒体教学保证了课堂的信息量，而严格的推理证明可以让学生深刻理解相关结论，领悟理论的精要，掌握课程的重点和难点。

东南大学移动通信国家重点实验室
22
“信息论与编码”课件
4.2 信息传输速率和编码效率
4.2.2 编码效率 信源的最大熵对应着信道容量，故信源编码器 的编码效率又可表示为

H ( X) / b 100 % H max ( X) / b
(4.9)
(4.10)
或
H (X K ) / B 100 % K H max ( X ) / B
11
“信息论与编码”课件
4.1 信源编码的模型
中文电报的编码方法
中文电报的基本编码方法是将每一个汉字或字符用4位 十进制数来表示，每一个十进制数再用5位二进制数来 表示。 例如，“信息论”三个字的电码分别是(0207)，(1873)， (6158)。以“信”为例，首先将它编成4位十进制的码 0207，再将它们变换成20位二进制的码:01101 11001 01101 11100，由此可见，其编码过程为 汉字查“标准电报电码” 电码 十~二变换 二进制码 字组
东南大学移动通信国家重点实验室
3
“信息论与编码”课件
第4章
离散信源的信源编码
从编码结果使信源消息的信息量有无损失角度，可 分为无失真信源编码和限失真信源编码两种。 无失真信源编码和限失真信源编码的理论基础分别 为香农第一定理和香农第三定理。 本章仅讨论无失真信源编码并仅限于离散信源 引出信源编码的一般模型，讨论离散信源的无失真 编码，导出香农第一定理， 给出最佳编码的概念，几种最佳编码的实例， 介绍和分析几种文本、图像的编码方法，并对译码 中可能出现的错误扩展问题提出了讨论。
i 1
这时信息传输速率为
R H (X ) / B
K
(4.6)

实验一信息熵与图像熵计算（2 学时）一、实验目的1.复习MATLAB的基本命令，熟悉MATLAB下的基本函数；2.复习信息熵基本定义,能够自学图像熵定义和基本概念。

二、实验容1.能够写出MATLAB源代码，求信源的信息熵；2.根据图像熵基本知识，综合设计出MATLAB程序，求出给定图像的图像熵。

三、实验仪器、设备1.计算机－系统最低配置256M存、P4 CPU；2.MATLAB编程软件。

四实验流程图五实验数据及结果分析四、实验原理1.MATLAB中数据类型、矩阵运算、图像文件输入与输出知识复习。

2.利用信息论息熵概念，求出任意一个离散信源的熵（平均自信息量）。

自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。

所发出的消息不同，它们所含有的信息量也就不同。

任何一个消息的自信息量都代表不了信源所包含的平均自信息量。

不能作为整个信源的信息测度，因此定义自信息量的数学期望为信源的平均自信息量：1( ) 1 ( ) [log ] ( ) log ( ) i n i i p a i H E p a p a X 信息熵的意义：信源的信息熵H是从整个信源的统计特性来考虑的。

它是从平均意义上来表征信源的总体特性的。

对于某特定的信源，其信息熵只有一个。

不同的信源因统计特性不同，其熵也不同。

3.学习图像熵基本概念，能够求出图像一维熵和二维熵。

图像熵是一种特征的统计形式，它反映了图像中平均信息量的多少。

图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量，令Pi表示图像中灰度值为i的像素所占的比例，则定义灰度图像的一元灰度熵为：2550 log i i i p p H图像的一维熵可以表示图像灰度分布的聚集特征，却不能反映图像灰度分布的空间特征，为了表征这种空间特征，可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。

选择图像的邻域灰度均值作为灰度2分布的空间特征量，与图像的像素灰度组成特征二元组，记为(i,j)，其中i表示像素的灰度值(0<=i<=255)，j表示邻域灰度(0<=j<=255),2 ( , ) / ij p f i j N上式能反应某像素位置上的灰度值与其周围像素灰度分布的综合特征，其中f(i,j)为特征二元组(i,j)出现的频数，N为图像的尺度，定义离散的图像二维熵为:2550 log ij ij i p p H构造的图像二维熵可以在图像所包含信息量的前提下，突出反映图像中像素位置的灰度信息和像素邻域灰度分布的综合特征。

一、实验目的1. 深入理解通信系统的基本原理和组成。

2. 掌握通信系统各模块的功能和作用。

3. 学会使用通信实验设备进行实验操作。

4. 分析实验结果，提高通信系统的分析和设计能力。

二、实验内容本次实验主要涉及以下内容：1. 通信系统概述- 通信系统的基本概念和组成。

- 通信系统的分类和特点。

2. 模拟通信系统- 模拟信号的产生和传输。

- 模拟调制和解调技术。

- 模拟通信系统的性能分析。

3. 数字通信系统- 数字信号的产生和传输。

- 数字调制和解调技术。

- 数字通信系统的性能分析。

4. 通信信道- 通信信道的分类和特点。

- 信道容量和香农公式。

- 信道编码和解码技术。

5. 通信系统设计- 通信系统设计的基本流程。

- 通信系统性能指标的确定。

- 通信系统设备的选型和配置。

三、实验步骤1. 通信系统概述- 学习通信系统的基本概念和组成。

- 了解通信系统的分类和特点。

2. 模拟通信系统- 使用模拟通信实验设备，产生模拟信号。

- 进行模拟调制和解调实验，观察调制和解调过程。

- 分析模拟通信系统的性能。

3. 数字通信系统- 使用数字通信实验设备，产生数字信号。

- 进行数字调制和解调实验，观察调制和解调过程。

- 分析数字通信系统的性能。

4. 通信信道- 学习通信信道的分类和特点。

- 使用信道模拟设备，模拟信道特性。

- 分析信道容量和香农公式。

5. 通信系统设计- 根据实验需求，设计通信系统。

- 选择合适的通信设备和参数。

- 进行系统测试和性能分析。

四、实验结果与分析1. 模拟通信系统- 通过实验，观察到模拟调制和解调过程，验证了调制和解调技术的正确性。

- 分析模拟通信系统的性能，得出系统带宽、信噪比等指标。

2. 数字通信系统- 通过实验，观察到数字调制和解调过程，验证了数字调制和解调技术的正确性。

- 分析数字通信系统的性能，得出系统带宽、信噪比、误码率等指标。

3. 通信信道- 通过实验，模拟信道特性，分析信道容量和香农公式。

1、 熵 是香农信息论最基本最重要的概念。

2、 单符号离散信源一般用随机变量描述，而多符号离散信源一般用 随机矢量 描述。

3、 两个相互独立的随机变量的联合自信息量等于 两个自信息量之和 。

4、 离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍 。

5、 对于n 元m 阶马尔可夫信源，其状态空间共有 n m 个不同的状态。

6、 若一离散无记忆信源的信源熵H （X ）等于4.2，对信源进行等长的无失真二进制编码，则编码长度至少为 5 。

7、 同时掷两个正常的骰子，各面呈现的概率都为1/6，则“3和6同时出现”这件事的自信息量是 log 218或（1+2 log 23）。

8、 一副充分洗乱的扑克牌（52张），从中任意抽取1张，然后放回，若把这一过程看作离散无记忆信源，则其信源熵为 52log 2 。

9、 具有一一对应关系的无噪信道的信道容量C= log 2n 。

10、 信道编码定理是一个理想编码的存在性定理，即：信道无失真传递信息的条件是 信息率小于信道容量 。

11、 信源的消息通过信道传输后的误差或失真越大，信宿收到消息后对信源存在的不确定性就 越大 ，获得的信息量就越小12、 平均失真度的下限取0的条件是失真矩阵的 每一行至少有一个零元素 。

13、 率失真函数对允许的平均失真度是 单调递减和连续的 。

14、 对于离散无记忆信源的率失真函数的最大值是 log 2n 。

15、 信源编码的目的是： 提高通信的有效性 。

16、 对具有8个消息的单符号离散无记忆信源进行4进制哈夫曼编码时，为使平均码长最短，应增加 2 个概率为0的消息。

17、 对于香农编码、费诺编码和哈夫曼编码，编码方法惟一的是 香农编码 。

18、 游程序列的熵 等于 原二元序列的熵。

19、 n 位重复码的编码效率是 1/n 。

20、 若纠错码的最小距离为d min ，则可以纠正任意小于等于t= ⎥⎦⎥⎢⎣⎢-21min d 个差错。