控制理论(Control Theory)
- 格式:pdf
- 大小:824.44 KB
- 文档页数:5

德勒兹控制论
德勒兹控制论(Deleuze's Control Theory)是法国哲学家吉尔·德勒兹(Gilles Deleuze)提出的一种社会政治理论。
该理论于1990年代初开始发展,是对传统的权力和社会控制理论的批判和重构。
德勒兹控制论认为,传统的社会控制理论主要基于禁止、纪律和监管的方式,通过建立规则和制度来统治和管理社会。
然而,在当代社会,信息科技、全球化和新媒体的出现,导致了权力的变异和社会关系的复杂性。
德勒兹控制论认为,传统的禁止式的控制已经变得不再有效,社会中的控制机制已发生转变。
德勒兹控制论提出了几个关键概念:
1. 控制社会(Societies of Control):德勒兹认为,当代社会不再是固定的禁止和纪律的社会,而是通过控制和操控来达到统治的目的。
这种控制是更加隐蔽、持续而流动的,并且通过全面的监视、管制和技术手段来实现。
2. 阀值(Threshold):阀值是指个体或群体进入特定状态的点,它可以是信息系统中的某个节点,也可以是个人在社会中所处的位置。
通过触发阀值,控制力量可以实施更加精确和个性化的控制。
3. 可塑性(Plasticity):控制论强调了个体的可塑性,即个体受到控制力量的影响,不断被塑造和改变。
个体在控制论中不再是单一和固定的,而是可变化和多样化的。
德勒兹控制论对社会政治的理论和实践提出了一种新的观点,强调了控制力量的变异性和复杂性。
它对于理解当代社会中的权力运行和社会关系具有重要的意义。

最优控制理论最优控制理论(optimal control theory),是现代控制理论的一个主要分支,着重于研究使控制系统的性能指标实现最优化的基本条件和综合方法。
最优控制理论是研究和解决从一切可能的控制方案中寻找最优解的一门学科。
它是现代控制理论的重要组成部分。
简介这方面的开创性工作主要是由贝尔曼(R.E.Bellman)提出的动态规划和庞特里亚金等人提出的最大值原理。
这方面的先期工作应该追溯到维纳(N.Wiener)等人奠基的控制论(Cybernetics)。
1948年维纳发表了题为《控制论—关于动物和机器中控制与通讯的科学》的论文,第一次科学的提出了信息、反馈和控制的概念,为最优控制理论的诞生和发展奠定了基础。
研究内容最优控制理论所研究的问题可以概括为:对一个受控的动力学系统或运动过程,从一类允许的控制方案中找出一个最优的控制方案,使系统的运动在由某个初始状态转移到指定的目标状态的同时,其性能指标值为最优。
这类问题广泛存在于技术领域或社会问题中。
例如,确定一个最优控制方式使空间飞行器由一个轨道转换到另一轨道过程中燃料消耗最少,选择一个温度的调节规律和相应的原料配比使化工反应过程的产量最多,制定一项最合理的人口政策使人口发展过程中老化指数、抚养指数和劳动力指数等为最优等,都是一些典型的最优控制问题。
最优控制理论是50年代中期在空间技术的推动下开始形成和发展起来的。
苏联学者Л.С.庞特里亚金1958年提出的极大值原理和美国学者R.贝尔曼1956年提出的动态规划,对最优控制理论的形成和发展起了重要的作用。
线性系统在二次型性能指标下的最优控制问题则是R.E.卡尔曼在60年代初提出和解决的。
主要方法为了解决最优控制问题,必须建立描述受控运动过程的运动方程,给出控制变量的允许取值范围,指定运动过程的初始状态和目标状态,并且规定一个评价运动过程品质优劣的性能指标。
通常,性能指标的好坏取决于所选择的控制函数和相应的运动状态。


社会控制理论(social control theory)亦称“社会键理论”。
解释人为什么不犯罪的理论。
美国犯罪学家T.赫希提出。
基本观点:人性本来就是恶的,每个人都有可能犯罪,犯罪是缺乏社会控制的产物。
T.赫希在《少年犯罪的原因》(1969)中认为,人是不道德的动物,每个人都有犯罪的自然倾向,故无需解释人为什么会犯罪,而应解释人为什么不犯罪。
认为人之所以不犯罪,是在社会化过程中形成各种社会控制机制(社会键)的结果。
社会键有四种成分:
(1)依恋,即个体对父母、学校和同辈朋友的感情依恋。
这种感情依恋越强烈,人就越不可能犯罪;
(2)奉献,即个体对传统的生活目标的追求。
若人渴望获得社会承认的、传统的成功,就不可能冒损害自己前途的危险去违法犯罪;
(3)参与,即参加传统的活动,如学术活动、体育运动等。
人若用全部的时间和精力参与传统的活动,就不可能进行违法犯罪活动;
(4)信仰,即对社会的道德、法律规范等的尊重。
人若尊重道德与法律规范,就不会出现违反这些规范的行为。



《控制理论基础》课程简介06191310控制理论基础 3Fundamentals of control theory 3-0预修课程:微积分,线性代数,常微分方程,大学物理面向对象:三、四年级本科生内容简介:控制科学是由数学、工程学和计算机科学交叉发展形成的一门学科。
本课程介绍控制系统的描述、分析、设计和综合的数学基础理论,内容包括:系统的输入-输出描述、状态变量描述、频率描述及其相互关系;控制系统分析、能控性和能观性、稳定性;极点配置、观测器和调节器设计等。
选用教材或参考书:教材:《控制理论基础》,李训经等著,高等教育出版社,2002参考书:1、《工程控制论》,钱学森著,科学出版社,19582、《线性系统理论与设计》,陈启宗著,科学出版社,1988《控制理论基础》教学大纲06191310控制理论基础 3Fundamentals of control theory 3-0预修课程:微积分,线性代数,常微分方程,大学物理面向对象:三、四年级本科生一、教学目的和基本要求:通过本课程的学习使学生获得以下知识和能力:1. 理解“控制理论”是工程控制过程的数学理论这一学科特点,理解控制的数学模型和概念的工程控制背景,理解“数学控制原理”的“工程控制意义”;2. 了解控制系统的基本组成及其功能,掌握对控制系统建立数学模型的方法和步骤;3.掌握线性控制系统的各种描述方法及其相互关系;3. 掌握线性定常系统的基本分析、设计和综合方法。
二、主要内容及学时分配:第一章控制论概貌(3学时)第二章线性系统模型(13学时)输入-输出描述、状态变量描述、频域描述以及相互关系和转换方法,几种典型环节,离散时间系统,等价动态方程。
第三章能控性和能观性(10学时)概念,能控性子空间,秩条件,频域条件,能控(能观)规范分解,最小实现。
第四章稳定性分析(8学时)输入-输出稳定性,Routh-Hurwitz判局,线性动态方程的稳定性,Lyapunov定理,第五章状态反馈与观测器设计(8学时)状态反馈及其不变量,极点配置定理,能稳性,能检测性与观测器设计第六章最优调节器设计(6学时)反馈镇定,控制参数选择,LQR问题,代数Riccati方程,跟踪问题。

控制理论的发展与一些存在的问题段志生北京大学工学院什么是自动化?一般是指生产、管理和科研过程中,在没有人的直接干预下,通过一定的技术装置,就能达到预定的目标。
其中有关的技术装置,就是自动控制装置。
控制理论-自动化的基础自然科学--认识世界控制--改造世界北京大学一、控制论的产生与发展社会背景现代社会的生产和管理对于高度自动化水平的需要数学分析, 微分方程, 统计数学, 信息科学社会一旦有技术上的需要,则这种需要就会比十所大学更能把科学推向前进。
——恩格斯标志二战期间,维纳参加了火炮控制和电子计算机的研制工作。
1948年维纳发表了著名的《控制论—关于在动物和机器中控制和通讯的科学》标志着控制论作为一门科学诞生。
1、我国古代、近代的自动化装置北京大学及其反映的控制思想李约瑟中国科学技术史北京大学瓦特离心式调速器1787年J.C. Maxwell 1868年发表论文“论调速器”对反馈作了理论论述,并从数学上作了探讨。
2、直接推动近代科技发展的调速器北京大学3、控制论的基本概念和方法(1)目的有无目的是区分人与机器的根本问题, 目的论与机械论的根本对立.(2)行为、控制为了改善某个对象的功能,需要获得并使用信息,以这种信息为基础而选出的,加于该对象上的作用。
(3)黑箱——灰箱——白箱“知人知面不知心”输入输出中医“望、闻、问、切”(1)按偏差进行补偿的系统特点:系统中至少有一个将输出量加以回输的闭合环路,是具有反馈的闭环系统。
(2)按扰动进行调节的系统特点:输入量按负荷的变化而成比例的改变以趋近目标值,是开环系统,抗干扰能力差。
基本控制思想二、技术层次控制科学的发展1、自动化的实现一般自动控制系统的结构图2、控制论的应用与主要分支1、工程控制论控制论在工程技术方面(机械的、电机的和电子的自动控制系统)上的运用。
又称自动控制理论,或简称控制理论(control theory)我国著名科学家钱学森1954年在美国出版了《工程控制论》一书。
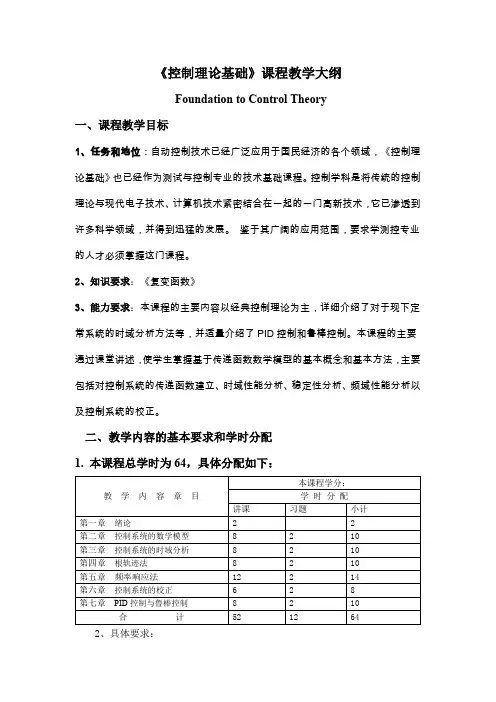
《控制理论基础》课程教学大纲Foundation to Control Theory一、课程教学目标1、任务和地位:自动控制技术已经广泛应用于国民经济的各个领域,《控制理论基础》也已经作为测试与控制专业的技术基础课程。
控制学科是将传统的控制理论与现代电子技术、计算机技术紧密结合在一起的一门高新技术,它已渗透到许多科学领域,并得到迅猛的发展。
鉴于其广阔的应用范围,要求学测控专业的人才必须掌握这门课程。
2、知识要求:《复变函数》3、能力要求:本课程的主要内容以经典控制理论为主,详细介绍了对于现下定常系统的时域分析方法等,并适量介绍了PID控制和鲁棒控制。
本课程的主要通过课堂讲述,使学生掌握基于传递函数数学模型的基本概念和基本方法,主要包括对控制系统的传递函数建立、时域性能分析、稳定性分析、频域性能分析以及控制系统的校正。
二、教学内容的基本要求和学时分配1. 本课程总学时为64,具体分配如下:2、具体要求:第一章绪论[目的要求] 掌握控制系统的一般概念以及控制系统的分类。
[教学内容] 自动控制系统的一般概念、开环控制与闭环控制、自动控制系统的分类、对控制系统性能的要求和本课程的任务[重点难点] 开环控制与闭环控制[教学方法] 课堂讲授[作业][课时] 2第二章控制系统的数学模型[目的要求] 掌握线性定常控制系统的传递函数数学模型的建立。
[教学内容] 列写系统微分方程的一般方法、非线性数学模型的线性化、传递函数、框图和系统的传递函数、信号流图和梅逊公式的应用[重点难点] 列写系统微分方程的一般方法、传递函数、框图和系统的传递函数、信号流图和梅逊公式的应用[教学方法] 课堂讲授、课堂练习[作业] 习题2[课时] 10第三章控制系统的时域分析[目的要求] 对线性控制系统进行分析时域分析[教学内容] 典型的试验信号、一阶系统的时域响应、二阶系统的时域响应、高阶系统的时域响应、线性定常系统的稳定性、Routh稳定判据、控制系统的稳态误差、控制系统对参数变化的灵敏度[重点难点] 一阶系统的时域响应、二阶系统的时域响应、线性定常系统的稳定性、Routh稳定判据、控制系统的稳态误差[作业] 习题3[课时] 10第四章根轨迹法[目的要求] 用根轨迹法对线性控制系统进行分析[教学内容] 根轨迹的基本概念、绘制根轨迹的基本规则、参量根轨迹的绘制、非最小相位系统的根轨迹、特征方程根的灵敏度、用根轨迹分析控制系统[重点难点] 绘制根轨迹的基本规则、参量根轨迹的绘制[教学方法] 课堂讲授、课堂练习[作业] 习题4[课时] 10第五章频率响应法[目的要求] 用频率响应法对线性控制系统进行分析[教学内容] 频率特性、对数坐标图、极坐标图、乃氏稳定判据、相对稳定性分析、频域性能指标与时域性能指标间的关系、传递函数的实验确定[重点难点] 对数坐标图、极坐标图、乃氏稳定判据[教学方法] 课堂讲授、课堂练习[作业] 习题5[课时] 14第六章控制系统的校正[目的要求] 线性控制系统的校正[教学内容] 超前校正、滞后校正、滞后-超前校正[重点难点] 超前校正、滞后校正、滞后-超前校正[作业] 习题6[课时] 8第七章 PID控制与鲁棒控制[目的要求] PID控制与鲁棒控制[教学内容] PID控制器及其参数的调整、控制系统的鲁棒性和灵敏度、控制系统的鲁棒性分析、鲁棒控制系统的设计[重点难点] PID控制器及其参数的调整、控制系统的鲁棒性和灵敏度、控制系统的鲁棒性分析[教学方法] 课堂讲授、课堂练习[作业] 习题7[课时] 10三、大纲说明主要围绕执行本大纲优化教学过程中相关问题作必要说明,一般有:1、考试要求与考试方法:闭卷考试。


主要心理治疗理论简介展开全文一、精神分析治疗法创始人物,Sigmind Freud(1856-1939),对於心理学的影响非常深远,几乎所有的咨询与心理治疗理论都与精神分析治疗法有关。
其主要的观点是人的行为受制於心理能量与幼年时性心理事件的影响。
潜意识是行为产生的驱力,会受到性冲动(生之本能)与攻击冲动(死之本能)的驱使。
Freud提出了性心理发展阶段,包含口欲期(0-1岁)、肛门期(1-3岁)、性器期(3-6岁)、潜伏期(6-12岁)、性征期(12-18岁),而其中幼年时(六岁之前)的心理冲突会影响人格发展的健全。
继Freud之后,Erikson提出心理社会化发展阶段论, Jung的集体潜意识理论;Klein, Wincott, Fairbairn, Guntrip, Balint, Mahler 等人提出客体关系理论(object rel-ations theory);其中Mahler 所提出的理论是客体关系理论中,很重要的理论之一,Mahler, Pine & Bergman(1975)有系统地提出分离─个体(separation-individuation)过程的理论,这个过程包含了分离与个体过程,为探讨幼年三岁前与母亲的互动关系。
「分离」是指个体一开始与母亲共生关系,之后就开始了分离的过程;而「个体」是个体在经历「分离─独立」过程,对自己特质假设的过程。
个体必须经过这些历程,个体才算是「心理上的诞生」(psychological birth),并成一个真正的人,建立自己与他人的稳固关系。
而边缘性人格异常(borderline personality disorder)就是发生在分离─个体历程中的不顺利,母亲无法适应与忍受幼儿进行个体化的历程,因而造成个体情绪不稳定、易怒、自我破坏行为及无法忍受焦虑等。
二、阿德勒学派治疗法创始人物Alfred Adler(1856- 1939),又称个体心理学,为抛弃Freud的基本理论,强调人性的正面观点,认为行为受到社会兴趣、追求意义与目标的影响,探讨个人的成长模式,强调负起责任,创造出自己的命运。
control theory 国外教程以下是一些关于Control Theory的国外教程资源:1. "Control Engineering: An Introduction with the Use of MATLAB" by Derek P. Atherton这本书是关于控制工程的入门教程,结合使用MATLAB进行实践应用。
2. "Modern Control Engineering" by Katsuhiko Ogata这本经典教材涵盖了现代控制工程的核心概念和技术,包括系统建模、系统响应和系统稳定性等方面。
3. "Control Systems Engineering" by Norman S. Nise这本教材介绍了控制系统工程的基础知识,包括控制器设计、系统建模和性能评估等内容。
4. "Feedback Control of Dynamic Systems" by Gene F. Franklin, J. David Powell, and Abbas Emami-Naeini这本教材深入介绍了反馈控制理论和实践应用,包括线性系统和非线性系统控制等方面的内容。
5. "Control Engineering: A Guide for Beginners" by Paul Lynn这本教材专为初学者编写,讲解了控制工程的基础概念和技术,并提供了实际问题的解决方法。
6. "Control Systems: Principles and Design" by M. Gopal这本教材介绍了控制系统原理和设计方法,结合了理论和实践应用,适合学习控制系统的基础知识。
7. "System Dynamics and Control" by Eronini Uduehi and Charles Ampadu这本教材探讨了系统动力学和控制的概念和原理,包括线性和非线性系统的分析和设计。
系统科学中的控制论交通运输学院张心哲系统科学中的控制论交通运输学院张心哲摘要: 控制论是近年来发展起来的一门新科学,并且正迅速地应用到各个领域。
本文概述了控制论的基本概念与发展历史,说明了控制系统的一般理论与控制论的研究方法,而且介绍了应用控制论的基本理论与方法形成的控制论的各分支学科。
此外,提出了控制论面临的挑战问题。
关键词:控制论、控制理论、系统科学、控制系统Cybernetics of the System ScienceJang Sim CholAbstract: Cybernetics is a new school subject which is developed recently, now, it is applying to various field rapidly. This paper summarize about the basic concept and development history of the cybernetics. Also, this paper explain the general theory of control system and the study direction of cybernetics, and it introduce a various school subject of cybernetics that is formed by applying to the basic theory and method of cybernetics. And others, put forward a difficult problem of the cybernetics.Keyword: Cybernetics, Control theory, System Science, Control System1.控制论的基本理论1.1 控制论的发展过程与研究对象1.1.1 控制论的形成及发展过程控制论(cybernetics)这个词不是现代才有的。