坐标正反算(带高程,可以算任何线性)

坐标正反算计算公式坐标的正反算是指根据点的经纬度坐标计算出该点所对应的位置，或者根据位置信息计算出该位置的经纬度坐标。

在地理信息系统中，正反算是非常重要的基本操作。

下面将分别介绍坐标的正算和反算的计算公式。

坐标正算即通过经纬度坐标计算出该点所对应的位置。

设经度为L，纬度为B，L0为中央经度（通常取地理区域中心点的经度），E为横轴坐标，N为纵轴坐标，M0为中央经线的投影，f为椭球扁率。

（1）将地球视为一个椭球体，对于小范围的区域，可以采用球面近似。

此时可以使用平面直角坐标系进行计算，并忽略地球的扁率和曲率。

具体计算公式如下：E=L-L0N=B-B0其中，B0为中央纬度。

（2）在地表为曲面的情况下，需要考虑地球的扁率和曲率。

此时可以使用高斯平面直角坐标系进行计算，公式如下：K = (a / √(1 - e^2 * sin^2B)) * √(1 + t^2)L = (L - L0) * cosBX=K*[L+(1-t^2+q^2)*L^3/6+(5-18*t^2+t^4+14*q^2-58*t^2*q^2)*L^5/120]Y=K*(M-M0+(1-t^2+q^2)*L^2/2+(5-14*t^2+3*t^4+14*q^2-28*t^2*q^2)*L^4/24)其中，a为椭球长半轴，e为椭球第一偏心率，M为曲面子午线弧长，t = tanB，q = (ωL)^2 * cosB，ω为地球自转角速度。

坐标反算即通过位置信息计算出该位置的经纬度坐标。

（1）对于小范围的区域，可以近似为平面直角坐标系，使用直角坐标系的计算公式即可反算出经纬度坐标。

具体计算公式如下：L=L0+EB=B0+N（2）对于地球曲面的情况，使用高斯平面直角坐标系进行反算时，可以采用交迭算法（迭代计算）。

迭代计算公式如下：L1 = [(X / K) - (1 - t^2 + q^2)(L1^3) / 6 - (5 - 18 * t^2 +t^4 + 14 * q^2 - 58 * t^2 * q^2)(L1^5) / 120] / cosBB1 = [(Y / K) - M - (1 - t^2 + q^2)(L1^2) / 2 - (5 - 14 *t^2 + 3 * t^4 + 14 * q^2 - 28 * t^2 * q^2)(L1^4) / 24] / (a /√(1 - e^2 * sin^2B))其中，L1、B1为迭代计算的经纬度坐标，X、Y为已知的平面坐标，K为局部坐标系绘图比例尺系数，t、q的计算和上述正算公式相同。

测量坐标正反算的方法测量坐标是一种常见的测量方法，用于确定物体在平面或者空间中的位置。

在实际测量中，我们往往需要进行坐标的正反算，即根据已知的坐标计算未知物体的位置或者根据已知物体的位置计算其坐标。

本文将介绍常见的测量坐标正反算的方法。

一、坐标的正算坐标的正算是指根据已知物体的位置计算其坐标。

在实际测量中，我们常用的方法有：1. 三角测量法三角测量法是一种基于三角关系的测量方法，适用于平面测量。

它利用视线方向的角度和边长关系推导出物体的坐标。

在三角测量法中，首先需要选择至少两个已知基准点，并确定其坐标。

然后，通过测量目标点与基准点之间的角度和边长，利用三角关系计算出目标点的坐标。

三角测量法的优点是精度较高、适用范围广，但需要测量目标点与基准点之间的角度和边长，测量过程比较复杂。

2. 几何测量法几何测量法是一种基于几何关系的测量方法，适用于平面和空间测量。

它利用测量物体与多个基准点之间的几何关系计算出物体的坐标。

在几何测量法中，首先需要选择至少三个已知基准点，并确定其坐标。

然后，通过测量目标点与基准点之间的距离、角度和方向等几何关系，利用几何图形和计算方法计算出目标点的坐标。

几何测量法的优点是简单易懂、计算方便，但需要选择合适的基准点和利用几何关系进行计算，对测量者的几何知识要求较高。

二、坐标的反算坐标的反算是指根据已知坐标计算出物体的位置。

在实际测量中，我们常用的方法有：1. 三角反算法三角反算法是一种基于三角关系的计算方法，适用于平面测量。

它利用已知基准点的坐标和目标点与基准点之间的角度和边长关系推导出目标点的位置。

在三角反算法中，首先需要选择至少两个已知基准点，并确定其坐标。

然后，通过测量目标点与基准点之间的角度和边长，利用三角关系计算出目标点的位置。

三角反算法的优点是计算简单、精度较高，但需要测量目标点与基准点之间的角度和边长。

2. 几何反算法几何反算法是一种基于几何关系的计算方法，适用于平面和空间测量。

第六章→第三节→导线测量内业计算导线计算的目的是要计算出导线点的坐标，计算导线测量的精度是否满足要求。

首先要查实起算点的坐标、起始边的方位角，校核外业观测资料，确保外业资料的计算正确、合格无误。

一、坐标正算与坐标反算1、坐标正算已知点的坐标、边的方位角、两点间的水平距离，计算待定点的坐标，称为坐标正算。

如图6-6 所示，点的坐标可由下式计算：式中、为两导线点坐标之差，称为坐标增量，即：【例题6-1】已知点A坐标，=1000、=1000、方位角=35°17＇"，两点水平距离=，计算点的坐标？35o17＇"=35o17＇"=2、坐标反算已知两点的坐标，计算两点的水平距离与坐标方位角，称为坐标反算。

如图6-6可知，由下式计算水平距离与坐标方位角。

（6-3）（6-4）式中反正切函数的值域是-90°～+90°，而坐标方位角为0°～360°，因此坐标方位角的值，可根据、的正负号所在象限，将反正切角值换算为坐标方位角。

【例题6-2】=、=、=、=，计算坐标方位角计算坐标方位角、水平距离。

=62°09＇"+180°=242°09＇"注意：一直线有两个方向，存在两个方位角，式中：、的计算是过A点坐标纵轴至直线的坐标方位角，若所求坐标方位角为，则应是A点坐标减点坐标。

坐标正算与反算，可以利用普通科学电子计算器的极坐标和直角坐标相互转换功能计算，普通科学电子计算器的类型比较多，操作方法不相同，下面介绍一种方法。

【例题6-3】坐标反算，已知=、=、=、=，试计算坐标方位角、水平距离。

键入按等号键［=］等于纵坐标增量，按储存键［］，键入按等号键［=］等于横坐标增量，按［］键输入，按［］显示横坐标增量，按［］键输入，按第二功能键［2ndF］，再按［］键，屏显为距离，再按［］键，屏显为方位角。

【例题6-4】坐标正算，已知坐标方位角=294°42＇51"，=，试计算纵坐标增量横坐标增量。

坐标正算和坐标反算名词解释
坐标正算和坐标反算是地理学和测量学中两个重要的术语，用于描述地球上某一地点的确定和定位。

坐标正算（Forward Calculation）是指根据已知的地理坐标系统或投影坐标系统的参数，通过数学计算得出地球上某一点的具体位置。

这一过程通常涉及到大地测量技术、三角测量和测量学等方法。

坐标正算被广泛应用于地图制作、导航系统、地理信息系统（GIS）等领域。

坐标反算（Inverse Calculation）是指通过已知地球上某一点的经纬度或投影坐标，利用反向的数学计算方法得出该点所在的地理或投影坐标系统的参数。

坐标反算可用于测量点的地理位置的确定，具体应用包括GPS定位系统、地图制作、地理勘测等领域。

坐标正算和坐标反算分别描述了地球上某一点的确定和定位过程。

坐标正算通过已知的参数计算出具体位置，而坐标反算则通过已知的位置反向计算出相应的参数。

这两个概念在地理学和测量学中起着重要的作用，为地理信息系统和定位导航系统等提供了基础支持。

坐标正反算定义及公式一、坐标正算（地理坐标转平面坐标）坐标正算是将地球上的地理坐标（经纬度）转换为平面坐标（笛卡尔坐标或者极坐标）。

坐标正算是地图制图的一项基本工作。

1.大地参考椭球体模型在进行坐标正算之前，需要先定义一个大地参考椭球体模型，用于近似地球的形状。

常用的大地参考椭球体模型有WGS84、北京54等。

这些模型定义了地球的椭球体参数，如长半轴、扁率等。

2.经度、纬度的度分秒表示法地理坐标通常使用度分秒表示法来表示经度和纬度。

经度是以东西方向为正负，以本初子午线（通常是格林威治子午线）为基准；纬度是以南北方向为正负，以赤道为基准。

3.大地坐标系和平面坐标系大地坐标系是地球表面的经纬度坐标系，平面坐标系是一个笛卡尔坐标系或者极坐标系，用于表示地球表面的平面位置。

4.坐标正算公式坐标正算的公式根据大地参考椭球体模型的不同而有所不同，这里以WGS84椭球体模型为例。

假设待转换的地理坐标是经度λ、纬度φ，转换后的平面坐标是X、Y。

首先，计算出椭球体的参数e：e=√(a^2-b^2)/a其中，a是椭球体的长半轴，b是椭球体的短半轴。

然后，计算出曲率半径N：N = a / √(1 - e^2 * sin^2(φ))接着，计算出当前点的平面坐标：X = (N + h) * cos(φ) * cos(λ)Y = (N + h) * cos(φ) * sin(λ)其中，h是当前点的海拔高度。

以上就是坐标正算的基本公式，可以将地理坐标转换为平面坐标。

二、坐标反算（平面坐标转地理坐标）坐标反算是将平面坐标（笛卡尔坐标或者极坐标）转换为地理坐标（经纬度）。

坐标反算是地图制图或者位置定位的一项重要工作。

1.平面坐标的原点和单位平面坐标通常以其中一点为原点，单位长度为米或者其他距离单位。

原点可以在任意位置，但是通常选择区域的中心或者其中一突出地物为原点。

2.坐标反算的过程坐标反算的过程是根据平面坐标和大地参考椭球体模型，计算出对应的地理坐标。

工程测量坐标正反算公式工程测量坐标正反算公式是指基于已知控制点坐标和测量仪器测量数据，通过计算获得被测物体或地形的坐标点。

在这个过程中，正算指的是从控制点计算被测点坐标的过程，而反算则是从已知被测点坐标计算控制点坐标的过程。

在本文中，我将详细介绍工程测量坐标正反算公式的原理和实际应用场景。

一、工程测量坐标正反算公式原理工程测量坐标正反算公式的原理主要是基于三角测量和距离测量原理。

三角测量法利用三角形的几何关系，通过测量三角形内角或边长，计算出三角形的各个顶点坐标。

而距离测量法则是通过测量被测物体或地形与仪器的距离，然后利用三角函数计算出被测物体或地形的坐标。

在实际工作中，测量仪器主要有全站仪、经纬仪、水准仪和电子测距仪等。

全站仪是一种常用的测量仪器，它可以测量水平角、垂直角和斜距，并输出相应的坐标值。

而经纬仪则是一种测量方位角和高度差的仪器，它常用于野外导线路线测量；水准仪则用于测量高差，电子测距仪则用于测量地形点到仪器的直线距离。

在进行工程测量坐标正反算时，需要先确定控制点坐标。

控制点分为基准控制点和工作控制点，基准控制点是指通过已知的测量结果或GPS测量等方式已知其坐标的点，而工作控制点则是在进行实测工作时测量得到的坐标点。

基准控制点与工作控制点之间的坐标关系构成了控制网络，该网络是工程测量的基础。

对于工程测量坐标正算来说，可以利用如下公式计算：X = XC + D × cos(V)Y = YC + D × sin(V) × cos(H)Z = ZC + D × sin(V) × sin(H) + hX、Y、Z为被测点的坐标；XC、YC、ZC为控制点的坐标；D为控制点与被测点的距离；V为控制点与被测点之间的垂直角；H为控制点与被测点之间的水平角；h为控制点与被测点之间的高差。

该公式利用三角函数计算出被测点的坐标，精度高且适用于不同的测量场景。

测量坐标正反算公式是什么引言在测量领域中，坐标正反算是一种常用的计算方法，用于将实际测量值转换为地理坐标或者将地理坐标转换为实际测量值。

本文将介绍测量坐标正反算的基本原理和公式，并通过示例进行说明。

坐标正算坐标正算是将实际测量值（如长度、角度等）转换为地理坐标的过程。

在进行坐标正算时，通常需要已知一些控制点的地理坐标，并通过测量的实际值来计算待测点的地理坐标。

点的水平坐标正算对于点的水平坐标正算，通常使用以下公式：X = X₀ + ∑(Di * cos ai)Y = Y₀ + ∑(Di * sin ai)其中，X₀和Y₀为已知控制点的地理坐标，Di为待测点到控制点的实测距离，ai 为待测点到控制点的真方位角（或差角）。

点的高程坐标正算对于点的高程坐标正算，通常使用以下公式：Z = Z₀ + ∑(Hi)其中，Z₀为已知控制点的高程坐标，Hi为待测点到控制点的高差。

坐标反算坐标反算是将已知的地理坐标转换为实际测量值的过程。

在进行坐标反算时，通常需要已知一些控制点的地理坐标，并通过测量待测点与已知控制点的实际值来计算实际测量值。

点的水平坐标反算点的水平坐标反算根据已知的控制点的地理坐标和实测距离，计算待测点与已知控制点的方位角（或差角）和距离。

其中，方位角可使用以下公式计算：tan α = (Y-Y₀) / (X-X₀)其中，X₀和Y₀为已知控制点的地理坐标，α为待测点到控制点的方位角。

待测点的距离可以使用以下公式计算：D = √((X-X₀)² + (Y-Y₀)²)点的高程坐标反算点的高程坐标反算根据已知的控制点的高程坐标和实测高差，计算待测点与已知控制点的高差。

已知控制点的高程坐标和高差可以通过以下公式计算：Hi = Z-Z₀其中，Z₀为已知控制点的高程坐标，Hi为待测点到控制点的高差。

示例为了更好地理解坐标正反算的原理，这里给出一个示例。

假设有一个测量任务，要求测量某点A的地理坐标。

坐标正反算定义及公式1.坐标正算：坐标正算是指根据给定的地球坐标系的椭球体参数、基准椭球体参数和初始二维坐标，通过一系列计算，求解出地球上对应的三维坐标。

这是将地图中的二维信息转换为地球上的三维信息的过程。

坐标正算的公式如下：X=cosB*cosL*HY=cosB*sinL*HZ=sinB*H其中，X、Y、Z分别表示地球上的三维坐标，B表示纬度，L表示经度，H表示高程。

2.坐标反算：坐标反算是指根据给定的地球坐标系的椭球体参数、基准椭球体参数和地球上的三维坐标，通过一系列计算，求解出地图上对应的二维坐标。

这是将地球上的三维信息转换为地图中的二维信息的过程。

坐标反算的公式如下：L=atan(Y/X)B=atan(Z/sqrt(X^2+Y^2))H=sqrt(X^2+Y^2+Z^2)其中，L表示经度，B表示纬度，H表示高程，X、Y、Z表示地球上的三维坐标。

在坐标正反算中，还需要考虑一些特殊情况，如椭球体的椭率偏差、大地基准面的形状等。

根据这些特殊情况，需要进行一些修正和适用于不同地区的公式。

此外，还有其他一些常见的坐标系统，如平面坐标系统、高斯投影坐标等，它们都有相应的坐标正反算公式。

值得注意的是，坐标正反算在实际应用中非常广泛，例如地图的绘制、GPS定位、导航系统等都需要通过坐标正反算来实现。

因此，熟练掌握坐标正反算的原理和公式对于地理信息专业人员至关重要。

总之，坐标正反算是将地图上的二维坐标与地球上的三维坐标相互转换的过程。

通过实际坐标的正算，可以确定地球上的位置，而通过坐标的反算，可以确定地图上的位置。

坐标正反算是地理信息系统中的一项重要技术，对于许多实际应用具有重要意义。

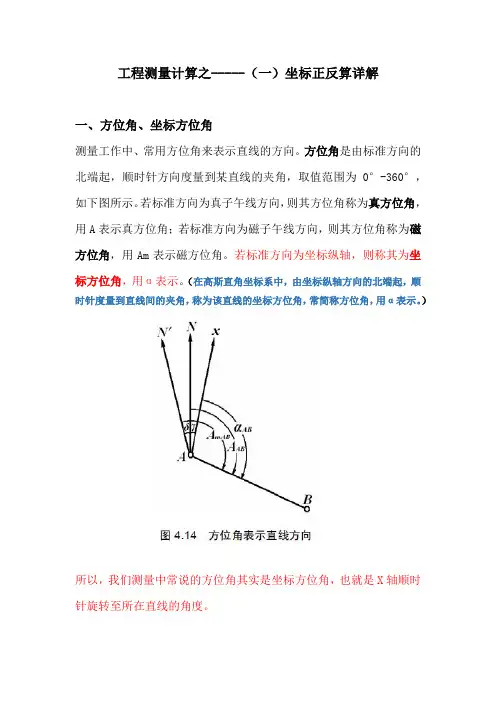
工程测量计算之-----（一）坐标正反算详解一、方位角、坐标方位角测量工作中、常用方位角来表示直线的方向。

方位角是由标准方向的北端起，顺时针方向度量到某直线的夹角，取值范围为0°-360°，如下图所示。

若标准方向为真子午线方向，则其方位角称为真方位角，用A表示真方位角；若标准方向为磁子午线方向，则其方位角称为磁方位角，用Am表示磁方位角。

若标准方向为坐标纵轴，则称其为坐标方位角，用α表示。

（在高斯直角坐标系中，由坐标纵轴方向的北端起，顺时针度量到直线间的夹角，称为该直线的坐标方位角，常简称方位角，用α表示。

）所以，我们测量中常说的方位角其实是坐标方位角，也就是X轴顺时针旋转至所在直线的角度。

二、象限角以基本方向北端或南端起算，顺时针或逆时针方向量至直线的水平角，称为象限角，用R表示。

象限角不但要表示角度大小，而且还要注明该直线所在的象限。

从坐标纵轴的北端或南端顺时针或逆时针起算至直线的锐角称为坐标象限角。

其角值变化从0°~90°，为了表示直线的方向，应分别注明北偏东、北偏西或南偏东、南偏西。

如北东85°，南西47°等。

显然，如果知道了直线的方位角，就可以换算出它的象限角，反之，知道了象限也就可以推算出方位角。

三、坐标正反算公式详解坐标正算根据直线的坐标方位角、边长和一个已知端点的坐标计算直线上另一端点坐标的过程。

或若两点间的平面位置关系由极坐标化为直角坐标，称为坐标正算。

1、坐标计算条件①起算点（定位点）的平面坐标（X0，Y0），②起算点至待求点的坐标方位角α，③起算点至待求点的平面距离D。

2、坐标计算过程坐标反算根据两已知点的平面坐标，计算该直线的方位角及两点间平面距离的过程。

或若两点间的平面位置关系由直角坐标化为极坐标，称为坐标反算。

α=arctan(△y / △x)D=√(△x*△x + △y*△y)其中，用计算器计算出的α称为象限角，之后还要根据△x、△y的正负号转换为坐标方位角。

第五节、坐标正、返算及应用实例1、基本概念所谓坐标正算，即已知一点的坐标和至另一已知点的起始方位，以及起始点至待定点的转角和边长，推求待定点坐标的计算称之为坐标正算。

所谓坐标返算，即已知两点的坐标，进行两点间的边长及边长方位角的计算，称之为坐标返算。

所谓点的坐标是指该点在某一坐标系统中相对纵、横坐标轴线的垂距。

在测量坐标系统中，纵、横轴分别以x、y表示。

坐标增量是指一点的坐标相对另一点坐标的增值。

在测量坐标系统中分别用△x、△y表示纵、横坐标增量。

所谓边的方位角是指该边与坐标纵轴的夹角。

方位角有正、反方位之分，正方位角即为以坐标纵轴正方向为零，顺时方向转至边起止方向的夹角。

相反方向的则为反向方位角，正、反方位角相差180°。

在坐标系统中，四个象限的划分是以东北方向开始按顺时方向规定为Ⅰ、Ⅱ、Ⅲ、Ⅳ象限，如图9所示。

轴线方向规定纵轴往北为正，反之为负，横轴往东为正，反之为负。

xⅣⅠyⅢⅡ图9由此可见：在Ⅰ象限中，X、Y均正值，在Ⅱ象限中，X为负Y为正，在Ⅲ象限中，X、Y均为负，在Ⅳ象限中，X为正Y为负。

弄清以上概念以后，便可进行坐标的正、返算运算。

如图10所示：正算公式：已知Ａ、Ｂ两点坐标和转角β，及ＢＰ的边长Ｓ，推算Ｐ点坐标。

P =XB+ScosαBPx . P= X B+Scos（αBA+β）YP =YB+SsinαBPA βS= YB +Ssin（αBA+β） B注意：在进行坐标推算 Y 时，推算方位角所用的转折 (0,0) 图10 角为左角时则应加转角，所用的转折角为右角时，则应减转角。

返算公式：已知A、B两点坐标，计算AB的边长和方位角。

SAB =（（XB-XA）2+（YB-YA）2）1/2=(ΔX2BA +ΔY2BA) 1/2αBA =tg-1((YA-YB)/ （XA-XB）)2、坐标正、返算实例。

如图11所示：已知中山路上m、n两测量控制点的坐标为：Xm =76.11Ym=179.51Xn =137.00 Yn=182.84设计给定拟建建筑物角点A、Ｄ两点(设计图纸中的)坐标为：X A =117.82YA=134.20X D =148.50 YD=120.04根据以上已知资料，对拟建建筑物进行定位。

坐标正算和坐标反算的原理及应用一、坐标正算坐标正算是指根据给定的点坐标和直线之间的水平距离 DAB 与坐标方位角 AB，推算出另一条直线的坐标方位角 AB 和水平距离DAB 的方法。

坐标正算的计算公式为:XB = XA + DAB·cos(AB)YB = YA + DAB·sin(AB)其中，XB 和 YB 分别称为 A～B 的纵、横坐标增量，XA、YA 分别是直线 AB 的起点和终点的坐标，DAB 是直线 AB 的水平距离。

需要注意，XB 和 YB 均有正、负号，其符号取决于直线 AB 的坐标方位角所在的象限。

二、坐标反算坐标反算是指根据给定的两个点坐标和直线之间的水平距离DAB，推算出直线 AB 的坐标方位角 AB 和水平距离 DAB 的方法。

坐标反算的计算公式为:AB = (YB - YA) / (XB - XA) - 90°其中，AB 是直线 AB 的坐标方位角，XB、YA 分别是直线 AB 的起点和终点的坐标，YB 和 XA 分别是 A～B 和 B～A 的横纵坐标增量。

需要注意，坐标反算得到的方位角是一个锐角，必须先根据 YB-YA 与 XB-XA 的正负号，确定直线 AB 所在的象限，再将象限角换算为坐标方位角。

三、坐标正算和坐标反算的应用坐标正算和坐标反算在实际应用中有着广泛的应用，下面列举几个典型的应用:1. 航空航天领域：在航空航天领域中，坐标正算和坐标反算被用来确定飞行器的位置和方向，从而确保飞行器的安全和准确性。

2. 机械设计领域：在机械设计中，坐标正算和坐标反算被用来计算机械零部件的位置和方向，从而确保机械设计的精确性和合理性。

3. 地理信息系统：在地理信息系统中，坐标正算和坐标反算被用来确定地图中各个点的位置和方向，从而支持地图数据的采集、管理和分析。

4. 机器人领域：在机器人领域中，坐标正算和坐标反算被用来确定机器人的位置和方向，从而确保机器人的准确移动和作业。

坐标正反算1. 前言坐标正反算是在测量和导航领域中常用的技术，用于在地球上确定位置的过程。

正算是根据已知参数计算给定地点的坐标，反算则是根据已知地点的坐标计算相应的参数。

本文将介绍坐标正反算的基本原理和常用方法。

2. 坐标系统为了确定地球上任意点的位置，使用了不同的坐标系统。

最常用的是地理坐标系（经纬度坐标系）和平面坐标系（如UTM坐标系）。

地理坐标系使用经度和纬度表示一个点的位置，而平面坐标系使用坐标轴上的数值表示。

坐标系统的选择取决于具体的应用需求和地理区域。

例如，地理坐标系常用于导航和地图制作，而平面坐标系则常用于测量和土地调查。

3. 坐标正算坐标正算是根据已知的参数计算给定点的坐标。

例如，在地理坐标系中，已知一个点的经度和纬度，可以通过正算计算出该点在地球上的位置。

正算的具体方法根据不同的坐标系统而异。

在地理坐标系中，常用的正算方法是球面三角法和大地测量学方法。

而在平面坐标系中，使用的方法通常是基于平面几何原理的。

4. 坐标反算坐标反算是根据已知的地点坐标计算相应的参数。

例如，在地理坐标系中，已知两个点的经纬度坐标，可以通过反算计算出这两个点之间的距离和方位角。

坐标反算的方法也因不同的坐标系统而异。

在地理坐标系中，常用的反算方法包括球面三角法和大地测量学方法。

在平面坐标系中，反算的方法则通常是基于平面几何原理的。

5. 常用工具和软件进行坐标正反算时，可以使用许多工具和软件来简化计算过程。

一些常用的工具包括地图和测量仪器，如全球定位系统（GPS）。

此外，还有一些专门用于坐标正反算的软件，如ArcGIS、AutoCAD和Google Earth等。

这些软件提供了各种功能和工具，可以帮助用户进行精确的正反算计算。

6. 总结坐标正反算是在测量和导航领域中常用的技术，在确定地球上任意点的位置和计算相关参数时发挥着重要作用。

本文介绍了坐标正反算的基本原理和常用方法，以及一些常用工具和软件。

虽然坐标正反算在实际应用中可能会更加复杂和多样化，但通过理解基本原理和使用适当的工具，可以更有效地进行坐标计算和位置确定。

测量学坐标正反算测量学是一门致力于研究测量方法和技术的学科，广泛应用于各个领域，如工程测量、地理测量、建筑测量等。

在测量学中，坐标正反算是一项重要的工作，用于确定任意点在坐标系统中的位置。

坐标系统简介在测量学中，坐标系统是一种用来描述和表示空间点位置的一种数学模型。

坐标系统通常由坐标系和坐标轴组成。

坐标系是一个框架，用来确定点的位置。

坐标轴则是坐标系的辅助线，用来定位具体的点。

常见的坐标系统有笛卡尔坐标系和极坐标系。

在笛卡尔坐标系中，一个点的位置可以由其在水平和垂直方向上的坐标表示。

而在极坐标系中，一个点的位置则由其距离原点的径向距离和与特定方向的角度表示。

坐标的正算在测量学中，坐标的正算是指已知一个点的坐标系中的坐标，通过测量和计算得到该点在其他坐标系中的坐标的过程。

正算的目的是确定点在其他坐标系中的位置，以便进行进一步的计算或分析。

坐标的正算通常涉及从已知坐标系到未知坐标系的转换。

这个转换过程可以使用一些数学模型和算法完成。

例如，在平面测量中，可以使用旋转和平移等几何变换来进行坐标的正算。

坐标的反算坐标的反算是指已知一个点在一个坐标系中的坐标，通过测量和计算得到该点在另一个坐标系中的坐标的过程。

反算的目的是确定点在其他坐标系中的位置，以便进行进一步的计算或分析。

坐标的反算也需要使用一些数学模型和算法。

在平面测量中，常用的反算方法包括旋转和平移等几何变换。

通过这些变换，可以将点在一个坐标系中的坐标转换为在另一个坐标系中的坐标。

坐标正反算的应用测量学坐标正反算在实际应用中具有广泛的用途。

在工程测量中，测量人员可以通过坐标的正反算来确定不同点的位置，以便进行工程规划和设计。

此外，在地理测量中，坐标的正反算也是常见的任务。

通过坐标的正反算，地理学家可以确定地球上不同地点的位置，而不论是经度和纬度表示的极坐标系，还是平面坐标系，都可以应用于地理测量中。

总之，测量学坐标正反算是测量学中重要的一环，用于确定点在不同坐标系中的位置。

曲线任意里程中边桩坐标正反算(CASIO fx-5800P计算器)程序一、程序功能及原理1.功能说明：本程序由一个主程序(TYQXJS)和五个子程——正算子程序(SUB-ZS)、反算子程序(SUB-FS)等构成，可以根据曲线段——直线、圆曲线、缓和曲线（完整或非完整型）的线元要素（起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径）及里程边距或坐标，对该曲线段范围内任意里程中边桩坐标进行正反算。

本修改版程序既可实现正算全线贯通，亦可实现反算全线贯通。

本程序在CASIO fx-5800P计算器运行。

2．计算原理：利用Gauss-Legendre 5点通用公式正算线路中边桩坐标、线外测点至曲线元起点和终点的垂距的符号是否相异（即Dca×Dcb<0=>该测点在其线元内）进行判断并利用该线元要素反算中桩里程、支距，最后计算出放样数据。

二、源程序1.主程序(TYQXJS)Deg:fix 3119→DimZ“INPUT(0) Or DATA(Else)”?ILbl 0:“1.SZ=>XY,2.XY=>SZ，3.TF=>CK,4.SD=>FY，5.TW=>FY”?NIf N=1 Or N=5:Then Goto 1Else If N=2 Or N=3 Or N=4:Then Goto 2Else Goto 3IfEnd:IfEndLbl 1:“K(m)=”?SIf S<0:Then Goto 0:IfEnd“JL(m)=”?ZIf Z≠0:Then “ANGLE→R(Deg)=”?M:IfEndIf I=0:Then Prog “DAT1”:Else Prog “DAT2”:IfEndS-O→W:If W<0:Then Goto 0:Else If W>H:Then Goto 0:IfEnd:IfEndProg “SUB-ZS”:Prog “SUB-GC”If Z<0:Then“XL(m)=”:X◢“YL(m)=”:Y◢If N=5:Then Prog “SUB-TW”:IfEndElse If Z>0:Then “XR(m)=”:X◢“YR(m)=”:Y◢If N=5:Then Prog “SUB-TW”:IfEndElse “X(m)=”:X◢“Y(m)=”:Y◢“Hs(m)=”:L◢“FWJ=”: F►DMS◢IfEnd:IfEndGoto 1Lbl 2:“X(m)=”?X:If X<0:Then Goto 0:IfEnd“Y(m)=”?YIf N=3 Or N=4:Then “H(m)=”?→Z[2]:IfEndX→Z[4]:Y→Z[5]:90→MIf I=0:Then Prog “DAT1”G+QEH(C+HD)→F:1→J:U→Z[8J]:V→Z[8J+1]G-M→A:F-M→B:Prog “SUB-ZX1”:Goto BG+M→A:F+M→B:Prog “SUB-ZX1”:Goto B:IfEnd0→J:Lbl A: Isz JZ[8J+3]-M→A:Z[8(J+1)+3]-M→B:Prog “SUB-ZX1”If Z[6]Z[7]<0:Then J→J:Prog“DAT1” :Goto B:IfEndZ[8J+3]+M→A:Z[8(J+1)+3]+M→B:Prog “SUB-ZX1”If Z[6]Z[7]<0:Then J→J:Prog “DAT1” :Goto B:Else Goto A:IfEndLbl B:Prog“SUB-FS”O+W→S:Prog “SUB-GC”“K(m)=”:S◢“Hs(m)=”:L◢“JL(m)=”:Z◢If N=3:Then Prog “WIDE”:IfEndIf N=4:Then Prog “SDFY”:IfEndGoto 2Lbl 3:“TYQXJS→END”2. 正算子程序(SUB-ZS)0.1184634425→A: 0.2393143352→B:0.2844444444→Z[1]:0.0469100770→K:0.2307653449→L:0.5→Z[3]U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Z[1]cos(G+QEZ[3]W(C+Z[3]WD))+Bcos(G+QE(1 -L)W(C+(1-L)WD))+Acos(G+QE(1-K)W(C+(1-K)WD)))→XV+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Z[1]sin(G+QEZ[3]W(C+Z[3]WD))+Bsin(G+QE(1-L)W(C+(1-L)WD))+Asin(G+QE(1-K)W(C+(1-K)WD)))→YG+QEW(C+WD)+M→FX+Zcos(F)→X:Y+Zsin(F)→YF-M→F:If F<0:Then F+360→F:IfEndReturn3. 反算子程序(SUB-FS)G-M→T:Abs((Y-V)cos(T)-(X-U)sin(T))→W:0→ZLbl C:Prog “SUB-ZS”T+QEW(C+WD)→L:(Z[5]-Y)cos(L)-(Z[4]-X)sin(L)→ZIf Abs（Z）<10-6:Then Goto D:Else W+Z→W：Goto C:IfEndLbl D:0→Z:Prog “SUB-ZS”:(Z[5]-Y)÷cos(F)→Z:Return4．高程计算子程序（SUB-GC）Prog “DAT3”0．5RAbs(0.01(E-D))→TIf E>D:Then 1→C:Else -1→C:IfEndIf S<A:Then -0.01D→W:Else 0.01E→W:IfEndAbs(A-S)→LIf L>T:Then B+WL→L:Else B+WL+C(T-L)2÷2÷R→L:IfEndReturn5. 垂距计算子程序(SUB-ZX1)(Z[5]-Z[8J+1])cos(A)-(Z[4]-Z[8J])sin(A)→Z[6](Z[5]-Z[8(J+1)+1])cos(B)-(Z[4]-Z[8(J+1)])sin(B)→Z[7]Return6.曲线元要素数据库：DAT1(两条线路，可扩充为多条线路)If I=0:Then Goto E: Else If I=2:Then Goto F:IfEnd:IfEndJ=1=>***→Z[8]:***→Z[9]:***→Z[10]:***→Z[11]:***→Z[12]:***→Z[13]:***→Z[14]:*** →Z[15]：IfEndJ=2=>***→Z[16]:***→Z[17]:***→Z[18]:***→Z[19]:***→Z[20]:***→Z[21]:***→Z[22]:***→Z[23]:IfEndJ=3=>***→Z[24]***→Z[25]:***→Z[26]:***→Z[27]:***→Z[28]:***→Z[29]:***→Z[30]:***→[31]:IfEnd………………………………………………..Goto HLbl F: J=1=>***→Z[8]:***→Z[9]:***→Z[10]:***→Z[11]:***→Z[12]:***→Z[13]:***→Z[14]:*** →Z[15]：IfEndJ=2=>***→Z[16]:***→Z[17]:***→Z[18]:***→Z[19]:***→Z[20]:***→Z[21]:***→Z[22]:***→Z[23]:IfEndJ=3=>***→Z[24]***→Z[25]:***→Z[26]:***→Z[27]:***→Z[28]:***→Z[29]:***→Z[30]:***→[31]:IfEnd(注：如有多个曲线元要素继续添加入数据库DAT1中)Goto GLbl E:“X0=”?U:“Y0=”?V:“S0=”?O:“F0=”?G:“LS=”?H:“R0=”?P:“RN=”?R:“Q=”?Q Lbl G:1÷P→C:(P-R)÷(2HPR)→D:180÷π→E:Return7．隧道放样子程序：SDFY5.5→A:8.5→B:L+1.5→CIf I=1:Then -1→K:Else 1→K:IfEnd 给左右隧道符号赋值1.25K→F:4.25K→L:7.25K→K 给各圆心距路线的偏距赋值Z[2]-C→D 计算测点至圆心的高差D，If D>A:Then Goto 1:Else If D<0:Then Goto 2:IfEnd:IfEndZ-L→E:Abs(E)→E:√(D2+E2)→W:W-A→T: 计算测点至圆心的平距E，实测半径W “R(m)=”:W◢“DR(m)=”:T◢If E≤A:Then D-√(A2-E2)→C:E-√(A2-D2)→L 计算测点水平偏移量L、垂直偏移量C “Dh(m)=”:C◢显示测点垂直偏移量C“DL(m)=”:L◢显示测点水平偏移量LElse E-√(A2-D2)→L“DL(m)=”:L◢IfEnd:ReturnLbl 1Z-L→E:Abs(E)→E:√(D2+E2)→W:W-A→T: 计算测点至圆心的平距E，实测半径W “R(m)=”:W◢“DR(m)=”:T◢If E≤A:Then D-√(A2-E2)→C“Dh(m)=”:C◢IfEnd:ReturnLbl 2:Abs(D)→D:Abs(Z)→Z:Abs(K)→K:Abs(F)→FIf Z>K:Then Z-F→E:Else Z+K→E:IfEnd√(D2+E2)→W:W-B→T“R(m)=”:W◢“Rc(m)=”:T◢If E≤B:Then D-√(B2-E2)→C:E-√(B2-D2)→L 计算测点水平偏移量L、垂直偏移量C “Dh(m)=”:C◢显示测点垂直偏移量C“DL(m)=”:L◢显示测点水平偏移量LElse E-√(B2-D2)→L“DL(m)=”:L◢显示测点水平偏移量LIfEnd:Return8．曲线元要素判断数据库：DAT2(两条线路，可扩充为多条线路)If I=2:Then Goto A:IfEndIf S<第一线元终点里程:Then 1→J:Prog “DAT1”:ReturnElse If S<第二线元终点里程:Then 2→J:Prog “DAT1”:ReturnElse If S<第三线元终点里程:Then 3→J:Prog “DAT1”:ReturnElse If S<第四线元终点里程:Then 4→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEndIf S≥第四线元起点里程And S<第五线元终点里程：Then 5→J：Prog “DAT1”：Return .................................Else If S<第n线元里程：Then n→J：Prog “DAT1”：ReturnIfEnd:IfEnd:IfEnd:IfEndLbl AIf S<第一线元终点里程:Then 1→J:Prog “DAT1”:ReturnElse If S<第二线元终点里程:Then 2→J:Prog “DAT1”:ReturnElse If S<第三线元终点里程:Then 3→J:Prog “DAT1”:ReturnElse If S<第四线元终点里程:Then 4→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEndIf S≥第四线元起点里程And S<第五线元终点里程：Then 5→J：Prog “DAT1”：Return Else If S<第n线元里程：Then n→J：Prog “DAT1”：ReturnIfEnd:IfEnd:IfEnd:IfEnd .................................9．高程数据库子程序：DAT3（两条线路，可扩充为多条线路）If I=0:Then Goto A:Else If I=2:Then Goto B:IfEnd:IfEndIf S≤46500:Then 46150→A:361.26→B:40000→R:-0.3→D:-1.2→E:ReturnElse If S≤47200:Then 46800→A:353.46→B:20000→R:-1.2→D:1→E:ReturnElse If S≤48400:Then 47500→A:360.46→B:20000→R:1→D:-1.6→E:ReturnElse If S≤49600:Then 48700→A:341.26→B:10000→R:-1.6→D:2.45→E:Return IfEnd:IfEnd:IfEnd:IfEndIf S>49600 And S≤50300:Then 49840→A:369.19→B:100000→R:2.45→D:2.8→E:Return Else If I=2:Then49800→A:368.21→B:150000→R:2.45→D:2.7→E:ReturnIfEnd:IfEndLbl A:“C PEG(m)=”?→A“C H(m)=”?→B“R(m)=”?→R“I1=”?→D“I2=”?→EReturnLbl B49800→A:368.21→B:150000→K:2.45→D:2.7→E:Return10.填方路基宽度检查子程序（WIDE）“WIDTH CHECK”◢“H→MID(m)=”?→A 起坡点与中桩高差常数“DIST→MID(m)=”?→B 起坡点与中桩距离常数“i=”?→C 路基填筑坡度CAbs(Z[2]-L+A)→DAbs(Z)-B-D→E“DL(m)=”:E◢显示实有宽度与应有宽度之差值Return11.坡口坡脚线坐标计算子程序:SUB-TW“TIANWA LINE”◢“DIST→MID(m)=”?A 起坡点与中桩距离常数“H→MID(m)=”?B 起坡点与中桩高差常数“T(1) Or W(Else)=”?C 填方边坡为1，其它为挖方边坡“i=”?E 填方或挖方边坡坡度Abs(Z)-A→D: DE→KIf C=1:Then L-B-K→W:Else L+B+K→W:IfEnd“JS H(m)=”:W◢计算出应有高程“SC H(m)=”？→D 输入实测高程D-W→T“GC(m)=”:T◢显示实测高程与计算高程的差异Return三、使用说明1、规定(1) 以道路中线的前进方向（即里程增大的方向）区分左右；当线元往左偏时，Q=-1；当线元往右偏时，Q=1；当线元为直线时，Q=0。

工程测量坐标正反算1. 引言工程测量是为了获取、分析和处理地面或工程对象的几何、位置、形状等信息，以便于工程设计、施工和管理。

在工程测量中，坐标正反算是一项重要的技术，用于将实际测得的数据转换为坐标，并在需要时将坐标转换为实际测量的数据。

2. 坐标正算坐标正算是指根据场地实际测量的数据，计算出点的坐标值。

在进行坐标正算之前，需要确定一个已知点作为基准，以及一组已知的方向角和距离。

常用的坐标正算方法有三角测量法、导线测量法和平差测量法。

2.1 三角测量法三角测量法是通过测量三角形的三个内角和至少一个边长来确定点的坐标。

首先，在已知点上设立三角形的起始基线，并通过观测角度和距离来确定其他两个顶点的位置。

然后，利用三角函数计算出这两个顶点的坐标。

2.2 导线测量法导线测量法是通过测量导线的方向角和距离来确定点的坐标。

首先，在已知点上设立导线的起始基线，并通过观测方向角和距离来确定其他点的位置。

然后，根据已知点的坐标和观测值，利用三角函数计算出其他点的坐标。

2.3 平差测量法平差测量法是通过多次测量和计算，将测得的观测值进行平差，然后根据得到的平差值计算点的坐标。

平差测量法包括最小二乘法和最小二乘平差法等。

在平差测量法中，需要利用数学模型和观测误差理论来进行计算，以提高测量精度。

3. 坐标反算坐标反算是指根据已知点的坐标和观测数据，计算出点的实际测量值。

在进行坐标反算之前，需要确定一个已知点作为基准，并记录已知点的坐标值。

常用的坐标反算方法有正算法、闭合差平差法和误差分析法。

3.1 正算法正算法是根据已知点的坐标和观测数据，通过计算得到其他点的实际测量值。

根据已知点的坐标和观测数据，可以利用三角函数计算出其他点的方向角和距离。

然后，根据已知点的坐标和观测值，利用三角函数计算出其他点的坐标值。

3.2 闭合差平差法闭合差平差法是通过多次测量和计算，将测得的观测值进行平差，以减小误差，并根据得到的平差值计算点的实际测量值。

工程测量计算之-----（一）坐标正反算详解一、方位角、坐标方位角测量工作中、常用方位角来表示直线的方向。

方位角是由标准方向的北端起，顺时针方向度量到某直线的夹角，取值范围为0°-360°，如下图所示。

若标准方向为真子午线方向，则其方位角称为真方位角，用A表示真方位角；若标准方向为磁子午线方向，则其方位角称为磁方位角，用Am表示磁方位角。

若标准方向为坐标纵轴，则称其为坐标方位角，用α表示。

（在高斯直角坐标系中，由坐标纵轴方向的北端起，顺时针度量到直线间的夹角，称为该直线的坐标方位角，常简称方位角，用α表示。

）所以，我们测量中常说的方位角其实是坐标方位角，也就是X轴顺时针旋转至所在直线的角度。

二、象限角以基本方向北端或南端起算，顺时针或逆时针方向量至直线的水平角，称为象限角，用R表示。

象限角不但要表示角度大小，而且还要注明该直线所在的象限。

从坐标纵轴的北端或南端顺时针或逆时针起算至直线的锐角称为坐标象限角。

其角值变化从0°~90°，为了表示直线的方向，应分别注明北偏东、北偏西或南偏东、南偏西。

如北东85°，南西47°等。

显然，如果知道了直线的方位角，就可以换算出它的象限角，反之，知道了象限也就可以推算出方位角。

三、坐标正反算公式详解坐标正算根据直线的坐标方位角、边长和一个已知端点的坐标计算直线上另一端点坐标的过程。

或若两点间的平面位置关系由极坐标化为直角坐标，称为坐标正算。

1、坐标计算条件①起算点（定位点）的平面坐标（X0，Y0），②起算点至待求点的坐标方位角α，③起算点至待求点的平面距离D。

2、坐标计算过程坐标反算根据两已知点的平面坐标，计算该直线的方位角及两点间平面距离的过程。

或若两点间的平面位置关系由直角坐标化为极坐标，称为坐标反算。

α=arctan(△y / △x)D=√(△x*△x + △y*△y)其中，用计算器计算出的α称为象限角，之后还要根据△x、△y的正负号转换为坐标方位角。

坐标正反算公式范文一、坐标正算（后方交汇计算）：已知起点坐标及观测角度和距离的情况下，求目标点的坐标。

1.观测角度求目标点坐标：在测量中，常常通过角度观测来确定目标点的坐标。

如果已知起点坐标和观测角度，可以通过以下公式求解目标点的坐标：X = X0 + L * sin(α + θ)Y = Y0 + L * cos(α + θ)其中，X0和Y0是起点的坐标，L为观测点到起点的距离，α为起点和观测点之间的方位角，θ为观测角度。

2.观测距离求目标点坐标：在一些情况下，可以通过观测距离来确定目标点的坐标。

已知起点坐标和观测距离的情况下，可以通过以下公式求解目标点的坐标：X = X0 + L * sinαY = Y0 + L * cosα其中，X0和Y0是起点的坐标，L为观测点到起点的距离，α为起点和观测点之间的方位角。

3.观测角度和距离求目标点坐标：在一些情况下，需要同时使用观测角度和观测距离来确定目标点的坐标。

已知起点坐标、观测角度和观测距离的情况下，可以通过以下公式求解目标点的坐标：X = X0 + （L * sinθ）/ sinαY = Y0 + （L * cosθ）/ cosα其中，X0和Y0是起点的坐标，L为观测点到起点的距离，α为起点和观测点之间的方位角，θ为观测角度。

二、坐标反算（前方交汇计算）：已知起点坐标和目标点坐标或两点坐标之间的距离和角度的情况下，求观测角度和距离。

1.目标点坐标求观测角度和距离：当已知起点坐标和目标点坐标时，可以通过以下公式求解观测角度和距离：L=√((X-X0)^2+(Y-Y0)^2)tanα = (X - X0) / (Y - Y0)θ = atan((X - X0) / (Y - Y0)) - α其中，X0和Y0是起点的坐标，X和Y是目标点的坐标，L为目标点到起点的距离，α为起点和观测点之间的方位角，θ为观测角度。

2.两点坐标之间的距离和角度求观测角度和距离：当已知起点坐标、目标点坐标和两点之间的距离时，可以通过以下公式求解观测角度和距离：L=√(a^2+b^2)sinθ = a / Lcosθ = b / Ltanα = a / b其中，a和b分别为起点和目标点之间的ΔX和ΔY坐标差，L为目标点到起点的距离，α为起点和观测点之间的方位角，θ为观测角度。

坐标正反算计算公式引言在数学和计算机科学领域中，坐标转换是一种常见的操作。

坐标正反算是指从一个坐标系中的点转换到另一个坐标系中的点，并且可以从目标坐标系中的点转换回原始坐标系中的点。

这种计算在许多应用中都非常有用，例如地理信息系统、计算机图形学和机器人学。

坐标正算坐标正算是将一个坐标点从原始坐标系转换到目标坐标系的过程。

在二维平面中，我们可以使用以下公式将点(x, y)从原始坐标系转换到目标坐标系：x' = x * cos(θ) - y * sin(θ) + dxy' = x * sin(θ) + y * cos(θ) + dy其中，(x, y)是原始坐标系中的点，(x’, y’)是目标坐标系中的点，θ是旋转角度，dx和dy是平移量。

这些参数确定了坐标转换的方式。

坐标反算坐标反算是将一个坐标点从目标坐标系转换回原始坐标系的过程。

在二维平面中，我们可以使用以下公式将点(x’, y’)从目标坐标系转换回原始坐标系：x = (x' - dx) * cos(-θ) - (y' - dy) * sin(-θ)y = (x' - dx) * sin(-θ) + (y' - dy) * cos(-θ)同样地，(x’, y’)是目标坐标系中的点，(x, y)是原始坐标系中的点，θ是旋转角度，dx和dy是平移量。

应用举例坐标正反算的计算公式在各种应用中都有广泛的应用。

•地理信息系统（GIS）中，坐标转换用于将地球表面的经纬度坐标转换为平面坐标系（如投影坐标系）。

这种转换对于地图制图和空间数据分析非常重要。

•在计算机图形学中，坐标转换用于将三维物体的顶点坐标从模型空间转换到世界空间，然后转换到相机空间或屏幕空间。

通过坐标转换，我们可以实现物体的旋转、缩放和平移等操作。

•在机器人学中，坐标转换用于描述机器人的位置和姿态，以及机器人在不同坐标系中的运动。

这对于路径规划、目标追踪和运动控制非常重要。