人教版必修一之对数函数

人教版必修一之对数函数全方位教学辅导教案M）＝logaM－logaN；N②loga（n③logaM＝nlogaM（n∈R）④logaNlogmN（换底公式）；logma⑤logablogba1；⑥logambnnlogab （a,b>0且均不为1）.m（2）对数恒等式：①logaabb（0a1）③logaa1（二）例题分析例1求下列各式的值：（1）log2（4某2）；（2）lg5100．练习75④loga10[]2.下列等式成立的是[]二、对数函数的定义、图象、性质（一）复习引入1．指数函数的定义、图象、性质。

2．回忆学习指数函数时的实例——细胞分裂问题：细胞的个数是分裂次数的指数函数y2．反之，细胞分裂的次数是细胞个数的函数，由对数定义：某log2y，即：次数y是个数某某的函数ylog2某．（二）新课讲解1．对数函数的定义：函数yloga某(a0且a1)叫做对数函数。

2．对数函数的性质：（1）定义域、值域：对数函数yloga某(a0且a1)的定义域为(0,)，值域为(,)．（2）图象：由于对数函数是指数函数的反函数，所以对数函数的图象只须由相应的指数函数图象作关于y某的对称图形，即可获得。

同样：也分a1与0a1两种情况归纳，以ylog2某（图1）与ylog1某（图2）为例。

y211某2y某1y()某211y某ylog2某ylog1某2（3）对数函数性质列表：（图1）（图2）a1图象0a1某1yloga某某1(1,0)(1,0)yloga某（1）定义域：(0,)性质（2）值域：R（3）过点(1,0)，即当某1时，y0（4）在（0，+∞）上是增函数3．例题分析例1.根据对数函数的图象和性质填空．1已知函数ylog2某，则当某0时，y；当某1时，y；○当0某1时，y；当某4时，y．2已知函数ylog1某，则当0某1时，y；当某1时，y；○3（4）在(0,)上是减函数当某5时，y；当0某2时，y；当y2时，某（3）已知函数yloga1某,yloga2某,yloga3某,yloga4某的图象，则底数之间的关系：例2．求下列函数的定义域：（1）yloga某2；（2）yloga(4某)；（3）yloga(9某2)．．教某24例2.试求函数f(某)的定义域。

§2.2对数函数2．2.1对数与对数运算1．对数的概念一般地，如果ax＝N (a>0，且a≠1)，那么数x叫做以a为底N的对数，记作x＝logaN，其中a叫做对数的底数，N叫做真数．说明：(1)实质上，上述对数表达式，不过是指数函数y＝ax的另一种表达形式，例如：34＝81与4＝log381这两个式子表达是同一关系，因此，有关系式ax＝N?x＝logaN，从而得对数恒等式：alogaN＝N.(2)“log”同“＋”“×”“”等符号一样，表示一种运算，即已知一个数和它的幂求指数的运算，这种运算叫对数运算，不过对数运算的符号写在数的前面．(3)根据对数的定义，对数logaN(a>0，且a≠1)具有下列性质：①零和负数没有对数，即N>0；②1的对数为零，即loga1＝0；③底的对数等于1，即logaa＝1.2．对数的运算法则利用对数的运算法则，可以把乘、除、乘方、开方的运算转化为对数的加、减、乘、除运算，反之亦然．这种运算的互化可简化计算方法，加快计算速度．(1)基本公式①loga(MN)＝logaM＋logaN (a>0，a≠1，M>0，N>0)，即正数的积的对数，等于同一底数的各个因数的对数的和．②loga＝logaM－logaN (a>0，a≠1，M>0，N>0)，即两个正数的商的对数，等于被除数的对数减去除数的对数．③logaMn＝n·logaM (a>0，a≠1，M>0，n∈R)，即正数的幂的对数等于幂的底数的对数乘以幂指数．(2)对数的运算性质注意点①必须注意M>0，N>0，例如loga[(－3)×(－4)]是存在的，但是loga(－3)与loga(－4)均不存在，故不能写成loga[(－3)×(－4)]＝loga(－3)＋loga(－4)．②防止出现以下错误：loga(M±N)＝logaM±logaN，loga(M·N)＝logaM·logaN，loga＝，logaMn ＝(logaM)n.3．对数换底公式在实际应用中，常碰到底数不为10的对数，如何求这类对数，我们有下面的对数换底公式：logbN＝(b>0，且b≠1；c>0，且c≠1；N>0)．证明设logbN＝x，则bx＝N.两边取以c为底的对数，得xlogcb＝logcN.所以x＝，即logbN＝.换底公式体现了对数运算中一种常用的转化，即将复杂的或未知的底数转化为已知的或需要的底数，这是数学转化思想的具体应用．由换底公式可推出下面两个常用公式：(1)logbN＝或logbN·logNb＝1 (N>0，且N≠1；b>0，且b≠1)；(2)logbnNm＝logbN(N>0；b>0，且b≠1；n≠0，m∈R).题型一正确理解对数运算性质对于a>0且a≠1，下列说法中，正确的是()①若M＝N，则logaM＝logaN；②若logaM＝logaN，则M＝N；③若logaM2＝logaN2，则M＝N；④若M＝N，则logaM2＝logaN2.A．①与③B．②与④C．②D．①、②、③、④题型二对数运算性质的应用求下列各式的值：(1)2log32－log3＋log38－；(2)lg25＋lg8＋lg5·lg20＋(lg2)2；(3).题型三对数换底公式的应用计算：(log2125＋log425＋log85)(log52＋log254＋log1258)．已知log(x＋3)(x2＋3x)＝1，求实数x的值．1．对数式log(a－3)(7－a)＝b，实数a的取值范围是()A．(－∞，7) B．(3,7) C．(3,4)∪(4,7) D．(3，＋∞)3．log56·log67·log78·log89·log910的值为()A．1 B．lg5 C. D．1＋lg24．已知loga(a2＋1)<loga2a<0，则a的取值范围是()A．(0,1) B. C. D．(1，＋∞)5．已知函数f(x)＝ax－1＋logax (a>0，a≠1)在[1,3]上最大值与最小值之和为a2，则a的值为()A．4 B. C．3 D.7．已知f(log2x)＝x，则f＝________.8．log(－1)(＋1)＝________.一、对数式有意义的条件例1求下列各式中x的取值范围：(1)log2(x－10)；(2)log(x－1)(x＋2)；(3)log(x＋1)(x－1)2.二、对数式与指数式的互化例2将下列对数形式化成指数形式或将指数形式转化为对数形式：(1)54＝625；(2)log8＝－3；(3)－2＝16; (4)log101 000＝3.变式迁移2将下列对数式化为指数式求x值：(1)logx27＝；(2)log2x＝－；(3)log5(log2x)＝0; (4)x＝log27；(5)x＝log16.一、选择题1．下列指数式与对数式互化不正确的一组是()A．100＝1与lg1＝0 B．27－＝与log27＝－C．log3＝9与9＝3 D．log55＝1与51＝5 2．指数式b6＝a (b>0，b≠1)所对应的对数式是()A．log6a＝a B．log6b＝a C．logab＝6 D．logba＝63．若logx(－2)＝－1，则x的值为()A.－2B.＋2C.－2或＋2 D．2－4．如果f(10x)＝x，则f(3)等于()A．log310 B．lg3 C．103 D．3105．21＋·log25的值等于()A．2＋B．2 C．2＋D．1＋二、填空题6．若5lgx＝25，则x的值为________．7．设loga2＝m，loga3＝n，则a2m＋n的值为________．三、解答题9．求下列各式中x的值(1)若log3＝1，则求x值；(2)若log2 003(x2－1)＝0，则求x值．二、对数运算性质的应用例2计算：(1)log535－2log5＋log57－log51.8；(2)2(lg)2＋lg·lg5＋；(3)；(4)(lg5)2＋lg2·lg50.(1)log535＋2log－log5－log514；(2)[(1－log63)2＋log62·log618]÷log64.一、选择题1．lg8＋3lg5的值为()A．－3 B．－1 C．1 D．33．若lga，lgb是方程2x2－4x＋1＝0的两个根，则2的值等于()A．2 B. C．4 D.5．设函数f(x)＝logax (a>0，且a≠1)，若f(x1x2…x2 005)＝8，则f(x)＋f(x)＋…＋f(x)的值等于()A．4 B．8 C．16 D．2loga8二、填空题6．设lg2＝a，lg3＝b，那么lg＝__________.7．若logax＝2，logbx＝3，logcx＝6，则logabcx的值为____．8．已知log63＝0.613 1，log6x＝0.386 9，则x＝________.三、解答题9．求下列各式的值：(1)lg－lg＋lg；(2)(lg5)2＋2lg2－(lg2)2.2．2.2对数函数及其性质1．对数函数的概念形如y＝logax (a>0且a≠1)的函数叫做对数函数．对于对数函数定义的理解，要注意：(1)对数函数是由指数函数变化而来的，由指数式与对数式关系知，对数函数的自变量x恰好是指数函数的函数值y，所以对数函数的定义域是(0，＋∞)；(2)对数函数的解析式y＝logax中，logax前面的系数为1，自变量在真数的位置，底数a必须满足a>0，且a≠1；(3)以10为底的对数函数为y＝lgx，以e为底的对数函数为y＝lnx.2．对数函数的图象及性质：a>10<a<1图象性质函数的定义域为(0，＋∞)，值域为(－∞，＋∞)函数图象恒过定点(1，0)，即恒有loga1＝0当x>1时，恒有y>0；当0<x<1时，恒有y<0当x>1时，恒有y<0；当0<x<1时，恒有y>0函数在定义域(0，＋∞)上为增函数函数在定义域(0，＋∞)上为减函数3.指数函数与对数函数的关系比较名称指数函数对数函数解析式y＝ax (a>0，且a≠1)y＝logax(a>0，且a≠1)定义域(－∞，＋∞)(0，＋∞)值域(0，＋∞)(－∞，＋∞)函数值变化情况a>1时，；0<a<1时，xa>1时，logax；0<a<1时，logax图象必过定点点(0,1)点(1,0)单调性a>1时，y＝ax是增函数；0<a<1时，y＝ax是减函数a>1时，y＝logax是增函数；0<a<1时，y＝logax是减函数图象y＝ax的图象与y＝logax的图象关于直线y＝x对称实际上，观察对数函数的图象不难发现，对数函数中的值y＝logmn有以下规律：(1)当(m－1)(n－1)>0，即m、n范围相同(相对于“1”而言)，则logmn>0；(2)当(m－1)(n－1)<0，即m、n范围相反(相对于“1”而言)，则logmn<0.有了这个规律，我们再判断对数值的正负就很简单了，如log2<0，log52>0等，一眼就看出来了！题型一求函数定义域求下列函数的定义域：(1)y＝log3x－1；题型二对数单调性的应用(1)log43，log34，log的大小顺序为()A．log34<log43<logB．log34>log43>logC．log34>log>log43D．log>log34>log43已知loga<1，那么a的取值范围是________．设函数f(x)＝lg(ax2＋2x＋1)，若f(x)的值域是R，求实数a的取值范围．1．已知函数f(x)＝的定义域为集合M，g(x)＝ln(1－x)的定义域为集合N，则M∩N等于() A．{x|x>－1} B．{x|x<1} C. D．?2．已知函数f(x)＝lg，若f(a)＝，则f(－a)等于()A. B．－C．－2 D．23．已知a＝log23，b＝log32，c＝log42，则a，b，c的大小关系是()A．c<b<a B．a<b<c C．b<c<a D．c<a<b4．函数f(x)＝lg|x|为()A．奇函数，在区间(0，＋∞)上是减函数B．奇函数，在区间(0，＋∞)上是增函数C．偶函数，在区间(－∞，0)上是增函数D．偶函数，在区间(－∞，0)上是减函数5．函数y＝ax与y＝－logax (a>0，且a≠1)在同一坐标系中的图象只可能为()6．设函数f(x)＝log2a(x＋1)，若对于区间(－1,0)内的每一个x值都有f(x)>0，则实数a的取值范围为()A．(0，＋∞) B. C. D.7．若指数函数f(x)＝ax (x∈R)的部分对应值如下表：x－22f(x)0.69411.44则不等式loga(x－1)<0的解集为__________．8．函数y＝logax (1≤x≤2)的值域为[－1,0]，那么a的值为________．9．已知函数f(x)＝是实数集R上的减函数，那么实数a的取值范围为__________．一、对数函数的图象例1下图是对数函数y＝logax的图象，已知a值取，，，，则图象C1，C2，C3，C4相应的a 值依次是()A. B．C．D．二、求函数的定义域例2求下列函数的定义域：(1)y＝；(2)y＝；(3)y＝log(x＋1)(2－x)．三、对数函数单调性的应用例3比较大小：(1)log0.81.5与log0.82；(2)log35与log64.变式迁移3比较下列各组中两个值的大小：(1)log0.52.7，log0.52.8；(2)log34，log65；(3)logaπ，logae (a>0且a≠1)．例4若－1<loga<1，求a的取值范围．一、选择题1．当a>1时，在同一坐标系中，函数y＝a－x与y＝logax的图象是()2．函数y＝的定义域是()A．[1，＋∞) B.C. D.3．已知a＝log0.70.8，b＝log1.10.9，c＝1.10.9，则a、b、c的大小关系是()A．a<b<c B．a<c<b C．b<a<c D．c<a<b4．设a>1，函数f(x)＝logax在区间[a,2a]上的最大值与最小值之和为4，则a等于() A. B．2 C．2 D．45．若loga<1，则a的取值范围是()A．a>1 B．0<a<或a>1 C．0<a< D.<a<1二、填空题6．若f(x)＝则满足f(x)＝的x的值为________．7.函数f(x)＝log3x的反函数为__________．,答案f(x)＝3x,8.对数函数f(x)的图象过点P(8,3)，则f＝______.三、解答题9．已知f(x)＝loga (a>0且a≠1)，其定义域为(－1,1)，试判断f(x)的奇偶性并证明．。

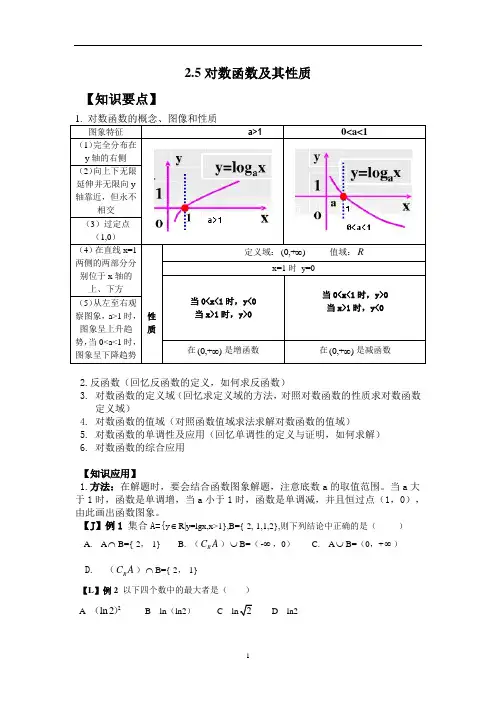
2.5对数函数及其性质【知识要点】2.反函数（回忆反函数的定义，如何求反函数）3. 对数函数的定义域（回忆求定义域的方法，对照对数函数的性质求对数函数定义域）4. 对数函数的值域（对照函数值域求法求解对数函数的值域）5. 对数函数的单调性及应用（回忆单调性的定义与证明，如何求解）6. 对数函数的综合应用【知识应用】1.方法：在解题时，要会结合函数图象解题，注意底数a 的取值范围。

当a 大于1时，函数是单调增，当a 小于1时，函数是单调减，并且恒过点（1，0），由此画出函数图象。

【J 】例1 集合A={y ∈R|y=lgx,x>1},B={-2,-1,1,2},则下列结论中正确的是（ ）A. A ⋂B={-2，-1}B. （R C A ）⋃B=（-∞，0）C. A ⋃B=（0，+∞）D. （R C A ）⋂B={-2，-1}【L 】例2 以下四个数中的最大者是（ ）A 2ln 2（） B ln （ln2） C D ln2【C 】例3 已知1<x<10，试比较2(lg )x 、2lg x lg （lgx ）的大小。

2. 方法：（1）由反函数定义可知，原函数的定义域是反函数的值域，原函数的值域是反函数的定义域。

因此，求反函数时，首先都要对原函数的定义域和值域进行研究，对于分段函数的反函数，应先分别求出每一段函数的反函数，再将它综合成一个函数即可。

（2）反函数的求法：a..由y=f(x)解出x b.把x 与y 的位置互换 c.写出解析式的定义域（注意：并不是每个函数都有反函数，有些函数没有反函数，如y=2x ；一般来说，单调函数有反函数）（3）反函数的性质：a.互为反函数的两个函数的图像关于直线y=x 对称 b.若函数y=f(x)图像上有一点（a ，b ），则（b ，a ）必在其反函数图像上，反之若（b,a ）在反函数图像上，则（a ，b ）必在原函数图像上。

c.互为反函数的函数具有相同的单调性、奇偶性。

高一数学必修一对数函数的基本性质对数函数是高中数学中重要的一类函数，具有许多特殊的性质和应用。

本文将介绍对数函数的基本性质。

1. 对数函数的定义对数函数是指以某个正数为底的对数函数，一般表示为$y=\log_{a}x$，其中 $a>0$，$a\neq 1$，$x>0$。

其中，$a$ 为底数，$x$ 为真数，$y$ 为对数值。

2. 对数函数的图像特征对数函数的图像呈现出以下特征：- 当 $0<x<1$ 时，$\log_{a}x<0$；- 当 $x=1$ 时，$\log_a1=0$；- 当 $x>1$ 时，$\log_a x>0$；- 对数函数的图像在 $x$ 轴的正半轴上单调递增，但增长速度越来越慢；- 对数函数的图像通过点 $(1, 0)$，并且与 $x$ 轴和 $y$ 轴分别渐近。

3. 对数函数的基本性质对数函数具有以下基本性质：- $\log_ab$ 为 $x=a^y$ 的反函数，即 $\log_ab=y\Rightarrowa^y=x$；- $\log_a(mn)=\log_am+\log_an$，即可以将乘积化为求和；- $\log_a\frac{m}{n}=\log_am-\log_an$，即可以将商化为差；- $\log_aa^x=x$；- $a^{\log_ax}=x$。

4. 对数函数的常用公式对数函数的常用公式有：- $\log_aa=1$；- $\log_a1=0$；- $\log_a a^k=k$。

5. 对数函数的应用对数函数在实际问题中具有广泛的应用，例如：- 在科学计算中，对数函数可以用于简化复杂的数值计算；- 在经济学中，对数函数可以用于描述指数增长和指数衰减的现象；- 在物理学中，对数函数可以用于描述某些物理现象的特性；- 在生物学中，对数函数可以用于研究生物体的生长和衰退规律。

以上就是对数函数的基本性质和应用的简要介绍。

对数函数在数学中具有重要的地位，通过深入理解对数函数的性质和应用，可以更好地解决实际问题。

目录对数函数 (2)模块一：对数与对数运算 (2)考点1：对数运算 (3)模块二：对数函数图像与性质的应用 (3)考点2：对数比较大小 (4)模块二：对数型复合函数 (5)考点3：对数函数相关的复合函数 (5)课后作业： (7)对数函数模块一：对数与对数运算1.对数的概念：一般地，如果b a N =(0a >，且1)a ≠，那么我们把b 叫做以a 为底N 的对数，记作log a b N =，其中a 叫做对数的底数，N 叫做真数．2.常用对数与自然对数对数log a N （0a >且1a ≠），当底数 （1）10a =时，叫做常用对数，记做lg N ；（2）e a =时，叫做自然对数，记做ln N （e 为无理数，e 2.71828≈）． 3.对数的运算性质：如果，且，那么： （1）；（积的对数等于对数的和） 推广（2） ；（商的对数等于对数的差） （3） ．（幂的对数等于底数的对数乘以幂指数）4.换底公式：（）．5.换底公式的几个基本使用： ①； ②；③；④. 0a >100a M N ≠>>，，log ()log log a a a M N M N ⋅=+1212log ()log log log a k a a a kN N N N N N ⋅⋅⋅=+++log log log aa a MM N N=-log log ()a a M M ααα=∈R log log log a b a NN b=010a b a b N >≠>，，，，log log 1a b b a ⋅=log log log a b a b c c ⋅=1log log n a a b b n=log log n m a a mb b n=考点1：对数运算例1.（1）化简求值：253948(log 212)(log 313)2log og og +++； 【解答】解：2539482233231113525(log 212)(log 313)2()()5(1)()55323223232223264log lg lg lg lg lg lg og og lg lg lg lg lg lg +++=+++=+++=⨯+= （2）2525(2)lg lg lg lg ++= ．【解答】解：2525(2)52(52)521lg lg lg lg lg lg lg lg lg lg ++=++=+=． 故答案为：1．例2.（1）若496m n ==，则11m n+= ． 【解答】解：由496m n ==， 得4log 6m =，9log 6n =， 即614log m =，61log 9n=， 所以66611log 4log 9log 362m n+=+==， 故答案为：2．（2）已知72p =，75q =，则2lg 用p ，q 表示为 ． 【解答】解：72p =，75q =， 72plg lg ∴=，75qlg lg =，∴2512qlg lg lg p==-， 化为2plg p q =+， 故答案为：pp q+． 模块二：对数函数图像与性质的应用1.对数函数：我们把函数且）叫做对数函数，其中是自变量，函数的定义域是，值域为实数集．2.对数函数的图象与性质：log (0a y x a =>1a ≠x (0)+∞，R考点2：对数比较大小例3.（1）若log 0.5log 0.50m n >>，则( ) A ．1m n <<B ．1m n <<C ．1n m <<D ．1n m <<【解答】解：log 0.5log 0.50m n >>；∴0.50.5110log m log n>>；0.50.5log log 0n m ∴>>；1n m ∴<<．故选：D ．（2）设4log 9a =，4log 25b =，5log 9c =，则( ) A ．a b c >> B ．c a b >> C ．b c a >> D ．b a c >>【解答】解：454995log log log =； 44log 9log 51>>；∴444995log log log <； 54log 9log 9∴<；又44log 9log 25<； b a c ∴>>．故选：D ．（3）已知2log 6a =，3log 2b =，3log 6c =，则( ) A ．a b c <<B ．b c a <<C ．a c b <<D ．c b a <<【解答】解：22log 6log 42>=，330log 2log 31<<=，3331log 3log 6log 92=<<=； b c a ∴<<．故选：B ．例4.求不等式2log (583)2x x x -+>的解集． 【解答】解：133252⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭，，模块二：对数型复合函数单调性、定义域、值域、奇偶性为本模块重点考点3：对数函数相关的复合函数例5.函数212log (12)y x x =--的单调增区间是 ．【解答】解：由2120x x -->得3x <-或4x >． 令2()12g x x x =--，则当3x <-时，()g x 为减函数，当4x >时，()g x 为增函数函数．又12y log u =是减函数，故212(12)y log x x =--在(,3)-∞-为增函数．故答案为：(,3)-∞-． 例6.（1）求函数21124log log 5⎛⎫=-+ ⎪⎝⎭y x x 在[]24，上的最值． 【解答】解：max10=y ，min 132=y ．（2）已知()32log ([19])f x x x =+∈，，求函数22[()]()y f x f x =+的最大值与最小值． 【解答】解：1x =时，y 有最小值6；3x =时，y 有最大值13．例7.已知函数22()log 2xf x x+=- （Ⅰ）求()f x 的定义域； （Ⅱ）讨论()f x 的奇偶性；（Ⅲ）求使()0f x >的x 的取值范围． 【解答】解：()I 由对数函数的定义知202xx+>-． 如果2020x x +>⎧⎨->⎩，则22x -<<；如果2020x x +<⎧⎨-<⎩，则不等式组无解．故()f x 的定义域为(2,2)- 2222()()()22x xII f x log log f x x x-+-==-=-+-， ()f x ∴为奇函数． 22()log 02x III x +>-等价于212x x+>-，① 而从()I 知20x ->，故①等价于22x x +>-，又等价于0x >．∴当(0,2)x ∈时有()0f x >例8.已知函数()log (1)log (1)a a f x x x =+--，其中0a >且1a ≠． （1）求函数()f x 的定义域；（2）判断()f x 的奇偶性，并说明理由；（3）若3()25f =，求使()0f x >成立的x 的集合．【解答】解：（1）要使函数有意义，则1010x x +>⎧⎨->⎩，解得11x -<<，即函数()f x 的定义域为(1,1)-； （2）()log (1)log (1)[log (1)log (1)]()a a a a f x x x x x f x -=-+-+=-+--=-，()f x ∴是奇函数． （3）若3()25f =，33log (1)log (1)log 4255a a a ∴+--==，解得：2a =，22()log (1)log (1)f x x x ∴=+--，若()0f x >，则22log (1)log (1)x x +>-， 110x x ∴+>->，解得01x <<，故不等式的解集为(0,1)．课后作业：1．计算2(2)205lg lg lg +⨯的结果是( ) A ．1B ．2C ．2lgD ．5lg【解答】解：因为22(2)205(2)(12)(12)1lg lg lg lg lg lg +⨯=++-=， 故选：A ．2．若3412a b c ==，且0abc ≠，则c ca b+等于( ) A ．4B ．3C ．2D ．1【解答】解：设3412a b c k ===， 则3log a k =，4log b k =，12log c k =， 则12123434112k k k log log log k log k c c a b log k log k log ++=+==． 故选：D ．3．已知52log a =，122b =，c =( )A ．a c b >>B ．a b c >>C ．c a b >>D ．c b a >>【解答】解：5512log log 32log 22a b =>==，7log 3c =，a c ∴>，52log 41b =<，72log 91c =>，c b ∴>．a cb ∴>>．故选：A ．4．若函数()log (0a f x x a =>且1)a ≠在区间[a ，22]a 上的最大值比最小值多2，则(a =) A ．2B ．3或13C ．4或12D ．2或12【解答】解：由22(21)0a a a a -=->，有12a >且1a ≠， ①当1a > 时，2(2)2a a log a log a -=，得2a =，②当112a << 时，2(2)2a a log a log a -=，得a ， 故2a =，故选：A ．5．已知函数()(2)(2)f x lg x lg x =++-．（1）求函数()f x 的定义域并判断函数()f x 的奇偶性； （2）记函数()()103f x g x x =+，求函数()g x 的值域； （3）若不等式()f x m >有解，求实数m 的取值范围． 【解答】解：（1）函数()(2)(2)f x lg x lg x =++-， ∴2020x x +>⎧⎨->⎩，解得22x -<<．∴函数()f x 的定义域为(2,2)-．()(2)(2)()f x lg x lg x f x -=-++=， ()f x ∴是偶函数．（2）22x -<<，2()(2)(2)(4)f x lg x lg x lg x ∴=++-=-． ()()103f x g x x =+，∴函数22325()34()24g x x x x =-++=--+，(22)x -<<，325()()24max g x g ∴==，()(2)6min g x g →-=-， ∴函数()g x 的值域是(6-，25]4． （3）不等式()f x m >有解，()max m f x ∴<， 令24t x =-，由于22x -<<，04t ∴< ()f x ∴的最大值为4lg ．∴实数m 的取值范围为{|4}m m lg <．。

对数函数__________________________________________________________________________________ __________________________________________________________________________________1、体会对数函数是一类重要的函数模型；能借助计算器或计算机画出具体对数函数的图像，探索并了解对数函数的单调性与特殊点.2、掌握对数函数的性质，并能应用对数函数解决实际中的问题. 知道指数函数 y =a x 与对数函数y =log a x 互为反函数. （a >0,a ≠1）一、对数函数的定义：函数x y a log =)10(≠>a a 且叫做对数函数。

二、对数函数的图像和性质：a >1 01a <<图 像性 质定义域：()0,+∞值域：R过点()1,0，即当1x =时，0y =)1,0(∈x 时，0<y ；),1(+∞∈x 时， 0>y)1,0(∈x 时，0>y ；),1(+∞∈x 时，0<y在()0,+∞上是增函数在()0,+∞上是减函数三、比较对数值的大小，常见题型有以下几类：1、比较同底数对数值的大小：利用函数的单调性；当底数是同一参数时，要对对参数进行分类讨论；2、比较同真数对数值的大小：可利用函数图像进行比较；3、比较底数和真数都不相同的对数值的大小：可选取中间量如：“1”、“0”等进行比较。

四、对数不等式的解法：()()()()()()()()()() 1 log log 0 01log log 0a a a a f x g x a f x g x f x f x g x a f x g x f x >⎧>>⎨>⎩<⎧<<>⎨>⎩当时，与同解。

对数函数高一必修一知识点对数函数是高一必修一数学课程中的重要知识点之一。

它是解决指数函数的反问题时所应用的数学工具。

在实际应用中，对数函数起着很大的作用。

本文将介绍对数函数的基本定义、性质及其在实际生活中的应用。

一、对数函数的基本定义对数函数的定义基于指数函数，而指数函数又是以指数为底数的常数幂函数。

设a是一个正实数，且a ≠ 1，x是任意实数，则以a为底数的对数函数定义如下：y = logₐx其中，a称为底数，x称为真数，y称为以a为底x的对数。

二、对数函数的性质1. 定义域和值域：由对数函数的定义可知，底数a为正实数且a ≠ 1，因此对数函数的定义域为(0, +∞)。

而对数函数的值域则为R（实数集）。

2. 对数函数的图象特点：对数函数y = logₐx的图象是一条曲线，对于a > 1时，该曲线从左下方逐渐上升，且永远不会超过x轴；对于0 < a < 1时，该曲线从左上方逐渐下降，且永远不会超过x轴。

此外，对于任意a 值，对数函数的图象均会通过点(1, 0)。

3. 对数函数的性质：（1）相等性质：logₐa = 1，即a的以a为底的对数等于1。

（2）互逆性质：logₐa = x 等价于aˣ = a。

（3）对数的连乘性：logₐ(ab) = logₐa + logₐb。

（4）对数的连除性：logₐ(a/b) = logₐa - logₐb。

（5）对数的连乘法则：logₐaⁿ = nlogₐa。

（6）对数的换底公式：logₐx = logᵦx / logᵦa。

三、对数函数在实际生活中的应用1. 比特率计算：对数函数在信息论中扮演着重要的角色。

在计算机科学中，比特率常被用于衡量数据传输的速率。

其计算公式为：log₂N，其中N为表示不同状态的离散符号数量。

对数函数在这里帮助我们将离散的符号数量转化为连续的比特率。

2. pH值计算：生活中，我们经常会用到pH值来衡量一个溶液的酸碱程度。