北京交通大学信号与系统第四章典型例题
- 格式:doc
- 大小:5.58 MB
- 文档页数:33


信号与系统_北京交通大学中国大学mooc课后章节答案期末考试题库2023年1.某连续周期信号如题1图所示,该信号的频谱成分有( )【图片】参考答案:直流、奇次谐波的余弦分量2.已知描述某连续时间LTI系统的状态方程的矩阵分别为【图片】【图片】【图片】【图片】则该系统的系统函数【图片】为参考答案:3行3列矩阵3.关于连续非周期信号的频域表示,正确的说法是( )参考答案:将信号表示为不同频率正弦信号的线性组合4.连续非周期信号频谱的特点是( )参考答案:连续、非周期5.已知某线性连续时间系统,其在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】;该系统在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】试求初始状态为【图片】,激励为【图片】时系统的完全响应【图片】=( )。
参考答案:,6.连续非周期信号频谱的特点是参考答案:连续、非周期7.已知信号【图片】,其频谱【图片】在【图片】的值【图片】参考答案:88.连续周期信号【图片】是功率信号,其傅里叶变换【图片】都不存在。
参考答案:错误9.已知信号【图片】的最高频率分量为【图片】 Hz,若抽样频率【图片】,则抽样后信号的频谱一定混叠。
参考答案:错误10.连续时间周期信号【图片】的平均功率为( )参考答案:1111.利用状态变量分析法分析连续时间LTI系统时,输出方程【图片】可能与哪些因素有关参考答案:与输入和状态变量有关12.关于连续周期信号频谱的特性,正确的说法是( )参考答案:同时具有离散特性和幅度衰减特性。
13.若描述离散时间系统的差分方程为【图片】,该系统为( )。
参考答案:因果、线性时不变系统14.连续周期信号在有效带宽内各谐波分量的平均功率之和占整个信号平均功率的很大一部分。
参考答案:正确15.连续时间信号在时域展宽后,其对应的频谱中高频分量将增加。
参考答案:错误16.信号时域时移,其对应的幅度频谱不变,相位频谱将发生相移。

![[工学]4第四章_波形估计_OK](https://uimg.taocdn.com/a2ef38296f1aff00bfd51eea.webp)


第四章部分习题解答4-7求下列各序列的DFT ,已知N=4。
(1))(0n n -δ 300≤≤n解:044300)()]([kn kn n WWn n n n X =-=-∑=δδ(2))(n G N解:∑∑=====344304)(4)()]([n kn knn N k W Wn G n G X δ (利用正交性)或用矩阵法解 j eW j-==-4214π⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0004111111111111111111111111111)]([946434644424342414j j j j W W W W W W W W W n G X N (3))(n G a N n , 1≠a 解:1,111)(1)()(43044444≠--=--==∑=a aW a aW aW Wn G a k X kn k k kn n(4)}3,2,1,0{)(=n nG N解:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=2222263210111111111111)]([4j j j j j j n nG X(5))(0n G e N n j ω解:kj j k j k j knn nj W e e W e W e Wn G ek X 444444300000111)(1)()(ωωωωω--=--==∑=4-8有限长序列x(n)如题图4-2所示,若题图 4-2)())3(()(441n G n x n x -= )())3(()(442n G n x n x -=给出)(1n x 和)(2n x 序列图形,并计算)(1n x 和)(2n x 的离散傅里叶变换。
解:由圆周移位特性知:}1,4,3,2{)(1=n x⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=j j j j j j k X 22222101432111111111111][1 }1,2,3,4{)(2↑=n x⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=j j j j j j k X 22222101234111111111111][2 4-9两有限长序列x(n)和h(n)如题图4-3所示,求)()(n h n x *。

1试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6试画出下列信号的波形图:⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。



1.某900MHz蜂窝系统中同时存在对数正态阴影衰落和瑞利衰落,阴影衰落的标准差为6dB,调制方式为DPSK,运营商可以容忍0。
01的中断率.非中断时,语音业务对平均误比特率的要求是10-3,假设噪声的功率谱密度为N0/2,N0=10—16mW/Hz,信号的带宽为30kHz.路径损耗采用自由空间传播模型,发送和接收均采用全向天线(增益为0),不考虑馈线损耗,移动终端的最大发射功率为100mW,求:(1) DPSK采用相干解调,考虑信号受瑞利衰落,求接收信号的平均信噪比,接收信号的平均功率?(2)考虑信号受对数正态阴影衰落,接收功率应该提高为多少?(3)计算小区的最大半径。
注:对于一个均值为μ,标准差为σ的正态分布随机变量X,则Xμσ-服从标准正态分布.标准正态分布的累计概率密度函数(CDF)()xΦ的值2.已知(7,4)循环汉明码的生成多项式为g(X)= X3+ X2+1。
(1)写出系统码形式的生成矩阵;(2) 写出该码的校验矩阵;(3) 假设接收码字为R=[1010011],求其伴随式;3.某移动通信系统的工作频率为900MHz,符号速率为270。
833kbps,移动台的移动速率为80km/h,求均衡器一次训练后能够传输的最大符号数。
4.考虑N支路的分集合并系统,每个支路是SNR=10dB的AWGN信道。
假设采用M=4的MQAM调制,误码率近似为P b=0。
2e—1。
5γ/(M-1),其中γ是接收信噪比。
(1)求N=1时的P b。
(2)MRC下,求使P b<10—6的N.1.(1)在瑞利信道下,DPSK经相干解调,误码率P b=1/(4γb)=10—3,∴接收信号信噪比γb=250噪声功率为N 0B=3*10-12mW∴P 瑞=γb *N 0B =7.5*10-10mW=-91。
2dBm (2)中断概率P out =P (P r 〈P 瑞)=P(ψ<P 瑞- P r )=Φ((P 瑞- P r )/σ)=0。
1. 请推导出三阶巴特沃思低通滤波器的系统函数,设1/c rad s W =。
解:幅度平方函数是:2261()()1A H j W =W =+W 令:令: 22s W =- ,则有:61()()1a a H s H s s-=- 各极点满足121[]261,26k j k s ek p -+==所得出的6个 k s 为:为:105==j e s 2321321je s j +-==p 12-==p j e s 2321343je s j --==p 2321354j es j -==p 2321316j es j +==p15==j e s 2321321je s j +-==p 12-==p j e s 2321343je s j --==p 2321354j es j -==p 2321316j es j +==p 122))()(()(233210+++=---=s s s k s s s s s s k sH a 1221)(23+++==s s s sHa 代入s=0时, ,可得,故:1=)s (H a 10=k2. 设计一个满足下列指标的模拟Butterworth 低通滤波器,要求通带的截止频率6,p f kHz =,通带最大衰减3,pA dB =,阻带截止频率12,s f kHz =,阻带的最小衰减25sAdB =,求出滤波器的系统函数。
,求出滤波器的系统函数。
解:解: 2,2s s p pf f p p W =W =0.10.1101lg 101N 2lg()s pA A s pæö-ç÷-èø³W W =4.15 取N=5,查表得H(p)为:为: 221()(0.6181)( 1.6181)(1)H p p p p p p =+++++因为3,pAdB =所以c p W =W[]52222()()0.618 1.618cs p cc c c c c H s H p s s s s s =W =W =éùéù+W -W +W -W +W ëûëû3. 设计一个模拟切比雪夫低通滤波器,设计一个模拟切比雪夫低通滤波器,要求通带的截止频率要求通带的截止频率要求通带的截止频率 f p =3kHz,通带衰减要不大于0.2dB ,阻带截止频率,阻带截止频率 f s = 12kHz ,阻带衰减不小于,阻带衰减不小于,阻带衰减不小于 50dB 。
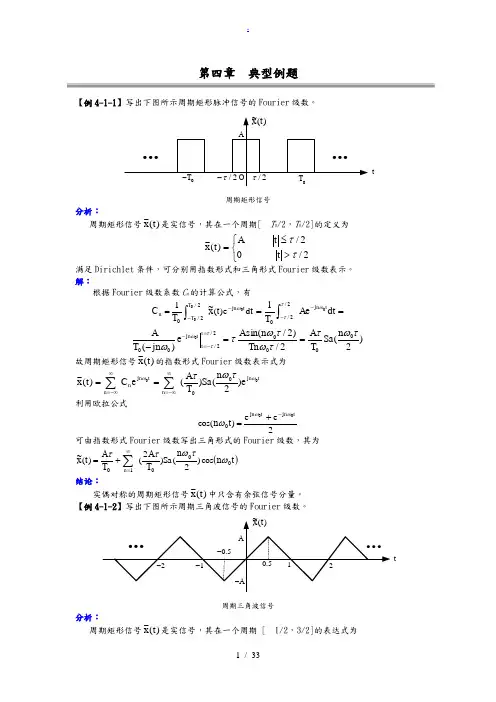
第四章 典型例题【例4-1-1】写出下图所示周期矩形脉冲信号的Fourier 级数。
t周期矩形信号分析:周期矩形信号)(~t x 是实信号,其在一个周期[-T 0/2,T 0/2]内的定义为⎩⎨⎧>≤=2/02/ )(~ττt t A t x满足Dirichlet 条件,可分别用指数形式和三角形式Fourier 级数表示。
解:根据Fourier 级数系数C n 的计算公式,有t t x T C t n T T n d e )(~1000j 2/2/0ω--⎰===--⎰t A T t n d e 10j 2/2/0ωττ 2/2/j 000e )j (ττωω=-=--t t t n n T A 2/)2/sin(00τωτωτTn n A =)2(Sa 00τωτn T A =故周期矩形信号)(~t x 的指数形式Fourier 级数表示式为t n n t n n n n T A C t x 00j 00j e )2(Sa )(e )(~ωωτωτ∑∑∞-∞=∞-∞===利用欧拉公式2e e )cos(00j j 0tn t n t n ωωω-+=可由指数形式Fourier 级数写出三角形式的Fourier 级数,其为()t n n T A T A t x n 00010cos )2(Sa )2()(~ωτωττ∑∞=+=结论:实偶对称的周期矩形信号)(~t x 中只含有余弦信号分量。
【例4-1-2】写出下图所示周期三角波信号的Fourier 级数。
t周期三角波信号分析:周期矩形信号)(~t x 是实信号,其在一个周期 [-1/2,3/2]的表达式为⎪⎩⎪⎨⎧≤<-≤=2321 )1(221 2)(~t t A t At t x满足Dirichlet 条件,可分别用指数形式和三角形式Fourier 级数表示。
解:由于该三角波信号)(~t x 的周期T 0=2,所以ππ200==T ω。
根据Fourier 级数系数的计算公式,有t t x T C t n T T n d e )(~1000j 2/2/0ω--⎰=t t A t At t n tn d e )1(221d e 221πj 2/32/1πj 2/12/1----+=⎰⎰计算上式积分可得三角波信号的频谱C n 为⎪⎩⎪⎨⎧=≠-=0,00),2πsin(πj422n n n n A C n 所以周期三角波信号的Fourier 级数表示式为tn n n n n A t x πj 220,e )2πsin(πj 4)(~-=∑∞≠-∞= 利用欧拉公式j2e e )sin(00j j 0tn t n t n ωωω--=可由指数形式Fourier 级数写出三角形式的Fourier 级数,其为==∑∞=t n n n A t x n πsin )2πsin(π8)(~221⎥⎦⎤⎢⎣⎡+-+- t t t t A π7sin 491π5sin 251π3sin 91πsin π82 结论:(1) 实奇对称的周期三角波信号)(~t x 中只含有正弦信号分量。
(2) 例4-1-1的周期矩形信号和例4-1-2的周期三角波信号均可用Fourier 级数tn nn C t x 0j e)(~ω∑∞-∞==表示,所不同的是两者的Fourier 系数不同。
因此,研究Fourier 系数也可获得信号的某些特性。
【例4-1-3】判断下图所示周期矩形信号和周期三角波信号的Fourier 系数的特性。
t(a)周期矩形信号t(b)周期三角波信号分析:首先判断信号时域的对称关系,再利用周期信号的对称特性和Fourier 系数的关系,即可得出相应信号Fourier 系数的特性。
解:(a)信号为实偶对称,满足)(~)(~t x t x -=,故Fourier 系数C n 实偶对称,其三角形式Fourier 级数表示式中只含有直流项和余弦项。
(b) 信号既满足)(~)(~t x t x --=,又满足)2/(~)(~0T t x t x ±=,为实奇对称半波镜像信号,其三角形式Fourier 级数表示式中只含有奇次谐波的正弦信号分量。
结论:利用周期信号的对称特性和Fourier 系数的关系可以建立信号时频的对应关系,定性地判断信号的频谱成份。
【例4-1-4】判断下图所示周期信号)(~t x 的Fourier 系数的特性。
t分析:从信号)(~t x 的波形来看,其不具有任何对称关系。
在这种情况下可以去掉信号的直流分量,再观察波形的对称性。
解:信号的直流分量为A t t x T C T 4.0d )(~10000==⎰)(~t x 去掉直流分量后的波形如下图所示,是半波镜像信号,故只含有奇次谐波分量。
t综合上面的分析,)(~t x 的三角形式Fourier 级数表示式中含有直流项、奇次谐波(正弦和余弦)分量。
结论:某些信号波形经上下或左右平移后,才呈现出某种对称特性。
【例4-1-5】利用连续时间Fourier 级数的性质,写出下图所示周期矩形信号)(~t x 的Fourier 级数表示式。
t分析:周期信号)(~t x 可以看成直流分量与例4-1-1周期矩形信号之差,利用Fourier 级数的线性特性和例4-1-1周期矩形信号Fourier 级数表示即可求解本题。
解:周期信号)(~t x 可以看成下图所示直流分量)(~1t x 和周期矩形信号)(~2t x 之差,即 )(~2)(~)(~)(~221t x t x t x t x -=-= 令例4-1-1中周期矩形信号的A =1,2=τ,40=T ,可得)(~2t x 的Fourier 级数表示式为()t n n T A T A t x n 000102cos )2(Sa )2()(~ωτωττ∑∞=+=)2πcos()2π(Sa 5.01tn n n ∑∞=+= 因此)(~t x 的Fourier 级数表示式为)(~2)(~2t x t x -=)2πcos()2π(Sa 5.11tn n n ∑∞=-=tt结论:利用常用周期信号的Fourier 系数和Fourier 级数的性质,可计算其它周期信号的Fourier 系数。
【例4-1-6】利用连续时间Fourier 级数的性质,写出下图所示周期矩形信号)(~t g的Fourier 级数表示式。
周期信号g (t )分析:周期信号)(~t g可以看成例4-1-1周期矩形信号右移0.5,利用Fourier 级数的时移特性和例4-1-1周期矩形信号Fourier 级数表示即可求解本题。
解:周期信号)(~t g 可以表示为)5.0(~)(~-=t x t g 。
令例4-1-1中周期矩形信号的1=τ,20=T , ω0=2π/ T 0=π,可得)(~t x 的Fourier 系数为)2(Sa 00τωτn T A C n =)2π(Sa 2n A =令)(~t g的Fourier 系数为D n ,利用Fourier 级数的时移特性可得 n n n C D 05.0j e ω-=2/πj e )2π(Sa 2n n A -=因此,周期信号)(~t g的Fourier 级数表示式为 ==∑∞-∞=n tn nC t g0j e)(~ωt n n n n A πj π/2j e e )2/π(/2)Sa (-∞-∞=∑⎥⎦⎤⎢⎣⎡++++= t t t A A π5sin 51π3sin 31πsin π22/t结论:)(~t g 与)(~t x 具有)5.0(~)(~-=t x t g 的关系,两者Fourier 级数的模相等,即n n D C =,但相位不同。
这充分体现了周期信号Fourier 级数时移特性的物理含义,即信号在时域的时移对应其在频域的相移。
【例4-1-7】画出例4-1-1以原点为中心对称的周期矩形信号)(~t x 的频谱。
t周期矩形信号分析:周期信号的Fourier 系数就是该信号的频谱。
解:由例4-1-1的计算结果,以原点为中心对称的周期矩形信号)(~t x 的频谱为)2(Sa 00τωτn T A C n =, 2,1,0±±=n由于C n 为实数,因而各谐波分量的相位或为零(C n 为正)或为±π(C n 为负),因此不需分别画出幅度频谱| C n |与相位频谱φ n 。
可以直接画出Fourier 系数C n 的分布图。
根据抽样函数Sa( t )的曲线便可得信号)(~t x 的频谱图。
ω00周期矩形信号的频谱结论:周期矩形脉冲的频谱具有以下特性:(1)离散频谱特性:频谱是以基频ω0为间隔分布的离散频谱。
由于谱线的间隔ω0=2π/T 0,故信号的周期T 0越大,其基频ω0就越小,谱线越密。
频谱都是由间隔为ω0的谱线组成的离散谱。
不同的周期信号其频谱分布的形状不同,但都 (2)幅度衰减特性:随着谐波n ω0增大,幅度频谱|C n |不断衰减,并最终趋于零。
不同的周期信号对应的频谱不同,但上述特性是周期信号频谱的普遍性质。
【例4-1-8】画出周期信号)(~t x =1+cos(ω0t -π/2)+0.5 cos(2ω0t +π/3)的频谱。
分析:根据周期信号的频谱基本概念,将)(~t x 表示为虚指数信号t n 0j e ω的线性组合(指数形式Fourier 级数),虚指数信号t n 0j e ω的系数就是该信号的频谱。
解:由Euler 公式,周期信号)(~t x 可表示为)e e e e (41)e e e e (211)(~00002j 3j π2j 3/j πj 2/j πj 2/j πt /t t t t x ωωωω----++++=与∑∞-∞==n tn nC t x 0j e)(~ω比较,可得3j π23/j π22/j π12/j π10e 41,e 41,e 21,e 21,1/C C C C C ----=====所以周期信号)(~t x 的频谱C n 如下图所示。
ω周期信号)(~t x 的幅度频谱和相位频谱结论:根据周期信号)(~t x 的幅度频谱和相位频谱,可以清楚看到周期信号中各谐波分量分布情况。
如果已知周期信号的频谱C n ,则可由式∑∞-∞==n tn nC t x 0j e)(~ω重建信号)(~t x 。
信号的时域描述和频域描述是深入分析和研究信号的理论基础。
【例4-2-1】试求图(a )所示非周期矩形脉冲信号x (t )的频谱函数X (j ω)。
tω(a ) 非周期矩形脉冲信号 (b ) 信号频谱函数分析:非周期矩形脉冲信号x (t )满足Dirichlet 条件,其Fourier 变换X (j ω)存在。