广东省佛山市2019-2020学年上学期普通高中高三教学质量检测(一)数学理科试题(解析版)

学校:1 •已知集合 A . B . 2.若复数 A . B . C. 20佃佛山一模（理）姓名:班级:W 口 考号:，则 C. D. （为虚数单位）在复平面内对应的点在虚轴上, D . 3 .设变量 满足约束条件 A . 7 B . 8 C. 15 D . 16 4 .已知： A .充分不必要条件 则实数，则目标函数 的最大值为（）”，则 B.必要不充分条件 5.已知-,则 - ()A.-B.-C. -D.-6 .已知向量( )A .B .C. 6 D . 87.展开式中的系数为（)A . B. 120 C . 160 D . 200C .充分必要条件 既不充分也不必要条件D . 8.某几何体的三视图如图所示，则该几何体的体积为（ A . B. C. D . 9.将偶函数 的图象向右平移-个单位,得到的图象，则 的一个单调递增区间为（ A . B . C. D . 10.已知矩形的中点，现分别沿翻折，使点 重合，记为点，则几何体的外接球表面积为（A .B . C. D .11 .双曲线 的左、右焦点分别为,且恰好为抛物线的焦点，设双曲线与12 •设为常数，函数 ① 若 ，则在区间② 若 ，则存在实数 ③ 若，则当 时，其中正确结论的个数是(A . 0B . 1 C. 2•给出以下结论:上有唯一零点；，当时，；)D . 3从中随机摸出2个球，则两个球不同色的概率为 ___________________16•在 中，角的对边分别为 ，且 ， 一•若当 变化时,存在最大值，则正数 的取值范围是 ________________17 .数列 中， ，，其中为常数(1) 若 成等比数列，求的值；(2)是否存在，使得数列 为等差数列？并说明理由.A .B . C. D .13 .已知双曲线一一 的一条渐近线为 一，则实数 _______________14 .不透明的布袋中有3个白球，2个黑球，5个红球共 10个球(除颜色外完全相同)15 .已知，则使得 成立的的取值范围是学号为22号的同学由于严重感冒导致物理考试发挥失常，学号为31号的同学因故未能参加物理学科的考试，为了使分析结果更客观准确，老师将两同学的成绩（对应于图中两点）剔除后，用剩下的42个同学的数据作分析，计算得到下列统计指标：数学学科平均分为110.5，标准差为18.36，物理学科的平均分为74，标准差为11.18,数学成绩与物理成绩的相关系数为，回归直线（如图所示）的方程为（1）若不剔除两同学的数据，用全部44人的成绩作回归分析，设数学成绩与物理成绩的相关系数为，回归直线为，试分析与的大小关系，并在图中画出回归直线的大致位置；（2）如果同学参加了这次物理考试，估计同学的物理分数（精确到个位）；（3）就这次考试而言，学号为16号的同学数学与物理哪个学科成绩要好一些？（通常为了比较某个学生不同学科的成绩水平，可按公式——统一化成标准分再进行比较，其中为学科原始分，—为学科平均分，为学科标准差）.19 .如图，多面体中，底面为菱形，且平面底面，平面底面（1）证明: 平面;（2）求一面角的余弦值.20 .已知过点的直线与椭圆交于不同的两点其中，为坐标原点.(1)若，求的面积；(2)在轴上是否存在定点，使得直线与的斜率互为相反数?21 .已知常数，函数(1)讨论函数在区间上的单调性;(2)若存在两个极值点，且，求的取值范围.22 .在直角坐标系中，曲线的参数方程为(为参数，)，直线的参数方程为(为参数)•(1)若，求曲线与的普通方程；(2)若上存在点，使得到的距离为—，求的取值范围.参考答案1. B【解析】【分析】求出集合A, B,然后直接取并集即可.【详解】集合 B = {x|- 1 v x v 1},A = {x|x2- 2x<0} = {x|0<x<2},则{x|0<x<2} {x|—1 v x v 1} = {x|-1<x v 2}故选：B.【点睛】本题考查集合的并集运算，属简单题•2. D【解析】【分析】计算出复数的表达式，由题意中复数在复平面内对应的点在虚轴上计算出结果【详解】复数在复平面内对应的点在虚轴上，则，-故选【点睛】本题主要考查了复数的几何意义，只需计算出复数在复平面内的对应点，结合题意即可计算出答案，较为基础3. B【解析】【分析】由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组得到最优解的坐标，代入目标函数得到答案【详解】作出变量x，y满足的约束条件如图:由z= 2x+y知，动直线y=- 2x+z的纵截距z取得最大值时，目标函数取得最大值.由得A （3，2）,结合可行域可知当动直线经过点 A （3，2）时,目标函数取得最大值z= 2X3+2 = &故选：B.52J 斗\y<321£ f \\-5 -4 -3 -2 -1-1-3--4L-5【点睛】本题考查线性规划中利用可行域求目标函数的最值，求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）（3 ）将最优解坐标代入目标函数求出最值.4. C【解析】【分析】先证充分性，然后再证明必要性，继而判定结果【详解】①充分性当时，成立,②必要性当时，当时，一，不成立，故舍去则是的充分必要条件故选【点睛】本题主要考查了充分条件和必要条件，在判定结果时左右两边分别进行证明充分性和必要性,继而得到结果，较为基础5. C【解析】【分析】运用两角差的余弦公式展开后再计算平方的结果，结合已知条件得到答案【详解】故选【点睛】本题主要考查了两角差的余弦公式以及二倍角公式，熟练运用公式来解题是关键，较为基础6. A【解析】【分析】先用坐标表示出，然后由向量垂直代入计算求出结果【详解】则解得故选【点睛】本题主要考查了向量的垂直计算，只需运用点坐标表示向量，然后点乘得零即可得到结果, 较为简单7.B【解析】【分析】结合二项展开式计算出含的项，从而得到系数【详解】展开式中的项为5则展开式中的系数为120故选【点睛】本题主要考查了二项展开式的运用，求特定项的系数，熟练运用公式进行求解8.D【解析】【分析】由题目中的三视图还原几何体，可知是由半圆锥和四棱锥组成，然后计算几何体的体积【详解】由三视图可得该组合体是由半圆锥和四棱锥组成由已知图中数量可得：故选【点睛】本题主要考查了三视图，要先还原几何体，然后再计算体积，还原几何体是难点，还需要有一定空间想象能力。

2019-2020学年上学期高三级期中考考试题理科数学本试卷共4页，22小题，满分150分，考试时间120分钟。

注意事项：1．答题前，考生务必用黑色笔迹的钢笔或签字笔将自己的姓名、考号填写在答题卷上。

2．每小题选出答案后，用2B 铅笔把答题卷上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

3．作答选做题时，请先用2B 铅笔填涂选做题的题组号对应的信息点，再作答。

漏涂、错涂、多涂的，答案无效。

第一部分选择题（共60分）一、选择题:本题共12小题，每小题5分，共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1．已知0||2,||3a b a b ===，且(32)()a b a b λ+⊥-则λ的值是( ) A ．32B ． 32±C ．32-D ．12．已知圆C 与直线30x y ++=相切，直线10mx y ++=始终平分圆C 的面积，则圆C 方程为( )A ．2222x y y +-=B ．2222x y y ++=C ．2221x y y +-=D ．2221x y y ++=3. 在ABC ∆中．角A 、B 、C 所对的边分别为a 、b 、c ．如果22tan tan a Ab B=．则ABC ∆的形状是( )A ．等腰三角形B ．等腰直角三角形C ．等腰三角形或直角三角形D ．直角三角形 4．设, 则的大小关系是：A ．B ．C ．D ．5. 设函数且(2)3f a =，则(2)(f a += )A ．2B ．3C ．2或3D ．36．已知两个圆1O 和2O ，它们的半径分别是2和4，且12||8O O =，若动圆M 与圆1O 内切，又与2O 外切，则动圆圆心M 的轨迹方程是( ) A ．圆B ．椭圆C ．双曲线一支D ．抛物线7．已知双曲线C ：()222210,0x y a b a b-=>>，斜率为1的直线与双曲线C 交于两点,A B ，若线段AB 的中点为(4，1)，则双曲线C 的渐近线方程是（ ）0y ±=B.20x y ±=C. 0x =D. 20x y ±=8. 在ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c ．已知b =，c =，tan()24A π+=，则(a = )A ．15B ．C ．3D ．9. 已知函数()cos()(f x A x A ωϕ=+，ω，ϕ为常数，0ω>，0)A <的部分图象如图所示，则(A = ) A ．2- B ．3-C ．D ． -10. 方程有三个不同的解，则的取值范围是()A ．B ．C ．D ．11．直线0x -+ 经过椭圆22221(0)x y a b a b+=>>的左焦点F ，交椭圆于A ，B 两点，交y 轴于C 点，若2FC CA =，则该椭圆的离心率是( )A1B C ．2 D 112．已知函数1()ax f x xe lnx ax -=--，21(,]a e ∈-∞-，函数()f x 的最小值M ，则实数M 的最小值是( ) A ．1-B ．1e-C ．0D ．31e -第二部分非选择题（90分）二、填空题:本题共4小题,每小题5分，共20分.13．直线0x =、直线1y e =+与曲线1x y e =+ 围成的图形的面积为 ． 14．直线与抛物线相交于A, B 两点，O 为原点，则三角形AOB 面积为 .15. 已知ABC ∆中，角、B 、C 对应边分别为 a b c 、、,且 0302A a ∠==，，则ABC ∆ 面积最大值为 . 16. 曲线C:与直线:1l y kx =-有4个交点，则 的取值范围是 .三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤. 17．(10分)ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，若．（1）求cos B ；（2）若2AB =，3sin 2sin A B =，求ABC ∆的面积．18．(12分)已知曲线12cos :(2sin x C y θθθ=⎧⎨=⎩为参数），曲线21cos (1sin x t C t y t αα=+⎧=⎨=-+⎩为参数）．（1）若4πα=，求曲线2C 的普通方程，并说明它表示什么曲线；（2）曲线1C 和曲线2C 的交点记为M 、N ，求||MN 的最小值．19．(12分)已知函数()()3+40,0.f x x a x b a b =-+>>（1）当11a b ==-，时，解不等式；（2）若()f x 的最小值为1，求13a b+的最小值．20．(12分)已知椭圆()2222:10x y E a b a b+=>>的左右焦点分别是12F F 、， 离心率12e =，点31,2⎛⎫- ⎪⎝⎭在椭圆E 上.（1）求椭圆E 的方程；（2）如图，分别过12F F 、作两条互相垂直的弦AC 与BD ，求AC BD +的最小值.21.(12分)如图，已知抛物线()2=20C x py p >：的焦点F 到直线20x y --=的距离为.223AB 是过抛物线C 焦点F 的动弦,O 是坐标原点，过B A ,两点分别作此抛物线的切线，两切线相交于点P . （1）求证：PB PA ⊥.（2）若动弦AB 不经过点(2,1)M ，直线AB 与准线l 相交于点N ，记,,MA MB MN 的斜率分别为123,,.k k k 问：是否存在常数λ，使得12311k k k λ+=+在弦AB 运动时恒成立？若存在，求λ的值；若不存在，说明理由.22. (12分)已知函数()ln x af x x ea -=-+（其中e 是自然对数的底数）.（1）当0a =时，求证：()2f x <-；（2）若函数()f x 有两个零点，求实数a 的取值范围.2019-2020 学年上学期高三级期中考理科数学答案2019年11月一、选择题:二、填空题:13. 1 ； 14. ； 15. ； 16. .三、解答题:17. 解：（1）,所以， …………………………………………………（3分）（2）因为1cos 3B =，所以, 所以sin 3B =．………………………（5分） 又3sin 2sin A B =，由正弦定理，32a b =．……………………………………………（6分）根据余弦定理2222cos b a c ac B =+-， 得43a =，2b =，………………………………………………………………………（8分）所以ABC ∆的面积为1sin 2S ac B ==．…………………………………………（10分）18. 解：（1）4πα=∴1(1x t y ⎧=⎪⎪⎨⎪=-+⎪⎩为参数） 11x y ∴-=+，∴曲线2C 的普通方程是2y x =-…………………………………（2分）它表示过(1,1)-，倾斜角为4π的直线………………………………………………（4分） （2）曲线1C 的普通方程为224x y +=……………………………………………（6分） 设(1,1)G -，过G 作MN OG ⊥，此时||MN 最小…………………………………（8分） 以下证明此时||MN 最小，过G 作直线M N ''，M N ''与MN不重合|||M N MN ''==在Rt △OG G '中，||||||||OG OG MN M N >'∴<''…………………………………（10分）此时，||MN ==12分）19 解：（1）当当11a b ==-，时()3 4.f x x x =-+-………………………………（1分）当3x <时，不等式化为，,；……………（2分）当时，不等式化为, 明显成立；………………………（3分）当4x >时，不等式化为，；………………（5分）综上所述，不等式的解集为；……………………………………………………（6分） （2）()()()0,03+43+43434a b f x x a x b x a x b a b a b >>∴=-+≥--=--=+当且仅当()()3+40x a x b -⋅≤时取等号341a b ∴+=…………………………（8分）()131349341515151227b a a b a b a b a b ⎛⎫∴+=+⋅+=++≥+=+= ⎪⎝⎭…（11分）当且仅当34149a b b a a b +=⎧⎪⎨=⎪⎩，即1916a b ⎧=⎪⎪⎨⎪=⎪⎩时，13a b ∴+的最小值为27. …………………（12分）20. 解：（1）由已知222222114243c a b e e a b a a -==∴==∴=2222314x y b b∴+=……（1分） 将点31,2⎛⎫- ⎪⎝⎭代入得22222393+13,444b a b b b==∴== ∴椭圆E 方程为:22143x y +=. ………………………………………………………（3分）（2）解法一：由已知()11,0F -， ①当AC x ⊥轴或在x 轴上时，3,4,4,3+=7AC BD AC BD AC BD ====∴或…………………………（4分）②当直线斜率存在且不为0时，()()121,0,1,0F F -设直线AC 方程为：()1y k x =+联立22143x y +=得：()()2222438430k x k x k +++-=………………………（5分）设()()1122,,,A x y B x y 则()22121222438,.4343k k x x x x k k -+=-⋅=++………………（6分）。

2019届广东省佛山市高三1月教学质量检测（一）数学（理）试题一、单选题1．已知集合，，则（）A．B．C．D．【答案】B【解析】求出集合A，B,然后直接取并集即可．【详解】集合B＝{x|﹣1＜x＜1}，A＝{x|x2﹣2x<0}＝{x|0<x<2}，则{x|0<x<2}{x|﹣1＜x＜1}＝{x|-1<x＜2}故选：B．【点睛】本题考查集合的并集运算，属简单题.2．若复数（为虚数单位）在复平面内对应的点在虚轴上，则实数（）A．B．2 C．D．【答案】D【解析】计算出复数的表达式，由题意中复数在复平面内对应的点在虚轴上计算出结果【详解】复数在复平面内对应的点在虚轴上，则，故选【点睛】本题主要考查了复数的几何意义，只需计算出复数在复平面内的对应点，结合题意即可计算出答案，较为基础3．设变量满足约束条件，则目标函数的最大值为（）A．7 B．8 C．15 D．16【答案】B【解析】由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组得到最优解的坐标，代入目标函数得到答案.【详解】作出变量x，y满足的约束条件如图：由z＝2x+y知，动直线y＝﹣2x+z的纵截距z取得最大值时，目标函数取得最大值．由得A（3，2）,结合可行域可知当动直线经过点A（3，2）时，目标函数取得最大值z＝2×3+2＝8．故选：B．【点睛】本题考查线性规划中利用可行域求目标函数的最值，求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.4．已知：“”，：“”，则是的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【答案】C【解析】先证充分性，然后再证明必要性，继而判定结果【详解】①充分性当时，成立，②必要性当时，,,,当时，，不成立，故舍去则是的充分必要条件故选【点睛】本题主要考查了充分条件和必要条件，在判定结果时左右两边分别进行证明充分性和必要性，继而得到结果，较为基础5．已知，则（）A．B．C．D．【答案】C【解析】运用两角差的余弦公式展开后再计算平方的结果，结合已知条件得到答案【详解】，，，本题主要考查了两角差的余弦公式以及二倍角公式，熟练运用公式来解题是关键，较为基础6．已知向量，，，则（）A．B．C．6 D．8【答案】A【解析】先用坐标表示出，然后由向量垂直代入计算求出结果【详解】，，，，则解得故选【点睛】本题主要考查了向量的垂直计算，只需运用点坐标表示向量，然后点乘得零即可得到结果，较为简单7．展开式中的系数为（）A．B．120 C．160 D．200【答案】B【解析】结合二项展开式计算出含的项，从而得到系数【详解】展开式中的项为,则展开式中的系数为120本题主要考查了二项展开式的运用，求特定项的系数，熟练运用公式进行求解8．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【答案】D【解析】由题目中的三视图还原几何体，可知是由半圆锥和四棱锥组成，然后计算几何体的体积【详解】由三视图可得该组合体是由半圆锥和四棱锥组成由已知图中数量可得：故选【点睛】本题主要考查了三视图，要先还原几何体，然后再计算体积，还原几何体是难点，还需要有一定空间想象能力。

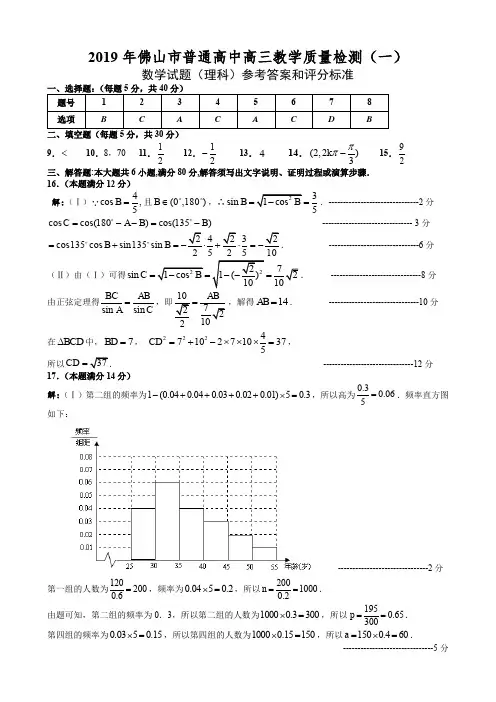
2019年佛山市普通高中高三教学质量检测（一）数学试题（理科）参考答案和评分标准二、填空题（每题5分，共30分） 9．< 10．8，70 11．12 12．12- 13．4 14．(2,2)3k ππ- 15．92三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤．16．（本题满分12分） 解：（Ⅰ）4cos ,5B =且(0,180)B ∈，∴3sin 5B ==．-------------------------------2分cos cos(180)cos(135)C A B B =--=-------------------------------- 3分243cos135cos sin135sin2B B =+=-+10=-． -------------------------------6分 （Ⅱ）由（Ⅰ）可得sinC === -------------------------------8分 由正弦定理得sin sin BC ABA C =7AB =，解得14AB =． -------------------------------10分 在BCD ∆中，7BD =， 22247102710375CD =+-⨯⨯⨯=，所以CD = -------------------------------12分17．（本题满分14分）解：（Ⅰ）第二组的频率为1(0.040.040.030.020.01)50.3-++++⨯=，所以高为0.30.065=．频率直方图如下：-------------------------------2分第一组的人数为1202000.6=，频率为0.0450.2⨯=，所以20010000.2n ==． 由题可知，第二组的频率为0．3，所以第二组的人数为10000.3300⨯=，所以1950.65300p ==． 第四组的频率为0.0350.15⨯=，所以第四组的人数为10000.15150⨯=，所以1500.460a =⨯=．-------------------------------5分（Ⅱ）因为[40,45)岁年龄段的“低碳族”与[45,50)岁年龄段的“低碳族”的比值为60:302:1=，所以采用分层抽样法抽取18人，[40,45)岁中有12人，[45,50)岁中有6人． -------------------------------6分 随机变量X 服从超几何分布．031263185(0)204C C P X C ===，1212631815(1)68C C P X C ===， 2112631833(2)68C C P X C ===，3012631855(3)204C C P X C ===． -------------------------------10分 所以随机变量的分布列为-------------------------------12分∴数学期望5153355012322046868204EX =⨯+⨯+⨯+⨯=．-------------------------------14分 18．（本题满分12分）解：（Ⅰ）∵11S a =，212122S a a a =+=+，3123136S aa a a =++=+，-------------------------------2分 ==解得11a =，故21n a n =-； ---------------------------------------4分（Ⅱ）211(21)()222nn n n n a n b n -===-， ---------------------------------------5分 法1：12311111()3()5()(21)()2222nn T n =⨯+⨯+⨯++-⨯， ①①12⨯得，23411111111()3()5()(23)()(21)()222222n n n T n n +=⨯+⨯+⨯++-⨯+-⨯， ②①-②得，2311111112()2()2()(21)()222222n n n T n +=+⨯+⨯++⨯--⨯11111(1)113121222(21)()12222212n n n n n n +-+--=⨯---⨯=---， ---------------------------------------10分 ∴4212333222n n n nn n T -+=--=-． ---------------------------------------12分 法2：121112222n n n n n na nb n --===⋅-， 设112nn k k k F -==∑，记11()()n k k f x kx -==∑，则()1111(1)()1(1)n n nn kk nk k x x n nx x f x x x x x +==''⎛⎫--+-⎛⎫'==== ⎪ ⎪--⎝⎭⎝⎭∑∑，∴114(2)2n n F n -⎛⎫=-+ ⎪⎝⎭， ---------------------------------------10分故111(1)1123224(2)13122212n n n n n n n T F n --+=-=-+⋅-+=--． ---------------------------------------12分 19．（本题满分14分） 解：法1：（Ⅰ）连结BD ，∵PA ⊥平面ABCD ，BD ⊂平面ABCD ，∴PA BD ⊥， 又∵BD AC ⊥，AC PA A =，∴BD ⊥平面PAC ，又∵E ，F 分别是BC 、CD 的中点，∴//EF BD ， ∴EF ⊥平面PAC ，又EF ⊂平面NEF ，∴平面PAC ⊥平面NEF ；---------------------------------------4分 （Ⅱ）连结OM ，∵//PC 平面MEF ，平面PAC 平面MEF OM =，∴//PC OM ， ∴14PM OC PA AC ==，故:1:3PM MA = -------------------------------8分 （Ⅲ）∵EF ⊥平面PAC ，OM ⊂平面PAC ，∴EF ⊥OM ，在等腰三角形NEF 中，点O 为EF 的中点，∴NO EF ⊥，∴MON ∠为所求二面角M EF N --的平面角， ---------------------------------------10分 ∵点M 是PA 的中点，∴2AM NC ==，所以在矩形MNCA中，可求得MN AC ==NO =MO = --------------------12分在MON ∆中，由余弦定理可求得222cos 233MO ON MN MON MO ON +-∠==-⋅⋅，∴二面角M EF N --的余弦值为33-． ---------------------------------------14分 法2：（Ⅰ）同法1；（Ⅱ）建立如图所示的直角坐标系，则(0,0,4)P ，(4,4,0)C ，(4,2,0)E ，(2,4,0)F ， ∴(4,4,4)PC =-，(2,2,0)EF =-，设点M 的坐标为(0,0,)m ，平面MEF 的法向量为(,,)n x y z =，则(4,2,)ME m =-，所以00n ME n EF ⎧⋅=⎪⎨⋅=⎪⎩，即420220x y mz x y +-=⎧⎨-+=⎩，令1x =，则1y =，6z m =，故6(1,1,)n m=，∵//PC 平面MEF ，∴0PC n ⋅=，即24440m+-=，解得3m =，故3AM =，即点M 为线段PA 上靠近P 的四等分点；故:1:3PM MA = --------------------------8分（Ⅲ）(4,4,2)N ，则(0,2,2)EN =，设平面NEF 的法向量为(,,)m x y z =，则00m EN m EF ⎧⋅=⎪⎨⋅=⎪⎩，即220220y z x y +=⎧⎨-+=⎩，令1x =，则1y =，1z =-，即(1,1,1)m =-， 当M 是PA 中点时，2m =，则(1,1,3)n =，∴cos ,m n <>== ∴二面角M EF N --的余弦值为．-------14分 20．（本题满分14分）解：（Ⅰ）由题意可得圆的方程为222x y b +=， ∵直线20x y -+=与圆相切，∴d b ==，即b =， ---------------------------------------1分又c e a ==，即a =，222a b c =+，解得a =1c =， 所以椭圆方程为22132x y +=． ---------------------------------------3分 （Ⅱ）设000(,)(0)P x y y ≠，(A，B ，则2200132x y +=，即2200223y x =-，则1k =2k =， ---------------------------------------4分即22200012222000222(3)2333333x x y k k x x x --⋅====----， ∴12k k 为定值23-． ---------------------------------------6分（Ⅲ）设(,)M x y，其中[x ∈．由已知222OP OMλ=及点P 在椭圆C 上可得2222222222633()x x x x y x y λ+-+==++， 整理得2222(31)36x y λλ-+=，其中[x ∈． -------------------------------------8分①当3λ=时，化简得26y =， 所以点M的轨迹方程为y x =≤≤，轨迹是两条平行于x 轴的线段； --------------------9分②当λ≠2222166313x y λλ+=-，其中[x ∈，-------------------------------------11分当03λ<<时，点M 的轨迹为中心在原点、实轴在y轴上的双曲线满足x ≤≤当13λ<<时，点M 的轨迹为中心在原点、长轴在x轴上的椭圆满足x ≤≤ 当1λ≥时，点M 的轨迹为中心在原点、长轴在x 轴上的椭圆． ---------------------------------------14分21．（本题满分14分）解：（Ⅰ）∵函数()f x 过点(1,2)-，∴(1)2f a b c -=-+-=， ① 又2()32f x ax bx c '=++，函数()f x 点(1,(1))f 处的切线方程为20y +=， ∴(1)2(1)0f f =-⎧⎨'=⎩，∴2320a b c a b c ++=-⎧⎨++=⎩， ②由①和②解得1a =，0b =，3c =-，故 3()3f x x x =-； ---------------------------------------4分 （Ⅱ）由（Ⅰ）2()33f x x '=-，令()0f x '=，解得1x =±， ∵(3)18f -=-，(1)2f -=，(1)2f =-，(2)2f =， ∴在区间[]3,2-上max ()2f x =，min ()18f x =-，∴对于区间[]3,2-上任意两个自变量的值12,x x ，12|()()|20f x f x -≤，∴20t ≥，从而t 的最小值为20； ---------------------------------------8分（Ⅲ）∵2()32f x ax bx c '=++，则 (0)(1)32(1)32f c f a b c f a b c '=⎧⎪'-=-+⎨⎪'=++⎩，可得6(1)(1)2(0)a f f f '''=-+-．∵当11x -≤≤时，1)(≤'x f ，∴(1)1f '-≤，(0)1f '≤，(1)1f '≤， ∴6||(1)(1)2(0)a f f f '''=-+-(1)(1)2(0)4f f f '''≤-++≤，∴23a ≤，故a 的最大值为23， 当23a =时，(0)1(1)221(1)221f c f b c f b c '⎧==⎪'-=-+=⎨⎪'=++=⎩，解得0b =，1c =-，∴a 取得最大值时()323f x x x =-． ---------------------------------------14分。

2019-2020学年广东省佛山一中高三（上）期中数学试卷（理科）一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知0,||2,||3a b a b ===且(32)()a b a b λ+⊥-，则λ的值是( ) A ．32B ．32-C ．32±D ．12．已知圆C 与直线30x y ++=相切，直线10mx y ++=始终平分圆C 的面积，则圆C 方程为( )A ．2222x y y +-=B ．2222x y y ++=C ．2221x y y +-=D ．2221x y y ++=3．在ABC ∆中．角A 、B 、C 所对的边分别为a 、b 、c ．如果22tan tan a Ab B =．则ABC ∆的形状是( ) A ．等腰三角形B ．等腰直角三角形C ．等腰三角形或直角三角形D ．直角三角形4．设2log 3a =，b =23c e =，则a ，b ，c 的大小关系是( ) A ．a b c <<B ．b a c <<C ．b c a <<D ．a b c <<5．设函数21,0()1,0x x f x x -⎧-⎪=+>…，且(2)3f a =，则(2)(f a += )A ．2B ．3C ．2或3D ．36．已知两个圆1O 和2O ，它们的半径分别是2和4，且12||8O O =，若动圆M 与圆1O 内切，又与2O 外切，则动圆圆心M 的轨迹方程是( ) A ．圆B ．椭圆C ．双曲线一支D ．抛物线7．已知双曲线2222:1(0,0)x y C a b a b -=>>，斜率为1的直线与双曲线C 交于两点A ，B ，若线段AB 的中点为(4,1)，则双曲线C 的渐近线方程是( ) A0y ±=B ．20x y ±=C．0x ±=D ．20x y ±=8．在ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c．已知b =，c =，tan()24A π+=，则(a = )A ．15B ．C ．3D ．9．已知函数()cos()(f x A x A ωϕ=+，ω，ϕ为常数，0ω>，0)A <的部分图象如图所示，则(A = )A ．2-B ．3-C ．-D ．10．方程2()10lnx lnx m x x--=有三个不同的解，则m 的取值范围是( ) A ．1(e e-，)+∞B ．1(,)e e-∞-C ．1(e e+，)+∞D ．1(,)e e-∞--11．直线0x -=经过椭圆22221(0)x y a b a b +=>>的左焦点F ，交椭圆于A ，B 两点，交y 轴于C 点，若2FC CA =，则该椭圆的离心率是( )A 1-B C ．2- D 112．已知函数1()ax f x xe lnx ax -=--，21(,]a e ∈-∞-，函数()f x 的最小值M ，则实数M 的最小值是( ) A ．1-B ．1e-C ．0D ．31e -二、填空题：本题共4小题，每小题5分，共20分.13．直线0x =、直线1y e =+与曲线1x y e =+围成的图形的面积为 ．14．直线1)y x =-与抛物线24y x =相交于A ，B 两点，O 为原点，则三角形AOB 面积为 ．15．已知ABC ∆中，角A 、B 、C 对应边分别为a 、b 、c ，且30A ∠=︒，2a =，则ABC ∆面积最大值为 ．16．曲线22:|1|1C x y --=与直线:1l y kx =-有4个交点，则k 的取值范围是 ． 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.17．ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，若22223a c acb +-=．（1）求cos B ；（2）若2AB =，3sin 2sin A B =，求ABC ∆的面积．18．已知曲线12cos :(2sin x C y θθθ=⎧⎨=⎩为参数），曲线21cos (1sin x t C t y t αα=+⎧=⎨=-+⎩为参数）． （1）若4πα=，求曲线2C 的普通方程，并说明它表示什么曲线；（2）曲线1C 和曲线2C 的交点记为M ，N ，求||MN 的最小值．19．已知函数()|3||4|(0f x x a x b a =-++>，0)b >． （1）当1a =，1b =-时，解不等式()2f x …； （2）若()f x 的最小值为1，求13a b+的最小值．20．已知椭圆2222:1(0)x y E a b a b +=>>的左右焦点分别是1F 、2F ，离心率12e =，点3(1,)2-在椭圆E 上．（1）求椭圆E 的方程；（2）如图，分别过1F 、2F 作两条互相垂直的弦AC 与BD ，求||||AC BD +的最小值．21．如图，已知抛物线2:2(0)C x py p =>的焦点F 到直线20x y --=AB 是过抛物线C 焦点F 的动弦，O 是坐标原点，过A ，B 两点分别作此抛物线的切线，两切线相交于点P ．（1）求证：PA PB ⊥．（2）若动弦AB 不经过点(2,1)M ，直线AB 与准线l 相交于点N ，记MA ，MB ，MN 的斜率分别为1k ，2k ，3k ．问：是否存在常数λ，使得12311k k k λ+=+在弦AB 运动时恒成立？若存在，求λ的值；若不存在，说明理由．22．已知函数()x a f x lnx e a -=-+（其中e 是自然对数的底数）． （1）当0a =时，求证：()2f x <-；（2）若函数()f x 有两个零点，求实数a 的取值范围．2019-2020学年广东省佛山一中高三（上）期中数学试卷（理科）参考答案与试题解析一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知0,||2,||3a b a b ===且(32)()a b a b λ+⊥-，则λ的值是( ) A ．32B ．32-C ．32±D ．1【解答】解：a b ⊥∴0a b =(32)()a b a b λ+⊥-即(32)()0a b a b λ+-= 即2232320a a b a b b λλ+--= 即12180λ-= 解得32λ=故选：A ．2．已知圆C 与直线30x y ++=相切，直线10mx y ++=始终平分圆C 的面积，则圆C 方程为( )A ．2222x y y +-=B ．2222x y y ++=C ．2221x y y +-=D ．2221x y y ++=【解答】解：直线10mx y ++=始终平分圆C 的面积， ∴直线10mx y ++=始终过圆的圆心(0,1)-，又圆C 与直线30x y ++=相切，则圆的半径r ==∴圆C 的方程为22(1)2x y ++=，即2221x y y ++=．故选：D ．3．在ABC ∆中．角A 、B 、C 所对的边分别为a 、b 、c ．如果22tan tan a Ab B =．则ABC ∆的形状是( ) A ．等腰三角形B ．等腰直角三角形C ．等腰三角形或直角三角形D ．直角三角形【解答】解：在ABC ∆中．角A 、B 、C 所对的边分别为a 、b 、c ．如果22tan tan a A b B=．利用正弦定理得：22sin sin cos sin sin cos AAA BB B=，整理得：sin cos sin cos A A B B =， 即：11sin 2sin 222A B =，则：22A B =或22A B π+=， 所以：A B =或2A B π+=．故：ABC ∆为等腰三角形或直角三角形． 故选：C ．4．设2log 3a =，b =23c e =，则a ，b ，c 的大小关系是( ) A ．a b c <<B ．b a c <<C ．b c a <<D ．a b c <<【解答】解： 1.72221log 2log 32 1.7a log =<=<=，1.732b ==，232c e =>，则a ，b ，c 的大小关系为a b c <<． 故选：A ．5．设函数21,0()1,0x x f x x -⎧-⎪=+>…，且(2)3f a =，则(2)(f a += )A ．2B ．3C ．2或3D ．3【解答】解：01当20a …时，2(2)213a f a -=-=，22242a -∴==22a ∴-=， 1a ∴=-；∴(2)(12)(1)12f a f f +=-+===；02当20a >时，(2)13f a =+=，∴2=，2a ∴=．∴(2)(22)(4)13f a f f +=+===．故选：C ．6．已知两个圆1O 和2O ，它们的半径分别是2和4，且12||8O O =，若动圆M 与圆1O 内切，又与2O 外切，则动圆圆心M 的轨迹方程是( ) A ．圆B ．椭圆C ．双曲线一支D ．抛物线【解答】解：设动圆圆心为M ，半径为R ，由题意 1||2MO R =-，2||4MO R =+，所以21||||6MO MO -=（常数）且1268||O O <= 故M 点的轨迹为以，12O O 为焦点的双曲线的一支． 故选：C ．7．已知双曲线2222:1(0,0)x y C a b a b -=>>，斜率为1的直线与双曲线C 交于两点A ，B ，若线段AB 的中点为(4,1)，则双曲线C 的渐近线方程是( ) A0y ±=B ．20x y ±=C．0x ±=D ．20x y ±=【解答】解：设1(A x ，1)y ，2(B x ，2)y ， 则2211221x y a b -=，2222221x y a b-=， 两式作差可得1212121222()()()()x x x x y y y y a b -+-+=，∴2121221212()()y y b x x x x a y y -+=-+，则2241b a=， 得2214b a =，∴12b a =． 则双曲线C 的渐近线方程是12y x =±，即20x y ±=．故选：D ．8．在ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c ．已知b =，c =，tan()24A π+=，则(a = )A ．15B ．C ．3D ．【解答】解：由tan 1tan()241tan A A A π++==-，解得1tan 3A =，cos A ∴=，由余弦定理可得2222cos 45729a b c bc A =+-=+-=， 3a ∴=．故选：C ．9．已知函数()cos()(f x A x A ωϕ=+，ω，ϕ为常数，0ω>，0)A <的部分图象如图所示，则(A = )A ．2-B ．3-C ．-D ．【解答】解：由图象可得3115324121224T ππππω=-==，解得3ω=． 可得：()cos(3)f x A x ϕ=+， 由于点5(12π，0)在函数图象上，可得5cos(3)012A πϕ⨯+=， 解得：53122k ππϕπ⨯+=+，即：34k πϕπ=-，k Z ∈， 又由于点(2π，2)-在函数图象上，可得3cos(3)224A k πππ⨯+-=-，k Z ∈，可得：3cos()24A k ππ+=-，k Z ∈，解得：A =-，或． 故选：C ． 10．方程2()10lnx lnx m x x--=有三个不同的解，则m 的取值范围是( )A ．1(e e -，)+∞B ．1(,)e e -∞-C ．1(e e +，)+∞D ．1(,)e e-∞--【解答】解：令()lnx f x x =，则21()lnxf x x -'=， ∴当x e >时，()0f x '<，当0x e <<时，()0f x '>，()f x ∴在(0，]e 上单调递增，在(,)e +∞上单调递减． ()max f x f ∴=（e ）1e=． 作出()f x 的大致函数图象如下：由图象可知当10k e<<时，()f x k =有两解， 当0k …或1k e =时，()f x k =有一解，当1k e>时，()f x k =无解．令2()1g x x mx =--，则(())g f x 有三个零点，()g x ∴在1(0,)e 上有一个零点，在(-∞，10]{}e上有一个零点．()g x 的图象开口向上，且(0)1g =-，()g x ∴在(,0)-∞上必有一个零点， 1()0g e ∴>，即2110me e-->，解得：1m e e<-； 故选：B ．11．直线0x -=经过椭圆22221(0)x y a b a b +=>>的左焦点F ，交椭圆于A ，B 两点，交y 轴于C 点，若2FC CA =，则该椭圆的离心率是( )A 1-B C ．2- D 1【解答】解：由0x -+=，取0y =，得x =取0x =，得1y =，(F ∴0)，(0,1)C ，设0(A x ，0)y ，则(3,1)FC =，00(,1)CA x y =-， 由2FC CA =，得00(2,22)x y =-，∴002122x y ==-⎪⎩，即0032x y ⎧=⎪⎪⎨⎪=⎪⎩3)2A ．把A 的坐标代入椭圆22221(0)x y a b a b+=>>，可得2239144a b +=，即22394a b +=．又223b a =-，解得2a =，又23c =，∴222(2c a ===，1e ∴=-．故选：A ．12．已知函数1()ax f x xe lnx ax -=--，21(,]a e ∈-∞-，函数()f x 的最小值M ，则实数M 的最小值是( ) A ．1-B ．1e-C ．0D ．31e -【解答】解：函数1()ax f x xe lnx ax -=--，21(,]a e ∈-∞-， 11111()(1)()ax ax ax g x e axe a ax e x x---∴'=+--=+-， 由110ax e x --=，解得：1lnxa x-=，设1()lnxp x x -=， 则22()lnx p x x -'=， 当2x e >时，()0p x '>，当20x e <<，()0p x '<， 从而()p x 在2(0,)e 上单调递减，在2(e ，)+∞上单调递增， 221()()min p x p e e ==-， 当21a e -…，1lnx a x -…，即110ax e x--…， 在1(0,)a-上，10ax +>，()0g x '…，()g x 单调递减，在1(a-，)+∞上，10ax +<，()0g x '…，()g x 单调递增， 1()()min g x g M a∴=-=，设1(0t a =-∈，2]e ，2()1tM h t lnt e ==-+，2(0)t e <…，211()0h t e t'=-…，()h x 在，(0∈，2]e 上单调递减， 2()()0h t h e ∴=…，M ∴的最小值为0．故选：C ．二、填空题：本题共4小题，每小题5分，共20分.13．直线0x =、直线1y e =+与曲线1x y e =+围成的图形的面积为 1 ． 【解答】解：依题意，令11x e e +=+，得1x =，所以直线0x =，1y e =+与曲线1x y e =+围成的区域的面积为 (Tex translation failed)，故答案为：1．14．直线1)y x =-与抛物线24y x =相交于A ，B 两点，O 为原点，则三角形AOB 面积【解答】解：联立21)4y x y x ⎧=-⎪⎨=⎪⎩，得231030x x -+=．设1(A x ，1)y ，2(B x ，2)y ， 则12103x x +=，121x x =．12|||AB x x ∴=-=163==．原点O 0y --=的距离d =．∴三角形AOB 面积为11623S =⨯=．15．已知ABC ∆中，角A 、B 、C 对应边分别为a 、b 、c ，且30A ∠=︒，2a =，则ABC ∆面积最大值为 2+【解答】解：30A ∠=︒，2a =，∴由余弦定理得：2222242cos (2a b c bc A b c bc ==+-=+-…，即4(2bc =+…，当且仅当b c =时等号成立，11sin 22ABC S bc A ∆∴=⨯ (1)4(222+⨯=+，当且仅当b c =时等号成立，则ABC ∆面积的最大值为2+．故答案为：2+．16．曲线22:|1|1C x y --=与直线:1l y kx =-有4个交点，则k 的取值范围是 (1)(1--⋃，1)⋃ 【解答】由曲线22:|1|1C x y --=，得2211x y --=±，222x y ∴-=或y x =±．图象如图：联立2212y kx x y =-⎧⎨-=⎩，得22(1)230k x kx -+-=． 由△222412(1)1280k k k =+-=-=，解得k = 又直线:1l y kx =-过定点(0,1)-，由图可知，要使曲线22:|1|1C x y --=与直线:1l y kx =-有4个交点， 则k的取值范围是(1)(1--⋃，1)(1⋃．故答案为：(1)(1--⋃，1)(1⋃．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.17．ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，若22223a c acb +-=．（1）求cos B ；（2）若2AB =，3sin 2sin A B =，求ABC ∆的面积． 【解答】解：（1）22223a c ac b +-=，22223a cb ac ∴+-=， 222213cos 223aca cb B ac ac +-∴===．（2）1cos 3B =， (0,)2B π∴∈，sin B = 又3sin 2sin A B =， ∴由正弦定理，32a b =，2AB c ==，∴根据余弦定理2222cos b a c ac B =+-，可得22221()44333b b b =+-⨯⨯，得2b =，43a =， ABC ∴∆的面积为1sin 2S ac B ==18．已知曲线12cos :(2sin x C y θθθ=⎧⎨=⎩为参数），曲线21cos (1sin x t C t y t αα=+⎧=⎨=-+⎩为参数）． （1）若4πα=，求曲线2C 的普通方程，并说明它表示什么曲线；（2）曲线1C 和曲线2C 的交点记为M ，N ，求||MN 的最小值．【解答】解：（1）4πα=∴1(1x t y ⎧=+⎪⎪⎨⎪=-+⎪⎩为参数） 11x y ∴-=+，∴曲线2C 的普通方程是2y x =-（2分）它表示过(1,1)-，倾斜角为4π的直线（2）曲线1C 的普通方程为224x y += 设(1,1)G -，过G 作MN OG ⊥， 以下证明此时||MN 最小，过G 作直线M N ''，M N ''与MN不重合||||M N MN ''== 在Rt △OG G '中，||||||||OG OG MN M N >'∴<''此时，||MN ==19．已知函数()|3||4|(0f x x a x b a =-++>，0)b >．（1）当1a =，1b =-时，解不等式()2f x …； （2）若()f x 的最小值为1，求13a b+的最小值． 【解答】解：（1）当1a =，1b =-时，()|3||4|f x x x =-+-． 当3x <时，不等式化为342x x -+-+…，解得52x …，∴532x <…；当34x 剟时，不等式化为342x x --+…，明显成立； 当4x >时，不等式化为342x x -+-…，解得942x <<； 综上所述，不等式的解集为59[,]22；（2）0a >，0b >，()|3||4||(3)(4)||34|34f x x a x b x a x b a b a b ∴=-++--+=--=+…当且仅当(3)(4)0x a x b -+…时取等号，341a b ∴+= ∴13134949()(34)151********b a b a a b a b a b a b a b+=++=+++=+=… 当且仅当34149a b b a a b +=⎧⎪⎨=⎪⎩，即1916a b ⎧=⎪⎪⎨⎪=⎪⎩时等号成立， ∴13a b+的最小值为27． 20．已知椭圆2222:1(0)x y E a b a b +=>>的左右焦点分别是1F 、2F ，离心率12e =，点3(1,)2-在椭圆E 上．（1）求椭圆E 的方程；（2）如图，分别过1F 、2F 作两条互相垂直的弦AC 与BD ，求||||AC BD +的最小值．【解答】解：（1）由已知12c e a ==，得222214a b e a -==，则2243a b =，∴椭圆方程为2222314x y b b +=，将点3(1,)2-代入得222393144b b b +==，得23b =，24a =．∴椭圆E 方程为：22143x y +=； （2）由已知1(1,0)F -，①当AC x ⊥轴或在x 轴上时，||3AC =，||4BD =，或||4AC =，||3BD =，||||7AC BD ∴+=； ②当直线斜率存在且不为0时，1(1,0)F -，2(1,0)F ，设直线AC 方程为：(1)y k x =+．联立22143x y +=得：2222(43)84(3)0k x k x k +++-=． 设1(A x ，1)y ，2(B x ，2)y ，则2212122284(3),4343k k x x x x k k -+=-=++． ∴221212(1)|||43k AC x x k +=-==+． AC BD ⊥，由椭圆对称性，以1k -代换上式中的k 得：22222112(1)12(1)||34143k k BD k k++==++． 222222222222212(1)12(1)84(1)84(1)48||||(43)(34)4334(43)(34)7[]2k k k k AC BD k k k k k k ++++∴+=+==+++++++…． 当且仅当224334k k +=+，即1k =±时，取“=”． 而4877<，||||AC BD ∴+有最小值487．21．如图，已知抛物线2:2(0)C x py p =>的焦点F 到直线20x y --=AB 是过抛物线C 焦点F 的动弦，O 是坐标原点，过A ，B 两点分别作此抛物线的切线，两切线相交于点P ．（1）求证：PA PB ⊥．（2）若动弦AB 不经过点(2,1)M ，直线AB 与准线l 相交于点N ，记MA ，MB ，MN 的斜率分别为1k ，2k ，3k ．问：是否存在常数λ，使得12311k k k λ+=+在弦AB 运动时恒成立？若存在，求λ的值；若不存在，说明理由．【解答】解：（1）证明：22(0)(0,)2px py p F =>∴，由F 到直线20x y --=2p ===，故抛物线方程为24x y =， (0,1)F ，依题意，设直线AB 方程为1(0)y kx k =+≠，联立24x y =得：2440x kx --=，设1(A x ，1)y ，2(B x ，2)y ，124x x k ∴+=，124x x =-，2/42x x y y =∴=，∴12124,12244PA PB PA PB x x x x k k k k -==∴===-，PA PB ∴⊥；（2）将1y =-代入1y kx =+得2(,1)N k--，(2,1)M ，2212112212112211121244,224224x x y x y x k k x x x x ---+-+======----， ∴1212122244414444x x x x k k k k ++++++=+===+， 31(1)212()k k k k--==+--， 若有12311k k k λ+=+成立，则有1111k k k λ+=++解得1λ=-，故存在1λ=-，使12311k k k λ+=+成立．22．已知函数()x a f x lnx e a -=-+（其中e 是自然对数的底数）． （1）当0a =时，求证：()2f x <-；（2）若函数()f x 有两个零点，求实数a 的取值范围．【解答】解：（1）证明：当0a =时，()x f x lnx e =-，求导，1()x f x e x'=-，(0)x >， 令()0f x '=，得：01(,1)2x x =∈，即001x e x =，也即00lnx x =-，且()f x 在0(0,)x 上单增，在0(x ，)+∞上单减， ∴00000011()()2x max f x lnx e x x x x =-=--=-+<-． ()2f x ∴<-；（2）()x a f x lnx e a -=-+，求导，1()x a f x e x-'=-，(0)x >， 故等价于()f x 在(0,)+∞上有唯一极大值点1x ，且1()0f x >， 则1()0f x =，111x a e x -=，则11lnx x a -=-， 11a x lnx ∴=+故11111()2f x lnx x x =-+， 令1()2,(1)0h x lnx x h x=-+=221()10h x x x '=++>， ()0h x ∴>，则1x >，则11x >，又y x lnx =+在(0,)+∞上单增，由11x >，得111a x lnx =+>． 综上，1a >，a ∴的取值范围(1,)+∞．。

2020年广东省佛山市高考数学一模试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）在复平面内，复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限2．（5分）已知集合A＝{x|x2﹣x﹣2＜0}，B＝{x||x|＞1}，则A∩B＝（）A．（﹣2，﹣1）B．（﹣1，1）C．（0，1）D．（1，2）3．（5分）已知x，y∈R，且x＞y＞0，则（）A．cos x﹣cos y＞0 B．cos x+cos y＞0C．lnx﹣lny＞0 D．lnx+lny＞04．（5分）函数f（x）的图象向左平移一个单位长度，所得图象与y＝e x关于y轴对称，则f（x）＝（）A．e﹣x+1B．e﹣x﹣1C．e x﹣1D．e x+15．（5分）希尔宾斯基三角形是一种分形，由波兰数学家希尔宾斯基在1915年提出，先作一个正三角形，挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色代表挖去的面积，那么黑三角形为剩下的面积（我们称黑三角形为希尔宾斯基三角形）．在如图第3个大正三角形中随机取点，则落在黑色区域的概率为（）A．B．C．D．6．（5分）已知等比数列{a n}满足a1﹣a2＝36，a1﹣a3＝24，则使得a1a2…a n取得最大值的n为（）A．3 B．4 C．5 D．67．（5分）已知α为锐角，cosα＝，则tan（+）＝（）A．B．C．2 D．38．（5分）已知双曲线C：，O为坐标原点，直线x＝a与双曲线C的两条渐近线交于A，B两点，若△OAB是边长为2的等边三角形，则双曲线C的方程为（）A．﹣y2＝1 B．x2＝1C．＝1 D．＝19．（5分）地球上的风能取之不尽，用之不竭．风能是清洁能源，也是可再生能源．世界各国致力于发展风力发电，近10年来，全球风力发电累计装机容量连年攀升，中国更是发展迅猛，在2014年累计装机容量就突破了100GW，达到114.6GW，中国的风力发电技术也日臻成熟，在全球范围的能源升级换代行动中体现出大国的担当与决心．以下是近10年全球风力发电累计装机容量与中国新增装机容量图．根据以上信息，正确的统计结论是（）A．截止到2015年中国累计装机容量达到峰值B．10年来全球新增装机容量连年攀升C．10年来中国新增装机容量平均超过20GWD．截止到2015年中国累计装机容量在全球累计装机容量中占比超过10．（5分）已知函数f（x）＝+2x+1，且f（a2）+f（2a）＞3，则a的取值范围是（）A．（﹣∞，﹣3）∪（1，+∞）B．（﹣∞，﹣2）∪（0，+∞）C．（﹣2，0）D．（﹣1，3）11．（5分）已知函数f（x）＝sin x+sin（πx），现给出如下结论：①f（x）是奇函数；②f（x）是周期函数；③f（x）在区间（0，π）上有三个零点；④f（x）的最大值为2．其中正确结论的个数为（）A．1 B．2 C．3 D．412．（5分）已知正三棱柱ABC﹣A1B1C1的侧棱长为4，底面边长为2，用一个平面截此棱柱，与侧棱AA1，BB1，CC1分别交于点M，N，Q，若△MNQ为直角三角形，则△MNQ面积的最大值为（）A．3 B．C．D．3二、填空题：本大题共4小题，每小题5分，满分20分．13．（5分）从进入决赛的6名选手中决出1名一等奖，2名二等奖，3名三等奖，则可能的决赛结果共有种．（用数字作答）14．（5分）在△ABC中，AB＝2，AC＝3，P是边BC的垂直平分线上一点，则•＝．15．（5分）函数f（x）＝lnx和g（x）＝ax2﹣x的图象有公共点P，且在点P处的切线相同，则这条切线方程为．16．（5分）在平面直角坐标系xOy中，对曲线C上任意一点P，P到直线x+1＝0的距离与该点到点O的距离之和等于2，则曲线C与y轴的交点坐标是；设点A（﹣，0），则|PO|+|PA|的最小值为．三、解答题：本大题共5小题，共70分，解答须写出必要的文字说明、证明过程或演算步骤．17．（12分）绿水青山就是金山银山．近年来，祖国各地依托本地自然资源，打造旅游产业，旅游业正蓬勃发展．景区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念，合力使旅游市场走上规范有序且可持续的发展轨道．某景区有一个自愿消费的项目：在参观某特色景点入口处会为每位游客拍一张与景点的合影，参观后，在景点出口处会将刚拍下的照片打印出来，游客可自由选择是否带走照片，若带走照片则需支付20元，没有被带走的照片会收集起来统一销毁．该项目运营一段时间后，统计出平均只有三成的游客会选择带走照片．为改善运营状况，该项目组就照片收费与游客消费意愿关系作了市场调研，发现收费与消费意愿有较强的线性相关性，并统计出在原有的基础上，价格每下调1元，游客选择带走照片的可能性平均增加0.05，假设平均每天约有5000人参观该特色景点，每张照片的综合成本为5元，假设每个游客是否购买照片相互独立．（1）若调整为支付10元就可带走照片，该项目每天的平均利润比调整前多还是少？（2）要使每天的平均利润达到最大值，应如何定价？18．（12分）在△ABC中，内角A，B，C的对边分别为a，b，c，已知a sin B＝b sin（A﹣）．（1）求A；（2）D是线段BC上的点，若AD＝BD＝2，CD＝3，求△ADC的面积．19．（12分）已知椭圆C：+＝1（a＞b＞0）的离心率为，点A（1，）在椭圆C上，直线l1过椭圆C的有交点与上顶点，动直线l2：y＝kx与椭圆C交于M、N两点，交l1于P点．（1）求椭圆C的方程；（2）已知O为坐标原点，若点P满足|OP|＝|MN|，求此时|MN|的长度．20．（12分）如图，三棱锥P﹣ABC中，平面PAB⊥平面ABC，PA＝PB，∠APB＝∠ACB＝90°，点E，F分别是棱AB，PB的中点，点G是△BCE的重心．（1）证明：GF∥平面PAC；（2）若GF与平面ABC所成的角为60°，求二面角B﹣AP﹣C的余弦值．21．（12分）已知函数f（x）＝1+x﹣2sin x，x＞0．（1）求f（x）的最小值；（2）证明：f（x）＞e﹣2x．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分，作答时请写清楚题号．[选修4-4：坐标系与参数方程选讲]22．（10分）在直角坐标系xOy中，曲线C的参数方程为（m为参数）．（1）写出曲线C的普通方程，并说明它表示什么曲线；（2）已知倾斜角互补的两条直线l1，l2，其中l1与曲线C交于A，B两点，l2与C交于M，N两点，l1与l2交于点P（x0，y0），求证：|PA|•|PB|＝|PM|•|PN|．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣a|+|x﹣1|．（1）若f（a）＜2，求a的取值范围；（2）当x∈[a，a+k]时，函数f（x）的值域为[1，3]，求k的值．2020年广东省佛山市高考数学一模试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）在复平面内，复数对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】利用复数代数形式的乘除运算化简，求出复数所对应点的坐标得答案．【解答】解：∵＝，∴在复平面内，复数对应的点的坐标为（2，1），位于第一象限．故选：A．【点评】本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．2．（5分）已知集合A＝{x|x2﹣x﹣2＜0}，B＝{x||x|＞1}，则A∩B＝（）A．（﹣2，﹣1）B．（﹣1，1）C．（0，1）D．（1，2）【分析】可以求出集合A，B，然后进行交集的运算即可．【解答】解：A＝{x|﹣1＜x＜2}，B＝{x|x＜﹣1或x＞1}，∴A∩B＝（1，2）．故选：D．【点评】本题考查了描述法、区间的定义，一元二次不等式和绝对值不等式的解法，交集的运算，考查了计算能力，属于基础题．3．（5分）已知x，y∈R，且x＞y＞0，则（）A．cos x﹣cos y＞0 B．cos x+cos y＞0C．lnx﹣lny＞0 D．lnx+lny＞0【分析】根据题意，结合函数的单调性分析选项A、C，可得A错误，C正确，对于B、D，利用特殊值分析可得其错误，综合即可得答案．【解答】解：根据题意，依次分析选项：对于A，y＝cos x在（0，+∞）上不是单调函数，故cos x﹣cos y＞0不一定成立，A错误；对于B，当x＝π，y＝时，cos x+cos y＝﹣1＜0，B不一定成立；对于C，y＝lnx在（0，+∞）上为增函数，若x＞y＞0，则lnx＞lny，必有lnx﹣lny＞0，C正确；对于D，当x＝1，y＝时，lnx+lny＝ln＜0，D不一定成立；故选：C．【点评】本题考查函数单调性的应用，涉及实数大小的比较，属于基础题．4．（5分）函数f（x）的图象向左平移一个单位长度，所得图象与y＝e x关于y轴对称，则f（x）＝（）A．e﹣x+1B．e﹣x﹣1C．e x﹣1D．e x+1【分析】根据函数图象变换关系，利用逆推法进行求解即可．【解答】解：y＝e x关于y轴对称的函数为y＝e﹣x，然后向右平移一个单位得到f（x），得y＝e﹣（x﹣1），即f（x）＝e﹣x+1，故选：A．【点评】本题主要考查函数图象变换，结合条件进行逆推法是解决本题的关键．比较基础．5．（5分）希尔宾斯基三角形是一种分形，由波兰数学家希尔宾斯基在1915年提出，先作一个正三角形，挖去一个“中心三角形”（即以原三角形各边的中点为顶点的三角形），然后在剩下的小三角形中又挖去一个“中心三角形”，我们用白色代表挖去的面积，那么黑三角形为剩下的面积（我们称黑三角形为希尔宾斯基三角形）．在如图第3个大正三角形中随机取点，则落在黑色区域的概率为（）A．B．C．D．【分析】我们要根据已知条件，求出第3个大正三角形的面积，及黑色区域的面积，代入几何概型计算公式，即可求出答案．【解答】解：由题意可知：每次挖去的面积为前一个三角形剩下面积的，不妨设第一个三角形的面积为1．∴第三个三角形的面积为1；则阴影部分的面积之为：第3个大正三角形中随机取点，则落在黑色区域的概率：，故选：B．【点评】几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P＝求解．6．（5分）已知等比数列{a n}满足a1﹣a2＝36，a1﹣a3＝24，则使得a1a2…a n取得最大值的n 为（）A．3 B．4 C．5 D．6【分析】结合等比数列的通项公式可求通项，然后结合项的正负及增减性可求．【解答】解：∵等比数列{a n}满足a1﹣a2＝36，a1﹣a3＝24，，解可得，q＝，a1＝27，∴a n＝，若使得a1a2…a n取得最大值，则n应该是偶数，且n＞4时，|a n|＜1，故当n＝4时，a1a2…a n取得最大值．故选：B．【点评】本题主要考查了等比数列的通项公式的简单应用，分析数列的项的特点是求解问题的关键．7．（5分）已知α为锐角，cosα＝，则tan（+）＝（）A．B．C．2 D．3【分析】求出tanα＝＝，从而tan＝，由此能求出tan（+）的值．【解答】解：∵α为锐角，cosα＝，∴sinα＝＝，tanα＝＝＝，解得tan＝，或tan＝﹣2，∴tan（+）＝＝＝3．故选：D．【点评】本题考查三角函数值的求法，考查诱导公式、正切函数的二倍角公式、正切加法定理等基础知识，考查运算求解能力，是基础题．8．（5分）已知双曲线C：，O为坐标原点，直线x＝a与双曲线C的两条渐近线交于A，B两点，若△OAB是边长为2的等边三角形，则双曲线C的方程为（）A．﹣y2＝1 B．x2＝1C．＝1 D．＝1【分析】求出双曲线的渐近线方程，令x＝a，求得A，B的坐标，由等边三角形的性质可得a，b的值，进而得到双曲线的方程．【解答】解：双曲线C：的渐近线方程为bx﹣ay＝0和bx+ay＝0，由x＝a与双曲线C的两条渐近线交于A（a，b），B（a，﹣b），△OAB是边长为2的等边三角形，即有2b＝2，即b＝1，且a＝×2＝，可得双曲线的方程为﹣y2＝1．故选：A．【点评】本题考查双曲线的方程和性质，主要是渐近线方程的应用，考查等边三角形的性质，以及化简运算能力，属于基础题．9．（5分）地球上的风能取之不尽，用之不竭．风能是清洁能源，也是可再生能源．世界各国致力于发展风力发电，近10年来，全球风力发电累计装机容量连年攀升，中国更是发展迅猛，在2014年累计装机容量就突破了100GW，达到114.6GW，中国的风力发电技术也日臻成熟，在全球范围的能源升级换代行动中体现出大国的担当与决心．以下是近10年全球风力发电累计装机容量与中国新增装机容量图．根据以上信息，正确的统计结论是（）A．截止到2015年中国累计装机容量达到峰值B．10年来全球新增装机容量连年攀升C．10年来中国新增装机容量平均超过20GWD．截止到2015年中国累计装机容量在全球累计装机容量中占比超过【分析】通过图结合选项分析．【解答】解：由图1知没有在截止到2015年中国累计装机容量达到峰值，A错；由图2知，10年来全球新增装机容量起伏，B错；由图1知，10年中国新增装机总容量为13.8+18.9+17.7+13+16.1+23.2+30.8+23.4+19.7+21.1＝197.7，则10年来中国新增装机容量平均为19.77GW，C错；故选：D．【点评】本题考查频率直方图，属于基础题．10．（5分）已知函数f（x）＝+2x+1，且f（a2）+f（2a）＞3，则a的取值范围是（）A．（﹣∞，﹣3）∪（1，+∞）B．（﹣∞，﹣2）∪（0，+∞）C．（﹣2，0）D．（﹣1，3）【分析】设F（x）＝f（x）﹣＝+2x+1﹣＝+2x，分析函数F（（x）的奇偶性，单调性，f（a2）+f（2a）＞3，转化为F（a2）＞﹣F（2a），即可解出答案．【解答】解：根据题意，设F（x）＝f（x）﹣＝+2x+1﹣＝+2x，则F（0）＝f（0）﹣＝0，又由F（﹣x）＝+2（﹣x）＝﹣（+2x）＝﹣F（x），即函数F（x）为奇函数；又由F′（x）＝＝＝＞0，所以函数F（x）单调递增，若f（a2）+f（2a）＞3，则f（a2）﹣＞，f（a2）﹣＞﹣[f（2a）﹣]，F（a2）＞﹣F（2a），F（a2）＞F（﹣2a），所以a2＞﹣2a，解得，a＜﹣2或a＞0，故选：B．【点评】本题考查函数的奇偶性与单调性的综合应用，涉及构造法的应用，属于基础题．11．（5分）已知函数f（x）＝sin x+sin（πx），现给出如下结论：①f（x）是奇函数；②f（x）是周期函数；③f（x）在区间（0，π）上有三个零点；④f（x）的最大值为2．其中正确结论的个数为（）A．1 B．2 C．3 D．4【分析】①根据函数奇偶性定义进行判断，②用反证法推出函数的函数无周期，③f（x）＝sin x+sin（πx）＝2sin cos，函数的零点为方程sin＝0或cos＝0，x＝或x＝，x∈（0，π），进而得出结论，④用反证法推出函数的函数最大值不是2．【解答】解：因为f（﹣x）＝sin（﹣x）+sin（﹣πx）＝﹣sin x﹣sin（πx）＝﹣f（x），所以f（x）是奇函数，①正确．假设存在周期T，则sin（x+T）+sin（π（x+T））＝sin x+sinπx，sin（x+T）﹣sin x＝﹣[sin（π（x+T））﹣sinπx]，所以sin•cos＝﹣sin•cos①，存在x0∈R，使得cos＝0，而cos≠0，将x0∈R，﹣sin•cos＝0，由于，故﹣sin＝0，所以sin＝0，sin＝0，＝kπ，＝mπ，k，m∈Z，所以kπ＝m，矛盾，所以函数f（x）＝sin x+sin（πx），没有周期，②错误．f（x）＝sin x+sin（πx）＝2sin cos，函数的零点为方程sin＝0或cos＝0，x＝或x＝，x∈（0，π）x＝，或，所以f（x）在区间（0，π）上有三个零点；故③正确．假设存在这样的x0使得f（x）最大值为2，x0＝且πx0＝，（k∈Z）即x0＝且x0＝，所以＝，k＝﹣，与k∈Z矛盾，故④错误．故选：B．【点评】本题考查三角函数的图象和性质，属于难题．12．（5分）已知正三棱柱ABC﹣A1B1C1的侧棱长为4，底面边长为2，用一个平面截此棱柱，与侧棱AA1，BB1，CC1分别交于点M，N，Q，若△MNQ为直角三角形，则△MNQ面积的最大值为（）A．3 B．C．D．3【分析】不妨设N在B处，AM＝h，CQ＝m，则有MB2＝h2+4，BQ2＝m2+4，MQ2＝（h﹣m）2+4由MB2＝BQ2+MQ2⇒m2﹣hm+2＝0．△＝h2﹣8≥0⇒h2≥8，且h≤4，可得S2＝1+h2，就可求出S最大值．【解答】解：解：如图，不妨设N在B处，AM＝h，CQ＝m，则有MB2＝h2+4，BQ2＝m2+4，MQ2＝（h﹣m）2+4由MB2＝BQ2+MQ2⇒m2﹣hm+2＝0．得h＝＝m+①△＝h2﹣8≥0⇒h2≥8，且h≤4，即8≤h2≤16，S＝，S2＝×|MQ|2×|BQ|2＝[（h﹣m）2+4]×（m2+4）把①代入得S2＝×[（m+﹣m）2+4]×（m2+4）＝[+4]×（m2+4）＝5+＝5+（+m）2﹣4＝1+（+m）2＝1+h2，所以S2＝1+h2∈[9，17]，S2max＝17，S max＝，故选：C．【点评】本题考查了空间线面位置关系，考查了转化思想，属于中档题．二、填空题：本大题共4小题，每小题5分，满分20分．13．（5分）从进入决赛的6名选手中决出1名一等奖，2名二等奖，3名三等奖，则可能的决赛结果共有60 种．（用数字作答）【分析】6名选手中决出1名一等奖有种方法，2名二等奖，种方法，利用分步计数原理即可得答案．【解答】解：依题意，可分三步，第一步从6名选手中决出1名一等奖有种方法，第二步，再决出2名二等奖，有种方法，第三步，剩余三人为三等奖，根据分步乘法计数原理得：共有•＝60种方法．故答案为：60．【点评】本题考查排列、组合及简单计数问题，掌握分步计数原理是解决问题的关键，属于中档题．14．（5分）在△ABC中，AB＝2，AC＝3，P是边BC的垂直平分线上一点，则•＝．【分析】取BC的中点D，＝（+）＝（（+）+），⊥，再利用两个向量垂直的性质及向量的运算法则，可得结果．【解答】解：取BC的中点D，由条件得•＝（+）•（﹣）＝（（+）+）•（﹣）＝﹣+＝﹣+•＝+0＝，故答案为：．【点评】此题是基础题．本题考查两个向量的运算法则及其意义，两个向量垂直的性质．15．（5分）函数f（x）＝lnx和g（x）＝ax2﹣x的图象有公共点P，且在点P处的切线相同，则这条切线方程为y＝x﹣1 ．【分析】分别求得f（x），g（x）的导数，设P（x0，y0），则lnx0＝ax02﹣x0①，结合f′（x0）＝g′（x0），联立消掉a可得关于x0的方程，构造函数，根据函数单调性可求得唯一x0值，进而可求P的坐标，以及切线的斜率和切线方程．【解答】解：f（x）＝lnx的导数为f′（x）＝，g（x）＝ax2﹣x的导数为g′（x）＝2ax﹣1，设P（x0，y0），则lnx0＝ax02﹣x0①，f′（x0）＝g′（x0），即＝2ax0﹣1，化简得1＝2ax02﹣x0②，联立①②消a得，lnx0＝，令φ（x）＝lnx﹣，φ′（x）＝+＞0，易知φ（x）在（0，+∞）上单调递增，又φ（1）＝0，所以φ（x）＝lnx﹣有唯一解1，即x0＝1，则y0＝f（1）＝0，a＝1．故P（1，0），切线的斜率为1，切线的方程为y＝x﹣1．故答案为：y＝x﹣1．【点评】本题考查利用导数研究函数的单调性及导数的几何意义，考查学生灵活运用所学知识分析问题解决问题的能力，属于中档题．16．（5分）在平面直角坐标系xOy中，对曲线C上任意一点P，P到直线x+1＝0的距离与该点到点O的距离之和等于2，则曲线C与y轴的交点坐标是（0，±1）；设点A（﹣，0），则|PO|+|PA|的最小值为．【分析】设P（x，y），P到直线x+1＝0的距离与该点到点O的距离之和等于2，求出P 的轨迹方程为抛物线，根据抛物线的性质，求出曲线C与y轴的交点坐标和|PO|+|PA|的最小值．【解答】解：设P（x，y），P到直线x+1＝0的距离与该点到点O的距离之和等于2，则|x+1|＝，化简得y2＝2x+1，令x＝0，y＝1，故曲线C与y轴的交点为（0，1），（0，﹣1），A（﹣，0），根据题意，当O，P，A三点共线时，则|PO|+|PA|的最小，最小值长等于|OA|＝，故答案为：（0，±1）；．【点评】考查直线与抛物线的综合，求曲线的轨迹方程，中档题．三、解答题：本大题共5小题，共70分，解答须写出必要的文字说明、证明过程或演算步骤．17．（12分）绿水青山就是金山银山．近年来，祖国各地依托本地自然资源，打造旅游产业，旅游业正蓬勃发展．景区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念，合力使旅游市场走上规范有序且可持续的发展轨道．某景区有一个自愿消费的项目：在参观某特色景点入口处会为每位游客拍一张与景点的合影，参观后，在景点出口处会将刚拍下的照片打印出来，游客可自由选择是否带走照片，若带走照片则需支付20元，没有被带走的照片会收集起来统一销毁．该项目运营一段时间后，统计出平均只有三成的游客会选择带走照片．为改善运营状况，该项目组就照片收费与游客消费意愿关系作了市场调研，发现收费与消费意愿有较强的线性相关性，并统计出在原有的基础上，价格每下调1元，游客选择带走照片的可能性平均增加0.05，假设平均每天约有5000人参观该特色景点，每张照片的综合成本为5元，假设每个游客是否购买照片相互独立．（1）若调整为支付10元就可带走照片，该项目每天的平均利润比调整前多还是少？（2）要使每天的平均利润达到最大值，应如何定价？【分析】（1）当收费为20元时，照片被带走的可能性为0.3，不被带走的概率为0.7，设每个游客的利润为Y1元，则Y1是随机变量，求出5000个游客的平均利润为5000元，当收费为10元时，照片被带走的可能性为0.3+0.05×10＝0.8，不被带走的概率为0.2，设每个游客的利润为Y2，则Y2是随机变量，求出5000个游客的平均利润为15000元，由此能求出该项目每天的平均利润比调整前多10000元．（2）设降价x元，则0≤x＜15，照片被带走的可能性为0.3+0.05x，不被带走的可能性为0.7﹣0.05x，设每个游客的利润为Y元，则Y是随机变量，求出其分布列，从而E（Y）＝（15﹣x）×（0.3+0.05x）﹣5×（0.7﹣0.05x）＝0.05[69﹣（x﹣7）2]，由此求出当定价为13元时，日平均利润取最大值为17250元．【解答】解：（1）当收费为20元时，照片被带走的可能性为0.3，不被带走的概率为0.7，设每个游客的利润为Y1元，则Y1是随机变量，其分布列为：Y1 15 ﹣5P 0.3 0.7E（Y1）＝15×0.3﹣5×0.7＝1（元），则5000个游客的平均利润为5000元，当收费为10元时，照片被带走的可能性为0.3+0.05×10＝0.8，不被带走的概率为0.2，设每个游客的利润为Y2，则Y2是随机变量，其分布列为：Y2 5 ﹣5P 0.8 0.2E（Y2）＝5×0.8﹣5×0.2＝3（元），则5000个游客的平均利润为5000×3＝15000（元），该项目每天的平均利润比调整前多10000元．（2）设降价x元，则0≤x＜15，照片被带走的可能性为0.3+0.05x，不被带走的可能性为0.7﹣0.05x，设每个游客的利润为Y元，则Y是随机变量，其分布列为：Y 15﹣x﹣5P 0.3+0.05x 0.7﹣0.05xE（Y）＝（15﹣x）×（0.3+0.05x）﹣5×（0.7﹣0.05x）＝0.05[69﹣（x﹣7）2]，当x＝7时，E（Y）有最大值3.45元，∴当定价为13元时，日平均利润取最大值为5000×3.45＝17250元．【点评】本题考查离散型随机变量的分布列和数学期望的求法，考查二项分布等基础知识，考查运算求解能力，是中档题．18．（12分）在△ABC中，内角A，B，C的对边分别为a，b，c，已知a sin B＝b sin（A﹣）．（1）求A；（2）D是线段BC上的点，若AD＝BD＝2，CD＝3，求△ADC的面积．【分析】（1）由正弦定理，三角函数恒等变换的应用化简已知等式可得tan A＝﹣，结合范围A∈（0，π），可求A的值．（2）设∠B＝θ，，由题意可得∠BAD＝θ，∠ADC＝2θ，∠DAC＝﹣θ，∠ACD＝﹣θ，在△ADC中，由正弦定理，三角函数恒等变换的应用可求sinθ＝cosθ，可求sinθ，cosθ，利用二倍角的正弦函数公式可求sin2θ，进而根据三角形的面积公式可求S△ADC的值．【解答】解：（1）由正弦定理可得a sin B＝b sin A，则有b sin A＝b（sin A﹣cos A），化简可得sin A＝﹣cos A，可得tan A＝﹣，因为A∈（0，π），所以A＝．（2）设∠B＝θ，，由题意可得∠BAD＝θ，∠ADC＝2θ，∠DAC＝﹣θ，∠ACD＝﹣θ，在△ADC中，，则＝，所以＝，可得sinθ＝cosθ，又因为sin2θ+cos2θ＝1，可得sinθ＝，cosθ＝，则sin2θ＝2sinθcosθ＝，所以S△ADC＝sin∠ADC＝＝．【点评】本题主要考查了正弦定理，三角函数恒等变换的应用，三角形的面积公式在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．19．（12分）已知椭圆C：+＝1（a＞b＞0）的离心率为，点A（1，）在椭圆C上，直线l1过椭圆C的有交点与上顶点，动直线l2：y＝kx与椭圆C交于M、N两点，交l1于P点．（1）求椭圆C的方程；（2）已知O为坐标原点，若点P满足|OP|＝|MN|，求此时|MN|的长度．【分析】（1）由离心率及过的点和a，b，c之间的关系求出椭圆的方程；（2）直线l2的方程与椭圆联立求出点M的坐标，由|OP|＝|MN|得P点坐标，P的直线l1上求出k值，进而求出MN|的值．【解答】解：（1）由题意得：e＝＝，+＝1，b2＝a2﹣c2，解得：a2＝4，b2＝3，所以椭圆的方程：＝1；（2）由题意直线l2的方程：y＝kx，代入椭圆中整理：（3+4k2）x2＝12，解得x＝，令M的坐标（，k）∵|OP|＝|MN|，由对称性可知，点P为OM的中点．故P的坐标（，），由P在直线l1：x+y﹣＝0，所以+﹣＝0，解得：k＝0或k＝，故M的坐标为（2，0），或（，），所以|OM|＝2，或，所以|MN|的长度为4或．【点评】考查直线与椭圆的综合，属于中难题．20．（12分）如图，三棱锥P﹣ABC中，平面PAB⊥平面ABC，PA＝PB，∠APB＝∠ACB＝90°，点E，F分别是棱AB，PB的中点，点G是△BCE的重心．（1）证明：GF∥平面PAC；（2）若GF与平面ABC所成的角为60°，求二面角B﹣AP﹣C的余弦值．【分析】（1）连结EF，连结EG并延长，交BC于点D，由点D是BC的中点，推导出DE ∥AC，EF∥AP，从而DE∥平面PAC，EF∥平面PAC，进而平面EFG∥平面PAC，由此能证明GF∥平面PAC．（2）连结PE，连结CG并延长交BE于点O，则O为BE的中点，连结OF，则OF∥PE，以O为原点，OC为x轴，OB为y轴，OF为z轴，建立空间直角坐标系，利用向量法能求出二面角B﹣AP﹣C的余弦值．【解答】解：（1）证明：连结EF，连结EG并延长，交BC于点D，由点D是BC的中点，∴D，E，F分别是棱CB，AB，PB的中点，∴DE∥AC，EF∥AP，∵DE，EF⊄平面PAC，AC，AP⊂平面PAC，∴DE∥平面PAC，EF∥平面PAC，∵DE，EF⊂平面EFG，DE∩EF＝E，∴平面EFG∥平面PAC，∵GF⊂平面EFG，∴GF∥平面PAC．（2）解：连结PE，∵PA＝PB，E是AB的中点，∴PE⊥AB，∵平面PAB⊥平面ABC，平面PAB∩平面ABC＝AB，PE⊂平面PAB，∴PE⊥平面ABC，连结CG并延长交BE于点O，则O为BE的中点，连结OF，则OF∥PE，∴OF⊥平面ABC，∴∠FGO是GF与平面ABC所成角，∴∠FGO＝60°，在Rt△FGO中，设GF＝2，则OG＝1，OF＝，∴OC＝3，PE＝2，∴AB＝4，CE＝2，OE＝，∴OE2+OC2＝CE2，∴OC⊥AB，以O为原点，OC为x轴，OB为y轴，OF为z轴，建立空间直角坐标系，则A（0，﹣3，0），C（3，0，0），P（0，﹣，2），＝（3，3，0），＝（0，2），设平面PAC的一个法向量＝（x，y，z），则，取z＝1，得＝（），平面PAB的法向量＝（1，0，0），设二面角B﹣AP﹣C的平面角为θ，则cosθ＝＝＝，∴二面角B﹣AP﹣C的余弦值为．【点评】本题考查线面平行的证明，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．21．（12分）已知函数f（x）＝1+x﹣2sin x，x＞0．（1）求f（x）的最小值；（2）证明：f（x）＞e﹣2x．【分析】（1）求导可知时f（x）单减，时f（x）单增，进而求得最小值；（2）即证x＞0时，g（x）＝（1+x﹣2sin x）e2x＞1，利用导数容易得证．【解答】解：（1）f′（x）＝1﹣2cos x，令f′（x）＝0，得，故在区间[0，π]上，f′（x）的唯一零点是，当时，f′（x）＜0，f（x）单调递减；当时，f′（x）＞0，f（x）单调递增，故在区间[0，π]上，f（x）的极小值为，当x＞π时，，∴f（x）的最小值为；（2）要证x＞0时，f（x）＞e﹣2x，即证x＞0时，g（x）＝（1+x﹣2sin x）e2x＞1，g′（x）＝2（1+x﹣2sin x）e2x+（1﹣2cos x）e2x＝（3+2x﹣4sin x﹣2cos x）e2x，令h（x）＝x﹣sin x，x＞0，则h′（x）＝1﹣cos x≥0，即h（x）是（0，+∞）上的增函数，∴h（x）＞h（0）＝0，即x＞sin x，∴3+2x﹣4sin x﹣2cos x＞3+2sin x﹣4sin x﹣2cos x＝3﹣2（sin x+cos x）＝，∴g′（x）＝（3+2x﹣4sin x﹣2cos x）e2x＞0，即g（x）是（0，+∞）上的增函数，g（x）＞g（0）＝1，故当x＞0时，f（x）＞e﹣2x，即得证．【点评】本题考查利用导数研究函数的最值及证明不等式，考查推理论证及运算能力，属于中档题．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分，作答时请写清楚题号．[选修4-4：坐标系与参数方程选讲]22．（10分）在直角坐标系xOy中，曲线C的参数方程为（m为参数）．（1）写出曲线C的普通方程，并说明它表示什么曲线；（2）已知倾斜角互补的两条直线l1，l2，其中l1与曲线C交于A，B两点，l2与C交于M，N两点，l1与l2交于点P（x0，y0），求证：|PA|•|PB|＝|PM|•|PN|．【分析】（1）由y＝4m，得m＝，代入x＝4m2，求出C的普通方程为y2＝4x，表示开口向右，焦点为F（1，0）的抛物线．（2）设直线l1的倾斜角为α，直线l2的倾斜角为π﹣α，直线l1的参数方程为，（t为参数），与y2＝4x联立，得t2sin2α+（2y0sinα﹣4cosα）t+y02﹣4x0＝0，由此能证明|PA|•|PB|＝|PM|•|PN|．【解答】解：（1）解：由y＝4m，得m＝，代入x＝4m2，得y2＝4x，∴曲线C的普通方程为y2＝4x，∴C的普通方程为y2＝4x，表示开口向右，焦点为F（1，0）的抛物线．（2）证明：设直线l1的倾斜角为α，直线l2的倾斜角为π﹣α，∴直线l1的参数方程为，（t为参数），与y2＝4x联立，得t2sin2α+（2y0sinα﹣4cosα）t+y02﹣4x0＝0，设方程的两个解为t1，t2，则t1t2＝，∴|PA|•|PB|＝|t1|•|t2|＝||，|PM|•|PN|＝||＝||，∴|PA|•|PB|＝|PM|•|PN|．【点评】本题考查曲线方程的求法，考查两组线段乘积相等的证明，考查直角坐标方程、极坐标方程、参数方程的互化等基础知识，考查运算求解能力，是中档题．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣a|+|x﹣1|．（1）若f（a）＜2，求a的取值范围；（2）当x∈[a，a+k]时，函数f（x）的值域为[1，3]，求k的值．【分析】（1）f（a）＝|a﹣1|＜2，即可得a的取值范围是（﹣1，3）；（2）对a分类讨论，由单调性即可得f（x）的单调性．【解答】解：（1）f（a）＝|a﹣1|＜2，得﹣2＜a﹣1＜2．即﹣1＜a＜3，所以a的取值范围是（﹣1，3）．（2）当a≥1时，函数f（x）在区间[a，a+k]上单调递增．则[f（x）]min＝f（a）＝a﹣1＝1，得a＝2，[f（x）]max＝f（a+k）＝a+2k﹣1＝3，得k ＝1．当a＜1时，f（x）＝则[f（x）]min＝f（a）＝1﹣a＝1，得a＝0，[f（x）]max＝f（a+k）＝a+2k﹣1＝3，得k＝2．综上所述，k的值是1或2．【点评】本题考查了绝对值不等式，属于中档题．。

高考数学精品复习资料2019.5佛山市普通高中高三教学质量检测（一）数 学（理科）本试卷共4页，21小题，满分150分．考试用时120分钟． 注意事项：1．答卷前，考生要务必填写答题卷上密封线内的有关项目．2．选择题每小题选出答案后，用铅笔把答案代号填在答题卷对应的空格内．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．请考生保持答题卷的整洁．考试结束后，将答题卷和答题卡交回． 参考公式：①柱体的体积公式V Sh =，其中S 为柱体的底面积，h 为柱体的高． ②锥体的体积公式13V Sh =，其中S 为柱体的底面积，h 为锥体的高． ③标准差222121[()()()]n s x x x x x x n=-+-++-，其中x 为样本12,,,n x x x 的平均数．一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．设i 为虚数单位，则复数i2i+等于 A ．12i 55+ B ． 12i 55-+ C ．12i 55- D ．12i 55--2．命题:p 2,11x x ∀∈+≥R ，则p ⌝是A ．2,11x x ∀∈+<R B ．2,11x x ∃∈+≤RC ．2,11x x ∃∈+<RD ．2,11x x ∃∈+≥R3．已知(1,2)=a ，(0,1)=b ，(,2)k =-c ，若(2)+⊥a b c ，则k = A ．2 B ．8 C ．2- D ．8-4．一个直棱柱被一个平面截去一部分后所剩几何体的 三视图如图所示，则该几何体的体积为 A ．9B ．102 21 31 正视图 侧视图俯视图第4题图C ．11D ．2325．为了从甲乙两人中选一人参加数学竞赛，老师将两人最近的6次数学测试的分数进行统计，甲乙两人的得分情况如茎叶图所示，若甲乙两人的平均成绩分别是x 甲，x 乙，则下列说法正确的是A ．x x >甲乙，乙比甲成绩稳定，应该选乙参加比赛B ．x x >甲乙，甲比乙成绩稳定，应该选甲参加比赛C ．x x <甲乙，甲比乙成绩稳定，应该选甲参加比赛D ．x x <甲乙，乙比甲成绩稳定，应该选乙参加比赛6．已知实数,x y 满足11y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则目标函数2z x y =-的最大值为A ．3-B ．12C ．5D ．6 7．已知集合{}|4||1|5M x x x =-+-<，{}6N x a x =<< ,且()2,MN b =,则a b +=A ．6B ．7C ．8D ．98．对于函数()y f x =，如果存在区间[,]m n ，同时满足下列条件：①()f x 在[,]m n 内是单调的；②当定义域是[,]m n 时，()f x 的值域也是[,]m n ，则称[,]m n 是该函数的“和谐区间”．若函数11()(0)a f x a a x+=->存在“和谐区间”，则a 的取值范围是 A ．(0,1) B ． (0,2) C ．15(,)22D ．(1,3)二、填空题：本大共7小题，考生作答6小题，每小题5分，满分30分． (一)必做题(9～13题)9．已知函数()y f x =是奇函数，当0x >时，()f x =2log x ，则1(())4f f 的值等于 ． 10．已知抛物线24x y =上一点P 到焦点F 的距离是5，则点P 的横坐标是_____．第5题图11．函数sin sin 3y x x π⎛⎫=+-⎪⎝⎭的最小正周期为 ，最大值是 ． 12．某学生在参加政、史、地 三门课程的学业水平考试中，取得A 等级的概率分别为54、53、52，且三门课程的成绩是否取得A 等级相互独立.记ξ为该生取得A 等级的课程数，其分布列如表所示，则数学期望ξE 的值为______________. 13．观察下列不等式： ①112<；②11226+<；③11132612++<；… 则第5个不等式为 ．(二)选做题(14～15题，考生只能从中选做一题)14．（坐标系与参数方程）在极坐标系中，直线l 过点(1,0)且与直线3πθ=（ρ∈R ）垂直，则直线l 极坐标方程为 ．15．（几何证明选讲）如图，M 是平行四边形ABCD 的边AB 的 中点，直线l 过点M 分别交,AD AC 于点,E F ． 若3AD AE =，则:AF FC = ．三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤．16．（本题满分12分）如图，在△ABC 中，45C ∠=，D 为BC 中点，2BC =. 记锐角ADB α∠=．且满足7cos 225α=-． （1）求cos α；（2）求BC 边上高的值．ξ 012 3P6125ab24125第15题图F ABCD E Ml第16题图CBD A17．（本题满分12分）数列{}n a 的前n 项和为122n n S +=-，数列{}n b 是首项为1a ，公差为(0)d d ≠的等差数列，且1311,,b b b 成等比数列．（1）求数列{}n a 与{}n b 的通项公式； （2）设nn nb c a =，求数列{}n c 的前n 项和n T ．18．（本题满分14分）如图所示，已知AB 为圆O 的直径，点D 为线段AB 上一点， 且13AD DB =，点C 为圆O 上一点，且3BC AC =． 点P 在圆O 所在平面上的正投影为点D ，PD DB =． （1）求证：PA CD ⊥；（2）求二面角C PB A --的余弦值．19．（本题满分14分）某工厂生产某种产品，每日的成本C （单位：万元）与日产量x （单位：吨）满足函数关系式3C x =+，每日的销售额S （单位：万元）与日产量x 的函数关系式PABDCO第18题图35, (06)814, (6)k x x S x x ⎧++<<⎪=-⎨⎪≥⎩ 已知每日的利润L S C =-，且当2x =时，3L =．（1）求k 的值；（2）当日产量为多少吨时，每日的利润可以达到最大，并求出最大值．20．（本题满分14分）设椭圆22221(0)x y a b a b+=>>的左右顶点分别为(2,0),(2,0)A B -，离心率32e =．过该椭圆上任一点P 作PQ x ⊥轴，垂足为Q ，点C 在QP 的延长线上，且||||QP PC =． （1）求椭圆的方程；（2）求动点C 的轨迹E 的方程；（3）设直线AC （C 点不同于,A B ）与直线2x =交于点R ，D 为线段RB 的中点，试判断直线CD 与曲线E 的位置关系，并证明你的结论．21．（本题满分14分）设()xg x e =，()[(1)]()f x g x a g x =λ+-λ-λ，其中,a λ是常数，且01λ<<． （1）求函数()f x 的极值；（2）证明：对任意正数a ，存在正数x ，使不等式11x e a x--<成立； （3）设12,λλ∈+R ，且121λλ+=，证明：对任意正数21,a a 都有：12121122a a a a λλ≤λ+λ．佛山市普通高中高三教学质量检测（一）数学试题（理科）参考答案和评分标准一、选择题：本大题共8小题，每小题5分，满分40分． 题号 12345678 答案A CBCD C BA二、填空题：本大共7小题，考生作答6小题，每小题5分，满分30分． 9．1- 10．4± 11．2π（2分），3 （3分） 12．59 13．11111526122030++++< 14．2sin()16πρθ+=（或2cos()13πρθ-=、cos 3sin 1ρθρθ+=） 15．1:4三、解答题：本大题共6小题，满分80分，解答须写出文字说明、证明过程或演算步骤．16．（本题满分12分） 解析：（1）∵27cos 22cos 125αα=-=-，∴29cos 25α=， ∵(0,)2πα∈，∴3c o s 5α=． -----------------5分 （2）方法一、由（1）得24sin 1cos 5αα=-=，∵45CAD ADB C α∠=∠-∠=-，∴2sin sin()sin cos cos sin 44410CAD πππααα∠=-=-=，-----------------9分在ACD ∆中，由正弦定理得：sin sin CD ADCAD C=∠∠， ∴21sin 25sin 210CD CAD CAD⨯⋅∠===∠，-----------------11分则高4sin 545h AD ADB =⋅∠=⨯=． -----------------12分 方法二、如图，作BC 边上的高为AH在直角△ADH 中，由（1）可得3cos 5DB AD α==， 则不妨设5,AD m = 则3,4DH m AH m ==-----------------8分第16题图 C BD AH注意到=45C ∠，则AHC ∆为等腰直角三角形，所以CD DH AH += ， 则134m m +=-----------------10分 所以1m =，即4AH =-----------------12分17．（本题满分12分） 解析：（1）当2n ≥，时11222n nn n n n a S S +-=-=-=， -----------------2分又111112222a S +==-==，也满足上式，所以数列{na }的通项公式为2n n a =． -----------------3分112b a ==，设公差为d ，则由1311,,b b b 成等比数列，得2(22)2(210)d d +=⨯+，-----------------4分解得0d =（舍去）或3d =，----------------5分 所以数列}{n b 的通项公式为31n b n =-． -----------------6分（2）由（1）可得312123n n nb b b b T a a a a =++++123258312222nn -=++++，-----------------7分121583122222n n n T --=++++，-----------------8分两式式相减得12133********n n n n T --=++++-，-----------------11分131(1)3135222512212n n n nn n T ---+=+-=--，-----------------12分18．（本题满分14分）解析：（Ⅰ）法1：连接CO ，由3AD DB =知，点D 为AO 的中点， 又∵AB 为圆O 的直径，∴AC CB ⊥， 由3AC BC =知，60CAB ∠=，∴ACO ∆为等边三角形，从而CD AO ⊥．-----------------3分 ∵点P 在圆O 所在平面上的正投影为点D ， ∴PD ⊥平面ABC ，又CD ⊂平面ABC ， ∴PD CD ⊥，-----------------5分由PDAO D =得，CD ⊥平面PAB ，又PA ⊂平面PAB ，∴PA CD ⊥． -----------------6分（注：证明CD ⊥平面PAB 时，也可以由平面PAB ⊥平面ACB 得到，酌情给分．） 法2：∵AB 为圆O 的直径，∴AC CB ⊥， 在Rt ABC ∆中设1AD =，由3A D D B=，3AC BC =得，3DB =，4AB =，23BC =， ∴32BD BC BC AB ==，则BDC BCA ∆∆∽， ∴BCA BDC∠=∠，即C ⊥． -----------------3分∵点P 在圆O 所在平面上的正投影为点D ， ∴PD ⊥平面ABC ，又CD ⊂平面ABC ， ∴PD CD⊥，-----------------5分 由PDAO D =得，CD ⊥平面PAB ，又PA ⊂平面PAB，∴PA CD ⊥． -----------------6分 法3：∵AB 为圆O 的直径，∴AC CB ⊥， 在Rt ABC ∆中由3AC BC =得，30ABC ∠=， 设1AD =，由3AD DB =得，3DB =，23BC =，PABDCO由余弦定理得，2222cos303CD DB BC DB BC =+-⋅=， ∴222CD DB BC +=，即C ⊥． -----------------3分∵点P 在圆O 所在平面上的正投影为点D ， ∴PD ⊥平面ABC ，又CD ⊂平面ABC ， ∴PD CD⊥，-----------------5分 由PDAO D =得，CD ⊥平面PAB ，又PA ⊂平面PAB，∴PA CD ⊥． -----------------6分（Ⅱ）法1：（综合法）过点D 作DE PB ⊥，垂足为E ，连接CE ． -----------------7分由（1）知CD ⊥平面PAB ，又PB ⊂平面PAB ， ∴CD PB ⊥，又DE CD D =， ∴PB ⊥平面CDE ，又CE ⊂平面CDE ， ∴CE PB ⊥，-----------------9分∴DEC ∠为二面角C PB A --的平面角． -----------------10分 由（Ⅰ）可知3CD =，3PD DB ==，（注：在第（Ⅰ）问中使用方法1时，此处需要设出线段的长度，酌情给分．）∴32PB =，则932232PD DB DE PB ⋅===， ∴在Rt CDE ∆中，36tan 3322CD DEC DE ∠===， ∴15cos 5DEC ∠=，即二面角C P B --的余弦值为155． -----------------14分 法2：（坐标法）以D 为原点，DC 、DB 和DP 的方向分别为x 轴、y 轴和z 轴的正向，建立如图所示的空间直角坐标系． -----------------8分 （注：如果第（Ⅰ）问就使用“坐标法”时，建系之前先要证明CD AB ⊥，酌情给分．） 设1AD =，由3AD DB =，3AC BC =得，3PD DB ==，3CD =，PABDC OE∴(0,0,0)D ，(3,0,0)C ，(0,3,0)B ，(0,0,3)P ， ∴(3,0,3)PC =-，(0,3,3)PB =-，(3,0,0)CD =-， 由CD ⊥平面PAB，知平面PAB的一个法向量为(3,0,0)CD =-． -----------------10分设平面PBC 的一个法向量为(,,)x y z =n ，则00PC PB ⎧⋅=⎪⎨⋅=⎪⎩n n ，即330330x y y z ⎧-=⎪⎨-=⎪⎩，令1y =，则3x =，1z =， ∴(3,1,1)=n ，-----------------12分 设二面角C PB A --的平面角的大小为θ， 则315cos 5||53CD CD θ⋅-===-⋅⨯n |n |，-----------------13分 ∴二面角C PB A --的余弦值为155．-----------------14分19．（本题满分14分） 解析：（Ⅰ）由题意可得：22,06811,6k x x L x x x ⎧++<<⎪=-⎨⎪-≥⎩，-----------------2分 因为2x =时，3L =，所以322228k=⨯++-. -----------------4分解得18k =.-----------------5分（Ⅱ）当06x <<时，18228L x x =++-，所以 1818182818=[2(8)]182********L x x x x x x=-++--++--⋅+=---≤（）（）．-----------------8分 当且仅当182(8)8x x-=-，即5x =时取得等号． -----------------10分 当6x ≥时，1L x =-≤． -----------------12分 所以当5x =时，L 取得最大值6．PABDCOyz x所以当日产量为5吨时，每日的利润可以达到最大值6万元． -----------------14分20．（本题满分14分）解析：（1）由题意可得2a =，32c e a ==，∴3c =， -----------------2分∴2221b a c =-=，所以椭圆的方程为2214x y +=． -----------------4分 （2）设(,)C x y ，00(,)P x y ，由题意得002x x y y =⎧⎨=⎩，即0012x x y x =⎧⎪⎨=⎪⎩， -----------------6分 又220014x y +=，代入得221()142x y +=，即224x y +=． 即动点C 的轨迹E 的方程为224x y +=． -----------------8分（3）设(,)C m n ，点R 的坐标为(2,)t ，∵,,A C R 三点共线，∴//AC AR ，而(2,)AC m n =+，(4,)AR t =，则4(2)n t m =+， ∴42n t m =+， ∴点R 的坐标为4(2,)2n m +，点D 的坐标为2(2,)2n m +，-----------------10分∴直线CD 的斜率为222(2)22244n n m n n mn m k m m m -+-+===---， 而224m n +=，∴224m n -=-，∴2mn m k n n ==--， -----------------12分∴直线CD 的方程为()m y n x m n-=--，化简得40mx ny +-=， ∴圆心O 到直线CD 的距离224424d r m n ====+， 所以直线CD与圆O 相切． -----------------14分21．（本题满分14分）解析：（1）∵()[(1f x g x ag x λλλλ'''=+--， -----------------1分由()0f x '>得，[(1)]()g x a g x λλ''+->，∴(1)x a x λλ+->，即(1)()0x a λ--<，解得x a <，-----------------3分故当x a <时，()0f x '>；当x a >时，()0f x '<；∴当x a =时，()f x 取极大值，但()f x 没有极小值．-----------------4分（2）∵111x x e e x x x----=， 又当0x >时，令()1xh x e x =--，则()10x h x e '=->， 故()(0)0h x h >=，因此原不等式化为1x e x a x--<，即(1)1x e a x -+-<， -----------------6分 令()(1)1xg x e a x =-+-，则()(1)x g x e a '=-+，由()0g x '=得：1x e a =+，解得ln(1)x a =+，当0ln(1)x a <<+时，()0g x '<；当ln(1)x a >+时，()0g x '>． 故当l n (1x a =+时，()g x 取最小值[ln(1)](1)ln(1)g a a a a +=-++， -----------------8分 令()ln(1),01a s a a a a=-+>+，则2211()0(1)1(1)a s a a a a '=-=-<+++． 故()(0)0s a s <=，即[ln(1)](1)ln(1)0g a a a a +=-++<．因此，存在正数ln(1)x a =+，使原不等式成立． -----------------10分（3）对任意正数12,a a ，存在实数12,x x 使11x a e =，22x a e =， 则121122112212x x x x a a ee e λλλλλλ+=⋅=，12112212x x a a e e λλλλ+=+， 原不等式12121122a a a a λλλλ≤+11221212x x x x e e e λλλλ+⇔≤+，11221122()()()g x x g x g x λλλλ⇔+≤+ -----------------14分由（1）()(1)()f x g a λ≤-恒成立，故[(1)]()(1)()g x a g x g a λλλλ+-≤+-，取1212,,,1x x a x λλλλ===-=，即得11221122()()()g x x g x g x λλλλ+≤+，即11221212x x x x e e e λλλλ+≤+，故所证不等式成立． -----------------14分。

2019～2020学年佛山市普通高中高一教学质量检测数学参考答案与评分标准一、选择题：本大题共12小题，每小题5分，满分60分．二、填空题：本大共4小题，每小题5分，满分20分．13． 2114． 11516．142625（或26.56）；13 三、解答题：本大题共6小题，满分70分．解答须写出文字说明、证明过程或演算步骤． 17.（10分）解析：法1：（1）由题意得，tan 2α=，所以2222sin cos 2tan 4sin 22sin cos sin cos tan 15ααααααααα====++． （5分）（2）因为29(sin cos )12sin cos 5αααα+=+=，所以sin cos αα+=，故sin()cos )4πααα++==．（10分） 法2：（1）由22sin 2cos sin cos 1αααα=⎧⎨+=⎩解得，sin cos αα⎧=⎪⎪⎨⎪=⎪⎩，或sin cos αα⎧=⎪⎪⎨⎪=⎪⎩（舍去）； 所以4sin 22sin cos 25ααα===． （5分） （2）sin()cos )422πααα+=+=+= （10分） 18.（12分）解析：（1）因为(1)(1)0f f +-=，所以224ln ln(2)ln 033m m m --++==， （1分）所以243m -=，又0m >，解得1m =． （2分） 由202xx->+得，(2)(2)0x x -+>，所以()f x 的定义域为(2,2)-． （3分） 因为1222()lnln()ln222x x xf x x x x-+---===--++． （5分） 即()()f x f x -=-，所以()f x 是奇函数； （6分）（2）()f x 在(2,2)-上单调递减； （8分）（3）()f x 是奇函数，不等式等价于：()()2ln3f x f x <-+． （9分）所以2()2ln3f x <，即()ln3(1)f x f <=-． （10分）由（2）知()f x 在(2,2)-单调递减，所以1x >-，同时由定义域22x -<<． （11分） 所以x 的取值集合为{|12}x x -<<． （12分） 19.（12分）解析：（1）由数据表可知，位移的最大值为20mm ，即20A =；周期为0.6s ，即20.6πω=，解得103πω=；再由0t =时的位移为20-，可得sin 1ϕ=-，解得2πϕ=-．所以振子位移关于时间的函数解析式为1020sin()32y t ππ=-，[0,)t ∈+∞． （6分） （2）作出函数一个周期的图象如下： （8分）（3）由表格或图象可知，一个周期内当10y =mm 时，0.2t =或0.4t =，所以当位移为10mm 的时间t 的取值集合为{|0.20.6t t k =+或}0.40.6,t k k =+∈N ． （12分）20.（12分）解析：（1）因为()()2x f x g x +=，所以()()()()2x f x g x f x g x --=-+-=，两式相加得，2()22xxf x -=+，解得22()2x xf x -+=． （4分）（2）函数()f x 在[0,)+∞上是增函数．证明如下：设任意12,[0,)x x ∈+∞，且12x x <，则，112212121212121212222111(22)(21)()()(22)222222x x x x x x x x x x x x x x f x f x --+++++---=-=⨯-+-=， 因为12x x <，所以1222x x <，则12220x x -<；又120x x +>，所以12210x x +->． 从而12()()f x f x <，即12()()f x f x <．因此，()f x 在[0,)+∞上单调递增． （8分）（3）因为1252(1)24f +==，且偶函数()f x 在[0,)+∞上单调递增，故原不等式等价于||1x ≥． 因此，原不等式的解集为(,1][1,)-∞-+∞U ． （12分） 21.（12分）解析：（1）表格和散点图如下：（4分）（2两组数据带入函数解析式得26.55085.4100a ba b =+⎧⎨=+⎩，解得 1.178a =，32.4b =-， 故 1.17832.4d v =-．对于模型二：2d av bv =+．将点(50,26.5)和(100,85.4)两组数据带入函数解析式得2226.5505085.4100100a b a b ⎧=+⎪⎨=+⎪⎩，解得0.00648a =，0.206b =， 故20.006480.206d v v =+． （8分）（3）当180v =时，对于模型一，停车距离 1.17818032.4212.0432.4179.64d =⨯-=-=m ；对于模型二，停车距离20.006481800.206180209.95237.08247.032d =⨯+⨯=+=m ，显然模型二计算得到数据与试验数据245.5m 更接近，说明选择函数模型二进行拟合效果好．（12分） 22.（12分）解析：（1）当1a =时，21()4f x x x =++在(0,)+∞上单调递增，12()log g x x =在(0,)+∞上单调递减． 由于11()()122f g ==，所以当102x <<时，()1()f x g x<<；当12x >时，()1()f x g x >>． 因此，2211,0,42()1log ,.2x x x h x x x ⎧++<≤⎪⎪=⎨⎪->⎪⎩由于()h x 在1(0,]2上单调递增，在1[,)2+∞上单调递减，所以当12x =时，()h x 取得最大值1()12h =． （4分） （2）当(1,)x ∈+∞时，2()log 0g x x =-<，从而()min{(),()}()0h x f x g x g x =≤<，故()h x 在(1,)+∞无零点．当1x =时，若54a ≥-，则5(1)04f a =+≥，(1)min{(1),(1)}(1)0h f g g ===，故1x =是()h x 的零点；若54a <-，则5(1)04f a =+<，(1)min{(1),(1)}(1)0h f g f ==<，故1x =不是()h x 的零点．当(0,1)x ∈时，2()log 0g x x =->．所以只需考虑()f x 在(0,1)的零点个数． （ⅰ）若0a ≥，则()f x 在(0,1)上单调递增，()f x 在(0,1)内没有零点． （ⅱ）若0a <，则()f x 在(0,)2a-单调递减，在(,)2a -+∞单调递增，当2ax =-时，()f x 取得最小值21()24a a f --=． ①若10a -<<，则21()024a a f --=>，()f x 在(0,1)无零点；②若1a =-，则21()024a a f --==，()f x 在(0,1)有唯一零点12x =；③若514a -<<-，则()f x 在(0,)2a -单调递减，在(,1)2a -单调递增，且1(0)04f =>，21()024a a f --=<，5(1)04f a =+>，()f x 在(0,1)有两个零点；④若524a -<≤-，则()f x 在(0,)2a -单调递减，在(,1)2a-单调递增，且1(0)04f =>，21()024a a f --=<，5(1)04f a =+≤，()f x 在(0,1)有一个零点；⑤若2a ≤-，则()f x 在(0,1)单调递减，且1(0)04f =>，5(1)04f a =+<，()f x 在(0,1)有一个零点． 综上所述，当1a >-或54a <-时，()h x 有一个零点；当1a =-或54a =-时，()h x 有两个零点；当514a -<<-时，()h x 有三个零点． （12分）。

2018~2019学年佛山市普通高中高三教学质量检测（一）数学（理科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合，，则（）A. B. C. D.【答案】B【解析】【分析】求出集合A，B,然后直接取并集即可．【详解】集合B＝{x|﹣1＜x＜1}，A＝{x|x2﹣2x<0}＝{x|0<x<2}，则{x|0<x<2}{x|﹣1＜x＜1}＝{x|-1<x＜2}故选：B．【点睛】本题考查集合的并集运算，属简单题.2.若复数（为虚数单位）在复平面内对应的点在虚轴上，则实数（）A. B. 2 C. D.【答案】D【解析】【分析】计算出复数的表达式，由题意中复数在复平面内对应的点在虚轴上计算出结果【详解】复数在复平面内对应的点在虚轴上，则，故选【点睛】本题主要考查了复数的几何意义，只需计算出复数在复平面内的对应点，结合题意即可计算出答案，较为基础3.设变量满足约束条件，则目标函数的最大值为（）A. 7B. 8C. 15D. 16【答案】B【解析】【分析】由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组得到最优解的坐标，代入目标函数得到答案.【详解】作出变量x，y满足的约束条件如图：由z＝2x+y知，动直线y＝﹣2x+z的纵截距z取得最大值时，目标函数取得最大值．由得A（3，2）,结合可行域可知当动直线经过点A（3，2）时，目标函数取得最大值z＝2×3+2＝8．故选：B．【点睛】本题考查线性规划中利用可行域求目标函数的最值，求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.4.已知：“”，：“”，则是的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C【解析】【分析】先证充分性，然后再证明必要性，继而判定结果【详解】①充分性当时，成立，②必要性当时，,,,当时，，不成立，故舍去则是的充分必要条件故选【点睛】本题主要考查了充分条件和必要条件，在判定结果时左右两边分别进行证明充分性和必要性，继而得到结果，较为基础5.已知，则（）A. B. C. D.【答案】C【解析】【分析】运用两角差的余弦公式展开后再计算平方的结果，结合已知条件得到答案【详解】，，，故选【点睛】本题主要考查了两角差的余弦公式以及二倍角公式，熟练运用公式来解题是关键，较为基础6.已知向量，，，则（）A. B. C. 6 D. 8【答案】A【解析】【分析】先用坐标表示出，然后由向量垂直代入计算求出结果【详解】，，，，则解得故选【点睛】本题主要考查了向量的垂直计算，只需运用点坐标表示向量，然后点乘得零即可得到结果，较为简单7.展开式中的系数为（）A. B. 120 C. 160 D. 200【答案】B【解析】【分析】结合二项展开式计算出含的项，从而得到系数【详解】展开式中的项为,则展开式中的系数为120故选【点睛】本题主要考查了二项展开式的运用，求特定项的系数，熟练运用公式进行求解8.某几何体的三视图如图所示，则该几何体的体积为（）A. B. C. D.【答案】D【解析】【分析】由题目中的三视图还原几何体，可知是由半圆锥和四棱锥组成，然后计算几何体的体积【详解】由三视图可得该组合体是由半圆锥和四棱锥组成由已知图中数量可得：故选【点睛】本题主要考查了三视图，要先还原几何体，然后再计算体积，还原几何体是难点，还需要有一定空间想象能力。

广东省佛山市2019-2020年度高三上学期期末数学试卷（理科）A卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）(2018·全国Ⅲ卷理) 已知集合，则（）A .B .C .D .2. （2分）直线x+y-1=0的倾斜角是（）A . 150ºB . 135ºC . 120ºD . 30º3. （2分） (2016高一下·新疆期中) 在△ABC中，角A，B，C的对应边分别为a，b，c，若，则角C的值为（）A .B .C . 或D . 或4. （2分）设动点坐标(x,y)满足，则的最小值为（）A .B .C .D . 105. （2分）已知a=log1.20.8，b=0.81.2 ， c=1.21.2 ，则a，b，c的大小关系为（）A . a＞b＞cB . a＜b＜cC . a＜c＜bD . b＜a＜c6. （2分） (2017高二上·宜昌期末) 若p是真命题，q是假命题，则（）A . p∧q是真命题B . p∨q是假命题C . ﹁p是真命题D . ﹁q是真命题7. （2分）若函数的图象上每一点的纵坐标保持不变，横坐标缩小到原来的，再将整个图象向右平移个单位，沿y轴向下平移1个单位，得到函数的图象，则函数是（）A .B .C .D .8. （2分）已知正六边形ABCDEF的边长为1，则(+)的值为（）A .B . -C .D . -9. （2分）函数y= 的零点的个数为（）A . 2B . 0C . 1D . 310. （2分）(2017·深圳模拟) 直线l：kx+y+4=0（k∈R）是圆C：x2+y2+4x﹣4y+6=0的一条对称轴，过点A （0，k）作斜率为1的直线m，则直线m被圆C所截得的弦长为（）A .B .C .D . 2二、填空题 (共5题；共6分)11. （1分）(2017·南京模拟) 射击运动员打靶，射5发，环数分别为9，10，8，10，8，则该数据的方差为________．12. （1分）已知函数f（x）=tan，x∈（﹣4，4），则满足不等式（a﹣1）[f（a﹣1）+]≤2的实数a的取值范围是________13. （1分）(2013·上海理) 在xOy平面上，将两个半圆弧（x﹣1）2+y2=1（x≥1）和（x﹣3）2+y2=1（x≥3），两条直线y=1和y=﹣1围成的封闭图形记为D，如图中阴影部分，记D绕y轴旋转一周而成的几何体为Ω．过（0，y）（|y|≤1）作Ω的水平截面，所得截面积为4π +8π．试利用祖暅原理、一个平放的圆柱和一个长方体，得出Ω的体积值为________．14. （2分）(2017·温州模拟) 如图，一个简单几何体三视图的正视图与侧视图都是边长为1的正三角形，其俯视图的轮廓为正方形，则该几何体的体积是________，表面积是________．15. （1分） (2019高三上·双流期中) 已知直线l:y=k(x-2)与抛物线C:y2=8x交于A,B两点，F为抛物线C 的焦点，若|AF|=3|BF|，则直线l的倾斜角为________。

广东佛山普通高中2019年高三教学质量检测（一）数学（理）理科数学本试卷共4页,21小题,总分值150分.考试用时120分钟. 本卷须知1.答卷前,考生要务必填写答题卷上密封线内的有关项目.2.选择题每题选出答案后，用铅笔把答案代号填在答题卷对应的空格内.3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.请考生保持答题卷的整洁.考试结束后，将答题卷和答题卡交回. 【一】选择题:本大题共8小题,每题5分,总分值40分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的.1、i 是虚数单位，m 、n ∈R ，且i 1i m n +=+，那么i im n m n +=-A 、1-B 、1C 、i -D 、i2、以下函数中既是奇函数，又在区间()1,1-上是增函数的为A 、y x=B 、sin y x =C 、x x y e e -=+D 、3y x =-3、设{}n a 是公差不为0的等差数列，12a =且136,,a a a 成等比数列，那么{}n a 的前5项和5S =A 、10B 、15C 、20D 、304、“关于x 的不等式220x ax a -+>的解集为R ”是“01a ≤≤”A 、充分而不必要条件B 、必要而不充分条件C 、充要条件D 、既不充分也不必要条件5、一个体积为A.36 B 、8 C 、38D 、126、点P 是抛物线24x y =上的一个动点，那么点P 到点(2,0)M 的距离与点P 到该抛物线准线的距离之和的最小值为A、2BC、 D 、927、某市要对两千多名出租车司机的年龄进行调查，现从中随机抽出100名司机，抽到的司机年龄都在[)20,45岁之间，依照调查结果得出司机的年龄情况残缺的频率分布直方图如下图，利用那个残缺的频率分布直方图可能该市出租车司机年龄的中位数大约是A 、31.6岁B 、32.6岁C 、33.6岁D 、36.6岁8、关于非空集合,A B ，定义运算：{|,}A B x x AB x A B ⊕=∈∉且，}|{},|{d x c x N b x a x M <<=<<=，其中d c b a 、、、满足a b c d +=+，0ab cd <<，那么=⊕N MA.(,)(,)a d b c B.(,][,)c a b d C.(,][,)a c d b D.(,)(,)c a d b【二】填空题:本大共7小题,考生作答6小题,每题5分，总分值30分〕 (一)必做题(9～13题)9、某学校三个社团的人员分布如下表〔每名同学只参加一个社团〕学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，那么a =_______________. 10、函数sin()2y x x π=++的最小正周期是___________.11、不等式组02,20,20x x y kx y ≤≤⎧⎪+-≥⎨⎪-+≥⎩所表示的平面区域的面积为4，那么k 的值为__________.12、向量=a (,2)x ，=b (1,)y ，其中0,0x y >>.假设4=a b ，那么12x y+的最小值为. 13、对任意实数b a ,，函数|)|(21),(b a b a b a F --+=，假如函数2()23,f x x x =-++ ()1g x x =+，那么函数()()(),()G x F f x g x =的最大值等于.(二)选做题(14～15题,考生只能从中选做一题) 14、〔坐标系与参数方程〕在极坐标系下，直线l 的方程为1)3cos(=-πθρ，那么点)2,1(πM 到直线l 的距离为__________.15.〔几何证明选讲〕如图，P 为圆O 外一点，由P 引圆O 的切线PA 与圆O 切于A 点，引圆O 的割线PB 与圆O 交于APC 点.AC AB ⊥，1,2==PC PA .那么圆O 的面积为.【三】解答题:本大题共6小题,总分值80分,解答须写出文字说明、证明过程或演算步骤. 16、〔此题总分值12分〕在△ABC 中，角A 、B 、C 的对边分别为a b c 、、，满足2A C B +=，且1411)cos(-=+C B . 〔1〕求C cos 的值；〔2〕假设5=a ，求△ABC 的面积. 17、〔此题总分值14分〕如图，三棱锥ABC P -中，PB ⊥底面ABC ，90BCA ∠=，2===CA BC PB ，E 为PC 的中点，点F 在PA 上，且FA PF =2.〔1〕求证：平面PAC ⊥平面BEF ；〔2〕求平面ABC 与平面BEF 所成的二面角的平面角〔锐角〕的余弦值. 18、〔此题总分值13分〕佛山某学校的场室统一使用“佛山照明”的一种灯管，这种灯管使用寿命ξ〔单位：月〕服从正态分布2(,)N μσ，且使用寿命许多于12个月的概率为0.8，使用寿命许多于24个月的概率为0.2.〔1〕求这种灯管的平均使用寿命μ；〔2〕假设一间功能室一次性换上4支这种新灯管，使用12个月时进行一次检查，将差不多损坏的灯管换下〔中途不更换〕，求至少两支灯管需要更换的概率. 19、〔此题总分值12分〕圆221:(4)1C x y -+=，圆222:(2)1C x y +-=，动点P 到圆1C ,2C 上点的距离的最小值相等.〔1〕求点P 的轨迹方程；〔2〕点P 的轨迹上是否存在点Q ，使得点Q 到点(0)A -的距离减去点Q 到点0)B 的距离的差为4，假如存在求出Q 点坐标，假如不存在说明理由.20、〔此题总分值14分〕设a R ∈,函数()ln f x x ax =-.(1)假设2a =，求曲线()y f x =在()1,2P -处的切线方程；(2)假设()f x 无零点,求实数a 的取值范围；(3)假设()f x 有两个相异零点12,x x ,求证:212x x e ⋅>. 21、〔此题总分值14分〕设*N n ∈，圆nC ：222(0)n n x y R R +=>与y 轴正半轴的交点为M，与曲线y =的交点为1(,)n N y n，直线MN 与x 轴的交点为(,0)nA a . (1)用n 表示n R 和n a ;(2)求证:12n n a a +>>; (3)设123n n S a a a a =++++,111123n T n =++++,求证:27352n n S n T -<<. 2018年佛山市一般高中高三教学质量检测〔一〕数学试题〔理科〕参考答案和评分标准【一】选择题：〔每题5分，共40分〕 题号 1 2 3 4 5678选项 D B B A A B C C【二】填空题〔每题5分，共30分〕 9、3010、2π11、112、9413、314、213-15、π49【三】解答题:本大题共6小题,总分值80分,解答须写出文字说明、证明过程或演算步骤、16、〔此题总分值12分〕 解：〔1〕∵2A C B +=，且A B C π++=，∴3B π=…………………1分∵1411)cos(-=+C B ,∴1435)(cos 1)sin(2=+-=+C B C B …………………3分 ∴()cos cos cos()cos sin()sin C B C B B C B B C B=+-=+++⎡⎤⎣⎦7123143521411=⨯+⨯-=…………………6分〔2〕由〔1〕可得734cos 1sin 2=-=C C …………………8分在△ABC 中，由正弦定理Aa Bb Cc sin sin sin ==∴8sin sin ==A C a c ,5sin ==aAb b …………………10分 三角形面积11sin 58222S ac B ==⨯⨯⨯=…………………12分17、〔此题总分值14分〕〔1〕证明：∵⊥PB 底面ABC ，且⊂AC 底面ABC ，∴AC PB ⊥…………………1分 由90BCA ∠=，可得CB AC ⊥…………………………2分 又 PBCB B =，∴AC ⊥平面PBC …………………………3分注意到⊂BE 平面PBC ，∴AC BE ⊥…………………………4分BC PB = ,E 为PC 中点，∴BE PC ⊥…………………………5分PCAC C =，BE ⊥平面PAC …………………………6分而⊂BE 平面BEF ，∴BEF PAC 平面平面⊥…………………………7分〔2〕方法【一】如图，以B 为原点、BC 所在直线为x 轴、BP 为z 轴建立空间直角坐标系.那么)1,0,1(,)2,0,0(,)0,2,2(,)0,0,2(E P A C …………………………8分1224(,,)3333BF BP PF BP PA =+=+=.…………………………10分设平面BEF 的法向量(,,)m x y z =.由0,0m BF m BE ⋅=⋅=得0343232=++z y x ， 即02=++z y x (1)0=+z x (2)取1=x ，那么1,1-==z y ，(1,1,1)m =-.…………………………12分取平面ABC 的法向量为)1,0,0(=n那么3cos ,||||m n m n m n ⋅<>=-，故平面ABC 与平面PEF 所成角的二面角〔锐角〕的余弦值为33.……………14分 方法【二】取AF 的中点G ，AB 的中点M ，连接,,CG CM GM ，的中点为PC E ，AF PF =2，∴//EF CG .……………8分BEF EF BEF CG 平面平面⊂⊄, ，∴//CG BEF 平面.……………9分同理可证：BEF GM 平面//.又CG GM G =，∴//CMG BEF 平面平面 (10)分那么CMG 平面与平面ABC 所成的二面角的平面角〔锐角〕就等于平面ABC 与平面BEF 所成的二面角的平面角〔锐角〕ABC PB 底面⊥，2==BC AC ，⊂CM 平面ABC∴CM PB ⊥，∴CM AB ⊥…………11分 又PBAB B =，∴CM ⊥平面PAB由于⊂GM 平面PAB ，∴CM GM ⊥ 而CM 为CMG 平面与平面ABC 的交线， 又⊂AM 底面ABC ，⊂GM 平面CMGAMG ∠∴为二面角A CM G --的平面角…………12分依照条件可得2=AM ，33231==PA AG 在PAB ∆中，36cos ==∠AP AB GAM在AGM ∆中，由余弦定理求得36=MG …………13分 332cos 222=⋅-+=∠GM AM AG GM AM AMG故平面ABC 与平面PEF 所成角的二面角〔锐角〕的余弦值为33.…………14分18、〔此题总分值13分〕 解：〔1〕∵2(,)N ξμσ，(12)0.8P ξ≥=，(24)0.2P ξ≥=，∴(12)0.2P ξ<=，显然(12)(24)P P ξξ<=>…………………3分 由正态分布密度函数的对称性可知，1224182μ+==， 即每支这种灯管的平均使用寿命是18个月；…………………5分〔2〕每支灯管使用12个月时差不多损坏的概率为10.80.2-=，…………………6分 假设使用12个月时该功能室需要更换的灯管数量为η支，那么(4,0.B η，…………………10分 故至少两支灯管需要更换的概率1(0)(1)P P P ηη=-=-=041314411310.80.80.2625C C =--⨯=〔写成≈0.18也能够〕.…………………13分19、〔此题总分值13分〕解：〔1〕设动点P 的坐标为(,)x y ，圆1C 的圆心1C 坐标为(4,0)，圆2C 的圆心2C 坐标为(0,2)，……………………2分因为动点P 到圆1C ,2C 上的点距离最小值相等，因此12||||PC PC =, (3)分=23y x =-，……………………4分因此点P 的轨迹方程是23y x =-；……………………5分 〔2〕假设如此的Q 点存在， 因为Q 点到(A -点的距离减去Q 点到B 点的距离的差为4， 因此Q 点在以(A -和B 为焦点，实轴长为4的双曲线的右支上，即Q 点在曲线221(2)44x y x -=≥上，……………………9分又Q 点在直线:23l y x =-上，Q 点的坐标是方程组2223144y x x y =-⎧⎪⎨-=⎪⎩的解，……………………11分消元得2312130x x -+=，21243130∆=-⨯⨯<，方程组无解， 因此点P 的轨迹上不存在满足条件的点Q .……………………13分 20、〔此题总分值14分〕 解：方法一在区间()0,+∞上,11()ax f x a xx-'=-=.……………………1分〔1〕当2a =时，(1)121f '=-=-，那么切线方程为(2)(1)y x --=--，即10x y ++=…………3分〔2〕①假设0a <,那么()0f x '>,()f x 是区间()0,+∞上的增函数,(1)0f a =->Q ,()(1)0a a a f e a ae a e =-=-<,(1)()0a f f e ∴⋅<,函数()f x 在区间()0,+∞有唯一零点.…………6分②假设0a =,()ln f x x =有唯一零点1x =.…………7分 ③假设0a >,令()0f x '=得:1x a=. 在区间1(0,)a 上,()0f x '>,函数()f x 是增函数; 在区间1(,)a+∞上,()0f x '<,函数()f x 是减函数;故在区间()0,+∞上,()f x 的极大值为11()ln 1ln 1f a aa=-=--.由1()0,f a <即ln 10a --<,解得:1a e>.故所求实数a 的取值范围是1(,)e+∞.…………9分方法【二】函数()f x 无零点⇔方程ln x ax =即ln x a x=在()0,+∞上无实数解…………4分 令ln ()x g x x =，那么21ln ()x g x x -'=由()0g x '=即21ln 0xx-=得：x e =…………6分在区间(0,)e 上,()0g x '>,函数()g x 是增函数; 在区间(,)e +∞上,()0g x '<,函数()g x 是减函数; 故在区间()0,+∞上,()g x 的极大值为1()g e e=.…………7分注意到(0,1)x ∈时，()(),0g x ∈-∞；1x =时(1)0g =；()1,x ∈+∞时，1()0,g x e ⎛⎤∈ ⎥⎝⎦故方程ln x a x =在()0,+∞上无实数解⇔1a e>. 即所求实数a 的取值范围是1(,)e+∞.…………9分[注:解法二只说明了()g x 的值域是1,e ⎛⎤-∞ ⎥⎝⎦,但并没有证明.] (3)设120,x x >>12()0,()0,f x f x ==Q 1122ln 0,ln 0x ax x ax ∴-=-=1212ln ln ()x x a x x ∴+=+,1212ln ln ()x x a x x -=-原不等式21212ln ln 2x x e x x ⋅>⇔+>12()2a x x ⇔+>121212ln ln 2x x x x x x -⇔>-+1122122()ln x x x x x x -⇔>+ 令12x t x =,那么1t >,因此1122122()2(1)ln ln 1x x x t t x x x t -->⇔>++.…………12分 设函数2(1)()ln 1t g t t t -=-+(1)t >,求导得:22214(1)()0(1)(1)t g t t t t t -'=-=>++故函数()g t 是()1,+∞上的增函数,()(1)0g t g ∴>=即不等式2(1)ln 1t t t ->+成立,故所证不等式212x x e ⋅>成立.……………………14分 21、〔此题总分值14分〕 解：(1)由点N在曲线y =1(N n ,……………………1分 又点在圆nC上，那么222111(),nn n R R n n n n+=+==,……………………2分 从而直线MN 的方程为1n nx y a R +=,……………………4分由点1(N n 在直线MN 上得:11n na +=,将n R n=代入化简得:11n a n =++……………………6分(2)111n +>>,*1,12n n N a n ∴∀∈=++>……………………7分又11111n n +>+>+111111n n a a n n +∴=+>++=+……………………9分 (3)先证:当01x ≤≤时,11)12x x +≤+.事实上,不等式11)12x x +≤≤+22[11)]1(1)2x x x ⇔+≤+≤+22211)1)114x x x x x ⇔++≤+≤++2223)1)04xx x⇔+≤≤后一个不等式显然成立,而前一个不等式2001x x x⇔-≤⇔≤≤. 故当01x≤≤时,不等式11)12xx+≤+成立.1111)12n n∴+≤<+,……………………11分1132122nan n n∴+≤=++<+(等号仅在n=1时成立) 求和得:3222n n nn T S n T+≤<+⋅27352nnS nT-∴<≤<……………………14分。