北师大版数学七年级下册尺规作图(绝对经典)汇编

北师大版《数学》（七年级下册）知识点总结第一章整式的运算一、单项式、单项式的次数：只含有数字与字母的积的代数式叫做单项式。

单独的一个数或一个字母也是单项式。

一个单项式中，所有字母的指数的和叫做这个单项式的次数。

二、多项式1、多项式、多项式的次数、项几个单项式的和叫做多项式。

其中每个单项式叫做这个多项式的项。

多项式中不含字母的项叫做常数项。

多项式中次数最高的项的次数，叫做这个多项式的次数。

三、整式：单项式和多项式统称为整式。

四、整式的加减法：整式加减法的一般步骤：（1）去括号；（2）合并同类项。

五、幂的运算性质：（1）同底数幂的乘法：a m ﹒a n =a m+n （同底，幂乘，指加）逆用： a m+n =a m ﹒a n （指加，幂乘，同底）（2）同底数幂的除法：a m ÷a n =a m-n （a ≠0）。

（同底，幂除，指减）逆用：a m-n = a m ÷a n （a ≠0）（指减，幂除，同底）（3）幂的乘方：（a m ）n =a mn （底数不变，指数相乘）逆用：a mn =（a m ）n（4）积的乘方：（ab ）n =a n b n 推广：逆用， a n b n =（ab ）n （当ab=1或-1时常逆用）（5）零指数幂：a 0=1（注意考底数范围a ≠0）。

（6）负指数幂：11()(0)pppa aa a-==≠(底倒，指反)六、整式的乘除法：1、单项式乘以单项式：法则：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余的字母连同它的指数不变，作为积的因式。

2、单项式乘以多项式：m(a+b+c)=ma+mb+mc 。

法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的每一项，再把所得的积相加。

3、多项式乘以多项式：(m+n)(a+b)=ma+mb+na+nb 。

多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。

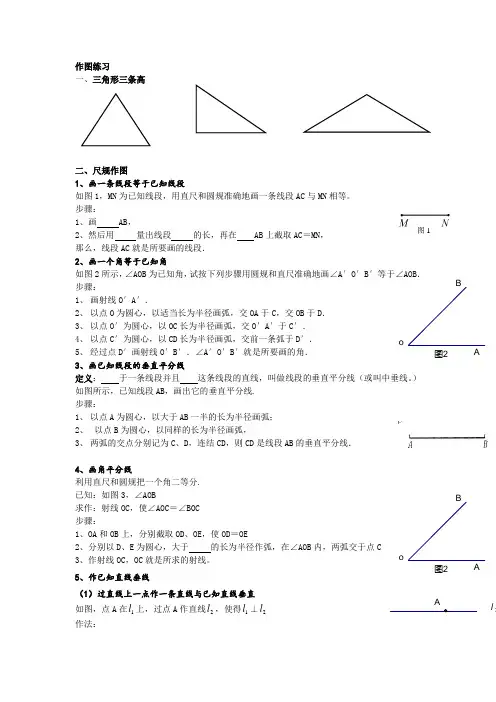
图 1作图练习一、三角形三条高二、尺规作图1、画一条线段等于已知线段如图1，MN 为已知线段，用直尺和圆规准确地画一条线段AC 与MN 相等。

步骤：1、画 AB ，2、然后用 量出线段 的长，再在 AB 上截取AC ＝MN ， 那么，线段AC 就是所要画的线段． 2、画一个角等于已知角 如图2所示，∠AOB 为已知角，试按下列步骤用圆规和直尺准确地画∠A ′O ′B ′等于∠AOB ． 步骤：1、 画射线O ′A ′．2、 以点O 为圆心，以适当长为半径画弧，交OA 于C ，交OB 于D ．3、 以点O ′为圆心，以OC 长为半径画弧，交O ′A ′于C ′．4、 以点C ′为圆心，以CD 长为半径画弧，交前一条弧于D ′．5、 经过点D ′画射线O ′B ′．∠A ′O ′B ′就是所要画的角． 3、画已知线段的垂直平分线定义： 于一条线段并且 这条线段的直线，叫做线段的垂直平分线（或叫中垂线。

） 如图所示，已知线段AB ，画出它的垂直平分线. 步骤：1、 以点A 为圆心，以大于AB 一半的长为半径画弧；2、 以点B 为圆心，以同样的长为半径画弧，3、 两弧的交点分别记为C 、D ，连结CD ，则CD 是线段AB 的垂直平分线．4、画角平分线利用直尺和圆规把一个角二等分. 已知：如图3，∠AOB求作：射线OC ，使∠AOC ＝∠BOC 步骤：1、OA 和OB 上，分别截取OD 、OE ，使OD ＝OE2、分别以D 、E 为圆心，大于 的长为半径作弧，在∠AOB 内，两弧交于点C3、作射线OC ，OC 就是所求的射线。

5、作已知直线垂线（1）过直线上一点作一条直线与已知直线垂直 如图，点A 在1l 上，过点A 作直线2l ，使得1l ⊥2l 作法：o BA图2Al 1o BA图21、以点A 为圆心，以为适当长为半径画弧交1l 于B 、C2、分别以点B 、C 为圆心，以大于21BC 为半径，在1l 一侧作弧，交点为D 3、连接AD那么，AD 就是所求的直线直线2l（2）过直线上一点作一条直线与已知直线垂直1、以点A 为圆心，以大于点A 到1l 的距离的长度为半径画弧交1l 于B 、C2、分别以点B 、C 为圆心，以大于21BC 为半径，在另一侧作弧，交点为D 3、连接AD那么，AD 就是所求的直线直线2l 练习一1、已知线段AB 和CD ，如下图，求作一线段，使它的长度等于AB ＋2CD.2、如图，已知∠A 、∠B ，求作一个角，使它等于∠A-∠B.5、如图，已知∠AOB 及M 、N 两点，求作：点P ，使点P 到∠AOB 的两边距离相等，且到M 、N 的两点也距离相等。

北师大版《数学》（七年级下册）知识点总结第一章整式的运算一、单项式、单项式的次数：只含有数字与字母的积的代数式叫做单项式。

单独的一个数或一个字母也是单项式。

一个单项式中，所有字母的指数的和叫做这个单项式的次数。

二、多项式1、多项式、多项式的次数、项几个单项式的和叫做多项式。

其中每个单项式叫做这个多项式的项。

多项式中不含字母的项叫做常数项。

多项式中次数最高的项的次数，叫做这个多项式的次数。

精典例题分析：基础例题：例1、下列整式哪些是单项式，哪些是多项式？它们的次数分别是多少？ 2223312,,21,,7,1,26,35a x y x x xy y h xy ab x by --++++- 单项式：多项式：次数： 例2、下列多项式分别有几项？每一项的系数和次数分别是多少？(1)2123x x y π--+ (2) 322223x x y y -+例3、多项式232312522a b ab b -+-是单项式___________、___________、___________、________的和，所以它是_______项式，次数最高的项的次数是___________，所以这个多项式的次数是__________，于是这个多项式称为______次_______项式例4、代数式:πab x x x abc ,213,0,52,17,52--+-中,单项式共有( )个.A.1个B.2个C.3个D.4个例5、若y b a 25.0与b a x 34的和仍是单项式，则正确的是( )A.x=2,y=0B.x=－2,y=0C.x=－2,y=1D.x=2,y=1 例6、当k = 时,多项式8313322+---xy y kxy x 中不含xy 项.例7、()()212-+-x mx x 的积中x 的二次项系数为零，则m 的值是：A ．1B ．–1C ．–2D ．2三、整式：单项式和多项式统称为整式。

四、整式的加减法：整式加减法的一般步骤：（1）去括号；去括号法则（1）括号前是“+”，把括号和它前面的“+”号去掉后，原括号里各项的符号都不改变。

第一环节：知识梳理(要点)1、尺规作图的定义： 尺规作图是指用没有刻度的直尺和圆规作图。

最基本，最常用的尺规作图通常称基本作图。

一些复杂的尺规作图都是由基本作图组成的。

2、五种基本作图：1、 作一条线段等于已知线段;2、 作一个角等于已知角；3、 作已知线段的垂直平分线；4、 作已知角的角平分线；5、 过一点作已知直线的垂线(1) 题目一：作一条线段等于已知线段。

已知：如图，线段 a .求作：线段AB 使AB = a .作法：(1)作射线AP ; (2) 在射线AP 上截取AB=a .则线段AB 就是所求作的图形。

(2) 题目二：作已知线段的中点。

已知：如图，线段 MN. 求作：点 0,使M0=N Q 即0是MN 的中点) 作法： (1) 分别以M N 为圆心，大于 占1门 的相同线段为半径画弧， 两弧相交于P , Q(2) 连接 PQ 交 MN 于 0.则点0就是所求作的MN 的中点。

(3) 题目三：作已知角的角平分线。

已知：如图，/ A0B求作：射线 0P,使/ A0P=Z B0P(即0P 平分/ A0B 。

作法：(1) 以0为圆心，任意长度为半径画弧， 分别交0A 0B于 M, N;(2) 分别以M N 为圆心，大于的线段长为半径画(3) 作射线0P 。

则射线0P 就是/ A0B 的角平分线。

(4) 题目四：作一个角等于已知角。

已知：如图，/ A0B求作：/ A ' 0 B',使 A ' 0' B' =/ A0B教学过程(1) 作射线O' A ;(2) 以O为圆心，任意长度为半径画弧，交OA于M,交OB于N;(3)以O'为圆心，以OM勺长为半径画弧，交O A'于M ;(4)以M为圆心，以MN的长为半径画弧，交前弧于N';(5)连接O' N'并延长到B'。

则/ A'OB'就是所求作的角。