当前位置：文档之家 › 频数分布表的编制举例

频数分布表的编制举例

  • 格式：ppt
  • 大小：658.50 KB
  • 文档页数：37

下载文档原格式

  / 37

合集下载

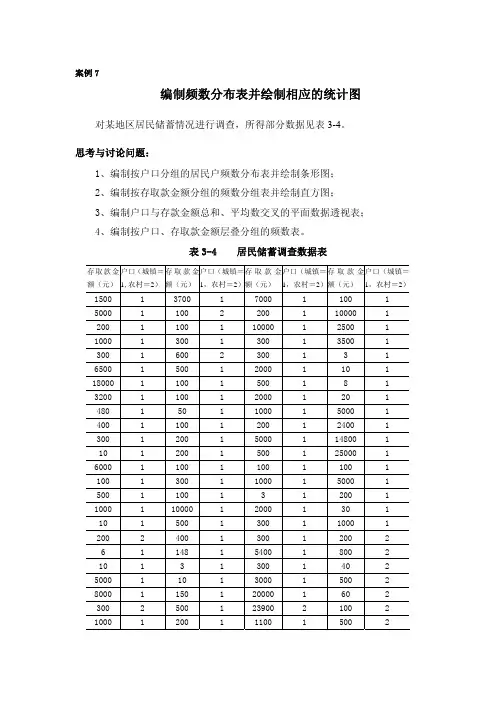
案例2编制频数分布表

案例2编制频数分布表

案例7编制频数分布表并绘制相应的统计图对某地区居民储蓄情况进行调查，所得部分数据见表3-4。

思考与讨论问题：1、编制按户口分组的居民户频数分布表并绘制条形图；2、编制按存取款金额分组的频数分组表并绘制直方图；3、编制户口与存款金额总和、平均数交叉的平面数据透视表；4、编制按户口、存取款金额层叠分组的频数表。

表3-4 居民储蓄调查数据表存取款金额（元） 户口（城镇＝1,农村＝2） 存取款金额（元） 户口（城镇＝1，农村＝2）存取款金额（元）户口（城镇＝1，农村＝2）存取款金额（元） 户口（城镇＝1，农村＝2）1500 1 3700 1 7000 1 100 1 5000 1 100 2 200 1 10000 1 200 1 100 1 10000 1 2500 1 1000 1 300 1 300 1 3500 1 300 1 600 2 300 1 3 1 6500 1 500 1 2000 1 10 1 18000 1 100 1 500 1 8 1 3200 1 100 1 2000 1 20 1 480 1 50 1 1000 1 5000 1 400 1 100 1 200 1 2400 1 300 1 200 1 5000 1 14800 1 10 1 200 1 500 1 25000 1 6000 1 100 1 100 1 100 1 100 1 300 1 1000 1 5000 1 500 1 100 1 3 1 200 1 1000 1 10000 1 2000 1 30 1 10 1 500 1 300 1 1000 1 200 2 400 1 300 1 200 2 6 1 148 1 5400 1 800 2 10 1 3 1 300 1 40 2 5000 1 10 1 3000 1 500 2 8000 1 150 1 20000 1 60 2 300 2 500 1 23900 2 100 2 1000120011100150023268250001100110002 70001100011000018002 800150150015002 1000110001500014002 1000131300012002 5001600130000130002 10001315000110002 201120021000150002 311000146001102 5190012000282 12001500013501502 10012000110001102 50011000011000152 30013600130015002 20011000150017002 3001300135001502 600220011000151 10001500120018002 301100011000122 80001300011000192 9001500150001142 1000190013000110002 3000011001200120002 60018001900115002 200130016029802 1500110002100025002 70001250001100025002 100011000110000210002 805022100013000252 3110001200252 100110001120282 10001200001800262 312000110021102 9016002100028002 8001100001400212 100012017021002 90250250112602 1000155001400210002 170011500290027002 10000155001700230002 100115001100017002500120001300015002 100150001100012002 100011500110110002 400015001600112002 80120011015002 1001700115000113002 10012601450012002 1001500011500111002 200150001500120002 10011000150016002 20013250021002 40012001200120001500011001100012000130001资料来源：薛薇，《SPSS统计分析方法及应用》，电子工业出版社，2007年4月。

40第021章频数分布表及其绘制

40第021章频数分布表及其绘制

48
46
42
49
51
50
51
56
42
59
49
48
52
42
49
55
53
51
45
47
47
47
50
48
51
51
53
46
47
57
45
46
51
46
51
47
51
55
47
52
47
48
54
47
54Leabharlann 49445354
45
48
44
48
42
47
48
50
55
50
53
56
49
50
56
41
53
53
49
44
49
48
45
52
52
46
48
51
51
53
46
47
57
45
46
51
46
51
47
51
55
47
52
47
48
54
47
54
49
44
53
54
45
48
44
48
42
47
48
50
55
50
53
56
49
50
56
41
53
53
49
44
49
48
45
52
52
46
54
50
44
53

实验一 频数表的制作(示例)-

实验一 频数表的制作(示例)-

实验一：频数分布表的编制统计学的最基本工作是收集数据。

把原始数据收集上来之后，首先要对数据进行整理并分析这些数据的特性和变化规律。

生物统计学中经常遇到的数据有两种类型，一种是连续型数据（continuous data），又称为计量数据（measurement data）；另一种是离散型数据（discrete data），又称为计数数据（count data）。

描述数据变化规律的最简单方法是将这些数据列成频数表（frequency table）。

1、离散型数据频数分布表的制作例1：检查200丛稻遗株，每丛内越冬三化螟幼虫的原始调查资料如下（见SAS程序），试编制频数分布表。

data freq_01; input x @@; cards;1 1 0 02 0 0 1 0 2 1 0 1 1 0 1 0 03 0 2 1 0 0 1 0 1 0 0 1 0 1 0 1 0 0 0 0 5 0 1 0 0 0 04 2 0 0 3 0 4 1 3 1 4 0 1 2 6 0 3 2 1 0 2 0 0 1 1 0 0 0 0 0 0 0 0 2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 02 0 1 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 0 1 0 0 0 1 1 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 1 1 0 0 0 0 0 1 0;proc freq; run;运行结果：2 连续型数据频数分布表的制作例2：在广州天河区称量106头越冬三化螟幼虫的体重（单位：毫克），根据原始资料（见SAS程序），以6毫克为组距，分成13组，第一组下限为10毫克，制作频数分布表。

Excel频数分布表制作的方法总结

Excel频数分布表制作的方法总结

Excel频数分布表制作的方法总结Excel可以使用函数或者数据透视表制作一组数据的频数分布表。

划分的组比较少时，可以使用函数"COUNTIFS(数据，条件1，条件2，...)"，相关的介绍有很多，本文对此不作赘述。

组数较多时，则建议使用函数"FREQUENCY(数据，分组)"或者数据透视表，但不同的方法中对于每组的划分有细微的差别，会导致结果不一样，下面将一一总结。

工具/原料MS Excel方法一：FREQUENCY函数1. 1以制作一次考试成绩的频数分布表为例，分数范围为0-100分，以5分为组距：2. 2先在空白处写下每组的分割点，本例为5,10,15,...,95,100，如图中F列；然后选中准备写入相应频数的区域“H2:H21”，在输公式处输入“=FREQUENCY(C2:C564,F2:F21)”，再按Ctrl+Shift+Enter，选中的区域“H2:H21”中就会出现相应的频数。

3. 3从上图中已可见，用FREQUENCY函数算出的每组频数是不包括左端而包括右端的。

例如组“(15,20]”中，成绩为15分的人数不会被算入该组，而成绩为20分的人数会被算入该组。

END方法二：数据透视表1. 1仍用上例，选择要统计的数据区域，点击菜单栏中的“插入->数据透视表”。

2. 2在数据透视表页面，将需要统计的数据（本例为“分数”）拖入“行标签”和“数值”中；点击“数值”中“求和项：分数”，选择“值字段设置”，在弹出的对话框中的“值汇总方式”选择“计数”；3. 3在得到的数据透视表中点击“行标签”列中的任意一格，便可以看到菜单中有一个“将字段分组”的选项，点击该选项后，就可以在弹出的对话框中设置要分组的起点、终点和步长，本例中应该分别设置为0,100,5。

4. 4点击确定后，便可得到所要的频数分布表，如下图中左边的表。

注意，用数据透视表统计的频数分布中，可能会缺少频数为0的组（如本例中得到的结果中缺少“5-10”这一组，），因此最后需要检查一遍各分组，添上缺少的组，相应的频数为0。

定量资料数据的统计描述

定量资料数据的统计描述

f lg X lg f
1
X1，X2…Xn 为各组段的滴度或滴度倒数。 f1，f2…fn分别为各组段的频数。
例2-6 52例慢性迁延性肝炎患者的HBsAg滴度 数据见表2-4，求其平均滴度。
2 1.20412 7 1.50515 ... 7 2.7027 G lg 1 52 lg 1 108.06977/ 52 lg 2.7017 119.74705
①两端的组段应分别包含最小值或 步骤： 最大值； （1） 求全距：（极差） R=29.64-7.42=22.22 ②尽量取较整齐的数值作为组段的 端点，便于对数据进行表述； （2） 定组段数与组距 ： 8～15个组段，组距i=全距/组段数 ③组距以相等为宜。 （3） 划组段：以一个稍小于或等于最小值的整数作为第一个
理的各种因素在个体之间都不会完全相同，即个体间存在差
异，因此导致某地18-35岁健康男性居民血清铁含量不会完全 相同，而是呈现或大或小的离散趋势。
一、描述集中趋势的统计指标
平均数：描述一组同质计量资料的集中趋势；反映一组观察值 的平均水平。 常用的平均数有算术均数，几何均数和中位数。 （一）算术均数(mean)：简称均数，总体均数用希腊字母µ 表
四、频数分布的类型
对称分布型：指集中位置在正中，左右 两侧频数分布大体对称。
偏态分布型：指集中位置偏向一侧，频数 分布不对称。 正偏态分布：集中位置偏向数值小的一侧。
偏态分布型
频数分布
负偏态分布：集中位置偏向数值大的一侧。
频数表的用途
1. 揭示频数分布的分布特征和分布类型。文献中常 将频数表作为陈述资料的形式。
图中横轴为血清铁含量，纵轴为频率密度，直条面 积等于相应组段的频率。

2.1 频率分布表与频率分布图

2.1 频率分布表与频率分布图
26～ 28～30 合计
频数 (2)
1 3 6 8 12 20 27 18 12 8 4 1 120
频率(%) (3) 0.83 2.50 5.00 6.67 10.00 16.67 22.50 15.00 10.00 6.67 3.33 0.83
100.00
累计频数 (4) 1 4 10 18 30 50 77 95 107 115 119 120 —
100.0
累计频率(%) （5） 4.2 11.5 22.9 36.5 63.5 87.5 100.0
4
频率分布 图
30 频 率 25 (%)
20
15
10
5
0
0
1
2
3
4
5 >5
产前检查次数
图21 某地96名妇女产前检查次率分布
横坐标：产前检查次数； 纵坐标：频率, 检查k次的妇女 所占的比例（%） 等宽矩形长条：高度为检查次 数的频率
试编制血清含量的频率分布表。
6
编 制 步 骤 ： 2
计 算 全 距 （range，R），又 称 极 差
（1）找• 出R = 最最大 值小－值最=小7值.4=229.647.42 = 22.22
3
确 定 组 段 数最与大组值距 = 29.64
•组 段 数 一 般 在 10 左 右 下 限 ： 组 段 的 左 端 点
第二章 定量资料的统计描述
一、频率分布表与频率分布图
定
义
当变量值个数较多时，对各变量值出现的频率列表即为频 率分布表（frequency distribution table），简称频率表。
频率分布表的图形表示即为频率分布图。
2
1、离散型定量变量的频率分布

5-2 编制频率频数分布表客户调查与数据分析

5-2 编制频率频数分布表客户调查与数据分析
组对应的频数分别为：2、5、8、12、6、2。
三、组距式分布数列
任务1 【步骤5】绘制频率频数分布表。
三、组距式分布数列
任务2：将上述表格制成Word表格。 【步骤1】新建word文件，点击“插入”菜单，选择“表格”
菜单中的“插入表格”，输入“行数”为“8”，输入“列数” 为“3”，并输入相关内容。 【步骤2】点击表格左上角的十字箭头，选择整个表格，点击 “表格工具”中的“设计”，选择“擦除”按钮。 【步骤3】将两边的竖线以及组与组之间的横线用橡皮擦除。
以是非数量标志。
二、分布数列及其分类
2.分布数列分类 （1）变量分布数列 按照数量标志进行分组所得到的分布数列，称为变量
分布数列。 如按照房型需求、成交总价等变量分组就是变量分布
数列。
二、分布数列及其分类
2.分布数列分类 （1）变量分布数列
房型需求频率频数分布表
二、分布数列及其分类
2.分布数列分类 （2）品质分布数列 按照非数量标志进行分组所得到的分布数列，称为品
三、组距式分布数列
组距式分布数列简称组距数列，是指在变量数列中的 每一个组，并不是由一个变量值来表示，而是一定数 值范围形成的数列。
三、组距式分布数列
江苏省第6次全国人口普查人口分布频率频数分布表
上表中的分组变量是人口年龄，而每组的年龄不是一个数值， 而是年龄段，因此这样的分布数列就称为组距式分布数列。
不超过10%。1.5/73.5=2%，小于10%，组距75可以采用。
三、组距式分布数列
任务1 如果分5组，组距=294/5=58.8。为了让组限整齐，组距取整
为60，组限是10的倍数。 误差为1.2。1.2/58.8=2%，小于10%，组距60可以采用。

用Excel_作频数分布表和统计图表

用Excel_作频数分布表和统计图表

“健力芬达682.00%雪碧9100.00% 二、用Excel作数值数据的频数分布表和直方图例2 某班50名学生的统计学原理考试成绩数据如下：798878507090547258728091959181726173978374616263747499846475657566758567697586597688697787步骤一：输入数据并排序（一）打开Excel工作簿，把本例中的数据输入到A1至A50单元格中。

（二）对上述数据排序。

结果放到B1至B50。

具体步骤如下：1.拖曳鼠标选中A1：A50单元格区域。

在该处，单击鼠标右键，选中“复制”命令。

2.拖曳鼠标选中B1：B50单元格区域。

在该处，单击鼠标右键，选中“粘贴”命令。

3.再次选中B1：B50，选择“数据”下拉菜单中的“排序”选项。

出现对话框，选中按递增 排序即可。

4.单击确定。

步骤二：指定上限在C3至C7单元格中输入分组数据的上限59，69，79，89，100。

I 提示：Excel在作频数分布表时，每一组的频数包括一个组的上限值。

这与统计学上的“上限不在组”做法不一致。

因此50-60这一组的上限为59。

以此类推。

步骤三：生成频数分布表和直方图（一）选择“工具”下拉菜单中的“数据分析”选项。

出现该对话框。

（二）在“数据分析”对话框种选择“直方图”。

（三）当出现直方图对话框时，1.在“输入区域”方框中输入数据所在单元格区域B1：B50。

2.在“接受区域”方框中输入分组数据上限所在单元格区域C3：C7。

3.在“输出区域”方框中输入D3，表示输出区域的起点。

4.在输出选项中，选择“输出区域”、“累计百分比”和“图表输出”。

（四）点击确定。

（五）为了便于阅读，单击频数分布表中的有“接受”字样的单元格，输入“考试成绩”；同样，用50-60代替频数分布表中的第一个上限值59，60-70代替第二个上限值69，以此类推，最后，用90-100代替频数分布表中最后一个上限值100。

频数分布表和频数分布直方图

频数分布表和频数分布直方图

4.25~4.55 6
0.12
4.55~4.85 23
0.46
4.85~5.15 18
0.36
5.15~5.45 1
0.02
合计
50
1.00
（1）、请你把上表补充完整；
（2）、请你根据频数分布表，画出频数分布直方图
如果视力在4.85以下就属于不正常范围，
人数
那么请你分析一下我们学校的视力情况，
28
(3)确定分点; 确定分点的方法有多 种。通常为了使得每 个数据都落在相应的 组内，可取比数据多 一位小数来分组;
(4)列频数分布表： 把数据划记到相应的 组中，统计每组中相 应数据出现的频数.
(5)画频数分布直方图.注意：各个“条形”之间就 应该是连续的，不应该有间隔，当各组的组距相等 时，所画的各个条形的宽度也应该是相同的；
这就是频数分布表
53 65 74 77
成绩段 49.5~ 59.5~ 69.5~ 79.5~ 89.5~
59.5 69.5 79.5 89.5 99.5
频数记录
正 正正 正正 正
频数
2
9
10 14
5
人数
16
15 14 13 12 11 10
9 8
7 6 5 4 3 2 1
这就是频数 分布直方图
49.5 59.5 69.5 79.5 89.5 99.5 分数
在怎这样组描数述据、中分1析6这3c5m0的名频学数生是身多高少的？分布情况呢？
频率呢？
7.4 频数分布表和频数分布直方图
某中学为了了解八年级学生身高的范围和整体分布 情况，抽样调查了八年级50名同学的身高，结果如下 （单位：㎝） 150 148 159 156 157 163 156 164 156 159 169 163 170 162 163 164 155 162 153 155 160 165 160 161 166 159 161 157 155 167 162 165 159 147 163 172 156 165 157 164 152 156 153 164 165 162 167 151 161 162

(完整)频数分布表和频数分布图

(完整)频数分布表和频数分布图

频数分布表与频数分布图频数是指某一随机事件在n次试验中出现的次数。

各种随机事件在n次试验中出现的次数分布就称为频数分布。

对一批数据，将其频数分布用表格的形式表示出来就构成了频数分布表。

(1）编制频数分布表的步骤编制频数分布表是数据整理的基本方法，下面我们结合一个实例来说明频数分布表的编制步骤。

例1．一次物理测验之后，某班48位同学的成绩如下.86 77 63 78 92 72 66 87 75 83 74 47 83 81 76 82 97 69 82 88 7167 65 75 70 82 77 86 60 93 71 80 76 78 57 95 78 64 79 82 68 7473 84 76 79 86 68；根据这一成绩编制频数分布表，其具体步骤是：①求全距（用R表示)。

全距是原始数据中的最大值与最小值之差，即R=max{xi｝-min｛xi｝。

式中R是全距，max｛xi}为这批数据中的最大数，min{xi｝为这批数据中的最小数.在本例中,max{xi｝=97，min｛xi}=47，因此R=97—47=50.②定组数（用K表示）。

根据全距决定组数（K）。

组数就是对这批数据分组的个数。

一般而言，组数以10组为宜，多至20组，少至5组。

若组数太多，便会失去实行分组化繁为简的作用；若组数太少,又会引起计算结果的失真。

组数与数据的个数有关,若数据多时,要分10组以上；数据少时，可分5—10组。

③定组距（用i表示）。

组距就是每一个组内包含的间距，即组距（i）是指每个小组的组上限（即组的终点值）与组下限（即组的起点值）之间的距离.显然,在一批数据中,组距一般是相同的.组数与组距有关,组距越小,则组数越多；组距越大,则组数越少.根据上面的讨论,我们得到全距R、组距i、组数K三者之间的关系即i=或K=根据上式，由全距R、组距i决定组数时，将全距R除以组距后取整数即得组数i。

在本例中，全距R=50,若取组距i=5，则组数K=10.④列组限。

【资料】频数分布表课件汇编

【资料】频数分布表课件汇编

2 (X= )2 N
(2)样本方差:
(XX)2
S2
n1
▪ 方差性质:方差越大说明数据的变异越大 ▪ 自由度(degree of freedom,简记为DF)
(1)定义:随机变量能自由取值的个数 (2)计算公式:υ=n-限制条件个数
▪ 例:有一四个(n=4)数据样本,受到 的条件限制,在自由确定4,2,5三个数据 后,第四个数只能是9, 因而 υ=n-1=3 。
三、中位数（median) 中位数是将一组观察值按大小顺序排列后， 位次居中的观察值。 （一）计算方法
1.直接法：适用于样本量较小的计量资料。 当 为奇数时
当 为偶数时
2.频数表法（百分位数法）：适用于样本量 较大的计量资料，如频数表资料。
（二）中位数的应用注意事项 1.中位数可用于各种分布的资料。 2.中位数不受极端值的影响，因此，实际 工作中主要用于： （1）偏态分布资料 （2）端点无确切值的资料 （3）分布不明确的资料
常用的平均数——算术平均数、几何均 数、中位数
一、算术均数
算术均数简称均数（mean)，描述一组同质 资料的平均水平。
总体均数：
样本均数：
（一）计算方法 1.直接法：适用于样本量较小的计量资料。
2.加权法：适用于样本量较大的计量资料。
（二）均数的特性 1.各观察值与均数之差（离均差）的总 和等于零，即
频数分布表课件
第一节 频数分布表和频数分布图
频数表适用于: 观察例数较多的计量资料。 一、频数分布表:
频数（frequency):不同组别内的观察
值个数称为频数，表示观察值在各组内出 现的频繁程度。
频数表：将分组标志和相应的频数列表，
即为频数分布表，简称频数表。

卫生统计学--集中趋势的统计描述(第一节 频数分布)

卫生统计学--集中趋势的统计描述(第一节 频数分布)

脉搏组段
(1) 56～ 59～ 62～ 65～ 68～ 71～ 74～ 77～ 80～ 83～85
合计
组中值（Xi）
(2)
57.5 60.5 63.5 66.5 69.5 72.5 75.5 78.5 81.5 84.5
频数， fi (3)
2 5 12 15 25 26 19 15 10 1
N＝∑f 130
料，特别是服从对数正态分布资料
第二节 集中趋势的描述
（三） 中位数 11个大鼠存活天数：
4，10，7，50，3，15，2，9，13，60， 70 平均存活天数? 1、中位数（median）
第二章 集中趋势的 统计描述
第一节 频数分布
第一节 频数分布
一、数值变量的频数分布 1、频数：即变量值的个数 2、频数表：同时列出观察指标的可能取值区间
及其在各区间出现的频数。 3、频数分布通常用频数分布表和频数分布图来
表示。 注意：了解频数分布是分析资料的第一步。 （一）频数分布表（frequency table）
之间，尤以组段的人数71~（次/分）最多。 且上下组段的频数分布基本对称。
3．便于发现一些特大或特小的可疑值
组段
频数 f
(1)
(2)
2.30～
12.60～02.90～03.20～
0
3.50～
17
3.80～
20
4.10～
17
4.40～
12
4.70～
9
5.00～
0
5.30～
0
5.60～5.90
8
合计
图 2-1 130 名 正 常 成 年 男 子脉搏的 频 数 分 布
第一节 频数分布

医学统计学--第二章 计量资料的统计描述

医学统计学--第二章 计量资料的统计描述

4.13 4.28 4.91 3.95 4.23 3.75 4.57 3.51
2.78 3.26 3.18 5.08 3.57 3.98 3.80 3.86
4.26 3.50 3.68 4.53 4.83 4.13 3.93 3.02
3.58 2.70 4.83 3.92 3.52 4.26 3.78 3.70
1
lg X ) lg (
n
1
ቤተ መጻሕፍቲ ባይዱ
lg10 lg 20 lg 40 lg 40 lg160 ( ) 34.8 5
（2）加权法 公式：
G lg (
1
f lg X f
)
例2-5 69例类风湿关节炎（RA）患者血清EBV-VCAlgG抗体滴度的分布见表2-4第(1)、(2)栏，求其平均 抗体滴度。
三、频数表和频数分布图用途
1．描述频数分布的 类型 （1）对称分布 ：若 各组段的频数以频数 最多组段为中心左右 两侧大体对称，就认 为该资料是对称分布
25
20 15
Æ µ Ê ý
10 5
0
2.45
3.05
3.65
4.25
4.85
5.45
6.10
Ñ Ç × µ ¹ ´ £ mmol/L£ ª å Ü ¨Ì ¼ ¨ ©
G 公式： X 1 X 2 X n
n
或
G lg
1
lg X ) (
n
例2-4 某地5例微丝蚴血症患者治疗七年后用间接 荧光抗体试验测得其抗体滴度倒数分别为，10， 20，40，40,160，求几何均数。
G 10 20 40 40 160 34.8
5
G lg

7编制频数分布表

7编制频数分布表

第7课时编制频数分布表教学目标1、掌握编制频数(率)分布表的步骤2、能对一组数据进行统计，会根据确定组数的经验法则合理分组3、学生通过对数据的整理、制表和分析，更好地理解和掌握频数和频率的概念;从中体会数据有多种不同的表示方法，能分析讨论得出各种方法的优缺点;逐步学会用多种方法来表示统计数据重点难点重点：编制频数(率)分布的步骤难点：确定组数、组距及每一组的上下界限教学过程一、复习引入前面几节课，我们己经知道要全面地掌握一组数据，了解数据的分布情况，通过编制频数(率)分布表可以给我们提供关于数据的更多信息，怎样编制频数(率)分布表呢?二、创设情境小明调查了他住的那栋宿舍30户职工家庭月收人情况，见教科书P132"统计活动"根据小明的统计表能直观、明确地获知月收人情况吗?如果不能，怎么办呢?三、探究新知分析:1.小明给出的数据是没有经过整理的数据，数据多，而且数量表示上不简单也不直观，各个数据所占人数多少也看不出来，要经过计算才知道.2.看来根据学生现在已有的经验所绘制的统计图不一定能很好地反映频数的分布状况.怎么办呢?(在编制频数分布表时，若不同的数据不多，可以直接算出每种数据在数据组中出现的次数，然后列表表示;若不同的数据较多，分布比较零散，可以先适当分组，计算数据在各组中出现的频数，然后列表表示.)3.引导学生观察、分析、创造出新的编制方法:分组划定数据取值的不同范围，然后统计数据在各范围中出现的频数引导学生自己动手设计，再与同伴交流，最后统一具体做法如下:(1)分组①确定最大值M和最小值m.②确定组数的各组界限.为了分组的方便，我们取略小于m的数作为第一组的下限，例如取720;而取略大于m 的数作为最后一组的上限，例如取960.再适当分组(960-720=240)，可分为6组，每组的长度(240÷6=40)即为组距.故所分6组为:720~759,760~799.800~。

实验一计量资料频数表的整理与统计描述

实验一计量资料频数表的整理与统计描述

实验一计量资料频数表的整理与统计描述一、测得12人的血红蛋白含量（g/L）121，118，130，120，122，118，116，124，127，129，125，132。

请计算其均数，几何均数，中位数，标准差，极差，变异系数。

二、某地101例30~49岁健康男子血清总胆固醇值（mmol/L）测定结果如下：4.77 3.37 6.14 3.95 3.56 4.23 4.31 4.715.69 4.12 4.56 4.375.396.30 5.217.22 5.54 3.93 5.21 6.51 5.18 5.77 4.79 5.12 5.20 5.10 4.70 4.74 3.50 4.69 4.38 4.89 6.25 5.32 4.50 4.63 3.61 4.44 4.43 4.25 4.03 5.85 4.09 3.35 4.08 4.79 5.30 4.973.18 3.97 5.16 5.10 5.864.795.34 4.24 4.32 4.776.36 6.384.885.55 3.04 4.55 3.35 4.87 4.17 5.85 5.16 5.09 4.52 4.38 4.31 4.58 5.726.55 4.76 4.61 4.17 4.03 4.47 3.40 3.91 2.704.60 4.095.96 5.48 4.40 4.55 5.38 3.89 4.60 4.47 3.64 4.345.186.14 3.24 4.90 3.051、编制频数分布表并绘制直方图，简述其分布特征。

2、选择适当的集中趋势指标、离散趋势指标并计算。

三、某市1974年为了解该地居民发汞（μmol/kg）的基础水平，为汞污染的环境监测积累资料，调查了留住该市一年以上，无明显肝、肾疾病，无汞接触史地2382、计算均数X、几何均数G和中位数M，何者较大？为什么？何者用于说明本资料的集中位置较适合？3、选用何种指标描述其离散程度较好？请计算。

1-2 编制频率频数分布表

1-2 编制频率频数分布表
三、分布数列的分类 （2）变量分布数列 ② 组距式分布数列 再次，确定组限，组限即组距的上下限，一般也是整数，如
100～150。 最后，统计各组的频数。在统计每组的频数时，要遵守一个
原则，每组上限不在本组内；最后，绘制频率频数分布表。
1-2 编制频率频数分布表
三、分布数列的分类 子任务1：某市35 个旅游网点某月销售额（单位：万元）资
比如在客户年龄统计中，由于客户人数众多，如果不对年龄 进行分组，很难找出年龄分布的规律，为了更好地反映数据 的特征，常用的处理方法是编制统计表格汇总数据。
1-2 编制频率频数分布表
二、分布数列及其分类 1.分布数列 分布数列是指将数据在统计分组的基础上，汇总各组内的
频数和频率，形成总体中个体在各组间的分布。 分布数列是统计整理的成果，揭示了总体的特征。
1-2 编制频率频数分布表
三、分布数列的分类 （2）变量分布数列 ② 组距式分布数列 其次，确定分组与组距。组距式分布数列中一般可以分为4～
12 组，即组数一般为4～12，每组的波动范围可以用全部的 波动范围除以组数，即组距=全距÷组数。组距一般要求是整 数，如5、10、20、50 等。
1-2 编制频率频数分布表
1-2 编制频率频数分布表
三、分布数列的分类
（1）品质分布数列
房型需求频率频数分布表
1-2 编制频率频数分布表
三、分布数列的分类 （2）变量分布数列 ① 单项式分布数列 变量分布数列中每一组都是由单一的组值表示，则称为单项
式分布数列，如按照房间数量分组就是变量分布数列，因为 每一组的取值只能是1、2、3、4……
1-2 编制频率频数分布表
三、分布数列的分类 （2）变量分布数列 ① 单项式分布数列

3.1频数分布表(开课用)

3.1频数分布表(开课用)
请说出每分脉搏跳动次数在 82.5—87.5次这一范围内的人数？
请说出每分脉搏跳动次数在 82.5—87.5次这一范围内的人数？
某班20名学生每分脉搏跳动次数频数分布表
组别(次) 67.5～72.5 72.5～77.5 77.5～82.5
划 记
正
频数（人数） 2 4 9
82.5～87.5 87.5～92.5 合计
绘制频数分布表的一般步骤：
（1）求极差；
（2）确定组距、组数； （3）分组；
（4）列频数分布表。
别忘记写标题！！！
为了了解班级学生在校午餐所需的时 间，抽查了20名同学午餐所花的时间，获
得如下数据（单位：分）： 10，12，15，10，16，18，19，18，20，38，
22，25，20，18，18，20，15，16，21，16。
3 2 20
抽查某班20名学生每分脉搏跳动次数，获得如下数据（单位：次）：
81 78 80 72
73 85 89 83
77 80 82 77
79 68 81 79
80 90 84 75
1.求极差 最大值 － 最小值 ＝ 极差 极差为：90－68＝ 22(次)
极差为： 22次
68～73 69～74 73～78 78～83
组距
5
？
3.分组
极差为： 22次
81 78 80 72
组别（次） 人数 2 67.5～ 72.5
72.5～ 77.5 77.5～ 82.5 82.5～ 87.5
87.5～ 92.5
4 9
3 2
77 79 80 80 68 90 70 82 81 84 77 79 75 边界值怎么取？ 为了使数据不落在各组的 边界上，在组距不变的情 况下，一般将边界值比实 际数据多取一位小数 2 = 极差 = 组数= 5 的整数部分 ＋1 0.4 组距

熟练使用SPSS创建频数分布表

熟练使用SPSS创建频数分布表

熟练使用SPSS创建频数分布表
试验内容:
[试验]
下表为10个人对两个不同的问题作出的回答（回答为“Yes”或“No”）后得到的数据，利用SPSS为该数据创建频数分布表。

表1 调查结果表
sample1sample2gender
No Yes女
Yes No女
No Yes女
No No女
No No女
Yes Yes男
Yes Yes男
Yes Yes男
No Yes男
No Yes男
1.在数据输入区域输入需要进行描述性统计分析的数据,如下图所示。

图1 数据录入界面
2.选择“analyze”下拉菜单。

3.选择“Descriptive Statistics”选项。

4.在子菜单中选择“Frequencies”。

图2 选择分析工具5.在左侧选择需要分析的参数添加到右侧的分析列表。

图3 选取变量进入右侧列表6.在“Statistics”选项中选择需要进行分析的参数。

图4 设置分析参数SPSS输出的结果:
图5 分析结果显示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
在一个组中（组距分组中）最大的可能值就
是该 组的上限；最小的可能值就是该组下限。
1、选择分组标志的原则 （1）要根据调查目的和任务选择分组标志
调查对象具有若干特征，都可作为分组 的依据，如何从这些特征中选择作为分组依 据的标志，就应该根据调查的目的和任务来 选择。
（2）要选择能够反映研究对象本质的标志 在研究对象所具有的特征中，有的是 事物的本质特征，有的是一般特征，我们 应从中选择本质特征作为分组标志。同时 要注意将事物的本质特征作为分组标志时， 应注意社会发展变迁的影响。
• 2.统计图的制作 统计图是表现数字资料的一种重要形式， 它具有形象、生动、直观、概括、活泼、 醒目等特点，可使读者一目了然，具有较 强的吸引力和说服力。 按照表现形式的不同，统计图可分为条形 图，直方图，饼图，环形图茎叶图和箱线 图和折线图四种类型。
1. 分组数据：直方图
概念：用矩形的宽度和高度（面积）来表示频 数分布的图形，叫直方图。 直方图一般可用横轴表示数据分组纵轴 表示频数或频率，这样各组和相应的频率就 形成一个矩形，即直方图。 对于等距分组可以用矩形的高度直接表示频数 分布； 对于不等距分组一般用矩形的面积来表示频数 分布，这时需要计算频数密度或频率密度。
（3）应多角度选择分组标志
事物或现象的分组标志不是唯一的，从 多角度选择分组标志，会使我们对社会现象 的认识更加深入。
分组方法
分组方法
单变量值分组 （适用于离散 变量）
组距分组
等距分组
异距分组
组距分组
•将变量值的一个区间作为一组 适合于连续变量 适合于变量值较多的情况 要遵循“不重不漏”的原则 采用等距分组，也可采用不等距分组
3. 用Excel制作频数分布表
等距分组表
(上下组限重叠)
三、汇总 • 所谓汇总，就是根据研究目的把分组后的 数据汇集至有关表格中，并进行计算和加 总，以集中、系统的形式反映调查对象总 体的数量情况。 汇总的方法，可分为手工汇总和电子计算 机汇总两大类。
四、制作统计表和统计图 • 汇总的数字资料，一般都要通过表格或图 形表现出来，为此，就要制作统计表和统 计图。 1.统计表的制作 （1）统计表的结构 （2）统计表的分类 （3）制作统计表应该注意的问题
直方图可观察一组数据的分布状况，但没有给出具体的数值； 茎叶图既能给出数据的分布状况，又能给出每一个原始数值，保 留了原始数据的信息。
未分组数据—茎叶图(例题分析)
分析市场调查资料
• 一、调查资料分析的意义
• 1、资料分析的含义 • 指将收集到的各类信息资料，按照一定的 程序和方法，进行分类计算、分析和选择等，使 之成为适用的信息资料的过程。 • 指通过对市场调查所获得的资料分解成较 为简单的组成部分，辩析出这些部分的本质属性 和彼此之间的关系，从而对研究的事物、现象有 更清晰、更本质的认识和把握的过程。
市场调查资料整理
二、调查资料分析的基本原则
及时性
1.
2.
3. 4.
5.
6.
用于显示未分组的原始数据的分布。 由“茎”和“叶”两部分构成，其图形是由数字组成的。 以该组数据的高位数值作树茎，低位数字作树叶 树叶上只保留一位数字。 对于 n(20 n 300) 个数据，茎叶图最大行数不超过 L = [ 10 × lg n ]。茎叶的行数可以拉长。 茎叶图类似于横置的直方图，但又有区别：
第三、 数字资料的整理
数字资料的整理，一般要经过检验、分组、 汇总、制作统计表或统计图等四个步骤。 一、检验 检验，就是检查、验证各种数字资料是否完 整和正确。 数字资料的正确性检验，一般采用三种方法： 1.经验判断 2.逻辑检验 3.计算审核
二、分组 就是根据社会调查研究的目的和要 求，按照一定的标志，将所研究的事物 或现象区分为不同的类型或组的一种整 理资料的方法。
浅谈市场调查资料的整理与分析
社会调查资料的整理
第一、资料整理的步骤和内容
1、步骤
1）资料审核
2）资料的编码和登录
3）资料的分组
4）资料的汇总
5）制作统计图和统计表
2、审查内容
1）资料的真实性
2）资料的准确性
3）资料的完整性
• 第二、整理资料的意义 整理资料，就是根据调查研究的目的，运 用科学的方法，对调查所获得的资料进行审 核、检验、分类、汇编等初步加工，使之系 统化和条理化，并以集中、简明的方式反映 调查对象总体情况的工作过程。 • 整理资料的重要意义在于： 1.它是提高调查资料质量及其使用价值的必 要步骤。 2.它是研究资料的重要基础。 3.它是保存资料的客观要求。
3. 统计出各组的频数并整理成频数分布表
频数分布表的编制 (例题分析)
【例】某电 脑 公 司 2007 年前四个月 各天的销售 量数据（单 位：台）。 试对数据进 行分组。
原始 数据
频数分布表的编制 举例(步骤)
1. 确定组数 2. 确定各组的组距： 组距＝( 237 - 141)÷ 10=9.6 10
①根据统计研究的需要，将原始数据按照不 同的数量级别划分为不同的组别的过程。 ②分组以后的数值型数据称为分组数据。 ③数值型数据分组可分为单变量分组和组距 分组。
1）把整个数据中，每一数据值（变量值）作为
一 组，这样的分组称为单变量分组。
2）将全部变量值一次划分若干数量区域，并将
在此区域的变量值作为一组称为组距分组。
~ ~ ~ ~ ~
组距分组 (步骤)
1. 确定组数：组数的确定应以能够显示数据的分 布特征和规律为目的。建议组数=1+lg N/lg2
2. 确定组距：组距 (Class Width) 是一个组的上限与下 限之差，可根据全部数据的最大值和最小值及所分 的组数来确定，即 组距＝( 最大值 - 最小值据绘制）
我一眼就看出 来了，销售量 在 170 ～ 180 之间的天数最 多!
频 数
30 25
直方图下的面 积之和等于1
(天) 20 15
10
5
140 150 160 170 180 190 200 210 220 230 240
某电脑公司销售量分布的直方图
2.未分组数据：茎叶图