纠错编码习题解答汇总
- 格式:doc
- 大小:387.04 KB
- 文档页数:14

信息论与纠错编码课后练习题含答案前言信息论与纠错编码是计算机科学与通信工程中非常重要的领域。
本文档将介绍该领域中一些常见的练习题,并且配有答案供参考。
第一部分:信息论题目一假设在信道中有两个符号a和b,其发生概率分别为P(a)和P(b)。
则符号a和b在信道中的平均传输信息量为多少?答案一符号a和b分别传输的信息量为 $I(a)=-\\log_2P(a)$ 和 $I(b)=-\\log_2P(b)$。
因此,符号a和b在信道中的平均传输信息量为:$$I_{avg}=\\frac{1}{2}(I(a)+I(b))=\\frac{1}{2}(-\\log_2P(a)-\\log_2P(b))=-\\frac{1}{2}\\log_2(P(a)P(b))$$题目二以上一题中的符号为例,若P(a)=0.2,P(b)=0.8,则符号b传输的信息量是符号a的多少倍?答案二符号a和b的信息量为:$$I(a)=-\\log_2P(a)=-\\log_2(0.2)=2.322$$$$I(b)=-\\log_2P(b)=-\\log_2(0.8)=0.321$$因此,符号b传输的信息量为符号a的 $\\frac{0.321}{2.322}=0.138$ 倍。
第二部分:纠错编码题目三对于一个二元码,其生成矩阵为$G=\\begin{bmatrix}1&0&1\\\\0&1&1\\end{bmatrix}$。
请问该码的最小汉明距离是多少?答案三对于二元码,最小汉明距离等于最小权值。
该码的所有码字是:$$\\begin{bmatrix}1&0&0\\end{bmatrix},\\begin{bmatrix}0&1&0\\end{bmatrix},\\begin{bmatrix}1&1&0\\end{bmatrix},\\begin{bmatrix}0&0&1\\end{bmatrix},\\begin{bmatrix}1&0&1\\end{bmatrix},\\begin{bmatrix}0&1&1\\end{bmatrix},\\begin{bmatrix}1&1&1\\end{bmatrix},\\begin{bmatrix}0&0&0\\end{bmatrix}$$因此,该码的最小汉明距离是d min=1。

1、供食用的活珍珠鸡(重量大于2千克)归类步骤:①活珍珠鸡属于活动物,应到第一章“活动物”中去查找。
然后按列名归入品目0105“家禽,即鸡、鸭、鹅、火鸡及珍珠鸡”。
②由于重量大于2千克,故归入一级子目“其他”③由于珍珠鸡未在二级子目列名,故应归入二级子目“其他”④由于题目未明确是“改良种用”,故归入三级子目“其他” 最后按列名归入四级子目01059993“珍珠鸡”提示:本题的关键是子目的判断2、冷冻的煮熟甜玉米粒,塑料袋装归类步骤:根据第十章章注二和第七章注二可知,甜玉米属于蔬菜。
由于冷冻的著述甜玉米粒符合品目0710条文“冷冻蔬菜(不论是否曾煮熟)”的规定,所以应归入品目0710。
然后按列名归入一级子目07104000“甜玉米”,所以正确的商品编码是07104000。
提示:本题的关键是不能误认为煮熟的甜玉米就归入第20章。
3、精制的玉米油归类步骤:玉米油属于植物油,故应到第十五章“动、植物油、脂及其分解产品;精制的食用油脂;动植物蜡”中找。
由于玉米油在品目1507~1514没有列名,故应归入1515“其他固定植物油、脂及其分离品,不论是否精制,但未经化学改性的”;然后按列名归入一级子目“玉米油及其分离品”由于题目中的玉米油是“精制的”故归入二级子目15152900“其他” 。
正确的商品编码是:151529004、煮熟的猪肝罐头归类步骤:由于猪肝已煮熟属于深加工,故应到第16章“肉、鱼、甲壳动物及其他水生无脊椎动物的制由于猪肝属于食用的杂碎,故归入1602;在归入一级子目时,肝可归入两个“动物肝的”和“猪的”按“具体列名”的总规则,应归入“动物肝的” 。
所以最后的商品编码是:16022000。
提示:本题关键是子目归类时首先要确定一级子目,而不能直接按“猪的罐头”误归入16024910,其次是确定一级子目时要正确运用归类总规则三(一)的“具体列名优先”的原则。
5、菠萝原汁中加入20%的水组成的混合物归类步骤:菠萝原汁属于品目2009“水果汁”,但是如果加水进行了稀释,则成了人们习惯饮用的饮料(其他果汁也是如此),故应归入第22章“饮料、酒及醋” ;然后按饮料归入品目2202“其他无酒精饮料,但不包括品目2009的水果汁或蔬菜汁” ;由于由果汁配成的饮料不属于一级子目“加味、加糖或其他甜物质的水,包括矿泉水及汽水”的范围,故归入22029000。

第6章习题参考答案6.6 解:(1)首先求联合概率矩阵111412611164121111264XYP ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦最大后验概率准则即最小错误概率准则,也等同于最大联合概率准则,因此,从联合概率矩阵的每一列中选联合概率最大的发送符号作为译码输出,因此将112233,,y x y x y x →→→此时正确译码概率为11223313()()()344c p p x y p x y p x y =++=⨯=错误概率为114e c p p =-=(2)当信源等概率分布时,极大似然准则等价于最大后验概率准则,因此从信道矩阵的每一列中取转移概率最大的一个发送符号作为相应接收符号的译码输出,即是最佳译码方案,因此将112233,,y x y x y x →→→此时正确译码概率为112233111()()()(3)322c p p x y p x y p x y =++=⨯⨯=错误概率为112e c p p =-=6.10 解:(1)(;)()()D R I X Y H Y H Y X ==- 设信源的四个消息等概率出现,则有0114p p ==,12e p =[]01101111111424222201qq ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦111()()log 2[()(1)2]10.50.5224D R H Y H Y X H H =-=-+⨯=-=bit/符号 (2)按照译码准则译码时,由于后两位始终译为ee ,与发送代码后两位始终相同,故不存在误码;前两位,由于1000→→,1111→→,也不存在译码错误,因此所有码字的错误概率均为0。
或由联合概率矩阵1041188104XYP ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 正确译码的概率为111(00)(11)()1442c p p x y p x y p ee ===+==+=++=(发送e 时始终可以正确译码),因此所有码字的错误概率为0。
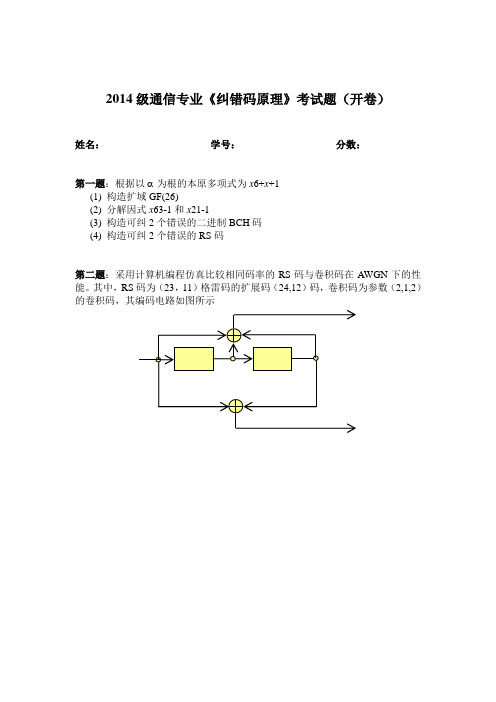
2014级通信专业《纠错码原理》考试题(开卷)姓名:学号:分数:第一题:根据以 为根的本原多项式为x6+x+1(1) 构造扩域GF(26)(2) 分解因式x63-1和x21-1(3) 构造可纠2个错误的二进制BCH码(4) 构造可纠2个错误的RS码第二题:采用计算机编程仿真比较相同码率的RS码与卷积码在AWGN下的性能。
其中,RS码为(23,11)格雷码的扩展码(24,12)码,卷积码为参数(2,1,2)的卷积码,其编码电路如图所示第一题根据以α为根的本原多项式为16++x x 1.构造扩域)2(6GF已知,01)(6=++=αααp ,即αα+=16,由这个等式,可构造扩域)2(6GF :267)1(ααααααα+=+⋅=⋅=32278)(αααααααα+=+⋅=⋅=433289)(αααααααα+=+⋅=⋅= 5443910)(αααααααα+=+⋅=⋅=5655410111)(αααααααααα++=+=+⋅=⋅=22625111211)1(ααααααααααααα+=+++=++=++⋅=⋅= 321213)1(ααααααα+=+⋅=⋅= 4231314)(αααααααα+=+⋅=⋅= 53421415)(αααααααα+=+⋅=⋅=4645315161)(αααααααααα++=+=+⋅=⋅=5241617)1(ααααααααα++=++⋅=⋅=326325217181)(ααααααααααααα+++=++=++⋅=⋅= 432321819)1(ααααααααααα+++=+++⋅=⋅=54324321920)(αααααααααααα+++=+++⋅=⋅=5436543543220211)(αααααααααααααααα++++=+++=+++⋅=⋅= 542654254321221)1(αααααααααααααααα+++=++++=++++⋅=⋅=5365354222231)1(ααααααααααααα++=+++=+++⋅=⋅=4645323241)1(αααααααααα+=++=++⋅=⋅= 542425)1(ααααααα+=+⋅=⋅=262525261)(αααααααααα++=+=+⋅=⋅= 3222627)1(ααααααααα++=++⋅=⋅=432322728)(αααααααααα++=++⋅=⋅=5434322829)(αααααααααα++=++⋅=⋅=5465454329301)(ααααααααααααα+++=++=++⋅=⋅= 526525430311)1(ααααααααααααα++=+++=+++⋅=⋅= 3635231321)1(αααααααααα+=++=++⋅=⋅= 433233)1(ααααααα+=+⋅=⋅= 5243334)(αααααααα+=+⋅=⋅=3635234351)(αααααααααα++=+=+⋅=⋅=4233536)1(ααααααααα++=++⋅=⋅=532423637)(αααααααααα++=++⋅=⋅=4364353237381)(ααααααααααααα+++=++=++⋅=⋅= 542433839)1(ααααααααααα+++=+++⋅=⋅=532653254239401)(αααααααααααααααα++++=+++=+++⋅=⋅= 432643253240411)1(αααααααααααααααα+++=++++=++++⋅=⋅= 5434324142)1(ααααααααααα+++=+++⋅=⋅=542654254342431)(αααααααααααααααα++++=+++=+++⋅=⋅= 532653254243441)1(αααααααααααααααα+++=++++=++++⋅=⋅=4364353244451)1(ααααααααααααα++=+++=+++⋅=⋅=54434546)1(ααααααααα++=++⋅=⋅=526525446471)(ααααααααααααα+++=++=++⋅=⋅=326325247481)1(ααααααααααααα++=+++=+++⋅=⋅= 43324849)1(ααααααααα++=++⋅=⋅=542434950)(αααααααααα++=++⋅=⋅=5365354250511)(ααααααααααααα+++=++=++⋅=⋅= 426425351521)1(ααααααααααααα++=+++=+++⋅=⋅= 53425253)1(ααααααααα++=++⋅=⋅=426425353541)(ααααααααααααα+++=++=++⋅=⋅= 532425455)1(ααααααααααα+++=+++⋅=⋅=432643253255561)(αααααααααααααααα++++=+++=+++⋅=⋅= 54324325657)1(ααααααααααααα++++=++++⋅=⋅=543265432543257581)(ααααααααααααααααααα+++++=++++=++++⋅=⋅=543265432543258591)1(ααααααααααααααααααα++++=+++++=+++++⋅=⋅=5436543543259601)1(αααααααααααααααα+++=++++=++++⋅=⋅=5465454360611)1(ααααααααααααα++=+++=+++⋅=⋅= 5655461621)1(αααααααααα+=++=++⋅=⋅= 1)1(656263=+=+⋅=⋅=ααααααα得到扩域)2(6GF 的元素表如下:幂表示6维向量表示幂表示6维向量表示α0100100 000000 33α0010011 100000 34α010000 35α110100 2α001000 36α011010 3α000100 37α001101 4α000010 38α110110 5α000001 39α011011 6α110000 40α111101 7α011000 41α101110 8α001100 42α010111 9α000110 43α111011 10α101101 α000011 4411α110001 45α100110 12α010011 α101000 4613α010100 47α111001 14α101100 α001010 4815α010110 α000101 4916α001011 α110010 5017α011001 51α110101 18α101010 α111100 5219α010101 α011110 5320α 001111 54α 111010 21α110111 55α011101 22α 101011 56α 111110 23α 100101 57α 011111 24α 100010 58α 111111 25α 010001 59α 101111 26α 111000 60α 100111 27α011100 61α100011 28α 001110 62α 100001 29α 000111 63α1 30α 110011 31α 101001 32α1001002.分解因式163-x 和121-x由共轭根系概念,将除0、1以上元素划分,同属一个根系的元素为一组:2481632361224334851017203440714283549569183611222537445013192638415215303951576021422329434653582745,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,ααααααααααααααααααααααααααααααααααααααααααααααααααααααα54314755596162,,,,,ααααααα分别求取每组共轭根系的最小多项式,化简得:248163261361224334864225101720344065237142834()()()()()()()1()()()()()()()1()()()()()()()1()()()()(x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ααααααααααααααααααααααΦ=++++++=++Φ=++++++=++++Φ=++++++=++++Φ=++++54956639183632511222537445065326131926384152643715308)()()1()()()()1()()()()()()()1()()()()()()()1()()(x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ααααααααααααααααααα++=++Φ=+++=++Φ=++++++=++++Φ=++++++=++++Φ=++39515760654221422923294346535865410274554311314755512)()()()()1()()()1()()()()()()()1()()()()1()()()()(x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ααααααααααααααααααα++++=++++Φ=++=++Φ=++++++=++++Φ=+++=++Φ=++++9616265)()()1x x x x αα++=++所以,因式分解结果为126311()i i x x =-=Φ∏(2.2) 分解因式x 21-1x 21-1中n=21,且找不到一个整数m 使等式n=2m -1成立,因此需要寻找非原元β。

8-1 某码字的集合为 00000000 1000111 0101011 0011101 1101100 1011010 0110110 1110001求:(1)该码字集合的最小汉明距离;(2)根据最小汉明距离确定其检错和纠错能力。
解:(1)通过两两比较每个码字,可知该码字集的最小汉明距离为4;(2)因为检错能力与最小码距的关系为:1min +=e d ,所以检错能力为3141min =-=-=d e又因为纠错能力与最小码距的关系为:12min +=t d ,所以纠错能力为5.121421min =-=-=d t取整后可得,纠错能力为1=t 。
8-2 已知二进制对称信道的差错率为210-=P 。
(1)(5,1)重复码通过此信道传输,不可纠正错误的出现概率是多少?(2)(4,3)偶校验码通过此信道传输,不可检出错误的出现概率是多少?解: (1)当(5,1)重复码发生3个或3个以上的错误时不可纠正,此时不可纠正的错误出现的概率为()()()60555144523351085.9111-⨯≈-+-+-=P P C P P C P P C P e (2)当(4,3)偶校验码发生偶数个错误时这些错误不可检出,这些错误出现的概率为()()4044422241088.511-⨯≈-+-=P P C P P C P e8-3 等重码是一种所有码字具有相同汉明重量的码,请分析等重码是否线性码?解:因为该码字集中所有的码字均有相同的码重,因此全零码字不包括在内,而线性码在输入信息位均为零时,输出也全为零,因此一定包含全零码。
因此等重码不是线性码。
8-4 对于一个码长为15,可纠正2个随机错误的线性分组码,需要多少个不同的校正子?至少需要多少位监督码元?解:对于一个码长为15的线性码,1个及2个随机错误的图样数为120215115=+C C所以至少需要121个校正子因为12712120631272151156=-<=+<=-C C所以至少需要7位监督码元。

第1章 信息论基础1.7 ⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡36136236336436536636536436336236112111098765432)(X q X 1.8 p (s 0 ) = 0.8p (s 0 ) + 0.5p (s 2 )p (s 1 ) = 0.2p (s 0 ) + 0.5p (s 2 ) p (s 2 ) = 0.5p (s 1 ) + 0.3p (s 3 ) p (s 3 ) = 0.5p (s 1 ) + 0.7p (s 3 ) p (s 0 ) + p (s 1 ) + p (s 2 ) + p (s 3 ) = 1 p (s 0 ) =3715, p (s 1 ) = p (s 2 ) = 376,p (s 3 ) = 37101.9 P e = q (0)p + q (1)p = 0.06(1-0.06)﹡1000﹡10 = 9400 < 9500 不能1.10 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------------=22222222)1(0)1()1(00)1(0)1()1(000000)1()1(0)1(00000)1()1(0)1(p p p pp p p p p p p p p p p p p p p p p p p p P 第2章 信息的度量2.4 logk2.5 I (X ; Y Z )= I (X ; Y )+ I (X ; Z ∣Y ) 2.7 010434()()()111111p s p s p s === H = 0.25(Bit/符号)2.8 H = 0.82(Bit/符号) 2.10 (1)1()log225.6()52!i I x Bit =-= (2)1352!()log ()log 413!39!i i I x q x =-=(3))/(4.713log 234log 52log 521log )(符号-Bit U H ==⨯===(4))/(7.313log 131log )(符号Bit X H ==- 2.11(1)H (X ) = log6 = 2.58 (Bit/符号) (2)H (X ) =2.36 (Bit/符号)(3)I (A+B=7) = - log1/6 = log6 = 2.585 (Bit) 2.12 (1)I (x i ) = -log1/100 = log100(2)H(X)=log100.2.13 039.0log )(-=Y X I2.14 R t =1000/4 (码字/秒) × H (U ) =250×9=2250(Bit/秒) 2.15 ―log p = log 55/44。
第二章作业参考答案1. 补充作业解:设{0,1,2}X =,1p p =-(1) 转移概率矩阵/2/2/2/2/2/2p p p P p p p p p p ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(2) 平稳分布001211022201012()2()2()21p p pp p p p p pp p p p p pp p p p p p ⎧=++⎪⎪⎪=++⎪⎨⎪=++⎪⎪⎪++=⎩解得01213p p p ===(3) 信源熵321()()i i i H X p H X s ==∑0(,,)322(,,)22(log log)2p p p H p p pH p p p p p =⨯==-+(4) 当做无记忆信源时,信源熵为()log 3H X =bit/符号 (5) 2()(,,)22p p H X H p =当12p p p =-=,2/3p =,即信源符号等概率分布时,2()H X 达到极大值2m a x ()l o g 3H X =bit/符号;0p =时,2()(1,0,0)0H X H ==; 1p =时,211()(0,,)log 2122H X H ===bit/符号 2.8 解:将其看作一阶马尔科夫信源转移概率矩阵为223310P ⎡⎤⎢⎥=⎢⎥⎣⎦,由P 可画出香农线图。
x 1:2/3x 2:1/31由香农线图列方程组求解平稳分布112211221()()()331()()3()()1p x p x p x p x p x p x p x ⎧=+⎪⎪⎪=⎨⎪+=⎪⎪⎩解得12()3/4()1/4p x p x =⎧⎨=⎩ 信源熵23211()(,)(1,0)0.6894334H X H H =+=bit/符号 2.11 解:(1)点数集合记为{1,2,3,4,5,6}X =,出现各点数的概率分别记为,1,...,6i p i =信源概率空间为123456111111666666X P ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦掷骰子的熵记为信源熵()log 6 2.585H X ==bit/符号 (2)由题意可得61111121i p i p ==⇒=∑,1,...,621i i p i ⇒==此时的信源熵为61()log 2.399i i i H X p p ==-=∑bit/符号(3)总点数为7这个事件集合为1212{(,)7}{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}x x x x +==,其中每个组合出现的概率均为1/36,故点数和为7这个事件发生的概率为6/36=1/6,从而这个事件的自信息量为1log log log 6 2.5856i I p =-=-==bit2.16 解:由题意可写出该系统的转移概率矩阵为10000000.500.2500.2500100000.2500.500.2500001000.250.250.5P ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦由题目的已知条件,每个符号等概率发出,可求得接收每个符号的概率[]01234510000000.500.2500.25001000111111[]00.2500.500.2566666600001000.250.250.5111111[]666666qq q q q q ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=11()log 6log 6 2.58566H Y ⎛⎫=-⨯== ⎪⎝⎭bit/符号51111()()()(,,)3(1)30.756244i i i H Y X p x H Y x H H =⎡⎤==⨯+⨯=∑⎢⎥⎣⎦bit/符号 (;)()() 2.5850.75 1.835I X Y H Y H Y X =-=-=bit/符号2.17 解:用“1”表示收到1,“10”表示收到10,“100”表示收到100()q ⋅表示接收符号的概率(1) 由4(14)(1;)log(1)p u I u q =,先求(1)q711(1)()(1)[4(1)4]82i i i q p u p u p p ===-+=∑代入上式可得4(14)(1)(1;)logloglog 2(1)(1)1/2p u p I u p q -===-或可由4444(1)(1;)(;1)log()p u I u I u p u ==,先求(1)q ,再求4(14)(4)1(1)(1)4p u p u p p u q -==,代入到定义式中求解(2) 由4(104)(10;)log(10)p u I u q =,先求(10)q72211(10)()(10)[4(1)22(1)]84i i i q p u p u p p p p ===-++-=∑代入上式可得24(104)(1)(10;)loglog2log 2(1)(10)1/4p u p I u p q -===-(24(104)(4)(1)(10)(10)2p u p u p p u q -==)(3) 由4(1004)(100;)log(100)p u I u q =,先求(100)q771(100)()(100)()(1)(0)(0)8i i i i i i i i q p u p u p u p u p u p u =====∑∑代入上式可得34(1004)(1)(100;)loglog3log 2(1)(10)1/8p u p I u p q -===-(34(1004)(4)(100)(1)(100)p u p u p u p q ==-)2.24 解:(法一)由(;)()()I X Y H Y H Y X =- 设信宿符号接收概率分别为0q 和1q01010.760.240.760.2411[][][][0.540.46]0.320.680.320.6822q q p p ⎡⎤⎡⎤===⎢⎥⎢⎥⎣⎦⎣⎦()(0.54,0.46)0.9954H Y H ==bit/符号[]11()()(0.76,0.24)(0.32,0.68)0.84972i i H Y X p H Y i H H ===+=∑bit/符号从而(;)()()I X Y H Y H Y X =-=0.9954-0.8497=0.146bit/符号(法二)直接由平均互信息量的定义式,()(;)()log()X Yp y x I X Y p xy q y =∑由信源分布及信道转移概率矩阵可得XY 的联合分布0.380.120.160.34XY P ⎡⎤=⎢⎥⎣⎦,将其代入到定义式中可得 0.760.240.320.68(;)0.38log 0.12log 0.16log 0.34log0.540.460.540.46I X Y =+++=0.146bit/符号2.25 解:由联合概率分布可求得X 和Y 的一维概率分布[]0.10.30.50.1X P =,[]0.30.40.3Y P =及转移概率矩阵100210333205501YXP ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦()(0.1,0.3,0.5,0.1) 1.685H X H ==bit/符号()(0.3,0.4,0.3) 1.571H Y H ==bit/符号2132()()()0.1(1,0,0)0.3(,,0)0.5(,,0)0.1(0,0,1)3355XH Y X p x H Y x H H H H ==+++∑21320.3(,)0.5(,)0.7613355H H =+=bit/符号 ()()() 1.6850.761 2.446H XY H X H Y X =+=+=bit/2符号(;)()()()() 1.5710.7610.81I X Y H X H X Y H Y H Y X =-=-=-=第三章作业参考答案:3.2 答:(1)当log ()n D LH X ≥时,可实现无失真编码;(2)等长编码时,从总的趋势来说,增加L 可提高编码效率,且当L →∞时,1η→。
第五章 纠错编码习题解答1、已知一纠错码的三个码组为(001010)、(101101)、(010001)。
若用于检错,能检出几位错码?若用于纠错,能纠正几位错码?若纠检错结合,则能纠正几位错码同时检出几位错码?[解]该码的最小码距为d 0=4,所以有:若用于检错,由d 0≥e +1,可得e =3,即能检出3位错码; 若用于纠错,由d 0≥2t +1,可得t =1,即能检出1位错码; 若纠检错结合,由d 0≥e +t +1 (e >t ),可得t =1,e =2,即能纠正1位错码同时能检出2位错码。
2、设某(n ,k )线性分组码的生成矩阵为:001011100101010110G ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦①试确定该(n ,k )码中的n 和k ; ②试求该码的典型监督矩阵H ; ③试写出该码的监督方程; ④试列出该码的所有码字; ⑤试列出该码的错误图样表; ⑥试确定该码的最小码距。
[解] ①由于生成矩阵G 是k 行n 列,所以k =3,n =6。
②通过初等行变换,将生成矩阵G 变换成典型生成矩阵[]100101010110001011k G I Q ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦由于101110110011011101T Q P Q ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦, ==,可知典型监督矩阵为 []110100011010101001r H PI ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦= ③监督方程为542431530000a a a a a a a a a ⊕⊕=⎧⎪⊕⊕=⎨⎪⊕⊕=⎩④所有码字见下表⑤错误图样表即错误图样与校正子关系表,见下表⑥线性码的最小码距为码字的最小重量(全零码除外),所以该码的最小码距为3。
3、已知一种(7,3)循环码的全部码组为:0000000 0101110 1001011 1100101 0010111 0111001 1011100 1110010试求该码的生成多项式g (x )、典型生成矩阵G 和典型监督矩阵H ;[解]由循环码的原理知,生成多项式g (x )对应的码字为前k -1位码元均为“0”的码字,即“0010111”,所以有g (x )=x 4+x 2+x +1则生成矩阵为2643253242()1011100()0101110()10010111x g x x x x x G xg x x x x x g x x x x ⎡⎤⎡⎤+++⎡⎤⎢⎥⎢⎥⎢⎥==+++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎣⎦ 典型化可得典型生成矩阵[]100101101011100010111k G I Q ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦由于110101101111101110111101TQ P Q ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦, ==,可得典型监督矩阵为 []1101000011010011100101010001r H PI ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦=4、已知一个(3,1,4)卷积码编码器的输出和输入关系为:11212343134c b c b b b b c b b b ==⊕⊕⊕=⊕⊕试画出该编码器的电路方框图和码树图。
纠错编码习题解答第一章1.1 Solution: p=0.05(1)The correct decoding P c is P c= P0 =C40p0(1-p)4=0.8145(2)The decoding error P e is P e = P2+P4 = C42p2(1-p)2 + C44p4(1-p)0 = 0.0135(3)The decoding failure P f is P f= C41p(1-p)3 + C43p3(1-p) = 0.17201.2 Solution:Because the success rate does not fall below 99%,then the decoding failure P f <1% .And p<<1, P f = P1 = n*0.001*0.999n-1 < 0.01So n<=10 .then the maximum blocklength n such that the success rate does not fall below 99% is 10.1.3 Solution: p=0.01P f = P2 = C42p2(1-p)2 = C42 * 0.012 * 0.992 = 0.000588So the decoding failure rate is 0.000588.1.4 Solution:(a)Error: There is one error(b)Correct(c)Failure(d)Error: There is two error1.5 Solution:S1 = v1+v2+v3+v4+v6+v8+v9+v12S2 = v2+v3+v4+v5+v7+v9+v10+v13S3 = v3+v4+v5+v6+v8+v10+v11+v144 12357811151.6 Solution(1)s=(0000) ~e = 0000 0000 0000 000~c= ~e+v1 = (000000000000000)+(100010011001001)= (100010011001001)(2)s=(1011) ~e = 0000 0001 0000 000~c= ~e+v2 = (000000010000000)+(001001110100110)= (001001100100110)1.7 Solution(1) v=(1011 110) s=(110)~e = (001 0000) ~c=(1001 110)(2) v=(1100 110) s=(100)~e = (0000 100) ~c=(1100 010)(3) v=(0001 011) s=(000)~e=(0000 000) ~c=(0001 011)第二章i j .2.2 Solution1 1 1 1 1 1 1 r1-r2 1 0 0 0 1 0 1G2= 0 1 1 1 0 1 0 r2-r3 0 1 0 0 1 1 1 = G10 0 1 1 1 0 1 0 0 1 0 1 1 00 0 0 1 0 1 1 r3-r40 0 0 1 0 1 1G1 is systematic form.And every liner coder is equivalent to a systematic linear codeSo the (7,4) linear codes generated by G1 and G2 equivalent.2.3 Solution(a) C 0 = (000) G = (000000) C 1 = (001) G = (001110) C 2 = (010) G = (010101) C 3 = (011) G = (011011) C 4 = (100) G = (100011) C 5 = (101) G = (101101) C 6 = (110) G = (110110) C 7 = (111) G = (111000)(b)If p=0 thenIf p=1 then2.4 SolutionBecause the (4,3) even-parity code is a linear code , The minimum distance d(C i ,C j )= W min = 2 The error detection limit is L=2-1=1The error correction is t=(2-1)/2=ly 0.2.5 Solution1 1 1 0 1 0 0 01 1 1 0 1 0 0 0 0 1 1 1 0 1 0 0 r4-r3-r2-r1 0 1 1 1 0 1 0 0 H= 1 1 0 1 0 0 1 0 1 1 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 1 1 0 0 0 1So the systematic forms is 1 1 1 0 1 0 0 00 1 1 1 0 1 0 01 1 0 1 0 0 1 01 0 1 1 0 0 0 1Because H = [P T | I n-k] and G=[I k | P]Then G = 1 0 0 0 1 0 1 10 1 0 0 1 1 1 00 0 1 0 1 1 0 10 0 0 1 0 1 1 12.6 Solution1 1 1 0 1 0 0 0 1 0 1 10 1 1 1 0 1 0 0 H T = 1 1 1 1H= 1 1 0 1 0 0 1 0 1 1 0 11 1 1 1 1 1 1 1 0 1 1 11 0 0 10 1 0 10 0 1 10 0 0 1第三章3.1 solutionBecause x3+1x4+x+1 x7+x3+1x7+x4+x3x4+1x4+x+1then q(x)= x3+1 and r(x)= xcheck answer : p1(x)q(x)+r(x)= (x3+1)( x4+x+1)+x= x7+x3+1 = p2(x) so the solution is correct.3.2 Solution(a) x3+x2+1x+1 x4+x2+x+1x4+x3x3+x2+x+1x3+x2x+1x+1R(x+1) (x4+x2+x+1) = 0(b) x3+x2+x+1x2+x+1 x5+x3+x2+x+1x5+x4+x3x4+x2+x+1x4+x3+x2x2+x+1x3+x2+xx3+x2x2+x+1xso R(x2+x+1) (x5+x3+x2+x+1) = x3.3 Solution(1) Systematic code :x3i(x)=x3(x3+x2+x+1)= x6+x5+x4+x3x3+x2+1x3+x+1 x6+x5+x4+x3x6+x4+x3x5x5+x3+x2x3+x2x3+x+1x2+x+1so q(x)= Q g(x) (x3i(x)) = x3+x2+1r(x)= R g(x) (x3i(x)) = x2+x+1then c(x)= x3i(x) +r(x)= x6+x5+x4+x3 +x2+x+1or c(x)=q(x)g(x)=( x6+x5+x4+x3)( x3+x+1) = x6+x5+x4+x3 +x2+x+1(2)Nonsystematic code :C(x)=i(x)g(x)=( x3+x2+x+1)( x3+x+1)= x6+x5+x3+13.4 SolutionWhen the codeword polynomials is x6+x3+x2+xThen s(x)= R g(x) (c(x)+e(x))= R g(x) (x6+x3+x2+x+x3)= R g(x) (x6+x2+x)x3+x+1x3+x+1 x6+x2+xx6+x4+x3x4+x3+x2+xx4 +x2+xx3x3+x+1x+1so s(x)= R g(x) (c(x)+e(x))= x+1When the codeword polynomials is x5+x3+x2The s(x)= R g(x) (c(x)+e(x)) = R g(x) (x5+x3+x2+x3)= R g(x) (x5+x2)x2 +1x3+x+1 x5+x2x5+x3+x2x3x3+x+1x+1so s(x)= R g(x) (c(x)+e(x))= x+1so the resulting syndrome polynomials are the same .3.5 Solution(a)The number of cyclic codes with blocklength 15 isC51+C52+C53+C54 =5+10+10+5=30(b)The number of (15,11)cyclic codes is 3 .when g(x)= x4+x+1 or g(x)= x4+x3+1 or g(x)= x4+x3+ x2+x+1 (c)The generator polynomials for the (15,7) cyclic codes isg1(x) =(x4+x+1)(x4+x3+1)=x8+x7+x5+x4+x3+x+1g2(x) =(x4+x+1)(x4+x3+ x2+x+1)=x8+x7+x6+x4 +1g3(x) =(x4+x3+1)(x4+x3+ x2+x+1)=x8+x4+x2+x+13.6 SolutionThe parity-check polynomial h(x)=( x15+1)/g(x)And g(x) = x10+x8+x5+x4+x2+x+1x5+x3+x+1x10+x8+x5+x4+x2+x+1 x15+1x15+x13+x10+x9+x7+ x6+x5x13+x10+x9+x7+x6+x5+1x13+x11+x8+x7+x5+ x4+x3x11+x10+x9+x8+x6+ x4+x3+1x11+x9+x6+x5+x3+ x2+xx10+x8+x5+x4+x2+x+1x10+x8+x5+x4+x2+x+1So h(x)= x5+x3+x+1h*(x)= x5(x-5+x-3+x-1+1)= x5+x4+x2+1So the blocklength of the cyclic code that is dual to the (15,5) codeis 15 and the information length is 15-5=10第四章4.1 Solution p(x)= x5+x4+x32q(x)=x5+x3+1 g(x)=x3+x2+x+1 r(x)= x2+x+1so q(x)g(x)+r(x)=( x5+x3+1)( x3+x2+x+1)+( x2+x+1)= x3(x5+x4+x)=x r p(x)4.2 Solution g(x)= x4+x3+13f2f210in fq(x)=x r(x)= x2+x+1So q(x) g(x)+r(x)= x(x4+x3+1)+( x2+x+1)=x5+x4+x2+1=p(x)4.3 Solution r(x)= R g(x)[x8i(x)]=R(x8+x4+x+1)[x8(x5+x2+1)]x5+x2+x+1x8+x4+x+1 x13+x10+x8x13+x9+x6+x5x10+x9+x8+x6+x5x10+x6+x3+x2x9+x8+x5+ x3+x2x9+x5+x2+xx8+x3+xx8+x4+x+1x4+x3+1so r(x)= x4+x3+1then the codeword is 010010100011001.4.4 Solutiong(x)g(x)n-k4.5 SolutionLow-order input i(x)=x8+x6+x+1 with g(x)=x4+x+1c(x)=x12+x10+x5+x4 +x3+x2+14.6 Solutionv(x)=x6+x4+x3+x2s(x)=R g(x)[v(x)]= x+1e(x)=x4So c(x)=v(x)+e(x)=x6+x3+x2第五章5.1 Solution(a)No. Because this set does not have a unique identity element. (b)No. Because this set does not have a unique inverse. (c)Yes.(d)No. Because this set does not satisfy the property of closure.5.2 Solution x 属于{0,1,2,3,4,5}5.3 SolutionModule-5 multiplication5.4 SolutionModulo-5 arithmetic(a)2*7+6=2*2+6=4+6=4+1=0(b)(4-8)*3-2=(4+2)*3-2=1*3-2=1(c)(3+6)/2-4/3=4*3-4*2=2-3=2+2=4Modulo-7 arithmetic(a)2*7+6=2*0+6=6(b)(4-8)*3-2=(4+6)*3-2=3*3-2=2-2=0(c)(3+6)/2-4/3=2*4-4*5=1-6=1+1=25.5 SolutionBecause (01010)+(10110)=(11100)(10011)+(10110)=(00101)(11001)+(10110)=(01111)do not belong to any one of the set of vectors.So the set of vectors does not form a vector subspace of V5.5.6 SolutionThe three vectors are (00101),(11100)and (01111)10 Take any 2 linearly independent vectors ,say (01010).(10110) as the initial set of vectorswhich is not a basis of the given subspace.20 Of the remaining 5 nonzero vectors (11100)=(01010)+(10110) is linearly dependent on the 2 vector already in the set .Any one of the remaining 5 nonzero vectors except (11100) can be appended to the initial set.30 Taking ,say, (00101) as the 3rd basis vector we find all the vectors with in the subspace.123because there are 3 basis vectors.5.7 SolutionBecause r=n-k=k the code is (8,4), then it satisfy this law.Because a self-dual code should satisfy H=G.G = [I k|P]1 1 1 0 1 0 0 0 1 0 0 1 1 1 0 0H = [P T|I n-k]= 0 1 1 1 0 1 0 0 r1+r2 1 0 1 0 0 1 1 01 1 0 1 0 0 1 0 r2+r30 1 1 0 0 0 1 11 0 1 1 0 0 0 1 r3+r4 1 0 1 1 0 0 0 10 0 1 0 1 1 0 1 0 0 1 0 1 1 0 1r1+r4 1 0 0 0 1 0 1 0 r4+r1+r2 1 0 0 0 1 0 1 1r2+r1 0 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0r3+r3 1 0 1 1 0 0 0 1 0 0 0 1 0 1 1 11 0 0 0 1 0 1 10 1 0 0 1 1 1 0 =G0 0 1 0 1 1 0 10 0 0 1 0 1 1 11 0 1 1 1 1 1 0 1 0 0 0PP T= 1 1 1 0 0 1 1 1 = 0 1 0 0 = I1 1 0 1 1 1 0 1 0 0 1 00 1 1 1 1 0 1 1 0 0 0 1So the (8,4) code with generator matrix is self-dual.第六章6.1 Solution(1)p1(x)=x4+x3+x+1(a) p1(1)=1+1+1+1=0Then p1(x) is not irreducible.(b) p1(x) is not primitive.(2) p 2(x)= x 2+x+1 (a) p 2(0)= p 2(1)=1Then p 2(x) is irreducible.(b)Image a 2+a+1=0 ,then a 2=a+1 a is a root and a ∈GF(22) So p 2(x) is primitive. (3) p 3(x)= x 3+x 2+1 (a) p 3(0)= p 3(1)=1.Then p 2(x) is irreducible.(b) Image a 3+a 2+1=0 ,then a 3=a 2+1 a is a root and a ∈GF(23) So p 3(x) is primitive.6.2 SolutionImage a 2+a+1=0 ,then a 2=a+1 The field elements of GF(22) P(0)=0+0+1=1 P(1)=1+1+1=1P(a)= a 2+a+1= a+1+a+1=0 P(a 2)= a 4+a+1= (a+1)2+a+1=0So the root of p(x)=0 are x=a and x=a 26.3 SolutionWhen β3+β2+1=0 then β3=β2+13When β3+β+1=0 then β3=β+1 The field element of GF(23)Xx3+x2+1 is the same as that constructed using x3+x+1 ,they differ only in the way in which elements are labeled.6.4 SolutionTo m1(x)=x5+x2+1m1(0)=1 , m1(1)=1 , m1(α)= α5+α2+1=α2+1+α2+1=0So the minimal polynomials of αis m1(x)=x5+x2+1To m3(x)=x5+ x4+x3+x2+1m3(0)=1 ,m3(1)=1 ,m3(α)= α5+α4+α3+α2+1=α2+1+α4+α3+α2+1=α4+α3m3(α2)= α10+α8+α6+α4+1=(α4+1)+( α3+α2+1)+(α3+α)+ α4+1=α2+α+1m3(α3)= α15+α12+α9+α6+α3=(α4+α3+α2+α+1)+( α3+α2+α)+( α4+α3+α)+( α3+α)+1=0So the minimal polynomials of α3 is m3(x)= x5+x4+x3+x2+16.5 Solution(1) Over GF(24)1 α4 x α5α5 α2 y = α3Then x = 14 -1α5 = (1/α11) α2 α4α5y α5 α2 αα5 1 α3= (1/α11) α2 *α5+α4*α3α5 *α5+1 *α3=(1/α11) 0 = 0α12 α[α2 *α5+α4*α3=α7+α7 =0α5 *α5+1 *α3=α10+α3= (α2+α+1)+ α3=α12]so the linear equations have a solution x=0 over GF(24)y=α(2) Over GF(23)Simplify the linear equations x+(α2+α)y=(α2+α+1)(α2+α+1)x+α2y=(α+1)Then the linear equations have a solution x=1 over GF (23y=1。