2014年福建省莆田市中考数学试卷含答案

九年 数学A第1页，共6页2013-2014学年（上）期末考试试卷九年 数学(满分: 150分；考试时间:120分钟)一、精心选一选：本大题共8小题，每小题4分，共32分．每小题给出的四个选项中有且只有一个选项是符合题目要求的．答对的得4分，答错、不答或答案超过一个的一律得O 分．1. 下列各式一定是二次根式的是（ ）A.B.C.2. 已知关于的方程有两个不同的实数根，则的取值范围是（ ）A 、 B、C、 D 、3. 下列图形中，是中心对称图形，但不是轴对称图形是（ ）A 、正方形B 、矩形C 、菱形D 、平行四边形 4. 下列命题中，假命题是（ ）A.两条弧的长度相等，它们是等弧B.等弧所对的圆周角相等C.直径所对的圆周角是直角D.一条弧所对的圆心角等于它所对圆周角的2倍.5. 把二次函数23x y =的图象向左平移2个单位，再向上平移1个单位，所得到的A()1232+-=x y ; ()1232-+=x y ;C()1232--=x y D()1232++=x y6. 下图中几何体的左视图是（ ）.7. 当锐角30>α时，则αcos 的值是（ ）A ．大于12 B ．小于12C ．大于D 8、 如图，AB ∥CD ，AC 、BD 交于O ，BO =7，DO =3，AC =25， 则AO 长为（ ） A ．10 B ．12．5 C ．15 D ．17．5二、细心填一填：本大题共8小题，每小题4分，共32分．。

10. x 取值范围是 。

11. 已知圆锥的底面半径是2，母线长是4，则圆锥的侧面积是________。

12. 如果，则________。

13. 已知方程8322=-x x 的两个根为21x x ，那么=⋅21x x ．第3页，共14.如图，△ABC绕点A旋转后到达△ADEA、B分别为切点，若∠C=62°，则∠APB= 。

16.将4个数a b c d，，，排成2行、2列，两边各加一条竖直线记成a bc d，定义a bc dad bc=-，上述记号就叫做2阶行列式．若1111x xx x+--+6=，则x=．三、耐心做一做：本大题共9小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤．17. 计算：(1-)2008－(π－3)0sin60°·tan45°（8分）18计算：.⎛÷⎝（8分）19.解方程：4x2-3x-1=0（8分）20.如图，在平面直角坐标系中，将四边形ABCD称为“基本图形”，且各点的坐标分别为A（4，4），B（1，3），C（3，3），D（3，1）.（8分）（1）画出“基本图形”关于原点O对称的四边形A1B1C1D1，并求出A1，B1，， )，， ) ；（8分）(1)求随机抽取一张卡片，恰好得到数字2的概率；(2)小贝和小晶想用以上四张卡片做游戏，游戏规则见信息图．你认为这个游戏公平吗?请用列表法或画树形图法说明理由．22.如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE CD⊥，垂足为E，DA平分BDE∠．（1）求证：AE是⊙O的切线；（2）若301cmDBC DE∠==，，求BD的长．23.某商厦今年一月份销售额为60万元，二月份由于经营不善，销售额下降10%，以后改进管理，大大激发全体员工的积极性，月销售额大幅度上升，到四月份销售额猛增到96万元，求三、四月份平均每月增长的百分率是多少？（精确到0.1%）（10分）24.在△ABC中，AB＝BC＝2，∠ABC＝第20题图B九年 数学A第5页，共6页120°，将△ABC 绕点B 顺时针旋转角α(0°＜α＜90°)得△A 1BC 1，A 1B 交AC 于点E ，A 1C 1分别交AC ，BC 于D ，F 两点．(12分)(1)如图(a)，观察并猜想，在旋转过程中，线段EA 1与FC 是怎样的数量关系?并证明你的结论；(2)如图(b)，当α＝30°时，试判断四边形BC 1DA 的形状，并说明理由；(3)在(2)的情况下，求ED 的长． 图(a) 图(b)25. 如图，已知抛物线234y x b x c =-++与坐标轴交于A B C ，，三点，点A 的横坐标为1-，过点(03)C ，的直线334y x t =-+与x 轴交于点Q ，点P 是线段BC 上的一个动点，PH OB ⊥于点H ．若5P B t =，且01t <<．（1）求b c ，的值（2）求出点B Q P ，，的坐标（其中Q P ，用含t 的式子表示）： （3）依点P 的变化，是否存在t 的值，使PQB △为等腰三角形？若存在，求出所有t 的值；若不存在，说明理由．。

莆田中考数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是正确的比例关系？A. 2:3 = 4:6B. 3:4 = 6:8C. 5:7 = 10:14D. 8:9 = 16:18答案：C2. 如果一个数的平方等于这个数本身，那么这个数可能是：A. 0B. 1C. -1D. 以上都是答案：D3. 一个圆的直径是10厘米，那么它的周长是：A. 31.4厘米B. 62.8厘米C. 314厘米D. 628厘米答案：B4. 下列哪个方程的解是x=2？A. 2x + 3 = 7B. 3x - 5 = 1C. 4x = 8D. 5x - 10 = 0答案：C5. 一个班级有40名学生，其中20名男生和20名女生。

随机选择一名学生，是男生的概率是：A. 0.5B. 0.4C. 0.25D. 0.8答案：A6. 一个长方体的长、宽、高分别是5厘米、4厘米和3厘米，那么它的体积是：A. 60立方厘米B. 120立方厘米C. 180立方厘米D. 240立方厘米答案：A7. 如果一个角的补角是120度，那么这个角的度数是：A. 60度B. 30度C. 90度D. 120度答案：B8. 下列哪个选项是正确的三角函数关系？A. sin(30°) = 1/2B. cos(45°) = √2/2C. tan(60°) = √3D. All of the above答案：D9. 一个等腰三角形的两个底角相等，如果其中一个底角是40度，那么顶角的度数是：A. 100度B. 80度C. 60度D. 40度答案：B10. 如果一个数的立方等于8，那么这个数是：A. 2B. -2C. 1/2D. -1/2答案：A二、填空题（每题3分，共15分）11. 一个数的相反数是-5，那么这个数是________。

答案：512. 如果一个数的绝对值是7，那么这个数可能是________或________。

A ．第6题2013-2014学年度荔城区中考模拟试卷（三）数学考试时间：120分钟 满分：150分一、精心选一选 ：本大题共8小题，每小题4分，共32分。

每个小题给出的四个选项中有且只有一个选项是符合要求，答对的得4分，答错、不答或答案超过一个的一律得0分。

1、在-3,-1，0,2四个数中，绝对值最小的数是（ ）A.-3B.－2C.0D.22、下列运算正确的是 （ ） A ．236a a a ⋅= B ．()325aa =C ．325a a a +=D ．632a a a ÷=3、为了解某小区居民的日用电量情况，居住在该小区的一名同学随机抽查了15户家庭的日用则关于这15户家庭的日用电量，下列说法错误的是（ ） A ．众数是6度 B ．平均数是6.8度 C ．极差是5度D ．中位数是6度4、下列图形中是中心对称图形但不是轴对称图形的是（ ） A ． 等腰三角形 B ．平行四边形 C ．矩形 D ．菱形5、如图①放置的一个水管三叉接头，若其主视图如图②，则其俯视图是（ ）6、如图，在Rt △ABC 中，∠ACB ＝90°，∠BAC ＝60°，AB ＝6，Rt A C B '' 可以看作是由Rt △ABC 绕点A 逆时针方向旋转60°得到的，则线段C B ' 的长为（ ）A 、33B 、6C 、73D 、367、如图，已知AB 是半圆O 的直径，∠BAC=32º，D 是弧AC 的中点，那么∠DAC 的度数是（ ） A、25º B 、29º C 、30º D 、32°8、如图，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角线 BD 重合，折痕为DG ,记与点A 重合的点为A ’,则△A ’BG 的面积与该矩形 的面积比为（ ） A 、121 B 91 C 81 D 61二、细心填一填：本大题共8小题，每小题4分，共32分9、不等式组2430x x >-⎧⎨-<⎩的解集是 ．10、许多人由于粗心，经常造成水龙头“滴水”或“流水”不断．根据测定，一般情况下一个水龙头“滴水”1个小时可以流掉3．5千克水．若1年约流掉30700千克水，将数据30700用科学计数法表示为 ．11、如图所示，AB =DB ，∠ABD =∠CBE ，请你添加一个适当的条件 ，使ΔABC ≌ΔDBE ． (只需添加一个即可)（第11题） （第12题）12、如图，在Rt△ABC 中，∠ACB=90°，CD 是AB 边上的中线，若BC=6，AC=8，则tan∠ACD 的值为 。

福建莆田秀屿下屿中学 2014 届九年级中考模拟卷 数学（满分：150 分，考试时间：120 分钟） 一、精心选一选：本大题共 8 小题，每小题 4 分，共 32 分．每小题给出的四个选项中有只 有一个选项是符合题目要求的．答对的得 4 分，答错、不答或答案超过一个的一律得 O 分． 1、化简|－2014|等于（ ） A．2014 B．－2014 C．±2 014 2、观察下列图案，既是中心对称图形又是轴对称图形的是（ D．-2013 ）A、 3、下列计算正确的是（ A．a+2a=3a2B、 ）2 3 5C、D、B．a •a =aC．a ÷a=323D． （﹣a） =a334、地球上的陆地面积约为 149000000 千米 ，用科学记数法表示为（ A.149³ 10 千米6） ．92B. 149³ 10 千米72C.1．49³ 10 千米82D.1．49³ 10 千米25、 如图， 将三角尺的直角顶点放在直线 a 上， a∥ b， ∠ 1=50° ， ∠ 2=60° ， 则∠ 3 的度数为 （）A、50° B、60° C、70° D、80° 6、若一个圆锥的侧面积是 10，则下列图象中表示这个圆锥母线 l 与底面半径 r 之间的函数 关系的是（ ）ABCD7、如图，在△ ABC 中，∠ B=30° ，BC 的垂直平分线交 AB 于 E，垂足为 D．若 ED=5，则 CE 的 长为（ ） A．10 B．8 C．5 D．2.58、如图，已知□ABCD 中，AB=4,AD=2,E 是 AB 边上的一动点（与点 A、B 不重合） ，设1 1AE= x ,DE 的延长线交 CB 的延长线于点 F，设 BF= y ，则下列图象能正确反映 y 与 x 的函 数关系的是D A E B FCy 2 O 4 xy 2 O 4 xyy 2O4xO4xABCD二、细心填一填：本大题共 8 小题，每小题 4 分，共 32 分． 9、-2 的倒数为______________ 10、使分式x 有意义的 x 的取值范围是 _________ x211、分解因式：a3﹣9a= _________ ． 12、一个多边形的内角和是外角和的 2 倍，则这个多边形为 ______边形 13、已知两圆半径分别为 2 和 3，圆心距为 d ，若两圆有唯一公共点，则 d 的值是 _____________ 14、 在半径为 2 的圆中有一个内接正方形，现随机地往圆内投一粒米，落在正方形内的概 率为_______（注：π 取 3）x＋y＝7 15、若方程组 ，则 3(x＋y)－(3x－5y)的值是__________． 3x－5y＝－316.新概念：[a，b]为一次函数 y=ax+b（a≠0，a，b 为实数）的“关联数”．若“关联数”[1，m-2] 的一次函数是正比例函数，则关于 x 的方程 三、解答题 17、 （8 分）计算题、 3 8 1 1 + =1 的解为 x 1 m．3  2  2 sin 60018、 （8 分）解不等式组：  3x  2  2 x  1(1) 并把它们的解集在数轴上表示出来。

福建省莆田市2014年中考数学试卷一、精心选一选：本大题共8小题，每小题4分，共32分。

每小题给出的四个选项中有且只有一个选项是符合题目要求的，答对的得4分，答错、不答或答案超过一个的一律得0分。

1． 2013的相反数是（ ）2．下列运算正确的是（ ）3．对于一组统计数据：2，4，4，5，6，9．下列说法错误的是（ ）4．如图，一次函数y=（m ﹣2）x ﹣1的图象经过二、三、四象限，则m 的取值范围是（ ）5．如图是一个圆柱和一个长方体的几何体，圆柱的下底面紧贴在长方体的上底面上，那么这个几何体的俯视图可能是（ ）C6．如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A 按顺时针方向旋转到△AB 1C 1的位置，使得点C 、A 、B 1在同一条直线上，那么旋转角等于（ ）7．如图，△ABC内接于⊙O，∠A=50°，则∠OB C的度数为（）8．下列四组图形中，一定相似的是（）二、细心填一填：本大题共8小题，每小题4分，共32分）9．不等式2x﹣4＜0的解集是．10．小明同学在“百度”搜索引擎中输入“中国梦”，搜索到相关的结果个数约为8650000，将这个数用科学记数法表示为．11．如图，点B、E、C、F在一条直线上，AB∥DE，BE=CF，请添加一个条件，使△ABC≌△DEF．12．已知在R t△ABC中，∠C=90°，sinA=，则tanB的值为．13．（4分）如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别为2，5，1，2．则最大的正方形E的面积是．14．（4分）经过某个路口的汽车，它可能继续直行或向右转，若两种可能性大小相同，则两辆汽车经过该路口全部继续直行的概率为．15．（4分）如图，正方形ABCD的边长为4，点P在DC边上且DP=1，点Q是AC上一动点，则DQ+PQ的最小值为．16．（4分）统计学规定：某次测量得到n个结果x1，x2，…，x n．当函数y=++…+取最小值时，对应x的值称为这次测量的“最佳近似值”．若某次测量得到5个结果9.8，10.1，10.5，10.3，9.8．则这次测量的“最佳近似值”为．三、耐心做一做：本大题共9小题，共86分。

莆田市2014年初中毕业（升学）考试试卷物理试题（满分：100分；考试时间：90分钟）注意：本试卷分为“试卷”和“答题卡”两部分，答题时请按答题卡中的“注意事项”要求认真作答，答案写在答题卡上相应位置。

一、单项选择题（每小题2分，共30分）1. 电功的国际单位是A.伏特（V）B.安培（A）C.瓦特（W）D.焦耳（J）2. 金属导体之所以具有良好的导电性，是因为金属导体中存在大量的A.原子B.自由电子C.质子D.中子3. 如图是2013年10月19日凌晨发生的月偏食现象，它的成因是A.光的直传播B.光的反射C.光的折射D.光的色散4. 验电器的两片金属箔片因带电而张开，则这两片金属箔片一定带A.正电B.负电C.同种电荷D.异种电荷5. 我们通过电视观看王亚平太空授课时，不看电视画面，仅凭声音就知道是王亚平在讲话，判断的依据是声音的A.响度B.音色C.音调D.频率6. 下列不符合．．．安全用电原则的是A.发现有人触电时，应先切断电源B.同一插座不要同时使用多个大功率电器C.大功率用电器的金属外壳应接地D.导线或用电器起火时，可立即用水扑灭7. 关于电磁波和声波，下列说法正确的是A.它们都可以在真空中传播B.它们传播的速度都为3×108 m/sC.它们都可以传递信息D.它们都不会对人类和环境造成危害8. 下图中能正确表示光从空气进入玻璃的光路是（）A B C D9. 四冲程汽油机的做功冲性，其能量转化过程是A.机械能转化成内能B.内能转化成机械能C.化学能转化成内能D.内能转化成化学能10. 运动员跳运时总是先助跑一段距离后再起跳，这是为了A.利用惯性B.克服惯性C.增大惯性D.减小惯性11. 关于温度、内能和热量，下列说法正确的是A.温度为0℃的冰没有内能B.温度高的物体比温度低的物体内能大C.温度高的的物体含有的热量多D.物体吸收或放出的热量可以为零，但物体的内能不会为零12. 利用图中甲、乙两种装置，将同一重物分别匀速提升同一高度，不计摩擦及绳子的重量，则A.以各自的滑轮为参照物，重物都是静止的B.拉力甲F 一定比拉力乙F 大C.两种装置的机械效率不一样D.两次重物增加的重力势能不一样13. 高考时，工作人员拿着金属探测仪对考生进行检查，以防止考生将手机等含有金属部分的作弊工具带入考场（如图）。

2014年莆田市九年数学中考模拟试卷（一）满分：150分，考试时间：120分钟一、精心选一选。

（每小题4分，共32分） 1.－3的绝对值是（ ） A 、－3 B 、3 C 、31 D 、－312.下列计算正确的是（ ） A 、()623a a -=－ B 、()222b a b a -=-C 、532523a a a =+ D 、336a a a =÷ 3.下列说法不正确的是（ ）A 、了解一批电视机的使用寿命适合用抽样调查B 、若甲组数据方差S 2甲＝0.27，乙组数据方差S 2乙＝0.2,则乙组数据比甲组数据稳定 C 、某种彩票中奖的概率是10001，买1000张该种彩票一定会中奖 D 、在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件 4.某种的细胞的直径是4105－⨯毫米，这个数是（ ）A 、0.05毫米B 、0.005毫米C 、0.0005毫米D 、0.00005毫米5.如图，下列四个几何体中，它们各自的三视图有两个相同，而另一个不同的几何体是（ ）①正方体 ②圆柱 ③圆锥 ④球 A 、①② B 、②③ C 、②④ D 、③④6.在△ABC 中，∠C ＝900； AC=4，BC=3，则cos ∠B 的值是（ ） A 、54 B 、53C 、34D 、437.如图，已知⊙O 的半径OA ＝6，∠AOB ＝900，则∠AOB 所对的弧AB 的长为（ ） A 、2π B 、3π C 、6π D 、12π8. 已知二次函数2(0)y ax bx c a =++≠的图象如图所示， 给出以下结论①0a b c ++<；②0a b c -+<；③20b a +<； ④0abc >其中所有正确结论的序号是（ ） 二、细心填一填。

（每小题4分，共32分） 9.当有意义。

时，二次根式2_________-x x 10.分解因式：______________422=-a a 11.已知圆锥的底面半径为3cm ，母线长为5cm ， 则这个圆锥的侧面积为_____________。

福建省莆田市中考数学试卷及答案（满分：150分，考题时间：120分钟）一、细心填一填（本大题共10小题，每小题4分，共40分．直接把答案填在题中的横线上．）1．3-的相反数是 ．2．莆田市参加初中毕业、升学考题的学生总人数约为43000人，将43000用科学记数法表示是___________．3．在组成单词“Probability ”（概率）的所有字母中任意取出一个字母，则取到字母“b ”的概率是 ．4．如图，A B 、两处被池塘隔开，为了测量A B 、两处的距离，在AB 外选一适当的点C ，连接AC BC 、，并分别取线段AC BC 、的中点E F 、，测得EF =20m ，则AB =__________m ．5．一罐饮料净重500克，罐上注有“蛋白质含量≥0.4%”，则这罐饮料中蛋白质的含量至少为__________克．6．如图，菱形ABCD 的对角线相交于点O ，请你添加一个条件： ，使得该菱形为正方形．7．甲、乙两位同学参加跳高训练，在相同条件下各跳10次，统计各自成绩的方差得22S S <乙甲，则成绩较稳定的同学是___________．（填“甲”或“乙”）8．已知1O ⊙和2O ⊙的半径分别是一元二次方程()()120x x --=的两根，且122O O =，则1O ⊙和2O ⊙的位置关系是 ．9．出售某种文具盒，若每个获利x 元，一天可售出()6x -个，则当x = 元时，一天出售该种文具盒的总利润y 最大．10．如图，在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====，过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x =≠的图象相交于点12345P P P P P 、、、、，得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、，并设其面积分别为12345S S S S S 、、、、，则5S 的值为 ．二、精心选一选（本大题共6小题，每小题4分，共24分，每小题给出的四个选项中有且只有一个是正确的，请把正确选项的代号写在题后的括号内，答对的得4分；答错、不答或(第4题图) A BDD C BA O （第6题图）O（第10题图）2答案超过一个的一律得0分）．11x 的取值范围是（ ）A ．x ≥0B ．0x <C ．0x ≠D ．0x > 12．下列各式运算正确的是（ ）A ．22a a a ÷= B ．()2224aba b =C ．248a a a ·= D ．55ab b a -= 13．如图是一房子的示意图，则其左视图是（ ）A ．B ．C ． Ｄ． 14．某班5位同学参加“改革开放30周年”系列活动的次数依次为12333、、、、，则这组数据的众数和中位数分别是（ ）A ．22、B ． 2.43、 C．32、 D ．33、15．不等式组2410x x <⎧⎨+>⎩，的解集在数轴上表示正确的是（ ）A ．CD16．如图1，在矩形MNPQ 中，动点R 从点N 出发，沿N →P →Q →M 方向运动至点M 处停止．设点R 运动的路程为x ，MNR △的面积为y ，如果y 关于x 的函数图象如图2所示，则当9x =时，点R 应运动到（ ）A ．N 处B ．P 处C ．Q 处D ．M 处三、耐心做一做（本大题共9小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤．）17．（8分）计算：0133⎛⎫ ⎪⎝⎭．（第16题图）（图1）18．（8分）先化简，再求值：2244242x x x x x x +++÷---，其中1x =．19．（8分）已知：如图在ABCD 中，过对角线BD 的中点O 作直线EF 分别交DA 的延长线、AB DC BC 、、的延长线于点E M N F 、、、．（1）观察图形并找出一对全等三角形：△________≌△____________，请加以证明； （2）在（1）中你所找出的一对全等三角形，其中一个三角形可由另一个三角形经过怎样的变换得到？20．（8分）（1）根据下列步骤画图．．并标明相应的字母:（直接在图１中画图） ①以已知线段AB （图1）为直径画半圆O ；②在半圆O 上取不同于点A B 、的一点C ，连接AC BC 、； ③过点O 画OD BC ∥交半圆O 于点D ． （2）尺规作图．．：（保留作图痕迹，不要求写作法、证明） 已知：AOB ∠（图2）． 求作：AOB ∠的平分线．图2OBABA图1 （第20题图）E B M OD N FC （第19题图） A21．（8分）某校课题研究小组对本校九年级全体同学体育测试情况进行调查，他们随机抽查部分同学体育测试成绩（由高到低分A B C D 、、、四个等级），根据调查的数据绘制成如下的条形统计图和扇形统计图．请根据以上不完整的统计图提供的信息，解答下列问题：（1）该课题研究小组共抽查了__________名同学的体育测试成绩，扇形统计图中B 级所占的百分比b =___________； （2）补全条形统计图；（3）若该校九年级共有400名同学，请估计该校九年级同学体育测试达标（测试成绩C 级以上，含C 级）约有___________名． 22．（10分）已知，如图，BC 是以线段AB 为直径的O ⊙的切线，AC 交O ⊙于点D ，过点D 作弦DE AB ⊥，垂足为点F ，连接BD BE 、．． （1）仔细观察图形并写出四个不同的正确结论：①________，②________ ，③________，④____________（不添加其它字母和辅助线，不必证明）； （2）A ∠=30°，CD，求O ⊙的半径r ．（第22题图）（第21题图）23．（10分）面对全球金融危机的挑战，我国政府毅然启动内需，改善民生．国务院决定从2月1日起，“家电下乡”在全国范围内实施，农民购买人选产品，政府按原价购买总额的．．．．．13%．．．给予补贴返还．某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电，已知购买冰箱的数量是电视机的2倍，且按原价购买冰箱总额为40000元、电视机总额为15000元．根据“家电下乡”优惠政策，每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元，求冰箱、电视机各购买多少台？（2）列出方程（组）并解答．24.（12分）已知：等边ABC △的边长为a ． 探究（1）：如图１，过等边ABC △的顶点A B C 、、依次作AB BC CA 、、的垂线围成MNG △，求证：MNG △是等边三角形且．MN =；探究（2）：在等边ABC △内取一点O ，过点O 分别作OD AB OE BC OF CA ⊥⊥⊥、、，垂足分别为点D E F 、、．①如图2，若点O 是ABC △的重心，我们可利用三角形面积公式及等边三角形性质得到两个正确结论（不必证明）：结论1．OD OE OF ++=；结论2．32AD BE CF a ++=； ②如图3，若点O 是等边ABC △内任意一点，则上述结论12、是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．NM A G CB A FC E BD A F CE B D（图1） （图2） （图3） （第24题图）O A F CE BD （图4）O O25．（14分）已知，如图1，过点()01E -，作平行于x 轴的直线l ，抛物线214y x =上的两点A B 、的横坐标分别为-1和4，直线AB 交y 轴于点F ，过点A B 、分别作直线l 的垂线，垂足分别为点C 、D ，连接CF DF 、．（1）求点A B F 、、的坐标； （2）求证：CF DF ⊥；（3）点P 是抛物线214y x =对称轴右侧图象上的一动点，过点P 作PQ PO ⊥交x 轴于点Q ，是否存在点P 使得OPQ △与CDF △相似？若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．（图1）备用图（第25题图）参照答案说明：（一）考生的解法与“参照答案”不同时，可参照“答案的评分标准”的精神进行评分 （二）如解答的某一步计算出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得分数的二分之一；如属严重的概念性错误，就不给分． （三）以下解答各行右端所注分数表示正确做完该步骤应得的累计分数． （四）评分的最小单位是１分，得分或扣分都不能出现小数． 一、细心填一填（本大题共10小题，每小题4分，共40分．）1．3 2．44.310⨯（不必考虑有效数字） 3．2114．40 5．2 6．AB BC ⊥或AC BD =或AO BO =等 7．甲 8．相交 9．3 10．15二、精心选一选（本大题共6小题，每小题4分，共24分．） 11．A 12．B 13．C 14．D 15．A 16．C 三、耐心做一做（本题共9小题，共86分）17．（1）解：原式=341+ ························ 6分=···························· 8分注：33=（2分）4=（2分），13⎛⎫ ⎪⎝⎭=1（2分）18.解：原式=()()()222222x x x x x x +-⨯-+-+···················· 6分=1x - ····························· 7分当1x =时原式=110-= ························ 8分 注：()()()22222442422?22x x x x x x x x x x +-++=+-=+-÷=⨯-+、、？（各2分） 19． （1）DOE BOF ①△≌△； ······ 2分证明：∵四边形ABCD 是平行四边形∴AD BC ∥ ··········· 3分 ∴EDO FBO E F ∠=∠∠=∠， ········ 4分又∵OD OB =∴()DOE BOF AAS △≌△ ····················· 5分BOM DON ②△≌△ ························ 2分证明：∵四边形ABCD 是平行四边形∴AB CD ∥ ···························· 3分∴MBO NDO BMO DNO ∠=∠∠=∠， ················ 4分 又∵BO DO =EB M O DNFC（第19题图）A∴()BOM DON AAS △≌△ ····················· 5分ABD CDB ③△≌△； ······················· 2分证明：∵四边形ABCD 是平行四边形∴AD CB AB CD ==， ······················· 3分又∵BD DB = ··························· 4分∴()ABD CDB SSS △≌△ ······················ 5分 （2）绕点O 旋转180°后得到或以点O 为中心作对称变换得到． ········ 8分 20．（1）正确完成步骤①、②、③，各得1分，字母标注完整得1分，满分4分．（2）说明：①以点O 为圆心，以适当长为半径作弧交OA OB 、于两点C D 、 ··· 5分②分别以点C D 、为圆心，以大于12CD 长为半径作弧， 两弧相交于点E ······················· 7分③作射线OE ························· 8分21．（1）80 ······················ 2分40% ························· 4分 （2）补全条形图（如右图） ··············· 6分（3）380 ························ 8分 22．（1）BC AB AD BD ⊥⊥，，DF FE BD BE ==，，BDF BEF △≌△， BDF △∽BAD △，BDF BEF ∠=∠，A E DE BC ∠=∠，∥等 （每写出一个正确结论得１分，满分４分．） （2）解:AB 是O ⊙的直径90ADB ∴∠=° ········ 5分又30E ∠=°30A ∴∠=° ····················· 6分12BD AB r ∴== ··················· 7分 又BC 是O ⊙的切线90CBA ∴∠=° ····················· 8分 60C ∴∠=︒在Rt BCD △中，3CD =（第22题图）B A 图1 （第20题图） 图2 O B A E D OC CD（第21题图）tan 602BD rDC ∴==° ···························· 9分 2r ∴= ··································· 10分 23（2）解:依题意得2x -65x= ················ 7分解得10x = ·································· 8分经检验10x =是原分式方程的解 ························· 9分220x ∴=． 答:冰箱、电视机分别购买20台、10台 ·········· 10分 24．证明：如图1，ABC △为等边三角形 60ABC ∴∠=°BC MN BA MG ⊥⊥，∴90CBM BAM ∠=∠=° 9030ABM ABC ∴∠=∠=︒°- ············· 1分9060M ABM ∴∠=︒∠=︒- ·············· 2分 同理：60N G ∠=∠=︒ MNG ∴△为等边三角形． ··························· 3分 在Rt ABM △中，sin sin 603AB a BM a M ===︒在Rt BCN △中，tantan 60BC a BN N ===︒ ················· 4分 MNBM BN ∴=+= ·························· 5分（2）②：结论1成立.证明；方法一：如图2，连接AO BO CO 、、 由ABC AOB BOC AOC S S S S =++△△△△=()12a OD OE OF ++ ··· 7分 作AH BC ⊥，垂足为H ，则sin sin 60AH AC ACB a =∠=⨯︒= 11222ABC S BC AH a ∴==△·· N MA G CB （图1） A FCE BD（图2）OH()11222a OD OE OF a ∴++=·2OD OE OF ∴++=···························· 8分 方法二：如图3，过点O 作GH BC ∥，分别交AB AC 、于点G H 、，过点 H 作HM BC ⊥于点M ， 6060DGO B OHF C ∴∠=∠=∠=∠=°，° AGH ∴△是等边三角形GH AH ∴= ···················6分 OE BC ⊥ OE HM ∴∥∴四边形OEMH 是矩形HM OE ∴= ··················· 7分在Rt ODG △中，sin sin 602OD OGDGO OG =∠=︒=·· 在Rt OFH △中，sin sin 602OF OHOHF OH =∠=︒=·· 在Rt HMC △中，sin sin 602HM HCC HC HC ==︒=··OD OE OF OD HM OF HC ∴++=++=++)GH HC AC =+== ······· 8分 （2）②:结论2成立．证明：方法一：如图４，过顶点A B C 、、依次作边AB BC CA 、、的垂线围成MNG △，由（1）得MNG △为等边三角形且MN = ············· 9分 过点O 分别作OD MN '⊥于D ',OE NG '⊥于NG 于点E OF MG ''⊥，于点F ' 由结论1得：32OD OE OF a '+'+'=== ·················· 10分 又OD AB AB MG OF MG ⊥⊥'⊥，，90ADO DAF OF A ∴∠=∠'=∠'=︒A F CEBD（图4）O F 'D 'MGNE 'AF CE BD （图3）OM HG∴四边形ADOF '为矩形 OF ∴'=AD同理：OD BE '=，OE CF '= ························· 11分32AD BE CF OD OE OF a ∴++='+'+'= ··················· 12分方法二：（同结论1方法二的辅助线） 在Rt OFH △中，tan 3OF FH OHF ==∠在Rt HMC △中，sin HM HC C == ······ 9分CF HC FH ∴=+=+同理：3333AD OF OD BE =+=+， ············· 10分 AD BE CF ∴++=+++=)OD OE OF ++ ····························· 11分由结论1得：OD OE OF ++=32AD BE CF a ∴++== ······················· 12分 方法三：如图5，连接OA OB OC 、、，根据勾股定理得：22222BE OE OB BD OD +==+① 22222CF OF OC CE OE +==+②22222AD OD AO AF OF +==+③ ······················· 9分①+②+③得：222222BE CF AD BD CE AF ++=++ ····················· 10分()()()222222BE CF AD a AD a BE a CF ∴++=-+-+-222222222a AD a AD a BE a BE a CF a CF =-++-++-+ ··········· 11分A FC EBD（图5）OAF CBD（图3）OHG整理得：()223a AD BE CF a ++=32AD BE CF a ∴++= ···························· 12分25．（1）解:方法一，如图1，当1x =-时,14y = 当4x =时,4y =∴1A ⎛⎫- ⎪⎝⎭1，4 ····················· 1分()44B ， ······················· 2分设直线AB 的解析式为y kx b =+ ············ 3分则1444k b k b ⎧-+=⎪⎨⎪+=⎩ 解得341k b ⎧=⎪⎨⎪=⎩ ∴直线AB 的解析式为314y x =+ ············ 4分 当0x =时,1y =()01F ∴， ··································· 5分 方法二:求A B 、两点坐标同方法一,如图2,作FG BD ⊥,AH BD ⊥,垂足分别为G 、H ,交y 轴于点N ,则四边形FOMG 和四边形NOMH 均为矩形,设FO x = ·············· 3分BGF BHA △∽△BG FGBH AH ∴=441544x -∴=- ································· 4分解得1x =()0F ∴，1 ·································· 5分(2)证明：方法一：在Rt CEF △中，1,2CE EF ==22222125CF CE EF ∴=+=+=CF ∴= ·································· 6分（图1）（图2）在Rt DEF △中，42DE EF ==，222224220DF DE EF ∴=+=+=DF ∴=由（1）得()()1141C D ---，，，5CD ∴=22525CD ∴==222CF DF CD ∴+= ··························· 7分90CFD ∴∠=°∴CF DF ⊥ ······························· 8分方法二：由 （1）知5544AF AC ===，AF AC ∴= ······························· 6分同理：BF BD = ACF AFC ∴∠=∠ AC EF ∥ACF CFO ∴∠=∠AFC CFO ∴∠=∠ ···························· 7分 同理：BFD OFD ∠=∠90CFD OFC OFD ∴∠=∠+∠=°即CF DF ⊥ ······························· 8分（3）存在.解：如图3，作PM x ⊥轴，垂足为点M ··· 9分 又PQ OP ⊥Rt Rt OPM OQP ∴△∽△ PM OMPQ OP∴= PQ PMOP OM∴= ·············· 10分 设()2104P x x x ⎛⎫> ⎪⎝⎭，，则214PM x OM x ==， ①当Rt Rt QPO CFD △∽△时，12PQ CF OP DF ===··························· 11分图321142xPM OM x ∴== 解得2x =()121P ∴， ································· 12分 ②当Rt Rt OPQ CFD △∽△时，2PQ DF OP CF === ···························13分 2142xPM OM x ∴== 解得8x =()2816P ∴，综上，存在点()121P ，、()2816P ，使得OPQ △与CDF △相似. ········· 14分。

2013-2014学年（上）期末考试试卷九年数学 A(满分:150分；考试时间:120分钟)一、精心选一选：本大题共8小题，每小题4分，共32分．每小题给出的四个选项中有且只有一个选项是符合题目要求的．答对的得4分，答错、不答或答案超过一个的一律得O分．1.下列各式一定是二次根式的是（）2.已知关于的方程有两个不同的实数根，则的取值范围是（）A、 B、C、 D、3.下列图形中，是中心对称图形，但不是轴对称图形是（）A、正方形B、矩形C、菱形D、平行四边形4. 下列命题中，假命题是（）A.两条弧的长度相等，它们是等弧B.等弧所对的圆周角相等C.直径所对的圆周角是直角D.一条弧所对的圆心角等于它所对圆周角的2倍.5.把二次函数23xy=的图象向左平移2个单位，再向上平移1个单位，二次函数关系式是（）A ()1232+-=xy; B ()1232-+=xy;C ()1232--=xy D ()1232++=xy6.下图中几何体的左视图是（）.7. 当锐角30>α时，则αcos的值是（）A．大于12B．小于12C8、如图，AB∥CD，AC、BD交于O，BO=7，DO=3，AC=25，则AO长为（）A．10 B．12．5 C．15 D．17．5二、细心填一填：本大题共8小题，每小题4分，共32分．。

10. x取值范围是。

11. 已知圆锥的底面半径是2，母线长是4，则圆锥的侧面积是________。

12.如果，则________。

APB= 。

16.将4个数a b c d，，，排成2行、2列，两边各加一条竖直线记成a bc d，定义a bc dad bc=-，上述记号就叫做2阶行列式．若1111x xx x+--+6=，则x=．A B C D第8题图第3页，共8页 第4页，共8页三、耐心做一做：本大题共9小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤．17. 计算：(1-)2008－(π－3)0°·tan45°（8分）18计算：.⎛÷ ⎝（8分） 19. 解方程：4x 2-3x-1=0（8分）20. 如图，在平面直角坐标系中，将四边形ABCD 称为“基本图形”，且各点的坐标分别为A （4，4），B （1，3），C （3，3），D （3，1）. （8分） （1）画出“基本图形”关于原点O 对称的四边形A 1B 1C 1D 1，并求出A 1，B 1，C 1，D 1的坐标.A 1( ， )，B 1( ， )，C 1( ， )，D 1( ， ) ； （2）画出“基本图形”关于x 轴的对称图形A 2B 2C 2D 2 ； （3）画出四边形A 3B 3C 3D 3，使之与前面三个图形组成的图形既是中心对称图形又是轴对称图形.21. 四张质地相同的卡片如图所示．将卡片洗匀后，背面朝上放置在桌面上．（8分）(1)求随机抽取一张卡片，恰好得到数字2的概率；(2)小贝和小晶想用以上四张卡片做游戏，游戏规则见信息图．你认为这个游戏公平吗?请用列表法或画树形图法说明理由．22.如图，四边形ABCD 内接于⊙O ，BD 是⊙O 的直径，AE CD ⊥BDE ∠． （1）求证：AE 是⊙O 的切线； （2）若301cm DBC DE ∠==，，求BD 的长．23.某商厦今年一月份销售额为60万元，二月份由于经营不善，销售额下降10%，以后改进管理，大大激发全体员工的积极性，月销售额大幅度上升，到四月份销售额猛增到96万元，求三、四月份平均每月增长的百分率是多少？（精确到0.1%）（10分）24. 在△ABC 中，AB ＝BC ＝2，∠ABC ＝120°，将△ABC 绕点B 顺时针旋转角α(0°＜α＜90°)得△A 1BC 1，A 1B 交AC 于点E ，A 1C 1分别交AC ，BC 于D ，F 两点．(12分)(1)如图(a)，观察并猜想，在旋转过程中，线段EA 1与FC 是怎样的数量关系?并证明你的结论；(2)如图(b)，当α＝30°时，试判断四边形BC 1DA 的形状，并说明理由； (3)在(2)的情况下，求ED 的长．图(a) 图(b)25. 如图，已知抛物线234y x bx c =-++与坐标轴交于A B C ，，三点，点A 的横坐标为1-，过点(03)C ，的直线334y x t=-+与x 轴交于点Q ，点P 是线段BC 上的一个动点，PH OB ⊥于点H ．若5PB t =，且01t <<． （1）求b c ，的值（2）求出点B Q P ，，的坐标（其中Q P ，用含t 的式子表示）（3）依点P 的变化，是否存在t 的值，使PQB △若存在，求出所有t 的值；若不存在，说明理由．第20题图2013-2014学年（上）期末考试答题卷九年数学 A(满分:150分；考试时间:120分钟)一、精心选一选：本大题共8小题，每小题4分，共32分．每小题给出的四个选项中有且只有一个选项是符合题目要求的．答对的得4分，答错、不答或答案超过一个的一律得O分．二、细心填一填：本大题共8小题，每小题4分，共32分．9. ________。

莆田市2014年初中毕业（升学）考试试卷英语试题（满分：150分；考试时间：120分钟）听力部分（满分30分）I. 听音选图听句子，根据你所听到的内容，选择正确的图画顾序。

每个句子读两遍。

（6分）1. ________2. ________3. ________4. ________5. ________6. ________Ⅱ．听对话根据你所听到的内容，选择正确的答案。

每段对话读两遍。

（12分）第一节听下面4段对话，每段对话后有1个小题，从题中所给的A、B、C三个选项中选出最佳选项。

（6分）( )7. Who wrote the letter?A. Kate.B. Sally.C. Jane.( )8. What did Linda buy for her dad on Father's Day?A. A watch.B. A shirt.C. A tie.( )9. When are they going to meet tomorrow?A. At 7:30 a.m.B. At 8:00 a.m.C. At 8:30 a.m. .( )10. What does the man ask the woman to do?A. To buy a hat.B. To leave the company.C. To keep some secret.第二节听下面2段对话，每段对话后有2个小题，从题中所给的A、B、C三个选项中选出最佳选项。

（6分）听第5段材料，回答第11. 12题。

( )II. What day is it today?A. Thursday.B. Friday.C. Saturday.( )12. Where are they going tomorrow?A. Nanri Island.B. Meizhou Island.C. Huanggua Island.听第6段材料，回答第13、14题。

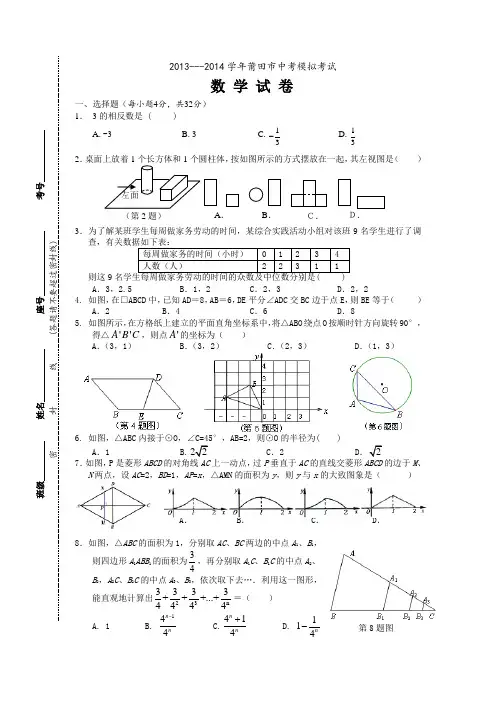
2013---2014学年莆田市中考模拟考试数 学试 卷一、选择题（每小题4分，共32分）1． 3的相反数是 ( )A .-3B .3C .13-D.132．按如图所示的方式摆放在一起，其左视图是（ ）3．为了解某班学生每周做家务劳动的时间，某综合实践活动小组对该班9名学生进行了调则这9A ．3，2.5 B ．1，2 C ．2，3 D ．2，2 4. 如图，在□ABCD 中，已知AD ＝8，AB ＝6，DE 平分∠ADC 交BC 边于点E ，则BE 等于（ ） A ．2 B ．4 C ．6 D ．8 5. 如图所示，在方格纸上建立的平面直角坐标系中，将△ABO 绕点O 按顺时针方向旋转90°，得△''A B C ，则点'A 的坐标为（ ） A ．（3，1） B ．（3，2） C ．（2，3） D ．（1，3）6. 如图，△ABC 内接于⊙O，∠C=45°，AB=2，则⊙O 的半径为( )A ．1 B.．2 D 7．如图，P 是菱形ABCD 的对角线AC 上一动点，过P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点，设AC =2，BD =1，AP =x ，△AMN 的面积为y ，则y 与x 的大致图象是（ ）A ．B ．C ．D ．8．如图，△ABC 的面积为1，分别取AC 、BC 两边的中点A 1、B 1，则四边形A 1ABB 1的面积为34，再分别取A 1C 、B 1C 的中点A 2、 B 2，A 2C 、B 2C 的中点A 3、B 3，依次取下去…．利用这一图形，能直观地计算出23n 3333+++...+4444＝（ ） A. 1 B. 144n n - C.414n n+ D. 114n -第8题图（第2题）A ．B ．Ｃ．Ｄ．二、填空题（每小题4分，共32分） 921011是边长相等的正方形），则小鸟落在阴影方格地面上的概率为_______．12．不等式组⎪⎩⎪⎨⎧->-≥-xx x 3111221的解集是 ．13141516．小赵对芜湖科技馆富有创意的科学方舟形象设计很有兴趣，他回家后将一正五边形纸片沿其对称轴对折．旋转放置，做成科学方舟模型．如图所示，该正五边形的边心距OB 长为AC 为科学方舟船头A 到船底的距离，请你计算12AC AB += ． 三、解答题（共86分，解答应写出文字说明、证明过程或推演步骤） 17．（8101()(3)2π-+-18.（8分）先化简，再求值：22282()24a a a a a a+-+÷--，其中2sin 602tan 45a =︒-︒．19．（8分）“五·一”假期，某公司组织部分员工分别到A 、B 、C 、D 四地旅游，公司按定额购买了前往各地的车票.下图是未制作完的车票种类和数量的条形统计图，根据统计图回答下列问题：（1）若去D 地的车票占全部车票的10%，请求出D 地车票的数量，并补全统计图；（2）若公司采用随机抽取的方式分发车票，每人抽取一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么员工小胡抽到去A 地的概率是 .（3）若有一张车票，小王、小李都想要，决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定，具体规则是：“每人各抛掷一次，若小王掷得着地一面的数字比小李掷得着地一面的数字小，车票给小王，图”的方法分析，这个规则对双方是否公平？第16题图20.（8分）已知A(n ，-2)，B(1，4)是一次函数y kx b =+的图象和直线AB 与y 轴交于点C ． (1) 求反比例函数和一次函数的关系式； (2)(直接写出答案)．使△AMN 与△ABC 相似，求线段MN 的长； （2）如图2，是由100个边长为1的小正方形组成的10×10正方形网格，设顶点在这些小正方形顶点的三角形为格点三角形．试直接写出在所给的网格中与△ABC 相似且面积最大的格点三角形的个数，并画出其中的一个（不需证明）．22.（10分）如图，D 为⊙O 上一点，点C 在直径BA 的延长线上，且∠CDA =∠CBD .（1）求证:CD 是⊙O 的切线； （2） 过点B 作⊙O 的切线交CD 的延长线于点E ，若BC =6，tan ∠CDA =23，求BE 的长。

1. 下列哪个数是质数？
- A. 15
- B. 18
- C. 29
- D. 42
2. 一个长方形的周长是36厘米，长是宽的两倍。

那么这个长方形的面积是多少平方厘米？
- A. 72
- B. 80
- C. 96
- D. 108
3. 一个角的度数是60度，它的补角是多少度？
- A. 30
- B. 45
- C. 60
- D. 120
4. 下列方程中，哪个方程的解是x = 3？
- A. 2x + 5 = 11
- B. 3x - 7 = 2
- C. x/2 + 4 = 7
- D. 5x - 3 = 12
5. 已知直角三角形的两个角分别为30度和60度，那么第三个角的度数是？
- A. 30
- B. 45
- C. 60
- D. 90
6. 一个圆的半径为7厘米，那么它的直径是多少厘米？
- A. 7
- B. 14
- C. 21
- D. 28
7. 如果一个数的平方是49，那么这个数的绝对值是？
- A. 7
- B. 14
- C. 49
- D. 0
8. 在一个等边三角形中，每个角的度数是多少？
- A. 45
- B. 60
- C. 90
- D. 120
9. 已知一个正方形的周长为32厘米，那么它的边长是多少厘米？
- A. 4
- B. 8
- C. 12
- D. 16
10. 在下面的选项中，哪个数不是一个偶数？
- A. 14
- B. 22
- C. 31
- D. 46。

第1页，共8页第2页，共8页2013-2014学年（上）期末考试试卷九年 数学 A(满分: 150分；考试时间: 120分钟)一、精心选一选：本大题共8小题，每小题4分，共32分．每小题给出的四个选项中有且只有一个选项是符合题目要求的．答对的得4分，答错、不答或答案超过一个的一律得O 分．1. 下列各式一定是二次根式的是（ ）2. 已知关于的方程有两个不同的实数根，则的取值范围是（ ）A 、B 、C 、D 、3. 下列图形中，是中心对称图形，但不是轴对称图形是（ ）A 、正方形B 、矩形C 、菱形D 、平行四边形4. 下列命题中，假命题是（ ）A.两条弧的长度相等，它们是等弧B.等弧所对的圆周角相等C.直径所对的圆周角是直角D.一条弧所对的圆心角等于它所对圆周角的2倍. 5. 把二次函数23x y =的图象向左平移2个单位，再向上平移1个单位，二次函数关系式是（ ）A ()1232+-=x y ; B ()1232-+=x y ;C ()1232--=x y D ()1232++=x y6. 下图中几何体的左视图是（ ）.7. 当锐角30>α时，则αcos 的值是（ ）A ．大于12 B ．小于12 C 8、 如图，AB ∥CD ，AC 、BD 交于O ，BO =7，DO =3，AC =25， 则AO 长为（ ）A ．10B ．12．5C ．15D ．17．5二、细心填一填：本大题共8小题，每小题4分，共32分．。

10. x 取值范围是 。

11. 已知圆锥的底面半径是2，母线长是4，则圆锥的侧面积是________。

12. 如果，则________。

APB= 。

16. 将4个数a b cd ，，，排成2行、2列，两边各加一条竖直线记成a bc d ，定义a b c d ad bc =-，上述记号就叫做2阶行列式．若1111x x x x +--+6=，则x = ．A B C D第8题图第3页，共8页第4页，共8页三、耐心做一做：本大题共9小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤．17. 计算：(1-)2008－(π－3)0°·tan45°（8分）18计算：.⎛÷ ⎝．（8分） 19. 解方程：4x 2-3x-1=0（8分）20. 如图，在平面直角坐标系中，将四边形ABCD 称为“基本图形”，且各点的坐标分别为A （4，4），B （1，3），C （3，3），D （3，1）. （8分）（1）画出“基本图形”关于原点O 对称的四边形A 1B 1C 1D 1，并求出A 1，B 1，C 1，D 1的坐标. A 1( ， )，B 1( ， )，C 1( ， )，D 1( ， ) ； （2）画出“基本图形”关于x 轴的对称图形A 2B 2C 2D 2 ； （3）画出四边形A 3B 3C 3D 3，使之与前面三个图形组成的图形既是中心对称图形又是轴对称图形.21. 四张质地相同的卡片如图所示．将卡片洗匀后，背面朝上放置在桌面上．（8分）(1)求随机抽取一张卡片，恰好得到数字2的概率；(2)小贝和小晶想用以上四张卡片做游戏，游戏规则见信息图．你认为这个游戏公平吗?请用列表法或画树形图法说明理由．22.如图，四边形ABCD 内接于⊙O ，BD 是⊙O 的直径，AE CD ⊥BDE ∠． （1）求证：AE 是⊙O 的切线； （2）若301cm DBC DE ∠==，，求BD 的长．23.某商厦今年一月份销售额为60万元，二月份由于经营不善，销售额下降10%，以后改进管理，大大激发全体员工的积极性，月销售额大幅度上升，到四月份销售额猛增到96万元，求三、四月份平均每月增长的百分率是多少？（精确到0.1%）（10分）24. 在△ABC 中，AB ＝BC ＝2，∠ABC ＝120°，将△ABC 绕点B 顺时针旋转角α(0°＜α＜90°)得△A 1BC 1，A 1B 交AC 于点E ，A 1C 1分别交AC ，BC 于D ，F 两点．(12分)(1)如图(a)，观察并猜想，在旋转过程中，线段EA 1与FC 是怎样的数量关系?并证明你的结论；(2)如图(b)，当α＝30°时，试判断四边形BC 1DA 的形状，并说明理由； (3)在(2)的情况下，求ED 的长．图(a) 图(b)25. 如图，已知抛物线234y x bx c =-++与坐标轴交于A B C ，，三点，点A 的横坐标为1-，过点(03)C ，的直线334y x t=-+与x 轴交于点Q ，点P 是线段BC 上的一个动点，PH OB ⊥于点H ．若5PB t =，且01t <<． （1）求b c ，的值（2）求出点B Q P ，，的坐标（其中Q P ，用含t 的式子表示）（3）依点P 的变化，是否存在t 的值，使PQB △若存在，求出所有t 的值；若不存在，说明理由．第20题图第5页，共8页第6页，共8页2013-2014学年（上）期末考试答题卷九年 数学 A(满分: 150分；考试时间: 120分钟)一、精心选一选：本大题共8小题，每小题4分，共32分．每小题给出的四个选项中有且只有一个选项是符合题目要求的．答对的得4分，答错、不答或答案超过一个的一律得O 分．二、细心填一填：本大题共8小题，每小题4分，共32分．9. ________。

一、选择题（共10小题，每小题4分，满分40分）1．（4分）﹣2的相反数是（ ）A ．12B ．2C ．12- D ．﹣2 2．（4分）下列运算正确的是（ ）A ．235()a a =B ．246a a a +=C ．331a a ÷=D ．32()a a a a -÷= 3．（4分）右边几何体的俯视图是（ ）A ．B ．C ．D ．4．（4分）下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A ． 等边三角形B ． 平行四边形C ． 矩形D ．正五边形5．（4分）不等式组21112x x +>⎧⎪⎨≤⎪⎩的解集在数轴上可表示为（ ） A ． B ． C ． D ．6．（4分）如图，AE ∥DF ，AE =DF ，要使△EAC ≌△FDB ，需要添加下列选项中的（ ）A ．AB =CD B ．EC =BF C ．∠A =∠D D ．AB =BC7．（4分）在一次定点投篮训练中，五位同学投中的个数分别为3，4，4，6，8，则关于这组数据的说法不正确的是（ ）A ．平均数是5B ．中位数是6C ．众数是4D ．方差是3.28．（4分）如图，在⊙O 中，AB AC =，∠AOB =50°，则∠ADC 的度数是（ ）A ．50°B ．40°C ．30°D ．25°9．（4分）命题“关于x 的一元二次方程210x bx ++=，必有实数解．”是假命题．则在下列选项中，可以作为反例的是（ ）A ．b =﹣3B ．b =﹣2C ．b =﹣1D ．b =210．（4分）数学兴趣小组开展以下折纸活动：（1）对折矩形ABCD ，使AD 和BC 重合，得到折痕EF ，把纸片展平；（2）再一次折叠纸片，使点A 落在EF 上，并使折痕经过点B ，得到折痕BM ，同时得到线段BN ． 观察，探究可以得到∠ABM 的度数是（ ）A ．25°B ．30°C ．36°D ．45°二、细心填一填（共6小题，每小题4分，满分24分）11．（4分）要了解一批炮弹的杀伤力情况，适宜采取 （选填“全面调查”或“抽样调查”）．12．（4分）八边形的外角和是 ． 13．（4分）中国的陆地面积约为9 600 000km 2，把9 600 000用科学记数法表示为．14．（4分）用一根长为32cm 的铁丝围成一个矩形，则围成矩形面积的最大值是 cm 2．15．（4分）如图，AB 切⊙O 于点B ，OA =23，∠BAO =60°，弦BC ∥OA ，则BC 的长为 （结果保留π）．16．（4分）谢尔宾斯基地毯，最早是由波兰数学家谢尔宾斯基制作出来的：把一个正三角形分成全等的4个小正三角形，挖去中间的一个小三角形；对剩下的3个小正三角形再分别重复以上做法…将这种做法继续进行下去，就得到小格子越来越多的谢尔宾斯基地毯（如图）．若图1中的阴影三角形面积为1，则图5中的所有阴影三角形的面积之和是 ．三、耐心做一做（共10小题，满分86分）17．（7分）计算：0229(1)--+-．18．（7分）解分式方程：232x x =+． 19．（8分）先化简，再求值：222a ab b a b b a----，其中13a =+，13b =-+． 20．（10分）为建设”书香校园“，某校开展读书月活动，现随机抽取了一部分学生的日人均阅读时间x （单位：小时）进行统计，统计结果分为四个等级，分别记为A ，B ，C ，D ，其中：A ：0≤x ＜0.5，B ：0.5≤x ＜1，C ：1≤x ＜1.5，D ：1.5≤x ＜2，根据统计结果绘制了如图两个尚不完整的统计图．（1）本次统计共随机抽取了名学生；（2）扇形统计图中等级B所占的圆心角是；（3）从参加统计的学生中，随机抽取一个人，则抽到“日人均阅读时间大于或等于1小时”的学生的概率是；（4）若该校有1200名学生，请估计“日人均阅读时间大于或等于0.5小时”的学生共有人．21．（8分）如图，菱形ABCD的对角线AC，BD相交于点O，点E，F分别是边AB，AD的中点．（1）请判断△OEF的形状，并证明你的结论；（2）若AB=13，AC=10，请求出线段EF的长．22．（8分）如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE=35．求证：CB是⊙O的切线．23．（8分）某动车站在原有的普通售票窗口外新增了无人售票窗口，普通售票窗口从上午8点开放，而无人售票窗口从上午7点开放，某日从上午7点到10点，每个普通售票窗口售出的车票数1y（张）与售票时间x （小时）的变化趋势如图1，每个无人售票窗口售出的车票数2y （张）与售票时间x （小时）的变化趋势是以原点为顶点的抛物线的一部分，如图2，若该日截至上午9点，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．（1）求图2中所确定抛物线的解析式；（2）若该日共开放5个无人售票窗口，截至上午10点，两种窗口共售出的车票数不少于900张，则至少需要开放多少个普通售票窗口？24．（8分）如图，矩形OABC ，点A ，C 分别在x 轴，y 轴正半轴上，直线6y x =-+交边BC 于点M （m ，n ）（m ＜n ），并把矩形OABC 分成面积相等的两部分，过点M 的双曲线k y x =（0x >）交边AB 于点N ．若△OAN 的面积是4，求△OMN 的面积．25．（10分）抛物线2y ax bx c =++，若a ，b ，c 满足b =a +c ，则称抛物线2y ax bx c =++为“恒定”抛物线．（1）求证：“恒定”抛物线2y ax bx c =++必过x 轴上的一个定点A ；（2）已知“恒定”抛物线233y x =-的顶点为P ，与x 轴另一个交点为B ，是否存在以Q 为顶点，与x 轴另一个交点为C 的“恒定”抛物线，使得以P A ，CQ 为边的四边形是平行四边形？若存在，求出抛物线解析式；若不存在，请说明理由．26．（12分）在Rt △ACB 和Rt △AEF 中，∠ACB =∠A EF =90°，若点P 是BF 的中点，连接PC ，PE ． 特殊发现：如图1，若点E ，F 分别落在边AB ，AC 上，则结论：PC =PE 成立（不要求证明）．问题探究：把图1中的△AEF绕着点A顺时针旋转．（1）如图2，若点E落在边CA的延长线上，则上述结论是否成立？若成立，请给予证明；若不成立，请说明理由；（2）如图3，若点F落在边AB上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）记ACkBC，当k为何值时，△CPE总是等边三角形？（请直接写出k的值，不必说明理由）。