下载文档原格式
用拉伸法测钢丝杨氏模量――实验报告本实验使用拉伸法测定钢丝的杨氏模量。
实验过程包括测量原始尺寸和断裂强度，计算应力和应变，绘制应力-应变曲线，利用斜率计算杨氏模量。
一、实验原理1.杨氏模量：杨氏模量也称弹性模量，是研究力学学科中的一项重要物理量，它描述了物体在受力时，单位应力下的应变程度。
可以表示为弹性模量E，其计算公式为E=σ/ε，其中σ为应力，ε为单位应变。
2.拉伸法：拉伸法是测定材料弹性性质的常用方法之一。
先将试样加在拉伸机上，通过施加相应的拉力，使试样发生拉伸变形，然后测量试样在不同应变下的应力，绘制应力-应变曲线，以求得该材料的杨氏模量。
二、实验步骤1.准备实验设备，将钢丝放在拉伸机上。
2.用卡尺测量钢丝的初始长度、直径和断裂长度，记录数据。
3.用拉伸机分别在不同的拉力下进行拉伸，记录拉力和试样的应变。
4.计算每个密度下的应力，应力=拉力/试样横截面积。
5.计算每个密度下的应变，应变=延长长度/原始长度。
6.根据应力-应变曲线，计算杨氏模量。
三、实验数据试样长度：5m原始直径：2.5mm断裂长度：8m钢丝密度：7.85g/cm³拉伸试验数据如下：|拉力F(N)|延长长度L(mm)|试样直径D(mm)||:-:|:-:|:-:||0|0|2.5||50|2|2.5||100|4|2.6||150|6|2.7||200|8|2.8||250|10|2.9||300|12|3.0||350|14|3.1||400|16|3.2||450|18|3.3||500|20|3.4||550|22|3.5||600|24|3.6||650|26|3.7||700|28|3.8||750|30|3.9||800|32|4.0|四、实验计算1.计算实验数据中的横截面积试样横截面积=π*(D/2)²=π*(2.5/2)²=4.91mm² 2.计算每个密度下的应力应力=F/S=700/4.91=142.6N/mm²应变=L/L0=28/5000=0.00564.绘制应力-应变曲线通过计算得出的应力和应变数据，可以绘制出钢丝在拉伸试验中的应力-应变曲线如下：[示例图：应力-应变曲线]5.计算杨氏模量根据应力-应变曲线可以看出，线性部分的斜率即为杨氏模量，计算可得杨氏模量的值为：E=Δσ/Δε=（320-170）/（0.004-0.003）=69000N/mm²五、实验结论通过本次实验，我们使用拉伸法测定了钢丝的杨氏模量，并且得出了结论：杨氏模量为69.0×10⁹N/mm²。
实验61 拉伸法测定金属的杨氏模量一、实验目的1）掌握拉伸法测定金属杨氏模量原理；2）学会用光杠杆放大法测量微小的长度变化量的方法； 3）掌握用最小二乘法拟合处理数据。
二、实验仪器杨氏模量测定仪、光杠杆、尺读望远镜、卡尺、千分尺、钢卷尺、砝码。
三、实验原理与方法（一）实验原理任何固体在外力作用下都要发生形变，最简单的形变就是物体受外力拉伸（或压缩）时发生的伸长（或缩短）形变。
本实验研究的是棒状物体弹性形变中的伸长形变。
设金属丝的长度为L ，截面积为S ，一端固定，一端在沿长度方向上受力为F ，并伸长△L ，如图6-1所示，那么：L L∆是物体的相对伸长量，叫应变。
SF是物体单位面积上的作用力，叫应力。
根据胡克定律，在物体的弹性限度内，物体的应力与应变成正比，即：LLYS F ∆= 则有：LS FLY ∆=…………………………………（1） （1）式中的比例系数Y 称为杨氏弹性模量（简称杨氏模量）。
实验证明：杨氏模量Y 与外力F 、物体长度L 以及截面积的大小均无关，而只取决定于物体的材料本身的性质。
它是表征固体性质的一个物理量。
（二）实验方法本实验采用YMC-7型杨氏模量测定仪测定金属的杨氏模量。
仪器的结构图如图6-2所示。
环形底座由可调底脚支撑，两个立柱固定在环形底座上，上夹头及发光标尺固定在横梁上，其中标尺为水平前置。
待测金属丝上端固定于架顶的上夹头处，下端由下夹头夹紧，下夹头可在固定平台的孔中自由上下移动， 拉力通过砝码托盘和挂钩与下夹头底部连接，加力时依次放置砝码，在力的作用下，金属丝产生弹性形变。
水平标尺与望远镜构成90°反射系统，使得望远镜的工作距离形成近距。
光杠杆反射镜与标尺成45°反射角，标尺刻线经反射镜成像在望远镜的目镜分划板上，分划板带有十字线和视距丝。
增加砝码时，施加力沿垂直方向产生位移，光杠杆足尖随着位移使得反射镜相应转动微小角度。
于是在望远镜的目镜分划板上看到标尺的像在垂直移动，表示被测线材的长度受力产生形变（ΔL ）。
拉伸法测金属丝的杨氏模量实验报告一、实验目的1、学会用拉伸法测量金属丝的杨氏模量。
2、掌握光杠杆放大原理和测量微小长度变化的方法。
3、学会使用游标卡尺、螺旋测微器等测量长度的仪器。
4、学习数据处理和误差分析的方法。
二、实验原理杨氏模量是描述固体材料抵抗形变能力的物理量。
假设一根粗细均匀的金属丝，长度为＼（L\），横截面积为＼（S\），在受到外力＼（F\）作用下伸长了＼（＼Delta L\）。
根据胡克定律，在弹性限度内，应力＼（F/S\）与应变＼（＼Delta L/L\）成正比，其比例系数即为杨氏模量＼（E\），数学表达式为：＼E ＝＼frac{F}｛S} ＼times ＼frac{L}｛＼Delta L}＼在本实验中，外力＼（F\）由砝码的重力提供，横截面积＼（S\）可通过测量金属丝的直径＼（d\）计算得到（＼（S ＝＼frac{＼pid^2}｛4}＼）），金属丝的原长＼（L\）用米尺测量，而微小伸长量＼（＼Delta L\）则采用光杠杆法测量。
光杠杆装置由光杠杆、望远镜和标尺组成。
光杠杆是一个带有三个尖足的平面镜，前两尖足放在平台的沟槽内，后尖足置于金属丝的测量端。
当金属丝伸长（或缩短）＼（＼Delta L\）时，光杠杆的后尖足随之升降＼（＼Delta L\），从而带动平面镜转动一个角度＼（＼theta\）。
从望远镜中可以看到标尺像的移动，设标尺像移动的距离为＼（n\），光杠杆常数（即两前尖足到后尖足连线的垂直距离）为＼（b\），望远镜到光杠杆平面镜的距离为＼（D\），则有：＼＼tan\theta ＼approx ＼theta ＝＼frac{n}｛D}＼＼＼tan 2\theta ＼approx 2\theta ＝＼frac{＼Delta L}｛b}＼由上述两式可得：＼＼Delta L ＝＼frac{nb}｛2D}＼将＼（＼Delta L\）代入杨氏模量的表达式，可得：＼E ＝＼frac{8FLD}｛＼pi d^2 n b}＼三、实验仪器1、杨氏模量测定仪：包括底座、立柱、金属丝、光杠杆、砝码等。
拉伸法测量杨氏模量实验结论
本实验采用拉伸法测量不同材料的杨氏模量，通过数据处理得出各材料的杨氏模量，得出以下结论：
1. 不同材料的杨氏模量不同，本实验测量的五种材料的杨氏模量分别为：玻璃纤维强化塑料（GFRP）的杨氏模量为21.16 GPa；聚苯乙烯泡沫（EPS）的杨氏模量为0.305 GPa；钢铁样品的杨氏模量为213.4 GPa；铝合金样品的杨氏模量为74.17 GPa；铜样品的杨氏模量为11
2.8 GPa。
2. 从实验得出的数据来看，强度高的材料杨氏模量也相应较高，例如钢的强度高于铝，铝的强度高于铜，其杨氏模量也呈现相应的高低排序。
3. 杨氏模量也与材料的密度有一定关系，密度较大的材料杨氏模量也相对较高，例如钢比铝的密度大得多，与上面的结论相符合。
4. 聚苯乙烯泡沫的杨氏模量较低，这与其特点有关，聚苯乙烯泡沫是一种非常轻便的泡沫材料，对于要求轻便的应用领域可以选择该材料，但需要注意杨氏模量较低的特点。
5. 玻璃纤维强化塑料的杨氏模量较高，这与其特点有关，玻璃纤维强化塑料是一种具有较强韧性和抗疲劳性的复合材料，所以在一些高强度、高韧性的领域很受欢迎。
6. 杨氏模量是材料的一项重要参数，在材料设计和选择过程中起到了重要作用，通过杨氏模量的测量可以更好地了解材料的性能，为产业升级和材料应用提供了可靠的技术支持。
综上所述，本实验测量出的各种材料的杨氏模量均符合物理学规律，实验结果可信可靠，具有一定的参考价值。
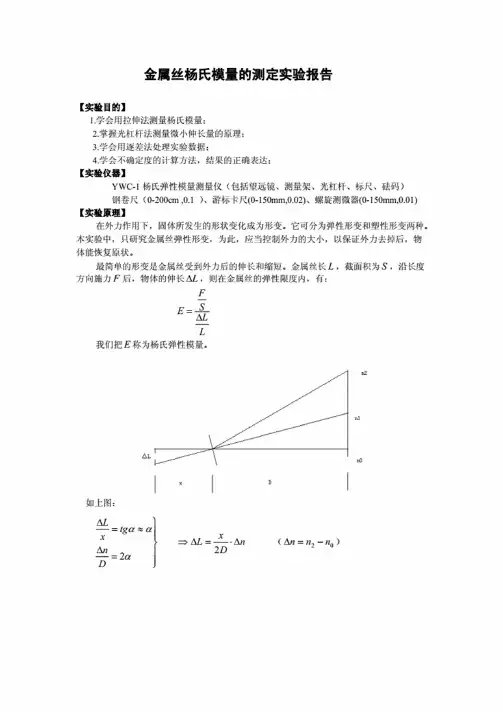
金属丝杨氏模量的测定实验报告【实验目的】1.学会用拉伸法测量杨氏模量：2.掌握光杠杆法测量微小伸长量的原理：3.学会用逐差法处理实验数据；4.学会不确定度的计算方法，结果的正确表达：【疝仪器】YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、破码)钢卷尺(0-200cm,0.1)、游标K•尺(0-150mm,0.02)、螺旋测微器(0-150mm,0.01)【实验原理】在外力作用下，固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中，只研究金属统弹性形变，为此.应当控制外力的大小，以保证外力去掉后，物体能恢复原状。
最简单的形变是金属统受到外力后的伸长和缩短。
金属税长乙，截面积为S,沿长度方向施力F后，物体的伸长则在金属统的弹性限度内.有：FE=i~L我们把E称为杨氏弹性模量。
8FLD F 1 , — —m£ = _5_ = ^_ _ ,亶 X7^1 X •——---M L W _L真实测量时放大倍数为4倍，即E=2£[实验内容】＜一＞仪器调整1、 杨氏弹性模量测定仪底座调节水平：2、 平面镜镜面放置与测定仪平面垂直：3、 将望远镜放置在平面镜正前方1.5-2.0m 左右位置上：4、 粗调望远镜：将镜面中心、标尺零点、望远镜调节等高，望远镜的缺口、准星对准平面镜中心，并能在望远镜外看到尺子的像：5、 调节物镜焦距能看到尺子清晰的像.调节目镜焦距能清晰的看到叉统：6、 调节叉税在标尺±2"〃以内，并使得视差不超过半格。
〈二〉测量1、 记下无挂物时刻度尺的读数〃°：2、 依次挂上】00g 的虢码，8次，计下〃],〃2，〃3，〃4，〃5，〃6，〃7 ：3、 依次取下 100g 的瑟码,8 次，计下 no 〃[ ,〃2 ,〃3 ,〃4，〃S ，〃6:4、 用米尺测量出金属税的长度L (两K •口之间的金属统)、镜面到尺子的距离。
用拉伸法测金属丝的杨氏模量实验报告结论
根据本次实验使用拉伸法测定金属丝的杨氏模量得出的结果，可以得出以下结论：
1. 金属丝的杨氏模量是一个物质固有的性质，与金属丝的形状、尺寸等无关。
2. 杨氏模量是表征材料纵向回复能力的物理量，它描述了材料纵向应力与应变的关系。
3. 在本次实验中，我们通过将金属丝固定于测量仪器上，施加一定的拉力，并测量此时金属丝的伸长量来计算出杨氏模量。
4. 实验测量得出的杨氏模量值应与理论值相近，如果出现大的偏差，可能是实验操作或者设备的误差所致。
5. 了解杨氏模量的大小和测量方法，对于材料力学、结构工程、材料科学等学科有着重要的应用价值。
用拉伸法测金属丝杨氏模量杨氏模量是表征固体材料弹性形变能力的一个重要物理量，是选定机械构件材料的依据之一、是工程技术中常用的参数。
本实验采用静态拉伸法，按光杠杆放大原理装置来测量金属丝的加载之形变，光杠杆法的原理已被广泛应用在测量技术中，如冲击电流计和光点检流计用光杠杆法的装置测量小角度的变化。
实验中的仪器结构、实验方法、数据处理、误差分析等内容较广，能使学生得到全面的训练。
【实验目的】1．掌握拉伸法测定钢丝杨氏模量的原理和方法。
1．掌握用光杠杆法测量长度微小变化量的原理和方法。
2．学习光杠杆和望远镜直横尺的调节与使用。
3．学会用逐差法处理实验数据。
【实验仪器及用具】YMC-1、2杨氏模量测定仪、YMC-1望远镜直横尺、光杠杆、砝码、钢卷尺、千分尺、游标卡尺【实验原理】在外力作用下，固体所发生的形状变化，称为形变。
它可分为弹性形变和范性形变两类。
外力撤除后物体能完全恢复原状的形变，称为弹性形变。
如果加在物体上的外力过大，以致外力撤除后，物体不能完全恢复原状，而留下剩余形变，就称之为范性形变。
在本实验中，只研究弹性形变。
为此，应当控制外力的大小，以保证此外力去除后物体能恢复原状。
最简单的形变是棒状物体（或金属丝）受外力后的伸长与缩短。
设一物体长为L ，截面积为S 。
沿长度方向施力F 后，物体的伸长（缩短）为ΔL 。
比值F/S 是单位面积上的作用力，称为胁强，它决定了物体的形变；比值ΔL/L 是物体的相对伸长，称为胁变，它表示物体形变的大小。
按照胡克定律，在物体的弹性限度内胁强与胁变成正比，比例系数Y 称为杨氏模量。
实验证明，杨氏模量与外力F 、物体的长度L 和截面积S 的大小无关，而只决定于棒（或金属丝）的材料。
它是描写物体形变程度的物理量。
根据式（1），测出等号右边各量后，便可算出杨氏模量。
其中F 、L 和S 可用一般的方法测得，唯有伸长量ΔL 之值甚小，用一般工具不易测准确。
因此，我们采用光杠杆法来测定伸长量ΔL 。
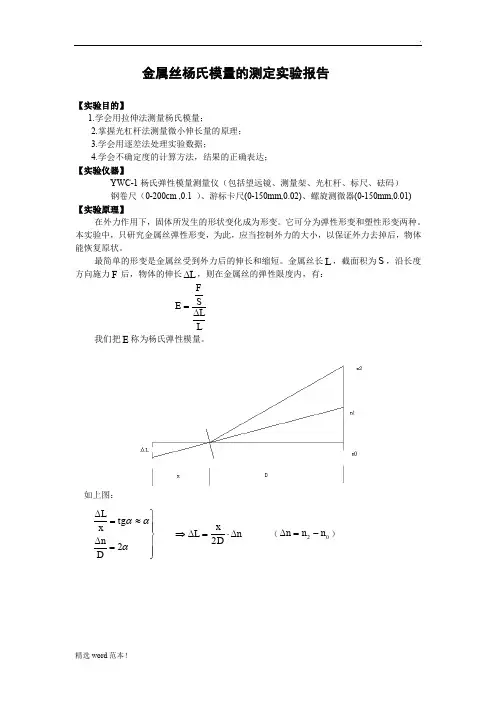
金属丝杨氏模量的测定实验报告【实验目的】1.学会用拉伸法测量杨氏模量；2.掌握光杠杆法测量微小伸长量的原理；3.学会用逐差法处理实验数据；4.学会不确定度的计算方法，结果的正确表达；【实验仪器】YWC-1杨氏弹性模量测量仪（包括望远镜、测量架、光杠杆、标尺、砝码） 钢卷尺（0-200cm ,0.1 ）、游标卡尺(0-150mm,0.02)、螺旋测微器(0-150mm,0.01)【实验原理】在外力作用下，固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中，只研究金属丝弹性形变，为此，应当控制外力的大小，以保证外力去掉后，物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。
金属丝长L ，截面积为S ，沿长度方向施力F 后，物体的伸长L ∆，则在金属丝的弹性限度内，有：FS E LL=∆ 我们把E 称为杨氏弹性模量。
如上图：⎪⎪⎭⎪⎪⎬⎫=∆≈=∆ααα2D n tg x L n D x L ∆⋅=∆⇒2 （02n n n -=∆）n x d FLD Ln Dx d FL L S F E ∆⋅=∆=∆=228241ππ 真实测量时放大倍数为4倍，即E=2E【实验内容】<一> 仪器调整1、杨氏弹性模量测定仪底座调节水平；2、平面镜镜面放置与测定仪平面垂直；3、将望远镜放置在平面镜正前方1.5-2.0m 左右位置上；4、粗调望远镜：将镜面中心、标尺零点、望远镜调节等高,望远镜的缺口、准星对准平面镜中心，并能在望远镜外看到尺子的像；5、调节物镜焦距能看到尺子清晰的像，调节目镜焦距能清晰的看到叉丝；6、调节叉丝在标尺cm 2±以内，并使得视差不超过半格。
<二>测量1、 记下无挂物时刻度尺的读数0n ；2、依次挂上100g 的砝码，8次，计下7654321,,,,,,n n n n n n n ；3、依次取下100g 的砝码，8次，计下n 0‘，'7'65'4'3'2'1,,,,,,'n n n n n n n ； 4、用米尺测量出金属丝的长度L （两卡口之间的金属丝）、镜面到尺子的距离D ；5、用游标卡尺测量出光杠杆x 、用螺旋测微器测量出金属丝直径d 。
用拉伸法测金属丝的杨氏模量实验报告用拉伸法测金属丝的杨氏模量实验报告引言：杨氏模量是材料力学性质的重要指标之一，它描述了材料在拉伸过程中的刚度和变形能力。
本实验通过拉伸金属丝的方法来测量杨氏模量，旨在了解金属丝的力学性质，并探讨拉伸过程中的变形行为。
实验装置和步骤：实验装置主要包括拉伸机、金属丝样品、刻度尺、电子天平和计算机。
具体的实验步骤如下：1. 将金属丝样品固定在拉伸机的夹具上，并调整夹具使其与拉伸机的拉伸轴心对齐。
2. 通过调整拉伸机的拉伸速度和加载范围，使实验能够在合适的条件下进行。
3. 使用刻度尺测量金属丝的初始长度，并记录下来。
4. 启动拉伸机，开始对金属丝进行拉伸。
5. 在拉伸过程中，使用电子天平测量金属丝的质量，并记录下来。
6. 当金属丝断裂时，停止拉伸机的运行，并记录下金属丝的最终长度。
实验数据处理：根据实验步骤所得到的数据，可以计算出金属丝的应力和应变。
应力定义为单位面积上的力，可以通过施加在金属丝上的拉力除以金属丝的横截面积得到。
应变定义为单位长度上的变形量，可以通过金属丝的伸长量除以初始长度得到。
根据胡克定律，应力与应变之间的关系可以用以下公式表示：应力 = 弹性模量× 应变其中，弹性模量即为杨氏模量。
通过绘制应力-应变曲线，可以得到金属丝的杨氏模量。
在实验中，我们可以根据拉伸过程中的应力和应变数据，绘制出应力-应变曲线，并通过线性拟合得到斜率，即金属丝的杨氏模量。
实验结果和讨论：根据实验数据处理得到的应力-应变曲线，我们可以得到金属丝的杨氏模量。
实验结果显示，金属丝的杨氏模量为XXX GPa（Giga Pascal）。
这个结果与文献中的数值相符合，证明了实验方法的可靠性。
在拉伸过程中，金属丝会发生塑性变形，即超过了材料的弹性限度。
这是因为金属丝在受到拉力的作用下，晶体结构发生了位错滑移，导致金属丝的形状发生变化。
当拉力超过金属丝的极限强度时，金属丝会发生断裂。
一、拉伸法 【实验目的】 1. 学会用拉伸法测量金属丝的杨氏模量 2. 掌握光杠杆法测量微小伸长量的原理 3. 掌握各种测量工具的正确使用方法 4. 学会用逐差法或最小二乘法处理实验数据 5. 学会不确定度的计算方法，结果的正确表达
【实验仪器】 杨氏模量仪如图 所示，主要由实验架和望远镜系统、数字拉力计、测量工具（图中未显示）组成。
标尺
金属丝 望远镜
拉力传感器 数字拉力计 光杠杆
施力螺母
水平卡座 垂直卡座
图 2-6-1 杨氏模量系统示意图 1. 实验架 实验架是待测金属丝杨氏模量测量的主要平台。金属丝通过一夹头与拉力传感器相连，采用螺母旋转加力方式，加力简单、直观、稳定。拉力传感器输出拉力信号通过数字拉力计显示金属丝受到的拉力值。光杠杆的反射镜转轴支座被固定在一台板上，动足尖自由放置在夹头表面。反射镜转轴支座的一边有水平卡座和垂直卡座。水平卡座的长度等于反射镜转轴与动足尖的初始水平距离（即小型测微器的微分筒压到0刻线时的初始光杠杆常数），该距离在出厂时已严格校准，使用时勿随意调整动足与反射镜框之间的位置。旋转小型测微器上的微分筒可改变光杠杆常数。实验架含有最大加力限制功能，实验中最大实际加力不应超过13.00kg。 2. 望远镜系统 望远镜系统包括望远镜支架和望远镜。望远镜支架通过调节螺钉可以微调望远镜。望远镜放大倍数12倍，最近视距0.3m，含有目镜十字分划线（纵线和横线）。望远镜如图所示。
图2-6-2 望远镜示意图 3. 数字拉力计 电源：AC220V±10%，50Hz 显示范围：0~±19.99kg（三位半数码显示） 最小分辨力：0.001kg 含有显示清零功能（短按清零按钮显示清零）。 含有直流电源输出接口：输出直流电，用于给背光源供电。 数字拉力计面板图：
图 2-6-3 数字拉力计面板图 4. 测量工具 实验过程中需用到的测量工具及其相关参数、用途： 量具名称 量程 分辨力 误差限 用于测量 标尺(mm) 80.0 1 0.5 Δx 钢卷尺(mm) 3000.0 1 0.8 L、H 游标卡尺(mm) 150.00 0.02 0.02 D 螺旋测微器(mm) 25.000 0.01 0.004 d 数字拉力计(kg) 20.00 0.01 0.005 m
【实验原理】
分划线 视度调节手轮 调焦手轮 物镜
O型连接圈 1. 杨氏模量的定义 设金属丝的原长为L，横截面积为S，沿长度方向施力F后，其长度改变ΔL，则金属丝单位面积上受到的垂直作用力σ=F/S称为正应力，金属丝的相对伸长量ε=ΔL/L称为线应变。实验结果指出，在弹性范围内，由胡克定律可知物体的正应力与线应变成正比，即： E
（2-6-1）
或 LLESF （2-6-2） 比例系数E即为金属丝的杨氏模量（单位：Pa或N/m2），它表征材料本身的性质，E越大的材料，要使它发生一定的相对形变所需要的单位横截面积上的作用力也越大。 由式（2-6-2）可知：
LLSFE// （2-6-3）
对于直径为d的圆柱形金属丝，其杨氏模量为：
LdmgLLLdmgLLSFE2
24/41///
（2-6-4）
式中L（金属丝原长）可由米尺测量，d（金属丝直径）可用螺旋测微器测量，F（外力）可由实验中数字拉力计上显示的质量m求出，即F=mg（g为重力加速度），而ΔL是一个微小长度变化（mm级）。本实验利用光杠杆的光学放大作用实现对金属丝微小伸长量ΔL的间接测量。 2.光杠杆光学放大原理 如图 2-6-42-6-4所示，光杠杆由反射镜、反射镜转轴支座和与反射镜镜固定连动的动足等组成。
x1
H O
x2
θ θ 2θ D ΔL
Δx
反射镜 望远镜 标尺
动足 图 2-6-4 光杠杆放大原理图 开始时，光杠杆的反射镜法线与水平方向成一夹角，在望远镜中恰能看到标尺刻度x1的像。当金属丝受力后，产生微小伸长ΔL，动足尖下降，从而带动反射镜转动相应的角度θ，根据光的反射定律可知，在出射光线（即进入望远镜的光线）不变的情况下，入射光线转动了2θ，此时望远镜中看到标尺刻度为x2。 实验中D>>ΔL，所以θ甚至2θ会很小。从图 2-6-44的几何关系中我们可以看出，2θ很小时有： ΔL≈D∙θ，Δx≈H∙2θ 故有： LDHx2 （2-6-5） 其中2H/D称作光杠杆的放大倍数，H是反射镜转轴与标尺的垂直距离。仪器中H>>D，这样一来，便能把一微小位移ΔL放大成较大的容易测量的位移Δx。将式（2-6-5）代入式（2-6-4）得到：
xDdmgLHE182
（2-6-6）
如此，可以通过测量式（2-6-6）右边的各参量得到被测金属丝的杨氏模量，式（2-6-6）中各物理量的单位取国际单位（SI制）。
【实验内容与步骤】 1. 调节实验架 实验前应保证上下夹头均夹紧金属丝，防止金属丝在受力过程中与夹头发生相对滑移，且反射镜转动灵活。 1) 将拉力传感器信号线接入数字拉力计信号接口，用DC连接线连接数字拉力计电源输出孔和背光源电源插孔。 2) 打开数字拉力计电源开关，预热10min。背光源应被点亮，标尺刻度清晰可见。数字拉力计面板上显示此时加到金属丝上的力。 3) 旋转光杠杆上的小型测微器的微分筒，使得光杠杆常数D为设定值（光杠杆常数等于水平卡座长度加小型测微器上读数）。旋转施力螺母，给金属丝施加一定的预拉力m0
（3.00±0.02kg），将金属丝原本存在弯折的地方拉直。
2. 调节望远镜 1) 将望远镜移近并正对实验架平台板（望远镜前沿与平台板边缘的距离在0~30cm范围内均可）。调节望远镜使从实验架侧面目视时反射镜转轴大致在镜筒中心线上（如图 2-6-1），同时调节支架上的三个螺钉，直到从目镜中看去能看到背光源发出的明亮的光。 2) 调节目镜视度调节手轮，使得十字分划线清晰可见。调节调焦手轮，使得视野中标尺的像清晰可见。 3) 调节支架螺钉（也可配合调节平面镜角度调节旋钮），使十字分划线横线与标尺刻度线平行，并对齐≤2.0cm的刻度线（避免实验做到最后超出标尺量程）。水平移动支架，使十字分划线纵线对齐标尺中心。
望远镜
平台板 反射镜转轴 反射镜
图 2-6-1 望远镜位置示意图 3. 数据测量 1) 测量L、H、D、d 用钢卷尺测量金属丝的原长L，钢卷尺的始端放在金属丝上夹头的下表面（即横梁上表面），另一端对齐平台板的上表面。 用钢卷尺测量反射镜转轴到标尺的垂直距离H，钢卷尺的始端放在标尺板上表面，另一端对齐垂直卡座的上表面（该表面与转轴等高）。 用游标卡尺和小型测微器测量光杠杆常数D，游标卡尺测量水平卡座长度，加上小型测微器上的读数（精确到0.01mm即可），便是光杠杆常数D。 以上各物理量为一次测量值，将实验数据记入表 2-6-1中。 用螺旋测微器测量不同位置、不同方向的金属丝直径视值d视j（至少6处），注意测量前记下螺旋测微器的零差d0。将实验数据记入表 2-6-2中，计算直径视值的算术
平均值d视，并根据0ddd视计算金属丝的平均直径。 2) 测量标尺刻度x与拉力m 点击数字拉力计上的“清零”按钮，记录此时对齐十字分划线横线的刻度值x1。 缓慢旋转施力螺母加力，逐渐增加金属丝的拉力，每隔1.00（±0.01）kg记录一次标尺的刻度xi+，加力至设置的最大值，数据记录后再加0.5kg左右（不超过1.0kg，且不记录数据）。 然后，反向旋转施力螺母至设置的最大值并记录数据，同样地，逐渐减小金属丝的拉力，每隔1.00（±0.01）kg记录一次标尺的刻度xi−，直到拉力为0.00（±0.01）kg。 将以上数据记录于表 2-6-3中对应位置。 注： 实验中不能再调整望远镜，并尽量保证实验桌不要有震动，以保证望远镜稳定。 加力和减力过程，施力螺母不能回旋。 3) 实验完成后，旋松施力螺母，使金属丝自由伸长，并关闭数字拉力计。
【数据记录】 表 2-6-1 一次性测量数据 L(mm) H(mm) D(mm)
表 2-6-2 金属丝直径测量数据 螺旋测微器零差d0= mm 序号i 1 2 3 4 5 6 平均值 直径视值d视i(mm)
表 2-6-3 加减力时标尺刻度与对应拉力数据 序号i 1 2 3 4 5 6 7 8 9 10 拉力视值mi (kg) 加力时标尺刻度xi+ (mm) 减力时标尺刻度xi− (mm) 平均标尺刻度(mm) xi =( xi++ xi−)/2 标尺刻度改变量(mm) Δxi=xi+5−xi
【注意事项】 1) 使用前请首先详细阅读本说明书。 2) 螺旋测微器和游标卡尺的使用说明请参见对应的说明书。 3) 为保证使用安全，三芯电源线须可靠接地。 4) 数字拉力计为市电供电的电子仪器，为了避免电击危险和造成仪器损坏，非指定专业维修人员请勿打开机盖。 5) 该实验是测量微小量，实验时应避免实验台震动。 6) 初始光杠杆常数与水平卡座的长度在出厂时已校为相等，实验时勿调整动足与反射镜框之间的连接件。 7) 加力勿超过实验规定的最大加力值。 8) 严禁改变限位螺母位置，避免最大拉力限制功能失效。 9) 光学零件表面应使用软毛刷、镜头纸擦拭，切勿用手指触摸镜片。 10) 严禁使用测装置观察强光源，如太阳等，避免人眼灼伤。 11) 实验完毕后，应旋松施力螺母，使金属丝自由伸长，并关闭数字拉力计。 12) 仪器应储存于干燥、清洁、通风良好的地方。 13) 金属丝不用时应涂上防锈油，避免生锈。 14) 仪器各部件仅限用于实验指导及操作说明书规定的实验内容，请勿作他用，否则，公司不承担由此带来的一切后果。
【思考题】 1) 螺旋测微计使用注意事项是什么？棘轮如何使用？螺旋测微计用完该如何处理？ 2) 从Y的不确定度计算分析哪个量的测量对Y的结果的准确度影响最大，测量中应注意哪些问题？ 3) 材料相同、粗细不同的两根钢丝，它们的杨氏模量是否相同？ 4) 怎样提高光杠杆测微小伸长量的灵敏度？这种灵敏度是否越高越好？ 5) 本实验可否用作图法计算钢丝的杨氏模量？如果能应该作怎样的关系曲线？
