堆排序过程实例

heap實例
"Heap" 是一個數據結構的種類，它可以實現有效率的插入和尋找最大（或最小）元素的操作。

以下是 heap 實例的 Python 語法：```python
import heapq
# 建立最大堆
heap = []
heapq.heappush(heap, 3)
heapq.heappush(heap, 1)
heapq.heappush(heap, 4)
print(heap) # 打印: [4, 3, 1]
# 堆的最大值即列表的最顶端元素
print(heapq.heappop(heap)) # 打印: 4
print(heap) # 打印: [3, 1]
```
在這個例子中，`heapq` 是 Python 的標準庫之一，提供了堆排序的基礎功能。

`heappush()` 方法將一個元素加入到堆中，而`heappop()` 方法則從堆中移除並回傳最大元素。

這裡的堆是一個最大堆，也就是說堆中的父节点总是大于或等於其子节点。

你也可以建立最小堆，只需要稍微改變一下元素的相加方式即可。

請注意，當使用 heapq 模組時，要確保列表是用小數點（float）
而不是其他數據類型（例如整數）來表示的。

這是因為 heapq 模組使用小數點來實現優秀的插入和尋找最大值操作。

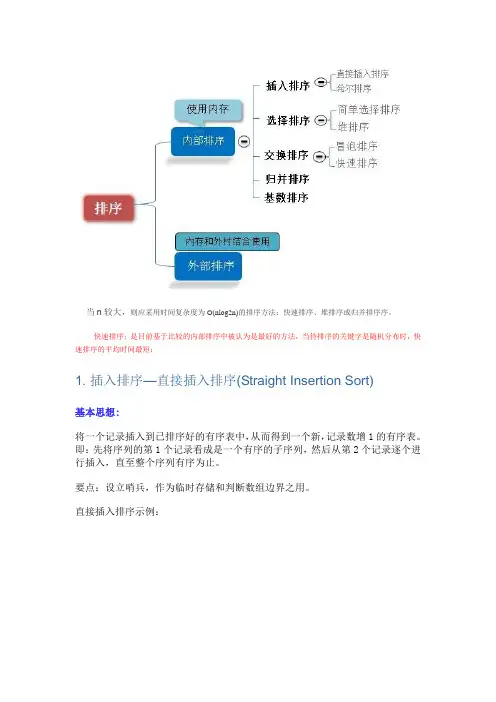
当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。

快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；1. 插入排序—直接插入排序(Straight Insertion Sort)基本思想:将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。

即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。

要点：设立哨兵，作为临时存储和判断数组边界之用。

直接插入排序示例：如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。

所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

算法的实现：效率：时间复杂度：O（n^2）.其他的插入排序有二分插入排序，2-路插入排序。

2. 插入排序—希尔排序（Shell`s Sort）希尔排序是1959 年由D.L.Shell 提出来的，相对直接排序有较大的改进。

希尔排序又叫缩小增量排序基本思想：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

操作方法：1.选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；2.按增量序列个数k，对序列进行k 趟排序；3.每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。

仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

希尔排序的示例：算法实现：我们简单处理增量序列：增量序列d = {n/2 ,n/4, n/8 .....1} n为要排序数的个数即：先将要排序的一组记录按某个增量d（n/2,n为要排序数的个数）分成若干组子序列，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。

⼗⼤排序算法算法之排序排序算法基本上是我们⽆论是在项⽬中还是在⾯试中都会遇到的问题，加上最近在看《算法》这本书，所以就准备好好的将排序算法整理⼀下。

所有排序算法都是基于 Java 实现，为了简单，只使⽤了int类型，从⼩到⼤排序基本排序⾼效的排序各⼤排序的时间测试如何选择排序排序之基本排序算法准备阶段：有⼀个交换位置的函数exc/*** 交换a数组中i和j的位置* @param a 需要交换的数组* @param i 位置* @param j 位置*/public static void exc(int a[],int i,int j){// 当他们相等的时候就没必要进⾏交换if(a[i] != a[j]){a[i] ^= a[j];a[j] ^= a[i];a[i] ^= a[j];}}基本排序算法主要是分为插⼊排序，选择排序，冒泡排序和梳排序。

选择排序原理：选择排序的原理很简单，就是从需要排序的数据中选择最⼩的（从⼩到⼤排序），然后放在第⼀个，选择第⼆⼩的放在第⼆个……代码：/*** 选择排序* @param a 进⾏排序的数组*/public static int[] selectionSort(int a[]){int min;for(int i=0;i<a.length;i++){min = i;// 这个for循环是为了找出最⼩的值for (int j = i+1; j < a.length; j++) {if(a[min]>a[j]){min = j;}}/** 如果第⼀个取出的元素不是最⼩值，就进⾏交换* 意思就是：如果取出的元素就是最⼩值，那么就没有必要进⾏交换了 */if(min != i){// 进⾏交换exc(a, i, min);}}return a;}选择排序的动画演⽰img假如数组的长度是N，则时间复杂度：进⾏⽐较的次数：(N-1)+(N-2)+……+1 = N(N-1)/2进⾏交换的次数：N特点：（稳定）1. 运⾏时间与输⼊⽆关。

排序之间的关系外部排序1，直接插入排序 (1)基本思想：在要排序的一组数中，假设前面(n-1) [n>=2]个数己经是排 好顺序的，现在要把第n 个数插到前面的有序数中，使得这n 个数也是排好顺序的。

如此反复循环，直到全部排好顺序。

(2)实例初始状态57 68 59 52 ❶ 57_68 59 52❸ 5759685268>57,不处理 I I I I O 52<57,插在57之前 ❷57 68 59 52结果：52 57 59 68I __ |57<59<68,插在57之后(3)用java 实现1. package com.njue;2. 2. public class insert Sort {3. public insertsort () { 5.inta[] = { 49,3 8, 65, 97, 76, 13,27, 4 9, 7 8, 34, 12, 64,5, 4, 62, 9 9, 9 8, 5 4, 56, 17, 18,2 3,34, 15,35,25,53,51); 4. int temp=0;5. for(int i=l;i<a.length;i++){6.int j=i-l;插入排序-只使用内存直接插入排序 希尔排序内部排序交换排序9冒泡排序 快速排序归并排序 基数排序内存和外存结合使用7.temp=a[i];10 . for(；j>=0&&temp<a[j];j―){11.a[j + 1] =a[j];〃将大于temp的值整体后移一个单位12.}13 . a [ j +1] =temp;14.}15.for(int i=0;i<a.length;i++)16.System. out. printin (a [ i ]);17- }18. }2,希尔排序（最小瞧排序）（1）基本思想：算法先将要排序的一组数技某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组, 在每组中再进行直接插入排序。

Java程序员必知的8大排序2012-06-28 14:01 without0815 博客园我要评论(5)字号：T | T本文主要详解了Java语言的8大排序的基本思想以及实例解读，详细请看下文AD：51CTO云计算架构师峰会抢票进行中！8种排序之间的关系:1，直接插入排序（1）基本思想：在要排序的一组数中，假设前面(n-1)[n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。

如此反复循环，直到全部排好顺序。

（2）实例（3）用java实现1.package com.njue;2.3.public class insertSort {4.public insertSort(){5.inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};6.int temp=0;7.for(int i=1;i<a.length;i++){8.int j=i-1;9. temp=a[i];10.for(;j>=0&&temp<a[j];j--){11. a[j+1]=a[j]; //将大于temp的值整体后移一个单位12. }13. a[j+1]=temp;14. }15.for(int i=0;i<a.length;i++)16. System.out.println(a[i]);17.}18.}2，希尔排序（最小增量排序）（1）基本思想：算法先将要排序的一组数按某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。

当增量减到1时，进行直接插入排序后，排序完成。

（2）实例：（3）用java实现1.public class shellSort {2.public shellSort(){3.int a[]={1,54,6,3,78,34,12,45,56,100};4.double d1=a.length;5.int temp=0;6.while(true){7. d1= Math.ceil(d1/2);8.int d=(int) d1;9.for(int x=0;x<d;x++){10.for(int i=x+d;i<a.length;i+=d){11.int j=i-d;12. temp=a[i];13.for(;j>=0&&temp<a[j];j-=d){14. a[j+d]=a[j];15. }16. a[j+d]=temp;17. }18. }19.if(d==1)20.break;21. }22.for(int i=0;i<a.length;i++)23. System.out.println(a[i]);24.}25.}3.简单选择排序（1）基本思想：在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

各种排序方法的比较与讨论现在流行的排序有：选择排序、直接插入排序、冒泡排序、希尔排序、快速排序、堆排序、归并排序、基数排序。

一、选择排序1．基本思想：每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。

2. 排序过程：【示例】：初始关键字[49 38 65 97 76 13 27 49]第一趟排序后13 ［38 65 97 76 49 27 49]第二趟排序后13 27 ［65 97 76 49 38 49]第三趟排序后13 27 38 [97 76 49 65 49]第四趟排序后13 27 38 49 [49 97 65 76]第五趟排序后13 27 38 49 49 [97 97 76]第六趟排序后13 27 38 49 49 76 [76 97]第七趟排序后13 27 38 49 49 76 76 [ 97]最后排序结果13 27 38 49 49 76 76 973.void selectionSort(Type* arr,long len){long i=0,j=0;/*iterator value*/long maxPos;assertF(arr!=NULL,"In InsertSort sort,arr is NULL\n");for(i=len-1;i>=1;i--){maxPos=i;for(j=0;jif(arr[maxPos]if(maxPos!=i)swapArrData(arr,maxPos,i);}}选择排序法的第一层循环从起始元素开始选到倒数第二个元素,主要是在每次进入的第二层循环之前,将外层循环的下标赋值给临时变量,接下来的第二层循环中,如果发现有比这个最小位置处的元素更小的元素,则将那个更小的元素的下标赋给临时变量,最后,在二层循环退出后,如果临时变量改变,则说明,有比当前外层循环位置更小的元素,需要将这两个元素交换.二.直接插入排序插入排序（Insertion Sort）的基本思想是：每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子文件中的适当位置，直到全部记录插入完成为止。

关于堆结构的详解⼀、定义堆的定义堆其实就是⼀棵完全⼆叉树（若设⼆叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最⼤个数，第 h 层所有的结点都连续集中在最左边），定义为：具有n个元素的序列（h1,h2,...hn），当且仅当满⾜（hi>=h2i,hi>=h2i+1）或（hi<=h2i,hi<=2i+1） (i=1,2,...,n/2)时称之为堆⼤顶堆堆顶元素（即第⼀个元素）为最⼤项，并且（hi>=h2i,hi>=h2i+1）⼩顶堆堆顶元素为最⼩项，并且（hi<=h2i,hi<=2i+1）⼆、构建堆（⼤顶堆）⽅法序列对应⼀个完全⼆叉树，从最后⼀个分⽀节点（n div 2）开始，到跟（1）为⽌，⼀次对每个分⽀节点进⾏调整（下沉），以便形成以每个分⽀节点为根的堆，当最后对树根节点进⾏调整后，整个树就变成⼀个堆实例先给出⼀个序列：45，36，18，53，72，30，48，93，15，35要想此序列称为⼀个堆，我们按照上述⽅法，⾸先从最后⼀个分⽀节点（10/2），其值为72开始，⼀次对每个分⽀节点53，18，36，45进⾏调整（下沉）图解流程代码实现/*根据树的性质建堆，树节点前⼀半⼀定是分⽀节点，即有孩⼦的，所以我们从这⾥开始调整出初始堆*/public static void adjust(List<Integer> heap){for (int i = heap.size() / 2; i > 0; i--)adjust(heap,i, heap.size()-1);System.out.println("=================================================");System.out.println("调整后的初始堆：");print(heap);}/*** 调整堆，使其满⾜堆得定义* @param i* @param n*/public static void adjust(List<Integer> heap,int i, int n) {int child;for (; i <= n / 2; ) {child = i * 2;if(child+1<=n&&heap.get(child)<heap.get(child+1))child+=1;/*使child指向值较⼤的孩⼦*/if(heap.get(i)< heap.get(child)){swap(heap,i, child);/*交换后，以child为根的⼦树不⼀定满⾜堆定义，所以从child处开始调整*/i = child;} else break;}}//把list中的a,b位置的值互换public static void swap(List<Integer> heap, int a, int b) {//临时存储child位置的值int temp = (Integer) heap.get(a);//把index的值赋给child的位置heap.set(a, heap.get(b));//把原来的child位置的数值赋值给index位置heap.set(b, temp);}三、堆排序堆排序的性能介绍（适合处理数据量⼤的序列）由于它在直接选择排序的基础上利⽤了⽐较结果形成。

三种查找算法:顺序查找，二分法查找（折半查找），分块查找，散列表（以后谈）一、顺序查找的基本思想：从表的一端开始，顺序扫描表，依次将扫描到的结点关键字和给定值（假定为a）相比较，若当前结点关键字与a相等，则查找成功；若扫描结束后，仍未找到关键字等于a的结点，则查找失败。

说白了就是，从头到尾，一个一个地比，找着相同的就成功，找不到就失败。

很明显的缺点就是查找效率低。

适用于线性表的顺序存储结构和链式存储结构。

计算平均查找长度。

例如上表，查找1，需要1次，查找2需要2次，依次往下推，可知查找16需要16次，可以看出，我们只要将这些查找次数求和（我们初中学的，上底加下底乘以高除以2），然后除以结点数，即为平均查找长度。

设n=节点数平均查找长度=（n+1）/2二、二分法查找（折半查找）的基本思想：前提：（1）确定该区间的中点位置：mid=（low+high）/2min代表区间中间的结点的位置，low代表区间最左结点位置，high代表区间最右结点位置（2）将待查a值与结点mid的关键字（下面用R[mid].key）比较，若相等，则查找成功，否则确定新的查找区间：如果R[mid].key>a，则由表的有序性可知，R[mid].key右侧的值都大于a，所以等于a的关键字如果存在，必然在R[mid].key左边的表中。

这时high=mid-1如果R[mid].key<a,则等于a的关键字如果存在，必然在R[mid].key右边的表中。

这时low=mid如果R[mid].key=a，则查找成功。

（3）下一次查找针对新的查找区间，重复步骤（1）和（2）（4）在查找过程中，low逐步增加，high逐步减少，如果high<low，则查找失败。

平均查找长度=Log2(n+1)-1注：虽然二分法查找的效率高，但是要将表按关键字排序。

而排序本身是一种很费时的运算，所以二分法比较适用于顺序存储结构。

为保持表的有序性，在顺序结构中插入和删除都必须移动大量的结点。

heap實例-回复什么是堆（Heap）？堆（Heap），是一种基于数组的完全二叉树结构，其特点是父节点的值总是大于（最大堆）或小于（最小堆）子节点的值。

堆常用于优先队列（Priority Queue）等数据结构的实现，可以高效地进行查找、删除和插入操作。

堆的基本操作：1. 堆的初始化：创建一个空堆，不包含任何元素。

可以使用数组或动态分配的内存来表示。

2. 插入元素：将元素插入堆的合适位置，保持堆的性质。

3. 删除元素：从堆中删除指定元素，保持堆的性质。

4. 堆化（Heapify）：将无序数组转换为堆，建立堆的性质。

堆的性质：1. 最大堆（Max Heap）：父节点的值大于或等于子节点的值。

根节点是堆中的最大元素。

2. 最小堆（Min Heap）：父节点的值小于或等于子节点的值。

根节点是堆中的最小元素。

堆的实现：1. 使用数组实现堆：最常见的堆实现方式是使用数组。

按照完全二叉树的特性，将堆的结构存储在数组中。

根节点位于数组下标为0的位置，其左子节点为2i+1，右子节点为2i+2，i表示父节点在数组中的下标。

2. 使用二叉堆实现堆：二叉堆是一种特殊的堆，满足父节点的值总是大于或小于子节点的值。

它可以通过二叉树来实现，具有高效的查找、删除和插入操作。

堆的应用：1. 优先队列（Priority Queue）：堆可以作为优先队列的底层数据结构，实现高效的元素插入、删除和查找操作。

根据堆的性质，优先队列可以根据元素的优先级进行操作。

2. 堆排序（Heap Sort）：堆排序是一种基于堆的排序算法，通过将无序数组转换为最大堆或最小堆，然后依次取出堆顶元素，以此获得有序数组。

堆排序的时间复杂度为O(nlogn)，具有稳定性。

3. 求Top K问题：使用堆可以高效地解决求解最大或最小的K个元素的问题。

通过维护一个大小为K的最小堆或最大堆，可以不断比较和更新堆顶元素，最终得到有序的K个元素。

总结：堆是一种基于数组的完全二叉树结构，具有快速的插入、删除和查找操作。

常见排序算法及对应的时间复杂度和空间复杂度转载请注明出处：（浏览效果更好）排序算法经过了很长时间的演变，产⽣了很多种不同的⽅法。

对于初学者来说，对它们进⾏整理便于理解记忆显得很重要。

每种算法都有它特定的使⽤场合，很难通⽤。

因此，我们很有必要对所有常见的排序算法进⾏归纳。

排序⼤的分类可以分为两种：内排序和外排序。

在排序过程中，全部记录存放在内存，则称为内排序，如果排序过程中需要使⽤外存，则称为外排序。

下⾯讲的排序都是属于内排序。

内排序有可以分为以下⼏类： (1)、插⼊排序：直接插⼊排序、⼆分法插⼊排序、希尔排序。

(2)、选择排序：直接选择排序、堆排序。

(3)、交换排序：冒泡排序、快速排序。

(4)、归并排序 (5)、基数排序表格版排序⽅法时间复杂度（平均）时间复杂度（最坏)时间复杂度（最好)空间复杂度稳定性复杂性直接插⼊排序O(n2)O(n2)O(n2)O(n2)O(n)O(n)O(1)O(1)稳定简单希尔排序O(nlog2n)O(nlog2n)O(n2)O(n2)O(n)O(n)O(1)O(1)不稳定较复杂直接选择排序O(n2)O(n2)O(n2)O(n2)O(n2)O(n2)O(1)O(1)不稳定简单堆排序O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(1)O(1)不稳定较复杂冒泡排序O(n2)O(n2)O(n2)O(n2)O(n)O(n)O(1)O(1)稳定简单快速排序O(nlog2n)O(nlog2n)O(n2)O(n2)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)不稳定较复杂归并排序O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(nlog2n)O(n)O(n)稳定较复杂基数排序O(d(n+r))O(d(n+r))O(d(n+r))O(d(n+r))O(d(n+r))O(d(n+r))O(n+r)O(n+r)稳定较复杂图⽚版①插⼊排序•思想：每步将⼀个待排序的记录，按其顺序码⼤⼩插⼊到前⾯已经排序的字序列的合适位置，直到全部插⼊排序完为⽌。