Matlab在常微分方程求解中的应用
- 格式:ppt
- 大小:463.50 KB
- 文档页数:50

matlab解常微分方程组摘要:一、引言1.常微分方程组简介2.Matlab 在解常微分方程组中的应用二、Matlab 解常微分方程组的基本步骤1.安装并配置Matlab2.准备常微分方程组模型3.使用Matlab 求解器求解方程组4.分析解的结果三、Matlab 解常微分方程组的常用命令1.初始化常微分方程组2.定义方程组3.使用ode45 等求解器解方程组4.输出结果四、Matlab 解常微分方程组的实际应用1.物理模型中的应用2.工程领域中的应用3.生物学和经济学模型中的应用五、结论1.Matlab 在解常微分方程组方面的优势2.需要注意的问题和技巧3.展望Matlab 在常微分方程组求解领域的发展前景正文:一、引言常微分方程组在自然科学、工程技术和社会科学等领域中有着广泛的应用。
随着科技的发展,Matlab 作为一种功能强大的数学软件,已经成为常微分方程组求解的重要工具。
本文将介绍Matlab 解常微分方程组的基本方法、常用命令以及实际应用。
二、Matlab 解常微分方程组的基本步骤1.安装并配置Matlab:首先需要在计算机上安装Matlab 软件。
安装完成后,需要对Matlab 进行配置,以便更好地使用相关功能。
2.准备常微分方程组模型:根据实际问题,建立相应的常微分方程组模型。
这包括确定变量、方程和边界条件等。
3.使用Matlab 求解器求解方程组:Matlab 提供了丰富的求解器,如ode45、ode23、ode113 等。
根据问题特点选择合适的求解器,调用相关函数求解常微分方程组。
4.分析解的结果:求解完成后,需要对结果进行分析,检查其合理性和准确性。
可以使用Matlab 内置的图形功能绘制解的图像,直观地了解解的变化规律。
三、Matlab 解常微分方程组的常用命令1.初始化常微分方程组:使用`pdsolve`函数可以求解常微分方程组。
首先需要定义微分方程和边界条件,然后调用`pdsolve`函数求解。

matlab解常微分方程例题当涉及到使用MATLAB解常微分方程(ODE)的例题时,我们可以采用MATLAB中的ode45函数来进行求解。
ode45是一种常用的ODE求解器,它基于龙格-库塔方法。
下面我将以一个简单的例题来说明如何使用MATLAB解常微分方程。
假设我们要解决以下的常微分方程:dy/dt = -2y + 4t.初始条件为y(0) = 1。
首先,我们需要定义一个匿名函数来表示方程右侧的表达式,即-2y + 4t。
在MATLAB中,可以这样定义这个函数:f = @(t, y) -2y + 4t.接下来,我们需要定义时间范围和初始条件:tspan = [0 5] % 时间范围从0到5。
y0 = 1 % 初始条件y(0) = 1。
然后,我们可以使用ode45函数进行求解:[t, y] = ode45(f, tspan, y0)。
最后,我们可以绘制出解的图像:plot(t, y)。
xlabel('t')。
ylabel('y')。
title('Solution of dy/dt = -2y + 4t')。
这样,我们就得到了常微分方程的数值解,并用图像表示出来。
需要注意的是,这只是一个简单的例题,实际应用中可能会涉及更复杂的常微分方程。
但是使用MATLAB的ode45函数求解常微分方程的基本步骤是相似的,定义方程右侧的函数,设定时间范围和初始条件,然后使用ode45函数进行求解,并绘制出解的图像。
希望以上的解答能够满足你的需求。
如果你有更多关于MATLAB 解常微分方程的问题,欢迎继续提问。

概述在工程和科学领域中,常微分方程是一种常见的数学建模工具。
其中,带积分的常微分方程更是一种需要特殊解法的方程形式。
MATLAB是一种功能强大的数学工具软件,而ode45是MATLAB中用于求解常微分方程的函数之一。
本文将详细介绍如何使用MATLAB中的ode45函数来求解带积分的常微分方程。
一、带积分的常微分方程简介带积分的常微分方程是指在微分方程中出现积分形式的项,通常表现为对某个函数进行积分。
这种形式的微分方程在工程和科学领域中有着广泛的应用,例如在电路分析、控制系统、生物学模型等领域中都能见到。
典型的带积分的常微分方程形式如下所示:y' = f(t,y) + ∫g(t,y)dt其中,y'表示y对自变量t的导数,f(t,y)为已知的函数,g(t,y)为未知的函数需要求解。
这种形式的微分方程要比普通的常微分方程更复杂,需要使用特定的求解方法来得到解析解或数值解。
二、MATLAB中的ode45函数介绍MATLAB是一种被广泛应用于科学计算和工程领域的数学软件工具,其中有丰富的数值计算函数库。
其中,用于求解常微分方程的ode45函数是应用较为广泛的函数之一。
ode45函数可以通过数值计算的方法来求解常微分方程的数值解,其基本调用格式如下:[t,y] = ode45(odefun,tspan,y0)其中,odefun是定义了微分方程的函数句柄,tspan是求解的时间范围,y0是初始条件。
ode45函数会返回微分方程在tspan范围内的数值解t和对应的y值。
三、使用MATLAB求解带积分的常微分方程对于带积分的常微分方程,我们需要将其转化为标准形式,然后利用MATLAB的ode45函数进行求解。
假设我们有如下形式的带积分的常微分方程:y' = f(t,y) + ∫g(t,y)dt我们将其转化为等价的无積分項的方程形式,例如∂F/∂t = f(t,y) + ∫g(t,y)dt我们可以利用MATLAB中的ode45函数来求解上述形式的微分方程。

matlab的odeset函数摘要:1.引言2.Matlab 简介3.ode45 函数4.ode23tb 函数5.ode113 函数6.结论正文:Matlab 是一款功能强大的数学软件,广泛应用于科学计算、数据分析等领域。
在Matlab 中,odeset 函数是一个用于求解常微分方程(ODE)的工具箱,支持多种数值积分方法。
本文将介绍三种常用的odeset 函数:ode45、ode23tb 和ode113。
1.引言常微分方程(ODE)是数学中研究函数的微分方程,描述了变量之间的关系。
在实际问题中,很多物理、化学、生物学等现象都可以用常微分方程来描述。
Matlab 中的odeset 函数可以帮助我们求解这些方程,得到数值解。
2.Matlab 简介Matlab 是一款由美国MathWorks 公司开发的数学软件,具有强大的数值计算、数据分析、图像处理等功能。
Matlab 提供了丰富的工具箱,使得用户可以方便地实现各种计算任务。
3.ode45 函数ode45 是Matlab 中用于求解常微分方程的一种数值方法。
它是一种四阶、五阶龙格库塔方法(RK45),具有较高的数值稳定性和精度。
ode45 函数可以处理非线性、刚性、多步长等问题,适用于大多数常微分方程求解场景。
4.ode23tb 函数ode23tb 是Matlab 中另一种常用的常微分方程求解函数。
它采用二阶、三阶龙格库塔方法(RK23)进行数值积分,具有较好的数值稳定性和精度。
ode23tb 函数适用于求解刚性、非线性、以及具有复杂输入输出的常微分方程。
5.ode113 函数ode113 是Matlab 中的一种高阶龙格库塔方法(RK113),用于求解常微分方程。
它具有较高的数值稳定性和精度,适用于处理非线性、刚性、多步长等问题。
相较于低阶方法,ode113 函数在求解过程中具有更高的精度,但计算时间也相对较长。
6.结论在Matlab 中,odeset 函数提供了多种数值积分方法,适用于不同类型的常微分方程求解。

主题:matlab常微分方程参数拟合1. 常微分方程(ODE)参数拟合的概念和作用常微分方程(ODE)是描述自然现象的数学模型之一,常常用来描述物理、生物、经济等领域的动态过程。
在实际应用中,我们往往需要通过实验数据来确定ODE中的参数,以使得模型能够更好地拟合实际情况。
这就是常微分方程参数拟合的作用所在。
2. MATLAB在常微分方程参数拟合中的应用MATLAB是一个功能强大的数学软件,其中包含丰富的ODE求解和参数拟合函数,可以帮助我们高效地进行常微分方程参数拟合的工作。
接下来,我们将介绍MATLAB中常微分方程参数拟合的具体方法和步骤。
3. 在MATLAB中进行常微分方程参数拟合的基本步骤在MATLAB中进行常微分方程参数拟合,一般包括以下几个基本步骤:3.1 确定ODE模型我们需要确定ODE模型的形式,即确定微分方程的形式和需要进行参数拟合的参数。
我们可以考虑一个简单的一阶ODE模型y’ = a*y,其中参数a需要进行拟合。
3.2 确定拟合的实验数据我们需要准备拟合的实验数据,即已知的ODE模型中的变量的取值。
这些数据可以来自实验测量、观测或者已有的数据集。
3.3 构建ODE方程组接下来,我们需要在MATLAB中构建ODE模型的方程组。
这可以通过MATLAB中的ode45等函数来完成,其中可以将ODE模型表示为一个函数,并将实验数据传入。
3.4 进行参数拟合在构建好ODE方程组之后,我们可以利用MATLAB中的参数拟合函数(如lsqcurvefit)来对ODE模型中的参数进行拟合。
此时,我们需要定义拟合的目标函数,以及给定初值。
3.5 验证拟合结果我们需要对拟合的结果进行验证。
这可以通过比较拟合参数和实际参数之间的差异,以及通过对比拟合结果和实验数据的拟合程度来完成。
4. MATLAB中常微分方程参数拟合的注意事项在进行常微分方程参数拟合时,我们需要注意一些问题,比如初值的选取、参数拟合方法的选择、拟合结果的评价等。

常微分方程是描述自然界和社会现象中许多现象的数学模型,它在科学工程技术中有着重要的应用。
而 MATLAB 是一个强大的科学计算软件,它提供了许多用于求解常微分方程的工具和函数。
本文将主要讨论在 MATLAB 中如何利用数值积分方法来求解常微分方程中的间断点问题。
1. 常微分方程与 MATLAB常微分方程是描述一个未知函数及其导数之间关系的方程。
在科学和工程中,常微分方程经常出现在物理、生物、经济等领域的建模过程中。
MATLAB 提供了丰富的工具箱和函数来求解常微分方程,包括ode45、ode23、ode15s 等。
2. 数值积分方法数值积分方法是求解微积分中定积分的数值近似值的方法。
在常微分方程的数值求解过程中,经常需要用到数值积分方法来处理积分项。
MATLAB 提供了许多数值积分的函数,如 quad、quadl、quadgk 等。
3. 间断点问题在常微分方程的求解过程中,经常会遇到间断点问题,即方程中存在函数的间断点。
这种情况下,传统的数值方法可能会失效,需要采用特殊的技巧来处理。
MATLAB 提供了一些专门用于处理间断点问题的函数和工具,如 bvp4c、bvp5c 等。
4. MATLAB 中的数值积分和间断点处理在 MATLAB 中,我们可以利用数值积分方法来处理常微分方程中的间断点问题。
我们需要将常微分方程转化为积分方程。
利用 MATLAB 提供的数值积分函数来求解积分方程。
如果方程中存在间断点,我们可以利用 MATLAB 提供的间断点处理函数来处理。
5. 实例分析接下来,我们将通过一个实例来详细介绍在 MATLAB 中如何利用数值积分方法来求解常微分方程中的间断点问题。
考虑如下的常微分方程:$$\frac{dy}{dx} = \frac{1}{y}, \quad 0 < x < 1$$初始条件为 $y(0) = 1$。
该常微分方程在 $x=0$ 处存在间断点,因此传统的数值方法可能会失效。

MATLAB是一种用于科学计算和工程应用的高级编程语言和交互式环境。
它在数学建模、模拟和分析等方面有着广泛的应用。
在MATLAB 中,常微分方程的数值求解是一个常见的应用场景。
在实际工程问题中,通常需要对常微分方程进行数值求解来模拟系统的动态行为。
本文将介绍MATLAB中对常微分方程进行数值求解的快速方法。
1. 基本概念在MATLAB中,可以使用ode45函数来对常微分方程进行数值求解。
ode45是一种常用的Runge-Kutta法,它可以自适应地选取步长,并且具有较高的数值精度。
使用ode45函数可以方便地对各种类型的常微分方程进行求解,包括一阶、高阶、常系数和变系数的微分方程。
2. 函数调用要使用ode45函数进行常微分方程的数值求解,需要按照以下格式进行函数调用:[t, y] = ode45(odefun, tspan, y0)其中,odefun表示用于描述微分方程的函数,tspan表示求解的时间跨度,y0表示初值条件,t和y分别表示求解得到的时间序列和对应的解向量。
3. 示例演示为了更好地理解如何使用ode45函数进行常微分方程的数值求解,下面我们以一个具体的例子来进行演示。
考虑如下的一阶常微分方程:dy/dt = -2*y其中,y(0) = 1。
我们可以编写一个描述微分方程的函数odefun:function dydt = odefun(t, y)dydt = -2*y;按照上述的函数调用格式,使用ode45函数进行求解:tspan = [0 10];y0 = 1;[t, y] = ode45(odefun, tspan, y0);绘制出解曲线:plot(t, y);4. 高级用法除了基本的函数调用方式外,MATLAB中还提供了更多高级的方法来对常微分方程进行数值求解。
可以通过设定选项参数来控制数值求解的精度和稳定性,并且还可以对刚性微分方程进行求解。
5. 性能优化在实际工程应用中,常常需要对大规模的常微分方程进行数值求解。

matlab 数学应用微分方程常微分方程非负ode解
在MATLAB中解决微分方程,特别是常微分方程(ODEs),通常使用内置的ode45函数。
这个函数可以解决非负的常微分方程。
以下是一个简单的示例,说明如何使用ode45来解决一个简单的非负常微分方程:
假设我们要解决以下方程:
dy/dt = y - y^2
这个方程描述了一个在生物学或经济学中常见的模型,其中y表示某种数量,t表示时间。
以下是MATLAB代码:
y) y - y^2;
% 初始条件
y0 = 0.5; % 初始值
tspan = [0, 10]; % 时间范围
% 使用ode45求解
[t, y] = ode45(dydt, tspan, y0);
% 绘制结果
plot(t, y(:,1));
xlabel('Time');
ylabel('y(t)');
title('Solution of the ODE');
代码首先定义了微分方程(使用匿名函数@(t, y))。
然后,它设置了初始条件和时间范围。
最后,它使用ode45来求解微分方程,并使用plot函数来绘制结果。
注意:ode45是默认使用四阶龙格-库塔法和五阶龙格-库塔法进行数值求解的,这两种方法都是相当稳定和可靠的。
但是,对于某些问题,可能需要尝试其他的数值方法或调整参数。

一、介绍迭龙格-库塔法(Runge-Kutta method)是一种数值求解常微分方程(ODE)的常用方法。
它是由卡尔·迭龙格(Carl Runge)和马丁·威尔黑尔姆·库塔(Wilhelm Kutta)在20世纪初提出的,该方法以两位数值分析家的名字来命名。
二、简单描述迭龙格-库塔法是通过数值逼近的方式,来计算常微分方程的近似解。
它是一种显式求解方法,适用于解非线性常微分方程和具有较大阶数的常微分方程。
三、数学原理迭龙格-库塔法主要是通过将微分方程转化为差分方程,利用数值解的方式来逼近微分方程的解。
它是一种显式方法,通过不断迭代得到下一个时间步的近似解。
四、matlab中的应用在matlab中,可以使用ode45函数来调用迭龙格-库塔法求解常微分方程。
ode45函数是matlab中集成的一个函数,通过调用ode45函数,可以直接求解常微分方程的数值解。
五、实例演示下面通过一个简单的例子来演示如何使用matlab中的ode45函数来求解常微分方程。
我们考虑一个简单的一阶常微分方程:dy/dt = -y初始条件为y(0) = 1。
在matlab中,可以通过以下代码来求解该微分方程:```定义微分方程的函数function dydt = myode(t, y)dydt = -y;调用ode45函数求解[t, y] = ode45(myode, [0, 5], 1);plot(t, y);```运行以上代码,即可得到微分方程的数值解,并通过绘图来展示解的变化。
六、总结迭龙格-库塔法是一种常用的数值解常微分方程的方法,它在matlab中有较为方便的调用方式。
通过ode45函数,可以快速求解常微分方程的数值解,并通过绘图来展示结果。
希望本篇文章对读者有所帮助,谢谢阅读。
七、应用场景和优势在实际应用中,迭龙格-库塔法广泛应用于各种科学和工程领域,如物理学、化学、生物学、经济学等。

matlab解常微分方程
Matlab是一种非常强大的数学软件,可以用来解决各种数学问题。
在工程、物理、生物学和其他科学领域中,常微分方程是一种非常重要的数学工具,用于模拟和解决许多问题。
使用Matlab可以方便地求解常微分方程。
Matlab提供了几种解常微分方程的函数,包括ode45、ode23、ode15s等。
这些函数可以解决一般常微分方程、刚性常微分方程、偏微分方程等。
使用这些函数可以简单地解决一些复杂的数学问题,并且可以快速地得到结果。
除了内置函数,Matlab还提供了一些工具箱,如Symbolic Math Toolbox和Partial Differential Equation Toolbox等。
这些工具箱提供了更高级的功能,可以用来求解更复杂的问题。
在使用Matlab解常微分方程时,需要了解一些数学知识,如常微分方程的基本概念、初值问题、边值问题、刚性问题等。
此外,还需要了解一些Matlab编程知识,如函数定义、变量赋值、循环、条件语句等。
总之,Matlab是一个非常强大的工具,可以用来解决各种数学问题,特别是常微分方程。
使用Matlab可以简单地解决一些复杂的数学问题,并且可以快速地得到结果。
- 1 -。
MATLAB ODE45函数用法在MATLAB中,ODE45函数是用于求解常微分方程(ODE)的一种常用工具。
它采用龙格-库塔法(Runge-Kutta)来数值求解微分方程,通常适用于非刚性的微分方程问题。
在本文中,我们将深入探讨ODE45函数的用法,并通过具体例子来演示它的实际应用。
1. ODE45函数概述ODE45函数的基本语法如下:```matlab[t, y] = ode45(@odefun, tspan, y0)```其中,@odefun是一个用户自定义的函数,用于定义微分方程的形式;tspan是时间范围;y0是初始条件。
这个函数返回两个参数:t是时间向量,y是对应时间点的解向量。
2. ODE45函数的详细用法2.1. 自定义微分方程函数在使用ODE45函数之前,我们需要先定义微分方程的形式。
通常,我们将微分方程表示为一个函数的形式,例如:```matlabfunction dydt = odefun(t, y)dydt = % 根据微分方程的具体形式对dydt进行计算end```在这个函数中,dydt表示微分方程的导数,t表示时间,y表示状态变量。
我们需要根据具体的微分方程形式来计算dydt的值。
2.2. 设定时间范围和初始条件在使用ODE45函数时,我们需要设定时间范围和初始条件。
时间范围可以用一个包含起始时间和结束时间的向量来表示,例如tspan = [0, 10];初始条件则是微分方程在起始时间点的状态变量值,例如y0 = 1。
2.3. 求解微分方程并获取结果一旦定义了ODE45函数的参数,我们就可以用它来求解微分方程了。
调用ODE45函数后,它将返回时间向量t和对应时间点的解向量y,我们可以利用这些结果来进行进一步的分析和应用。
3. ODE45函数的实际案例为了更好地理解ODE45函数的用法,让我们通过一个具体的案例来演示。
假设我们有一个简单的一阶微分方程:```matlabfunction dydt = odefun(t, y)dydt = -2*t*y;end```我们希望求解该微分方程在时间范围tspan = [0, 5],初始条件y0 = 1的情况下的解。
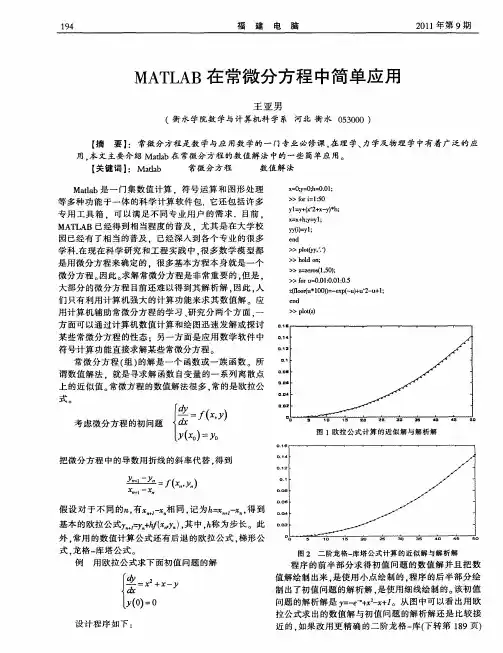
Matlab中欧拉法求解常微分方程初值问题一、概念介绍在数学和工程领域,常微分方程初值问题是一个广泛应用的数学概念。
它描述了一个未知函数在给定初始条件下的行为。
而欧拉法则是一种常用的数值方法,用来解决常微分方程初值问题。
在Matlab中,我们可以利用欧拉法来求解常微分方程问题,从而得到函数在给定初始条件下的近似解。
二、欧拉法的基本原理欧拉法的基本思想是通过离散化微分方程,将其转化为递推的差分方程。
考虑一个一阶常微分方程初值问题:\[ \frac{dy}{dx} = f(x, y), \quad y(x_0) = y_0 \]在欧拉法中,我们采用递推的方式,根据已知的初始条件和微分方程的性质,通过迭代来得到逼近解的数值结果。
具体地,我们首先将自变量$x$的范围进行等间距分割,得到$x_0, x_1, x_2, ..., x_n$,并将步长记为$h$。
根据微分方程的性质,我们可以根据已知的初始条件$y(x_0) = y_0$,通过迭代计算得到近似解$y(x_1), y(x_2), ..., y(x_n)$。
三、Matlab中的欧拉法求解在Matlab中,我们可以利用欧拉法来求解常微分方程初值问题。
以求解一阶常微分方程为例,假设我们需要求解以下的常微分方程初值问题:\[ \frac{dy}{dx} = -2xy, \quad y(0) = 1 \]我们可以利用欧拉法的思想,将自变量$x$的范围进行离散化,然后根据欧拉法的递推公式,利用迭代的方式得到近似解的数值结果。
具体地,在Matlab中,我们可以编写如下代码来实现欧拉法的求解过程:```matlabfunction y = euler_method(f, x0, y0, h, n)% 初始化存储结果的数组x = zeros(1, n+1);y = zeros(1, n+1);% 将初始条件存入数组x(1) = x0;y(1) = y0;% 利用欧拉法进行迭代for i = 1:nx(i+1) = x(i) + h;y(i+1) = y(i) + h * f(x(i), y(i));end% 返回近似解的数值结果plot(x, y); % 绘制解的图像end```在上述代码中,我们定义了一个名为`euler_method`的函数,其中包含了欧拉法的计算过程。
matlab求解常微分方程的准确解使用Matlab求解常微分方程的准确解一、引言常微分方程是研究自然界现象和工程实际问题中常见的数学工具之一。
求解常微分方程的准确解对于理解问题的本质和性质具有重要意义。
本文将介绍如何使用Matlab来求解常微分方程的准确解,并通过具体的例子进行演示。
二、常微分方程的基本概念常微分方程是指包含未知函数及其导数的方程。
一般形式为:dy/dx = f(x,y)其中,y是未知函数,x是自变量,f(x,y)是已知函数。
常微分方程的解是指能够满足方程的函数y(x)。
三、Matlab的符号计算工具箱Matlab提供了符号计算工具箱,可以对方程进行符号计算。
通过符号计算工具箱,我们可以求解常微分方程的准确解。
四、使用Matlab求解常微分方程的步骤1. 定义未知函数和自变量。
在Matlab中,可以使用符号变量来定义未知函数和自变量。
2. 定义常微分方程。
使用符号变量来定义常微分方程。
3. 求解常微分方程。
使用dsolve函数来求解常微分方程的准确解。
4. 绘制准确解的图像。
使用ezplot函数来绘制准确解的图像。
五、具体例子假设我们要求解一阶线性常微分方程:dy/dx + y = x其中,y是未知函数,x是自变量。
1. 定义未知函数和自变量。
在Matlab中,可以使用符号变量来定义未知函数和自变量。
syms y(x)2. 定义常微分方程。
使用符号变量来定义常微分方程。
eqn = diff(y,x) + y == x3. 求解常微分方程。
使用dsolve函数来求解常微分方程的准确解。
sol = dsolve(eqn)4. 绘制准确解的图像。
使用ezplot函数来绘制准确解的图像。
ezplot(sol)六、总结本文介绍了如何使用Matlab求解常微分方程的准确解。
通过符号计算工具箱,我们可以方便地求解常微分方程,并得到准确解的图像。
使用Matlab求解常微分方程的准确解可以帮助我们更好地理解问题的本质和性质,并为进一步的分析和应用提供基础。
在本文中,我将为您介细介绍MATLAB中的ode45函数的用法。
ode45函数是MATLAB中常用的求解常微分方程(ODE)的函数,可以对一阶或高阶ODE进行求解,并且能够处理刚体动力学、化学反应动力学、电路等各种领域的问题。
我将从ode45函数的基本用法、参数设定、示例应用以及个人理解这几个方面展开讨论。
1. ode45函数的基本用法ode45函数是MATLAB中常用的求解ODE的函数。
其基本用法为:[t, y] = ode45(odefun, tspan, y0)其中,odefun为自定义的求解函数,tspan为时间范围,y0为初值条件。
ode45函数通过自适应步长Runge-Kutta法对ODE进行求解,得到时间t与对应的解y。
2. 参数设定在使用ode45函数时,需要设定求解的ODE函数odefun、时间范围tspan和初值条件y0。
还可以设定相对误差容限RelTol和绝对误差容限AbsTol,以控制求解的精度。
还可以通过设定事件函数、输出函数等对求解过程进行控制和监测。
3. 示例应用下面通过一个简单的例子来说明ode45函数的应用。
考虑一个简单的一阶ODE问题:dy/dt = -y,y(0) = 1其MATLAB代码如下:```matlabodefun = @(t, y) -y;tspan = [0, 5];y0 = 1;[t, y] = ode45(odefun, tspan, y0);plot(t, y, '-o');```这段代码首先定义了ODE函数odefun,然后设定时间范围tspan和初值条件y0,最后利用ode45函数求解ODE并绘制解y随时间t的图像。
4. 个人观点和理解在我看来,ode45函数是MATLAB中非常强大且常用的求解ODE的工具。
它能够高效地对各种类型的ODE进行求解,并且通过设定参数和监控函数,可以实现对求解过程的精确控制。
在工程领域和科学研究中,ode45函数的灵活性和高效性使其成为了不可或缺的工具。
一、概述随着科技的发展,数学在各个领域中都扮演着非常重要的角色。
微分方程作为数学中的一个重要分支,在物理、工程、生物等领域都有着广泛的应用。
而 MATLAB 作为一个强大的数学软件工具,可以帮助我们快速高效地求解各种类型的微分方程组,从而为各领域的研究和应用提供有力的支持。
本文将详细介绍如何使用 MATLAB 求解常微分方程组的方法及步骤。
二、常微分方程组的定义常微分方程组是指这样一类微分方程组:一个或多个未知函数及其导数的方程组。
一般形式为:dx1/dt=f1(t,x1,x2,...,xn),dx2/dt=f2(t,x1,x2,...,xn),..., dxn/dt=fn(t,x1,x2,...,xn)。
其中x1,x2,...,xn 是未知函数,t是自变量,f1,f2,...,fn 是关于 t 和x1,x2,...,xn 的已知函数。
三、求解常微分方程组的方法MATLAB 提供了多种方法来求解常微分方程组,常用的方法有:欧拉法、四阶龙格库塔法、常微分方程组函数 ode45、ode23、ode113 等。
下面将分别介绍各种方法的具体步骤。
四、使用欧拉法求解常微分方程组欧拉法是一种简单粗糙的数值解法,通过分割等间距的步长满足微分方程初值问题。
其具体步骤如下:1. 定义微分方程组的初始条件和步长:x0=[x1(0),x2(0),...,xn(0)],h=步长。
2. 使用欧拉法逐步逼近微分方程组的解:for i=1:Nt(i)=t(i-1)+h;x(:,i+1)=x(:,i)+h*f(t(i),x(:,i));end其中 x(:,i)=[x1(i),x2(i),...,xn(i)] 为微分方程组在第 i 个时间节点的解。
五、使用四阶龙格库塔法求解常微分方程组四阶龙格库塔法是一种常用的数值解法,通过多次近似来计算微分方程组的数值解。
其具体步骤如下:1. 定义微分方程组的初始条件和步长:x0=[x1(0),x2(0),...,xn(0)],h=步长。