流体力学第4章习题

第四章 流体动力学基础4-1 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭，0y ≥总流的动能修正系数为何值?解：172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A A B y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4-2 如图示一股水流自狭长的缝中水平射出，其厚度00.03m δ=，平均流速V 0＝8m/s ，假设此射流受重力作用而向下弯曲，但其水平分速保持不变。

试求(1)在倾斜角45θ=o 处的平均流速V ；(2)该处的水股厚度δ。

解：（1）由题意可知：在45度水流处，其水平分速度仍为8m/s,由勾股定理可得：V=︒45sin 8=11.31m/s （2）水股厚度由流量守恒可得：VD D V δδ=000，由于缝狭长，所以两处厚度近似相等，所以000.0380.02111.31V V δδ⨯===m 。

4-3 如图所示管路，出口接一收缩管嘴，水流射人大气的速度V 2=20m/s ，管径d 1＝0.1m ，管嘴出口直径d 2＝0.05m ，压力表断面至出口断面高差H ＝5m ，两断面间的水头损失为210.5(/2)V g 。

试求此时压力表的读数。

解：取压力表处截面为截面1-1，收缩管嘴处截面为截面2-2，选择两截面包围的空间为控制体，由实际流体的恒定总流能量方程得：2211221222wV p V p z z h g g g g ρρ'++=+++， 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ，由上述两个方程可得压力表的读数（相对压强）：222112212wV V p p z z h g g ρ⎛⎫-'-=+-+ ⎪⎝⎭， 上式计算结果为：2.48at 。

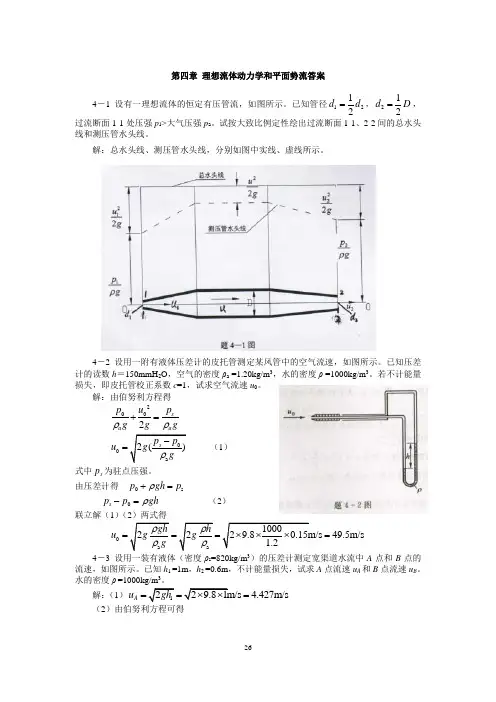
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。

已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。

试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。

解：总水头线、测压管水头线，分别如图中实线、虚线所示。

4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。

已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。

若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。

解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。

由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。

已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。

水的密度ρ =1000kg/m 3。

解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。

由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。

第四章 流体动力学基础4-1 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭，0y ≥总流的动能修正系数为何值?解：172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A A B y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4-2 如图示一股水流自狭长的缝中水平射出，其厚度00.03m δ=，平均流速V 0＝8m/s ，假设此射流受重力作用而向下弯曲，但其水平分速保持不变。

试求(1)在倾斜角45θ=o 处的平均流速V ；(2)该处的水股厚度δ。

解：（1）由题意可知：在45度水流处，其水平分速度仍为8m/s,由勾股定理可得：V=︒45sin 8=11.31m/s （2）水股厚度由流量守恒可得：VD D V δδ=000，由于缝狭长，所以两处厚度近似相等，所以000.0380.02111.31V V δδ⨯===m 。

4-3 如图所示管路，出口接一收缩管嘴，水流射人大气的速度V 2=20m/s ，管径d 1＝0.1m ，管嘴出口直径d 2＝0.05m ，压力表断面至出口断面高差H ＝5m ，两断面间的水头损失为210.5(/2)V g 。

试求此时压力表的读数。

解：取压力表处截面为截面1-1，收缩管嘴处截面为截面2-2，选择两截面包围的空间为控制体，由实际流体的恒定总流能量方程得：2211221222wV p V p z z h g g g g ρρ'++=+++， 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ，由上述两个方程可得压力表的读数（相对压强）：222112212w V V p p z z h g g ρ⎛⎫-'-=+-+ ⎪⎝⎭，上式计算结果为：2.48at 。

第四章习题答案选择题(单选题)4、1等直径水管,A-A 为过流断面,B-B 为水平面,1、2、3、4为面上各点,各点的流动参数有以下关系:(c)(a)1p =2p ;(b)3p =4p ;(c)1z +1p g ρ=2z +2p g ρ;(d)3z +3p g ρ=4z +4pgρ。

4、2伯努利方程中z +p g ρ+22v gα表示:(a)(a)单位重量流体具有的机械能;(b)单位质量流体具有的机械能;(c)单位体积流体具有的机械能;(d)通过过流断面流体的总机械能。

4、3水平放置的渐扩管,如忽略水头损失,断面形心点的压强,有以下关系:(c)p p 2(a)1p >2p ;(b)1p =2p ;(c)1p <2p ;(d)不定。

4、4黏性流体总水头线沿程的变化就是:(a)(a)沿程下降;(b)沿程上升;(c)保持水平;(d)前三种情况都有可能。

4、5黏性流体测压管水头线的沿程变化就是:(d)(a)沿程下降;(b)沿程上升;(c)保持水平;(d)前三种情况都有可能。

4、6平面流动具有流函数的条件就是:(d)无黏性流体;(b)无旋流动;(c)具有速度势;(d)满足连续性。

4、7一变直径的管段AB ,直径A d =0、2m,B d =0、4m,高差h ∆=1、5m,今测得A p =302/m kN ,B p =402/m kN , B 处断面平均流速B v =1、5s m /、。

试判断水在管中的流动方向。

解: 以过A 的水平面为基准面,则A 、B 点单位重量断面平均总机械能为:42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭(m)2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯(m)∴水流从B 点向A 点流动。

第四章 流体运动学基础一 选择题1. 用欧拉法表示流体质点加速度a等于 。

(A) t u (B) u u )( (C) u u t u)( (D) u u tu)(2. 恒定流就是流场中 的流动。

(A) 各断面流速分布相同 (B) 流线就是相互平行的直线 (C) 运动要素不随时间而变化 (D) 流动随时间按一定规律变化 3. 一元流动就是 。

(A) 运动参数就是一个空间坐标与时间变量的函数 (B) 速度分布按直线变化 (C) 均匀直线流 (D) 流动参数随时间而变化 4. 均匀流的 加速度为零。

(A) 当地 (B) 迁移 (C) 向心 (D) 质点 5. 在 流动中,流线与迹线重合。

(A) 恒定 (B) 非恒定 (C) 不可压缩流体 (D) 一元 6. 连续性方程表示流体运动遵循 守恒定律。

(A) 能量 (B) 动量 (C) 质量 (D) 流量7. 水在一条管道中流动,如果两断面的管径比为d 1/d 2 =2,则速度比v 1/v 2= 。

(A) 2 (B) 1/2 (C) 4 (D) 1/4 8. 流体微团 。

(A) 具有规则的几何形状 (B) 质量大小不受限制 (C) 就是由大量流体质点组成的微小质团 (D) 就是质量、体积均可忽略的微元 9. 在 流动中,伯努利方程不成立。

D(A) 恒定 (B) 理想流体 (C) 不可压缩 (D) 可压缩 10. 在总流伯努利方程中,速度 v 就是 速度。

B(A) 某点 (B) 断面平均 (C) 断面形心处 (D) 断面上最大 11. 文透里管用于测量 。

D(A) 点流速 (B) 压强 (C) 密度 (D) 流量 12. 毕托管用于测量 。

A(A) 点流速 (B) 压强 (C) 密度 (D) 流量13. 密度 = 800kg/m 3 的油在管中流动,若压强水头为2m 油柱,则压强为 N/m 2。

C(A) 1、96×104 (B) 2×103 (C) 1、57×104 (D) 1、6×103 14. 应用总流能量方程时,两断面之间 。

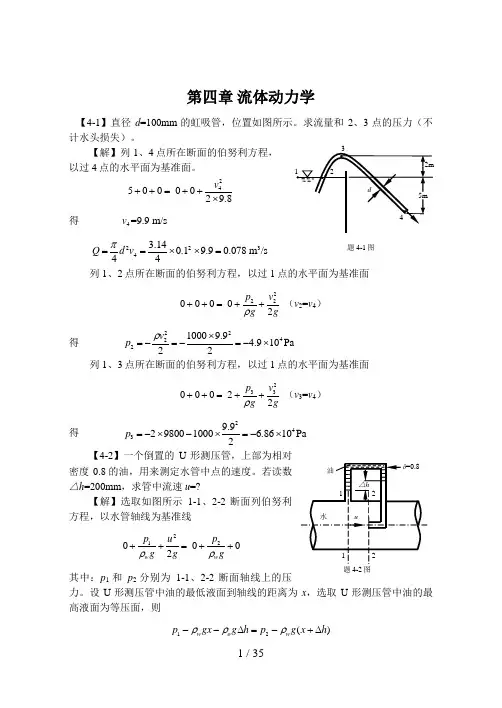
第四章 流体动力学【4-1】直径d =100mm 的虹吸管，位置如图所示。

求流量和2、3点的压力（不计水头损失）。

【解】列1、4点所在断面的伯努利方程，以过4点的水平面为基准面。

24500 0029.8v ++=++⨯得 4 =9.9 m/s v 2234 3.140.19.90.078 m /s 44π==⨯⨯=Q d v列1、2点所在断面的伯努利方程，以过1点的水平面为基准面222000 02p v g gρ++=++ （v 2=v 4）得 2242210009.9 4.910Pa 22ρ⨯=-=-=-⨯v p列1、3点所在断面的伯努利方程，以过1点的水平面为基准面233000 22p v g gρ++=++ （v 3=v 4）得 2439.9298001000 6.8610Pa 2=-⨯-⨯=-⨯p【4-2】一个倒置的U 形测压管，上部为相对密度0.8的油，用来测定水管中点的速度。

若读数△h =200mm ，求管中流速u =?【解】选取如图所示1-1、2-2断面列伯努利方程，以水管轴线为基准线212 0 002w w p p u g g gρρ++=++其中：p 1和p 2分别为1-1、2-2断面轴线上的压力。

设U 形测压管中油的最低液面到轴线的距离为x ，选取U 形测压管中油的最高液面为等压面，则12()w o w p gx g h p g x h ρρρ--∆=-+∆题 4-1图21()w o p p g h ρρ-=-∆则0.885m/s u ==【4-3】图示为一文丘里管和压力计，试推导体积流量和压力计读数之间的关系式。

当z 1=z 2时，ρ=1000kg/m 3，ρH =13.6×103kg/m 3，d 1=500mm ，d 2=50mm ，H =0.4m ，流量系数α=0.9时，求Q =？ 【解】列1-1、2-2断面的伯努利方程、以过1-1断面中心点的水平线为基准线。

李玉柱流体力学课后题解答-第四章————————————————————————————————作者：————————————————————————————————日期:第四章 流体动力学基础4-１ 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭,0y ≥总流的动能修正系数为何值?解:172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A AB y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4－2 如图示一股水流自狭长的缝中水平射出，其厚度00.03m δ=,平均流速V 0=8ｍ/s ，假设此射流受重力作用而向下弯曲，但其水平分速保持不变。

试求（1)在倾斜角45θ=处的平均流速V ;(２）该处的水股厚度δ。

解：（1)由题意可知:在45度水流处,其水平分速度仍为８m/s,由勾股定理可得:Ｖ=︒45sin 8=１1．３1m/s (2)水股厚度由流量守恒可得：VD D V δδ=000,由于缝狭长，所以两处厚度近似相等，所以000.0380.02111.31V V δδ⨯===m 。

4－3 如图所示管路,出口接一收缩管嘴,水流射人大气的速度V 2=2０m/s ，管径ｄ1＝０.1ｍ，管嘴出口直径d 2＝０．05ｍ,压力表断面至出口断面高差Ｈ=５m ，两断面间的水头损失为210.5(/2)V g 。

试求此时压力表的读数。

解:取压力表处截面为截面１-１，收缩管嘴处截面为截面2-2,选择两截面包围的空间为控制体，由实际流体的恒定总流能量方程得:2211221222wV p V p z z h g g g g ρρ'++=+++, 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ,由上述两个方程可得压力表的读数(相对压强）:222112212w V V p p z z h g g ρ⎛⎫-'-=+-+⎪⎝⎭, 上式计算结果为：2．48at 。

第四章 习题解答4-1 用直径为100mm 的管道输送流量为10kg/s 的水，如水温为5℃，试确定管内水的流态。

如用这管道输送同样质量流量的石油，已知石油密度为3/850m kg =ρ运动粘滞系数为s cm /14.12，试确定石油的流态。

解：水温为5℃时，其密度为3/1000m kg =ρ，运动粘滞系数为s m /10519.126−×=γ因此，水在管道中流动的体积流量为： s m mkg skg Q /01.0/1000/1033== 流速为：s m mm sm A Q /27.11000100(14.341/01.023=××==υ雷诺数为：83863/10519.11000100/27.1Re 26=××=−sm mms m 为紊流 当输送石油时： s m mkg s kg Q /012.0/850/1033== 流速为：s m mm sm A Q /5.1)1000100(14.341/012.023=××==υ雷诺数为：1316/1014.11000100/5.1Re 24=××=−sm mms m 为层流 4-2 一圆形风道，管径为300mm ，输送的空气温度为20℃，求气流保持层流时的最大流量。

若输送的空气量为200kg/h ，气流是层流还是紊流？解：空气温度为20℃时，运动粘滞系数s m /107.1526-×=γ，根据题意有：6107.1510003002000−××=mm υ 解方程得：s m /105.0=υ气体流量为： s m s m mm Q /0074.0/105.01000300(14.34132=×××=质量流量为：h kg s kg m kg s m Q /29/0081.0/093.1/0074.033==×= 若输送的空气量为200kg/h ，因此，空气在管道中流动的体积流量为：s m m kg hkg Q /051.03600/093.1/20033=×= 流速为：s m mm sm A Q /72.0)1000300(14.341/051.023=××==υ雷诺数为：13758/107.151000300/72.0Re 26=××=−sm mms m 为紊流 4-3 断面为矩形的排水沟，沟底宽为20cm ，水深为15cm ，流速为0.15m/s ，水温为15℃。

第四章 流体阻力与水头损失计算习题一、填空题1．雷诺数Re 是反映流体流动状态的准数，它反映了流体流动时 粘性力 与 惯性力 的对比关系，雷诺数Re 越大，说明液流的惯性力越大；雷诺数Re 越小，说明液流的粘滞力越大；2. 流体在管道中流动时，流动阻力包括 沿程阻力 和 局部阻力 ；3．流体流动阻力产生的根本原因是流体本身的 惯性 与 粘性 ，其中 粘性 是流动阻力的根本原因。

4．由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv '， 其中kv '称为 上临界速度 ，k v 称为 下临界速度 ； 5.达西公式的表达式为 22f L v h d g λ= ，计算局部水头损失的通用公式是22j v h gξ= ; 7、对圆管来说，临界雷诺数值=k Re 2000 。

8、雷诺数的表达公式为 vd vd Re ρμν==，当Re ≤2000,则液体的流动状态为层流，当Re ＞2000,则液体的流动状态为紊流；9、通过雷诺实验，可知，流体的流动状态分为层流与紊流；其中，质点以平行于管轴方向呈直线运动而无横向运动的流动状态，称为层流状态。

液体质点的互相撞击和掺混，有横向位移，称为紊流状态。

层流到紊流的过渡，称为临界状态。

10、紊流由紊流核心、层流边层和过渡层三部分组成。

11、我们把在管壁附近作层流运动的液层称为层流边界层，其厚度用“δ”，表示。

12、壁面的粗糙度有两种表示方法：绝对粗糙度和相对粗糙度。

13、绝对粗糙度△是壁面粗糙突出的平均高度。

14、紊流的三种类型有水力光滑管、水力粗糙管、混合摩擦管 。

二、选择题1、雷诺数的物理意义表示：（c ）A 、粘滞力与重力之比；B 、重力与惯性力之比；C 、惯性力与粘滞力之比；D 、压力与粘滞力之比。

2、圆管紊流粗糙区的沿程摩阻系数λ D ；A 、与雷诺数Re 有关B 、与和管长l 有关C 、与Re 和d∆有关 D 、与管壁相对粗糙度d D 有关 3、在圆管流动中，层流的断面速度分布符合 C ； A 、均匀规律 B 、直线变化规律 C 、抛物线变化规律 D 、对数曲线规律4、流体在管内作层流流动时，其沿程损失h f 值与断面平均流速v 的 A 次方成正比。

第四章习题简答4-2 管径cm d 5=，管长m L 6=的水平管中有比重为0.9油液流动，水银差压计读数为cm h 2.14=，三分钟内流出的油液重量为N 5000。

管中作层流流动，求油液的运动粘度ν。

解: 管内平均流速为s m d Q v /604.1)4/05.0/(180/)9.09800/(5000)4//(22=⨯⨯==ππ 园管沿程损失h f 为γ(h 水银γ/油)1-=0.142(13.6/0.9-1)=2.004m园管沿程损失h f 可以用达西公式表示： gvd l h f 22λ=,对层流, Re /64=λ, 有fgdhlv 264Re 2=, 但νvd=Re , 从而lvh gd f 6422=ν, 代入已知量, 可得到s m /10597.124-⨯=ν题 4-2 图4-4 为了确定圆管内径，在管内通过s cm /013.02=ν的水，实测流量为s cm /353，长m 15管段上的水头损失为cm 2水柱。

试求此圆管的内径。

解：422222212842642642642Re 64gdlQ d d g lQ gdlv gvd l vdgvd l h f πνπννν=⎪⎭⎫ ⎝⎛====m gdlQ d 0194.002.08.9210013.0351********4=⨯⨯⨯⨯⨯⨯==∴-ππν4-6 比重85.0, s m /10125.024-⨯=ν的油在粗糙度mm 04.0=∆的无缝钢管中流动，管径cm d 30=，流量s m Q /1.03=, 求沿程阻力系数λ。

解: 当78)(98.26∆d >Re>4000时，使用光滑管紊流区公式：237.0Re221.00032.0+=λ。

园管平均速度s m d q v /4147.1)4//(2==π, 流动的33953Re ==νvd, ：723908)(98.2678=∆d , 从而02185.0Re/221.00032.0237.=+=o λ4-8 输油管的直径mm d 150=,流量h m Q /3.163=，油的运动黏度s cm /2.02=ν,试求每公里长的沿程水头损失。

第四章流体动力学基本定理及其应用4-1欧拉运动微分方程和伯努利方程的前提条件是什么，其中每一项代表什么意义？答：（1）欧拉运动微分方程是牛顿第二定律在理想流体中的具体应用，其矢量表达式为:.:t其物理意义为：从左至右，方程每一项分别表示单位质量理想流体的局部惯性力、迁移惯性力、质量力和压力表面力。

（2）伯努利方程的应用前提条件是：理想流体的定常运动，质量力有势，正压流体，沿流2线积分。

单位质量理想流体的伯努利方程的表达式为：- p g^ C，从左至右方程2 P每项分别表示单位质量理想流体的动能、压力能和位能，方程右端常数称流线常数，因此方程表示沿流线流体质点的机械能守恒。

4-2设进入汽化器的空气体积流量为Q = 0.15m3 / S,进气管最狭窄断面直径D=40mm，喷油嘴直径d=10mm。

试确定汽化器的真空度。

又若喷油嘴内径d=6mm，汽油液面距喷油嘴高度为50cm，试计算喷油量。

汽油的重度=7355N/m3。

答：（1）求A点处空气的速度：设进气管最狭窄处的空气速度为V i，压力为p i，则根据流管的连续方程可以得到:丄二D2_d2V i =Q，44Q因此：v14Q 厂。

江（D2-d2）（2 ）求真空度p v选一条流线，流线上一点在无穷远处F，—点为A点；并且:在F点：P F二P o ，V F = 0 ；在A点：P A二P1 二？，V A二W。

将以上述条件代入到伯努利方程中，可以得到:2也.0. v_02g-—；v f ， v A = v 2 = ?， z A = h = 50cm = 0.5m ；2在 B 点：P B = p 0， V B = 0，Z B = 0 ； 代入到伯努利方程中，可以得到:Ip 0才v 22rh 』0 0；整理得到:v ；二」V 12 -2gh ；2因此汽油喷出速度为:1V 2 -2gh ；其中空气重度1 = Sg =1.226 9.81 =12N/m 3 ； V 1缪 龙，并注意到喷油嘴的 兀(D -d )直径是6mm ，而不是原来的10mm ，则计算得到:因此汽油流量为:12 _43 3因此真空度为:P v 二 P o - P i4Q冷心2] D2—d 28 322 JI(D 2 —d 2 2若取空气的密度为3::=1.226kg/m ，那么计算得到:8 1.226 0.152pv3.1421 32 =9.95 103Pa 。

4.1一变直径管段AB ，直径d A =0.2m ，d B =0.4m ，高差△h=1.5m，测得p A =30kPa ，p B =40kPa ，B 点处断面平均流速v B =1.5m/s ．水在管中的流动方向。

解：s m d d v v ABB A 62.04.05.1442222=⨯=⋅=ππ以过A 点的水平面为等压面，则OmH g v g p h H OmH g v g p H B B B A A A 2222226964.58.925.18.9405.128980.48.9268.9302=⨯++=++==⨯+=+=ρρ可以看出：，水将从B 点流向A 点。

A B H H >或：wB B B A A A h gvg p z g v g p z +++=++2222ρρ解得水头损失为：，水将从B 点流向A 点。

O mH h w 27984.0-=4.2利用毕托管原理，测量水管中的流速u 。

水银差压计读书⊿h =60mm ，求该点流速。

解：m/s8530606128922....h g u =⋅⋅⋅=∆=汞ρ4.3水管直径50mm ，末端阀门关闭时，压力表读值为21kPa ，阀门打开后读值降为5.5kPa ，求不计水头损失时通过的流量Q.解：所以 m/s 57555212221.g .g g p p g V =-=⎪⎪⎭⎫ ⎝⎛-=ρρQ=VA=5.57×π(0.05)2/4=10.9 l/s4.4水在变直径竖管中流动，已知粗管直径d 1=300mm ，流速v 1=6m/s ，为使两断面的压力表读值相同，试求细管直径（水头损失不计）。

gV g p g p 20221++=ρρ解： gvg P g v g P 223222211+⋅=+⋅+ρρ21P P =流量相等222121v d v d =mmd 2352=4.5 为了测量石油管道的流量，安装文丘里流量计，管道直径d 1 =200mm ，流量计喉管直径d 2 =100mm ，石油密度ρ=850kg/m ，流量计流量系数μ=0.95。

第四章习题答案选择题（单选题）4.1等直径水管，A-A 为过流断面，B-B 为水平面，1、2、3、4为面上各点，各点的流动参数有以下关系：（c ）（a ）1p =2p ；（b ）3p =4p ；（c ）1z +1p g ρ=2z +2p g ρ；（d ）3z +3p g ρ=4z +4pgρ。

4.2伯努利方程中z +p g ρ+22v gα表示：（a ）（a ）单位重量流体具有的机械能；（b ）单位质量流体具有的机械能；（c ）单位体积流体具有的机械能；（d ）通过过流断面流体的总机械能。

4.3水平放置的渐扩管，如忽略水头损失，断面形心点的压强，有以下关系：（c ）p p 2（a ）1p >2p ；（b ）1p =2p ；（c ）1p <2p ；（d ）不定。

4.4黏性流体总水头线沿程的变化是：（a ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。

4.5黏性流体测压管水头线的沿程变化是：（d ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。

4.6平面流动具有流函数的条件是：（d ）无黏性流体；（b ）无旋流动；（c ）具有速度势；（d ）满足连续性。

4.7一变直径的管段AB ，直径A d =0.2m ，B d =0.4m ，高差h ∆=1.5m ，今测得A p =302/m kN ，B p =402/m kN ， B 处断面平均流速B v =1.5s m /.。

试判断水在管中的流动方向。

解： 以过A 的水平面为基准面，则A 、B 点单位重量断面平均总机械能为：42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭（m ）2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯（m ）∴水流从B 点向A 点流动。