第六节微分法在几何上的应用.

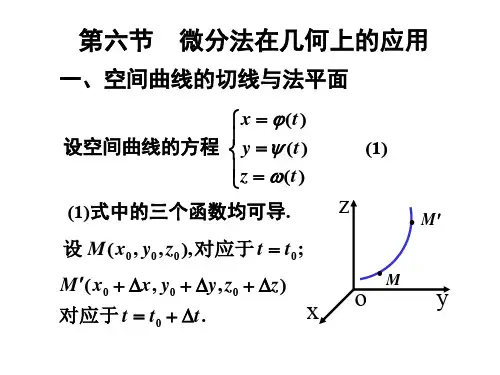
本学期《高等数学》的考试范围是：第五章定积分的应用，第六章至第十一章.内容为：空间解析几何与向量代数，多元函数的微积分，曲线积分，微积分的应用-级数理论及常微分方程的解法．我们用了90课时，讲了尽可能多的知识，保证了后继课程学习中对数学知识的需要，及将来考研同学对高数的知识点范围．对教学工作仍坚持一丝不苟、认真负责的态度，讲好每节课，对大题量的作业做到每周全收、认真批阅一次，耐心解答同学提出的问题．对同学的学习坚持从严要求，强调做好听课、记笔记、独立完成作业三个教学环节．逐步培养同学掌握学习数学课的方法：多动脑勤动手，数学书不是光靠看，还要动手演算才能理解深刻，记忆牢固．考试题型为：一.选择题（每小题3分，共15分） 二.填空题（每小题3分，共15分） 三.计算题（8小题，共40分） 四.应用题（2小题，共16分） 五.证明题（2小题，共14分）下面分章复习所学知识第五章 定积分的应用定积分在几何上的应用：求平面图形的面积（1） 直角坐标情形：由平面曲线(),()[()()]y f x y g x f x g x ==≥,()x a x b a b ==<所围图形的面积为[()()].baA f x g x dx =-⎰（2）极坐标情形：由曲线()r r θ=及射线,()θαθβαβ==<所围成的曲边扇形的面积为21().2A r d βαθθ=⎰例 （填空题）由曲线x y 1=及直线0,2,===y x x y 围成的平面图形的面积 .第六章 向量代数与空间解析几何（一）向量代数1.空间两点111(,,)A x y z 与222(,,)B x y z 的距离公式222121212()()()d x x y y z z =-+-+- 2.非零向量 {}123,,a a a a =的方向余弦公式 312222222222123123123cos ,cos ,cos a a a a a aa a aa a aαβγ===++++++3.向量的运算设 {}{}123123,,,,,a a a a b b b b ==，则112233123123,ijka b a b a b a b a b a aab b b ⋅=++⨯= 两非零向量垂直、平行的充要条件11223331212300//0a b a b a b a b a b a a a a b a b a b b b b λ⊥⇔⋅=⇔++=⇔=⇔⨯=⇔==4.向量{}123,,a a a a =在非零向量{}123,,b b b b =上的投影 112233222123Pr cos ,b b a b a b a ba b a j a a a b bb b b ++⋅∏==<>==++（二）平面与直线 1.平面方程（1）一般式：0;Ax By Cz D +++=（2）点法式：000()()()0;A x x B y y C z z -+-+-=（3）截距式：1;x y za b c++=（4）三点式：1112121213131310.x x y y z z x x y y z z x x y y z z ------=--- 2.直线方程（1）对称式（点向式、标准式）：000;x x y y z z m n p---== （2）一般式：111122220;0A xB yC zD A x B y C z D +++=⎧⎨+++=⎩（3）参数式：000,;x x mt y y nt t z z pt=+⎧⎪=+-∞<<+∞⎨⎪=+⎩（4）两点式：111212121.x x y y z z x x y y z z ---==--- 3.平面()∏与直线()l 平行、垂直的充要条件及夹角（1）1212121211112222()()0()//()A A B B C C A B C A B C ∏⊥∏⇔++=∏∏⇔==;(2)12121212111122220//l l m m n n p p m n pl l m n p ⊥⇔++=⇔==；（3）1111111111111111()()//0m n p l A B C l m A n B p C ∏⊥⇔==∏⇔++=；（4）1()∏与2()∏的夹角： 121212222222111222c o s A A B B C C A B C A BC ϕ++=++⋅++(5)1l 与2l 的夹角： 121212222222111222c o s m m n n p p m n p m np ϕ++=++⋅++（6）1()∏与1l 的夹角：111111222222111111s i n m A n B p C m n p A BC ϕ++=++⋅++4.距离设点0000(,,)M x y z ，平面():0Ax By Cz D ∏+++=直线111:x x y y z z l m n p---==（1）点到平面的距离公式：000222;Ax By Cz Dd A B C+++=++(2) 点到直线的距离公式：01M M ld l⨯=，其中 {}01101010,,M M x x y y z z =---，{}1,,,l m n p M =是直线上任一点． （三）曲面与空间曲线记住一些常见的曲面的方程 （1）旋转曲面园锥面：22z x y =+，旋转抛物面：22z x y =+，旋转椭球面：22222 1.x y z a c++= （2）柱面圆柱面：222,x y R +=椭圆柱面：22221x y a b+=，抛物柱面：220x py -=，双曲柱面：2222 1.x y a b-=（3）二次曲面球面：2222()()();x a y b z c R -+-+-=椭球面：2222221,(,,0)x y z a b c a b c++=>；椭球抛物面：22,(,22x y z p q p g +=同号）； 双曲抛物面：22,(,2x y z p q p q-+=同号）； 单叶双曲面：2222221,(,,0)x y z a b c a b c +-=>；双叶双曲面：2222221,(,,0)x y z a b c a b c+-=->．本章的考点：仅是一些简单的填空题或选择题．例1.设三角形ABC ，已知2,2,BA i j BC i j k D =+=++为BC 的中点，则BC 上 的中线长AD =10/2例2. 1.两向量a 与b 互相垂直的充要条件是0a b ⋅=.2.向量13(2),(1)a i j b i j k λλλ=-++=-+-平行，则λ= 1 .3.求同时垂直于向量{}{}2,3,1,1,2,0a b =-=-的单位向量是 0c ±.解 {}2312,1,1120i j kc a b =⨯=-=--，单位化 {}02222,1,1211,,66621(1)c c c --⎧⎫===⎨⎬⎩⎭++-. 例3.（选择题）过点(2,3,5)且平行于平面53210x y z -++的平面是（ C ）.53211A x y z ++-=.53211B x y z -++= .53211C xy z -+-=.53211D x y z +++= 例4.（选择题）在空间直角坐标系下，方程350x y +=的图形是（ D ）.A 过原点的一条直线； .B 斜率为35-的一条直线；.C 垂直于z 轴的一平面； .D 过z 轴的一平面.例5.（选择题）方程231x y +=在空间表示的图形是（ B ） .A 平行于XOY 坐标面的平面； .B 平行于z 轴的平面； .C 过oz 轴的平面； .D 直线． 例6.（选择题）方程22x y =在空间表示的是（ B ） .A 抛物线； .B 抛物柱面； .C 母线平行于x 轴的柱面； .D 旋转抛物面. 例7. (选择题) 下列平面方程中（ C ）过y 轴：.A 1x y z ++=； .B 0x y z ++=； .C 0x z +=； .D 1.x z +=例8. 曲线 2221z x y z ⎧=+⎨=⎩在XOY 平面上的投影方程为：22210x y z ⎧+=⎨=⎩第七章 多元函数微分法及其应用（一）基本概念1.二元函数：定义域和对应规律为(,)z f x y =的两要素，其定义域为平面上的点集．例9 (填空题)二元函数ln 1xyz y=+的定义域是0,0(,)0,10x y D x y x y ⎧⎫>>⎪⎪=⎨⎬<-<<⎪⎪⎩⎭或 二元函数221ln(1)x y z x y --=--的定义域为{}22(,)1,1D x y x y x y =+≤+<2.极限：函数(,)z f x y =的极限为A ，是指点(,)x y 以任何方式沿某路径趋于点00(,)x y 时，(,)f x y A →，记为00lim (,)x x y y f x y A →→=例10. 证明：极限2222200lim ()x y x y x y x y →→--不存在．证明 如果动点(,)P x y 沿y x =趋于点(0,0)时，则2242224000lim lim 1;()x x y x y x x y x y x →→→==-- 如果动点(,)P x y 沿2y x =趋于点(0,0)时，则2242224200024lim lim 0()4x x y y xx y x x y x y x x →→→===--+ 因沿不同路径，极限值不一，故原极限不存在.3.连续：函数(,)z f x y =在点00(,)x y 连续，必须同时满足三个条件，缺一不可：（1）在00(,)U x y 内有定义；（2）0lim (,)x x y y f x y →→存在；（3）0000lim (,)(,)x x y y f x y f x y →→=.否则间断．例11.（选择题）设221xy z x y=--，下面结论正确的是（ D ）.A 在XOY 平面上连续； .B 在XOY 平面上不连续；.C 在XOY 平面上只有(1,0),(0,1)为间断点；.D 在XOY 平面上，只有在区域221x y +<内，函数连续.例12． (选择题) 函数22222,(,)(0,0)(,)0,(,)(0,0)x y x y f x y x y x y ⎧+≠⎪=+⎨⎪=⎩在点(0,0)处（ C ）.A 连续； .B 有极限但不连续； .C 极限不存在； .D 无定义.（二）偏导数1.定义与计算偏导数,z zx y∂∂∂∂是整体记号，不具有商的意义，求z x ∂∂时，把(,)z f x y =中的y固定 （看作常数），利用一元函数的求导公式和法则求出．记住：偏导函数z x ∂∂与一点的偏导数000(,)x x x y y z f x y x==∂'=∂记号不同，及它们之间的关系例13.（填空题）设22(,)f x y x y x y =+-+，则(3,4)x f '=252.高阶偏导数（以二阶为主）：22(,)();xx z z f x y x x x ∂∂∂''==∂∂∂ 22(,)();yy z zf x y y y y∂∂∂''==∂∂∂ 2(,)();xy z z f x y x y y x ∂∂∂''==∂∂∂∂ 2(,)().yx z zf x y y x x y ∂∂∂''==∂∂∂∂（注意：二阶混合偏导数在定义域D 内连续时，相等）（三）全微分1.定义与计算：若函数(,)z f x y =在点00(,)x y 的全改变量（全增量）可表为()z A x B y ρ∆=∆+∆+，其中,A B 不依赖于,x y ∆∆，仅与00(,)x y 有关， 22()()x y ρ=∆+∆，则全增量的线性主要部分为为函数的全微分，记作 .z z dz A x B y dx dy x y∂∂=∆+∆=+∂∂ 例14.（选择题）函数(,)z z x y =由方程ln()0z xy +=所确定，则dz =（ A ）.;dx dy A x y -- .;dx dy B x y+ .;dx dy C z x + ..dx dy D xy xy+ 例15. 函数22ln()u x y z =++在点(1,0,1)处的全微分为： . 例16. 求22x y z e +=的全微分及二阶偏导数.解22222,2x y x y zz xe ye x y++∂∂==∂∂ 222222;x y x y d z x e d xy ed y++∴=+ 2222222222(12),4x y x y z z z ex x y e x x y y x++∂∂∂=+==∂∂∂∂∂22222,2(12).x y z e y y +∂=+∂2.二元函数在一点连续、可导（两个偏导数存在）与可微的关系．偏导数连续⇒可微⎧⎨⎩⇒⇒可导极限存在，反之不一定成立.例17.（选择题）二元函数22z x y =+在点(0,0)处（ C ）.A 不连续，两个偏导数不存在； .B 不连续，两个偏导数存在； .C 连续，两个偏导数不存在；.D 连续，两个偏导数存在．例18.（填空题）(,),(,)x y f x y f x y 连续是(,)z f x y =可微的充分条件.例19. 证明题：证明函数222222,0(,)0,0xyx y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩在(0,0)点处两个偏导数存在，但不连续.（用定义求偏导数，取两条路径如极限不一则不连续）3.方向导数与梯度（不做考试要求）（1）方向导数—函数在特定方向（指定方向）上的变化率：cos cos cos f f f fxy z l αβγ∂∂∂∂=++∂∂∂∂，其中,,αβγ为射线l 与,,x y z 轴正向夹角（2）梯度—不同点的方向导数不同，它在哪个方向上最大呢？函数(,,)u f x y z =在点(,,)x y z 处的梯度为：(,,).f f f gradf x y z i j k x y z∂∂∂=++∂∂∂ 例20.（填空题）函数22u xy z xyz =+-在点(1,1,2)处沿方向{}1,2,1l =的方向导数是 .（四）多元复合函数的导数1.锁链法则—先画出链式图，写出公式，然后计算.(,),(,),(,)z f u v u x y v x y ϕψ===，则有锁链公式：z z u z v x u x v x∂∂∂∂∂=+∂∂∂∂∂z z u z v y u y v y∂∂∂∂∂=+∂∂∂∂∂ 2.几种推广情形（1）若(,,)z f u v w =，而(,),(,),(,)u x y v x y w x y ϕψω===，则有锁链公式：z z u z v z w x u x v x w x∂∂∂∂∂∂∂=++∂∂∂∂∂∂∂z z u z v z w y u y v y w y∂∂∂∂∂∂∂=++∂∂∂∂∂∂∂ （2）若(,,),z f u x y =而(,)u u x y =，则有锁链公式： z f f u x x u x∂∂∂∂=+∂∂∂∂z f f u y y u y∂∂∂∂=+∂∂∂∂注意：这里z x ∂∂与f x ∂∂不同，zx∂∂是把复合后的函数，将y 看作常数，对x 求偏导；而fx∂∂是把复合前的函数，将,u y 看作常数对x 求偏导． （3）设(,,,)u f x y z t =，而(),(),()x x t y y t z z t ===，则复合函数只有一个自变量， t 求导dzdt ，称为全导数.d z u d x u d y u d z u d td t x d t y d x t d t t d t∂∂∂∂=+++∂∂∂∂何时用锁链法则：①函数关系不具体； ②中间变量多于一个.例21.（选择题）设22(,)()()f x y x y x y x y x y +-=-=+-，则()()f x y f x yxy∂⋅∂⋅+=∂∂（ C ）..22A x y - .22B x y+.;C x y + ..D x y --例22.22sin()1,yz x e xy =++求 2,.z zx x y∂∂∂∂∂例23.设arctan()z u x y =-，求,,.u u u x y z∂∂∂∂∂∂ 解 由锁链法则121();1()z z u z x y x x y -∂=⋅-∂+- 121();1()z zu z x y y x y -∂-=⋅-∂+-21()l n .1()z z u x y x y z x y ∂=-⋅-∂+- 例24.设二元函数(,)xz xy f xy y=+，其中f 是二阶可微函数，求,,.x y yy z z z ''''解 设1,2xxy u v y====，则 121;x z y yf f y'=++122;y xz x xf f y '=+- 11122212223222()()yy x x x x z x f x f f f x f y y y y ⎡⎤⎡⎤''=+-+-+-⎢⎥⎢⎥⎣⎦⎣⎦ 222111222224322.x x xx f f f f y y y=-++例25.设(5,)u f x y xyz =+，求22.ux∂∂解 12x u f yzf '=+； 2211122122.xx u f yzf yzf y z f ''=+++ （五）隐函数微分法：（只讨论一个方程的情形）1. 方程两边对自变量求导（复合函数的锁链法则）， 解出所求的偏导数（是,x y 的函数）.2.公式法：x z F z x F '∂=-'∂， .y z F zy F '∂=-'∂ 3.微分法：利用一阶全微分形式的＂不变性＂，对方程两边求全微分，即可求出所需的偏导数或导数．例26.（填空题）由方程2221x xyz z ++=确定(,)z z x y =，则z x ∂=∂124xy z-+. 例27.设ln ,x z z y =求,.z z x y∂∂∂∂ 解 由隐函数微分法 设 (,,)ln ln ln x z xF x y z z y z y z=-=-+ 因为 22111,,x y z x x zF F F z y z z z+'''===--=-所以 21x z F z z z x z x F x z z -'∂=-==+'∂+- 221.()y z F z z y x z y F y x z z -'∂=-==+'∂+-例28. 设(,)z z x y =是由方程2224x x y e z z ++=所确定的隐函数，求.dz例29.设2sin(23)23x y z x y z +-=+-，证明：1x z x y∂∂+=∂∂ 证明设(,,)2sin(23)23F x y z x y z x y z =+---+，则 2c o s (23)x F x y z '=+--,2c o s (23)2y F x y z '=+-⋅-2x F '= 2c o s (23)(3)3z x F x y z F ''=+--+=-133x x z x F F z x F F ''∂=-=-=''∂-, 2233y x z x F F zy F F ''∂=-=-=''∂-故12 1.33y x z z F F z zx y F F ''∂∂+=--=+=''∂∂ （六）微分法在几何上的应用（不做考试要求）1.空间曲线的切线与法平面设空间曲线Γ的参数方程 (),(),()x t y t z t ϕψω===，则Γ在点000(,,)x y z 处的切线方程为：000000()()()x x y y z zt t t ϕψω---==''' 法平面方程为： 000()()()()()()0t x x t y y t z zϕψω'''-+-+-= 2.空间曲线的切平面与法线隐函数的曲面方程：(,,)0F x y z =， 显函数的曲面方程：(,)z f x y =，（七）多元函数的极值及其求法1.极值的必要条件：见教材.264P 定理1（极值发生在可疑点，即驻点或偏导数不存在的点上.2.极值的充分条件：设00(,)x y 为为函数(,)z f x y =的驻点，000022222,,x x x x x xy y y y y yzz zA B C xx yy ======∂∂∂===∂∂∂∂,则下结论（1）20,0B AC A -<>有极小值，0A <有极大值； （2）20B AC ->，无极值；（3）20B AC -=,不定，另作讨论.例30.（选择题）下列说法中，正确的是（ ）.A 可微函数(,)f x y 在00(,)x y 达到极值，则必有0000(,)(,)0;x y f x y f x y ''==.B 二元函数(,)f x y 在00(,)x y 达到极值，则必有0000(,)(,)0;x y f x y f x y ''== .C 可微函数(,)f x y 在00(,)x y 有0000(,)(,)0;x y f x y f x y ''== .D 二元函数(,)f x y 在00(,)x y 的偏导数不存在，则必不存在极值. 例31求函数224(23)z x y =-+的极值.解 804(23)0x y z x z y ⎧'==⎪⎨'=-+=⎪⎩，得驻点3(0,)2-又22333(0,)(0,)(0,)222()xyxxyyB AC z z z ----=-⋅08(8)640-⋅-=>，故函数在3(0,)2-处无极值.3.用Lagrange 乘子法求条件极值的应用题解题步骤：（1）将实际问题化为二元或三元函数的条件极值问题； （2）作辅助函数(,,,)F x y z λ＝原函数+λ乘条件函数； （3）将辅助函数对,,,x y z λ分别求偏导数，得方程组； （4）解方程组，得唯一驻点（5）答：根据实际问题的意义，知此唯一驻点即极值点，也是最值点，并求出最值．例32 应用题：造一个容积为V 的长方体盒子，如何设计，才能使所用材料最少？解 设盒长为x ，宽为y 则高为V xy ，故表面积为：2()V V S xy x y=++， 于是，将问题化为求二元函数的最大值问题，222(02()0SV y x x S V x yy ∂⎧=-=⎪∂⎪⎨∂⎪=-=∂⎪⎩，解得唯一驻点33(,)V V ，根据实际问题的意义，此唯一驻点即为极大值点，也是最大值点， 答：当盒子的长宽高都是3V ，即正方体时，所用材料最少.例33. 应用题：利用Lagrange 乘子法求椭圆抛物面222z x y =+到平面232x y z +-=的最短距离.第八章 重 积 分（一）重积分的概念1.定义：二重积分表示一种类型的和式极限； 三重积分表示另一种类型的和式极限.2.几何与物理意义二重积分表示曲顶柱体的体积，平面薄板的质量； 三重积分表示空间物体的质量（无几何意义）． 3.性质与定积分类似性质3：如果在定义域D 上，函数(,)1f x y =，σ为D 的面积，则 1DDd d σσσ=⋅=⎰⎰⎰⎰（二）二重积分的计算1.直角坐标系下二重积分的计算步骤：面积元素 d dxdy σ= ①先通过解方程组曲线交点的坐标，然后画出积分域的草图； ②如是x -形积分域，将其化为先对y 后对x 的积分次序积出来 y -形积分域，将其化为先对x 后对y 的积分次序积出来. 注 利用“穿口法”的定限口诀是： 后积先定限，限内画条线； 先交下限写，后交上限见.2.极坐标系下二重积分的计算①何时采用极坐标：（ⅰ）积分域是园形或环形；（ⅱ）被积函数包含22x y +.②记住极坐标变换：cos x r θ= 面积元素：d rdrd σθ=， s i n y r θ=然后将积分化为先对r ，后对θ的次序积出来； ③积分限如下定：（ⅰ）若极点O 在域D 内，则2()(,)(cos ,sin );r Df x y d d f r r rdr πθσθθθ=⎰⎰⎰⎰（ⅱ）若极点O 在域D 的边界上，则()(,)(cos ,sin );r Df x y d d f r r rdr βθασθθθ=⎰⎰⎰⎰（ⅲ）若极点O 在域D 的外部，则21()()(,)(cos ,sin ).r r Df x y d d f r r rdr βθαθσθθθ=⎰⎰⎰⎰例34.（选择题）设(,)f x y 是连续函数，交换二重积分112203ydy x y dx -⎰⎰的的积分次序后的结果为（ C ） 11220.3;xA dx x y dy -⎰⎰11220.3;y B dx x y dy -⎰⎰21122.3;x C dx x y dy -⎰⎰ 211220.3.x D dx x y dy +⎰⎰例35.交换积分次序：22121(1)01(,)(,)x x odx f x y dy dx f x y dy --+=⎰⎰⎰⎰.例36.(选择题)设域22:1D x y +≤，且0,0x y ≥≥，则2Dxy dxdy =⎰⎰（ B ）112.;A dx xy dy ⎰⎰ 211200.;x B dx xy dy -⎰⎰2112.;y C dx xy dy -⎰⎰221120..y x D dx xy dy --⎰⎰例37.计算二重积分Ⅰ＝22y Dx e dxdy -⎰⎰，其中D 是由直线,1y x y ==及y轴所围的平面区域．解 画出积分区域草图，这是y -型积分域，故选取先对x 后对y 的积分次序，得Ⅰ＝221220yy y Dx edxdy edy x dx --=⎰⎰⎰⎰＝221113000111()366y t y t t y e dy te dt td e =---==-⎰⎰⎰令110112(1).66t t tee dt e--⎡⎤=-+=-⎢⎥⎣⎦⎰分部法例38.求二重积分 cos()Dx x y d σ+⎰⎰，其中D 是顶点分别为(0,0),(,0)π和(,)ππ的三角形区域.例39.计算Dydxdy ⎰⎰，其中D 由2,2y x y x x ==-围成．解 将22y x x =-改写为：11x y =+±-，则 {}(,)11,01D x y y x y y =--≤≤≤≤，所以原式＝11110(11)yyydy dx y y y dy --⋅=-+-⎰⎰⎰＝101514y ydy -+⋅-⎰ ＝2sin 2220442(1sin )sin .15815y tt tdt ππ==-+-=-⎰令例40.计算222DR x y d σ--⎰⎰，其中D 是由圆周22x y Rx +=所围成的闭区域 解 根据积分域和被积函数的特点，选用极坐标计算c o s22222202R DR x y d d R r rdrπθσθ--=-⋅⎰⎰⎰⎰＝33332024(sin )().333R R R d πθθπ--=-⎰例41.求二重积分22()xy De dxdy -+⎰⎰，其中222:0,0,.D x y x y a ≥≥+≤解 选用极坐标计算22222()221()(1).224aax yrraDedxdy d erdr e d r e πππθ-+----=⋅=⋅-=-⎰⎰⎰⎰⎰例42.应用题：求在XOY 平面上由2y x =与24y x x =-所围成区域的面积.例43.D 是由曲线24()y x y =+以及4x y +=所围成的图形，试求D 的面积.（以上两题，利用二重积分的几何意义，取被积函数(,)1f x y ≡，计算二重积分即得所谓区域的面积）例44.（填空题）设空间一光滑曲面S ：(,),z f x y D =是S 在坐标面XOY 上的投影，则D 的面积＝1Dd σ⋅⎰⎰例45.利用极坐标计算二重积分22ln(1)Dx y dxdy ++⎰⎰，其中 22:1,0,0.D x y x y +≤≥≥ 解 由于极点在D 的边界上，故原式＝1222ln(1)ln(1)Dr r drd d r r dr πθθ⋅+=+⎰⎰⎰⎰＝12201ln(1)(1)22r d r π⋅++⎰=分部法122100(1)l n (1)2(2l n 21).44r r rdr ππ⎡⎤++-=-⎢⎥⎣⎦⎰ 解 2244444464(4).43yy Dy S dxdy dy dx dy ---===-=⎰⎰⎰⎰⎰（三）三重积分的计算（只做简单的计算）1.直角坐标系下的计算 体积元素：dv dxdydz =1212(,)(,):()()z x y z z x y y x y y x a x b ≤≤⎧⎪Ω≤≤⎨⎪≤≤⎩，（这是上下张着的曲面，x -型的投影域）则2211()(,)()(,)(,,)(,,);by x z x y ay x z x y f x y z dv dx dy f x y z dz Ω=⎰⎰⎰⎰⎰⎰2.柱坐标系（＝极坐标z +轴）下的计算体积元素：dv rdrd dz θ=1212(,)(,):()()z r z z r r r r θθθθαθβ≤≤⎧⎪Ω≤≤⎨⎪≤≤⎩，(这是上下张着的曲面，极点在投影域外部)则2211()(,)()(,)(,,)(cos ,sin );r z r r z r f x y z dv d rdr f r r dz βθθαθθθθθΩ=⎰⎰⎰⎰⎰⎰3.球坐标系下的计算体积元素：2sin dv r drd d ϕϕθ=s i n c o s i n s i n c o s x r y r z r ϕθϕθϕ=⎧⎪=⎨⎪=⎩， 1212(,)(,):()()r r r ϕθϕθϕθϕϕθαθβ≤≤⎧⎪Ω≤≤⎨⎪≤≤⎩，则2211()(,)2()(,)(,,)(sin cos ,sin sin ,cos )sin r r f x y z dv d d f r r r r dr βϕθϕθαϕθϕθθϕϕθϕθθϕΩ=⋅⎰⎰⎰⎰⎰⎰例46.在柱坐标中，a θ=（常数）表示的曲面是：z 过轴的半平面. 例47.(填空题)设一立体由上半球面224z x y =--及锥面223()z x y =+所围成，则其在XOY 平面上的投影为：21y x y +≤.例48.（选择题）Ⅰ＝22()x y dv Ω+⎰⎰⎰，其中Ω是由锥面22z x y =+，平面(0)z a a =>所围成的闭区域，则它在柱坐标系下的三次积分是（ D ）2.;a arA d rdr r dz πθ⎰⎰⎰ 2220.;a arB d rdr r dz πθ⎰⎰⎰20.;a a C d rdr r dz πθ⎰⎰⎰ 220..a arD d rdr r dz πθ⎰⎰⎰例49（选择题）设区域{}222(,,)(1)1x y z x y z Ω=++-≤，且()f t 是连续函数，则222()f x y z dv Ω++=⎰⎰⎰（ A ） 22c o s220.()sin A d d f r r dr ππϕθϕϕ⎰⎰⎰；22c o s220.(2cos 1)sin B d d f r r r dr ππϕθϕϕϕ++⎰⎰⎰； 22c o s 200.(2c o s)s i n C d d f r r d rππϕθϕϕϕ⎰⎰⎰； 22c o s 220.(2c o s )s i n .D d d f r r d r ππϕθϕϕϕ⎰⎰⎰例50. 求曲面22y x z +=与22y x z +=所围成立体的体积体积. 解 在柱坐标系下，将被积函数(,,)1f x y z ≡，则所围立体的体积为：2211.6rr V dv rdrd dz d rdr dz ππθθΩΩ=⋅===⎰⎰⎰⎰⎰⎰⎰⎰⎰第九章 曲线积分与曲面积分（曲面积分不做考试要求） （一）曲线积分1.第Ⅰ型曲线积分（对弧长的积分）2.第Ⅱ型曲线积分（对坐标的积分）3.两类积分之间的联系.4.计算方法（1）设曲线L 由它的的参数方程：(),()x t t y t ϕαβψ=⎧≤≤⎨=⎩给出(特例) ,()x xa xb y y x =⎧≤≤⎨=⎩)，则[]22(,)(),()()(),();Lf x y ds f t t t t dt εαϕψϕψαβ''=+<⎰⎰（2）若弧AB 由()()x t y t ϕψ=⎧⎨=⎩给出，起点A 对应t α=，终点B 对应,t β=则[][]{}(),()()(),()()ABPdx Qdy P t t t Q t t t dt βαϕψϕϕψψ''+=+⎰⎰. 5.Green （格林）公式：()DLQ Pdxdy Pdx Qdy x y∂∂-=+∂∂⎰⎰⎰ 应用：,P y Q x =-=，得D 得面积 12A xdy ydx =-⎰.6.平面曲线积分与路径无关的条件 （1）0;Pdx Qdy +=⎰（2）设G 是单连通域，,P Q 在G 内有一阶连续偏导数，则曲线积分LPdx Qdy +⎰在G 内与路径无关的充分必要条件是：P Q y x∂∂=∂∂在G 内恒成立. 例51.（选择题）设AB 为由点A (0,)π到点(,0)B π的直线段，则si n s i n ABydx xdy +=⎰（ C ）.2;A .1;B - .0;C .1.D例52.计算曲线积分22()()Lx y dx x y dyx y -+++⎰，其中L 是沿着园： 22(1)(1)1x y -+-=从点(2,1)到点(0,1)的上半圆弧. 解 2222(,),(,)x y x yP x y Q x y x y x y-+==++ 因为 222222,(0,0)()P y xy x Qx y y x y x∂--∂==≠≠∂+∂ 所以，在不含原点的任何闭曲线L 上0L=⎰，即在不含原点的任一闭区域内积分与路径无关.故选择路径为线段:,1,02,AB x x y x ==≤≤，在AB 上有：1,0y d y ==，故 原式＝02222()()11ABx y dx x y dyx dx x y x -++-=++⎰⎰ ＝22222011ln(1)arctan 12x dx x x x -+⎡⎤=-++⎢⎥+⎣⎦⎰ln 5arctan 2.2=-例53.计算曲线积分22()Lx y ds +⎰，其中L 是园的渐开线：(c o s s i n ),02.(s i n c o s )x at t t t y at t t π=+⎧≤≤⎨=-⎩ 解 [][]222222(cos sin )(sin )(1)x y a t t t a t t a t +=++-=+(s i n s i n c o s 0x at t tt a tt'=-++= (cos cos sin )sin y a t t t t at t '=-+= 22ds x y dt atdt ''=+=原式＝2222330(1)()a t atdt a t t dt ππ+=+⎰⎰＝24322320()2(12).24t t a a πππ+=+例54.（填空题）L 为园：224x y +=，计算弧长的曲线积分22Lx y ds +=⎰8π例55. 计算 222(sin ).Lx yx dx xy dy -+⎰L 为正向圆周：22 1.x y +=（应用Green 公式化为二重积分计算）第十章 无 穷 级 数（一）数项级数敛散性的判别 一.级数的概念12121,nn nnn uu u u Su uu∞==++++=+++∑ 若lim n n S S →∞=，则称级数收敛到和S级数收敛的必要条件：1n n u ∞=∑收敛，则lim 0.n n u →∞=二.逆否命题：若lim 0,n n u →∞≠则级数1n n u ∞=∑发散．三.收敛判别法1.正项级数的两个判别法：比较判别法，比值判别法；2.任意项级数的两个定理； （1）绝对收敛定理1nn u∞=∑与1n n u ∞=∑有如下关系：1nn u∞=∑收敛 ⇒1nn u∞=∑也收敛；1nn u∞=∑发散 ⇒1nn u∞=∑收敛或发散；1nn u∞=∑收敛 ⇒1nn u∞=∑收敛或发散；1nn u∞=∑发散 ⇒1nn u∞=∑必定发散.（2）比值判别法23.交错级数的Leibniz （莱布尼兹）判别法；4.从定义、性质判别.四.两个重要的参照级数：1.等比（几何）级数1211n n n aqa aq aq aq ∞--==+++++∑当1q <时，级数收敛；当1q ≥时，级数发散. 2.p 级数11111123pp p pn nn ∞==+++++∑当1p >时，级数收敛；当1p ≤时，级数发散；特例：1p =时，11n n∞=∑称为调和级数，发散.五.判别级数收敛的一般步骤： 1.先看通项n u 是否趋于零？若lim 0n n u →∞≠，则级数1n n u ∞=∑发散；若lim 0n n u →=，则需进一步判断.2.选用合适的判别法；3.实在不行，再用定义试试，即看极限lim n n S →∞是否存在？例56.（选择题）若级数1n n u ∞=∑收敛，则级数（ D ）收敛1.;n n A u ∞=∑ 21.;n n B u ∞=∑1.();n n C u c ∞=+∑ 1..n n D c u ∞=⋅∑例57.若级数1nn u∞=∑收敛，则级数1(100)nn u∞=+∑收敛还是发散？ .例58.判定级数12sin3n nn π∞=∑的收敛性解 这是正项级数法一.用比较判别法 因 22sin()33n nn n u ππ=≤⋅，而12()3n n π∞=∑是公比213q =<的等比级数，收敛，由比较判别法，知原级数收敛.法二.用比值判别法 因111112si n3l i m l i m 2si n 3223l i m 1.323n n n n n n n n n n n n nu u ππππ+++→∞→∞++→∞=⋅==<⋅无穷小替换，由比值判别法，知原级数收敛. 例59判断级数111(1)ln(1)n n n ∞-=-+∑的收敛性.解 因 111ln(1)ln(2)n n u u n n +=>=++(1,2,)n =1l i m 0l n (1)n n →∞=+ ，故由leibniz 判别法，知原交错级数收敛.例60（填空题 ）极限2!lim n n n n n→∞的值为0解 以2!n n n n u n=为通项的正项级数，根据比值判别法知其收敛，又据收敛级数的必要条件，知其通项的极限为零.例61证明：若0,lim 0n n n u nu a →∞>=≠，则级数1n n u ∞=∑发散.证明 因为 lim lim01nn n n u n u a n→∞→∞⋅==≠，由0n u >，根据正项级数比值判别法的极限形式，由于11n n ∞=∑为调和级数，发散，所以级数1n n u ∞=∑也发散.（二）求幂级数的收敛半径及收敛区间 1. 用比值判别法2 1()lim()n n n u x u x +→∞=（一般与x 有关），再讨论，求出收敛半径.2. 1l i m n n n aa ρ→∞+=， 则收敛半径为：1R ρ=3.对端点单独讨论后，确定收敛区间. 例62.求幂级数221212n nn n x ∞-=-∑的收敛域. 解 这是缺少奇数次项的幂级数，由比值判别法2，1()lim ()n n nu x u x +→∞=2221221)12(22)12(lim x x n x n n n n n n =-⋅+-+∞→ ⇒ 当2211,2,22x x x <<<时，原级数收敛，收敛半径2R =讨论端点的情况：当2±=x 时，原级数为∑∞=-1212n n 发散，故收敛域)2,2(-例63.将函数21()52x f x x x -=-+展为1x -的幂级数.例64.求幂级数2ln (1)nnn n x n∞=-∑的收敛域；当1x =时，是绝对收敛， 还是条件收敛？并给出证明.（三）利用幂级数和函数的分析性质，求和函数.设幂级数0n n n a x ∞=∑的收敛半径为(0)R >，则在(,)R R -内，和函数具有下列性质：（1）和函数是连续的；（2）()S x 逐项可导，且10()()nn n n n n S x a x na x ∞∞-==''==∑∑；（3）()S x 逐项可积，且10()1xx xnnn n n n n n n a S t dt a t dt a t dt x n ∞∞∞+======+∑∑∑⎰⎰⎰. 注意：求导和积分后的和函数收敛半径不变，但在收敛区间端点可能不同．例65.求幂级数41141n n x n +∞=+∑的和函数.解 设和函数411()41n n x S x n +∞==+∑，易得收敛区间为(1,1)-，利用逐项微分和积分，414442411()()()()41n n n n n x S x x x x x n +∞∞==''===+++++∑∑这是41q x =<的等比级数，由因(0)0S =，故 44440001(1)()()11xxx x x S x S x dx dx dx x x--'===--⎰⎰⎰ ＝4220011111(1)(1)12121x x dx dx x x x-=-+⋅+⋅-+-⎰⎰ ＝111arctan ln .241xx x x+-+- (11)x -<< 例66. 求幂级数21121n n x n +∞=+∑的收敛区间，并求其和函数.（四）傅立叶级数(不做考试要求)第十一章 微 分 方 程（一）一阶微分方程的求解1.可分离变量的方程：()()dyf xg y dx=的解法 分离变量后，两边同时积分得通解；2.齐次方程：()dy yF dx x =的解法： 令 y u x =，则()duxu F u dx+=，分离变量并积分，得通解； 3.一阶线性非齐次方程：()()dyp x y q x dx+=的解法解法-常数变易法通解公式为：()()()p x dx p x dx y e q x e dx c -⎡⎤⎰⎰=⋅+⎢⎥⎣⎦⎰ 注：解方程一般直接用常数变易法，当然，也可代通解公式，但公式复杂，且计算和化简时较繁，易出错．（二）二阶线性微分方程的通解结构1.齐次方程：()()0y p x y q x '''++=的通解：是两个线性无关特解12(),()y x y x 的线性组合，即1122()()y c y x c y x =+；2.非齐次方程：()()()y p x y q x y f x '''++=的通解 非齐通（y ）＝齐通（y ）+非齐特（y *）（三）二阶常系数线性齐次方程：0y py q '''++=通解的特征根解法； 二阶常系数线性非齐次方程的两种特殊右端特解的解法. 例67.（单选题）下列微分方程中，通解为212(cos sin )x y e c x c x =+的方程是（ B ）.450A y y y '''--= .450B y y y '''-+= .250C y y y '''-+= 2.45.x D y y y e '''++=解 B .的特征方程为：2450λλ-+= 4162042222i i λ±-±===±， 2,1αβ== 故通解为： 212(cos sin )x y e c x c x =+.例68.求微分方程0340,,5x x y y y yy ==''''--==-的特解.例69.（填空题）微分方程ln 0xy y y '-=的通解为cx y e =. 这是可分离变量的方程 ln dyx y y dx= 分离变量ln dy dxy y x = 两边积分(l n )ln d y dx y x =⎰⎰得 1l n l n l nl ny x c =+ 111ln ,ln ,.c x cx y c x y c x y e e ±==±== 例70. 求微分方程x y y y 2345-=+'+''的通解。

第五节 函数的微分在理论研究和实际应用中，常常会遇到这样的问题：当自变量x 有微小变化时，求函数)(x f y =的微小改变量)()(x f x x f y -∆+=∆. 这个问题初看起来似乎只要做减法运算就可以了，然而，对于较复杂的函数)(x f ，差值)()(x f x x f -∆+却是一个更复杂的表达式，不易求出其值. 一个想法是：我们设法将y ∆表示成x ∆的线性函数，即线性化，从而把复杂问题化为简单问题. 微分就是实现这种线性化的一种数学模型.分布图示★ 引言★ 问题的提出 ★ 微分的定义 ★ 可微的条件 ★ 例1-2 ★ 基本微分公式 ★ 微分四则运算法则 ★ 例3★ 例4 ★ 微分的几何意义★ 复合函数的微分法★ 例5 ★ 例6 ★ 例7 ★ 例8★ 例9★ 例10★ 微分近似计算公式 ★ 例11 ★ 例12★ 例13 ★ 例14★ 常用函数的近似计算公式★ 例15 ★ 例16★ 误差计算 ★ 例17 ★ 内容小结 ★ 课堂练习 ★ 习题 2- 6内容要点：一、 微分的定义：定义1 设函数)(x f y =在某区间内有定义, 0x 及x x ∆+0在这区间内, 如果函数的增量)()(00x f x x f y -∆+=∆可表示为)(x o x A y ∆+∆⋅=∆ (5.1)其中A 是与x ∆无关的常数, 则称函数)(x f y =在点0x 可微, 并且称x A ∆⋅为函数)(x f y =在点0x 处相应于自变量改变量x ∆的微分, 记作dy , 即x A dy ∆⋅= (5.2)二、函数可微的条件dx x f dy )('= (5.8))(x f dxdy '= (5.9)即，函数的导数等于函数的微分与自变量的微分的商. 因此，导数又称为“微商”.三、 微分的几何意义四、基本初等函数的微分公式与微分运算法则 五、 微分形式不变性：无论u 是自变量还是复合函数的中间变量, 函数)(u f y =的微分形式总是可以按微分定义的形式来写，即有du u f dy )('=这一性质称为微分形式的不变性. 利用这一特性，可以简化微分的有关运算. 六、利用微分进行近似计算： 近似值的计算 误差计算dy y ≈∆. (5.10)例题选讲：微分的定义例1（E01）求函数2x y =当x 由1改变到1.01的微分.解 因为,2xdx dy =由题设条件知 ,1=x 01.0101.1=-=∆=x dx 所以 .02.001.012=⨯⨯=dy例2（E02）求函数3x y =在2=x 处的微分. 解 函数3x y =在2=x 处的微分为 dx x dy x 2'3)(==.12dx =基本初等函数的微分公式与微分运算法则的应用例3（E03）求函数x e x y 23=的微分. 解 因为'23')(xex y =xxex ex 232223+=)23(22x ex x+=所以 dx x e x dx y dy x )23(22'+== 或利用微分形式不变性)()(2332xxed x x d edy +=dx ex dx x e xx232223⋅+⋅=.)23(22dx x ex x+=例4（E04）求函数xx y sin =的微分.解因为''sin ⎪⎭⎫⎝⎛=x x y 2sin cos x x x x -=所以 dx y dy '=.s i n c o s 2dx xxx x -=微分形式的不变性例5（E05）设),12sin(+=x y 求dy . 解 设,sin u y =,12+=x u 则)(sin u d dy =udu cos =)12()12cos(++=x d x dx x 2)12cos(⋅+=.)12cos(2dx x +=注: 与复合函数求导类似, 求复合函数的微分也可不写出中间变量, 这样更加直接和方便.例6 设),1ln(2x e y += 求.dy解 )1l n (2xe d dy +=)1(1122xxed e++=)(11222x d eexx+=x d x eexx2122+=.1222dx exe xx+=例7（E06）设,2sinxe y =求.dy解 应用微分形式不变性, 有 .2sin cos sin 2sin sin 2sin2222sin sinsin2sindx xexdxx ex xd ex d edy xxxx=⋅=⋅==例8（E07）已知,22xey x = 求dy .解 222222)()()(x x d eed x dy xx-=422222xxdxedx ex xx⋅-⋅=.)1(232dx xx ex-=例9（E08）在下列等式的括号中填入适当的函数, 使等式成立.(1) ;cos )(tdt d ω= (2) ).()()(sin 2x d x d = 解 ,cos )(sin tdt t d ωωω= ∴)(s i n 1c o s td t d t ωωω=);sin 1(t d ωω=一般地，有.cos sin 1tdt C t d ωωω=⎪⎭⎫⎝⎛+例10（E09）求由方程32y x e xy +=所确定的隐函数)(x f y =的微分dy . 利用微分进行近似计算解 对方程两边求微分, 得 ),2()(3y x d e d xy +=),()2()(3y d x d xy d exy+= ,32)(2dy y dx xdy ydx e xy +=+于是 .322dx yxeye dy xyxy --=例11(E09) 求x )x (f +=1在0=x 与3=x 处的线性化.解 首先不难求得xx f +='121)( ，则413(21)0(23(1)0(='='==），，），f f f f ，于是，根据上面线性化定义知)(x f 在0=x 处的线性化121)0)(0()0()(+=-'+=x x f f x L ，在3=x 处的线性化为4541)3)(3()3()(+=-'+=x x f f x L))(()()(000x x x f x f x L -'+=示意图见右,故x x 2111+≈+（在x=0处）， 45411+≈+x x （在x=3处）．例12(E11) 求)x ln()x (f +=1在0=x 的线性化． 解 首先求得)(x f 'x+=11，得1)0(='f ，又0)0(=f ，于是)(x f 在x=0处的线性化x x f f x L =-'+=)0)(0()0()(例13（E12）半径10厘米的金属圆片加热后, 半径伸长了0.05厘米, 问面积增大了多少?解 设,2r A π=10=r (厘米), 05.0=∆r (厘米).∴dA A ≈∆r r ∆⋅=π205.0102⨯⨯=ππ=（厘米2）.例14（E13）计算0360cos ' 的近似值.解 设x x f cos )(=⇒,sin )('x x f -=x (为弧度),取,30π=x 360π=∆x⇒,21)3(=πf .23)3('-=πf所以 ⎪⎭⎫⎝⎛+=3603cos 3060cos 'ππ 3603s i n 3c o s πππ⋅-=3602321π⋅-=.4924.0≈例15计算下列各数的近似值.(1) (E14)35.998的近似值. (2) .03.0-e解 (1)335.110005.998-=310005.111000⎪⎭⎫ ⎝⎛-=30015.0110-=⎪⎭⎫ ⎝⎛⨯-=0015.031110.995.9=(2) 03.0103.0-≈-e .97.0=例16(E15) 最后我们来看一个线性近似在质能转换关系中的应用. 我们知道，牛顿的第二运动定律αm F =（α为加速度）中的质量m 是被假定为常数的，但严格说来这是不对的，因为物体的质量随其速度的增长而增长. 在爱因斯坦修正后的公式中，质量为2201c/v m m -=,当v 和c 相比很小时，22c /v 接近于零，从而有⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+≈-=22002202201212111c v m m c v m c/v m m 即 ⎪⎭⎫ ⎝⎛+≈2200121c v m m m , 注意到上式中K v m =2021是物体的动能，整理得)K (m v m v m c )m m (∆=-=≈-202020200212121,或 )K (c )m (∆∆≈2. （1）换言之，物体从速度0到速度v 的动能的变化)K (∆近似等于2c )m (∆. 因为8103⨯=c 米/秒，代入式（1）中，得≈)K (∆90 000 000 000 000 000m ∆焦耳,由此可知，小的质量变化可以创造出大的能量变化．例如，1克质量转换成的能量就相当于爆炸一颗2万吨级的原子弹释放的能量．例17 正方形边长为005.041.2±米, 求出它的面积, 并估计绝对误差与相对误差. 解 设正方形的边长为x ,面积为y ,则.2x y = 当41.2=x 时,).(8081.5)41.2(22m y ==.82.4241.241.2'====x x xy边长的绝对误差为,005.0=x δ ∴面积的绝对误差为).(0241.0005.082.42m x =⨯=δ ∴面积的相对误差为%.4.08081.50241.0≈=yy δ课堂练习1.求函数x x y -=的微分dy .2.因为一元函数)(x f y =在0x 的可微性与可导性是等价的, 所以有人说“微分就是导数, 导数就是微分”，判断这种说法对吗?3.设,0>A 且n A B <||, 证明1-+≈+n n n nAB A B A (A , B 为常数), 并计算101000的近似值.。

目录一、高等数学电子教案第一章函数与极限第一节函数第二节初等函数第三节数列的极限第四节函数的极限第五节无穷小与无穷大第六节极限运算法则第七节极限存在准则,两个重要极限第八节无穷小的比较第九节函数的连续性与间断点第十节连续函数的运算与初等函数的连续性第十一节闭区间上连续函数的性质第二章导数与微分第一节导数的概念第二节函数的和、差、积、商的求导法则第三节反函数的导数、复合函数的求导法则第四节初等函数求导问题、双曲函数求导与反双曲函数的导数第五节高阶导数第六节隐函数导数,由参数方程所确定函数的导数,相关变化率第七节函数的微分第八节微分在近似计算中应用第三章微分中值定理与导数的应用第一节中值定理第二节洛必达法则第三节泰勒公式第四节函数单调性判别法第五节函数的极值及其求法第六节最大值、最小值问题第七节曲线的凹凸性与拐点第八节函数图形的描绘第九节曲率第十节第一、二、三章测验第四章不定积分第一节不定积分的概念与性质第二节换元积分法第三节分部积分法第四节几种特殊类型函数的积分第五章定积分第一节定积分的概念第二节定积分的性质中值定理第三节微积分基本公式第四节定积分的换元法第五节定积分的分部积分法第七节广义积分第六章定积分的应用第一节定积分的元素法第二节平面图形的面积第三节体积第四节平面曲线的弧长第五节功、水压力和引力第六节平均值第七章空间解析几何与向量代数第一节空间直角坐标系第二节向量及其加减法,向量与数的乘积第三节向量的坐标第四节数量积、向量积、混合积第五节曲面及方程第六节空间曲线及方程第七节平面及方程第八节空间直线及其方程第九节二次曲面第八章多元函数微分法及其应用第一节多元函数的基本概念第二节偏导数第三节全微分第四节多元复合函数的求导法则第五节隐函数的求导公式第六节微分法在几何上的应用第七节方向导数与梯度第八节多元函数的极值及其求法第九章重积分第一节二重积分的概念与性质第二节二重积分的计算法第三节二重积分的应用第四节三重积分的概念及其算法第五节利用柱面坐标和球面坐标计算三重积分第十章曲线积分与曲面积分第一节对弧长的曲线积分第二节对坐标的曲线积分第三节格林公式第四节对面积的曲面积分第五节对坐标的曲面积分第六节高斯公式、通量与散度第七节斯托克斯公式、环流量与旋度第十一章无穷级数第一节常数项级数的概念和性质第二节常数项级数的审敛法第三节幂级数第四节函数展开成幂级数第五节函数的幂级数展开式的应用第七节傅里叶级数第八节正弦级数和余弦级数第九节傅立叶级数简明版第十二章微分方程第一节微分方程的基本概念第二节可分离变量的微分方程第三节齐次微分方程第四节一阶线性微分方程第五节全微分方程第七节可降阶的高阶微分方程第八节二阶线性微分方程解的结构第九节二阶常系数线性齐次微分方程第十节二阶常系数线性非齐次微分方程第十一节二阶线性微分方程应用问题举例第十二节欧拉方程、常系数线性微分方程组求解第十三节二阶线性微分方程的幂级数解法。

第六节 微分方程的应用举例在学习了以上几节内容关于微分方程解法的基础上，本节将举例说明如何通过建立微分方程解决一些在几何上和物理上的实际问题。

例1 设曲线过（1，1），且其上任意点p 的切线在y 轴上的截距是切点纵坐标的三倍，求此曲线方程（图12-1）解：设所求的曲线方程为()()y x P x y y ,，=为其上任意点，则过点P 的切线方程为()x X y y Y -'=-. 其中()Y X ,是切线上动点，()y x ,是曲线上L令0=X ,的y x y Y '-=为切线在y 轴上的截距。

由x所给的条件得微分方程： 图12-1y y x y 3='-这是一阶线性齐次方程，易得其通解为2xCy =。

因曲线过点（1，1），代入上式，得1=C ，所以曲线方程为21x y =. 例2 设跳伞员开始跳伞后所受的空气阻力与他下落的速度成正比（比例系数为常数0>k ），起跳时的速度为0。

求下落的速度与时间之间的函数关系。

解：这是一个运动问题，我们可以利用牛顿第二定律ma F =建立微分方程。

首先，设下落速度为()t v ，则加速度()t v a '=。

再分析运动物体所受的外力。

在此，跳伞员只受重力和阻力这两个力的作用。

重力的大小为mg ，方向与速度方向一致；阻力大小为kv ，方向与速度方向相反。

因此，所受的外力为kv mg F -=，于是，由牛顿第二定律可得到速度()t v 应满足的微分方程为v m kv mg '=-，又因为假设起跳时的速度为0，所以，其初始条件为00==t v ， 至此，我们已将这个运动问题化为一个初值问题()⎩⎨⎧=-='.00,v kv mg v m 解此初值问题。

这是一个一阶线性非齐次微分方程，但由于v v '，的系数及自由项均为常数，故也可按分离变量方程来解。

求出方程的通解为t mk Cekv mg -=-.将初始条件()00=v 代入，得mg C =。