下载文档原格式
过程试验汇报班级: 通信1004班姓名: 杨靖学号: U13098试验目:了解数产生, 而且利用数来模拟均匀分布、 正态分布、 指数分布、 泊松分布而且计算均值和自相关序列。
试验工具:C++编程模拟试验原理:数产生原理: 经过数学算法产生伪数来, 模拟数产生。
数序列含有循环周期性。
能够证实, 任何产生伪数算法总会进入循环, 这么为了确保随机数序列不产生反复数据, 就要求循环周期足够长。
均匀分布产生原理:利用线性同余法（1）设置y0, 即设置种子（2）yn=kyn-1(mod N), un=yn/N泊松分布产生原理: 从泊松分布分布律可知, 采取前述方法很不适用。
因为: 所以, 采取递推法组成泊松分布: （1）产生均匀分布数u; （2） （3）若u<F, 令X=i, 停止; （4） （5）转向（3）。
正态分布产生原理:标准正态变量分布函数 反函数不存在显式, 所以也不能用逆变法产生。
故采取以下方法:设Ui ～U(0, 1), i=1,2,…,n, 且相互独立, 由中心极限定理可知, 当n 较大时设Ui ～U(0, 1), i=1,2,…,n, 且相互独立, E(Ui)=1/2, D(Ui)=1/12, 当n 较大时有:取n=12, 近似有:也就是说, 只要产生12个伪数u1,u2,…u12, 将它们加起来, 再减去6, 就能近似得到标准正态变量样本值。
{}!i i e p P X i i λλ-===11(1)!1i i i e p p i i λλλ+-+==++0,,;i p e F p λ-===/(1),,1;p p i F F p i i λ=+=+=+()~(0,1)n i i U nE U Z N -=∑~(0,1)ni n U Z N -=∑1216~(0,1)i i Z U N ==-∑指数分布产生原理:（1）产生均匀分布数{ui};（2）计算指数分布数: xi=-ln ui /λ试验代码:（1）数产生/*函数功效, 采取线性同余法, 依据输入种子数产生一个伪数, 假如种子不变,则将能够反复调用产生一个伪序列利用CMyRand类中定义全局变量: S, K, N, Y。
《随机过程》课程研究与实践本文将结合课堂教学和实践经验，以及相关理论知识，对《随机过程》课程进行研究和实践总结。
一、课程研究1.离散时间马尔可夫链：离散时间马尔可夫链是一种序列随机变量，其特点是过去的状态对下一个状态的概率分布没有影响，只与当前状态有关。
在研究中，我们要掌握马尔可夫链的转移矩阵、迭代计算等基本概念和方法。
2.连续时间马尔可夫链：与离散时间马尔可夫链相对应，连续时间马尔可夫链是一种连续随机变量，其特点是状态变量是连续的。
在研究中，我们要了解连续时间马尔可夫链的转移密度函数、平稳分布等基本概念和性质。
3.泊松过程：泊松过程是一种连续时间的独立增量随机过程，其特点是相邻两个事件的时间间隔服从指数分布。
在研究中，我们要掌握泊松过程的均值和方差计算、重要性质等基本理论和应用方法。
4.连续时间马尔可夫过程：连续时间马尔可夫过程是一种连续时间的马尔可夫链，其特点是状态变量是连续随机变量。
在研究中，我们要了解连续时间马尔可夫过程的转移密度函数、平稳分布等基本概念和性质。
二、课程实践1.实例分析：通过实践案例分析，将理论知识与实际问题相结合，加深学生对随机过程的理解和应用能力。
例如，通过分析金融领域中的股票价格变化，引导学生应用随机过程来建模并预测未来的价格变化。
2. 编程模拟：通过编程模拟的方式，让学生实际操作随机过程的理论知识，加深对概念和方法的理解。
例如，使用Python编写程序模拟随机过程并进行统计分析，进一步验证随机过程的性质和特点。
3.实验设计：设计实验，引导学生通过实验方法验证随机过程的基本特性。
例如，设计一组抛硬币实验，统计硬币正面朝上的次数，并利用极大似然估计法估计硬币正面朝上的概率。
4.论文研究：鼓励学生进行论文研究，深入探究随机过程在实际问题中的应用。
例如，学生可以选择在金融、通信或生物医学领域进行相关论文研究，分析和总结已有研究成果，并提出自己的见解。
三、总结与展望通过对《随机过程》课程的研究和实践，我们可以发现，这门课程的理论体系完备、应用广泛。
一、实验目的1. 理解随机过程的基本概念和性质。
2. 掌握随机过程的基本运算和性质。
3. 通过实验验证随机过程的性质和规律。
二、实验原理随机过程是指一系列随机变量按照一定规则排列而成的序列。
在现实生活中，随机过程广泛存在于自然界和人类社会，如股票价格、气象变化、生物进化等。
随机过程的研究有助于我们更好地理解和预测这些现象。
随机过程可以分为两类：离散随机过程和连续随机过程。
本实验主要研究离散随机过程。
三、实验设备与材料1. 计算机2. 随机过程模拟软件（如Matlab）3. 纸笔四、实验内容1. 随机过程的基本概念（1）随机变量的概念随机变量是指具有不确定性的变量，它可以取多个值。
在随机过程中，随机变量是基本的研究对象。
（2）随机过程的概念随机过程是由一系列随机变量按照一定规则排列而成的序列。
2. 随机过程的基本性质（1）无后效性无后效性是指随机过程的前后状态相互独立。
（2）无记忆性无记忆性是指随机过程的状态只与当前时刻有关，与过去时刻无关。
（3）马尔可夫性马尔可夫性是指随机过程的状态只与当前时刻有关，与过去时刻无关。
3. 随机过程的运算（1）随机过程的和设{Xn}和{Yn}是两个随机过程，则它们的和{Zn}定义为Zn = Xn + Yn。
（2）随机过程的差设{Xn}和{Yn}是两个随机过程，则它们的差{Zn}定义为Zn = Xn - Yn。
（3）随机过程的乘积设{Xn}和{Yn}是两个随机过程，则它们的乘积{Zn}定义为Zn = Xn Yn。
4. 随机过程的模拟利用随机过程模拟软件（如Matlab）模拟随机过程，观察其性质和规律。
五、实验步骤1. 初始化随机数生成器2. 定义随机过程（1）根据随机过程的基本性质，定义随机过程{Xn}。
（2）根据随机过程的运算，定义随机过程{Yn}。
3. 模拟随机过程（1）使用随机过程模拟软件（如Matlab）模拟随机过程{Xn}和{Yn}。
（2）观察模拟结果，分析随机过程的性质和规律。
2015-2016第一学期随机过程第二次上机实验报告实验目的：通过随机过程上机实验，熟悉Monte Carlo计算机随机模拟方法，熟悉Matlab的运行环境，了解随机模拟的原理，熟悉随机过程的编码规律即各种随机过程的实现方法，加深对随机过程的理解。
上机内容：(1 )模拟随机游走。
(2)模拟Brown运动的样本轨道。
(3)模拟Markov过程。
实验步骤：(1)给出随机游走的样本轨道模拟结果，并附带模拟程序。
①一维情形%—维简单随机游走% “从0开始，向前跳一步的概率为p，向后跳一步的概率为1-p”n=50;p=0.5;y=[0 cumsum(2.*(rand(1,n-1)v=p)-1)]; % n 步。
plot([0:n-1],y); %画出折线图如下。
w%一维随机步长的随机游动%选取任一零均值的分布为步长，比如，均匀分布。
n=50;x=rand(1,n)-1/2;y=[0 (cumsum(x)-l)];plot([0:n],y);②二维情形%在(u, v)坐标平面上画出点(u(k), v(k)), k=1:n,其中(u(k)) 和(v(k))是一维随机游动。
例%子程序是用四种不同颜色画了同一随机游动的四条轨道。
n=100000;colorstr=['b' 'r' 'g' 'y'];for k=1:4z=2.*(rand(2,n)<0.5)-1;x=[zeros(1,2); cumsum(z')];col=colorstr(k);plot(x(:,1),x(:,2),col);③%三维随机游走 ranwalk3dp=0.5;n=10000; colorstr=['b' 'r' 'g' 'y'];for k=1:4z=2.*(rand(3,n)v=p)-1; x=[zeros(1,3); cumsum(z')];col=colorstr(k);plot3(x(:,1),x(:,2),x(:,3),col);hold on end gridhold onendgrid4：04003?0-200-300-400-2OD20050、-100-200 -20D⑵给出一维，二维Brown运动和Poisson过程的模拟结果，并附带模拟程序，没有结果的也要把程序记录下来。
随机过程实验报告学院：专业：学号：姓名：一、实验目的通过随机过程的模拟实验，熟悉随机过程编码规律以及各种随机过程的实现方法，通过理论与实际相结合的方式，加深对随机过程的理解。
二、实验内容（1）熟悉Matlab工作环境，会计算Markov链的n步转移概率矩阵和Markov链的平稳分布。
（2）用Matlab产生服从各种常用分布的随机数，会调用matlab自带的一些常用分布的分布律或概率密度。
（3）模拟随机游走。
（4）模拟Brown运动的样本轨道的模拟。
（5）Markov过程的模拟。
三、实验原理及实验程序n步转移概率矩阵根据Matlab的矩阵运算原理编程，Pn = P ^n。
已知随机游动的转移概率矩阵为：P =0.5000 0.5000 00 0.5000 0.50000.5000 0 0.5000求三步转移概率矩阵p3及当初始分布为P{x0 = 1} = p{x0 = 2} = 0, P{x0 = 3} = 1 时经三步转移后处于状态3的概率。
代码及结果如下：P = [0.5 0.5 0; 0 0.5 0.5; 0.5 0 0.5] %一步转移概率矩阵P3 = P ^3 %三步转移概率矩阵P3_3 = P3(3,3) %三步转移后处于状态的概率1、两点分布x=0:1;y=binopdf(x,1,0.55);plot(x,y,'r*');title('两点分布');2、二项分布N=1000;p=0.3;k=0:N;pdf=binopdf(k,N,p);plot(k,pdf,'b*');title('二项分布');xlabel('k');ylabel('pdf');gridon;boxon3、泊松分布x=0:100;y=poisspdf(x,50);plot(x,y,'g.');title('泊松分布')4、几何分布x=0:100;y=geopdf(x,0.2);plot(x,y,'r*');title('几何分布');xlabel('x');ylabel('y');5、泊松过程仿真5.1 % simulate 10 timesclear;m=10; lamda=1; x=[];for i=1:ms=exprnd(lamda,'seed',1);x=[x,exprnd(lamda)];t1=cumsum(x);end[x',t1']5.2%输入：N=[];for t=0:0.1:(t1(m)+1)if t<t1(1)N=[N,0];elseif t<t1(2)N=[N,1];elseif t<t1(3)N=[N,2];elseif t<t1(4)N=[N,3];elseif t<t1(5)N=[N,4];elseif t<t1(6)N=[N,5];elseif t<t1(7)N=[N,6];elseif t<t1(8)N=[N,7];elseif t<t1(9)N=[N,8];elseif t<t1(10)N=[N,9];elseN=[N,10];endendplot(0:0.1:(t1(m)+1),N,'r-') 5.3% simulate 100 timesclear;m=100; lamda=1; x=[];for i=1:ms= rand('seed');x=[x,exprnd(lamda)];t1=cumsum(x);end[x',t1']N=[];for t=0:0.1:(t1(m)+1)if t<t1(1)N=[N,0];endfor i=1:(m-1)if t>=t1(i) & t<t1(i+1)N=[N,i];endendif t>t1(m)N=[N,m];endendplot(0:0.1:(t1(m)+1),N,'r-')6、泊松过程function I=possion(lambda,m,n)for j=1:mX=poissrnd(lambda,[1,n]); %参数为lambda的possion 过程N(1)=0;for i=2:nN(i)=N(i-1)+X(i-1);endt=1:n;plot(t,N)grid onhold onend7、布朗运动7.1一维布朗运动程序：function [t,w]=br1(t0,tf,h)t=t0:h:tf;t=t';x=randn(size(t));w(1)=0;for k=1:length(t)-1w(k+1)=w(k)+x(k);endw=sqrt(h)*w;w=w(:);end调用t0=1;tf=10;h=0.01;[t,w]=br1(t0,tf,h);figure;plot(t,w,'*');xlabel('t');ylabel('w');title('一维Brown运动模拟图'); 7.2二维布朗运动：function [x,y,m,n]=br2(x0,xf,y0,yf,h)x=x0:h:xf;y=y0:h:yf;a=randn(size(x));b=randn(size(y));m(1)=0;n(1)=0;for k=1:length(x)-1m(k+1)=m(k)+a(k);n(k+1)=n(k)+b(k);endm=sqrt(h)*m;n=sqrt(h)*n;end调用x0=0;xf=10;h=0.01;y0=0;yf=10;[x,y,m,n]=br2(x0,xf,y0,yf,h);figure;plot(m,n);xlabel('m');ylabel('n');title('二维Brown运动模拟图');7.3三维布朗运动：npoints =1000;dt = 1;bm = cumsum([zeros(1, 3); dt^0.5*randn(npoints-1, 3)]);figure(1);plot3(bm(:, 1), bm(:, 2), bm(:, 3), 'k');pcol = (bm-repmat(min(bm), npoints, 1))./ ...repmat(max(bm)-min(bm), npoints, 1);hold on;scatter3(bm(:, 1), bm(:, 2), bm(:, 3), ...10, pcol, 'filled');grid on;hold off;8、马尔科夫链离散服务系统中的缓冲动力学m=200;p=0.2;N=zeros(1,m); %初始化缓冲区A=geornd(1-p,1,m); %生成到达序列模型, for n=2:mN(n)=N(n-1)+A(n)-(N(n-1)+A(n)>=1);endstairs((0:m-1),N);9、随机数游走9.1 100步随机游走n = 100; %选取步数。
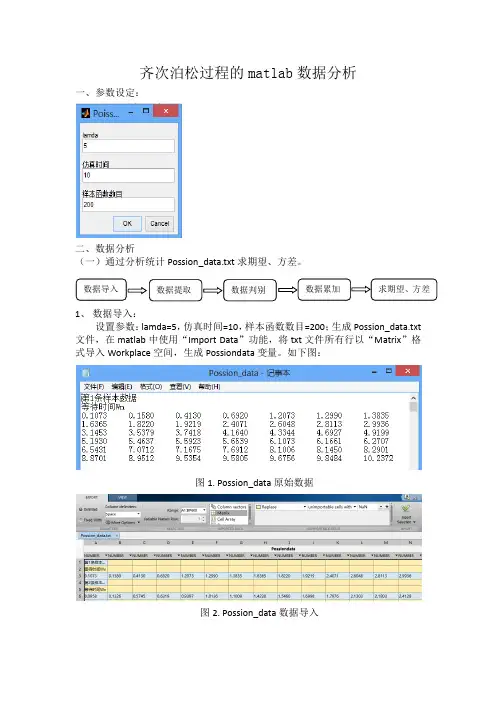
齐次泊松过程的matlab数据分析一、参数设定：二、数据分析（一）通过分析统计Possion_data.txt求期望、方差。
1、数据导入：设置参数：lamda=5，仿真时间=10，样本函数数目=200；生成Possion_data.txt 文件，在matlab中使用“Import Data”功能，将txt文件所有行以“Matrix”格式导入Workplace空间，生成Possiondata变量。
如下图：图1. Possion_data原始数据图2. Possion_data数据导入图3. 生成Possiondata2、数据提取编程将Possiondata数组中的第3,6,9…300行提取出来形成一个新的数值poiss。
图4. 提取有效数据3、数据判别（1）、按照试验指导大纲，将时间间隔设成0.1，将每一条样本函数按照0.1的时间间隔进行统计，将在同一个0.1间隔内的数据归为一类。
得到“t1”图5. 数据判别归类（2）、采用“length”函数将上表中的数据进行计数得到以下参数：图6. 统计类中数量（3）、将“t2”进行累加，并同样的方法计算所有样本函数得到“s”：图7. 得到样本计数样本图8. 第一条样本计数过程图9. SJGC生成的第一条样本函数4、计算期望、方差使用“mean”函数计算期望值，使用“var”函数计算方差得到下图：图10. 均值_方差图从图中可以看出，泊松过程的均值与方差具有一致性。
图11. SJGC生成的均值函数图（二）求泊松过程的速率方法1根据所得到的的均值函数，使用“polyfit”函数采用一次函数模拟得到斜率4.9138，即为泊松速率。
方法2考虑到泊松事件的时间间隔是指数分布，且均值为泊松过程速率的倒数。
对样本函数进行处理，将两次到达时间相减得到每相邻两次事件发生的时间间隔，使用“expfit”函数得到估计的均值，对其求倒得到泊松速率。
使用循环语句得到每一条样本函数的速率，最后求平均得到要求的泊松速率。
物业化管理调研报告8篇（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如调研报告、总结报告、述职报告、心得体会、自我鉴定、条据文书、合同协议、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as research reports, summary reports, job reports, reflections, self-evaluation, normative documents, contract agreements, teaching materials, essay summaries, and other sample essays. If you want to learn about different sample essay formats and writing methods, please stay tuned!物业化管理调研报告8篇认真撰写调研报告是对调研任务的最终总结，也是对相关领域的专业呈现，调研报告是一种详尽记录研究、分析和发现的文档，旨在提供全面的信息，以下是本店铺精心为您推荐的物业化管理调研报告8篇，供大家参考。
随机过程实验报告一、实验问题两赌徒模型对于上述模型现在假定赌徒甲的对手赌徒乙有N－i的初始财富，N为两个赌徒的总财富。
则赌徒甲破产的概率有多大？模拟之。
二、问题分析该问题实质上为带有两个吸壁的随机游动，我们可以仍可把它看作数学中的一个一维随机游动问题。
其马尔可夫链状态空间为{0，1，2，…，N}，N为赌徒甲、乙的总财富。
类似于赌徒与游戏机模型，我们也可以把财富抽象地看成是一个质点。
可知求赌徒甲破产的概率转化为现在的问题就是求质点从i点出发到达0状态先于到达N状态的概率。
这里较赌徒与游戏机模型中多出一个条件，即：赌徒甲先于赌徒乙到达0状态。
我们不难得到这一模型的解：三、问题解决1、先讨论p=q的随机游动情况对于简单的随机游动，如果从0开始，向前跳一步的概率为p，向后跳一步的概率为1－p，则由计算机可以模拟此情形。
这只是许多模拟结果中的一种。
现在我们假设，有A、B两个赌徒，他们共同用于赌博的财富M=100（元），A、B输赢的概率（即赌博的技巧相同）时，他们破产的概率。
假设，共同的财富中A、B分别投入的资金如下表：运算结果如下：由上图可知，当赌徒甲、乙输赢的概率相等时,其中一人破产的概率与对方所拥有的财富成正比关系。
这样我们可以得出结论：在两人的赌博游戏中,如果赌徒甲、乙的赌博技术差不多即输赢概率相当的话,那么谁要想最终获胜的最好方法就是多带赌本。
2、下面讨论p!=q时随机游动情况我们不妨将之具体为p=0.4，q=0.6。
用计算机模拟上述数据。
可得图如下：由上图可知，在每次输赢都为1元时，就算甲90元、乙10元，甲也几乎不可能赢。
如果我们把每次下的赌注加大到5元，修改程序三，模拟之，又可得图如下：由上图我们可以更清晰地看出：在两人的赌博游戏中,如果赌徒甲的赌博技术比乙的赌博技术差的话,那么甲要想最终获胜就要带比乙多很多的赌本。
四、结果拓展现实中的赌博还可能有三人、四人甚至更多的人一起进行。
下面我们简单地讨论当赌徒输赢概率相等时的二维随机游动。
2015-2016第一学期随机过程第二次上机实验报告实验目的：通过随机过程上机实验，熟悉Monte Carlo计算机随机模拟方法，熟悉Matlab的运行环境，了解随机模拟的原理，熟悉随机过程的编码规律即各种随机过程的实现方法，加深对随机过程的理解。
上机内容：（1）模拟随机游走。
（2）模拟Brown运动的样本轨道。
（3）模拟Markov过程。
实验步骤：（1）给出随机游走的样本轨道模拟结果，并附带模拟程序。
①一维情形%一维简单随机游走%“从0开始，向前跳一步的概率为p，向后跳一步的概率为1－p”n=50;p=0.5;y=[0 cumsum(2.*(rand(1,n-1)<=p)-1)]; % n步。
plot([0:n-1],y); %画出折线图如下。
%一维随机步长的随机游动%选取任一零均值的分布为步长, 比如，均匀分布。
n=50;x=rand(1,n)-1/2;y=[0 (cumsum(x)-1)];plot([0:n],y);②二维情形%在(u, v)坐标平面上画出点(u(k), v(k)), k=1:n, 其中(u(k))和(v(k)) 是一维随机游动。
例%子程序是用四种不同颜色画了同一随机游动的四条轨道。
n=100000;colorstr=['b' 'r' 'g' 'y'];for k=1:4z=2.*(rand(2,n)<0.5)-1;x=[zeros(1,2); cumsum(z')];col=colorstr(k);plot(x(:,1),x(:,2),col);hold onendgrid③%三维随机游走ranwalk3d p=0.5;n=10000;colorstr=['b' 'r' 'g' 'y'];for k=1:4z=2.*(rand(3,n)<=p)-1;x=[zeros(1,3); cumsum(z')]; col=colorstr(k);plot3(x(:,1),x(:,2),x(:,3),col);hold onendgrid(2) 给出一维，二维Brown运动和Poisson过程的模拟结果，并附带模拟程序，没有结果的也要把程序记录下来。
①一维Brown% 这是连续情形的对称随机游动,每个增量W(s+t)-W(s)是高斯分布N(0, t)，不相交区间上的增量是独立的。
典型的模拟它方法是用离散时间的随机游动来逼近。
n=1000;dt=1;y=[0 cumsum(dt^0.5.*randn(1,n))]; % 标准布朗运动。
plot(0:n,y);②二维Brownnpoints = 5000;dt = 1;bm = cumsum([zeros(1, 3); dt^0.5*randn(npoints-1, 3)]); figure(1);plot(bm(:, 1), bm(:, 2), 'k');pcol = (bm-repmat(min(bm), npoints, 1))./ ...repmat(max(bm)-min(bm), npoints, 1);hold on;scatter(bm(:, 1), bm(:, 2), ...10, pcol, 'filled');grid on;hold off;③三维Brownnpoints = 5000;dt = 1;bm = cumsum([zeros(1, 3); dt^0.5*randn(npoints-1, 3)]); figure(1);plot3(bm(:, 1), bm(:, 2), bm(:, 3), 'k');pcol = (bm-repmat(min(bm), npoints, 1))./ ...repmat(max(bm)-min(bm), npoints, 1);hold on;scatter3(bm(:, 1), bm(:, 2), bm(:, 3), ...10, pcol, 'filled');grid on;hold off;④%泊松过程的模拟、检验及参数估计syms Un X S;n=10;%生成n*n个随机数r=1;%参数temp=0;tem=0;Un=rand(n,1);%共产生n*n个随机数for i=1:1:nX(i)=-log(Un(i))/r;endX=subs(X);for i=1:1:nfor j=1:1:itemp=temp+X(j);endS(i)=temp;temp=0;endS=subs(S);%检验泊松过程使用第四条for i=1:1:ntem=tem+S(i);endsigmaN=tem;T=S(n);alpha=0.05;%置信水平p=sigmaN/T;p1=(1/2)*(n-1.96*(n/3)^(1/2)); p2=(1/2)*(n+1.96*(n/3)^(1/2)); c1=subs(p-p1)c2=subs(p-p2)if (c1<=0&c2>=0)|(c1>=0&c2<=0)disp('这是一个泊松过程！')%参数估计使用极大似然估计r_=subs(n/T);if abs(subs(r_-r))<0.1disp('参数估计正确！')disp('参数估计值为：')r_end%绘制轨迹y=0;x=0:0.001:subs(S(1));plot(x,y)for k=1:1:ny=k;x=subs(S(k)):0.001:subs(S(k+1));hold onplot(x,y)endelsedisp('这不是一个泊松过程！') end⑤%二维poisson2d lambda=100;nmb=poissrnd(lambda)x=rand(1,nmb);y=rand(1,nmb);gridscatter(x,y,5,5.*rand(1,nmb));⑥%三维poisson3d%单位体积的泊松点数强度为lambda lambda=100;nmb=poissrnd(lambda)x=rand(1,nmb);y=rand(1,nmb);z=rand(1,nmb);gridscatter3(x,y,z,5,5.*rand(1,nmb));（3）Markov过程的模拟结果。
①离散服务系统中的缓冲动力学%离散服务系统中的缓冲动力学m=200;p=0.2;N=zeros(1,m); %初始化缓冲区A=geornd(1-p,1,m); %生成到达序列模型, 比如，几何分布for n=2:mN(n)=N(n-1)+A(n)-(N(n-1)+A(n)>=1);endstairs((0:m-1),N);②M/M/1模型% [tjump, systsize] = simmm1(n, lambda, mu) % Inputs: n - number of jumps% lambda - arrival intensity% mu - intensity of the service times % Outputs: tjump - cumulative jump times% systsize - system size% set default parameter values if ommited Ⅰ：nargin=0nargin=0;if (nargin==0)n=500;lambda=0.8;mu=1;endi=0; %initial value, start on level itjump(1)=0; %start at time 0systsize(1)=i; %at time 0: level ifor k=2:nif i==0mutemp=0;elsemutemp=mu;endtime=-log(rand)/(lambda+mutemp); % Inter-step times:%Exp(lambda+mu)-distributedif rand<lambda/(lambda+mutemp)i=i+1; %jump up: a customer arriveselsei=i-1; %jump down: a customer is departing end %ifsystsize(k)=i; %system size at time itjump(k)=time;end %for itjump=cumsum(tjump); %cumulative jump times stairs(tjump,systsize);Ⅱ：nargin不为0时nargin=2;if (nargin==0)n=500;lambda=0.8;mu=1;endi=0; %initial value, start on level itjump(1)=0; %start at time 0systsize(1)=i; %at time 0: level ifor k=2:nif i==0mutemp=0;elsemutemp=mu;endtime=-log(rand)/(lambda+mutemp); % Inter-step times:%Exp(lambda+mu)-distributedif rand<lambda/(lambda+mutemp)i=i+1; %jump up: a customer arriveselsei=i-1; %jump down: a customer is departingend %ifsystsize(k)=i; %system size at time itjump(k)=time;end %for itjump=cumsum(tjump); %cumulative jump timesstairs(tjump,systsize);③M/D/1系统% function [jumptimes, systsize] = simmd1(tmax, lambda)% SIMMD1 simulate a M/D/1 queueing system. Poisson arrivals% of intensity lambda, deterministic service times S=1.% [jumptimes, systsize] = simmd1(tmax, lambda)% Inputs: tmax - simulation interval% lambda - arrival intensity% Outputs: jumptimes - time points of arrivals or departures % systsize - system size in M/D/1 queue% systtime - system times% Authors:% v1.2 07-Oct-02% set default parameter values if ommitedⅠ：nargin=0nargin=0;if (nargin==0)tmax=1500;lambda=0.95;endarrtime=-log(rand)/lambda; % Poisson arrivalsi=1;while (min(arrtime(i,:))<=tmax)arrtime = [arrtime; arrtime(i, :)-log(rand)/lambda];i=i+1;endn=length(arrtime); % arrival times t_1,...t_narrsubtr=arrtime-(0:n-1)'; % t_k-(k-1)arrmatrix=arrsubtr*ones(1,n);deptime=(1:n)+max(triu(arrmatrix)); % departure times%u_k=k+max(t_1,..,t_k-k+1)B=[ones(n,1) arrtime ; -ones(n,1) deptime'];Bsort=sortrows(B,2); % sort jumps in order jumps=Bsort(:,1);jumptimes=[0;Bsort(:,2)];systsize=[0;cumsum(jumps)]; % M/D/1 processsysttime=deptime-arrtime'; % system times% plot a histogram of system timeshist(systtime,30);Ⅱ：nargin不为0% function [jumptimes, systsize] = simmd1(tmax, lambda)% SIMMD1 simulate a M/D/1 queueing system. Poisson arrivals% of intensity lambda, deterministic service times S=1.%% [jumptimes, systsize] = simmd1(tmax, lambda)%% Inputs: tmax - simulation interval% lambda - arrival intensity% Outputs: jumptimes - time points of arrivals or departures% systsize - system size in M/D/1 queue% systtime - system times% Authors:% v1.2 07-Oct-02% set default parameter values if ommitednargin=2;if (nargin==0)tmax=1500;lambda=0.95;endarrtime=-log(rand)/lambda; % Poisson arrivalsi=1;while (min(arrtime(i,:))<=tmax)arrtime = [arrtime; arrtime(i, :)-log(rand)/lambda];i=i+1;endn=length(arrtime); % arrival times t_1,...t_n arrsubtr=arrtime-(0:n-1)'; % t_k-(k-1)arrmatrix=arrsubtr*ones(1,n);deptime=(1:n)+max(triu(arrmatrix)); % departure times%u_k=k+max(t_1,..,t_k-k +1)B=[ones(n,1) arrtime ; -ones(n,1) deptime'];Bsort=sortrows(B,2); % sort jumps in order jumps=Bsort(:,1);jumptimes=[0;Bsort(:,2)];systsize=[0;cumsum(jumps)]; % M/D/1 processsysttime=deptime-arrtime'; % system times% plot a histogram of system timeshist(systtime,30);④M/G/infinity系统%function [jumptimes, systsize] = simmginfty(tmax, lambda)% SIMMGINFTY simulate a M/G/infinity queueing system. Arrivals are% a homogeneous Poisson process of intensity lambda. Service times% Pareto distributed (can be modified).% [jumptimes, systsize] = simmginfty(tmax, lambda) %% Inputs: tmax - simulation interval% lambda - arrival intensity% Outputs: jumptimes - times of state changes in the system% systsize - number of customers in system% See SIMSTMGINFTY, SIMGEOD1, SIMMM1, SIMMD1, SIMMG1.% set default parameter values if ommitedⅠ: nargin=0nargin=0;if (nargin==0)tmax=1500;lambda=1;end% generate Poisson arrivals% the number of points is Poisson-distributednpoints = poissrnd(lambda*tmax);% conditioned that number of points is N,% the points are uniformly distributedif (npoints>0)arrt = sort(rand(npoints, 1)*tmax);elsearrt = [];end% uncomment if not available POISSONRND% generate Poisson arrivals% arrt=-log(rand)/lambda;% i=1;% while (min(arrt(i,:))<=tmax)% arrt = [arrt; arrt(i, :)-log(rand)/lambda];% i=i+1;% end% npoints=length(arrt); % arrival times t_1,...,t_n% servt=50.*rand(n,1); % uniform service times s_1,...,s_kalpha = 1.5; % Pareto service times servt = rand^(-1/(alpha-1))-1; % stationary renewal processservt = [servt; rand(npoints-1,1).^(-1/alpha)-1]; servt = 10.*servt; % arbitrary choice of meandept = arrt+servt; % departure times% Output is system size process N.B = [ones(npoints, 1) arrt; -ones(npoints, 1) dept];Bsort = sortrows(B, 2); % sort jumps in orderjumps = Bsort(:, 1);jumptimes = [0; Bsort(:, 2)];systsize = [0; cumsum(jumps)]; % M/G/infinity system size% process stairs(jumptimes, systsize);xmax = max(systsize)+5;axis([0 tmax 0 xmax]);gridⅡ: nargin不为0时%function [jumptimes, systsize] = simmginfty(tmax, lambda)% SIMMGINFTY simulate a M/G/infinity queueing system. Arrivals are% a homogeneous Poisson process of intensity lambda. Service times% Pareto distributed (can be modified).% [jumptimes, systsize] = simmginfty(tmax, lambda) %% Inputs: tmax - simulation interval% lambda - arrival intensity% Outputs: jumptimes - times of state changes in the system% systsize - number of customers in system% See SIMSTMGINFTY, SIMGEOD1, SIMMM1, SIMMD1, SIMMG1.% set default parameter values if ommitednargin=2;if (nargin==0)tmax=1500;lambda=1;end% generate Poisson arrivals% the number of points is Poisson-distributednpoints = poissrnd(lambda*tmax);% conditioned that number of points is N,% the points are uniformly distributedif (npoints>0)arrt = sort(rand(npoints, 1)*tmax);elsearrt = [];end% uncomment if not available POISSONRND% generate Poisson arrivals% arrt=-log(rand)/lambda;% i=1;% while (min(arrt(i,:))<=tmax)% arrt = [arrt; arrt(i, :)-log(rand)/lambda];% i=i+1;% end% npoints=length(arrt); % arrival times t_1,...,t_n% servt=50.*rand(n,1); % uniform service times s_1,...,s_kalpha = 1.5; % Pareto service times servt = rand^(-1/(alpha-1))-1; % stationary renewal process servt = [servt; rand(npoints-1,1).^(-1/alpha)-1]; servt = 10.*servt; % arbitrary choice of meandept = arrt+servt; % departure times% Output is system size process N.B = [ones(npoints, 1) arrt; -ones(npoints, 1) dept];Bsort = sortrows(B, 2); % sort jumps in orderjumps = Bsort(:, 1);jumptimes = [0; Bsort(:, 2)];systsize = [0; cumsum(jumps)]; % M/G/infinity system size% process stairs(jumptimes, systsize);xmax = max(systsize)+5;axis([0 tmax 0 xmax]);grid实验总结：通过这次实验，加深了我对随机过程这门课程的理解与认识，对各种随机过程的模拟有了更深刻的了解，同时也认识到模拟编程的重要性。
