实验一 秩亏自由网上机实验
- 格式:doc
- 大小:57.50 KB
- 文档页数:3

院系____________________ 班级____________________ 姓名____________________ 学号____________________目录(页码根据自己需要填写)一、实验项目须知.....................................二、实验一秩亏自由网上机实验........................三、实验二极大验后滤波、推估上机实验...............四、实验三最小二乘配置上机实验.....................五、实验四平差系统的统计假设检验上机实验...........六、编写实验报告要求................................实验项目须知一、课程介绍本课程是测绘工程类专业的专业选修课程之一,是在学生学习了误差理论与测量平差知识之后又开设的一门专业的数据处理课程,该课程主要讲授近现代测量数据处理理论、模型和方法,同时紧密结合计算机编程,从而提高学生的计算机应用能力、测量数据处理能力,培养学生养成严谨的科学态度,提高分析和解决问题的能力,更好的适应今后工作和学习。
二、测量数据处理实验教学要求1.掌握稳健估计方法处理测量数据;2.掌握极大验后滤波、推估理论和方法处理测量数据;3.初步掌握最小二乘配置理论和方法处理测量数据;4.初步掌握工程或科研项目中测量数据处理的理论、步骤、方法和技巧;5.掌握测量数据处理中常用的计算机语言和软件;6.服从实验指导教师的规定,认真、按时、独立完成任务每次实验结束,提交书写工整或按照规范打印实验报告。
7.在实验过程中,还应遵守纪律,爱护实验室设备、离开后将自己的随身物品带走,并记录仪器使用状况、将凳子整理好并放到电脑桌的下方。
8.上机实验后,提交实验报告,成绩评定重点考核算法、处理结果与结果分析。
三、实验选择要求可根据课堂讲课具体内容,完成4个实验,并要求写出实验报告。

论秩亏自由网平差的性质及稳健基准的意义
自由网平差是一种网络平差方法,它可以用来解决复杂的网络平差问题。
自由网平差具有三个特点:1、自由网平差是一种秩亏的网络平差方法,它可以解决复杂的网络平差问题;2、自由网平差是一种稳健的网络平差方法,它可以抵消网络中的噪声和误差;3、自由网平差是一种有效的网络平差方法,它可以有效地提高网络的精度和稳定性。
秩亏的自由网平差是指在网络平差过程中,网络的观测数据和计算结果之间存在着秩亏的状态,即观测数据和计算结果之间存在着不可解释的差异。
这种秩亏的状态可以通过调整网络中的参数来消除,从而达到网络平差的目的。
稳健基准是指在网络平差过程中,通过调整网络中的参数,使网络对噪声和误差具有较强的抗干扰能力,有效地抵消噪声和误差,从而提高网络的精度和稳定性。
稳健基准的意义在于,可以有效地抵消网络中的噪声和误差,保证网络的精度和稳定性。

§8-2 秩亏自由网平差2学时在前面介绍的经典平差中,都是以已知的起算数据为基础,将控制网固定在已知数据上。
如水准网必须至少已知网中某一点的高程,平面网至少要已知一点的坐标、一条边的边长和一条边的方位角。
当网中没有必要的起算数据时,我们称其为自由网,本节将介绍网中没有起算数据时的平差方法,即自由网平差。
在经典间接平差中,网中具备必要的起算数据,误差方程为111ˆ⨯⨯⨯⨯-=n t t n n l xB V (8-2-1)式中系数阵B 为列满秩矩阵,其秩为t B R =)( 。
在最小二乘准则下得到的法方程为0ˆ11=-⨯⨯⨯t t tt bb W xN (8-2-2)由于其系数阵的秩为t B R PB B R N R Tbb ===)()()(,所以bb N 为满秩矩阵,即为非奇异阵,具有凯利逆bb N 1-,因此具有唯一解,即W N xbb 1ˆ-= (8-2-3)当网中无起算数据时,网中所有点均为待定点,设未知参数的个数为u ,误差方程为111ˆ⨯⨯⨯⨯-=n u u n n l xB V (8-2-4)式中d t u +=d 为必要的起算数据个数。
尽管增加了d 个参数,但B 的秩仍为必要观测个数,即u t B R <=)(其中B 为不满秩矩阵,称为秩亏阵,其秩亏数为d 。
组成法方程0ˆ11=-⨯⨯⨯u u u u W xN(8-2-5)式中PlB W PB B N T u T uu ==⨯⨯1,,且u t B R PB B R N R T<===)()()(,所以N 也为秩亏阵,秩亏数为:t u d -=(8-2-6)由上式知,不同类型控制网的秩亏数就是经典平差时必要的起算数据的个数。
即有:⎪⎩⎪⎨⎧=测角网网测边网、边角网、导线水准网、测站平差,4,3,1d在控制网秩亏的情况下,法方程有解但不唯一。
也就是说仅满足最小二乘准则,仍无法求得xˆ的唯一解,这就是秩亏网平差与经典平差的根本区别。

地质工程与测绘学院实习报告课程名称:近代测量数据处理与应用实习名称:秩亏自由网平差程序设计上机实习班级:学号:姓名:指导教师:实习时间:2013年10月28日一、 实习目的1. 理解秩亏自由网平差的函数模型和随机模型;2. 理解广义逆、最小范数逆、伪逆的概念3. 学会如何求解最小范数逆和伪逆;4. 理解秩亏自由网平差数据的处理的一般过程。
5. 加强程序的理解力、使用给定的程序处理数据; 二、 实验基本原理误差方程⎪⎭⎪⎬⎫=-=-⨯∧⨯⨯⨯P l D lX A V n u u n n 121110)(σ由最小二乘原理min =PV V T ,可得 1n n n u 1u u u ⨯⨯⨯∧⨯⨯=n Tl P AX N由于R(N)=R (A )=t<u ,故N 为奇异矩阵,其正则逆不存在,得不到唯一解。
增加约束条件min =∧∧X X T组成新的函数:求偏导数并令其等于零,得:为最小范数逆求解方法有:1) 最小范数逆法A. 在法方程系数阵N 的对角线元素加微小量,将秩亏问题转化为经典自由网平差B. 采用降秩法求解最小范数逆--=)(NN N N m Pl A N X T m r -=ˆ)ˆ(2ˆˆPl A X N K X X T T T --=Φ02ˆ2ˆ=-=∂Φ∂N K X XT T Pl A NN N Pl A NN N X PlA NN K T T T T rTT ---===)()(ˆ)(--=)(NN N N m2) 伪逆解法采用满秩分解法求解伪逆三、 程序操作流程Pl A N X T +=ˆ)()(N N N NN N N T T T -+=四、实验结果(一) 水准网水准网如图所示,测得观测高差为h 1=12.345m h 2=3.478m h 3=-15.817m各段路线距离相等(等权),取H 10=0 H 20=12.345m H 30=15.823m1)误差方程V=B*X-lB=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---101110011,l=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡600 P=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100010001,X0=[ 0 12.345 15.823 ] T(二)平面网如图所示的测边自由网(假定各边等权),观测数据如表所示,各点近似坐标给定如下。


秩亏自由网平差的研究刘 阳(江苏师范大学,城建学部,江苏 徐州 )摘要:秩亏自由网是因为控制网中没有足够的起始数据, 即缺乏基准的平差问题,因此按间接平差进行平差时, 其误差方程的系数阵 B 不能满足列满秩的要求, 相应的法方程系数阵T bbN B PB 是秩亏阵.为了求定未知参数的唯一确定解, 除了遵循最小二乘准则外, 还需增加新的基准约束条件 , 从而得到未知参数的唯一确定解.本文主要利用MATLAB 从传统的测量平差的观点出发, 来计算例题,分析,和论述亏秩自由网平差之解的性质,讨论了附加矩阵S 的形式了确定的方式,讨论了秩亏自由网平差之解与传统自由网平差之解的关系, 给出了详细的解答过程,并且比较了俩种方法的各自的优缺点,给出总结。
关键词:秩亏自由网;平差;间接平差Research Rank Defect Free NetworkAdjustmentLiuyang(School of Urban construction and design, Jiangsu Normal University, 221116)Abstract:Rank Defect Free Network control network because of not enough initial data,That lack of adjustment problems benchmark.Therefore, when carried out by indirect adjustment adjustment, the coefficient matrix B error equation does not meet the requirements of full rank.Corresponding normal equation coefficient matrix is rank deficient matrix.In order to find a unique set of unknown parameters to determine the solution, in addition to following the least squares criterion, the need to add a new benchmark constraints, resulting in a unique solution to determine the unknown parameters.The main advantage of MATLAB article from the traditional viewpoint of Surveying Adjustment,Analysis of the nature of the calculation examples, and discusses the loss of rank free net adjustment of the solution,Additional discussion of the form of the S matrix determined, discusses the relationship between solutions of rank defect free network adjustment of the solution with the traditional free network adjustment, the process gives a detailed answer, and compare the two methods of their advantages and disadvantages.Gives summary.Key words: Rank-defect free net adjustment; adjustment; condition comparison引言在现代测量数据处理过程中,秩亏自由网平差在近几十年得到了广泛应用,是重要的数据处理方法之一,特别是在变形监测、最优化设计中,秩亏自由网平差都展现出其优势。


《计量经济学》上机实验参考答案实验一:线性回归模型的估计、检验和预测(3 课时)实验设备:个人计算机,计量经济学软件Eviews,外围设备如U 盘。
实验目的:(1)熟悉Eviews 软件基本使用功能;(2)掌握一元线性回归模型的估计、检验和预测方法;正态性检验;(3)掌握多元线性回归模型的估计、检验和预测方法;(4)掌握多元非线性回归模型的估计方法;(5)掌握模型参数的线性约束检验与参数的稳定性检验。
实验方法与原理:Eviews 软件使用,普通最小二乘法(OLS),拟合优度评价、t 检验、F 检验、J-B 检验、预测原理。
实验要求:(1)熟悉和掌握描述统计和线性回归分析;(2)选择方程进行一元线性回归;(3)选择方程进行多元线性回归;(4)进行经济意义检验、拟合优度评价、参数显著性检验和回归方程显著性检验;(5)掌握被解释变量的点预测和区间预测;(6)估计对数模型、半对数模型、倒数模型、多项式模型模型等非线性回归模型。
实验内容与数据1(第2 章思考与练习:三、简答、分析与计算题第12 小题):12. 表1 数据是从某个行业的5 个不同的工厂收集的,请回答以下问题:ˆˆˆˆ(1)估计这个行业的线性总成本函数:yˆt= b0 + b1 x t ;(2)b0 和b1 的经济含义是什么?;(3)估计产量为10 时的总成本。
表1 某行业成本与产量数据参考答案:(1)总成本函数(标准格式):yˆt = 26.27679 + 4.25899xts = (3.211966) (0.367954)t = (8.180904) (11.57462)R 2 = 0.978098 S.E = 2.462819 DW =1.404274 F =133.9719ˆˆ(2) b0 =26.27679 为固定成本,即产量为0 时的成本;b1 =4.25899 为边际成本,即产量每增加1 单位时,总成本增加了4.25899 单位。


§8-2 秩亏自由网平差2学时在前面介绍的经典平差中,都是以已知的起算数据为基础,将控制网固定在已知数据上。
如水准网必须至少已知网中某一点的高程,平面网至少要已知一点的坐标、一条边的边长和一条边的方位角。
当网中没有必要的起算数据时,我们称其为自由网,本节将介绍网中没有起算数据时的平差方法,即自由网平差。
在经典间接平差中,网中具备必要的起算数据,误差方程为111ˆ⨯⨯⨯⨯-=n t t n n l xB V (8-2-1)式中系数阵B 为列满秩矩阵,其秩为t B R =)( 。
在最小二乘准则下得到的法方程为0ˆ11=-⨯⨯⨯t t tt bb W xN (8-2-2)由于其系数阵的秩为t B R PB B R N R Tbb ===)()()(,所以bb N 为满秩矩阵,即为非奇异阵,具有凯利逆bb N 1-,因此具有唯一解,即W N xbb 1ˆ-= (8-2-3)当网中无起算数据时,网中所有点均为待定点,设未知参数的个数为u ,误差方程为111ˆ⨯⨯⨯⨯-=n u u n n l xB V (8-2-4)式中d t u +=d 为必要的起算数据个数。
尽管增加了d 个参数,但B 的秩仍为必要观测个数,即u t B R <=)(其中B 为不满秩矩阵,称为秩亏阵,其秩亏数为d 。
组成法方程0ˆ11=-⨯⨯⨯u u u u W xN(8-2-5)式中PlB W PB B N T u T uu ==⨯⨯1,,且u t B R PB B R N R T<===)()()(,所以N 也为秩亏阵,秩亏数为:t u d -=(8-2-6)由上式知,不同类型控制网的秩亏数就是经典平差时必要的起算数据的个数。
即有:⎪⎩⎪⎨⎧=测角网网测边网、边角网、导线水准网、测站平差,4,3,1d在控制网秩亏的情况下,法方程有解但不唯一。
也就是说仅满足最小二乘准则,仍无法求得xˆ的唯一解,这就是秩亏网平差与经典平差的根本区别。
秩亏自由网平差的应用一、 问题及解决方案水利工程布设控制网是为测量工作提供依据,在精度上起到控制作用。
平面、高程控制网的建立通常情况下需要起算基准。
按规划设计阶段的《水利水电工程测量规范》第2.1.4条要求,建立基本平面控制网时,在长度小于60km 的测区或任何长度的狭长带状测区时,可不进行高斯投影,采用任意平面直角坐标系统。
第3.1.1条要求,建立基本高程控制网时,对远离国家水准点的地区,引测有困难时,可采用独立高程系统[1]。
也有这种情况:由于时间紧急、未曾获得国家系统数据,而需要先进场开展测量工作。
此时,在没有起算数据的情况下,通常的做法是假设起算数据,但这样会导致观测精度相同而平差成果精度却不均匀:即离假设已知点越远,其精度越差。
解决方案:考虑使用秩亏自由网进行严密平差来建立基本平面、高程控制网,使精度均匀,误差按权分配。
二、秩亏自由网平差1、秩亏自由网我们知道,间接平差中观测误差方程为[2]:nxlV=^uxlnxu x B -nxll (1)法方程表示为:^uxluxu xN -uxlf = 0 (2)式中 uxuN =B T PB ,f = B T P l 。
由于缺乏起算基准,误差方程系数矩阵B 非满秩:R (B )= t < u ;法方程系数矩阵N 也非满秩:R (N )= t < u 。
秩亏数d = u – t 等于控制网必要起算数据个数。
在常用网中,对于水准网 d = 1;对于边角网 d = 3;对于测角网 d = 4。
为改善奇异性,为平差参数^uxlx 附加d 个基准条件:dxuS T ^uxlx= 0 (3)且线性无关,与法方程也线性无关,即:uxduxu SN = 0,R (S )=d 。
由此秩亏自由网平差模型为:nxlV=^uxlnxu xB - nxlldxuS T^uxlx= 0 (4)V TPV = Min法方程表示为:^000bb eT S xk f N S ⎛⎫⎛⎫⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (5)参数解为:^1()Tbb eex S Q ffN S -=+= (6)单位权中误差为:^0σ=2、秩亏网平差多种取自由网基准条件中一般用重心基准条件。
实验一 秩亏自由网上机实验
一、 实验目的
1. 掌握各种秩亏自由网平差的函数模型和随机模型;
2. 熟悉各种秩亏自由网平差解算的若干公式;
3. 结合算例能利用matlab 进行编程计算。
二、
实验内容
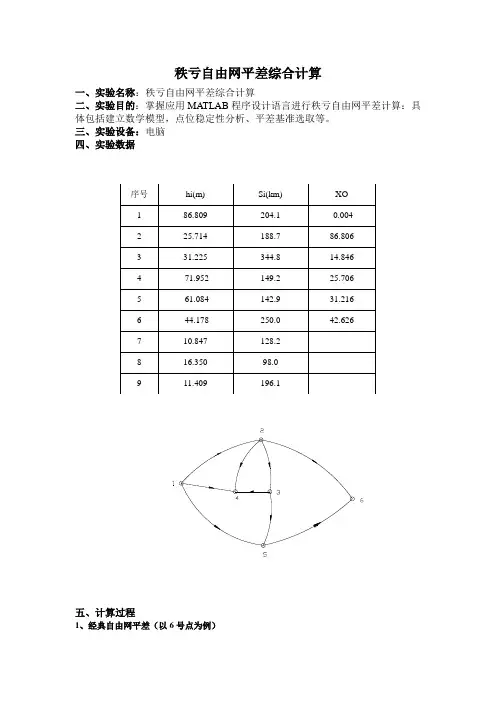
在下图水准网中,观测高差、距离和各待定点高程近似值见教材P43表2-1,分别进行下列自由网平差:
(1)以6号点为固定点的经典自由网平差; (2)以重心基准的自由网平差(P χ=E );
(3) 以1,2,5,6四个点为拟稳基准的拟稳平差. 解:(1)
5
693583
472662452341531421121∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
∧
-=-=-=-=-=-=-=-=-=X X h X X h X X h X X h X X h X X h X X h X X h X X h
.
)()(.
......)()(5605
06
991201
0211∧
∧
∧
∧-+-=+-+-=+x x X X V h x x X X V h
可得误差方程为:
(2)matlab 进行编程计算 l x B V -=∧
B=[-1 1 0 0 0 ;-1 0 0 1 0;-1 0 0 0 1 ;0 -1 1 0 0 ;0 -1 0 1 0 ...
;0 -1 0 0 0 ;0 0 -1 1 0 ;0 0 -1 0 1 ;0 0 0 0 -1 ]; l=[0;3;4;9;15;2;-12;-21;0];
S=[204.1 188.7 344.8 149.2 142.9 250 128.2 98 196.1];
P=diag(10./S);
N=B'*P*B;
x=inv(N)*B'*P*l V=B*x-l Qx=inv(N)
(2) 首先建立误差方程 l x B V -=∧
B=[-1 1 0 0 0 0;-1 0 0 1 0 0;-1 0 0 0 1 0;0 -1 1 0 0 0;0 -1 0 1 0 0 ... ;0 -1 0 0 0 1;0 0 -1 1 0 0;0 0 -1 0 1 0;0 0 0 0 -1 1];
l=[-1;4;5;8;16;2;-13;-20;-1]
S=[204.1 188.7 344.8 149.2 142.9 250 128.2 98 196.1];
P=diag(10./S); S1=[1;1;1;1;1;1]; W=B'*P*l;
Xr=inv(B'*P*B+S1*S1')*W
V=B*Xz-l
Qxr=inv(B'*P*B+S1*S1')-inv(B'*P*B+S1*S1')*S1*S1’*inv(B'*P*B+S1*S1')
(3) 首先建立误差方程 l x B V -=∧
B=[-1 1 0 0 0 0;-1 0 0 1 0 0;-1 0 0 0 1 0;0 -1 1 0 0 0;0 -1 0 1 0 0 ...
;0 -1 0 0 0 1;0 0 -1 1 0 0;0 0 -1 0 1 0;0 0 0 0 -1 1];
⎥⎥
⎥
⎥⎥
⎥
⎥
⎥⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢
⎢⎢⎢
⎢⎢⎢
⎢⎢⎢⎣
⎡=∧
02112215943000011-0
0000000101-00000011-000001000
1-000000101-000000011-00000100
01-000001001-00000
00
11-i i x V
l=[-1;4;5;8;16;2;-13;-20;-1]
S=[1;1;1;1;1;1];
S1=[204.1 188.7 344.8 149.2 142.9 250 128.2 98 196.1]; P=diag(10./S1);
N=B'*P*B
W=B’*P*l;
px=[1 1 0 0 1 1]
Px=diag(px)
Ss=Px*S
Xs=inv(B'*P*B+Ss*Ss')*W
V=B*Xs-l
Qxs=inv(B'*P*B+Ss*Ss')*N*inv(B'*P*B+Ss*Ss')。