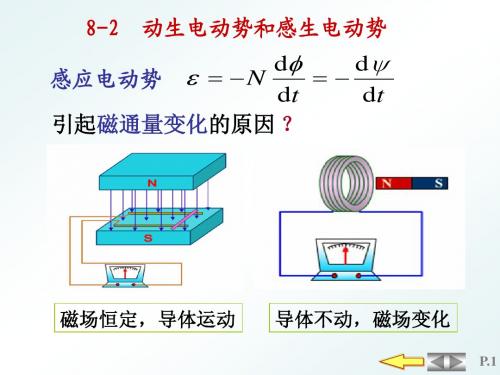
8_2动生电动势和感生电动势1

感生电动势与动生电动势的本质区别曹海斌（高新区第一中学 215011）一、问题的提出关于感生电动势和动生电动势的概念，不仅学生往往有错误的理解，有的老师也理解深度不够。

请看下面的问题：下图中所示：图1中通电螺线管A 不动，A 中电流大小也不变，金属圆环B 由远处向A 靠近；图2中金属圆环B 不动，通电螺线管A 也不动，但使A 中的电流变大；图3中金属圆环B 不动，通电螺线管A 中电流大小不变，让A 从远处插入B 。

问这三种情况下产生的电动势分别是什么电动势？这三种情况下通过线框的磁通量都发生了变化，其中图1中磁通量的变化是由于线框运动切割磁感线引起的，B 中产生的是动生电动势，这应该是没有争议的。

图2中磁通量的变化是由磁感应强度变化引起的，这是感生电动势也是没有争议的。

图3中当A 向B 靠近时，B 所在处的磁感应强度发生了变化，乍一看认为B 产生的感应电动势是感生电动势。

但从相对运动的角度看，虽然圆环B 不动，通电螺线管A 在运动，但也可以理解为：磁铁不动，线框在动。

这样图C 中的感应电动势就应该和图1相同产生的是动生电动势。

那么C 图中的感应电动势究竟是什么电动势呢？二、感生电动势和动生电动势的本质区别这就要弄清楚这两种电动势的本质区别。

在高中物理人教版新教材3-2中，P19-20中是这样解释的：“如果是感应电动势由感生电场产生的，这也叫做‘感生电动势’”。

“如果感应电动势是由于导体运动而产生的，它也叫做‘动生电动势’”。

对照动生电动势的定义，对上面的问题的解决还不是很清楚。

但对照感生电动势的定义，再深入思考一下，就能明白了。

也就是说有没有感生电场是关键。

感生电动势的本质是产生涡旋电场，涡旋电场产生非静电力，使导体中的电荷向两端积累产生电势差。

而动生电动势是洛伦兹力充当非静电力，使导体中的电荷向两端积累产生电势差。

C 图中磁通量变化貌似磁场变化引起的，其实这样的磁场是稳定的磁场，只不过是运动的稳定的磁场，由于磁场运动导致线框切割磁感线，使得线框中的自由电荷受到洛伦兹力而发生定向移动形成电流。

动生电动势和感生电动势的相对性和统一性
动生电动势（也称为发电机电动势）是指通过磁场运动而产生
的电动势，如发电机中电线在通过磁场运动时产生的电动势。

而感
生电动势则是指当磁场变化时，导体内产生的电动势，如变压器中
的感应电动势。

这两种电动势的相对性在于它们都是由磁场和运动（或变化）
导致的电动势。

一方面，动生电动势是一种主动性的过程，需要有
电力来驱动电线在磁场中运动产生电动势；另一方面，感生电动势
是一种被动性的过程，当磁场发生变化时，导体内就会产生电动势。

因此，动生电动势和感生电动势是相对的。

但是，在物理上，动生电动势和感生电动势也有一定的统一性。

它们都遵循法拉第电磁感应定律，即磁通量变化率与感应电动势成
正比。

此外，动生电动势和感生电动势都是由磁场和运动（或变化）导致的电动势，它们的本质都是由电子在磁场中运动和受力产生的。

因此，在一定程度上，动生电动势和感生电动势也具有一定的统一性。

Science &Technology Vision 科技视界1动生电动势如图1,一根金属棒在匀强磁场中沿与棒和磁场垂直的方向以速度V0向右运动。

自由电荷(电子)随棒运动。

必然受到洛仑磁力作用,而发生运动。

电子沿棒运动的速度为U。

这样自由电子具有随金属棒运动的速度V0同时还有沿棒运动的速度U,故自由电子相对磁场的合速度为V0。

金属棒ab 两端因正负电荷分别积累,而形成电动势,Uab>0。

图1由左手定则可知,由于自由电子相对磁场以速度V 运动,一定会受到洛仑磁力F 洛。

当F 洛的分力F1与F 外平衡,F 洛的另一分力F2与电场力FE 平衡时,金属棒两端建立了稳定的动生电动势。

F 洛=eBV 其分力F1=eBVcosα=eBu,F2=eBVsinα=eBV0金属棒ab 两端电动势U=BLV0,自由电子受到的电场力FE=eE=eBLV0/L=eBV0FE 与F2等大反向。

F 外与F1等大反向(图2)。

图2F E 与F 外的合力F'=eB V 02+U 2√=eBVH 合和F 洛等大反向。

此时自由电子受到的三个力F 洛、F 外、F E 作用达到平衡。

金属棒匀速垂直切割磁感线运动建立了稳定的电动势。

E=BLV 0从能量转化的观点来看:外力克服洛仑磁力的分力F1做功,机械能转化的电能。

在此过程中洛仑磁力起到中转能量的作用。

使机械能和电能之间发生转化。

那么洛仑磁力是否做功呢:F 洛的分力F 1与V 0反向做负功W1,另一分力F2与电子沿棒移动方向U 一致做正功W2,则有:W1=-F 1V 0t=-eBIV 0t W2=F 2Ut=eBV 0Ut W=W1+W1=0其实洛仑磁力F H 合与电子合速度V 垂直,其做功为零是肯定的。

我们可以看到动生电动势有以下几个特点:a.在能量转化上是机械能转化为电能。

b.洛仑磁力参与其全过程并传递能量,实现两种形式的能量转化。

c.因为洛仑磁力与自由电荷合速度方向垂直,洛仑磁力不做功。

11/2009谈谈感应电动势、感生电动势、动生电动势蔡薇(南京高等职业技术学校)动生电动势和感生电动势产生的缘由及其非静电力是不一样的。

而感应电动势是动生电动势的感生电动势的总称。

应当指出,这种分法在一定程度上只有相对意义。

文章阐述了感应电动势、感生电动势、动生电动势的不同运用。

感应电动势感生电动势动生电动势在物理教科书中常常看到感应电动势、感生电动势、动生电动势这三个名词。

其实,这三个名词的概念是不一样的。

大家知道:当穿过导体回路的磁通量发生变化时,回路中就产生感应电动势。

按照磁通量变化原因的不同,又有两种情形:一种是在稳恒磁场中运动着的导体内产生的感应电动势,叫做动生电动势;另一种是导体不动,因磁场的变化产生的感应电动势,叫做感生电动势。

动生电动势可以看成是由洛仑兹力所引起的。

导体在磁场中运动,导体内的自由电子也以同样速度向同样方向运动,自由电子从而受到洛仑兹力的作用,在洛仑兹力的作用下,自由电子向导体的一端聚集,使导体此端带负电,而导体另一端则带正电,从而产生动生电动势,形成电源。

由此可见,导体在磁场中运动产生动生电动势,其非静电力为洛仑兹力,并且动生电动势只可能存在于运动的这一段导体上,而不动的那一段导体上没有电动势。

感生电动势是由变化的磁场本身引起的。

变化的磁场在其周围也会激发一种电场,叫做感应电场或涡旋电场。

这种电场与静电场的共同点就是对电荷有作用力。

与静电场不同之处,一方面在于这种涡旋电场不是由电荷激发的,而是由变化的磁场所激发;另一方面在于描述涡旋电场的电力线是闭合的,从而它不是保守场。

产生感生电动势的非静电力正是这一涡旋电场。

从上述分析可见:动生电动势和感生电动势产生的缘由及其非静电力是不一样的。

而感应电动势是动生电动势的感生电动势的总称。

最后应当指出,这种分法在一定程度上只有相对意义。

例如,如图示,如果在以线圈为静止的参照系内观察,磁棒的运动引起空间磁场的变化,线圈中的电动势是感生的。

动生电动势和感生电动势之杨若古兰创作法拉第电磁感应定律：只需穿过回路的磁通量发生了变更，在回路中就会有感应电动势发生.而实际上，惹起磁通量变更的缘由不过乎两条：其一是回路绝对于磁场有活动；其二是回路在磁场中虽无绝对活动，但是磁场在空间的分布是随时间变更的，我们将前一缘由发生的感应电动势称为动生电动势，而后一缘由发生的感应电动势称为感生电动势. 留意:动生电动势和感生电动势的名称也是一个绝对的概念，因为在分歧的惯性系中，对同一个电磁感应过程的理解分歧：（1）设观察者甲随磁铁一路向左活动:线圈中的自在电子绝对磁铁活动，受洛仑兹力感化，作为线圈中发生感应电流和感应电动势的缘由.－动生电动势.（2）设观察者乙绝对线圈静止:线圈中的自在电子静止不动，不受磁场力感化.发生感应电流和感应电动势的缘由是活动磁铁（变更磁场）在空间发生一个感应（涡旋）电场，电场力驱动使线圈中电荷定向活动构成电流.－感生电动势一、动生电动势导体或导体回路在磁场中活动而发生的电动势称为动生电动势.动生电动势的来源: 如图，活动导体内每个电子受到方向向上的洛仑兹力为：；正负电荷积累在导体内建立电场；当时达到动态平衡，不再有宏观定向活动，则导体 ab 相当一个电源，a为负极（低电势），b为正极（高电势），洛仑兹力就是非静电力.可以使用法拉第定律计算动生电动势：对于全体或局部在恒定磁场中活动的闭合回路，先求出该回路的磁通F与t 的关系，再将对t求导，即可求出动生电动势的大小.（2）动生电动势的方向可由楞次定律确定. 二、感生电动势处在磁场中的静止导体回路，仅仅由磁场随时间变更而发生的感应电动势，称为感生电动势. 感生电场:变更的磁场在其四周空间激发一种电场，称之为感生电场.而发生感生电动势的非静电场恰是感生电场.感生电动势: 回路中磁通量的变更仅由磁场变更惹起，则电动势为感生电动势 .若闭合回路是静止的，它所围的面积S 也不随时间变更.感生电场与变更磁场之间的关系:（1）变更的磁场将在其四周激发涡旋状的感生电场，电场线是一系列的闭合线. （2）感生电场的性质分歧于静电场.静电场 感生电场 场源正负电荷 变更的磁场力线起源于正电荷，终止于负电荷 不闭合曲线 感化力法拉第电磁感应定律一、1、关于表达式t n E ∆∆=φ【公式在利用时容易漏掉匝数n ，变更过程中磁场方向改变的情况容易出错，而且感应电动势E与φ、φ∆、t ∆∆φ的关系容易混淆不清.】 2、利用法拉第电磁感应定律的三种特殊情况：（1）E=Blv, （2）ω221Bl E =,（3）E=nBs ωsin θ（或E=nBs ωcos θ）二、1、φ、φ∆、t ∆∆φ同v 、△v 、t v ∆∆一样都是容易混淆的物理量磁通量φ 磁通量变更量φ∆磁通量变更率t ∆∆φ物理意义磁通量越大，某时刻穿过磁场中某个面的磁感线条数越某段时间穿过某个面的末、初磁通量的差值 表述磁场中穿过某个面的磁通量变更快慢的物理量 计算注 意 若穿过某个面无方向相反的磁场，则不克不及直接用，应考虑相反方向的磁通量彼此抵消当前所剩余的磁通量 开始和转过1800时平面都与磁场垂直，穿过平面的磁通量是分歧的，一正一负，△φ=2 BS ，而不是零 既不暗示磁通量的大小，也不暗示变更的多少，在φ—t 图象顶用图线的斜率暗示2、明确感应电动势的三种特殊情况中各公式的具体用法及利用时须留意的成绩⑴导体切割磁感线发生的感应电动势E=Blv ，利用此公式时B 、l 、v 三个量必须是两两彼此垂直，若不垂直应转化成彼此垂直的无效分量进行计算.将无效分量代入公式E=Blv 求解.此公式也可计算平均感应电动势，只需将v 代入平均速度即可.⑵导体棒以端点为轴在垂直于磁感线的匀强磁场中匀速动弹，各点的线速度分歧，用平均速度（中点线速度）计算⑶矩形线圈在匀强磁场中，绕垂直于磁场的任意轴匀速动弹发生的感应电动势何时用E=nBs ωsin θ或E=nBs ωcos θ计算.其实这两个公式的区别是计时起点分歧.当线圈转至中性面（即线圈平面与磁场垂直的地位）时E=0，当线圈转至垂直中性面的地位（即线圈平面与磁场平行）时E=nBs ω.如许，线圈从中性面开始计时感应电动势按E=nBs ωsin θ规律变更，线圈从垂直中性面的地位开始计时感应电动势按E=nBs ωcos θ规律变更.用这两个公式可以求某时刻线圈的磁通量变更率△φ/△t ，.t →0的极限值才等于瞬时感应电动势.当△φ均匀变更时，平均感应电动势等于瞬时感应电动势.但三种特殊情况中的公式通经常使用来求感应电动势的瞬时值.【典例】例1：关于感应电动势，以下说法准确的是（）【答】CDA．穿过回路的磁通量越大，回路中的感应电动势就越大B．穿过回路的磁通量变更量越大，回路中的感应电动势就越大C．穿过回路的磁通量变更率大，回路中的感应电动势就大D．单位时间内穿过回路的磁通量变更量大，回路中感应电动势就大【总结】0是回路中存.例2：一个面积S=4×10-2m2，匝数N=100的线圈，放在匀强磁场中，磁场方向垂直线圈平面，磁场的磁感应强度B随时间变更规律为△B /△t=2T/s Wb/s，线圈中发生的感应电动势E=V.【审题N有关.与匝数N有关.【解析△B /△t=4×10-2×2 Wb/s=8×10-2Wb/s由E=N△φ/△t得E=100×8×10-2V=8V【总结】计算磁通量φ=BScosθ、磁通量变更量△φ=φ2-φ1、磁通量变更率△φ/△t 时不必考虑匝数N ，但在求感应电动势时必须考虑匝数N ，即E=N △φ/△t.求安培力时也要考虑匝数N ，即F=NBIL ，因为通电导线越多，它们在磁场中所受安培力就越大.例3：如图7-1所示，两条平行且足够长的金属导轨置于磁感应强度为B 的匀强磁场中，B 的方向垂直导轨平面.两导轨间距为L ，左端接一电阻R ，其余电阻不计.长为2L 的导体棒ab 如图所示放置， 开始时ab 棒与导轨垂直，在ab 棒绕a 点紧贴导轨滑倒的过程中，通过电阻R 的电荷量是.【解析】t BL t L L L B t S B t E ∆=∆-•=∆∆=∆∆=23421222φ，tR 2BL 3R E I 2∆== ∴R BL t I q 232=∆=答案：R BL 232【总结】用E=N △φ/△t 求的是平均感应电动势，由平均感应电动势求闭合回路的平均电流.而电路中通过的电荷量等于平均电流与时间的乘积，即R N t tR N t I q φφ∆=∆∆∆=∆=，留意这个式子在分歧情况下的利用.例4：如图7-2所示，在竖直向下的匀强磁场中，将一水平放置的金属棒以水平速度V 0抛出，设全部过程中，棒的取向不变，不计空气阻力，则金属棒活动过程中发生的感应电动势的大小变更情况应是（ ）A ．愈来愈大B ．愈来愈小C ．坚持不变D ．没法判断【解】导体切割磁感线发生的感应电动势E=Blv ，金属棒活动过程中B 、l 和v 的无效分量均不变，所以感应电动势E 不变，选C. 图7-图例5：如图7-3所示，长为L 的金属棒ab ，绕b 端在垂直于匀强磁场的平面内以角速度ω匀速动弹，磁感应强度为B ，求ab 两端的电势差.【审题】用棒的中点的速率作为平均切割速率代入公式E=Blv.也能够设△t 时间ab 棒扫过的扇形面积为△S ，根据E=n △φ/△t.【解析】解法一：E=Blv=BL ωL/2=BL 2ω/2，解法二：E=n △φ/△t= B △S/△t=t t L B ∆∆•/212ω= BL 2ω/2 ∴22ωBL E U ab ==【总结】若用E=Blv 求E ，则必须先求出平均切割速率；若用E=n △φ/△t 求E ，则必须先求出金属棒ab 在△t 时间扫过的扇形面积，从而求出磁通量的变更率.例6：如图7-4所示，矩形线圈abcd 共有n 匝，总电阻为R ，部分置于有理想鸿沟的匀强磁场中，线圈平面与磁场垂直，磁感应强度大小为B.让线圈从图示地位开始以ab 边为轴匀速动弹，角速度为ω.若线圈ab 边长为L 1，ad 边长为L 2，在磁场内部分为2L 52，则⑴线圈从图示地位转过530时的感应电动势的大小为.⑵线圈从图示地位转过1800的过程中，线圈中的平均感应电流为.⑶若磁场没有鸿沟，线圈从图示地位转过450时的感应电动势的大小为，磁通量的变更率为.【审题】磁场有鸿沟时，线圈abcd 从图示地位转过530的过程中，穿过线圈的磁通量始终没有变更，所以此过程感应电动势始终为零；在线圈abcd 从图示地位转过1800的过程中，初末形态磁通量大小不变，但方向改变，图图所以2121L BL 56L 53BL 2=•=φ∆.磁场没有鸿沟时，线圈abcd 从图示地位动弹发生的感应电动势按E=nBs ωsin θ规律变更.【解析】⑴线圈从图示地位转过530时的感应电动势的大小为零.⑵线圈从图示地位转过1800的过程中，πωωπφ56562121L nBL L BL n t n E ==∆∆=∴R L nBL R E I πω5621==⑶若磁场没有鸿沟，线圈从图示地位转过450时的感应电动势E=nBL 1L 2ωsin ωt=ω21L nBL 22，此时磁通量的变更率2221ωφL BL n E t ==∆∆【总结】磁通量的变更量的求法，开始和转过1800时平面都与磁场垂直，△φ=2 BS ，而不是零.例7：一个圆形闭合线圈固定在垂直纸面的匀强磁场中，线圈平面与磁场方向垂直，如图7-5甲所示.设垂直纸面向里的磁感应强度方向为正，垂直纸面向外的磁感应强度方向为负.线圈中顺时针方向的感应电流为正，逆时针方向的感应电流为负.已知圆形线圈中感应电流i 随时间变更的图象如图7-5乙所示，则线圈所在处的磁场的磁感应强度随时间变更的图象可能是（ ）【总结】若给出的是φ—t 图象，情况是一样的.答案：CD例8：如图7-6所示，金属导轨间距为d ，左端接一电阻R ，图图7-匀强磁场的磁感应强度为B ，方向垂直于平行金属导轨所在的平面，一根长金属棒与导轨成θ角放置，金属棒与导轨电阻不计.当金属棒沿垂直于棒的方向，以恒定速度v 在金属导轨上滑行时，通过电阻的电流强度为；电阻R 上的发热功率为；拉力的机械功率为.【审题】导体棒做切割磁感线活动，导体棒两端发生的感应电动势相当于闭合回路的电源，所以题中R 是外电阻，金属棒为电源且电源内阻不计.因为金属棒切割磁感线时，B 、L 、v 两两垂直，则感应电动势可直接用E=Blv 求解，从而求出感应电流和发热功率，又因为金属棒匀速活动，所以拉力的机械功率等于电阻R 上的发热功率，也能够用P=Fv=BILv 求拉力的机械功率.【解析】⑴θsin Bdv BLV E ==∴θsin R Bdv R E I ==⑵θ22222sin R v d B R I P ==热⑶θ2222sin R v d B P P ==热机械或者θθθ2222sin sin sin R v d B v d R Bdv B BILv Fv P ====机械例9：如图7-7所示，两根足够长的直金属导轨MN 、PQ 平行放置在倾角为θ的绝缘斜面上，两导轨间距为L.M 、P 两点间接有电阻值为R 的电阻，一根质量为m 的均匀直金属杆ab放在两导轨上，并与导轨垂直.整套安装处于磁感应强度为B的匀强磁场中，磁场方向垂直斜面向下.导轨和金属杆的电阻可忽略.让ab 杆沿导轨由静止开始下滑，导轨和金属杆接触良好，不计它们之间的摩擦.求：⑴在加速下滑过程中，当ab 杆的速度大小为v 时杆中的电流及杆的加速度大小；图7-图7-⑵鄙人滑过程中，ab 杆可以达到的速度最大值.【审题】根据受力情况还可以判断ab 杆的活动情况，ab 杆下滑过程中速度愈来愈大，安培力F 愈来愈大，其合外力愈来愈小，加速度愈来愈小，当加速度为零时速度最大，所以ab 杆做的是加速度逐步减小的加速活动，最初以最大速度匀速活动.根据ab 杆达最大速度时合外力为零可求其最大速度.【解析】⑴ab 杆的速度为v 时，感应电动势E=BLv ∴R v L B L R BLv B BIL F 22===根据牛顿第二定律，有ma=mgsin θ-F∴mR v L B g a 22sin -=θ⑵当F=mgsin θ时，ab 杆达最大速度v max ，所以22max L B sin mgR v θ=感生电动势与动生电动势同时存在的情况例1（江苏）如图所示，两根平行金属导轨固定在水平桌面上，每根导轨每米的电阻为r 0=0.10 Ω/m ，导轨的端点P 、Q 用电阻可忽略的导线相连，两导轨间的距离l =0.20 m.有随时间变更的匀强磁场垂直于桌面，已知磁感应强度B 与时间t 的关系为B = kt ，比例系数kt =0时刻，金属杆紧靠在P 、Q 端，在外力感化下，杆以恒定的加速度从静止开始导游轨的另一端滑动，求在t =6.0 s 时金属杆所受的安培力.【解1】以a 暗示金属杆活动的加速度，在t 时刻，金属杆与初始地位的距离 L ＝221at此时杆的速度v=at这时候，杆与导轨构成的回路的面积S＝Ll，回路的Blv，而B＝k，回路的总电阻R＝2Lr，回路中的感应电流i感化于杆的安培力F＝Bli 解得F代入数据为F×10－3 N【解2】分析法： F安=BILa 为金属杆的加速度）PQ的距离）知”，请求F安，应求B和I，请求I，应求E和R，慢慢推导，直到应求. 求解过程是：将②、⑤、⑥、⑦代入④求出E将⑨与⑧代入③求出I.将⑩与②代入①得F安最初将已知数据代入得F安=1.44×10-3N【本题的创新处也是易错处在式④式，即发生感应电动势的身分有两个，中未出现过的.因为感生电动势与动生电动势在回路中方向不异，所以总电动势等于二者之和.】例2（广东）如图所示，光滑的平行水平金属导轨MN 、PQ 相距l ，在M 点和P 点间连接一个阻值为R 的电阻，在两导轨间cdfe 矩形区域内有垂直导轨平面竖直向上、宽为d 的匀强磁场，磁感应强度为B .一质量为m 、电阻为r 、长度也刚好为l 的导体棒ab 垂直搁在导轨上，与磁场左鸿沟相距d 0.现用一个水平向右的力F 拉棒ab ，使它由静止开始活动，棒ab 离开磁场前已做匀速直线活动，棒ab 与导轨始终坚持良好接触，导轨电阻不计，F 随ab 与初始地位的距离x 变更的情况如图，F 0已知.求：（1）棒ab 离开磁场右鸿沟时的速度（2）棒ab 通过磁场区域的过程中全部回路所耗费的电能（3）d 0满足什么条件时，棒ab 进入磁场后不断做匀速活动【解】（1）设离开右鸿沟时棒ab 速度为υ，则有 υεBI =，r R I +=ε，对棒有：020=-BIl F ，得：220)(2l B r R F +=υ （2）在ab 棒活动的全部过程中，根据动能定理：02122000-=-+υm W d F d F 安 由功能关系： 安电W E =解得：4422000)(2)2(l B r R mF d d F E +-+=电（3）设棒刚进入磁场时的速度为0υ，则有0212000-=υm d F当υυ=0，即44200)(2l B r R m F d +=时，进入磁场后不断匀速活动.归纳：在同时存在感生电动势与动生电动势的情况下，总电动势等于二者R M N P Q ab c de f d 0 d BF O x F O xF 02F 0 d 0 d 0+d的代数和，二者方向不异时相加，方向相反时相减.须要留意的是，所谓方向不异或相反，是指感应电流在回路中的方向.2010年高考题电磁感应1. 2010·全国卷Ⅱ如图，空间某区域中有一匀强磁场，磁感应强度方向水平，且垂直于纸面向里，磁场上鸿沟b 和下鸿沟d水平.在竖直面内有一矩形金属统一加线圈，线圈上下边的距离很短，下边水平.线圈从水平面a开始着落.已知磁场上下鸿沟之间的距离大于水平面a、b之间的距离.若线圈下边刚通过水平面b、c（位于磁场中）和d时，线圈所受到的磁场力的大小分别为F、c F和d F，则bA．F>c F>b F B. c F<d F<b F C. c F>b F>d F D. c F<b F<d Fd2．2010·江苏物理一矩形线框置于匀强磁场中，线框平面与磁场方向垂直，先坚持线框的面积不变，将磁感应强度在1 s 时间内均匀地增大到本来的两倍，接着坚持增大后的磁感应强度不变，在1 s 时间内，再将线框的面积均匀地减小到本来的一半，前后两个过程中，线框中感应电动势的比值为（B）1 （C）2 （D）4答案：B（A）124.2010·新课标如图所示，两个端面半径同为R的圆柱形铁芯同轴水平放置，绝对的端面之间有一缝隙，铁芯上绕导线并与电源连自在着落，铜棒着落距离为E动势大小为2E，1E、2E的大小和铜棒离开磁场前两端的极1性，以下判断准确的是A、E>2E，a端为正B、1E>2E，b端为正 C、1E<2E，a端为正1D、E<2E，b端为正15. 2010·上海如右图，一有界区域内，存在着磁感应强度大小均为B ，方向分别垂直于光滑水平桌面向下和向上的匀强磁场，磁场宽度均为L ，边长为L 的正方形框abcd 的bc 边紧靠磁场边沿置于桌面上，使线框从静止开始沿x 轴正方向匀加速通过磁场区域，若以逆时针方向为电流的正方向，能反映线框中感应电流变更规律的是图【解析】在0-1t ，电流均匀增大，排除CD.2t ，在1t -2t ，两边感应电流方向不异，大小相加，故电流大.在32~t t ，因右侧离开磁场，只要一边发生感应电流，故电流小，所以选A.6．2010·海南一金属圆环水平固定放置.现将一竖直的条形磁铁，在圆环上方沿圆环轴线从静止开始释放，在条形磁铁穿过圆环的过程中，条形磁铁与圆环（）A ．始终彼此吸引B ．始终彼此排斥C ．先彼此吸引，后彼此排斥D ．先彼此排斥，后彼此吸引【答案】D【解析】由楞次定律可知，当条形磁铁靠近圆环时，感应电流障碍其靠近，是排斥力；当磁铁穿过圆环阔别圆环时，感应电流障碍其阔别，是吸引力，D 准确.8．2010·天津如图所示，质量m 1=0.1kg ，电阻R 1Ω，长度l=0.4m 的导体棒ab 横放在U 型金属框架上.框架质量m 2=0.2kg ，放在绝缘水平面上，与水平面间的动摩擦因数μ’、NN ’彼此平行，电阻不计且足够长.电阻R 2Ω的MN 垂直于MM ’.全部安装处于竖直向上的匀强磁场中，磁感应强度B=0.5T.垂直于ab施加F=2N的水平恒力，ab从静止开始无摩擦地活动，始终与MM’、NN’坚持良好接触，当ab活动到某处时，框架开始活动.设框架与水平面间最大静摩擦力等于滑动摩擦力，g取10m/s2.(1)求框架开始活动时ab速度v的大小；（2）从ab开始活动到框架开始活动的过程中，MN上发生的热量Q=0.1J，求该过程ab 位移x的大小.解析：（12）闭合回9．2010·江苏如图所示，两足够长的光滑金属导轨竖直放置，相距为L, 一理想电流表与两导轨相连，匀强磁场与导轨平面垂直.一质量为m、无效电阻为R的导体棒在距磁场上鸿沟h处静止释放.导体棒进入磁场后，流经电流表的电流逐步减小，终极波动为I.全部活动过程中，导体棒与导轨接触良好，且始终坚持水平，不计导轨的电阻.求：（1）磁感应强度的大小B；（2）电流波动后，导体棒活动速度的大小v；（310．2010·福建如图所示，两条平行的光滑金属导轨固定在倾角为缘斜面上，导轨上端连接一个定值电阻.导体棒a和b放在导轨上，与导轨垂直并良好接触.斜面上水平虚线PQ以下区域内，存在着垂直穿过斜面向上的匀强磁场.现对a棒施以平行导轨斜向上的拉力，使它沿导轨匀速向上活动，此时放在导轨下端的b棒恰好静止.当a棒活动到磁场的上鸿沟PQ 处时，撤去拉力，a棒将继续沿导轨向上活动一小段距离后再向下滑动，此时b棒已滑离导轨.当a棒再次滑回到磁场鸿沟PQ处时，又恰能沿导轨匀速向下活动.已知a棒、b棒和定值电阻的阻值均为R,b棒的质量为m，重力加速度为g，导轨电阻不计.求（1）a棒在磁场中沿导轨向上活动的过程中，a棒中的电流强度I，与定值电阻R中的电流强度I R之比；（2）a棒质量m a;（3）a棒在磁场中沿导轨向上活动时所受的拉力F. 11. 2010·上海如图，宽度L=0.5m的光滑金属框架MNPQ固定板个与水平面内，并处在磁感应强度大小B=0.4T，方向竖直向下的匀强磁场中，框架的电阻非均匀分布，将质量m=0.1kg，电阻可忽略的金属棒ab放置在框架上，而且框架接触良好，以P为坐标原点，PQ方向为x轴正方向建立坐标，金属棒从01x m=处以02/v m s=的初速度，沿x轴负方向做22/a m s=的匀减速直线活动，活动中金属棒仅受安培力感化.求：（1）金属棒ab活动0.5m，框架发生的焦耳热Q；（2）框架中aNPb部分的电阻R随金属棒ab的地位x变更的函数关系；（3）为求金属棒ab沿x轴负方向活动0.4s过程中通过ab的电量q，某同学解法为：先算出金属棒的活动距离s ，和0.4s 时回路内的电阻R ，然后代入q=BLs R R ϕ=2'02212222240318.85*10/M BLs R S cm p pal ml m R R q SE c N m E θθϕμμεε-=======⋅求解.指出该同学解法的错误的地方，并用准确的方法解出结果.解析：（1）F a m=，0.2F ma N ==因为活动中金属棒仅受安培力感化，所以F=BIL ，又E BLv I R R ==，所以0.4BLv BLat R t I I ===，且212S at =，得212S t s a ==，所以2220.40.2Q I Rt I t J ==•=（2）221112x at t =-=-，得1t x =-，所以0.41R x =-.（3）错误的地方：因框架的电阻非均匀分布，所求R 是0.4s 时回路内的电阻R ，不是平均值.准确解法：因电流不变，所以c c It q 4.04.01=⨯==.12. 2010·北京·19在如图所示的电路中，两个不异的小灯泡L 1和L 2分别串联一个带铁芯的电感线圈L 和一个滑动变阻器R .闭合开关S 后，调整R ，使L 1和L 2发光的亮度一样，此时流过两个灯泡的电流均为I .然后，断开S.若t 时刻再闭合S ，则在t 前后的一小段时间内，准确反映流过L 1的电流 i 1、流过L 2的电流i 2随时间t 变更的图像是A ．B ．C ．D ．答案；B13. 2010·江苏如图所示的电路中，电源的电动势为E,内阻为r,电感L 的电阻不计，电阻R 的阻值大于灯泡D 的阻值，在t=0时刻闭合开关S,经过一段时间后，在t=t 1时刻断开S,以下暗示A 、B 两点间电压U AB 随时间t变更的图像中，准确的是答案；B14.2010·全国×10-5T.一灵敏电压表连接在当地入海河段的两岸，河宽100m，该河段退潮和落潮时有海水（视为导体）流过.设落潮时，海水自西向东流，流速为2m/s.以下说法准确的是A．电压表记录的电压为5mV B．电压表记录的电压为9mVC．河南岸的电势较高D．河北岸的电势较高【答案】B、D15.2010·山东如图所示，空间存在两个磁场，磁感应强度大小均为B，方向相反且垂直纸面，MN、PQ为其鸿沟，OO′为其对称轴一导线折成边长为l的正方形闭合加在路abcd，回路在纸面内以恒定速度0v向右活动，叵活动到关于OO′对称的地位时BlvA．穿过回路的磁通量为零B．回路中感应电动势大小为20C．回路中感应电流的方向为顺时针方向D．回路中ab边与cd边所受安培力方向不异【答案】A、B、D16.2010·广东如图5所示，平行导轨间有一矩形的匀强磁场区域，细金属棒PQ沿导轨从MN处匀速活动到M'N'的过程中，棒上感应电动势E 随时间t 变更的图示，可能准确的是【答案】A 17.2010·安徽如图所示，水平地面上方矩形区域内存在垂直纸面向里的匀强兹场，两个边长相等的单线闭合正方形线I 和Ⅱ，分别用不异材料，分歧组细的导线绕制（I 为细导线）.两线圈在距兹场上界面h 高处由静止开始自在着落，再进入兹场，最初落到地面.活动过程中，线圈平面始终坚持在整直平面内且下边沿平行于磁场上功界.设线圈I 、Ⅱ落地时的速度大小分别为y 1、y 2在磁场中活动时发生的热量分别为Q 1、Q 2，不计空气阻力则A ．v 1<v 2,Q 1<Q 2B ．v 1=v 2,Q 1=Q 2C ．v 1<v 2,Q 1>Q 2D ．v 1=v 2,Q 1<Q 2【答案】D18.2010·四川如图所示，电阻不计的平行金属导轨固定在一绝缘斜面上，两不异的金属导体棒a 、b 垂直于导轨静止放置，且与导轨接触良好，匀强磁场垂直穿过导轨平面.现用一平行于导轨的恒力F 感化在a 的中点，使其向上活动.若b 始终坚持静止，则它所受摩擦力可能A ．变成0B . 先减小后不变C . 等于FD ．先增大再减小【答案】AB【解析】对a 棒所受合力为Blv mg F F F f a---=θsin 说明a 做加速度减小的加速活动，当加速度为0后匀速活动，所以a 所受安培力先增大后不变.如果θsin 2mg F F f +=，则最大安培力为θsin mg ，则b 所受摩擦力最初为0，A 准确.如果θsin 2mg F F f +〈，则最大安培力小于θsin mg ，则b 所受摩擦力不断减小最初不变，B准确.b所受摩擦力先减小后增大最初不变.可以看出b所受摩擦力先变更后不变，C D错误.。