单位根检验
- 格式:doc
- 大小:355.00 KB
- 文档页数:4

单位根检验单位根检验是一种用于检验指数时间序列是否稳定的方法。
在经济学中,许多变量都是随时间变化的,如股票价格、货币汇率、通货膨胀率等,而这些变量都可以被视为时间序列。
但是,这些时间序列是否稳定是一个重要的问题。
因为如果一个时间序列是不稳定的,那么它的预测结果就是不可靠的。
什么是单位根?单位根是指一个数学方程中的根等于1的根。
在统计学中,我们通常使用单位根来检验时间序列的稳定性。
如果时间序列有一个单位根,那么它就是不稳定的。
因此,我们需要通过时间序列的单位根检验来确定它是否是稳定的。
单位根检验是基于一个叫做“随机游走”的经济学理论的基础上的。
随机游走是指一个随机变量在未来的状态完全是随机的。
如果一个时间序列是随机游走的,那么它就是不稳定的。
因此,我们需要通过检验这个序列是否是随机游走来确定它是否是稳定的。
单位根检验的主要步骤如下:第一步:确定时间序列的类型。
我们需要确定这个时间序列的具体类型,是属于随机游走类型还是平稳类型,或者是介于两者之间的。
第二步:选择一种统计方法进行检验。
单位根检验有许多种不同的方法,每种方法都基于不同的假设。
第三步:计算检验统计量。
根据所选的统计方法,我们需要计算出检验统计量的值,然后与临界值进行比较。
第四步:做出结论。
如果检验统计量的值小于临界值,那么我们可以拒绝原假设,说明时间序列是稳定的;如果检验统计量的值大于临界值,那么我们接受原假设,说明时间序列是不稳定的。
常用的单位根检验方法包括ADF检验、PP检验,以及KPSS检验。
ADF检验ADF检验全称为“Augmented Dickey-Fuller test”。
这种检验方法用于检查一个时间序列是否具有单位根,并且可以给出序列是否是平稳序列的信息。
ADF检验的步骤如下:第一步:设定模型。
ADF模型可以通过以下方式表示:$\Delta Y_t=a+bY_{t-1}+\sum_{i=1}^{k-1}\delta\Delta Y_{t-i}+u_t $其中,$\Delta$表示差分运算符,$Y_t$表示时间序列,$k$表示差分的阶数,$u_t$是一个随机变量。

第2节 单位根检验由于虚假回归问题的存在,因此检验变量的平稳性是一个必须解决的问题。
在第十二章中介绍用相关图判断时间序列的平稳性。
这一章则给出序列平稳性的严格的统计检验方法,即单位根检验。
单位根检验有很多方法,这里主要介绍DF 和ADF 检验。
序列均值为0则无C ,序列无时间趋势则无trend在介绍单位根检验之前,先认识四种典型的非平稳随机过程。
1、四种典型的非平稳随机过程 (1)随机游走过程。
y t = y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) 其均值为零,方差无限大(?),但不含有确定性时间趋势。
(见图1a )。
-10-551020406080100120140160180200y=y(-1)+u12001400160018002000220050100150200250300图1a 由y t = y t -1+ u t 生成的序列 图1b 深证成指(2)随机趋势过程。
y t = α + y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) 其中α称作位移项(漂移项)。
由上式知,E(y 1)= α(过程初始值的期望)。
将上式作如下迭代变换,y t = α + y t -1 + u t = α+ (α+ y t -2 + u t -1) + u t = … = αt +y 0 +∑-ti i u 1y t 由确定性时间趋势项αt 和y 0 +∑-t i i u 1组成。
可以把y 0 +∑-ti i u 1看作随机的截距项。
在不存在任何冲击u t 的情况下,截距项为y 0。
而每个冲击u t 都表现为截距的移动。
每个冲击u t 对截距项的影响都是持久的,导致序列的条件均值发生变化,所以称这样的过程为随机趋势过程(stochastic trend process ),或有漂移项的非平稳过程(non-stationary process with drift ),见图2,虽然总趋势不变,但随机游走过程围绕趋势项上下游动。

单位根检验的方法主要有以下几种:
1. ADF检验:即Augmented Dickey-Fuller检验,是对Dickey-Fuller检验的扩展,可以处理含有高阶滞后项的时间序列数据。
它通过在回归模型中加入差分滞后项来控制序列相关的干扰。
2. PP检验:即Phillips-Perron检验,与ADF检验类似,但使用非参数方法来修正序列相关的问题,对小样本性质有一定的改进。
3. KPSS检验:即Kwiatkowski-Phillips-Schmidt-Shin检验,是一种基于平稳序列的检验方法,原假设是序列是平稳的,而备择假设是序列存在单位根。
4. ERS检验:即Elliott-Rothenberg-Stock检验,是一种基于误差修正模型的单位根检验方法,适用于存在长期均衡关系的非平稳时间序列。
5. NP检验:即Nelson-Plosser检验,是一种专门用于检验宏观经济时间序列是否存在单位根的方法。
6. DF-GLS检验:即Dickey-Fuller Generalized Least Squares检验,是一种改进的Dickey-Fuller检验,使用广义最小二乘法来估计模型参数,以提高检验的功效。
7. 霍尔斯检验:即Hall测试,也是一种单位根检验方法,主要用于检测分数整合的存在。
8. 其他检验:还有一些其他的单位根检验方法,如Fisher类型的检验、Maddala-Wu检验等,它们在不同的情况下有各自的适用性和优势。

adf检验通俗解释
ADF检验,即单位根检验(Augmented Dickey-Fuller Test),是一种经济学时间序列分析中常用的统计方法。
它用来判断一个时间序列数据是否存在单位根,即是否存在趋势。
通俗地说,单位根检验用来判断时间序列数据的变化趋势是否随机性的,或者说是否存在长期趋势。
如果数据存在长期趋势,就不能用简单的方法进行分析和预测,因为数据变化是有规律的。
而单位根检验可以帮助我们识别数据是否存在长期趋势,从而选择合适的模型来进行进一步分析。
ADF检验的思路是将时间序列数据拆分成趋势项、季节项、残差项等不同部分,然后分别对这些部分进行统计检验。
如果残差项(即剔除了趋势项和季节项后的数据)不存在单位根,那么我们可以认为原始数据也不存在单位根,即没有长期趋势。
通过ADF检验,我们可以得到一个统计量,根据这个统计量的显著性水平,来判断时间序列是否存在单位根。
如果统计量的值小于某个阈值,即p值小于显著性水平,那么我们可以拒绝存在单位根的假设,认为数据不存在长期趋势。
总之,ADF检验是一种用来判断时间序列数据是否存在长期趋势的方法,通过检验序列的残差项是否存在单位根,来判断原始数据是否存在单位根。


什么是单位根检验如何进行单位根检验单位根检验是时间序列分析中常用的一种方法,用于判断一个序列是否具有单位根。
本文将介绍单位根检验的概念及其常见方法,并详细说明如何进行单位根检验。
一、单位根检验的概念单位根检验是用来判断一个时间序列数据是否具有单位根的方法。
单位根是指时间序列中的随机游走部分,即序列具有无界的随机性。
如果一个序列是单位根序列,那么它的均值和方差都会随着时间的推移而改变,无法稳定在一个特定的水平上。
单位根检验是为了验证时间序列是否平稳而进行的,平稳序列的均值和方差在时间推移的过程中是固定的,与时间无关。
二、如何进行单位根检验常见的单位根检验方法包括ADF检验(Augmented Dickey-Fuller Test)和KPSS检验(Kwiatkowski–Phillips–Schmidt–Shin Test)。
ADF检验是一种常用的单位根检验方法,它的原假设是序列具有单位根,即非平稳;备择假设是序列是平稳的。
ADF检验会利用时间序列的滞后项来估计单位根系数,进而进行假设检验。
KPSS检验则是另一种常用的单位根检验方法,它的原假设是序列是平稳的;备择假设是序列具有单位根,即非平稳。
KPSS检验会计算序列的累积和,通过比较它与滞后项的关系来判断序列是否具有单位根。
在进行单位根检验时,一般需要确定检验的滞后阶数和选择合适的检验统计量。
通常会根据样本的性质和经验来选择合适的参数。
三、进行单位根检验的步骤下面将以ADF检验为例,介绍进行单位根检验的具体步骤。
1. 收集时间序列数据,确保数据已经按照时间顺序排列。
2. 导入统计软件,比如R或Python等,加载相关的统计函数库。
3. 指定滞后阶数。
根据样本的特点和经验选择合适的滞后阶数,一般建议初始滞后阶数为1或者自动选择。
4. 进行ADF检验,并取得检验统计量的值。
统计软件会输出检验统计量的值,一般为负数,可以与相应的临界值进行比较。
5. 进行假设检验。

第4章 单位根检验4.1 DF 分布由于虚假回归问题的存在,在回归模型中应避免直接使用非平稳变量。
因此检验变量的平稳性是一个必须解决的问题。
在第二章中介绍用相关图判断时间序列的平稳性。
这一章则给出严格的统计检验方法,即单位根检验。
在介绍检验方法之前,先讨论所用统计量的分布。
给出三个简单的自回归数据生成过程(d.g.p .), y t =y t -1+u t,y 0=0,u t~IID(0,2)(4.1)y t = μ + y t -1 + u t , y 0 = 0, u t ~ IID(0,2)(4.2)y t = μ + α t + y t -1 + u t , y 0 = 0, u t ~ IID(0,2)(4.3)其中μ 称作位移项(漂移项),α t 称为趋势项。
显然,对于以上三个模型,当< 1时,y t 是平稳的,当= 1时,y t是非平稳的。
以模型 (4.1) 为例,若 = 0,统计量,)ˆ(βt = )ˆ(ˆββs ~ t (T -1) , (4.4)的极限分布为标准正态分布。
若< 1,统计量,)ˆ(βt = )ˆ()ˆ(βββs - (4.5)渐进服从标准正态分布。
根据中心极限定理,当T → ∞ 时, T(Tβˆ- ) → N (0,2(1-2) )(4.6) 那么在= 1条件下,统计量 )ˆ(βt 服从什么分布呢?当= 1时,变量非平稳,上述极限分布发生退化(方差为零)。
首先观察= 1条件下,数据生成系统(4.1),(4.2) 和 (4.3)的变化情况。
= 1条件下的(4.1) 式是随机游走过程。
= 1条件下的 (4.2) 式是含有随机趋势项的过程。
将(4.2) 式作如下变换则展示的更清楚。
y t = μ + y t -1 + u t = μ + (μ + y t -2 + u t -1) + u t = … = y 0 + μ t +∑-t i i u 1= μ t + ∑-ti i u 1(4.7)-10-551020406080100120140160180200y=y(-1)+u12001400160018002000220050100150200250300图4.1 由y t = y t -1+ u t 生成的序列 图4.2深圳股票综合指数(file:stock )这是一个趋势项和一个随机游走过程之和。

单整:如果一个时间序列经过一次差分变成平稳的,则称原序列是1阶单整的,记为I(1)。
一般地,如果时间序列经过d次差分后变成平稳序列,则称原序列是d阶单整序列,记为I(d)。
单位根检验:单位根检验是指检验序列中是否存在单位根,因为存在单位根就是非平稳时间序列了.单位根就是指单位根过程,可以证明,序列中存在单位根过程就不平稳,会使回归分析中存在伪回归。
单位根检验是随机过程的问题。
定义随机序列{ x_t},t=1,2,…是一单位根过程,若x_t=ρx_t-1 +ε,t=1,2… 其中ρ=1,{ε }为一平稳序列(白噪声),且E[ε ]=0, V(ε )=σ <∞, Cov(ε ,ε )=μ <∞这里τ=1,2…。
特别地,若{ε}是独立同分布的,且E[ε]=0,V(ε)=σ<∞,则上式就变成一个随机游走序列,因此随机游走序列是一种最简单的单位根过程。
将定义式改写为下列形式:( 1-ρL)x_t =ε,t=1,2,…其中L 为滞后算子,1-ρL为滞后算子多项式,其特征方程为1-ρz=0,有根z= 1/ρ。
当ρ=1时,时间序列存在一个单位根,此时{x_t }是一个单位根过程。
当ρ<1时,{x_t }为[1]。
而当ρ〉1时,{x_t }为一类具有所谓爆炸根的非平稳过程,它经过差分后仍然为非平稳过程,因此不为单整过程。
一般情况下,单整过程可以称作单位根过程。
单位根检验时间序列的单位跟研究是时间序列分析的一个热点问题。
时间序列矩特性的时变行为实际上反映了时间序列的非平稳性质。
对非平稳时间序列的处理方法一般是将其转变为平稳序列,这样就可以应用有关平稳时间序列的方法来进行相应得研究。
对时间序列单位根的检验就是对时间序列平稳性的检验,非平稳时间序列如果存在单位根,则一般可以通过差分的方法来消除单位根,得到平稳序列。
对于存在单位根的时间序列,一般都显示出明显的记忆性和波动的持续性,因此单位根检验是有关协整关系存在性检验和序列波动持续性讨论的基础。
第6讲 单位根检验由于虚假回归问题的存在,在回归模型中应避免直接使用不存在协积关系的非平稳变量。
因此检验变量的平稳性是一个必须解决的问题。
在第二章中介绍用相关图判断时间序列的平稳性。
这一章则给出序列平稳性的严格的统计检验方法,即单位根检验。
在介绍单位根检验之前,先认识四种典型的非平稳随机过程。
4.1 四种典型的非平稳随机过程 (1)随机游走过程。
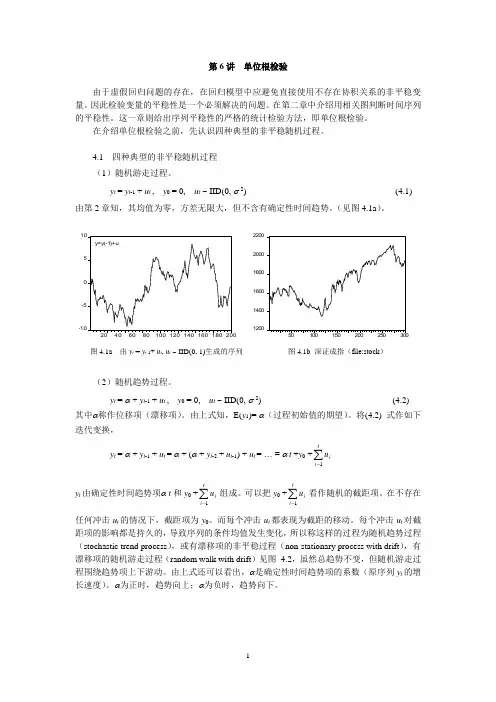
y t = y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) (4.1) 由第2章知,其均值为零,方差无限大,但不含有确定性时间趋势。
(见图4.1a )。
-10-551020406080140160y=y(-1)+u120014001600180020002200图4.1a 由y t = y t -1+ u t , u t ~ IID(0, 1)生成的序列 图4.1b 深证成指(file:stock )(2)随机趋势过程。
y t = α + y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) (4.2) 其中α称作位移项(漂移项)。
由上式知,E(y 1)= α(过程初始值的期望)。
将(4.2) 式作如下迭代变换,y t = α + y t -1 + u t = α + (α + y t -2 + u t -1) + u t = … = α t +y 0 +∑-ti i u 1y t 由确定性时间趋势项α t 和y 0 +∑-ti i u 1组成。
可以把y 0 +∑-ti i u 1看作随机的截距项。
在不存在任何冲击u t 的情况下,截距项为y 0。
而每个冲击u t 都表现为截距的移动。
每个冲击u t 对截距项的影响都是持久的,导致序列的条件均值发生变化,所以称这样的过程为随机趋势过程(stochastic trend process ),或有漂移项的非平稳过程(non-stationary process with drift ),有漂移项的随机游走过程(random walk with drift )见图 4.2,虽然总趋势不变,但随机游走过程围绕趋势项上下游动。

单位根检验原理
单位根检验原理指的是一种检验时间序列稳定性的方法,它通过检验时间序列是否存在单位根来判断该序列是否具有平稳性。
单位根检验原理的核心是检验序列是否具有随机游走特征,如果序列具有随机游走特征,那么该序列将不具有平稳性。
因此,在时间序列分析中,单位根检验是一种非常重要的方法,它可以帮助分析者判断时间序列的平稳性,从而选择合适的时间序列模型进行预测和分析。
在实践中,常用的单位根检验方法包括ADF检验、Phillips-Perron检验、KPSS 检验等。
- 1 -。
第八章 单位根检验由于非平稳过程可能存在严重的伪回归问题,所以在对序列进行估计之前,需要检验序列的平稳性。
本章介绍了严格的平稳性的统计检验方法--单位根检验。
在简要介绍四种主要的非平稳随机过程以产输出单位根检验原理之后,文章主要介绍ADF 检验及PP 检验法,以及介结构突变和单位根检验。
8.1 四种典型非平稳过程简介前面我们知道,若一个时间序列含有某种变动趋势,即该序列的均值或自协方差函数随时间而改变,则称该序列为非平稳序列。
下面介绍四种典型的非平稳过程。
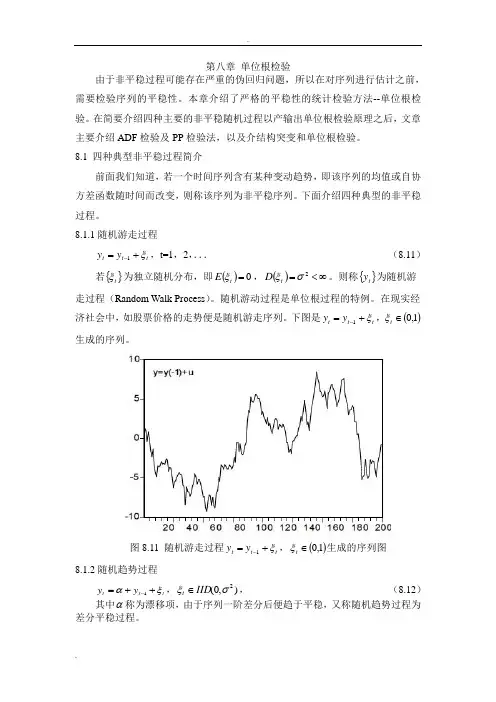
8.1.1随机游走过程t t t y y ξ+=-1,t=1,2,... (8.11) 若}{t ξ为独立随机分布,即()0=t E ξ,()∞<=2σξt D 。
则称}{t y 为随机游走过程(Random Walk Process )。
随机游动过程是单位根过程的特例。
在现实经济社会中,如股票价格的走势便是随机游走序列。
下图是t t t y y ξ+=-1,()1,0∈t ξ生成的序列。
图8.11 随机游走过程t t t y y ξ+=-1,()1,0∈t ξ生成的序列图8.1.2随机趋势过程t t t y y ξα++=-1,),0(2σξIID t ∈, (8.12)其中α称为漂移项,由于序列一阶差分后便趋于平稳,又称随机趋势过程为差分平稳过程。
图8.12 t t t y y ξ++=-11.0,()1,0∈t ξ生成的序列8.1.3趋势平稳过程t t t y ξβα++= ,其中t t t νρξξ+=-1,1<ρ,),0(2σν∈t (8.13)由于t t t y ξαβ+=-,即当减去退势后为平稳过程,故趋势平稳过程又称为退势平稳过程。
由t t t y ξβα++=,t t t νρξξ+=-1知:11)1(--+-+=t t t y ξβα (8.14)将(4)两边同时乘以ρ,与(3)两边同时相减,整理可得:t t t y t y νρβα+++=-1'' , ),0(2σν∈t (8.15)其中,ρβρααα+-=',ρβρβ-='这样便得出趋势平稳过程的另一种形式。
单位根检验和协整检验单位根检验和协整检验是时间序列分析中常用的两种方法。
本文将分别介绍这两种检验方法的概念、原理和应用。
一、单位根检验1.概念单位根检验,又称为ADF(Augmented Dickey-Fuller)检验,是一种用于判断时间序列是否具有平稳性的方法。
它的基本原理是通过对时间序列进行一定程度的差分,使得序列变得平稳,从而判断序列是否具有单位根。
2.原理在时间序列中,如果一个变量具有单位根,则说明它在长期内存在趋势或者周期性波动。
而如果一个变量具有平稳性,则说明它在长期内不存在趋势或者周期性波动。
因此,通过对时间序列进行差分,可以消除其中的趋势或者周期性波动,使得序列变得平稳。
ADF检验的基本原理就是通过比较差分后的时间序列与原始时间序列之间的关系来判断是否存在单位根。
具体地说,在ADF检验中,我们需要假设一个线性回归模型:ΔYt = α + βt + γYt-1 + δ1ΔYt-1 + … + δpΔYt-p + εt其中,Δ表示差分符号;Yt表示时间序列;α、β、γ、δ1~δp和εt分别表示回归系数和误差项。
如果该模型中的γ等于0,则说明时间序列具有单位根,即存在趋势或者周期性波动;如果γ小于0,则说明时间序列具有平稳性,即不存在趋势或者周期性波动。
3.应用ADF检验通常用于判断时间序列是否具有平稳性。
在金融领域中,它常被用于股票价格的分析和预测。
例如,通过对股票价格进行ADF检验,可以判断该股票是否处于上涨或下跌趋势,并进一步预测未来的走势。
二、协整检验1.概念协整检验是一种用于判断两个或多个时间序列之间是否存在长期稳定的关系的方法。
它的基本原理是通过构建线性组合,使得两个或多个时间序列之间的关系变得平稳。
2.原理在协整检验中,我们需要假设一个线性组合模型:Yt = α + βXt + εt其中,Yt和Xt分别表示两个时间序列;α、β和εt分别表示回归系数和误差项。
如果该模型中的β等于0,则说明Yt和Xt之间不存在长期稳定的关系;如果β不等于0,则说明Yt和Xt之间存在长期稳定的关系,即它们是协整的。
单位根检验法单位根检验法是一种统计方法,用于检验时间序列数据是否具有单位根。
单位根表示时间序列中的变量存在随机游走的趋势,即序列呈现非平稳性。
单位根检验的目的是验证序列是否平稳,因为平稳性对于许多时间序列分析方法的有效性至关重要。
常用的单位根检验方法包括:ADF检验(Augmented Dickey-Fuller test):ADF检验是一种常用的单位根检验方法之一,它基于Dickey-Fuller检验,通过扩展模型以处理序列中的自相关性问题。
ADF检验的原假设是序列存在单位根,备择假设是序列是平稳的。
如果检验统计量小于一定的临界值,我们就可以拒绝原假设,认为序列是平稳的。
PP检验(Phillips-Perron test):PP检验也是一种基于Dickey-Fuller 检验的单位根检验方法,它通过对序列进行回归分析来检验序列的平稳性。
与ADF检验相比,PP检验的计算方式略有不同,但原理和假设检验的思想是相似的。
KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin test):KPSS检验与ADF检验相反,它的原假设是序列是平稳的,备择假设是序列存在单位根。
如果检验统计量小于临界值,我们就可以接受原假设,认为序列是平稳的。
DF-GLS检验(Dickey-Fuller Generalized Least Squares test):DF-GLS 检验是ADF检验的一种泛化形式,它允许序列中的误差项存在序列相关性。
与ADF检验相比,DF-GLS检验在处理序列中的自相关性方面更加准确。
这些单位根检验方法在实践中经常用于验证时间序列数据的平稳性,从而为后续的时间序列分析提供可靠的基础。
在进行单位根检验时,需要注意选择合适的检验方法,并结合实际问题和数据特点进行分析和判断。
一、单位根检验面板数据增强了稳定性,但是也需要进行单位根检验。
面板数据单位根检验有四种方法:1、LLC检验需要安装命令search levinlin, net ,要求各截面单元具有同质性,H0:具有单位根命令:levinlin varname ,lags(n)2、IPS检验安装命令search ipshin, net,各截面存在异质单位根H0:具有单位根命令:ipshin varname ,lags(n)3、fisher ADF检验;命令:xtfisher varname ,lags(n) 对统计量样本容量和滞后期较为稳健,并且适用于非平衡面板数据4、fisher PP检验命令:xtfisher varname ,lags(n) pp N较大时必须对P进行修正,即为fisher PP test以上各种,还可以加入trend,时间趋势项。
加入存在单位根需要差分后再检验。
差分即注意:以上各种在使用前均需要xtset设置好面板数据。
help xtunitroot 默认带有截距项二、协整检验1、在Stata中对面板数据进行协整检验的命令是xtwest,命令安装ssc install xtwest命令:xtwest depvar varlist [if exp] [in range] , lags(# [#]) leads(# [#])具体使用时可以help通过了协整检验,说明变量之间存在着长期稳定的均衡关系,其方程回归残差是平稳的。
因此可以在此基础上直接对原方程进行回归,此时的回归结果是较精确的。
三、长面板的处理%长面板N相对较小,T相对较大,扰动项不一定服从iid分布,需要估计扰动项的具体形式,然后使用广义最小二乘法(FGLS)进行估计。
长面板数据关注的焦点在于设定扰动项相关的具体形式,用于提高估计的效率。
在对长面板估计时需要确定是否存在异方差或者自相关,因此需要进行检验。
1、组间异方差的检验quietly xtgls laddindu huil other ,igls panel(het)est store heteroquietly xtgls laddind huil other ,iglsest store homolocal df=e(N_g)-1lrtest hetero homo,df(`df')2)xttest3也用于组间异方差的检验。
单位根检验和协整检验一、单位根检验的概念和原理单位根检验是时间序列分析的重要工具,在经济学中广泛应用于研究时间序列数据的平稳性。
它用来判断一个时间序列是否具有单位根的存在,单位根表示一个时间序列具有非平稳的特性。
单位根检验的原理是基于自回归模型(Autoregressive Model,简称AR模型)。
AR模型是一种常用的时间序列分析模型,它假设当前观测值与过去的p个观测值存在线性关系。
在单位根检验中,通常使用的是ADF检验(Augmented Dickey-Fuller Test)和KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin Test)。
ADF检验是一种常用的单位根检验方法,它基于Dickey-Fuller单位根检验,并对原检验方法进行扩展和改进。
ADF检验的原假设是存在单位根,备择假设是不存单位根。
通过ADF检验的结果,可以判断一个时间序列是否平稳。
KPSS检验是另一种常用的单位根检验方法,它的原假设是存在单位根,备择假设是不存单位根。
KPSS检验的结果与ADF检验相反,当p值小于显著性水平时,拒绝存在单位根的原假设,即序列是平稳的。
二、单位根检验的应用场景单位根检验在经济学中有着广泛的应用场景。
以下是一些常见的应用场景:1.金融市场:单位根检验可用于判断金融市场的收益率时间序列数据是否具有平稳性。
平稳的收益率序列可以用于构建有效的投资组合和预测股票价格。
2.宏观经济:在宏观经济分析中,单位根检验可用于判断经济增长率、失业率等变量是否具有平稳性。
平稳的经济变量序列可以提供有效的经济政策参考。
3.国际贸易:单位根检验可用于判断国际贸易量和汇率等变量是否具有平稳性。
平稳的贸易量和汇率序列对于制定贸易政策和汇率政策具有重要意义。
三、协整检验的概念和原理协整检验是单位根检验的一种推广,它用于判断两个或多个时间序列之间是否存在长期均衡关系。
协整关系表示两个或多个时间序列的线性组合是平稳的,即它们在长期内是相互影响的。
多元回归单位根检验一、引言多元回归单位根检验是经济学中一种常用的检验方法,用于检验多个自变量是否存在单位根。
单位根表示时间序列变量具有非平稳性,而多元回归单位根检验则可以帮助我们确定自变量是否适合用于时间序列回归分析。
本文将介绍多元回归单位根检验的基本原理和步骤,并针对其应用进行详细阐述。
二、多元回归单位根检验的原理单位根检验是时间序列分析中的一项重要工作,用于判断时间序列数据是否具有非平稳性。
对于多元回归模型,我们通常使用ADF(Augmented Dickey-Fuller)检验来进行单位根检验。
ADF检验的基本原理是通过对时间序列模型进行多次回归,判断残差序列是否存在单位根。
三、多元回归单位根检验的步骤1. 收集数据:首先,我们需要收集相关自变量和因变量的时间序列数据。
确保数据的完整性和准确性,避免数据缺失或错误。
2. 构建模型:根据研究问题和数据特点,构建多元回归模型。
确定自变量和因变量,并进行模型的设定。
3. 进行回归分析:利用所选的多元回归模型,对数据进行回归分析。
计算回归系数和残差序列。
4. 进行ADF检验:对残差序列进行ADF检验,判断残差序列是否存在单位根。
若残差序列不存在单位根,则说明自变量是平稳的;若残差序列存在单位根,则说明自变量是非平稳的。
5. 解释结果:根据ADF检验的结果,解释自变量的平稳性。
如果自变量是平稳的,说明可以进行时间序列回归分析;如果自变量是非平稳的,说明需要进行差分处理或采取其他方法进行调整。
四、多元回归单位根检验的应用多元回归单位根检验在经济学研究中具有广泛的应用。
例如,在宏观经济学中,可以使用多元回归单位根检验来分析经济增长和收入分配等问题;在金融学中,可以使用多元回归单位根检验来研究股票价格和利率等变量的关系。
多元回归单位根检验也可以用于交叉领域的研究。
例如,在环境经济学中,可以使用多元回归单位根检验来分析环境污染和经济增长之间的关系;在教育经济学中,可以使用多元回归单位根检验来研究教育投资和劳动力市场的关系。
Exogenous: Constant, Linear TrendLag Length: 2 (Automatic - based on SIC, maxlag=13)t-StatisticProb.*Augmented Dickey-Fuller test statistic -1.605700 0.7863Test critical values:1% level-4.0216915% level -3.44068110% level -3.144830*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test Equation Dependent Variable: D(Y)Method: Least SquaresDate: 11/12/14 Time: 23:32Sample (adjusted): 4 150Included observations: 147 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob. Y(-1)-0.0196270.012223-1.6057000.1106D(Y(-1))0.2535480.081530 3.1098870.0023D(Y(-2))0.2146390.081798 2.6240080.0096C4.074679 2.403364 1.6954070.0922@TREND("1")0.0088840.0060791.4612690.1462R-squared0.148873 Mean dependent var 0.430612Adjusted R-squared 0.124898 S.D. dependent var 1.450725S.E. of regression 1.357109 Akaike info criterion 3.482012Sum squared resid 261.5277 Schwarz criterion 3.583727Log likelihood -250.9279 Hannan-Quinn criter. 3.523340F-statistic6.209410 Durbin-Watson stat 2.054851Prob(F-statistic)0.000124Lag length:2 即滞后阶数为2,则初始估计模型为0111122t t t t Y c c t Y Y Y λββ---∆=+++∆+∆因为ADF 的t=-1.6057> 5%level 的t=-3.440681,所以接受H 0,即存在单位根。
(或因为p=0.7863>α=0.05,所以接受H 0,即存在单位根。
)又因为@TREND(“1”)的p=0.1462>α=0.05,所以接受H 0,即c 1显著为0。
则模型改为011122t t t t Y c Y Y Y λββ---∆=++∆+∆Exogenous: ConstantLag Length: 2 (Automatic - based on SIC, maxlag=13)t-StatisticProb.*Augmented Dickey-Fuller test statistic -0.663786 0.8513Test critical values:1% level-3.4751845% level -2.88112310% level -2.577291*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test Equation Dependent Variable: D(Y)Method: Least SquaresDate: 11/12/14 Time: 23:38Sample (adjusted): 4 150Included observations: 147 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob. Y(-1)-0.0035350.005326-0.6637860.5079D(Y(-1))0.2496220.081808 3.0513070.0027D(Y(-2))0.2042410.081811 2.4964990.0137C1.0521581.2286900.8563250.3933R-squared0.136074 Mean dependent var 0.430612Adjusted R-squared 0.117950 S.D. dependent var 1.450725S.E. of regression 1.362485 Akaike info criterion 3.483332Sum squared resid 265.4604 Schwarz criterion 3.564704Log likelihood -252.0249 Hannan-Quinn criter. 3.516394F-statistic7.507838 Durbin-Watson stat 2.046101Prob(F-statistic)0.000106因为ADF 的t=-0.663786> 5%level 的t=-2.881123,所以接受H 0,即存在单位根。
(或因为p=0.8513>α=0.05,所以接受H 0,即存在单位根。
) 又因为C 的p=0.3933>α=0.05,所以接受H 0,即c 0显著为0。
则模型改为11122t t t t Y Y Y Y λββ---∆=+∆+∆Exogenous: NoneLag Length: 2 (Automatic - based on SIC, maxlag=13)t-StatisticProb.*Augmented Dickey-Fuller test statistic 1.940255 0.9875Test critical values:1% level-2.5807885% level -1.94301210% level -1.615270*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test Equation Dependent Variable: D(Y)Method: Least SquaresDate: 11/13/14 Time: 18:53Sample (adjusted): 4 150Included observations: 147 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob. Y(-1)0.0010040.000517 1.9402550.0543D(Y(-1))0.2492900.081732 3.0501040.0027D(Y(-2))0.2011300.0816552.4631830.0149R-squared0.131644 Mean dependent var 0.430612Adjusted R-squared 0.119584 S.D. dependent var 1.450725S.E. of regression 1.361223 Akaike info criterion 3.474841Sum squared resid 266.8216 Schwarz criterion 3.535870Log likelihood-252.4008 Hannan-Quinn criter. 3.499638Durbin-Watson stat2.043355因为ADF 的t=1.940255> 5%level 的t=-1.943012,所以接受H 0,即存在单位根。
(或因为p=0.9875>α=0.05,所以接受H 0,即存在单位根。
) 所以模型:11122t t t t Y Y Y Y λββ---∆=+∆+∆Exogenous: Constant, Linear TrendLag Length: 1 (Automatic - based on SIC, maxlag=13)t-Statistic Prob.*Augmented Dickey-Fuller test statistic-5.739450 0.0000 Test critical values:1% level-4.0216915% level-3.44068110% level-3.144830*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(Y,2)Method: Least SquaresDate: 11/12/14 Time: 23:41Sample (adjusted): 4 150Included observations: 147 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.D(Y(-1))-0.5510030.096003-5.7394500.0000D(Y(-1),2)-0.2007290.081786-2.4543200.0153 C0.2336790.233654 1.0001070.3189 @TREND("1")8.93E-050.0026530.0336640.9732R-squared0.371186 Mean dependent var0.004082 Adjusted R-squared0.357994 S.D. dependent var 1.703054 S.E. of regression 1.364577 Akaike info criterion 3.486400 Sum squared resid266.2762 Schwarz criterion 3.567773 Log likelihood-252.2504 Hannan-Quinn criter. 3.519463 F-statistic28.13737 Durbin-Watson stat 2.043400 Prob(F-statistic)0.000000对初始模型进行1阶差分后进行分析:因为ADF的p=0.0000<α=0.05,所以拒绝原假设H0,即不存在单位根。