第四章 四元数正态分布

《正态分布》讲义在统计学中，正态分布是一种极其重要的概率分布，它在自然科学、社会科学、工程技术等众多领域都有着广泛的应用。

下面，让我们一起来深入了解正态分布。

一、什么是正态分布正态分布，也被称为高斯分布，是一种连续型概率分布。

它的概率密度函数呈现出一种独特的“钟形”曲线，具有对称性。

从数学表达式上看，正态分布的概率密度函数为：＼ f(x) ＝＼frac{1}｛＼sigma ＼sqrt{2\pi}｝ e^｛＼frac{（x ＼mu)＾2}｛2\sigma^2}｝＼其中，＼（＼mu\）是均值，决定了曲线的位置；＼（＼sigma\）是标准差，决定了曲线的“胖瘦”程度。

二、正态分布的特点1、对称性正态分布曲线以均值\（＼mu\）为对称轴，左右两侧对称。

这意味着在均值两侧相同距离处，出现观测值的概率相等。

2、集中性大部分数据集中在均值附近，离均值越远，数据出现的概率越小。

3、均值和中位数、众数相等这三个统计量在正态分布中是重合的，反映了数据的中心趋势。

4、标准差的作用标准差\（＼sigma\）越大，曲线越“胖”，数据的分散程度越大；标准差越小，曲线越“瘦”，数据越集中。

三、正态分布的产生原因为什么在现实世界中会有如此多的现象符合正态分布呢？1、大量独立随机因素的综合作用许多自然和社会现象受到众多微小、相互独立的随机因素的影响。

例如，人的身高受到遗传、营养、环境等多种因素的影响，当这些因素的数量足够多且相互独立时，最终的结果往往呈现正态分布。

2、中心极限定理根据中心极限定理，当从一个总体中抽取大量独立同分布的随机样本，并计算其均值时，这些均值的分布将近似于正态分布。

四、正态分布的应用1、质量控制在生产过程中，通过对产品质量特征的测量，如果其符合正态分布，可以设定合理的控制界限，来监控生产过程是否处于稳定状态。

2、考试成绩评估考试成绩通常近似服从正态分布。

教师可以根据正态分布来确定合理的分数段，评估学生的学习情况。

《正态分布》讲义一、什么是正态分布在统计学中，正态分布是一种极其重要的概率分布。

它就像是自然界和人类社会中许多现象的“常客”，无处不在。

想象一下，我们测量一群人的身高，或者记录一段时间内某地区的气温，这些数据往往会呈现出一种特定的规律，这就是正态分布。

正态分布的形状就像一个钟形，中间高，两边逐渐降低并且对称。

这意味着大部分数据集中在平均值附近，而离平均值越远，数据出现的频率就越低。

二、正态分布的特点1、对称性正态分布曲线是关于均值对称的。

也就是说，如果均值是μ，那么在μ 左侧和右侧相同距离处的数据出现的频率是相等的。

2、集中性大部分数据都集中在均值附近。

这反映了在许多情况下，一个典型的或者最常见的值是存在的。

3、均匀变动性从均值向两侧，曲线的下降是均匀的。

这意味着数据的变化是相对平稳和有规律的。

三、正态分布的数学表达式正态分布的概率密度函数可以用下面的公式来表示：f(x) ＝（1 ／（σ √（2π)）） e^（（（x μ)＾2 ／（2σ^2)））在这里，μ 是均值，σ 是标准差，π 是圆周率，e 是自然常数。

这个公式看起来可能有点复杂，但它精确地描述了正态分布的形状和特征。

四、正态分布的应用1、质量控制在生产过程中，例如制造零件，产品的某些质量指标往往服从正态分布。

通过对这些指标的监控和分析，可以判断生产过程是否稳定，是否需要进行调整。

2、考试成绩学生的考试成绩通常也近似符合正态分布。

这有助于教师评估教学效果，确定合理的分数段和等级划分。

3、金融领域股票价格的波动、收益率等常常呈现正态分布的特征。

投资者可以利用这一特点进行风险评估和投资决策。

4、医学研究例如人体的生理指标，如血压、身高体重指数等，很多都符合正态分布。

这对于疾病的诊断和预防具有重要意义。

五、如何计算正态分布的概率为了计算给定区间内的概率，我们通常需要借助数学表或者使用统计软件。

例如，要计算某个值 x 以下的概率，可以通过将 x 标准化为 z 分数：z ＝（x μ) ／σ然后，查找标准正态分布表来获取对应的概率。

正态分布计算方法嘿，咱今儿就来聊聊正态分布计算方法！这正态分布啊，就像是生活中的很多事儿一样，有它自己的规律呢！你看哈，正态分布就像是一群人站成一排，大部分人都在中间，两边的人就比较少。

这中间的“大部队”就是最常见的情况呀！那怎么去算它呢？咱先得搞清楚几个关键的东西。

比如说均值，这就像是这群人的平均位置，是个很重要的参考点呢。

还有标准差，它就像是衡量这群人站得有多开或者多集中的一个指标。

计算正态分布的时候，咱可以想象成在给这些人排队分位置呢。

先找到均值这个中心，然后根据标准差来看看两边的范围有多大。

比如说，咱假设有个正态分布，均值是 50，标准差是 10。

那离均值一个标准差范围内的，不就是 40 到 60 之间嘛。

这一段里的情况就比较常见咯。

然后呢，咱可以通过一些公式来具体算算某个值出现的概率。

这就好像是在问，在这群人里，找到一个特定身高的人的可能性有多大。

哎呀，这正态分布计算方法其实也不难理解嘛，对吧？咱把它想象成生活中的例子，不就好懂多啦！你想想，考试成绩很多时候不就是正态分布嘛！大部分人都在中间的分数段，特别高和特别低的都比较少。

那咱要是会算正态分布，不就能大概知道自己的成绩在整个群体里处于啥位置啦？再比如说，人的身高啊、体重啊，很多也都符合正态分布呢。

咱知道了计算方法，就能更好地了解这些数据背后的意义呀！总之呢，正态分布计算方法虽然听起来有点高大上，但只要咱用心去理解，把它和生活中的例子联系起来，就会发现它其实挺有趣，也挺有用的呢！别被那些公式和概念吓住啦，勇敢地去探索，你肯定能掌握它的！就像咱生活中遇到困难，只要勇敢面对，总能找到解决办法一样！加油吧！。

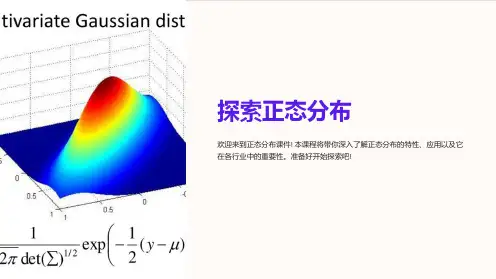
正态分布原理正态分布，又称高斯分布，是概率论和统计学中最重要的连续型概率分布之一。

它具有许多重要的性质，被广泛应用于自然科学、社会科学和工程技术等领域。

正态分布的形状是对称的钟形曲线，其均值、方差和标准差是其分布特征的重要参数。

在实际应用中，正态分布常常被用来描述各种随机变量的分布规律，因此了解正态分布的原理和特点对于数据分析和统计推断具有重要意义。

正态分布的原理可以从多个角度来解释。

首先，从数学角度来看，正态分布是由数学家高斯在研究误差理论时提出的。

它的概率密度函数可以表示为一个关于均值和标准差的函数，其曲线在均值处达到最大值，两侧逐渐下降，呈现出典型的钟形。

这种对称的形状使得正态分布在描述随机变量时具有很好的性质，例如可以方便地计算概率、求解置信区间等。

其次，从统计学角度来看，正态分布在中心极限定理中扮演着重要的角色。

中心极限定理指出，大量独立随机变量的均值的分布趋近于正态分布。

这意味着在很多情况下，当我们对一组随机变量进行统计分析时，可以假设其总体分布近似为正态分布，从而简化了问题的复杂性。

此外，从实际应用的角度来看，正态分布在自然界和社会现象中的广泛存在也为其原理提供了实际基础。

例如，身高、体重、考试成绩等许多现象都呈现出正态分布的特征。

这种普遍性使得正态分布成为了一种重要的模型，可以帮助我们更好地理解和分析现实世界中的各种现象。

总的来说，正态分布的原理涉及数学、统计学和实际应用等多个方面，其重要性不言而喻。

了解正态分布的原理有助于我们更好地理解概率统计的基本概念，提高数据分析和统计推断的能力，为科学研究和实际应用提供有力支持。

因此，对于学习者来说，深入理解正态分布的原理是非常重要的。

在实际应用中，我们可以通过计算机软件进行正态分布的模拟和分析，从而更好地理解其原理和特点。

同时，也可以通过实际数据的分析来验证正态分布在现实中的应用情况，进一步加深对正态分布原理的理解和掌握。

总之，正态分布作为概率论和统计学中的重要概率分布之一，其原理和特点具有重要的理论和应用价值。

正态分布的概念与计算正态分布（Normal Distribution），也称高斯分布（Gaussian Distribution），是概率论与统计学中非常重要的一种连续型概率分布。

它在自然界和人类社会的各个方面都有广泛应用，是描述随机变量分布的重要工具。

本文将介绍正态分布的概念，并说明如何计算正态分布。

一、正态分布的概念正态分布由其概率密度函数来定义，符号表示为：N(N, N²)，其中N为均值，N²为方差。

概率密度函数的形式为：N(N) = 1 / (N√2N) * N^(-((N−N)² / (2N²)))特点：1. 正态分布的图像呈钟形，中心对称，左右两边曲线对称，均值、中位数和众数相等，即N。

2. 在均值处有最高点，随着离均值的距离增加，曲线下降缓慢。

3. 标准差N的大小决定了曲线的陡峭程度，标准差越大，曲线越平缓。

二、正态分布的计算1. 概率密度计算：对于给定的正态分布N(N, N²)，可以通过概率密度函数计算任意N处的概率密度值。

例如，计算某个值N的概率密度，可以使用如下公式：N(N) = 1 / (N√2N) * N^(-((N−N)² / (2N²)))其中，N(N)表示N处的概率密度值。

2. 累积概率计算：对于给定的正态分布N(N, N²)，可以计算N≤ N的累积概率N(N≤ N)。

此时，可以使用标准正态分布表格或统计软件来查找概率值。

3. 标准化与反标准化：在实际计算过程中，常常需要将正态分布转化为标准正态分布，即N(0, 1)。

标准正态分布的均值N为0，方差N²为1。

标准化公式如下：N = (N−N) / N其中，N表示标准化后的值。

反标准化则是将标准正态分布转化为任意正态分布。

反标准化公式如下：N = N + NN4. 百分位数计算：对于给定的正态分布N(N, N²)，可以计算N对应的百分位数。

四级正态分布表1. 什么是正态分布？正态分布，又称为高斯分布，是概率论和统计学中最重要的分布之一。

它以钟形曲线为特征，对称分布于均值周围。

在自然界和社会科学中，许多现象都可以用正态分布来描述，因此它具有广泛的应用。

正态分布的概率密度函数可以用以下公式表示：其中，μ表示均值，σ表示标准差。

正态分布的均值决定了曲线的位置，标准差决定了曲线的形状。

2. 为什么需要四级正态分布表？四级正态分布表是一种用于计算正态分布概率的工具。

由于正态分布的概率密度函数没有一个简单的闭式表达式，因此需要借助正态分布表进行计算。

正态分布表中列出了标准正态分布（均值为0，标准差为1）的累积分布函数值，通过查表可以方便地计算出任意正态分布的概率。

3. 如何使用四级正态分布表？使用四级正态分布表进行计算需要以下几个步骤：步骤1：确定问题的条件首先，需要确定问题的条件，即给定的正态分布的均值和标准差。

这些条件通常是通过实验或观察得到的。

步骤2：标准化将给定的正态分布转化为标准正态分布，即均值为0，标准差为1的分布。

这可以通过以下公式进行计算：其中，X是给定的正态分布的随机变量，μ是均值，σ是标准差，Z是标准正态分布的随机变量。

步骤3：查表计算概率在四级正态分布表中，找到标准正态分布的Z值对应的概率。

四级正态分布表通常是按照Z值的整数部分和小数部分进行排列的。

通过查表可以得到对应Z值的概率。

步骤4：计算实际概率根据标准化公式，将步骤3中计算得到的概率转化为实际正态分布的概率。

如果给定的正态分布是左尾概率，需要计算1减去查表得到的概率；如果给定的正态分布是右尾概率，直接使用查表得到的概率。

4. 示例假设某城市的男性身高服从均值为170cm，标准差为5cm的正态分布。

现在需要计算身高在180cm以上的男性所占的比例。

步骤1：确定问题的条件均值为170cm，标准差为5cm。

步骤2：标准化X = 180，μ = 170，σ = 5，代入标准化公式得到： Z = (180 - 170) / 5 = 2步骤3：查表计算概率在四级正态分布表中查找Z = 2对应的概率为0.9772。