第十章(含耦合电感的电路)习题解答

第十章 耦合电感和变压器电路分析一 内容概述1 互感的概念及VCR ：互感、同名端、互感的VCR 。

2 互感电路的分析方法：①直接列写方程：支路法或回路法； ②将互感转化为受控源； ③互感消去法。

3 理想变压器：①理想变压器的模型及VCR ； ②理想变压器的条件；③理想变压器的阻抗变换特性。

本章的难点是互感电压的方向。

具体地说就是在列方程时，如何正确的计入互感电压并确定“＋、－”符号。

耦合电感1）耦合电感的伏安关系耦合电感是具有磁耦合的多个线圈 的电路模型，如图10-1(a)所示，其中L 1、 L 2分别是线圈1、2的自感，M 是两线圈之 间的互感，“．”号表示两线圈的同名端。

设线圈中耦合电感两线圈电压、电流 选择关联参考，如图10-1所示，则有：dtdiM dt di L )t (u dt di M dt di L )t (u 12222111±=±=若电路工作在正弦稳态，则其相量形式为： .1.2.2.2.1.1I M j I L j U I M j I L j U ωωωω±=±=其中自感电压、互感电压前正、负号可由以下规则确定：若耦合电感的线圈电压与电流的参考方向为关联参考时，则该线圈的自感电压前取正号(如图10-l (a)中所示)t (u 1的自感电压)，否则取负号；若耦合电感线圈的线圈电压的正极端与该线圈中产生互感电压的另一线圈的电流的流入端子为同名端时，则该线圈的互感电压前取正号(如图10-l (a)所示中)t (u 1的互感电压)，否则取负号(如图10-1(b)中所示)t (u 1的互感电压)。

2）同名端当线圈电流同时流人(或流出)该对端钮时，各线圈中的自磁链与互磁链的参考方向一致。

2 耦合电感的联接及去耦等效 1）耦合电感的串联等效两线圈串联如图10-2所示时的等效电感为：M 2L L L 21eq ±+= （10-1）图10-1（10-1）式中M前正号对应于顺串，负号对应于反串。

第10章含有耦合电感的电路1．试确定图10-1所示耦合线圈的同名端。

图10-1解：图10-1（a）先指定电流i1和i2从线圈1的1端和线圈2的2端流入，按照右手螺旋法则，电流i1所产生的磁通链（用实线表示）方向和电流i2所产生的磁通链（用虚线表示）方向相反，如图10-2所示，它们是相互消弱的，所以可以断定端子1与端子2为异名端，则同名端为（1，2＇）或（1＇，2）。

用同样的方法可得图10-1 （b）的同名端为（1，2＇）或（1，3＇）或（2，3＇）。

图10-22．两个耦合的线圈如图10-3所示（黑盒子）。

试根据图中开关S闭合时或闭合后再打开时，毫伏表的偏转方向确定同名端。

图10-3解：根据右手螺旋法可知，线圈的同名端为（1，2）。

当开关S闭合时，线圈1中随时间增大的电流i从电源正极流入线圈端子1，这时毫伏表的高电位与端子1为同名端；当开关S闭合后再打开时，电流i减小，毫伏表的低电位端与端子1为同名端。

3．若有电流i1＝2＋5cos（10t＋30°）A，i2＝10A，各从图10-4（a）所示线圈的1端和2端流入，并设线圈1的电感＝6H，线圈2的电感＝3H，互感为M＝4H。

试求：（1）各线圈的磁通链；（2）端电压和；（3）耦合因数k。

解：（1）（1，2）为异名端，两个线圈的磁通是相互消弱的，所以（2）根据电压和磁通的关系得：（3）耦合因数为：k＝＝0.943。

4．如图10-5所示电路中（1）＝8H，＝2H，M＝2H；（2）＝8H，＝2H，M＝4H；（3）＝＝M＝4H。

试求以上三种情况从端子1-1′看进去的等效电感。

图10-5解：（a）＝M＋（L1－M）//（L2－M）当L1＝8H，L2＝2H，M＝2H时，＝2H；当L1＝8H，L2＝2H，M＝4H时，＝0H；当L1＝L2＝M＝4H时，＝4H。

（b）＝－M＋（L1＋M）//（L2＋M）当L1＝8H，L2＝2H，M＝2H时，＝0.857H；当L1＝8H，L2＝2H，M＝4H时，＝0H；当L1＝L2＝M＝4H时，＝0H。

CH10含有耦合电感的电路第⼗章含有耦合电感电路§10-1 互感⼀、互感: 当两个线圈都有电流时，每⼀线圈的磁链为⾃磁链与互磁链的代数和： 1111211122L i M i ψψψ=±=± 2222122211L i M i ψψψ=±=±注意：1）互感系数M 12和M 21的值与线圈形状、⼏何位置、空间媒质有关，与线圈中的电流⽆关，因此，满⾜ M 12 =M 21 =M ，单位为（H ）2）⾃感系数L 总为正值，互感系数 M 值有正有负。

正值表⽰⾃感磁链与互感磁链def ⼀般有：1k ≤；当 k =1 称全耦合。

耦合因数 k 与线圈的结构、相互⼏何位置、空间磁介质有关。

三、耦合电感上的电压、电流关系I 注意：互感电压的正负：（1）与电流的参考⽅向有关（2）与线圈的相对位置和绕向有关。

四、互感线圈的同名端：当两个电流分别从两个线圈的对应端⼦同时流⼊或流出时，若产⽣的磁通相互增强，则这两个对应端⼦称为两互感线圈的同名端。

注意：当有多个线圈之间存在互感作⽤时，同名端必须两两线圈分别标定。

确定同名端的⽅法：(1) 当两个线圈中电流同时流⼊或流出同名端时，两个电流产⽣的磁场将相互增强。

(2) 当随时间增⼤的时变电流从⼀线圈的⼀端流⼊时，将会引起另⼀线圈相应同名端的电位升⾼。

同名端的实验测定：实验线路如图所⽰，当开关 S 闭合时，线圈 1 中流⼊*号⼀端的电流 i 增加，在线圈 2 的*号⼀端产⽣互感电压的正极，则电压表正偏。

如图所⽰（a ）、（b ）、（c ）、（d ），已知同名端和各线圈上电压电流参考⽅向，试写出每⼀互感线圈上的电压电流关系。

例 10-1 图（a ）例 10-1 图（b ）例 10-1 图（c ）例 10-1 图（d ）⼀、耦合电感的串联（1）顺向串联:122L L L M =++，互感起“增助”作⽤，耦合电感等效阻抗⼤于⽆互感时。

（2）反向串联: 122L L L M =+-，互感起“削弱”作⽤，耦合电感等效阻抗⼩于⽆互感时。

第十章 含有耦合电感的电路习题一、填空题1.电路如图1-1所示，已知负载R L =100Ω时可获得最大功率，则R o =（ ）2.图1-2所示理想变压器，若此时R L 可以获得最大功率，则变比n 为（ ）3. 图1-3电路，求输入电阻R ab =（ ）图1-1 图1-2 图1-34. 如图1-4所示单口网络的开路电压和等效电阻为（ ）V 和（ ）Ω8Ω3:1a b 2:1图1-4 图1-55.如图1-5所示电路的等效电阻Rab=（ ）。

二、计算题。

1.图1所示电路，V )cos(210t u s ω=，R 1=10 Ω，R 2=40 Ω， L 1=L 2=0.1mH ， M=0.02mH ， C 1=C 2=0.01µF ，ω=106rad/s 。

列出回路电流方程并求电流1i 和2i图12.图2所示，已知R=1Ω, ωL 1=2Ω, ωL 2=32Ω, 耦合系数k = 1，Ω=32C 1ω,求 1I •、2U •。

图23.图3示电路，电路原已稳定，t = 0时开关S 由1转向2，求t >0时的电容电流)(t i c 。

图34.图4示，已知正弦电源电压U=200V ，R=500Ω，L=5H ，L1=2H ，M=1H ，L2=0.5H ， C=200μF ，电流表的读数为零：求：（1）电源的角频率ω；（2）各支路的电流；（3）电路的P 、Q 、S 、功率因数图45.求图5所示，负载Z L 是：C L ＝1F 元件，求单口网络的输入阻抗Zab 。

1Ωa b 2Ωj2Ωj1Ωω＝1rad/s Zj1Ω图56.图6所示电路中R=50Ω，L 1=70mH ，L 2=25mH ，M=25mH ，C=1uF ，正弦电压5000U V =∠，ω=104rad/s 。

画出此电路的去耦等效图，并求各支路电流（相量形式）。

Rj ωL 1j ωL 2U +1I 2I I j ωM图67.电路如图7，已知u s = 20.2 cos(5t + 45°)V ，画出此电路的去耦等效电路图，分析计算负载Z 取何值时可获得最大功率？并计算最大功率max P 。

第10章含有耦合电感的电路10.1 复习笔记一、互感1．互感现象及互感磁链某个线圈中的电流产生的磁通链除穿过本线圈外，还与其他线圈相交，称为“互感”现象。

设有n个载流线圈，第k个线圈中的总磁通链为Ψk＝±Ψk1±Ψk2±…＋Ψkk±…±Ψk（n－1）±Ψkn其中，Ψkk为自感磁通链，Ψkj（j≠k）为互感磁通链。

“＋”表示互感磁通链和自感磁通链的方向一致，即同向耦合；“－”为反向耦合。

2．互感系数互感磁通链与产生它的电流比为互感系数，即M12＝Ψ12/i2M21＝Ψ21/i1式中，M12和M21称为互感系数，简称互感，单位为H（亨）。

当只有两个电感有耦合时，M＝M12＝M21。

3．耦合因数用来描述两个线圈间磁耦合的松紧程度，定义为4．互感元件的伏安关系（1）时域伏安关系图10-1-1（a）为互感元件的时域电路模型图，其时域伏安关系为图10-1-1 互感元件时域电路模型（2）相量伏安关系图10-1-1（b）为相量电路模型，其相量伏安关系为二、含有耦合电感电路的计算当耦合电感的两线圈串联、并联或各有一端相连成为三端元件时，其电路可以等效为无互感（无耦合）的等效电路，我们称这种等效电路为去耦合等效电路。

1．耦合电感的串联等效（1）同向串联：如图10-1-2（a）所示，等效电感为：L＝L1＋L2＋2M。

（2）反向串联：如图10-1-2（b）所示，等效电感为：L＝L1＋L2－2M。

图10-1-22．耦合电感的并联等效（1）同向并联如图10-1-3（a）所示，去耦等效电路如图10-1-3（b）所示，其中L a＝L1－M，L b ＝M，L c＝L2－M。

（2）反向并联如图10-1-3（c）所示，去耦等效电路如图10-1-3（d）所示，其中L a＝L1＋M，L b＝－M，L c＝L2＋M。

图10-1-33．其他连接图10-1-4（a）为含耦合电感的两个线圈的单侧同名端连接，其去耦等效电路如图10-1-4（b）所示。

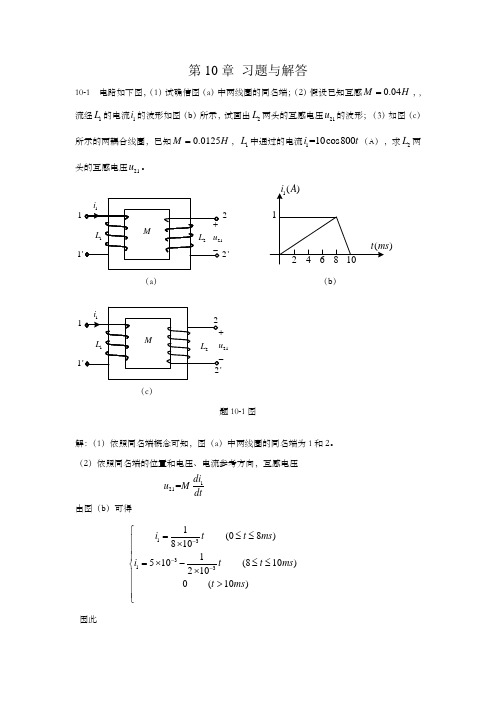
第10章 习题与解答10-1 电路如下图，（1）试确信图（a ）中两线圈的同名端；（2）假设已知互感0.04M H =，,流经1L 的电流1i 的波形如图（b ）所示，试画出2L 两头的互感电压21u 的波形；（3）如图（c ）所示的两耦合线圈，已知0.0125M H =，1L 中通过的电流1=10cos800i t （A ），求2L 两头的互感电压21u 。

122')（a ） （b ）121（c ）题10-1图解：（1）依照同名端概念可知，图（a ）中两线圈的同名端为1和2。

（2）依照同名端的位置和电压、电流参考方向，互感电压121=di u Mdt由图（b ）可得133131(08)8101510(810)2100(10)i t t ms i t t ms t ms ---⎧=≤≤⎪⨯⎪⎪=⨯-≤≤⎨⨯⎪>⎪⎪⎩因此3131125(/)(08)8101500(/)(810)2100(10)A s t ms di A s t ms dt t ms --⎧=≤≤⎪⨯⎪⎪=-=-≤≤⎨⨯⎪>⎪⎪⎩则1210.041255()0.04(500)20()0V di u M V dt ⨯=⎧⎪==⨯-=-⎨⎪⎩21u 的波形图为)-题10－1 附图(3) 依照同名端概念可知，图（c ）中两线圈的同名端为1和2',因此 1210.012510cos800di du Mt dt dt=-=-⨯ 0.012510(800sin800)100sin800100cos(80090)()t t t V =-⨯⨯-==-10-2有两组线圈，一组的参数为1=0.01L H ，2=0.04L H ，=0.01M H ；另一组的参数为1'=0.04L H ，2'=0.06L H ，'=0.02M H 。

别离计算每组线圈的耦合系数，通过比较说明，是不是互感大者耦合必紧？什么缘故？解：计算耦合系数0.5k == 0.41k ==比较：'M M <但'k k >，k 大者耦合较紧。

第十章（含耦合电感的电路）一、选择题1．图1-1所示电路的等效电感=eq L 。

Ａ．8H ； Ｂ．7H ； Ｃ．15H ； Ｄ．11H2．图1—2所示电路中，V )cos(18t u s ω=，则=2i A 。

Ａ．)cos(2t ω； Ｂ．)cos(6t ω； Ｃ．)cos(6t ω-； Ｄ．03．将图1─3（a ）所示电路化为图10—3（b ）所示的等效去耦电路，取哪一组符号取决于 。

Ａ．1L 、2L 中电流同时流入还是流出节点0；Ｂ．1L 、2L 中一个电流流入0，另一个电流流出节点0 ；Ｃ．1L 、2L 的同名端相对于0点是在同侧还是在异侧，且与电流参考方向无关； Ｄ．1L 、2L 的同名端相对于0点是在同侧还是在异侧，且与电流参考方向有关。

4．图1—4所示电路中，=i Z 。

A ．Ω2j ； Ｂ．Ωj1； Ｃ．Ωj3； Ｄ．Ωj85．在图1—5所示电路中，=i Z 。

A ．Ωj8； Ｂ．Ωj6； Ｃ．Ωj12； Ｄ．Ωj46.互感系数M 与下列哪个因素无关A ．两线圈形状和结构； Ｂ．两线圈几何位置；Ｃ．空间煤质； Ｄ．两线圈电压电流参考方向 7.理想变压器主要特性不包括A ．变换电压； Ｂ．变换电流； Ｃ．变换功率； Ｄ．变换阻抗8.对于图1-6所示电路中，下列电压、电流的关系叙述中，正确的是： A.12121122,di di di di u L M u M L dt dt dt dt=--=--； B.12121122,di di di di u L M u M L dt dt dt dt =-=-+； C.12121122,di di di diu L M u ML dt dtdt dt=+=--； 图1-6 D. 12121122,di di di diu L M u M L dt dt dt dt=+=+ 9.如果图1-7（b ）是图10-7（a ）的去耦等效电路，则图10-7（b ）中的1Z 等于： A. j M ω-； B. j M ω； C. ()1j L M ω-；D. ()1j L M ω+。

§10.1 互感耦合电感元件属于多端元件，在实际电路中，如收音机、电视机中的中周线圈、振荡线圈，整流电源里使用的变压器等都是耦合电感元件，熟悉这类多端元件的特性，掌握包含这类多端元件的电路问题的分析方法是非常必要的。

1. 互感两个靠得很近的电感线圈之间有磁的耦合，如图10.1所示，当线圈1中通电流 i 1 时，不仅在线圈1中产生磁通f 11，同时，有部分磁通 f 21 穿过临近线圈2，同理，若在线圈2中通电流i 2 时，不仅在线圈2中产生磁通f 22，同时，有部分磁通 f 12 穿过线圈1，f 12和f 21称为互感磁通。

定义互磁链：图 10.1ψ12 = N 1φ12 ψ21 = N 2φ21当周围空间是各向同性的线性磁介质时，磁通链与产生它的施感电流成正比，即有自感磁通链：互感磁通链：上式中 M 12 和 M 21 称为互感系数，单位为（H ）。

当两个线圈都有电流时，每一线圈的磁链为自磁链与互磁链的代数和：需要指出的是：１）M 值与线圈的形状、几何位置、空间媒质有关，与线圈中的电流无关，因此，满足M12 =M21 =M２）自感系数L 总为正值，互感系数 M 值有正有负。

正值表示自感磁链与互感磁链方向一致，互感起增助作用，负值表示自感磁链与互感磁链方向相反，互感起削弱作用。

2. 耦合因数工程上用耦合因数k 来定量的描述两个耦合线圈的耦合紧密程度，定义一般有：当k =1 称全耦合，没有漏磁，满足f11 = f21，f22 = f12。

耦合因数k 与线圈的结构、相互几何位置、空间磁介质有关。

3. 耦合电感上的电压、电流关系当电流为时变电流时，磁通也将随时间变化，从而在线圈两端产生感应电压。

根据电磁感应定律和楞次定律得每个线圈两端的电压为：即线圈两端的电压均包含自感电压和互感电压。

在正弦交流电路中，其相量形式的方程为注意：当两线圈的自感磁链和互感磁链方向一致时，称为互感的“增助”作用，互感电压取正；否则取负。

Chapter 10 含有耦合电感的电路一、填空题1. 有一对耦合线圈11',22'，现对2个线圈分别通入电流1i ,2i ，则线圈11'的自感电压的时域表达式为 ，线圈22'对11'的互感电压表达式为 。

(设线圈11',22'的自感系数分别为L 1、L 2，互感系数为M ）2. 当2个线圈的磁通链相互加强时，称为互感_________作用，此时互感系数前面的符号为 号。

当2个线圈的磁通链相互抵消时，称为互感_________作用，此时互感系数前面的符号为 号。

3. 耦合系数k 是表征2个耦合线圈的耦合紧疏程度，当2个线圈的结构，周围磁介质一定时，与_________有关，k 的变化范围是__________。

4. 当2个耦合线圈的绕向和相对位置一定时，如果2个线圈的电流都从同名端流入，产生的互感磁通链与自感磁通链方向为________，互感系数的符号为 ；反之，如果一个线圈的电流从同名端流入，另一个线圈的电流从同名端流出，则产生的互感磁通链与自感磁通链方向为________ ，互感系数的符号为 。

5. 含有耦合电感电路的正弦稳态分析可采用 法，注意耦合电感电压除了包括自感电压外还有____________。

6. 2个含耦合电感线圈顺向串联时，端口的等效电感为 ；2个含耦合电感线圈反向串联时，端口的等效电感为 。

7. 2个含耦合电感线圈并联时，可以列写回路电流法方程，但不能列写 ；但如果把电路转化为无耦合等效电路，则两种方法都 。

8. 空心变压器可以看作是把2个含耦合电感线圈分别接在 回路中构成的。

9. 空心变压器副边的回路阻抗通过互感反映到原边，变成等效导纳，即感性变为 ，电阻（电导）变为 。

10. 理想变压器匝数比为 n :1，当副边接上L R 时，原边等效电阻变为___________。

11. 理想变压器的功率=+=2211i u i u p 。

图（a ）理想变压的匝数比为1：10及V 10sin 10501S 21t u ,R ,R =Ω=Ω=，求2u 。

解法一：用回路电流法，根据图（a ）可得理想变压器的电压、电流关系为解得 V)10sin(3.333102t u u S-=-=解法二：用阻抗变换法，等效电路如图（b ）所示。

SS eqeq u u R R R u 3111=+=Su u nu 31112-=-=∴ V )10sin(3.332t u -=10-101、10-102、10-103、10-104、10-105、10-106、例10-1 如图所示（a ）、（b ）、（c ）、（d ）四个互感线圈，已知同名端和各线圈上电压电流参考方向，试写出每一互感线圈上的电压电流关系。

()a2()b 2()c+-2()d 21R 2R（a）（b）（c）（d）解：（a）（b）（c）（d）图示电路中，L 1=8mH ，L 2=0.3H ，R =2Ω，L 3= 0.5H ，R 1=4Ω，U 0=6V ，n=4，t u s 1000sin 28=，电流表的读数为0.6A ，求C 值及电流表的读数。

解：电路中有直流激励和正弦激励。

当直流激励单独作用时，A 6.0A A A,2.1//2110读数分别为、∴=+=RR R U I当正弦激励单独作用时，A 2的读数必为零。

故在L 3与C /（等效电容）并联处发生谐振。

A18.06.0A8.0321/1221212113222323=+=∴=++==='=='∴='上的读数）（）（A L R R U I FL nC n C L C L C Sωμωωωω例10-13 已知图（a ）电路的电源内阻R S =1k Ω ，负载电阻 R L =10Ω 。

为使R L 上获得最大功率，求理想变压器的变比 n。

解：把副边阻抗折射到原边，得原边等效电路如图（b ）所示，因此当 n 2R L =R S 时电路处于匹配状态，由此得： 10 n 2=1000 即 n 2=100 ， n =10 10-204、例10-14 求图（a ）所示电路负载电阻上的电压 2U .例 10 — 14 图 （ a ）解法 1 ：列方程求解。

§10.1 互感耦合电感元件属于多端元件，在实际电路中，如收音机、电视机中的中周线圈、振荡线圈，整流电源里使用的变压器等都是耦合电感元件，熟悉这类多端元件的特性，掌握包含这类多端元件的电路问题的分析方法是非常必要的。

1. 互感两个靠得很近的电感线圈之间有磁的耦合，如图10.1所示，当线圈1中通电流 i 1 时，不仅在线圈1中产生磁通f 11，同时，有部分磁通 f 21 穿过临近线圈2，同理，若在线圈2中通电流i 2 时，不仅在线圈2中产生磁通f 22，同时，有部分磁通 f 12 穿过线圈1，f 12和f 21称为互感磁通。

定义互磁链：图 10.1ψ12 = N 1φ12 ψ21 = N 2φ21当周围空间是各向同性的线性磁介质时，磁通链与产生它的施感电流成正比，即有自感磁通链：互感磁通链：上式中 M 12 和 M 21 称为互感系数，单位为（H ）。

当两个线圈都有电流时，每一线圈的磁链为自磁链与互磁链的代数和：需要指出的是：１）M 值与线圈的形状、几何位置、空间媒质有关，与线圈中的电流无关，因此，满足M12 =M21 =M２）自感系数L 总为正值，互感系数 M 值有正有负。

正值表示自感磁链与互感磁链方向一致，互感起增助作用，负值表示自感磁链与互感磁链方向相反，互感起削弱作用。

2. 耦合因数工程上用耦合因数k 来定量的描述两个耦合线圈的耦合紧密程度，定义一般有：当k =1 称全耦合，没有漏磁，满足f11 = f21，f22 = f12。

耦合因数k 与线圈的结构、相互几何位置、空间磁介质有关。

3. 耦合电感上的电压、电流关系当电流为时变电流时，磁通也将随时间变化，从而在线圈两端产生感应电压。

根据电磁感应定律和楞次定律得每个线圈两端的电压为：即线圈两端的电压均包含自感电压和互感电压。

在正弦交流电路中，其相量形式的方程为注意：当两线圈的自感磁链和互感磁链方向一致时，称为互感的“增助”作用，互感电压取正；否则取负。

第十章（含耦合电感的电路）习题解答一、选择题1．图10—1所示电路的等效电感=eq L A 。

Ａ．8H ； Ｂ．7H ； Ｃ．15H ； Ｄ．11H解：由图示电路可得 121 d d 2d d )63(u t i t i =++， 0d d 4d 221=+tit i d从以上两式中消去t i d d 2得tiu d d 811=，由此可见 8=eq L H2．图10—2所示电路中，V )cos(18t u s ω=，则=2i B A 。

Ａ．)cos(2t ω； Ｂ．)cos(6t ω； Ｃ．)cos(6t ω-； Ｄ．0解：图中理想变压器的副边处于短路，副边电压为0。

根据理想变压器原副边电压的关系可知原边的电压也为0，因此，有A )cos(29)cos(18 1t t i ω=ω=再由理想变压器原副边电流的关系ni i121= (注意此处电流2i 的参考方向)得A )cos(612t ni i ω==因此，该题应选B 。

3．将图10─3（a ）所示电路化为图10—3（b ）所示的等效去耦电路，取哪一组符号取决于 C 。

Ａ．1L 、2L 中电流同时流入还是流出节点0；Ｂ．1L 、2L 中一个电流流入0，另一个电流流出节点0 ；Ｃ．1L 、2L 的同名端相对于0点是在同侧还是在异侧，且与电流参考方向无关；Ｄ．1L 、2L 的同名端相对于0点是在同侧还是在异侧，且与电流参考方向有关。

解：耦合电感去耦后电路中的M 前面是取“+”还是取“–”，完全取决于耦合电感的同名端是在同侧还是在异侧，而与两个电感中电流的参考方向没有任何关系。

因此，此题选C 。

4．图10—4所示电路中，=i Z B 。

A ．Ω2j ； Ｂ．Ωj1； Ｃ．Ωj3； Ｄ．Ωj8解：将图10—4去耦后的等效电路如图10—4（a ），由图10—4（a ）得j1 j6j6j6j6j2Ω=+⨯+-=i Z因此，该题选Ｂ。

5．在图10—5所示电路中，=i Z D 。