电路分析基础第四章(李瀚荪)

线性电路和网络函数叠加定理叠加方法与功率计算§线性电路和网络函数独立电源：电路的输入，对电路起着激励的作用。

元件的电压、电流：激励引起的响应。

一、线性电路：一、线性电路：由线性元件及独立电源组成的电路。

su R R R R R R R i 13322132++=单输入的线性电路在单激励的线性电路中，激励增大（或减小）多少倍，响应也增大（或减小）相同倍数。

比例性或齐次性单激励sKu =叠加性两个以上激励若x1(t) Þy1(t), x2(t) Þy2(t)Þ叠加原理则x1(t) + x2(t) Þy1(t) + y2(t)对任何线性电阻电路，网络函数H 都是实数。

)(二、网络函数：对单一激励的线性、时不变电路，指定的响应对激励之比定义为网络函数，记为H 。

H=响应激励任一支路的电压或电流电压源电压或电流源电流若响应与激励在同一端口：激励策动点电导G i 策动点电阻R i 转移电导G T 转移电阻R T 转移电流比H i 转移电压比H u电流电压电压电流电流电压电流电压电压电流电流电压策动点函数转移函数策动点函数转移函数不在同一端口：+–U L R 1R 3R U s例：求电阻R L 的电压U L 。

例：求各支路电流和电压。

例：电桥电路如图，若输出电压为u o ，求转移电压比H u ＝u o u s 。

例：求转移电压比H u ＝u o u s 。

=1V，计算u和i；例5：在图中所示电路中，(1)若us(2)若u s=10V，计算u和i；(3)若图中每个1Ω电阻换为10V，计算u和i。

为10Ω电阻，usi2i1i§叠加原理在任何由线性电阻、线性受控源及独立源组成的电路中，每一元件的电流或电压可以看成是每一个独立源单独作用时，在该元件上产生的电流或电压的代数和。

当某一独立源单独作用时，其他独立源为零值，即独立电压源短路，独立电流源开路。

一、叠加原理：双节点1：i 1+i s =i 2回路：R 1i 1+R 2i 2=u si s =0，u s 单独作用时R 2中产生的电流叠加原理：叠加原理：在线性电路中，任一电流变量或电压变量，作为电路的响应y (t )，与电路各个激励x m (t )的关系可表示为式中x m (t )表示电路中的电压源电压或电流源电流，设独立电源的总数为M 个，H m 为相应的网络函数。

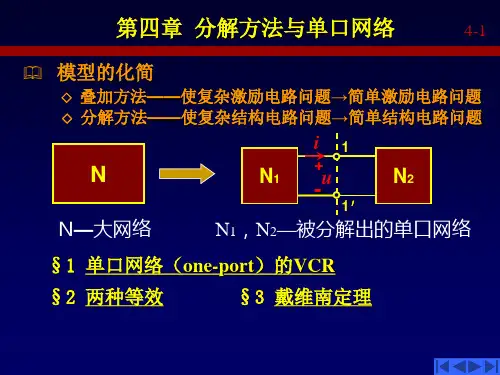
第4章分解方法及单口网络4.1 复习笔记一、分解的基本步骤1．划分原则一个元件的电压电流关系是由这个元件本身所确定的，与外接的电路无关。

从全面求解网络的角度来看，何处划分是随意的，视方便而定。

2．分解步骤分解的基本步骤为：（1）把给定网络划分为两个单口网络N1和N2；（2）分别求出N1和N2的VCR（计算或测量）；（3）联立两者的VCR或由它们伏安特性曲线的交点，求得N1和N2的端口电压、电流；（4）分别求解N1和N2内部各支路电压、电流。

二、单口网络的电压电流关系1．单口网络的伏安关系VCR单口网络的伏安关系可用以下方式来描述：（1）具体的电路模型；（2）方程或曲线的形式；（3）等效电路。

2．单口网络VCR的求解方法（1）在单口网络两端外施电流源i求单口网络两端电压u；（2）在单口网络两端外施电压源u求单口网络两端电流i。

3．注意事项（1）单口网络的VCR与外接电路无关；（2）可以在最简单的外接电路情况下，求得单口网络的VCR；（3）外施电流源求电压法和外施电压源求电流法是求解VCR常用的方法.三、单口网络的置换-置换定理1．置换定理内容置换定理可表述为：若网络N由两个单口网络N1和N2连接组成，且已知端口电压和电流值分别为α和β，则N1（或N2）可以用一个电压为α的电压源或用一个电流为β的电流源置换，不影响N1（或N2）内各支路电压、电流原有数值。

2．置换过程的图示置换过程如图4-1所示。

（a）（b）N2为电压源所置换（c）N2为电流源所置换图4-1 置换定理四、单口网络的等效电路两单口网络等效是指一个单口网络N和另一个单口网络N'的电压、电流关系完全相同，即它们在u-i平面上的伏安特性曲线完全重叠。

1．等效串联电路（1）典型电路图串联等效电路的典型电路图如图4-2所示。

图4-2 串联等效电阻（2）串联等效的公式串联等效的公式为（3）串联等效的表述串联等效电路的电阻为各电阻之和。

2．等效并联电路（1）并列等效的公式等效并联电阻公式为（2）并联等效的表述并联等效电阻的倒数等于各电阻倒数之和。

第1章1.1 复习笔记一、电路及集总电路模型1．基础元件图形实际电路是由电阻器、电容器、线圈、电源等部件和晶体管等器件相互连接组成的，各种部、器件可以用图形符号表示，如表1-1所示。

表1-1 部分电气图用图形符号2．集总电路（1）定义集总电路是指由集总参数元件组成的电路。

（2）应用条件当电路的尺寸远小于最高频率所对应的波长时，可以当做集总电路来处理。

二、电路变量电流、电压及功率1．电流（1）定义电流是指每单位时间内通过导体横截面的电荷量。

（2）表达式电流的表达式为（3）分类①恒定电流恒定电流是指大小和方向都不随时间变化的电流，简称直流。

②交变电流交变电流是指大小和方向都随时间作周期性变化的电流，简称交流。

2．电压（1）定义电路中a、b两点间的电压是指单位正电荷由a点转移到b点时所获得或失去的能量。

（2）表达式电压的表达式为（3）分类①恒定电压恒定电压是指大小和极性都不随时间而变动的电压，也叫直流电压。

②时变电压时变电压是指大小和极性都随时间变化的电压，也叫交流电压。

（4）关联参考方向：关联参考方向是指电流参考方向与电压参考方向一致，如图1-1所示。

图1-1 关联的参考方向3．功率（1）定义功率是指能量流动的速率。

（2）表达式功率的表达式为p（t）＝u（t）i（t）（3）功率的正负功率的正负表示能力的吸收与产生，电压电流取关联参考方向时：①当功率为正，电路吸收能量，p值即为吸收能量的速率；②当功率为负，电路提供能量，p值为产生能量的速率。

三、基尔霍夫定律1．基尔霍夫电流定律（1）定律内容基尔霍夫电流定律可表述为：对于任一集总电路中的任一节点，在任一时刻，流出（或流进）该节点的所有支路电流的代数和为零。

（2）表达式基尔霍夫电流定律的数学表示式为（3）理论基础基尔霍夫电流定律的理论基础是电荷守恒法。

2．基尔霍夫电压定律（1）定律内容基尔霍夫电压定律可表述为：对于任一集总电路中的任一回路，在任一时刻，沿着该回路的所有支路电压降的代数和为零。

电路分析基础第四版下册(李瀚荪著)课后答案下载电路分析基础第四版下册(李瀚荪著)内容简介下册第三篇动态电路的相量分析法和s域分析法第八章阻抗和导纳8—1 变换方法的概念8—2 复数8—3 振幅相量8—4 相量的线性性质和基尔霍夫定律的相量形式8—5 三种基本电路元件VCR的相量形式8—6 VCR相量形式的统一——阻抗和导纳的引入8—7 弦稳态电路与电阻电路分析方法的类比——相量模型的引入8—8 正弦稳态混联电路的分析8—9 相量模型的网孔分析和节点分析8—10 相量模型的等效8—11 有效值有效值相量8—12 两类特殊问题相量图法习题第九章正弦稳态功率和能量三相电路 9—1 基本概念9—2 电阻的平均功率9—3 电感、电容的平均储能9—4 单口网络的`平均功率9—5 单口网络的无功功率9—6 复功率复功率守恒9—7 弦稳态最大功率传递定理9—8 三相电路习题第十章频率响应多频正弦稳态电路 10一1 基本概念10—2 再论阻抗和导纳10—3 正弦稳态网络函数10—4 正弦稳态的叠加10—5 平均功率的叠加10—6 R1C电路的谐振习题第十一章耦合电感和理想变压器11—1 基本概念11—2 耦合电感的VCR耦合系数11—3 空心变压器电路的分析反映阻抗11—4 耦合电感的去耦等效电路11—5 理想变压器的VCR11—6 理想变压器的阻抗变换性质11—7 理想变压器的实现11—8 铁心变压器的模型习题第十二章拉普拉斯变换在电路分析中的应用 12一1 拉普拉斯变换及其几个基本性质12—2 反拉普拉斯变换——赫维赛德展开定理 12—3 零状态分析12—4 网络函数和冲激响应12—5 线性时不变电路的叠加公式习题附录A 复习、检查用题附录B 复习大纲部分习题答案(下册)索引结束语电路分析基础第四版下册(李瀚荪著)目录《电路分析基础》(下高等学校教材)第4版下册讲授动态电路的相量分析法和s域分析法。

具体内容有：阻抗和导纳、正弦稳态功率和能量/三相电路、频率响应/多频正弦稳态电路、耦合电感和理想变压器、拉普拉斯变换在电路分析中的应用。

电路分析基础李瀚荪版配套课件第四章第四章分解方法及单口网络4-1 分解的基本步骤 4-2 单口网络的伏安关系 4-3 单口网络的置换－置换定理 4-4 单口网络的等效电路 4-5 戴维南定理 4-6 诺顿定理4-7 最大功率传递定理 4-8 T形网络和П形网络的等效变换单口网络：由元件相连接组成、对外只有两个端钮的网络整体称为二端网络或单口网络，二端网络或直接称为单口。

单口N§4-1 分解的基本步骤1. 把给定的网络分为两个单口网络N1和N2。

2. 分别求N1，N2的VCR。

3. 联立VCR，或由它们伏安特性曲线交点，求单口网络端钮上的电压u和电流i。

4. 分别求单口网络N1，N2中的电压，电流。

Nu Us QOUs/Ri{ u = Riu = UsT{ i =U / Rsu = UsQ：工作点，坐标（Us/R，Us）§4-2 单口网络的伏安关系求解单口网络的伏安关系方法：1. 列电路方程：求u-i关系。

列电路方程：2. 外施电流源求电压法：端钮上加电流源，求入端电压，得到u-i关系。

3. 外施电压源求电流法：端钮上加电压源，求入端电流，得到u-i关系。

例1：求图示含电源和电阻的单口网络的 VCR。

例2：求图示含电源、电阻和受控源的单口网络的VCR。

例3：求图示只含电阻的单口网络的VCR。

(1)外施电压源法4 21(2)外施电流源法3§4-3单口网络的置换—置换定理若网络N由两个单口网络 N1 或 N2 连接组成，且已知端口电压和电流值分别为u=α ，i=β ，则 N2 （或 N1 ）可用一个电压为α的电压源或用一个电流为β的电流源置换，不影响 N1 （或 N2 ）内各支路电压、电流原有数值。

例1：求图示电路的各支路电流。

i1 = 3.75A i2 = 1.5A i3 = 2.25A4Ω电阻用电流源置换：置换后对其他支路没有影响。

i2 = 1.5Ai3 = 2.25A例2：图示电路的N1能否用结构更简单的电路代替而保持N2的电流电压不变？6Ω电阻可否置换为其他元件？i 2.5 1u=6u = 6iQi =1u = 10 - 4i10 uO N1 N26工作点：Q（6V, 1A）置换是一种基于工作点相同的“等效”替换。

第2部分课后习题详解说明：本部分对李瀚荪编写的《电路分析基础》（第4版）教材每一章的课后习题进行了详细的分析和解答，并对个别知识点进行了扩展。

课后习题答案经过多次修改，质量上乘，非常标准，特别适合应试作答和临考冲刺。

第1章集总参数电路中电压、电流的约束关系§1-2电路变量电流、电压及功率1-1接在图1-1所示电路中电流表A的读数随时间变化的情况如图中所示。

试确定t ＝1s、2s及3s时的电流i。

图1-1解：因图中以箭头所示电流i的参考方向是从电流表负端到正端，所以t＝1s，i＝－1At＝2s，i＝0At＝3s，i＝1A1-2设在图1-2所示元件中，正电荷以5C/s的速率由a流向b。

（1）如电流的参考方向假定为由a至b，求电流。

（2）如电流的参考方向假定为由b至a，求电流。

（3）如流动的电荷为负电荷，（1）、（2）答案有何改变？图1-2解：（1）根据电流的定义，5C/s＝5A，实际流动方向为a→b，若参考方向假定为a→b，两者吻合，该电流应记为i＝5A（2）若参考方向假定为b→a，而电流实际流向为a→b，两者不吻合，该电流应记为i＝－5A（3）以上均系指正电荷而言，若流动的是负电荷，则（1）、（2）的答案均须改变符号。

1-3各元件的情况如图1-3所示。

（1）若元件A吸收功率10W，求（2）若元件B吸收功率10W，求（3）若元件C吸收功率－10W，求（4）试求元件D吸收的功率；（5）若元件E提供的功率为10W，求（6）若元件F提供的功率为－10W，求（7）若元件G提供的功率为10mW，求（8）试求元件H提供的功率。

图1-3解：元件A、C、E、G的u和i为关联参考方向，在取关联参考方向前提下，可以使用P＝ui，功率为正表示这段电路吸收功率，功率为负表示该段电路提供功率。

而元件B、D、F、H的u和i为非关联参考方向，应注意在使用的公式中加负号，即使用P＝－ui。

（该元件吸收功率为－20μw，即提供功率20μw）；（该元件提供功率为4mW）。

第4章　分解方法及单口网络§4-2　单口网络的电压电流关系4-1　求图4-1所示单口网络的VCR。

图4-1解：标出端口u和i，电压u可认为是外施电压源电压，i流出网络，指向外施电源正极。

用网孔法列出电路方程。

设网孔电流和i均为顺时针方向。

找出i和u的关系得u＝－12.5i＋11.25 （1）如i指向网络内部，则u＝12.5i＋11.25 （2）u、i的单位分别为V、A。

列网孔方程就是如此规定的。

4-2　试用外施电源法求图4-2所示含源单口网络的VCR，并绘出伏安特性曲线。

图4-2解：图中u可认为是外施电压源的电压。

根据图中所示i的参考方向，可列出u＝（3 Ω）i＋（6 Ω）（i＋5 A）＋20 V＝（3 Ω＋6 Ω）i＋（6 Ω）（5 A）＋20 V＝（9 Ω）i＋50 V伏安特性曲线是条直线。

i＝0时u＝50 V，即u轴截距为50；u＝0时，即i轴截距为4-3　试求图4-3所示电路的VCR。

图4-3解：施加电压源u于a、b两端，由KVL和KCL，可得§4-3　单口网络的置换——置换定理4-4　在图4-4所示电路中已知N的VCR为5u＝4i＋5，试求电路中各支路电流。

图4-4解：分割出图4-4所示虚线框内电路，设外施电压为u，为求其VCR，可列出节点方程整理得VCRu＝2－1.2i以之与N的VCR联立可解出i，即5（2－1.2i）＝4i＋5解得i＝0.5 A，u＝1.4 V以1.4 V电压源置换N，可简便地估计到N存在的影响，由此可得4-5　试设法利用置换定理求解图4-5所示电路中的电压何处划分为好？置换时用电压源还是电流源为好？图4-5图4-6解：试从图4-6的虚线处将电路划分成两部分，对网络有整理得15u＝117－14i（1）对网络有 联立（1）、（2）两式解得i＝3 A。

用3 A电流源置换较为方便，置换后利用分流关系，可得4-6　电路如图4-7（a）所示，网络N的VCR如图4-7（b）所示，求u和i，并求流过两线性电阻的电流。

第4章　分解方法及单口网络一、选择题1．如图4-1所示电路，根据置换定理，一端口电路N可用支路（）替代。

图4-1【答案】C【解析】应先求出端口1-1＇的电压。

2．如图4-2所示电路中，N0为无源线性电阻电路。

当U S＝8V，I S＝2A时，开路电压U ab＝0；当U S＝8V，I S＝0A时，开路电压U ab＝6V和短路电流I ab＝6V。

当＝0V，I S＝2A，且a、b间外接电阻9 时，电流I ab为（）AUSA．－2/3B．2/3C．0.6D．－0.6图4-2【答案】D【解析】由叠加定理可设开路电压，由题设条件得解得α＝3/4，β＝－3。

由题设条件得端口戴维南等效电阻为当时a、b间开路电压，则a、b间外接电阻9Ω时，电流I ab为3．如图4-3所示电路中a、b端的诺顿等效电路是（）。

图4-3【答案】C【解析】如图4-3所示，有方程解得再者当如图4-3所示电路a、b间短路时的短路电流为从而4．如图4-4所示一端口电路的电压-电流关系为（）。

图4-4A．U＝25＋IB．U＝25－IC．U＝－25－ID．U＝－25＋I【答案】A【解析】可将戴维南支路等效为诺顿支路，和5 A电流源合并后即可求得电压－电流关系为二、填空题1．如图4-5所示电路中，电阻R L调至阻值4Ω时获得最大功率6.25 W，则U S＝______V。

图4-5【答案】9V【解析】对如图4-5所示电路，通过电源转移以及电源支路等效变换，可得如图4-6所示电路。

由R L ＝4Ω时获得最大功率6.25W ，可求得回路电流I ＝1.25A 。

根据如图4-6所示电路可列写KVL 方程，并求得U S ＝9V 。

图4-62．如图4-7所示电路的戴维南等效电路参数U oc ＝______V ，R 0＝______Ω。

图4-7【答案】9；63．如图4-8所示电路可用诺顿定理求电流I ，对应的诺顿等效电路参数I oc ＝______A ， R 0＝______Ω，求得电流I ＝______A 。