云南大学2009——2010第1学期高等代数期末考试试卷

高等代数 --复习资料一、单项选择题1、设为任意两个级方阵,则如下等式成立的是A.B.C.D.参考答案： C2、设向量组线性无关,则向量组线性无关的充分必要条件为A.B.C.D.参考答案： A3、若,则( ).A. 30mB. -15mC. 6mD. -6m参考答案： D4、实对称矩阵的特征值都是( )A. 非负整数B. 实数C. 正数参考答案： B5、实对称矩阵A的秩等于r,且它有m个正特征根,则它的符号差为 ( )A. rB. mC. 2m-rD. r-m参考答案： C6、设矩阵和分别是和的矩阵,秩,秩,则秩是A. 1B. 2C. 3D. 4参考答案： B7、是线性空间V上的线性变换,,那么关于V的基的矩阵是 ( )A.B.C.D.参考答案： B8、对于元方程组,下列命题正确的是( ).A. 如果只有零解,则也只有零解B. 如果有非零解,则有无穷多解C. 如果有两个不同的解,则有无穷多解D. 有唯一解的充分条件是参考答案： C9、若矩阵A的不变因子为,则A的全部初等因子为 ( )A.B.C.参考答案： A10、设为3次实系数多项式,则A. 至少有一个有理根B. 至少有一个实根C. 存在一对非实共轭复根D. 有三个实根.参考答案： B11、对于数域P上线性空间V的数乘变换来说 ( )不变子空间A. 只有一个B. 每个子空间都是C. 不存在参考答案： B12、下列运算中正确的是( )A. ；B. ；C. ；D. 。

参考答案： D13、为欧氏空间V上的对称变换,下面正确的是 ( )A.B.C.参考答案： C14、如果把代入实二次型都有,那么是 ( )A. 正定B. 负定C. 未必正定参考答案： C15、设向量组线性无关,线性相关,则( ).A. 一定能由线性表示B. 一定能由线性表示C. 一定不能由线性表示D. 一定不能由线性表示参考答案： B16、下列说法不正确的是( ).A. 任何一个多项式都是零次多项式的因式B. 如果f(x)∣g(x),g(x)∣h(x),则f(x)∣h(x)C. 如是阶矩阵,则D. 如是阶矩阵,则参考答案： A17、设是矩阵,是非齐次线性方程组所对应的齐次线性方程组,则下列结论正确的是( )A. 若仅有零解,则有唯一解；B. 若有非零解,则有无穷多个解；C. 若有无穷多个解,则仅有零解；D. 若有无穷多个解,则有非零解；参考答案： D18、是n维复空间V的两个子空间,且,则的维数为 ( )A.B.C.参考答案： C19、阶矩阵A可逆的充分必要条件是( ).A. ∣A∣=0B. r(A)<C. A是满秩矩阵D. A是退化矩阵参考答案： C20、设矩阵的秩为,为阶单位方阵,下述结论中正确的是( )A. 的任意个列向量必线性无关；B. 的任意一个阶子式不等于零；C. 若矩阵满足,则,或非齐次线性方程组,一定有无穷多组解D. 通过初等行变换,必可化为的形式。

云南大学经济学院经济学（含政治经济学、西方经济学）2006——2009经济学（含政治经济学和西方经济学）2005（A），2005（B）（试卷内容不全）经济学二2007经济学三（国际贸易学专业）2005西方经济学2005西方经济学（含宏观经济学、微观经济学）2006——2009西方经济学二2008经济学（含产业经济学和西方经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和世界经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和人口、资源与环境经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（资本主义部分）2004（A卷），2004（B卷）管理学原理（管理科学与工程专业）2006——2009管理学（企业管理专业）2004——2009（2004、2005年名称为“管理学原理”）会计学原理2005——2006统计学原理2005公共管理学院政治学原理2006——2009当代中国政府与政治2006——2009政治学概论2007——2009（2007、2008年试题名称为“国际政治学概论”）社会学人类学理论与方法2007——2009社会学基础2007——2009民族学基础2004——2006（注：2006年试卷为回忆版）社会文化人类学2005文化人类学理论与方法2004文化人类学2004行政管理2008——2009行政学概论2006——2009经济学（含政治经济学、西方经济学）2006——2009经济学（含政治经济学和西方经济学）2005（A），2005（B）（试卷内容不全）西方经济学二2008——2009西方经济学2005西方经济学（含宏观经济学、微观经济学）2006——2007西方经济学（含微观经济学和宏观经济学）（产业经济学专业）2008图书馆、情报与档案管理实务2006——2009图书馆学、情报学与档案学基础2006——2009法学院经济法学、民法学、刑法学2006——2009法理学、宪法学2006——2009马克思主义研究院马克思主义哲学原理2006——2009马克思主义基本原理概论2009毛泽东思想、邓小平理论和“三个代表”重要思想概论2009民族学理论与方法2009发展研究院经济学（含政治经济学、西方经济学）2006——2009经济学（含政治经济学和西方经济学）2005（A），2005（B）（试卷内容不全）经济学二2007经济学三（国际贸易学专业）2005西方经济学2005西方经济学（含宏观经济学、微观经济学）2006——2009西方经济学二2008经济学（含产业经济学和西方经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和世界经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和人口、资源与环境经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（资本主义部分）2004（A卷），2004（B卷）管理学原理（管理科学与工程专业）2006——2009管理学（企业管理专业）2004——2009（2004、2005年名称为“管理学原理”）会计学原理2005——2006统计学原理2005社会学人类学理论与方法2007——2008社会学基础2007——2008民族学基础2004——2006（注：2006年试卷为回忆版）社会文化人类学2005文化人类学理论与方法2004文化人类学2004人文学院马克思主义哲学原理2006——2009专业综合理论2007——2009中国语言文学基础2007——2009理论批评2007——2009传播理论2002——2005，2007——2009新闻传播实务2002——2005，2007——2009世界近现代史2005——2006中国通史2005——2006西方哲学史2006马克思主义政治经济学原理2006外国语学院二外日语2002，2004——2009二外德语2002，2004——2009二外法语2002，2004——2009二外英语2004，2006——2007，2009基础英语（含写作、翻译、阅读）2004——2009综合考试（英语语言文学专业）1999——2000，2004——2009综合考试（法语语言文学专业）2004，2006——2007，2009基础法语2004，2006——2007，2009翻译（法汉互译）2002法国文学2002英美文化与文学2002英美文学1999——2000英语写作1999——2000英汉互译1999——2000写作与翻译（英语专业）2002民族研究院马克思主义哲学原理2006——2009综合专业理论2007——2009社会学人类学理论与方法2007——2009社会学基础2007——2009人类学基础2009民族学基础2004——2006（注：2006年试卷为回忆版）民族学理论与方法2009社会文化人类学2005文化人类学理论与方法2004文化人类学2004马克思主义政治经济学原理2006工商管理与旅游学院经济学（含政治经济学、西方经济学）2006——2009经济学（含政治经济学和西方经济学）2005（A），2005（B）（试卷内容不全）经济学二2007经济学三（国际贸易学专业）2005西方经济学2005西方经济学（含宏观经济学、微观经济学）2006——2009西方经济学二2008经济学（含产业经济学和西方经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和世界经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和人口、资源与环境经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（资本主义部分）2004（A卷），2004（B卷）管理学原理（管理科学与工程专业）2006——2009管理学（企业管理专业）2004——2009（2004、2005年名称为“管理学原理”）会计学原理2005——2006统计学原理2005旅游综合考试2005国际关系研究院政治学概论2006——2009近现代国际关系史2007——2009世界民族与民族问题2007——2009民族学概论2007——2009经济学（含政治经济学、西方经济学）2006——2009经济学（含政治经济学和西方经济学）2005（A），2005（B）（试卷内容不全）经济学二2007经济学三（国际贸易学专业）2005西方经济学2005西方经济学（含宏观经济学、微观经济学）2006——2009西方经济学二2008经济学（含产业经济学和西方经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和世界经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（含西方经济学和人口、资源与环境经济学）2004（A卷），2004（B卷），2005（A卷），2005（B卷）经济学（资本主义部分）2004（A卷），2004（B卷）艺术与设计学院中外艺术史2004，2005，2009（其中2005年的试卷内容不全）艺术理论2009文化人类学2009艺术概论2004（A卷），2005（A卷）（其中2005年的试卷内容不全）高等教育研究院院教育学专业基础综合（全国统考试卷）2007——2009（2007——2009有答案）教育学综合（含教育学原理、中外教育史）2006马列主义教学研究部马克思主义哲学原理2006——2009马克思主义基本原理概论2009毛泽东思想、邓小平理论和“三个代表”重要思想概论2009 马克思主义哲学基本原理2007马克思主义政治经济学原理2006邓小平理论和三个代表重要思想概论2006——2007民族学理论与方法2007数学与统计学院数学分析2004，2007——2009高等代数2004，2007——2009数学分析与高等代数2003，2005——2006概率论数数理统计2005——2009（2006年试题有两份）西方经济学（含宏观经济学、微观经济学）2006——2009生命科学学院普通生物学2006——2009遗传学2005——2009生物化学2000——2003微生物学2002信息学院离散数学2002——2009信号与系统2003，2005——2006，2008——2009自动控制原理2007——2009数据结构与操作系统2003，2005——2008数据结构与数据库技术2003数据结构与算法2003数据结构2003计算机程序设计2007——2008数据结构与程序设计2003，2005，2007——2008数字电路2005——2006化学科学与工程学院化学（一）2005——2009化学（二）2005——2009化学（三）2005——2009分析化学2004有机化学2004综合化学2004物理科学技术学院量子力学2003，2007——2009大学物理（物理科学技术学院使用）2007——2009高等数学2005——2009程序设计与数值算法基础2007电路理论2008——2009电磁场原理2008电路与电磁场理论2007普通化学2006——2008普通化学（一）2007——2009普通物理2006——2009量子物理基础2008——2009固体物理基础2008固体物理2003，2007——2008材料科学基础2007，2009资源环境与地球科学学院城市与区域规划（人文地理专业）2005土地利用规划与管理2009高等数学2005——2009高等数学（二）2009综合地理学2009天气学2009地震学与地质学基础2009结构力学2009软件学院计算机程序设计2007——2009高等数学一（自命题）2009数据结构与程序设计2003，2005，2007——2008 数据结构与操作系统2003，2005——2006，2008 数据结构与数据库技术2003数据结构与算法2003数据结构2003离散数学2002——2009古生物重点实验室地质学基础2006普通生物学2006——2009古生物地史学2006城市建设与管理学院城市与区域规划（人文地理专业）2005土地利用规划与管理2009高等数学2005——2009高等数学（二）2009综合地理学2009天气学2009地震学与地质学基础2009结构力学2009文化产业研究院经济人类学2009民族文化与经济2009文化产业概论2009中外艺术史2004（A卷），2005（A卷）（其中2005年的试卷内容不全）社会文化人类学2005文化人类学理论与方法2004文化人类学2004工程技术研究院大学物理（工程技术研究院使用）2007——2009普通化学2006——2008普通化学（一）2007——2008普通化学（二）2009教育技术学基础2006——2009多媒体技术基础2006——2008计算机网络基础2009。

高等代数（II ）期末考试试卷及答案（A 卷） 一、 填空题（每小题3分，共15分）1、线性空间[]Px 的两个子空间的交()()11L x L x -+=2、设12,,...,n εεε与12,,...,n εεε'''是n 维线性空间 V 的两个基， 由12,,...,n εεε到12,,...,n εεε'''的过渡矩阵是C ，列向量X 是V 中向量ξ在基12,,...,n εεε下的坐标，则ξ在基12,,...,n εεε'''下 的坐标是3、设A 、B 是n 维线性空间V 的某一线性变换在不同基下的矩阵， 则A 与B 的关系是4、设3阶方阵A 的3个行列式因子分别为：()21,,1,λλλ+则其特征矩阵E A λ-的标准形是5、线性方程组AX B =的最小二乘解所满足的线性方程组是：二、 单项选择题（每小题3分，共15分）1、 （ ）复数域C 作为实数域R 上的线性空间可与下列哪一个 线性空间同构：（A ）数域P 上所有二级对角矩阵作成的线性空间； （B ）数域P 上所有二级对称矩阵作成的线性空间； （C ）数域P 上所有二级反对称矩阵作成的线性空间； （D ）复数域C 作为复数域C 上的线性空间。

2、（ ）设 是非零线性空间 V 的线性变换，则下列命题正确的是：（A ） 的核是零子空间的充要条件是 是满射； （B ） 的核是V 的充要条件是 是满射； （C ） 的值域是零子空间的充要条件是 是满射； （D ） 的值域是V 的充要条件是 是满射。

3、（ ）λ-矩阵()A λ可逆的充要条件是： ()()()()0;A AB A λλ≠是一个非零常数；()()C A λ是满秩的；()()D A λ是方阵。

4、（ ）设实二次型f X AX '=（A 为对称阵）经正交变换后化为：2221122...n n y y y λλλ+++， 则其中的12,,...n λλλ是：()()1;A B ±全是正数；()C 是A 的所有特征值；()D 不确定。

云南大学2009——2010第1学期数学分析期末考试试卷
一、叙述题：（每小题6分，共18分）
1、 牛顿-莱不尼兹公式
2、 ∑∞=1n n a
收敛的cauchy 收敛原理
3、 全微分
二、计算题：（每小题8分，共32分）
1、40202sin lim x dt t x x ⎰→
2、求由曲线2x y =和2y x =围成的图形的面积和该图形绕x 轴旋转而成的几何体的体积。

3、求∑∞
=+1)1(n n
n n x 的收敛半径和收敛域，并求和
4、已知z y x u = ，求y
x u ∂∂∂2 三、（每小题10分，共30分）
1、写出判别正项级数敛散性常用的三种方法并判别级数
∑∞
=1!n n n n 2、讨论反常积分⎰+∞
--01dx e x x p 的敛散性
3、讨论函数列),(1
)(22+∞-∞∈+=
x n x x S n 的一致收敛性 四、证明题（每小题10分，共20分）
1、设)2,1(11,01 =->>+n n x x x n n n ，证明∑∞=1
n n x 发散 2、证明函数⎪⎩
⎪⎨⎧=+≠++=000),(22222
2y x y x y x xy y x f 在（0，0）点连续且可偏导，但它在该点不可微。

，。

高等代数（II ）期末考试试卷及答案（A 卷） 一、 填空题（每小题3分，共15分）1、线性空间[]Px 的两个子空间的交()()11L x L x -+=2、设12,,...,n εεε与12,,...,n εεε'''是n 维线性空间 V 的两个基， 由12,,...,n εεε到12,,...,n εεε'''的过渡矩阵是C ，列向量X 是V 中向量ξ在基12,,...,n εεε下的坐标，则ξ在基12,,...,n εεε'''下 的坐标是3、设A 、B 是n 维线性空间V 的某一线性变换在不同基下的矩阵， 则A 与B 的关系是4、设3阶方阵A 的3个行列式因子分别为：()21,,1,λλλ+则其特征矩阵E A λ-的标准形是5、线性方程组AX B =的最小二乘解所满足的线性方程组是：二、 单项选择题（每小题3分，共15分）1、 （ ）复数域C 作为实数域R 上的线性空间可与下列哪一个 线性空间同构：（A ）数域P 上所有二级对角矩阵作成的线性空间； （B ）数域P 上所有二级对称矩阵作成的线性空间； （C ）数域P 上所有二级反对称矩阵作成的线性空间； （D ）复数域C 作为复数域C 上的线性空间。

2、（ ）设 是非零线性空间 V 的线性变换，则下列命题正确的是：（A ） 的核是零子空间的充要条件是 是满射； （B ） 的核是V 的充要条件是 是满射； （C ） 的值域是零子空间的充要条件是 是满射； （D ） 的值域是V 的充要条件是 是满射。

3、（ ）λ-矩阵()A λ可逆的充要条件是： ()()()()0;A AB A λλ≠是一个非零常数；()()C A λ是满秩的；()()D A λ是方阵。

4、（ ）设实二次型f X AX '=（A 为对称阵）经正交变换后化为：2221122...n n y y y λλλ+++， 则其中的12,,...n λλλ是：()()1;A B ±全是正数；()C 是A 的所有特征值；()D 不确定。

高等代数（北大版）第一学期考试卷答案一、选择题（每小题3分，共24分）1.Ｄ2.Ｃ3.Ｂ4.Ｄ5.Ａ6.Ｂ7.Ｃ8.Ａ二、填空题（每小题3分，共１８分）1．322(1)5(1)7(1)1x x x -+-+-- 2．2x + 3．1()2n n +- 4．)1,,1,1( c x = 5．d6．⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=-3/13/1003/23/100005200211A三、计算题（本大题共３个小题，共2２分.请写出必要的推演步骤和文字说明）１．（6分）设b ax x x x x f +++-=23463)(，1)(2-=x x g ，a 与b 是什么数时，)(x f 能被)(x g 整除？解：方法一、利用辗转相除法，得余式：7)3()(++-=b x a x r ，………………………………………..4分由已知， 7,3-==b a ……………………………………………..2分方法二、由于)(x f 能被)(x g 整除，而1)(2-=x x g 的零点为1和-1，所以1和-1也应是)(x f 的零点，即04)1(=++=b a f 和 010)1(=+-=-b a f …………5分 故7,3-==b a …………………………………………………...….1分２．（8分）已知B AX X +=，其中⎪⎪⎪⎭⎫ ⎝⎛---=101111010A ，⎪⎪⎪⎭⎫ ⎝⎛--=350211B ，求矩阵X 。

解：由 B AX X += 得 B X A E =-)(而 ⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=-201101011101111010100010001A E 可逆…………….2分可以求得 ⎪⎪⎪⎭⎫ ⎝⎛--=--11012312031)(1A E ……………………………………….. .3分 所以 ⎪⎪⎪⎭⎫ ⎝⎛--=-=-11012312031)(1B A E X ⎪⎪⎪⎭⎫ ⎝⎛--350211=⎪⎪⎪⎭⎫ ⎝⎛--110213………………3分３．（８）b a ,取什么值时,线性方程组⎪⎪⎩⎪⎪⎨⎧=-+++=+++=-+++=++++bx x x x x x x x x a x x x x x x x x x x 5432154325432154321334536223231有解？在有解的情形求一般解。

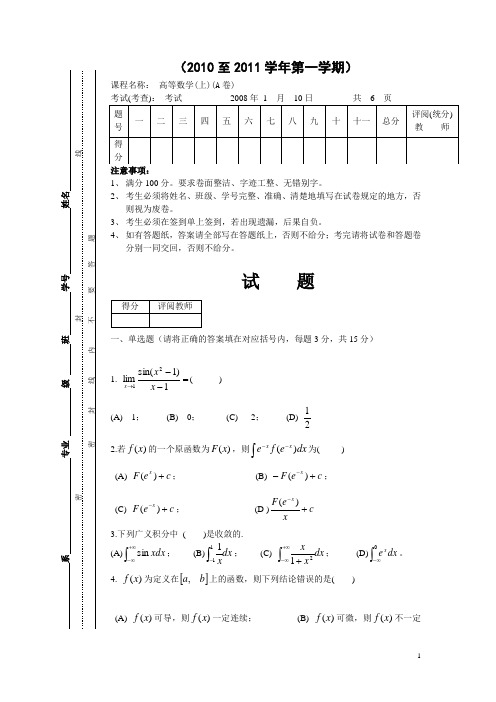
（2010至2011学年第一学期）课程名称： 高等数学(上)(A 卷)考试(考查)： 考试 2008年 1 月 10日 共 6 页 注意事项：1、 满分100分。

要求卷面整洁、字迹工整、无错别字。

2、 考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方，否则视为废卷。

3、 考生必须在签到单上签到，若出现遗漏，后果自负。

4、 如有答题纸，答案请全部写在答题纸上，否则不给分；考完请将试卷和答题卷分别一同交回，否则不给分。

试 题一、单选题（请将正确的答案填在对应括号内，每题3分，共15分）1. =--→1)1sin(lim21x x x ( ) (A) 1； (B) 0； (C) 2； (D)212.若)(x f 的一个原函数为)(x F ，则dx e f e xx )(⎰--为( )(A) c e F x +)(； (B) c eF x+--)(；(C) c e F x+-)(； (D )c xe F x +-)( 3.下列广义积分中 ( )是收敛的. (A)⎰+∞∞-xdx sin ； (B)dx x⎰-111； (C) dx x x ⎰+∞∞-+21； (D)⎰∞-0dx e x。

4. )(x f 为定义在[]b a ,上的函数，则下列结论错误的是( )(A) )(x f 可导，则)(x f 一定连续； (B) )(x f 可微，则)(x f 不一定可导；(C) )(x f 可积（常义），则)(x f 一定有界； (D) 函数)(x f 连续，则⎰xadt t f )(在[]b a ,上一定可导。

5. 设函数=)(x f nn x x211lim++∞→ ，则下列结论正确的为( )(A) 不存在间断点； (B) 存在间断点1=x ； (C) 存在间断点0=x ； (D) 存在间断点1-=x二、填空题（请将正确的结果填在横线上.每题3分，共18分）1. 极限=-+→xx x 11lim 20 _____.2. 曲线⎩⎨⎧=+=321ty t x 在2=t 处的切线方程为______. 3. 已知方程xxe y y y 265=+'-''的一个特解为x e x x 22)2(21+-，则该方程的通解为 .4. 设)(x f 在2=x 处连续，且22)(lim2=-→x x f x ，则_____)2(='f5．由实验知道，弹簧在拉伸过程中需要的力F （牛顿）与伸长量s 成正比，即ks F =（k 为比例系数），当把弹簧由原长拉伸6cm 时，所作的功为_________焦耳。

高等代数第一学期试卷及答案(A)1. 若 $b_1c_1=b_3m$，则 $a_2=$B. $-15m$2. $n$ 阶矩阵 $A$ 可逆的充分必要条件是 A. $\vertA\vert\neq0$3. 下列说法不正确的是 B. 如果 $f(x)\mid g(x)$，$g(x)\mid h(x)$，则 $f(x)\mid h(x)$4. 设向量组 $\alpha,\beta,\gamma$ 线性无关，$\alpha,\beta,\delta$ 线性相关，则() D. $\mathrm{\delta}$ 一定不能由 $\mathrm{\alpha,\beta,\gamma}$ 线性表示5. 对于 $n$ 元方程组，下列命题正确的是 B. 如果$Ax=0$ 只有零解，则 $Ax=b$ 也只有零解6. 若$A=\begin{pmatrix}1&2&3\\4&5&6\\5&6&7\end{pmatrix}$，则$\vert A\vert=$ $-3$7. $f(x)=x^4+x^3-1$，则 $f^\prime(x)=4x^3+3x^2$8. 已知 $\vert A\vert=-113$，则 $A_{12}-A_{22}+A_{32}-A_{42}=$ $-1145$9. 设$A=\begin{pmatrix}1&2&3\\2&4&6\\3&6&9\end{pmatrix}$，则$(A^{-1})^*=$ $\begin{pmatrix}0&0&1\\0&1&0\\1&0&0\end{pmatrix} $10. 若 $\alpha_1=(1,0,5,2)^T,\alpha_2=(3,-2,3,-4)^T,\alpha_3=(2,4,1,0)^T$，则 $\alpha_3$ 可以由$\alpha_1,\alpha_2$ 线性表示，且线性表示为 $\alpha_3=-\alpha_1+2\alpha_2$。

数学与应用数学专业本科期末考试试卷（A ）课程名称： 高等代数 任课教师： 考试时间： 120 分钟 考试性质（学生填写“√”）：正常考试（ ）缓考补考（ ）重修（ ）提前修读（ ）一、填空题（每小题2分）1. 设n x f =∂))((, 且)()(x f x g , )()(x g x f , 则))((x g ∂=_________．2. 在数域P 上有根, 但是在P 上不可约的多项式是__________多项式．3. )(x f 是首项系数为1的实系数三次多项式. 若0)()3(==i f f , 则)(x f =_________________．4. 在行列式55511511a a a a 中, 含有32a 且带有负号的项共有_________项．5. 在行列式1314021b a -中, b 的代数余子式为-24, 则a =________．6. 当矩阵A=______时, 秩A=0.7. 已知A 为三阶矩阵, 且A =1, 则A 2-=_________．8. 向量组{k ααα,,,21 }和{m βββ,,,21 }的秩分别是s 和t , 则{k αα,,1 ,m ββ,,1 }的秩r 与s ,t 适合关系式____________．9. 设A 为n 阶方阵, X 1, X 2均为方程组AX=B 的解, 且21X X ≠, 则A =____．10. 设A, B 都是三阶方阵, 秩A=3, 秩B=2, 则秩(AB)=____________．二、单选题（每小题2分））.(A) S 1={Z n m mn ∈,2}; (B) S 2={Z b a bi a ∈+,};(C) S 3={Z z nz ∈}; (D) S 4={Q b a b a ∈+,2}．2. 设0)(≠x f , 且)())(),((x d x g x f =, )()()()()(x d x v x g x u x f =+, 则错误的结．．．．论．是( ). (A) 1))()(,)()((=x d x g x d x f ; (B) )())(),((x d x v x u =; (C) )())(),()((x d x g x g x f =+; (D) )())(),((m m m x d x g x f =．3. 设行列式D 1=333231232221131211a a a a a a a a a , D 2=313233212223111213a a a a a a a a a ,则下面结论正确的有( ). (A)D 2=－D 1； (B)D 2=0； (C)D 2与D 1无关； (D)D 2=D 1．4. )(x f =xx x x x111123111212-中 4x 的系数为（ ）(A) 1, (B) 2, (C) 0, (D) 3．5. 22)13)()(1()(--+=x i x x x f 在复数域上的标准分解式是（ ）(A)22)13)()(1(--+x i x x ; (B) 22)13())((--+x i x i x ;(C)22)31())((--+x i x i x ; (D) 22)31())((9--+x i x i x ．6．若r ααα,,,21 是线性无关的向量组, 则r r k k k ααα,,,2211 也线性无关的条件是（ ）(A) r k k k ,,,21 不全为零, (B) r k k k ,,,21 全为零, (C) r k k k ,,,21 全不为零, (D)以上结论都错．7. 在一个含有n 个未知数m 个方程的线性方程组中，若方程组有解，则（ ） (A) m ＞n ； (B) m ＜n ； (C) m =n ； (D)与m ,n 的大小无关． 8. 若矩阵A 的秩为r ，则（ ）(A)A 有r 阶非零子式； (B)A 有r 阶非零子式且任意r +1阶子式为0； (C)A 的任意r +1阶子式为0； (D)A 的r 阶子式都不等于0． 9. 下列矩阵中( )不是初等矩阵(A)⎪⎪⎪⎭⎫ ⎝⎛-100010001; (B)⎪⎪⎪⎭⎫ ⎝⎛101010100; (C)⎪⎪⎪⎭⎫ ⎝⎛010100001; (D)⎪⎪⎪⎭⎫⎝⎛100010101．10. 若数域P 上三元齐次线性方程组0=AX 的基础解系中仅含有一个向量,则其系数矩阵的秩是( )(A) 0; (B) 1; (C) 2; (D) 3．三、判断正误（每小题2分）1. 若)()()(21x f x f x g +, 且)()()(21x f x f x g -, 则)()(1x f x g ,且)()(2x f x g .( )2. 若n 级行列式D ≠0, 则D 的n-1阶子式不全为零. ( )3. 初等矩阵的逆矩阵仍为初等矩阵. ( )4. 若A,B 均为n 阶可逆矩阵, 则A+B 也是n 阶可逆矩阵． ( )5. 等价的向量组含有相同个数的向量． ( ) 四、计算题（第1、2小题每题10分，第3小题15分）1. 计算n 阶行列式nnna a a a a a a a a a a a +++111321321321．2. 设111111022110110211X --⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭，求矩阵X ．3. 用导出组的基础解系表出线性方程组⎪⎪⎩⎪⎪⎨⎧=+-++-=---+=-++=+-++55493123236232335432154321432154321x x x x x x x x x x x x x x x x x x x 的全部解.五、证明题（第1小题7分，第2小题8分）1. 设P[x]的多项式)(x f 与不可约多项式)(x p 有一个公共根, 则)()(x f x p ．2. 若方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++++++11212111221111212111n n n n n n n n nn n n n n b x a x a x a b x a x a x a b x a x a x a 有解, 则行列式111111111+++n nn n n nnn n b a a b a a b a a=0．。

数学系《高等代数》期末考试试卷年级专业学号姓名注：考试时间120分钟，试卷满分100分。

题号一二三四五总分签名得分一装订线得分阅卷教师一．判断题（正确的在题后的括号内打“√”；错误的在题后的括号内打“×”.每小题2分，共18分）1．向量空间一定含有无穷多个向量. ( ) 2．若向量空间V的维数dimV2,则V没有真子空间. ( )3.n维向量空间中由一个基到另一个基的过渡矩阵必为可逆矩阵. ( ) 4．线性变换把线性无关的向量组映成线性无关的向量组. ( ) 5．每一个线性变换都有本征值. ( ) 6．若向量是线性变换的属于本征值的本征向量，则由生成的子空间为的不变子空间. ( )7．保持向量间夹角不变的线性变换是正交变换. ( ) 8．两个复二次型等价的充分必要条件是它们有相同的秩. ( )9.若两个n阶实对称矩阵A,B均正定,则它们的和A B也正定. ( )得二分阅卷教师二．单项选择题（在每小题的四个备选答案中，选出一个正确的答案，并将其号码填在题目的括号内.每小题2分，共10分）1.下列命题不正确的是 ( ).A.若向量组{1,2,,r}线性无关，则它的任意一部分向量所成的向量组也线性无关；B.若向量组{1,2,,r}线性相关，则其中每一个向量都是其余向量的线性组合；C.若向量组{1,2,,r}线性无关，且每一i可由向量{1,2,,s}线性表示，则r s ；D.n(n0)维向量空间的任意两个基彼此等价.2.下列关于同构的命题中，错误的是( ).A．向量空间V 的可逆线性变换是V 到V 的同构映射；B．数域F 上的n 维向量空间的全体线性变换所成向量空间与数域F 上的所有n 阶矩阵所成向量空间同构；C．若是数域F 上向量空间V 到W 的同构映射，则1是W 到V 的同构映射；D．向量空间不能与它的某一个非平凡子空间同构.3．n 阶矩阵A 有n 个不同的特征根是A 与对角矩阵相似的 ( ).A．充分而非必要条件； B．必要而非充分条件；C．充分必要条件； D.既非充分也非必要条件．21x14．二次型q(x 1,x 2,x 3)(x 1,x 2)31x的矩阵是( ).22121A．； B．3111；310210C．310； D．1100000005.实二次型q(x 1,x 2,x 3)x Ax 正定的充分且必要条件是 ( ).A．A0； B．秩为3；C．A 合同于三阶单位矩阵； D．对某一x (x 1,x 2,x 3)0,有x Ax 0.三得分阅卷教师三．填空题（每小题2分，共10分，把答案填在题中横线上）1.复数域C 作为实数域R 上的向量空间，它的一个基是________.2.设F n{(x 1,x 2,,x n)xiF ,i 1,2,,n}是数域F 上n 元行空间，对任意(x 1,x 2,,x n)F n ，定义((x 1,x 2,,x n ))(0,0,x 1,x 2,,x n 2)，则是一个线性变换，且的核Ker()的维数等于______.3.若A 是一个正交矩阵，则A 2的行列式A 2=________.4.在欧氏空间R 3中向量1(1,0,0)与2(0,1,0)的夹角=______.5.实数域Ｒ上5元二次型可分为_______类，属于同一类的二次型彼此等价，属于不同类的二次型互不等价.得四分阅卷教师四．计算题（每小题14分，共42分）1．求齐次线性方程组x 1x 2x 3x 403x 12x 2x 3x 40x 2x 2x 03425x14x 23x 33x4的解空间的一个基，再进一步实施正交化，求出规范正交基．1002．设A 021,求A 的特征根及对应的特征向量.问A 是否可以对角化？032若可以，则求一可逆矩阵T ，使T 1AT 为对角形.3．写出3元二次型q(x1,x2,x3)x1x24x2x3的矩阵．试用非奇异的线性变换，将此二次型变为只含变量的平方项.五得分阅卷教师五．证明题（每小题10分，共20分）1．设1,2为n阶矩阵A的属于不同特征根，1,2分别是A的属于1,2的特征向量，证明12不是A的特征向量.2．设是n维欧氏空间V的正交变换，且2为单位变换，某一规范正交基的矩阵，证明A为对称矩阵．A是关于V的数学系《高等代数》期末考试试卷（A 卷）年级专业学号姓名注：考试时间120分钟，试卷满分100分。

云南民族大学2009——2010第1学期高等代数期末试卷课程名称：高等代数专业： 学号： 年级：一年级 姓名：考试时间：200 年 月 日（星期 ） 午 ： -- ：题号 一 二 三 四 总分 阅卷人成绩一. 填空题 （将正确答案填在题中括号内。

每小题2分，共10分）1. 齐次线性方程组0332211=++x x x ααα的系数行列式0321=ααα，那么，此方程组有___________解，且系数列向量321,,ααα是线性___________.2. 已知 ()()(),.1,0,3,0,1,2,1,0321k TT-===ααα当k 満足___________时，321,,ααα构成3R 中的一个基。

3. 在3R 上的线性变換T 为()ααA T =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=541452121A则T 的秩为__________，T 的零度为__________。

4. 设1，-1，2是三阶矩阵A 的特征值, 且235A A B -=，则B 的特征值为___________________________.5. 实二次型2322213213),,(x x x x x x f +-=的秩为__________，正惯性指数为__________，负惯性指数为__________，符号差为__________。

二. 单项选择题 (每小题仅有一个正确答案, 将正确答案的番号填入下表内.每小题3分, 共24分)题号 1 2 3 4 5 6 7 8 答案番 号1. 三个方程四个未知量的非齐次线性方程组B AX =，若__________成立，则该方程组一定有解。

(A ) 1)(=A R ； (B) 2)(=A R ；(C ) 3)(=A R ; (D ) ()3=A R 。

2. 齐次线性方程组⎩⎨⎧=+++=+++0022112211nn n n x b x b x b x a x a x a的基础解系中含有1-n 个解向量，则必有__________成立),,2,1,0,0(n i b a i i =≠≠。

云南大学硕士研究生入学考试试题专业：基础数学、计算数学、应用数学、运筹学与控制论 考试科目：《高等代数A 卷》一、 (1)若()24224x ax bx -++，则a = ，b = 。

(2)方程23411111248013927x x x x = 的所有根为（3）设n 阶方阵A 的每个元素都等于1，则A 的n 个特征值为 （4）若矩阵A 满足220A A E +-=（其中E 为n 阶单位矩阵），则()12A E --=二、计算行列式510001100011000110011a a a a D a aa a a---=------三、求线性方程组1234512345123451234522122141055712147111x x x x x x x x x x x x x x x x x x x x -+-+=⎧⎪+-+-=⎪⎨-+-+=⎪⎪-+-+=-⎩ 的通解（用基础解系表示）四、设1000111011102220A ⎛⎫⎪---⎪= ⎪⎪⎝⎭（1）求A 的若当标准形 （2）求A 的最小多项式五、设f(x),g(x)分别为m 次和n 次多项式(),1m n ≥证明：f(x),g(x)不互素的充分必要条件是存在次数<n 的多项式u(x)和次数<m 的多项式v(x)使得u(x)f(x)=v(x)g(x) 六、设T A B ααβ⎛⎫=⎪⎝⎭其中A 为n 阶正定矩阵，α为n 维实列向量，β为实数，Tα为α的转置，证明：B 为正定矩阵的充分必要条件是1TAβαα->七、已知222254245A -⎛⎫ ⎪=- ⎪ ⎪--⎝⎭，求正交矩阵P ，使得T P AP （其中T P 是P 的转置矩阵）为对角形矩阵。

八、已知A ，B 均为n 阶方阵，且A ，B ，AB-E 皆可逆。

证明：1A B --和()111A BA -----都可逆，且有等式()()1111A BAABA A ------=-九、设A 为n 阶实对称矩阵且A 的主对角线上的元素之和等于正整数N ，求2E A +的最大值。

一、填空题（每小题2分，共10分）1．多项式22009320101()(2)()2f x x x =+-的常数项为 。

2．设,,a b c 是方程30x px q ++=的三个根，则a bcb c a c a b = 。

3．线性方程组m n A x b ⨯=有无穷多解的充要条件是______________________。

4．设矩阵123012001A ---⎛⎫ ⎪-- ⎪ ⎪-⎝⎭＝，则1A -的秩为 。

5．设实二次型123(,,)f x x x 的矩阵是111t ⎛⎫⎪⎝⎭，则123(,,)f x x x 是正定二次型的充要条件是 。

二、单选题（每小题2分，共10分）1．实数域上次数大于1的多项式()f x 有一实根是()f x 在实数域上可约的（ ）。

a) 必要非充分条件 b) 充分必要条件 c) 充分非必要条件 d) 既非充分又非必要条件2．行列式111213212223313233a a a a a a d a a a =，则332313322212312111a a a a a a a a a =（ ）。

a) d - b) d c) 0 d) 不确定3．λ=（ ），非齐次线性方程组12323232132(3)(4)(2)x x x x x x x λλλλλλ+-=-⎧⎪-=-⎨⎪-=--+-⎩有无穷多解。

a) 1 b) 2 c) 3 d) 4 4．若矩阵A 满足20A A E ++=，则9A =（ ）。

a) A b) A - c) E d) 05．矩阵（ ）合同与200010005-⎛⎫ ⎪⎪ ⎪⎝⎭ 。

a) 4000100010⎛⎫⎪⎪ ⎪⎝⎭b) 300020005⎛⎫⎪ ⎪ ⎪-⎝⎭c) 100010001-⎛⎫⎪- ⎪ ⎪⎝⎭d) 200020001⎛⎫⎪ ⎪ ⎪⎝⎭三、判断题（每小题2分，共10分）1．若()()()h x f x g x ，则()()h x f x 或()()h x g x 。

一、单选题（32分. 共8题, 每题4分）1.下列说法错误的是________.A)若向量组线性无关，则其中任意两个向量线性无关；B)若向量组中任意两个向量线性无关，则线性无关；C)向量组线性相关；D)若向量组线性无关，则线性无关.设n维列向量线性无关, 则n维列向量2.A)向量组可由向量组线性表示；B)向量组可由向量组线性表示；C)向量组与向量组等价；D)矩阵与矩阵相抵.3.设线性方程组的解都是线性方程组的解，则____.A) ；B) ；C) ； D).4.设n阶方阵A的伴随矩阵，非齐次线性方程组有无穷多组解，则对应的齐次线性方程组的基础解系____.A) 不存在； B) 仅含一个非零解向量；C) 含有两个线性无关的解向量； D) 含有三个线性无关的解向量.5.下列子集能构成的子空间的是________.A) ； B)；C) ； D).6.设V是数域K上的线性空间, V上的线性变换在基下的矩阵为A且，若在基下的矩阵为B, 则________.A) ； B) 2； C) ； D)不能确定.7.设V是维向量空间，和是V上的线性变换，则的充分必要条件是________.A) 和都是可逆变换； B) Ker=Ker；C) ； D) 和在任一组基下的表示矩阵的秩相同.8.设是线性空间V到U的同构映射, 则下列命题中正确的有________个.(Ⅰ) 为可逆线性映射；(Ⅱ) 若W是V的s维子空间, 则是U的s维子空间；(Ⅲ) 在给定基下的表示矩阵为可逆阵；(Ⅳ) 若, 则.A) 1 B) 2 C) 3D) 4二、填空题（32分. 共8题,每题4分）1.若矩阵经过行初等变换化为, 那么向量组的一个极大无关组是_________________, 其余向量由此极大无关组线性表示的表示式为________________.2.设3维向量空间的一组基为，则向量在这组基下的坐标为____.3.设，均为线性空间V的子空间，则____.4.数域上所有三阶反对称矩阵构成的线性空间的维数是____.而____是它的一组基.5.已知上的线性变换定义如下：，则Ker=____.Im=____.6.设是数域上维线性空间V到维线性空间U的线性映射, 则为满射的充分必要条件是____.（请写出两个）7.设和是线性空间V的两组基，从到的过渡矩阵为. 若是V上的线性变换且，则在基下的表示矩阵是____ .8.设是线性空间V上的线性变换，在基下的表示矩阵为，其中A为矩阵，则存在V的一个非平凡-不变子空间____.三、(8分) 设线性空间V的向量组线性无关，，考虑向量组.求证：或者该向量组线性无关，或者可由线性表示.四、(10分) 设,分别是数域上的齐次线性方程组与的解空间. 证明.五、(10分) 设. 证明：的充分必要条件是存在，，使得且.六、 (8分) 设V, U, W是有限维线性空间，，是线性映射. 求证：存在线性映射使得的充分必要条件是.附加题: (本部分不计入总分)设V, U, W 是有限维线性空间且，，是线性映射. 证明：存在可逆线性映射使得的充分必要条件是.一、填空：（每空2分，共30分）1、n 元二次型正定的充分必要条件是它的正惯性指数______________。

大学期末考试试卷（A 卷）2010学年第一学期 考试科目： 高等代数Ⅰ考试类型：（闭卷） 考试时间： 90 分钟学号 姓名 年级专业 题号 一二三四五总分得分 评阅人一、填空题（35=15分）1、设A 是n 阶方阵，12,X X 均为线性方程组AX b =的解，且12X X ≠，则A 的秩 ；2、已知213233220343131D-=--，则1112131433A A A A -+-＝ ；3、若A 为三阶方阵，*A 为A 的伴随矩阵，且|A |=12，则1*|(3)2|A A --= ；4、如果向量()()()21231,1,1,1,1,1,1,1,1,(1,)ααα=+λ=+λ=+λβ=λ,λ，β可以由123,,ααα唯一地线性表示，那么λ满足：；5、设2是多项式43228xx ax bx -++-的二重根，则a =，b =。

二、判别题（25=10分）（请在正确的小题对应的括号内打“√”，否则打“”）6、如果()d x 是多项式() f x 和()g x 的一个最大公因式且()()()d x u x f x =()()v x g x +，那么()u x 和()v x 唯一。

（ ） 7、设A 为n 阶方阵，若AX AY =，且0A ≠，则X Y =。

（ ） 8、若矩阵A 有一个非零r 阶子式，则()r A r ≥。

（ ）9、含有n 个未知数的线性方程组有解的充分必要条件是它的系数矩阵的秩等于n 。

（ ） 10、若A 是正定矩阵，那么1A -也是正定矩阵。

（ ）三、单项选择题（35=15分）11、若集合{}|,Fa bi ab R =+∈（这里R 是实数集）是数域，则,a b 应满足条件（ ）。

（A ）,a b 是整数 （B ）,a b 是无理数 （C ）a 是有理数，b 是实数 （D ）,a b 是任意实数 12、初等矩阵（ ）（A ）所对应的行列式的值等于1 （B ）都是可逆矩阵 （C ）相乘仍为初等矩阵 （D ）相加仍为初等矩阵 13、设rs <, 两个n 维向量组：{}12s α,α,⋯,α(1)， {}12r β,β,⋯,β(2) 下述正确的是（ ）（A ）若(1)可由(2)线性表出, 则(1)线性相关； （B ）若(1)可由(2)线性表出, 则(1)线性无关；（C ）若(1)可由(2)线性表出, 则当(2)线性无关时, (1)线性无关； （D ）若(1)可由(2)线性表出, 则仅当(2)线性相关时, (1)线性相关。