简单的推理 (1)

简单的推理
举一反三1
1、在甲、乙、丙、丁四人同住的一座四层的楼房里。

已知甲比乙住的楼层高，比丙住的楼层低，丁住第四层，甲、乙、丙、丁各住哪层？
2、四个小朋友站成一排，乙站在甲的右边，丙站在甲的左边，丁站在丙的左边。

请问：甲、乙、丙、丁四位小朋友是怎样站的？
举一反三2
1、A、B、C、D四人在同一个房间，其中一人在修指甲，一人在洗头，一人在画画，另一人在看书。

已知：A没修指甲，也没看书；B没画画，也没修指甲；若A没画画，则D没修指甲；C既没看书，也没修指甲；D没看书，也没画画。

请问：他们各自在干什么？
2、甲、乙、丙三人，一个姓张，一个姓李，一个姓王，他们一个是银行职员，一个是计算机程序员，一个是秘书。

又知甲不是银行职员也不是秘书；丙不是秘书；张不是银行职员；王不是乙，也不是丙。

问甲、乙、丙三人分别姓什么？
举一反三3
1、下图是标有1~6数字的正方体的三种不同摆法，问三个正方体朝左那一面的数字之和是多少？
2、下面是飞行棋的一颗骰子，根据图中三种状态所显示的数字，推出“？”处的数字是多少？
举一反三4
1、张三说：“李四在说谎。

”李四说：“王五在说谎。

”王五说：“张三、李四都在说谎。

”那么说真话的是谁？
2、甲、乙、丙、丁四人踢毽子比赛，赛前名次说法不一。

有的说：“甲第一名，丁第三名。

”有的说：“甲第一名，丁第二名。

”有的说：“丙第二名，丁第四名。

”实际上，这三种说法各对一半，请说出四人的名次。

第24讲简单推理一、知识要点数学课上，老师布置了一道题：□＋△=28 □=△＋△＋△□=（）△=（）要得出正确的结论，就要进行分析、推理。

学会了推理，能使你变得更聪明，头脑更灵活。

数学上有许多重大的发现和疑难问题的解决都离不开推理。

解答这类推理题时，要求小朋友仔细观察，认真分析等式中几个图形之间的关系，寻找解题的突破口，然后再利用等量代换、消去等方法来进行解答。

二、精讲精练【例题1】下式中，□和△各代表几？□＋△=28 □=△＋△＋△□=（）△=（）练习1：1．☆＋○=18 ☆=○＋○☆=（）○=（）2．△＋○=25 △=○＋○＋○＋○△=（）○=（）3．○＋□=36 ○=□＋□＋□＋□＋□○=（）□=（）【例题2】下式中，□和△各代表几？□×△=36 □÷△=4 □=（）△=（）练习2：1．○和□各表示几？○×□=16 □÷○=4 ○=（）□=（）2．想想，填填。

○×△=20 ○=△＋△＋△＋△＋△○=（）△=（）3．□和○各代表几？□=○＋○＋○＋○○×□=16□=（）○=（）【例题3】下式中，□和△各代表几？□＋□＋△=16 □＋△＋△=14□=（）△=（）练习3：1．下式中，□、○各代表几？□＋□＋○＋○=38 □＋□＋○=22□=（）○=（）2．下式中，□和△各代表几？□＋□＋□＋△＋△=52 □＋□＋△＋△＋△=48□=（）△=（）3．下式中，□、○和△各代表几？○＋△＋□＋□=10 △＋□＋△＋□=12 △＋○＋□＋○=12 ○=（）□=（）△=（）【例题4】下式中，□、○各代表几？□＋□＋○＋○＋○=34 ○＋○＋○＋○＋□＋□＋□=48 □=（）○=（）练习4：1．下式中，☆、△各代表几？☆＋☆＋△＋△＋△=24 △＋△＋△＋△＋☆＋☆＋☆=36 ☆=（）△=（）2．下式中，△和○各代表几？○＋○＋○＋△＋△=54 △＋△＋△＋○＋○＋○＋○=76 ○=（）△=（）3．下式中，□、△各代表几？□＋□＋□＋△＋△＋△＋△=96△＋△＋△＋△＋△＋□＋□＋□＋□=123□=（）△=（）【例题5】下式中，□、☆和△各代表几？☆＋☆=□＋□＋□□＋□＋□=△＋△＋△＋△☆＋□＋△＋△=80☆=（）□=（）△=（）练习5：1．下式中，□、△和○各代表几？△＋△=○＋○＋○○＋○＋○=□＋□＋□○＋□＋△＋△=100○=（）□=（）△=（）2．下式中，□、△和○各代表几？○＋○=□＋□＋□□＋□＋□=△＋△△＋□＋○=40 △=（）□=（）○=（）3．下式中，□、☆和○各代表几？□＋□=○＋○＋○○＋○＋○=☆＋☆＋☆＋☆＋☆＋☆＋☆＋☆□＋○＋☆＋☆＋☆＋☆=320○=（）□=（）☆=（）三、课后作业1、下式中，□、☆各代表几？□+□+☆＋☆＋☆＋☆=38☆＋☆＋☆＋☆＋☆＋☆＋☆+□+□=53□=（）☆=（）2、下式中，○和△各代表几？△＋△＋△＋○＋○=96○＋○+△＋△＋△＋△＋△＋△＋△=176△=（）○=（）3、下式中，☆和△各代表几？☆＋△＋△＋△＋△=70 △＋△＋△＋△+☆＋☆＋☆=90 △=（）☆=（）4、下式中，△和○各代表几？△=○＋○＋○＋○○×△=16△=（）○=（）5、下式中，□和○各代表几？○×□=20 □=○＋○＋○＋○＋○○=（）□=（）6、下式中，□、☆各代表几？□+□+☆＋☆＋☆=31☆＋☆＋☆＋☆+□+□+□=43□=（）☆=（）7、下式中，△和○各代表几？△＋△+○＋○＋○＋○＋○=56○＋○＋○＋○＋○＋○＋△＋△＋△=75△=（）○=（）8、下式中，△和○各代表几？△＋△＋△+○＋○＋○＋○=68○＋○＋○+△＋△=50△=（）○=（）9、下式中，□、☆和△各代表几？☆＋☆＋☆=□＋□＋□＋□□＋□=△＋△＋△☆+□+△=90☆=（）□=（）△=（）。

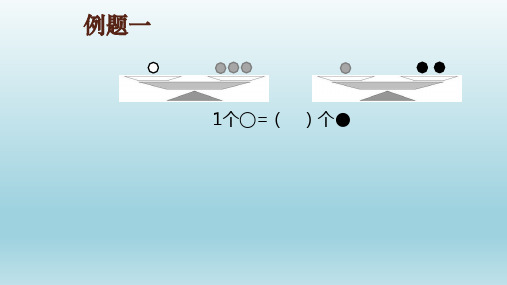
二年级简单推理（简单推理1）例1：一头猪的重量=两只羊的重量1只羊的重量＝5只兔的重量问：1只猪的重量＝（）只兔的重量练习1。

一壶水的重量=两瓶水的重量，一瓶水的重量=四杯水的重量，然后一壶水的重量=（）一杯水的重量。

练习2、1个苹果换2个椅子，1个椅子换6块糖，想想看，一个苹果可以换成糖果。

练习3、1头牛换4头猪，1头猪换3只羊，1只羊换10只兔，想一想，1头牛能换（）只兔子。

例2。

一个黑色球的重量=两个灰色球的重量，一个灰色球的重量=三个白色球的重量，三个黑色球的重量=（）白色球的重量。

练习1。

一头猪换两只羊，1只羊换2只兔子，4头猪换（）只兔子。

练习2。

一头大象的重量等于四头牛的重量，1头牛的重量等于3匹小马的重量，1匹小马的重量等于3头小猪的重量。

1头象的重量等于（）头小猪的重量。

一练习3、2只鸡的重量等于1只兔的重量，一只兔子的重量等于四只鸭子的重量，一只鸡的重量等于（）只鸭子的重量。

例3、☆、△、○各代表什么数字？☆＋☆＋☆＝18☆＝（）△＋☆＝14△＝（）△＋○＋○＋○＝20○＝（）练习1，○ + ○ + ○ = 15☆＋☆＋☆＝12△＋△＋△＝18○＋☆＋△＝（）练习2。

△ + ○ = 24,○＝△＋△＋△△＝（）○＝（）练习3、○＝△＋△＋△＋△＋△○×△＝20○＝（）△＝（）例4。

找出由△ 和☆ 在下面的公式中。

☆＋☆＋☆＋△＋△＝22△＋△＋☆＋☆＋☆＋☆＋☆＝30☆=()△=()二练习1、□＋□＋△＋△＋△＝21□＋□＋△＋△＋△＋△＋△＝27□＝（）△＝（）练习2、□＋□＋○＋○＝14□＋□＋○＝11□＝（）○=()练习3、春节到了，爸爸买了2只鸭、1只鸡共付33元，如果买2只鸭、3只鸡要付51元，问一只鸡和一只鸭各多少钱？例5。

找出由△ 和□ 在下面的公式中。

△＋□＝9△ + △ + □ + □ + □ + □ = 25△ = () □ = （）练习1，□ + □ + △ = 16□＋△＋△＝14□＝（）△＝（）练习2、○＋☆＋☆＝10○＋☆＋○＝8.○＝（）☆＝（）练习3。

简单推理例1：晴晴比珊珊高，珊珊比慧慧高，她们三人中，谁最高？练习1：东东比明明重，明明比力力重，他们三人中，谁最轻？谁最重？练习2：东东比明明矮，明明比军军矮，他们三人，谁最矮？例2：桌子上有三盘糖，小明说：“第一盘比第三盘多3个。

”小军说：“第三盘比第二盘少5个。

”哪盘糖最多？哪盘糖最少？练习1：三个小朋友比大小，根据下面的两句话，请你猜一猜，谁最大？谁最小？1：芳芳比阳阳大3岁， 2：宁宁比芳芳小2岁。

例3：红红，颖颖，慧慧三人都戴着太阳帽参加野炊活动，她们分别戴了红帽子，黄帽子和蓝帽子，只知道红红没有戴黄帽子，颖颖没戴蓝帽子也没黄帽子，请问她们三人分别戴了什么颜色的帽子？练习1：李颖，马娟和林红都穿了新裙子，她们穿的新裙子一个是花的，一个是粉的，一个是蓝的，已知李颖穿的不是粉裙子，林红穿的不是花裙子也不是粉裙子，她们三人分别穿了什么颜色的裙子？练习2、三年级举行英语竞赛，小王、小光和小明取得了前三名。

已知小王不是第一名，小光不是第一名也不是第二名，那么他们各是第几名？例4：一个正方体有6个面，每个面分别涂有红、黄、绿、白、蓝、黑六种颜色，你能根据这下正方体的三种不同摆法，判断出每一种颜色的对面是什么颜色吗？练习1、有一个正方体，它的六个面上分别写着六个汉字：我、们、喜、欢、数、学。

如图是三位同学从三个不同角度观察到的。

这个正方体相对面上各是什么汉字？练习2、冬冬、晨晨和方方三位小朋友分别出生在上海、北京和南京三个城市中。

已知冬冬从没有到过上海；上海出生的小朋友不叫晨晨；晨晨不出生在南京。

问：三位小朋友的出生地各是哪里？例5：甲、乙、丙，丁4个人同住一座4层的楼房里，他们之中有工程师，教师，医生和商人，如果已知：1：甲比乙住的楼层高，比丙住的楼层低、丁住在第1楼.2：教师住在医生楼上，在商人楼下。

工程师住在最顶楼。

请问：他们4人各住在第几层？各是什么职业？练习：一个院子里住了4户人家，房号分别是：1，2，3，4，主人有张三，李四，王五，赵六。

简单推理
1、李大爷家养了6只兔子，有2只黑兔子，4只白兔子，每只黑兔子生5只小兔，李大爷家一共有几只兔子？
2、1只钢笔可以换3只圆珠笔，1只圆珠笔可以换4只铅笔，1只钢笔可以换几支铅笔？
3、在一次书法比赛中，大刚，小刚，大毛小毛四人得了前四名，有人问他们各得了第几名，大刚说：“我得了第二名。

”小刚说：“我是第一名。

”大毛说：“我是第四名。

”小毛说：“我不是第三名。

”已知他们中有1人的名次说错了，请问：谁是第四名？
4、某校五年级三个班举行乒乓球混双表演，每班男女生各出一名，男生是甲乙丙，女生是
A、B、C、规定：同班男女生不能配对，第一盘甲、A对丙、B，第二盘丙、C对甲和乙班的同班女同学，问：甲的同班女同学是谁？
5、某商品编号是一个三位数，现有五个三位数：784、765、123、、394、927，其中每一个数与这个商品编号恰好在同一个数位上有一个相同的数字，这个商品编号是多少？
6、A、B、C、D、E五个人如下排列：A在C前面5米，B在C后面5米，A在E前面1米，E在D前面7米，那么
（1）C与E之间有多少米？
（2）紧跟在C后面的是谁？相距多少米？
（3）最前面的人与最后面的人相距多少米？。

15 简单推理（一）教学目标:1、通过解决一些简单的问题，向学生初步渗透等量代换的思想方法，为以后学习简单的代数知识做准备。

2、提高学生运用等量代换的数学思想解决一些简单的实际问题的能力。

3、培养学生逻辑推理能力，感受数学就在身边，体验用“数学”的乐趣。

教学重点:在观察和分析中，正确找到事物相互之间的等量关系，发现规律获得结论。

教学难点：在解决问题中理清数量之间的等量关系，从而解决等量代换的问题。

教学过程：一、情景体验课件出示曹冲称象的故事。

师：曹冲利用什么的重量称出了大象的重量？生：石头。

师：为什么曹冲称出了石头的重量也就知道了大象的重量？生：因为石头和大象的重量是相等的。

师：是呀！像这样两个完全相等的量是可以互换的，我们称之为等量代换，曹冲才7岁就有等量代换的方法解决了大人们都难以解决的问题，你们想不想学习这种方法吗？生：想！师：今天我们就一起来学习这种解决问题的方法吧！（板书课题：等量代换）二、思维探索（建立知识模型）展示例1例1：☆和△各代表几？☆+△=28 ☆=△+△+△师：根据题意，☆和△有怎样的数量关系呢？生：一个☆等于3个△。

师：既然一个☆等于3个△，那你知道几个△之和等于28吗？生：将等式1中的一个☆换成3个△，△+△+△+△=28，也就是4个△之和是28。

师：那△代表几吗？生：△=28÷4=7师：很好！那☆=？生：3×7=21师：对，请同学们将计算结果代入到题目中的等式进行验证。

小结：通过等量代换，将不同量转化为同一量进行计算，从而使问题得以解决。

例2：○和□各代表几？○×□=18，□÷○=2○=（），□=（）。

师：根据□÷○=2，说明□与○有怎样的数量关系呢？生：一个□等于○的2倍。

师：也就是说□=○×2，将□换成○代入到乘法算式中，该怎么书写呢?生：○×○×2=18师：你知道○代表几吗？生：○×○=9，所以○=3师：很好！那□=？生：2×3=6，所以□=6师：对，请同学们将计算结果代入到题目中的等式进行验证。