重力加速度表

2
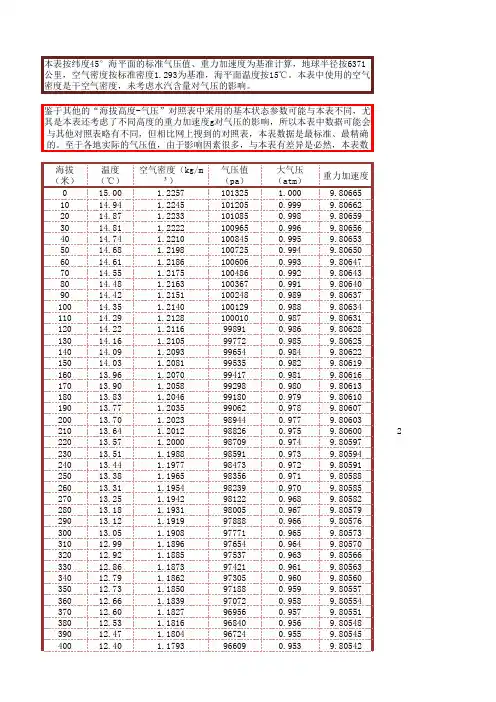
本表按纬度45°海平面的标准气压值、重力加速度为基准计算，地球半径按6371公里，空气密度按标准密度1.293为基准，海平面温度按15℃。

本表中使用的空气密度是干空气密度，未考虑水汽含量对气压的影响。

鉴于其他的“海拔高度-气压”对照表中采用的基本状态参数可能与本表不同，尤其是本表还考虑了不同高度的重力加速度g对气压的影响，所以本表中数据可能会与其他对照表略有不同，但相比网上搜到的对照表，本表数据是最标准、最精确的。

至于各地实际的气压值，由于影响因素很多，与本表有差异是必然，本表数
1。

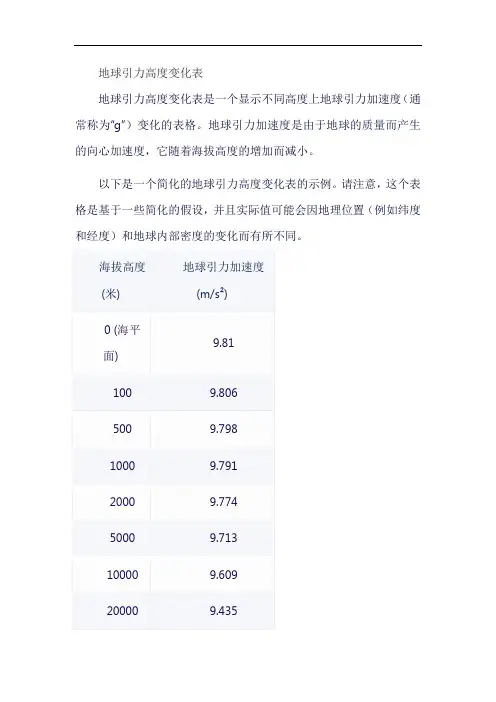
地球引力高度变化表地球引力高度变化表是一个显示不同高度上地球引力加速度（通常称为“g”）变化的表格。

地球引力加速度是由于地球的质量而产生的向心加速度，它随着海拔高度的增加而减小。

以下是一个简化的地球引力高度变化表的示例。

请注意，这个表格是基于一些简化的假设，并且实际值可能会因地理位置（例如纬度和经度）和地球内部密度的变化而有所不同。

这个表格显示了随着海拔的增加，地球引力加速度逐渐减小。

在海拔10000米以上，地球引力加速度的减小变得更为显著。

要生成更精确的地球引力高度变化表，您需要使用更复杂的数学模型，例如考虑地球的形状（不是完美的球体）和地球内部密度的变化。

此外，您还可以使用地理信息系统（GIS）软件或在线工具来生成特定地理位置的地球引力高度变化表。

地球引力随高度的变化而变化，但具体的引力高度变化表可能因地理位置、地球模型、大气条件等多种因素而有所不同。

通常情况下，地球引力随高度的增加而减小，因为引力与距离的平方成反比。

在地球表面附近，重力加速度约为9.81 m/s²，这意味着物体自由下落的速度将每秒增加约9.81米。

然而，随着高度的增加，地球引力逐渐减弱，重力加速度也会逐渐减小。

据估计，每升高1000米，重力加速度约减小3.1 m/s²。

需要注意的是，这个变化率并不是线性的，因为地球是一个球体，所以引力随高度的变化是非线性的。

此外，地球自转也会对引力产生影响，导致赤道处的重力加速度略低于两极处的重力加速度。

总的来说，地球引力的具体高度变化表需要根据具体的地理位置和地球模型进行计算。

在实际应用中，可以使用重力加速度随高度的变化公式进行计算，或者使用地球重力场模型进行更精确的预测。

重力加速度几种测量方法的比较引言：重力加速度是物理学中的一个十分重要的物理量，在地面上不同的地区，重力加速度g值不相同，它是由物体所在地区的纬度、海拔等因素决定，随着地球纬度和海拔高度的变化而变化，准确地确定它的量值，无论从理论上、还是科研上、生产上以及军事上都有极其重大的意义。

测量重力加速度的方法有很多，我所要做的就是通过学习前人的理论知识，经过思考，在现有的实验室条件下，进行实验，做出归纳和总结，提出自己的看法与体会。

且实验方法虽然多，但有的测量仪器的精确度受环境因素的影响比较大，不是每种方法都适用，所以有必要对测量方法进行研究，找出一种适合测量本地重力加速度的方法。

一、重力加速度的测量方法（一）用自由落体法测量重力加速度1.实验仪器：自由落体装置（如图一），数字毫秒计，光电门（两个），铁球。

图一自由落体装置2.实验原理、步骤、注意事项实验原理：设光电门A 、B 间的距离为s ，球下落到A 门时的速度为0v ，通过A 、B 间的时间为t ，则成立：2/20gt t v s += （1）两边除以t ,得：2//0gt v t s += （2）设t x =,t s y /=,则：2/0gx v y += （3）这是一直线方程，当测出若干不同s 的t 值，用t x =和t s y /=进行直线拟合，设所得斜率为b ，则由2/g b =可求出g ，b g 2=（4） 实验步骤：（1）调节实验装置的支架，使立柱为铅直，再使落球能通过A 门B 门的中点。

（2）测量A 、B 两光电门之间的距离s 。

（3）测量时间t 。

（4）计算各组的x ，y 值，用最小二乘法做直线拟合，求出斜率b 及其标准偏差b S 、)(b u （注意：在取b 的时，由于立柱调整不完善，落球中心未通过光电门的中点，立柱上米尺的误差均给s 值引入误差，也是b 的不确定度来源，一般此项不确定度（B 类评定）较小，可略去不计，所以b S b u =)(）。

2
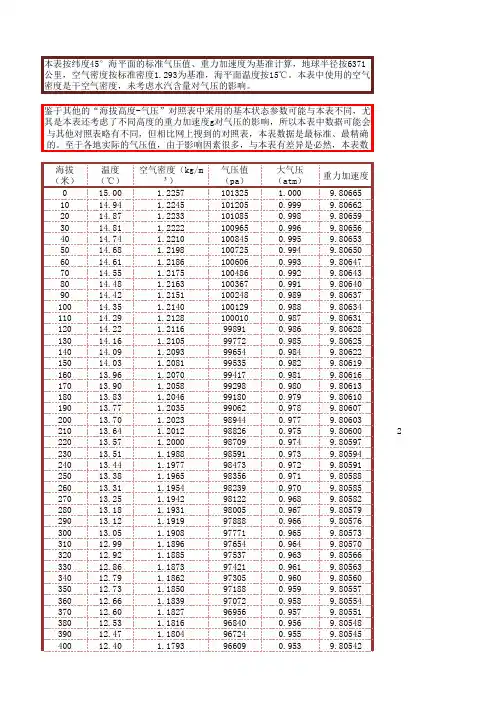
本表按纬度45°海平面的标准气压值、重力加速度为基准计算，地球半径按6371公里，空气密度按标准密度1.293为基准，海平面温度按15℃。

本表中使用的空气密度是干空气密度，未考虑水汽含量对气压的影响。

鉴于其他的“海拔高度-气压”对照表中采用的基本状态参数可能与本表不同，尤其是本表还考虑了不同高度的重力加速度g对气压的影响，所以本表中数据可能会与其他对照表略有不同，但相比网上搜到的对照表，本表数据是最标准、最精确的。

至于各地实际的气压值，由于影响因素很多，与本表有差异是必然，本表数
1。

凯特摆测重力加速度PB09206016 肖啸实验目的：(1)学习凯特摆的实验设计思想和技巧(2)掌握一种比较精确的测量重力加速度的方法实验仪器：凯特摆，光电探头，米尺，V AFN 多用数字测试仪数据处理：(1) 计算l 和1h 的平均值与不确定度由原始数据可得下表表一：l -1h 数值表a) 计算l 的平均值与不确定度 统计计算结果：l=∑l i3i=13=74.260cmσ(l )=√∑(l i −l )23i=1n−1=0.010cml 的A 类不确定度：P=0.683 n=3 取p t =1.32u A (l )=t p√n=1.32×√3=7.62×10−3cml 的B 类不确定度：∆仪=0.1cm k p =1 C =3 P=0.683u B (l )=k p∆仪C=1×0.13=0.033cm合成不确定度：u (l )=√u A (l )2+u B (l )2=√0.007622+0.0332=0.034cm综上，实验测得:l=l ±u (l )=(74.260±0.034)cm (P =0.683)b) 计算1h 的平均值与不确定度统计计算结果：1h =∑1h i3i=13=29.923cm σ(1h )=√∑(1h i −1h )23i=1n−1=0.025cm1h 的A 类不确定度：P=0.683 n=3 取p t =1.32u A (1h )=t pσ(1h )√n=1.32×√3=0.019cm1h 的B 类不确定度：∆仪=0.1cm k p =1 C =3 P=0.683u B (1h )=k p∆仪C=1×0.13=0.033cm合成不确定度：u(1h )=√u A (1h )2+u B (1h )2=√0.0192+0.0332=0.038cm综上，实验测得:1h =1h ±u (1h )=(29.923±0.038)cm (P =0.683)(2) 计算1T 和2T 的平均值与不确定度由原始数据可得下表表二：摆动周期数值表a) 计算1T 的平均值与不确定度 统计计算结果：T 1=110×∑T 1i5i=15=1.73505sσ(T 1)=110×√∑(T 1i −T 1)25i=1n−1=0.000046s1T 的A 类不确定度：P=0.683 n=5 取p t =1.14u A (T 1)=t p 1√n=1.14×√5=0.000023s1T 的B 类不确定度：∆仪=0.0001s k p =1 C =3 P=0.683u B (T 1)=k p∆仪C=1×0.00013=0.000033s合成不确定度：u (T 1)=√u A (T 1)2+u B (T 1)2=√0.0000232+0.0000332 =0.000040s综上，实验测得T 1=T 1±u (T 1)=(1.73503±0.00004)s (P =0.683)b) 计算2T 的平均值与不确定度 统计计算结果：T 2=110×∑T 2i5i=15=1.73429sσ(T 2)=110×√∑(T 2i −T 2)25i=1n−1=0.000032s2T 的A 类不确定度：P=0.683 n=5 取p t =1.14u A (T 2)=t p 2√n=1.14×√5=0.000016s2T 的B 类不确定度：∆仪=0.0001s k p =1 C =3 P=0.683u B (T 2)=k p∆仪C=1×0.00013=0.000033s合成不确定度：u (T 2)=√u A (T 2)2+u B (T 2)2=√0.0000162+0.0000332 =0.000037s综上，实验测得T 2=T 2±u (T 2)=(1.73429±0.00004)s (P =0.683)(3)计算重力加速度g 的平均值与不确定度由公式 2222212121422(2)T T T T a b g l h l π+-=+=+- 带入数值，得到重力加速度g ：1222221221214422(2)T T T T g a b l h l ππ-⎡⎤-+==+⎢⎥+-⎢⎥⎣⎦=4π2[1.735032+1.7342922×0.74260+1.735032−1.7342922×(2×0.29923−0.74260)]−1=9.7795m/s 2下面计算g 的不确定度由于221212(2)T T b h l -=- 的大小相对22122T T a l +=非常小因此 12222122212842T T l g l T T ππ-⎡⎤+≈⨯=⎢⎥+⎣⎦两边取对数 22221222128ln ln 8ln ()l g ln l ln T T T T ππ==+-++ 两边取全微分11222222121222T dT T dT dg dl g l T T T T =--++ 因此有()u g g =得到g 的合成不确定度公式()u g g =⨯=0.0045m/s2不确定度保留一位有效数字，因此：综上，实验测得g=g ±u (g )=(9.780±0.005) m/s 2 (P=0.683)误差分析：(1)本实验对周期的测量较精确，但是对等效摆长的测量却有很大的误差，由于钢卷尺较软，加之凯特摆形状的限制，对两刀口间距离（即l ）德德良存在很大误差。

地球表面重力加速度公式
地球表面重力加速度的公式是：g=GM/r²。

其中，g为重力加速度，G为万有引力常数，M为地球质量，r为距离地球表面的半径。

这个公式基于牛顿第二定律，表明重力加速度与距离的平方成反比，与质量M成正比。

另一个常用的公式是：g=9.7803(1+0.0052884sin²φ-
0.0000059sin²2φ)m/s²。

其中，φ为物体所在处的地理纬度。

这个公式将地球视为旋转椭球，并考虑了地球自转的影响。

请注意，地球表面重力加速度的值会随纬度和海拔的变化而变化。

在地球表面，重力加速度的平均值约为9.8m/s²，但在不同地方可能会有所不同。

因此，在实际应用中，需要根据具体情况选择合适的公式和参数进行计算。

分类号密级U D C 编号本科毕业论文(设计)题目测重力加速度的几种方法比较及误差分析系别专业名称物理学年级学生姓名学号指导教师二00 八年五月摘要：地球表面及附近的物体受到地球重力的作用，如果忽略空气摩擦的影响，则所有落地物体都将以同一加速度下落，这个加速度称为重力加速度。

重力加速度是一个重要的地球物理常数，准确测定它的量值，不仅在理论上，而且在生产上、科研上都有着极其重要的意义。

在实验室内测量重力加速度的方法有很多种。

本文利用实验室的仪器，通过单摆法、电磁打点计时器法、倾斜气垫导轨法以及复摆法进行测量重力加速度的实验。

通过实验原理、实验方法、实验记录数据、误差分析、最终结果等方面进行比较与研究，针对可能造成较大误差的变量，提出可实施的改进办法，提高实验测量值的可靠性。

关键词：重力加速度单摆电磁打点计时器气垫导轨复摆Abstract: On Earth, everything feels the downward force of gravity. If we neglect the friction force of the air, all the masses will be falling freely with the same downward acceleration because gravity is the only force acting. This is the acceleration of free fall. The constant acceleration, g, is very important. Measuring exactly plays a significant role in theory, production and scientific research. There are many methods for measuring g in laboratories. The major content about this thesis is doing experiments through using the simple pendulum, the electromagnetic pointing set, the sloping air track and the compound pendulum. Then compare the principle, method or result of the four experiments and analyze the error. At the end, suggest practicable and improvable measures in accordance with the larger error for raising accuracy.Key words: acceleration of gravity simple pendulum electromagnetic pointing set air track compound pendulum文献综述一、概述测量重力加速度的方法有很多种，包括用单摆测重力加速度、用电磁打点计时器测重力加速度、用自由落体法测重力加速度、用复摆测重力加速度、用凯特摆测重力加速度、倾斜气垫导轨上测重力加速度以及频闪照相法测重力加速度等。

液氯的物理性质-密度和饱和蒸汽压.温度℃饱和液密度kg/m3-20 152820 140640 134250 1307图1 液氯密度随温度变化图图2 液氯温度与饱和蒸汽压图1atm=1.0133*10^5Pa表1-1 全国各地区重力加速度表序号地区重力加速度序号地区重力加速度序号地区重力加速度1 包头9.798612海口9.786323沈阳9.80352 北京9.801513合肥9.794724石家庄9.79973 长春9.804814吉林9.804825太原9.79704 长沙9.791515济南9.798826天津9.80115 成都9.791316昆明9.783027乌鲁木齐9.80156 重庆9.791417拉萨9.779928西安9.79447 大连9.801118南昌9.792029西宁9.79118 广州9.783319南京9.79493张家口9.80009 贵阳9.79682南宁9.787731郑州9.79661 0 哈尔9.806621青岛9.7985滨1 1 杭州9.793622上海9.7964地球各点重力加速度近似计算公式:g=g(1-0.00265cos&)/1+(2h/R)g:地球标准重力加速度9.80665(m/平方秒)&:测量点的地球纬度h:测量点的海拔高度R:地球的平均半径(R=6370km)30m3的液氯储罐的设计2011133152目录1 引言 (6)2设计任务书 (7)3设计参数及材料的选择 (7)3.1 设备的选型与轮廓尺寸 (7)3.2 设计压力 (7)3.2 筒体及封头材料的选择 (11)3.3 许用应力 (11)4结构设计 (11)4.1筒体壁厚计算 (11)4.2 封头设计 (12)4.2.1 半球形封头 (12)4.2.2 标准椭圆形封头 (13)4.2.3 标准蝶形封头 (14)4.2.4 圆形平板封头 (14)4.2.5 不同形状封头比较 (15)4.3 压力试验 (16)4.4鞍座 (17)4.4.1鞍座的选择 (17)4.4.2 鞍座的位置 (18)5 结果 (20)参考文献 (22)1 引言液氯化学名称液态氯，为黄绿色液体，沸点-34.6℃，溶点-103℃，在常压下即气化成气体，吸入人体能严重中毒，有剧烈刺激作用和腐蚀性，在日光下与其它易燃气体混合时发生燃烧和爆炸，氯是很活泼的元素，可以和大多数元素（或化合物）起反应。

世界各地的重力加速度分别是多少一些城市的纬度和重力加速度地点纬度重力加速度附注赤道9.780 m/s2新加坡北纬1°17′9.7807马尼拉北纬14°35′9.7836南宁北纬22°43′9.7876广州北纬23°06′9.7883福州北纬28°02′ 9.7916杭州北纬30°16′ 9.7930武汉北纬30°33′ 9.7936上海北纬31°12′ 9.7940东京北纬35°42′ 9.7980海拔18m华盛顿北纬38°53′ 9.8011北京北纬39°56′ 9.8012罗马北纬41°54′ 9.8035海拔59m巴黎北纬48°50′ 9.8094海拔61m格林威治北纬51°29′ 9.81188伦敦北纬51°31′ 9.81199海拔30m柏林北纬52°31′ 9.8128海拔30m莫斯科北纬55°45′9.8156海拔139m好望角南纬33°56′9.7963海拔11m爪哇南纬6°9.7820北极909.832由于g随纬度变化不大，因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米／秒^2作为重力加速度的标准值。

在解决地球表面附近的问题中，通常将g作为常数，在一般计算中可以取g=9.80米／秒^2。

理论分析及精确实验都表明，随纬度的提高，重力加速度g的数值略有增大，如赤道附近g=9.780米／秒^2，北极地区g=9.832米／秒^2。

地球各点重力加速度近似计算公式:g=g0(1-0.00265cos&)/1+(2h/R)g0:地球标准重力加速度9.80665(m/平方秒)&:测量点的地球纬度 h:测量点的海拔高度 R:地球的平均半径(R=6370km) s:时间参考资料：/ 其他回答chenbinghui1988 2008-11-05 14:45:22地点纬度重力加速度附注赤道9.780 m/s2新加坡北纬1°17′9.7807马尼拉北纬14°35′9.7836南宁北纬22°43′9.7876广州北纬23°06′9.7883福州北纬28°02′ 9.7916杭州北纬30°16′ 9.7930武汉北纬30°33′ 9.7936上海北纬31°12′ 9.7940东京北纬35°42′ 9.7980海拔18m华盛顿北纬38°53′ 9.8011北京北纬39°56′ 9.8012罗马北纬41°54′ 9.8035海拔59m巴黎北纬48°50′ 9.8094海拔61m格林威治北纬51°29′ 9.81188伦敦北纬51°31′ 9.81199海拔30m柏林北纬52°31′ 9.8128海拔30m莫斯科北纬55°45′9.8156海拔139m好望角南纬33°56′9.7963海拔11m爪哇南纬6°9.7820北极909.832由于g随纬度变化不大，因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米／秒^2作为重力加速度的标准值。

重力加速度计算重力加速度是指物体受到地球引力作用下，其速度每秒增加9.8米/秒的加速度。

它是一个基本物理常数，被广泛应用于科学研究和工程实践中。

计算重力加速度的方法有多种。

其中一种常见的方法是使用质量和距离的关系来计算。

根据万有引力定律，两个物体之间的引力正比于它们的质量乘积，并且与它们之间的距离的平方成反比。

重力加速度可以通过以下公式计算：a = G * (m / r^2)其中，a表示重力加速度，G是引力常数（约等于6.67430 × 10^(-11) N·(m/kg)^2），m是物体的质量，r是物体与地球之间的距离。

以地球为例，如果我们想要计算在地球表面上的重力加速度，我们可以将物体的质量设定为单位质量（1千克），并将距离设定为地球半径（约为6371千米）。

代入上述公式进行计算，我们得出的结果是约9.8米/秒^2，这就是地球表面上的重力加速度。

除了上述方法，还有一种常用的计算重力加速度的方法是使用牛顿第二定律。

牛顿第二定律表明，物体的加速度与作用在它上面的力成正比，与物体的质量成反比。

在地球上，物体受到的力是由地球对物体的引力产生的。

因此，我们可以使用下述公式来计算重力加速度：a = F / m其中，a表示重力加速度，F表示物体所受到的重力，m表示物体的质量。

在地球上，物体所受到的重力可以用以下公式计算：F = m * g其中，g表示重力加速度。

通过将上述两个公式相结合，可以得出重力加速度的计算公式为：a = g也即，地球上物体的重力加速度等于常数9.8米/秒^2。

在其他天体或不同位置的重力加速度计算中，我们需要使用相应的质量和距离。

比如在月球上，我们可以将相应的地球到月球的平均距离和月球质量代入重力加速度的计算公式，得出约为1.6米/秒^2的结果。

总结来说，重力加速度的计算方法有多种，其中一种是使用万有引力定律以及地球的质量和距离来计算；另一种是使用牛顿第二定律以及物体质量和所受到的重力来计算。

我国主要城市的重力加速度：北京：9.80151天津：9.80106唐山：9.80164石家庄：9.79973昆明：9.78363南宁：9.78769柳州：9.78850乌鲁木齐：9.80146武汉：9.79361呼和浩特：9.79864吉林：9.80480长春：9.80476西安：9.79136成都：9.79134哈尔滨：9.80665开封：9.79660南昌：9.79196广州：9.78833青岛：9.79849南京：9.79494上海：9.79460福州：9.78910杭州：9.79362F=mg-V(&k)g=mg-(m/&f)g(&k)m:物体的质量g:物体所在地的重力加速度&k:空气密度(一般取1.2kg/立方厘米)&f:物体材料密度地球各点重力加速度近似计算公式:g=g0(1-0.00265cos&)/1+(2h/R)g0:地球标准重力加速度9.80665(m/平方秒) &:测量点的地球纬度h:测量点的海拔高度R:地球的平均半径(R=6370km)s:时间附录D 基本雪压和风压的确定方法D.1基本雪压D.1.1 在确定雪压时，观察场地应具有代表性。

场地的代表性是指下述内容:——观察场地周围的地形为空旷平坦；——积雪的分布保持均匀；——设计项目地点应在观察场地的地形范围内，或它们具有相同的地形。

对于积雪局部变异特别大的地区，以及高原地形的山区，应予以专门调查和特殊处理。

D.1.2 雪压是指单位水平面积上的雪重，单位以kN/㎡计。

当气象台站有雪压记录时，应直接采用雪压数据计算基本雪压；当无雪压记录时，可间接采用积雪深度，按下式计算雪压：式中h—积雪深度，指从积雪表面到地面的垂直深度(m)；ρ—积雪密度(t/m3)；g—重力加速度，9.8m/s2。

雪密度随积雪深度、积雪时间和当地的地理气候条件等因素的变化有较大幅度的变异，对于无雪压直接记录的台站，可按地区的平均雪密度计算雪压。