进制转换方法

进制转换规则⼀、⼗进制与⼆进制之间的相互转换⼗进制——>⼆进制1. 整数部分和⼩数部分分别转换，2.⼗进制整数转换为⼆进制整数：除2，由下往上取余3.⼗进制⼩数转换为⼆进制⼩数：乘2，由上往下取整⼆进制——>⼗进制将⼆进制数的每⼀位数乘以它的权，然后相加，即可求得对应的⼗进制数值。

⼆、⼋进制与⼗进制、⼆进制之间的相互转换⼆进制——>⼋进制从⼩数点起，每三位⼆进制位分成⼀组（不⾜3位时，在⼩数点左边时左边补0，在⼩数点右边时右边补0），然后写出每⼀组的等值⼋进制数，顺序排列起来就得到所要求的的⼋进制数。

⼋进制——>⼆进制将每⼀位⼋进制数⽤三位⼆进制数表⽰，就可以直接将⼋进制数转换成⼆进制数。

⼋进制——>⼗进制将⼋进制数的每⼀位数乘以它的权，然后相加，即可求得对应的⼗进制数值。

⼗进制——>⼋进制1. 整数部分和⼩数部分分别转换，2.⼗进制整数转换为⼋进制整数：除8，由下往上取余3.⼗进制⼩数转换为⼋进制⼩数：乘8，由上往下取整三、⼗六进制与⼗进制、⼆进制之间的相互转换⼗六进制——>⼗进制将⼗六进制数的每⼀位数乘以它的权，然后相加，即可求得对应的⼗进制数值。

⼗进制——>⼗六进制1. 整数部分和⼩数部分分别转换，2.⼗进制整数转换为⼗六进制整数：除16，由下往上取余3.⼗进制⼩数转换为⼗六进制⼩数：乘16，由上往下取整⼗六进制——>⼆进制将每⼀位⼗六进制数⽤四位⼆进制数表⽰，就可以直接将⼗六进制数转换成⼆进制数。

⼆进制——>⼗六进制从⼩数点开始，每4位⼆进制数为⼀组（不⾜4位时，在⼩数点左边时左边补0，在⼩数点右边时右边补0），将每⼀组⽤相应的⼗六进制数符来表⽰，即可得到正确的⼗六进制数。

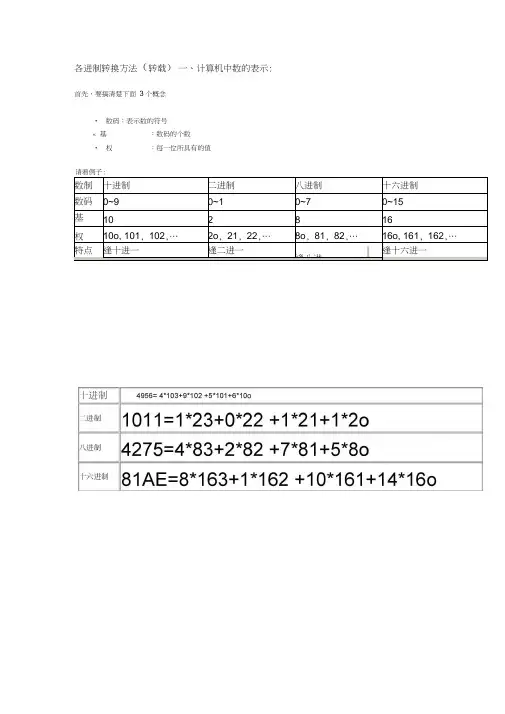
各进制转换方法（转载）一、计算机中数的表示: 首先，要搞清楚下面3个概念•数码：表示数的符号« 基：数码的个数•权：每一位所具有的值、各种进制的转换问题1. 二、八、十六进制转换成十进制2. 十进制转换成二、八、十六进制3. 二进制、八进制的互相转换4. 二进制、十六进制的互相转换1、二、八、十六进制转换成十进制方法：数码乘以相应权之和例(HloJ-l/25+lx24+l/23+0/22+ h2:+h20 -(59)10例(136)8=lx82+3x8l+6x8°=(94)10例(1F2^)1S=1X163+15X16S +2\16] + 10/16° = (7978)102、十进制转换成二、八、十六进制方法：连续除以基，直至商为0,从低到高记录余数例把十进制数159转换成八进制数 8| 198辽(159)IO =(237)8例把十进制数59转换成二进制数(59)IO =(111O11)22 余余余余余余8 159例把十进制数459转换成十六进制数u | 1| C| B(459)io=(1CB)ib '3、二进制、八进制的互相转换方法：*二进制转换成八进制：从右向左，每3位一组(不足3位左补0),转换成八进制*八进制转换成二进制：用3位二进制数代替每一位八进制数例(1101001)2=(001,101,001)2=(151)8例(246)8=(010,100,110)2=(10100110)24、二进制、十六进制的互相转换方法：二进制转换成十六进制：从右向左，每4位一组(不足4位左补0)，转换成十六进制*十六进制转换成二进制：用4位二进制数代替每一位十六进制数例(11010101111101)2=(0011,0101,0111,1101)2=(357D)16例(4B9E)16=(0100,1011,1001,1110)2=(100101110011110)2三、各种进制数的运算方法：逢满进具体计算与平时十进制的计算类似，以十六进制为例: 加法：05C3 + 3D2542 E83D25…05C3376205C3 X OOAB3F61 + 399E3D941。

各种进制之间的转换方法在计算机科学和数学领域中，我们经常会遇到各种不同进制的数，比如二进制、八进制、十进制和十六进制。

而在实际应用中，我们有时需要将一个数从一种进制转换成另一种进制。

本文将介绍各种进制之间的转换方法，帮助读者更好地理解和运用这些知识。

首先，我们来介绍二进制和十进制之间的转换方法。

二进制是计算机中最常用的进制，而十进制则是我们最为熟悉的进制。

将一个二进制数转换成十进制数，我们只需要按照权重相加的原理进行计算即可。

比如，二进制数1011，其对应的十进制数为12^3 +02^2 + 12^1 + 12^0 = 11。

而将一个十进制数转换成二进制数，则可以通过不断除以2取余数的方法进行计算，最后将余数倒序排列即可得到对应的二进制数。

接下来，我们来介绍八进制和十进制之间的转换方法。

八进制是基数为8的一种进制，而十进制则是基数为10的进制。

将一个八进制数转换成十进制数，同样可以按照权重相加的原理进行计算。

比如，八进制数36，其对应的十进制数为38^1 + 68^0 = 24。

而将一个十进制数转换成八进制数，则可以通过不断除以8取余数的方法进行计算，最后将余数倒序排列即可得到对应的八进制数。

再来介绍十六进制和十进制之间的转换方法。

十六进制是基数为16的一种进制，常用于表示颜色、存储地址等。

将一个十六进制数转换成十进制数，同样可以按照权重相加的原理进行计算。

比如，十六进制数2A，其对应的十进制数为216^1 + 1016^0 = 42。

而将一个十进制数转换成十六进制数，则可以通过不断除以16取余数的方法进行计算，最后将余数倒序排列即可得到对应的十六进制数。

除了以上介绍的几种进制之间的转换方法外，我们还可以利用计算机编程语言中的函数来进行进制转换。

比如，在Python语言中，可以使用bin()、oct()、hex()等函数将一个十进制数转换成二进制、八进制、十六进制数。

而int()函数则可以将一个二进制、八进制、十六进制数转换成十进制数。

一、二进制转十进制由二进制数转换成十进制数的基本做法是，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。

这种做法称为按权相加法。

二、十进制转二进制十进制数转换为二进制数时，由于整数和小数的转换方法不同，所以先将十进制数的整数部分和小数部分分别转换后，再加以合并。

1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用除2取余，逆序排列法。

具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

2．十进制小数转换为二进制小数十进制小数转换成二进制小数采用乘2取整，顺序排列法。

具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。

然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。

1．二进制与十进制的转换（1）二进制转十进制方法：按权展开求和例：（1011.01）2 ＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10＝（8＋0＋2＋1＋0＋0.25）10＝（11.25）10（2）十进制转二进制十进制整数转二进制数：除以2取余，逆序输出例：（89）10＝（1011001）22 892 44 12 22 02 11 02 5 12 2 12 1 00 1十进制小数转二进制数：乘以2取整，顺序输出例：(0．625)10= (0．101)20．625 X 21．25 X 20．5 X 21．02．八进制与二进制的转换例：将八进制的37.416转换成二进制数：37 ． 4 1 6011 111 ．100 001 110即：（37.416）8 ＝（11111.10000111）2例：将二进制的10110.0011 转换成八进制：0 1 0 1 1 0 . 0 0 1 1 0 02 6 . 1 4即：（10110.011）2 ＝（26.14）83．十六进制与二进制的转换例：将十六进制数5DF.9 转换成二十进制转二进制：用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如：302转化成二进制302/2 = 151 余0151/2 = 75 余175/2 = 37 余137/2 = 18 余118/2 = 9 余09/2 = 4 余14/2 = 2 余02/2 = 1 余0故二进制为100101110二进制转十进制从最后一位开始算，依次列为第0、1、2...位第n位的数（0或1）乘以2的n次方得到的结果相加就是答案例如:01101011.转十进制:第0位:1乘2的0次方=11乘2的1次方=20乘2的2次方＝01乘2的3次方＝80乘2的4次方＝01乘2的5次方＝321乘2的6次方＝640乘2的7次方＝0然后：1＋2＋0＋8＋0＋32＋64＋0＝107．二进制01101011＝十进制107．。

各种进制之间的转换方法⑴二进制B转换成八进制Q：以小数点为分界线，整数部分从低位到高位，小数部分从高位到低位，每3位二进制数为一组，不足3位的，小数部分在低位补0，整数部分在高位补0，然后用1位八进制的数字来表示，采用八进制数书写的二进制数，位数减少到原来的1/3。

例：◆二进制数转换成八进制数： = 110 110 . 101 100B↓↓ ↓ ↓6 6 . 5 4 =◆八进制数转换成二进制数：3 6 . 2 4Q↓ ↓ ↓ ↓011 110 . 010 100 =◆低位，每4位二进制数为一组，不足4位的，小数部分在低位补0，整数部分在高位补0，然后用1位十六进制的数字来表示，采用十六进制数书写的二进制数，位数可以减少到原来的1/4。

例：◆二进制数转换成十六进制数：.100111B = 1011 0101 1010 . 1001 1100B↓ ↓ ↓ ↓ ↓B 5 A . 9C = 5A◆十六进制数转换成二进制数：= A B . F EH↓ ↓ ↓ ↓1010 1011. 1111 1110 = .1111111B先把八进制数Q转换成二进制数B，再转换成十六进制数H。

例：◆八进制数转换成十六进制数：= 111 100 000 010 . 100 101B= .100101B= 1111 0000 0010 . 1001 0100B= F 0 2 . 9 4H=◆十六进制数转换成八进制数：= 0001 1011 . 1110B== 011 011 . 111B= 3 3 . 7Q=⑷二进制数B转换成十进制数D：利用二进制数B按权展开成多项式和的表达式，取基数为2，逐项相加，其和就是相应的十进制数。

例：◆二进制数转换成十进制数：= 1×25＋1×24＋0×23＋0×22＋1×21＋0×20＋1×2-1= 32＋16＋2＋=◆求8位二进制数能表示的最大十进制数值：最大8位二进制数是BB = 1×27＋1×26＋1×25＋1×24＋1×23＋1×22＋1×21＋1×20= 255⑸十进制数D转换成二进制数B：十进制数转换成二进制数时，整数部分和小数部分换算算法不同，需要分别进行。

一：简述：进位计数制：是人们利用符号来计数的方法。

一种进位计数制包含一组数码符号和两个基本因素。

（1）数码：用不同的数字符号来表示一种数制的数值，这些数字符号称为”数码”。

（2）基：数制所使用的数码个数称为”基”。

（3）权：某数制每一位所具有的值称为”权”。

二：进制转换的理论1、二进制数、十六进制数转换为十进制数：用按权展开法把一个任意R进制数a n a n-1 ...a1a0 . a-1a-2...a-m转换成十进制数，其十进制数值为每一位数字与其位权之积的和。

a n×R n+ a n-1×R n-1+…+ a1×R 1+ a0×R0+ a-1×R-1+ a-2×R-2 + …+ a-m×R-m2、十进制转化成R进制十进制数轮换成R进制数要分两个部分：整数部分：除R取余数，直到商为0，得到的余数即为二进数各位的数码，余数从右到左排列(反序排列)。

小数部分：乘R取整数，得到的整数即为二进数各位的数码，整数从左到右排列(顺序排列)。

3、十六进制转化成二进制每一位十六进制数对应二进制的四位，逐位展开。

4、二进制转化成十六进制将二进制数从小数点开始分别向左（对二进制整数）或向右（对二进制小数）每四位组成一组，不足四位补零。

三、具体实现1、二进制转换成十进制任何一个二进制数的值都用它的按位权展开式表示。

例如：将二进制数(10101.11)2转换成十进制数。

（10101.11）2＝1*24＋0*23＋1*22＋0*21＋1*20＋1*2-1＋1*2-2＝24＋22＋20＋2-1+2-2＝(21.75)102、十进制整理转换成二进制将十进制整数转换成二进制整数采用“除2取倒余法”。

即将十进制整数除以2，得到一个商和一个余数；再将商除以2，又得到一个商和一个余数；以此类推，直到商等于零为止。

每次得到的余数的倒排列，就是对应二进制数的各位数。

二进制，八进制，十进制，十六进制之间的相互转化1.转换为十进制二进制化为十进制例：将二进制数101.01转换成十进制数（101.01）2 = 1×22 + 0×21 + 1×20 + 0×2-1 + 1×2-2 = （5.25）10 八进制化为十进制例：将八进制数12.6转换成十进制数（12.6）8 = 1×81 + 2×80 + 6×8-1 = （10.75）10十六化为十进制例：将十六进制数2AB.6转换成十进制数：（2AB.6）16 = 2×162 + 10×161 + 11×160 + 6×16-1 = （683.375）102.转换为二进制八进制化为二进制规则：按照顺序，每1位八进制数改写成等值的3位二进制数，次序不变。

例：（17.36）8 = （001 111 .011 110）2 = （1111.01111）2十六进制化为二进制规则：每1位十六进制数改写成等值的4位二进制数，次序不变。

例：（3A8C.D6）16 =（0011 1010 1000 1100.1101 0110）2 =（11101010001100.1101011）2十进制整数化为二进制整数规则：除二取余，直到商为零为止，倒排。

例：将十进制数86转化为二进制2 | 86 02 | 43 (1)2 | 21 (1)2 | 10 02 | 5 (1)2 | 2 02 | 1 (1)结果：（86）10 = （1010110）2十进制小数化为二进制小数规则：乘二取整，直到小数部分为零或给定的精度为止，顺排。

例：将十进制数0.875转化为二进制数0.875× 21.75× 21.5×21.0结果：（0.875）10 = （0.111）23.转换为八进制二进制化为八进制整数部份从最低有效位开始，以3位一组，最高有效位不足3位时以0补齐，每一组均可转换成一个八进制的值，转换完毕就是八进制的整数。

二进制、八进制、十进制、十六进制之间转换一、十进制转换为其他进制方法：以二进制为例，除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

下面举例：例：将十进制的168转换为二进制步骤:第一步，将168除以2,商84,余数为0。

第二步，将商84除以2，商42余数为0。

第三步，将商42除以2，商21余数为0。

第四步，将商21除以2，商10余数为1。

第五步，将商10除以2，商5余数为0。

第六步，将商5除以2，商2余数为1。

第七步，将商2除以2，商1余数为0。

第八步，将商1除以2，商0余数为1。

最后，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000将十进制转化为八进制与十六进制，原理相同，每次做除法时把除数变成8或16即可。

例：将十进制的5621转换为八进制步骤:第一步，将5621除以8,商702,余数为5。

第二步，将商702除以8，商87余数为6。

第三步，将商87除以8，商10余数为7。

第四步，将商10除以8，商1余数为2。

第五步，将商1除以8，商0余数为1。

最后，读数，因为最后一位是经过多次除以8才得到的，因此它是最高位，读数字从最后的余数向前读，即12765（2）二进制转换为十进制方法：从最后一位开始算，依次列为第0、1、2...位第n位的数（0或1）乘以2的n次方得到的结果相加就是答案。

例如：二进制1101011 转十进制：第0位（最后一位）:1乘2的0次方=1第1位（最后第二位）：1乘2的1次方=2第2位（最后第三位）：0乘2的2次方＝0第3位（最后第四位）：1乘2的3次方＝8第4位（最后第五位）：0乘2的4次方＝0第5位（最后第六位）：1乘2的5次方＝32第6位（最后第七位）：1乘2的6次方＝64最后：1＋2＋0＋8＋0＋32＋64＋0＝107．二进制1101011＝十进制107．二、二进制、八进制与十六进制的关系首先，我们需要了解一个数学关系，即2^3=8，2^4=16，而八进制和十六进制是用这关系衍生而来的，即用三位二进制表示一位八进制，用四位二进制表示一位十六进制数。

进制转换方法
进制转换方法是将一个数从一种进制表示转换为另一种进制表示的过程。

常见的进制包括二进制、八进制、十进制和十六进制。

以下是一些进制转换方法：
1. 二进制转十进制：将二进制数的每一位与相应的权值相乘，然后将结果相加即可得到十进制数。

2. 十进制转二进制：用除2取余法，将十进制数除以2得到商和余数，将余数从下往上排列即可得到二进制数。

3. 八进制转十进制：将八进制数的每一位与相应的权值（8的幂）相乘，然后将结果相加即可得到十进制数。

4. 十进制转八进制：用除8取余法，将十进制数除以8得到商和余数，将余数从下往上排列即可得到八进制数。

5. 十六进制转十进制：将每一位的十六进制数值与相应的权值（16的幂）相乘，然后将结果相加即可得到十进制数。

6. 十进制转十六进制：用除16取余法，将十进制数除以16得到商和余数，将余数从下往上排列即可得到十六进制数。

这些是常见的进制转换方法，掌握这些方法可以更方便地在不同进制之间进行转换。

各种进制之间的转换方法⑴二进制B转换成八进制Q：以小数点为分界线，整数部分从低位到高位，小数部分从高位到低位，每3位二进制数为一组，不足3位的，小数部分在低位补0，整数部分在高位补0，然后用1位八进制的数字来表示，采用八进制数书写的二进制数，位数减少到原来的1/3。

例：◆二进制数转换成八进制数：110110.1011B = 110 110 . 101 100B↓↓↓↓6 6 . 5 4 = 66.54Q◆八进制数36.24Q转换成二进制数：3 6 . 2 4Q↓↓↓↓011 110 . 010 100 = 11110.0101B⑵二进制数B转换成十六进制数H：以小数点为分界线，整数部分从低位到高位，小数部分从高位到低位，每4位二进制数为一组，不足4位的，小数部分在低位补0，整数部分在高位补0，然后用1位十六进制的数字来表示，采用十六进制数书写的二进制数，位数可以减少到原来的1/4。

例：◆二进制数转换成十六进制数|：101101011010.100111B = 1011 0101 1010 . 1001 1100B↓↓↓↓↓B 5 A . 9C = B5A.9CH◆十六进制数转换成二进制数：AB.FEH = A B . F EH↓↓↓↓1010 1011. 1111 1110 = 10101011.1111111B◆十六进制数、十进制数和二进制数对应关系表⑶八进制数Q转换成十六进制数H：八进制数Q和十六进制数H的转换要通过二进制数B 来实现，即先把八进制数Q转换成二进制数B，再转换成十六进制数H。

例：◆八进制数转换成十六进制数：7402.45Q = 7 4 0 2 . 4 5Q↓↓↓↓↓↓111 100 000 010 . 100 101B= 111100000010.100101B= 1111 0000 0010 . 1001 0100B↓↓↓↓↓= F 0 2 . 9 4H = F02.94H◆十六进制数转换成八进制数：1B.EH =1 B. EH↓↓↓0001 1011 . 1110B= 11011.111B= 011 011 . 111B↓↓↓= 3 3 . 7Q = 33.7Q⑷二进制数B转换成十进制数D：利用二进制数B按权展开成多项式和的表达式，取基数为2，逐项相加，其和就是相应的十进制数。