数值分析实验六(分段三次Hermite插值)

求一次数x0xixn431hermitehermite插值问题的提出三次hermite插值基函数构造法满足插值条件的牛顿插值法误差估计2n1次hermite插值多项式hermite插值问题的提出由于理论与实践的需要在构造插值函数时不但要求在节点上函数值相等而且还要求它的高阶导数值也相等即要求在节点上具有一定的光滑度使得插值函数与被插函数贴近程度更好满足这种要求的插值多项式就是hermite项式有时也称为具有重节点插值或切触插值
由（2.3）可设
0 x x x1 a x x0 b ,
2
再由（2.2）可求得
b 1
x1 x0
2
, a
2
x1 x0
பைடு நூலகம்
3
x x1 x x0 0 x 1 2 x1 x0 x0 x1
4!
3. 2n+1 次Hermite 插值多项式
给定n+1个节点和相应的函数值和导数值：
f xi yi , yi f xi mi , i 0,1,, n
则可构造2n+1 次Hermite 插值多项式H x 满足条件：
H 1） x 是不超过2n+1 次多项式； H 2） xi yi , H xi mi , i 0,1,, n
2
2
f , x0 , x1 4!
4
于是有下述定理
定理：设 H3 x 是以 x0 , x1 为插值节点的三次 f x C 3 a, b , f 4 x 在 a, b Hermite 插值多项式， 内存在，其中 a, b 是包含 x0 , x1 的任一区 间，则对任意给定的 x a, b ，总存在依赖 于 x 的点 a, b ，使 4 f 2 2 R3 x f x H 3 x x x0 x x1 .

2
公式推导
参数三次曲线，简称 PC 曲线，表示为： ������(t) = ������0 + ������1 t + ������2 ������ 2 + ������3 ������ 3 , ������ ∈ [0,1] 确定四个系数矢量的方法是给定曲线两端点及其切矢。 对函数中参数 t 求导，得： ������������ ������′ (������) = = ������1 + 2������2 ������ + 3������3 ������ 2 ������������ 用������ = 0,1代入以上两式，得： ������0 = ������(0) ������0 + ������1 + ������2 + ������3 = ������(1) ������1 = ������′ (0) ������1 + 2������2 + 3������3 = ������′ (1) 写成矩阵形式： ������(0) 1 0 0 0 ������0 ������ ������(1) 1 1 1 1 1 [ ] [������ ] = ′ ������ (0) 0 1 0 0 2 ������ 0 1 2 3 3 [������′ (1)] 于是可得： ������0 1 0 0 0 ������(0) ������1 0 0 1 0 ������(1) [������ ] = [ ] 2 −3 3 −2 −1 ������′ (0) ������3 2 −2 1 1 [������′ (1)] 将上式代入函数方程，得： 1 0 0 0 ������(0) 0 0 1 0 ������(1) ������(t) = [1 ������ ������ 2 ������ 3 ] [ ] −3 3 −2 −1 ������′ (0) 2 −2 1 1 [������′ (1)] 上式即与标量形式的三次埃尔米特插值相对应的参数形式，即定义在区间������ ∈ [0,1]

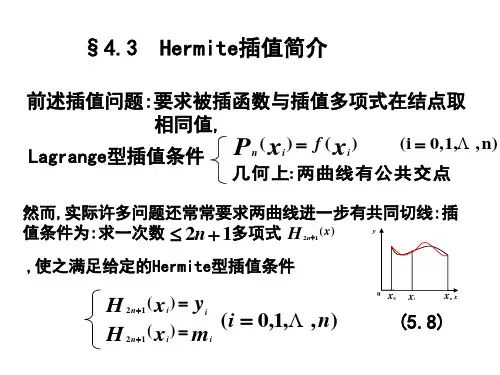
在第一个插值点上的hermite三点插
指公式
在第一个插值点上的hermite三点插指公式
Hermite三点插值法是一种采用三个插值点来求解函数f(x)在给定范围内的曲
线图的插值算法，通常是用来拟合y=f(x)在离散中提供的三个点的插值函数，在
第一个插值点的提出的这种特定的三点插值模型，即对第一个插值点位置
(x0,f(x0))，其中x0为插值点位置，f(x0)为其处的函数值，用的三点模型可写为：
f(x)=f(x0)+f'(x0)(x-x0)+[f''(x0)/2](x-x0)^2
即，把第一个插值点位置(x0,f(x0))处的点代入，可以得到其相应的函数拟合
多项式，当然，并不是每一个函数拟合多项式都能满足实际需求，这就需要注意函数拟合多项式的拟合度，可以在参数估计和函数估计的时候，使用一定的误差来估计函数值，从而获得函数拟合度较好的模型。

此外，在使用Hermite三点插值法时，需要注意三个点之间的位置关系，三个
点位于x0，x1，x2等位置，在确定每个点的位置时应该考虑到它们之间的距离，
一般来说，三个点之间的间距应保持一定，以使插值函数尽可能精确的反映函数的实际变化。

因此，要使得Hermite三点插值法能取得较好的效果，在确定三个插值点的位
置的时候要综合考虑它们之间的位置关系，以及在第一个插值点的估计时要注意拟合度，这样就能很好的进行三点插值，从而得到准确的结果。

Hermite 插值实验的目的及意义：分段线性插值多项式S(x)在差值区间[a,b]上只能保证连续性，而不光滑。

要想得到在插值区间上光滑的分段线性插值多项式，采用Hermite 插值。

（带有导数的插值多项式）。

如果已知函数y=f(x)在节点a=x0<x1<…<xn=b 处的函数值和导数值：()()n i x f y x f y i i i i ,...,2,1,0,'',===则在小区间],[1i i x x -上有四个插值条件：()11--=i i x f y ， ()i i x f y =()11''--=i i x f y ，()i i x f y ''=，故能构造一个三次多项式()x H i ，并称为三次Hermite 插值多项式。

这时在整个[a,b]上可以用分段三次Hermite 插值多项式来逼近f(x).()()()()10121,21,[,],[]......,[,]n n n H x x x x H x x x x H x H x x x x -∈⎧⎪∈⎪=⎨⎪⎪∈⎩ 数学公式：()()2211133[2]()[2()]()i i i i i i i i i iih x x x x h x x x x H x y y h h ---+-----=++2211122()()()()''i i i i i i iix x x x x x x x y y h h -------+算法描述：Step1: 输入未知数X 及ii i y y x ',,其中i=0,1,…,n ；Step2: For i=0,1,…,n 对于指定X,判断X 是否满足条件1i i x X x -〈〈； Step3:如果满足计算()()2211133[2]()[2()]()i i i i i i i i i iih x x x x h x x x x H x y y h h ---+-----=++2211122()()()()''i i i i i i iix x x x x x x x y y h h -------+，如果不满足不执行循环。

数值分析实验六（分段三次Hermite插值）《数值分析》实验报告实验编号：实验六课题名称：分段三次Hermite插值一、算法介绍给定的函数为f(x)=1/(25*x*x+1)，将给定区间分成10分，得到11个节点：x[0],x[1],...,x[10]，构造插值函数的基函数。

当x在(x[0],x[1])区间上时，H[0] = (x-x[0])*[((x-x[1])/(x[0]-x[1]))^2]。

其余的区间为H[0]=0。

h[0]= [1+2*(x-x[0])/(x[1]-x[0])]*[((x-x[1])/(x[0]-x[1]))^2]。

当x在[x[i-1],x[i]] (i=1,2,3, (9)区间上时，H[i]=(x-x[i])*[((x-x[i-1])/(x[i]-x[i-1]))^2]，h[i]=[1+2*(x-x[i])/(x[i-1]-x[i])]*[((x-x[i-1])/(x[i]-x[i-1]))^2)。

当x在(x[i],x[i+1]](i=1,2,3,…,10)区间上其余的区间为H[i]=(x-x[i])[((x-x[i+1])/(x[i]-x[i+1]))^2],h[i]=[1+2*(x-x[i])/(x[i+1]-x[i])]*[((x-x[i+1 ])/(x[i]-x[i+1]))^2]。

其余区间上均为H[i]=0,h[i]=0(i=1,2,…,10)。

当x在(x[9],x[10])区间上时，H[10] = (x-x[9])(((x-x[10])/(x[9]-x[10]))^2).其余的区间为H[10]=0.h[10]= (1+2*((x-x[9])/(x[10]-x[9])))(((x-x[10])/(x[9]-x[10]))^2).其余区间h[10]=0。

构造函数H(x) =∑(y[i]*h[i]+y'[i]*H[i],(i=0,1,…,10)。

二、程序代码// testV iew.cpp : implementation of the CT estV iew class//#include "stdafx.h"#include "test.h"#include "testDoc.h"#include "testView.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////// //////////// CTestV iewIMPLEMENT_DYNCREA TE(CTestView, CView)BEGIN_MESSAGE_MAP(CTestView, CView)//{{AFX_MSG_MAP(CTestView)// NOTE - the ClassWizard will add and remove mapping macros here.// DO NOT EDIT what you see in these blocks of generated code!//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CV iew::OnFilePrint) ON_COMMAND(ID_FILE_PRINT_PREVIEW,CView::OnFilePrintPreview)END_MESSAGE_MAP()/////////////////////////////////////////////////////////////////// //////////// CTestV iew construction/destructionCTestView::CTestV iew(){// TODO: add construction code here}CTestView::~CT estView(){}BOOL CTestView::PreCreateWindow(CREA TESTRUCT& cs){// TODO: Modify the Window class or styles here by modifying // the CREA TESTRUCT csreturn CV iew::PreCreateWindow(cs);}/////////////////////////////////////////////////////////////////// //////////// CTestV iew drawingvoid CTestView::OnDraw(CDC* pDC){CTestDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data hereint i,j,k;double x,y,p_x,p_y,l,xx[100],f[100],F[100],sum,p_sum;CPen MyPen,*OldPen;pDC->SetViewportOrg(400,400); //定义坐标原点for(i=-500;i<500;i++){pDC->SetPixel(0,i,RGB(0,0,0));pDC->SetPixel(i,0,RGB(0,0,0)); //画出坐标}pDC->TextOut(-210,5,"-1");pDC->TextOut(196,5,"1");//原函数MyPen.CreatePen(PS_SOLID,1,RGB(255,0,0));//定义画笔颜色OldPen=pDC->SelectObject(&MyPen);x=-1.0,y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->MoveTo(p_x,p_y);for (x=-1.0;x<=1.0;x+=0.0001){y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->LineT o(p_x,p_y);}pDC->SelectObject(OldPen);MyPen.DeleteObject();//分段三次Hermite插值MyPen.CreatePen(PS_SOLID,1,RGB(0,0,0)); OldPen=pDC->SelectObject(&MyPen); x=-1.0,y=1.0/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->MoveTo(p_x,p_y);x=-1.0;for(i=0;i<=10;i++){f[i]=1/(1+25*x*x);xx[i]=x;F[i]=-50*x/(1+25*x*x)/(1+25*x*x); //导数x+=0.2;}x=-1.0;for(j=0;j<=1000;j++){sum=0;for(i=0;i<=10;i++){if(x==xx[i]){sum=f[i];p_x=x*200,p_y=-sum*200;pDC->LineT o(p_x,p_y);break;}if(xxx[i]){y=(1+2*(x-xx[i])/(xx[i+1]-xx[i]))*(x-xx[i+1])*(x-xx[i+1])/(xx[i]-xx[i+1])/(xx[i]-xx[i+1]);sum+=f[i]*y;y=(1+2*(x-xx[i+1])/(xx[i]-xx[i+1]))*(x-xx[i])*(x-xx[i])/(xx[i+1]-xx[i])/(xx[i+1]-xx[i]);sum+=f[i+1]*y;y=(x-xx[i])*(x-xx[i+1])*(x-xx[i+1])/(xx[i]-xx[i+1])/(xx[i]-xx[i+1]);sum+=F[i]*y;y=(x-xx[i+1])*(x-xx[i])*(x-xx[i])/(xx[i+1]-xx[i])/(xx[i+1]-xx[i]);sum+=F[i+1]*y;p_x=x*200;p_y=-sum*200;pDC->LineT o(p_x,p_y);break;}}x+=0.002;}pDC->SelectObject(OldPen);MyPen.DeleteObject();/////////////////////////////////////////////////////////////////// //////////// CTestV iew printingBOOL CTestView::OnPreparePrinting(CPrintInfo* pInfo){// default preparationreturn DoPreparePrinting(pInfo);}void CTestView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add extra initialization before printing}void CTestView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add cleanup after printing}/////////////////////////////////////////////////////////////////// //////////// CTestV iew diagnostics#ifdef _DEBUGvoid CTestView::AssertV alid() const{CView::AssertV alid();}void CTestView::Dump(CDumpContext& dc) const{CView::Dump(dc);CTestDoc* CT estV iew::GetDocument() // non-debug version is inline{ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CT estD oc)));return (CT estDoc*)m_pDocument;}#endif //_DEBUG/////////////////////////////////////////////////////////////////// //////////// CTestV iew message handlers三、运算结果截屏红色的曲线为原函数图像，黑色曲线为分段三次Hermite插值曲线四、算法分析上述图像中黑色的曲线为分段分段三次Hermite插值多项式所对应的图像，由图像可看出黑色的分段三次Hermited插值函数图像和拉格朗日、分段线性插值相比与红色被逼近函数的重合度最好，说明分段三次Hermite插值在函数的各节点两边插值函数的导数是相等的，保证了在各节点的平滑性，且不会出现Runge现象。

2
由于0 ( x0 ) 0 ( x1 ) 0( x1 ) 0, 故 0 ( x) 含有 ( x x0 )( x x1 ) 因子。可设
0 ( x) c( x x0 )( x x1 )2
2
其中c为待定系数。
1 . 由 0( x0 ) 1, 可得 c 2 ( x0 x1 )
称 H3 ( x) 为三次Hermite插值多项式，上述条件称 为此问题的插值条件。
采用基函数的方法来构造 H3 ( x) 。
将 H3 ( x) 表示为：
H3 ( x) y00 ( x) y11( x) m00 ( x) m11( x)
其中 0 ( x),1 ( x), 0 ( x), 1 ( x)为插值基函数，且均为次数 不超过3的多项式。为满足插值条件，它们应满足
并给出余项公式。
( x1 ) m1, (i 0,1,2), H3 ( xi ) yi , H3 H3 ( x) y00 ( x) y11( x) y22 ( x) m11( x)
函数值
导数值
x0
x1
0
1
x2
0 0
1
x1
0 0 0
1
0 ( x)
1( x)
2 ( x )
作为多项式插值,三次已是较高的次数，次数再高就有 可能发生Runge现象,因此，对有n+1节点的插值问题， 我们可以使用分段两点三次Hermite插值
例1 对给定数表
x
y
x0 y0
x1 y1 m1
x2 y2
y
求一个三次Hermite插值多项式 H3 ( x) 满足条件
( x1 ) m1, (i 0,1,2), H3 ( xi ) yi , H3

检查插值多项式是否满足Hermite插 值的约束条件，即插值多项式和原函 数在节点处有相同的函数值和导数值 。
04 实例分析
CHAPTER
实例一：已知数据点的插值
总结词
利用已知数据点进行插值，可三次Hermite插值方法，利用已知的数据点来估计未知点的值。这 种方法能够更好地处理数据点的变化，并提高插值的精度。
CHAPTER
插值多项式的构造
定义
Hermite插值法是一种通过已知的离散数据点来构造一个多 项式，使其能够准确地经过这些数据点，并尽可能地平滑地 连接这些点的方法。
构造方法
Hermite插值多项式由两个部分组成，一个是线性函数，另 一个是二次函数。线性函数部分用于确保插值多项式能够准 确地经过数据点，而二次函数部分则用于保证插值多项式的 平滑性。
实例二：未知数据点的插值
总结词
在未知数据点的情况下，可以通过三次 Hermite插值方法，预测并估计未知点的值。
详细描述
在数据点未知的情况下，可以利用三次 Hermite插值方法，根据已知的数据点来预 测和估计未知点的值。这种方法能够为后续 的数据分析和处理提供重要的参考依据。
实例三：复杂函数的插值
三次Hermite插值能够提供高精度的插值结果，特别是在处理
复杂函数时。
稳定性好
02
该方法在处理大数据集时表现出良好的稳定性，不易受到噪声
和异常值的影响。
易于实现
03
三次Hermite插值的算法相对简单，易于在计算机上实现和优
化。
三次Hermite插值的局限性
对初始数据敏感
三次Hermite插值的结果对初始数据的选择 较为敏感，不同的初始数据可能导致不同的 插值结果。

实验六: 分段三次Hermite插值画函数图像学号: 姓名:指导老师：马季骕班级:计算机科学与技术（非师范）1、算法说明：分段三次Hermit插值的做法是在每一个小区间上作三次Hermit插值，因此在每一个插值节点上都需要构造两个插值基函数，然后再作它们的线性组合。

分段三次Hermit插值基函数如下：H(x)=Σ(yihi(x)+y’iHi(x))给定的函数为f(x)=1/(25*x*x+1)，将给定区间分成10分，得到11个节点：x[0],x[1],...,x[10]，构造插值函数的基函数。

当x在(x[0],x[1])区间上时，H[0] = (x-x[0])*[((x-x[1])/(x[0]-x[1]))^2]。

其余的区间为H[0]=0。

h[0]= [1+2*(x-x[0])/(x[1]-x[0])]*[((x-x[1])/(x[0]-x[1]))^2]。

当x在[x[i-1],x[i]] (i=1,2,3,...,9)区间上时，H[i]=(x-x[i])*[((x-x[i-1])/(x[i]-x[i-1]))^2]，h[i]=[1+2*(x-x[i])/(x[i-1]-x[i])]*[((x-x[i-1])/(x[i]-x[i-1]))^2)。

当x在(x[i],x[i+1]](i=1,2,3, (10)区间上其余的区间为H[i]=(x-x[i])[((x-x[i+1])/(x[i]-x[i+1]))^2],h[i]=[1+2*(x-x[i])/(x[i+1]-x[i])]*[((x-x[i+1])/(x[i]-x[i+ 1]))^2]。

其余区间上均为H[i]=0,h[i]=0(i=1,2,…,10)。

当x在(x[9],x[10])区间上时，H[10] = (x-x[9])(((x-x[10])/(x[9]-x[10]))^2).其余的区间为H[10]=0.h[10]= (1+2*((x-x[9])/(x[10]-x[9])))(((x-x[10])/(x[9]-x[10]))^2).其余区间h[10]=0。

M n1 (n 1)!
n1 ( x)
说明：
n=1时，
R1 ( x)

1 2
f
( )2 (x)

1 2
f
( )(x
x0 )(x
x1)
n=2时，
( [x0 , x1])
R2 (x)

1 6
f
( )(x
x0 )(x
x1)(x
x2 )
( [x0 , x2 ])
,
x1,
Hale Waihona Puke xn)1
x1
x12

x1n

n
( xi
ni j1

xj)
1 xn xn2 xnn
因 xi x j (i j) 故上式不为0。
据Cramer法则，方程组解存在且唯一。 故Pn (x)存在且唯一。虽然直接求解上述方程组 可求得插值多项式，但繁琐复杂，一般不用。
得关于a0,a1,…,an的n+1阶线性方程组
a0 a1x0 a0 a1x1
an x0n an x1n

y0 y1
a0 a1xn an xnn yn
其系数行列式是Vandermonde行列式
1 x0 x02 x0n
V
( x0
jk jk
(j,k=0,1)
称l0 (x)及l1 (x)为线性插值基函数。
2. 抛物插值：n=2情形
假定插值节点为x0, x1, x2 ，求二次插值多项式 L2 (x)，使 L2(xj)=yj (j=0,1,2) y= L2 (x)的几何意义就是过 (x0, y0)，(x1, y1) ， (x2, y2)三点的抛物线。 采用基函数方法，设

下 面 讨 论 当 自 由 变 量 α1 α 2 β1 β 2 取 何 值 时 ， 曲线
p(u) 的能量函数 f (α1 α 2 β1 β 2) 最小。
之满足如下条件：
ì p(u i ) = p i , p(u i + 1/3) = α1, p(u i + 2/3) = α 2 , p(u i + 1) = p i + 1 í î p′(u i ) = T i , p′(u i + 1/3) = β1, p′(u i + 2/3) = β 2 , p′(u i + 1) = T i + 1 α1 、 α 2 、β1 和 β 2 是四个自由变量。 其中，
光顺性是一个在 CAGD 中应用很普遍又很重要的
概念， 国内外许多学者对此作了大量研究， 提出了很多 光顺方法， 如 Kjellander 法、 量法及最小二乘法等 [13]。其 中， 能量法是一种整体优化方法， 其光顺效果好， 为人们 普遍采用的一种曲线光顺方法。光顺法的关键是： 能量 函数的确定， 优化问题的求解。 对于曲线 p(u) ， 一般选用 ||p(u)″||2 du 和 p ‴(u)du 作 为曲线的能量函数。其中，p″(u) 为 p(u) 的二阶导数， 体现了曲线的曲率因素。 p ‴(u) 为 p(u) 的三阶导数， 体 现了曲线的挠率因素。由于上述两个能量函数不依赖 曲线的参数化， 能取得较好的光顺效果， 且计算量较小， 便于在计算机上实现， 故在曲线光顺优化中得到了普遍 的应用。
f (α1 α 2 β1 β 2) = u ||p″(u)||2 du = u
i
ui + 1
ui + 1 3
i
||p″(u)||2 du + ||p″(u)||2 ห้องสมุดไป่ตู้u

山东师范大学数学科学学院实验报告x 0.1 0.5 1 1.5 2 2.5 3y 0.95 0.84 0.86 1.06 1.5 0.72 1.9y' 1 1.5 2 2.5 3 3.5 4求质点在时刻1.8时的速度，并画出插值多项式的图像。

1)运用Hermite插值法画出图像，如图4-1，并求质点在时刻1.8时的速度。

>>clear>>clc>>X=[0.1 0.5 1 1.5 2 2.5 3;0.95 0.84 0.86 1.06 1.5 0.72 1.9;1 1.5 2 2.5 3 3.5 4];>> x=0.1:0.01:3;>> H=Hermite1(X,x);>> plot(x,H)>> hold on>> plot(X(1,:),X(2,:),'r*')>> H1_8=Hermite(X,1.8);>> plot(1.8,H1_8,'go')>> legend('插值图像','原始点','目标点');图4-1二、验证高次插值的Runge现象问题分析和算法设计（一）Language插值代码function [Ln] =Lagrange(X,x)%请输入2*n+1矩阵X，X中第一行每个元素都是插值节点，X中第二行每个元素都是插值节点对应的函数值；%第二章P24例一拉格朗日插值n=size(X,2);d=0;for m=1:1:nif x==X(1,m);d=m;breakendend运行结果和总结 运行结果 例：给定函数55,11)(2≤≤-+=x xx f ； （1） 验证表2-10的误差结果（高次插值的Runge 现象）；（2） 以0.1为步长分别进行Language 插值、分段线性插值、分段三次Hermite插值，画出三种插值函数以及f(x)的图像，比较三种插值结果。

题目：利用Matlab实现数据的Hermite插值和分段三次Hermite插值小组成员：王晓波（38）蔡明宇（20）一、程序实现意义：一般的，从各种试验得来的数据总有一定的数量，而利用插值技术能够从有限的数据中获取整体的状态。

而Hermite插值不仅保证了插值函数与原函数在给定数据点处得拟合，同时保证了在相应点处导数的相同，从而在很大程度上保证了曲线的“光滑性”。

因此，通过Matlab实现Hermite插值具有很普遍的意义。

二、实现过程：1、Hermite插值由于并不是所有的Matlab版本都提供现有的Hermite插值函数包，故我们首先编写了实现给定五个观测点的Hermite插值的M程序，代码如下：function [f,f0] = Hermite1(x,y,y_1)syms t;f = ;!if(length(x) == length(y))if(length(y) == length(y_1))n = length(x);elsedisp('y和y的导数的维数不相等');return;endelsedisp('x和y的维数不相等！ ');return;end*for i=1:nh = ;a = ;for j=1:nif( j ~= i)h = h*(t-x(j))^2/((x(i)-x(j))^2);a = a + 1/(x(i)-x(j));endendf = f + h*((x(i)-t)*(2*a*y(i)-y_1(i))+y(i));<endf0 = subs(f,'t');其中x为给定点横坐标数组，y为给定点纵坐标数组，y_1为原函数在给定点处的导数数组。

测试证明该程序可以实现，例如输入如下数组：x=1::;y_1=[ ];y=[1 ];>> [f,f0] = Hermite1(x,y,y_1)；运行结果如下：f =$(390625*((3972231*t)/35 - 28321/0000)*(t - 1)^2*(t - 7/5)^2*(t - 8/5)^2*(t - 9/5)^2)/36 - (390625*(t - 1)^2*(t - 6/5)^2*(t - 7/5)^2*(t - 9/5)^2*((28557*t)/28 - 23/2000))/36 + (390625*((64*t)/3 - 61/3)*(t - 6/5)^2*(t - 7/5)^2*(t - 8/5)^2*(t - 9/5)^2)/576 + (390625*((763*t)/1984 + 043/6240000)*(t - 1)^2*(t - 6/5)^2*(t - 8/5)^2*(t - 9/5)^2)/16 - (390625*((77623*t)/28 - 931/60000)*(t - 1)^2*(t - 6/5)^2*(t - 7/5)^2*(t - 8/5)^2)/576f0 =．利用matlab绘制图像：2、程序的窗口化：利用Matlab提供的GUIDE工具以及callback函数实现相应函数的窗口化，GUI代码如下：function varargout = untitled(varargin)?% UNTITLED M-file for% UNTITLED, by itself, creates a new UNTITLED or raises the existing% singleton*.%% H = UNTITLED returns the handle to a new UNTITLED or the handle to% the existing singleton*.%% UNTITLED('CALLBACK',hObject,eventData,handles,...) calls the local% function named CALLBACK in with the given input arguments.%% UNTITLED('Property','Value',...) creates a new UNTITLED or raises the，% existing singleton*. Starting from the left, property value pairs are% applied to the GUI before untitled_OpeningFcn gets called. An% unrecognized property name or invalid value makes property application% stop. All inputs are passed to untitled_OpeningFcn via varargin.%% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one% instance to run (singleton)".%% See also: GUIDE, GUIDATA, GUIHANDLES% Edit the above text to modify the response to help untitled%% Last Modified by GUIDE 15-Sep-2011 22:24:48% Begin initialization code - DO NOT EDITgui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @untitled_OpeningFcn, ...'gui_OutputFcn', @untitled_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);】if nargin && ischar(varargin{1})= str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:}); elsegui_mainfcn(gui_State, varargin{:});end% End initialization code - DO NOT EDIT<% --- Executes just before untitled is made visible.function untitled_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn.% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA)% varargin command line arguments to untitled (see VARARGIN)% Choose default command line output for untitled= hObject;>% Update handles structureguidata(hObject, handles);% UIWAIT makes untitled wait for user response (see UIRESUME)% uiwait;% --- Outputs from this function are returned to the command line.function varargout = untitled_OutputFcn(hObject, eventdata, handles)% varargout cell array for returning output args (see VARARGOUT);…% hObject handle to figure% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Get default command line output from handles structurevarargout{1} = ;function edit1_Callback(hObject, eventdata, handles)% hObject handle to edit1 (see GCBO)…% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit1 as text% str2double(get(hObject,'String')) returns contents of edit1 as a double guidata(hObject, handles);% --- Executes during object creation, after setting all properties.function edit1_CreateFcn(hObject, eventdata, handles)% hObject handle to edit1 (see GCBO)（% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');end￥function edit2_Callback(hObject, eventdata, handles)% hObject handle to edit2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit2 as text% str2double(get(hObject,'String')) returns contents of edit2 as a double guidata(hObject, handles);% --- Executes during object creation, after setting all properties.、function edit2_CreateFcn(hObject, eventdata, handles)% hObject handle to edit2 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');end—function edit3_Callback(hObject, eventdata, handles)% hObject handle to edit3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit3 as text% str2double(get(hObject,'String')) returns contents of edit3 as a double guidata(hObject, handles);·% --- Executes during object creation, after setting all properties.function edit3_CreateFcn(hObject, eventdata, handles)% hObject handle to edit3 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');·endfunction edit4_Callback(hObject, eventdata, handles)% hObject handle to edit4 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit4 as text% str2double(get(hObject,'String')) returns contents of edit4 as a double '% --- Executes during object creation, after setting all properties.function edit4_CreateFcn(hObject, eventdata, handles)% hObject handle to edit4 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))；set(hObject,'BackgroundColor','white');end% --- Executes on button press in pushbutton1.function pushbutton1_Callback(hObject, eventdata, handles)% hObject handle to pushbutton1 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)x=str2num(get,'string'));y=str2num(get,'string'));<y_1=str2num(get,'string'));x0=str2num(get,'string'));syms t;f = ;if(length(x) == length(y))if(length(y) == length(y_1))n = length(x);elsedisp('yºÍyµÄµ¼ÊýµÄάÊý²»ÏàµÈ');return;end—elsedisp('xºÍyµÄάÊý²»ÏàµÈ£¡ ');return;endfor i=1:nh = ;a = ;for j=1:nif( j ~= i)h = h*(t-x(j))^2/((x(i)-x(j))^2);a = a + 1/(x(i)-x(j));、endendf = f + h*((x(i)-t)*(2*a*y(i)-y_1(i))+y(i));endf0 = subs(f,'t',x0);plot,x,y,'*');^function edit5_Callback(hObject, eventdata, handles)% hObject handle to edit5 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles structure with handles and user data (see GUIDATA)% Hints: get(hObject,'String') returns contents of edit5 as text% str2double(get(hObject,'String')) returns contents of edit5 as a doubleguidata(hObject, handles);{% --- Executes during object creation, after setting all properties.function edit5_CreateFcn(hObject, eventdata, handles)% hObject handle to edit5 (see GCBO)% eventdata reserved - to be defined in a future version of MATLAB% handles empty - handles not created until after all CreateFcns called% Hint: edit controls usually have a white background on Windows.% See ISPC and COMPUTER.if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))~set(hObject,'BackgroundColor','white');end程序运行结果：其中左上方纵列的三个对话框从上到下分别输入给定点的横坐标x，纵坐标y以及导数值y_1，右侧空白框输入维数，下方坐标图显示插值函数图像，例如仍插入上面所给定的点列，得出结果：从图上看拟合程度还是比较不错的。

两点三次hermite插值c++程序例题两点三次Hermite插值是一种数值分析方法，用于在给定的数据点之间估计函数值。

这种方法基于多项式插值，并使用导数信息来提高插值的准确性。

以下是一个C++程序，实现了两点三次Hermite插值：cpp#include <iostream>#include <vector>// 定义一个结构体，用于存储数据点和它们的导数struct Point {double x;double y;double dy;};// 计算两点之间的差值double difference(double a, double b) {return a - b;}// 计算两点之间的差值的平方double squareDifference(double a, double b) {return difference(a, b) * difference(a, b);}// 计算两点之间的差值的立方double cubeDifference(double a, double b) {return squareDifference(a, b) * difference(a, b);}// 两点三次Hermite插值函数double hermiteInterpolation(const std::vector<Point>& points, double x) {double result = 0.0;for (size_t i = 0; i < points.size(); ++i) {double term = points[i].y;double prod = 1.0;for (size_t j = 0; j < points.size(); ++j) {if (i != j) {double weight = cubeDifference(x, points[j].x) / (squareDifference(points[i].x, points[j].x) *squareDifference(x, points[i].x));prod *= weight;}}result += term * prod;}return result;}int main() {std::vector<Point> points = {{1.0, 2.0, 3.0},{2.0, 3.0, 4.0},{3.0, 5.0, 6.0},{4.0, 7.0, 8.0}};double x = 2.5;double y = hermiteInterpolation(points, x);std::cout << "The interpolated value at x = " << x << " is y = " << y << std::endl;return 0;}这个程序首先定义了一个结构体`Point`，用于存储数据点及其导数。

分段三次 hermite 插值多项式的数学表达Hermite插值多项式是一种用于在给定的点集上进行插值的数学工具。

与其他插值方法不同的是，Hermite插值多项式不仅考虑了函数在各个插值点上的函数值，还考虑了函数在该点上的导数值。

这使得Hermite插值多项式能够更准确地拟合函数的曲线特征，特别是在存在函数奇点或不连续点的情况下。

要理解Hermite插值多项式的具体数学表达，首先需要了解插值点和插值条件的概念。

设给定的插值点集为{(x0, f0, f'0), (x1, f1, f'1), ..., (xn, fn, f'n)}，其中xi为插值点的横坐标，fi为插值点的纵坐标，f'i为插值点的导数值。

我们的目标是构造一个多项式P(x)，满足以下条件：1.在每个插值点(xi, fi)处，多项式P(x)的函数值等于fi：P(xi) = fi；2.在每个插值点(xi, fi)处，多项式P(x)的导数值等于f'i：P'(xi) = f'i。

根据这些插值条件，我们可以得到Hermite插值多项式的数学表达式。

首先，我们需要定义一个Lagrange插值基函数Lk(x)，用于描述在插值点xi处的多项式P(x)的函数值。

Lagrange插值基函数可以通过以下公式计算得到：Lk(x) = Π(j ≠ k) [(x - xj) / (xk - xj)]其中Π是乘积符号，j和k分别表示插值点的索引。

然后，我们可以构造Hermite插值多项式Hk(x)，它的数学表达式可以通过Lagrange插值基函数和插值点的函数值、导数值得到：Hk(x) = [1 - 2(x - xi)L'i(xi)]Li(x)^2 + (x - xi)Li(x)^2 其中Li(x)表示第i个插值点处的Lagrange插值基函数，L'i(xi)表示第i个插值点处的Lagrange插值基函数的导数值。

分段三次Ｈｅｒｍｉｔｅ插值在水文上的应用作者：张旭臣来源：《南水北调与水利科技》2009年第05期摘要:Hermite插值是样条插值的基础,具有很强的适应性和可控性。

如果能够用适当的方法来计算出节点处的导数,则可以构造一种新的分段三次Hermit插值函数,它具有C1连续性并在子区间保持单调。

该方法在水文资料的计算机处理等领域具有很好的应用前景。

关键词:分段三次Hermit插值;线性插值;越界;差商中图分类号:TP183文献标识码:A 文章编号:1672-1683(2009)05-0092-03Piecewise Cubic Hermite Interpolation Function and Its Application to HydrologyZHANG Xu-chen(Chengde Bureau for Hydrology and Water Resources Survey of Hebei Province,Chengde 067000,China )Abstract: The Hermite Interpolating is foundation of spline interpolation,and it has very strong adaptability and controllability. If we can use suitable method to calculate the derivative at nodes, a new piecewise cubic hermit interpolation function can be proposed,which has C1 continuity and monotonicity preserving in the subinterval. This method has very broad prospect in many fields such as the application in hydrological data processing by computer.Key words: piecewise cubic Hermit interpolating;linear interpolating;cross-border;difference quotient1 问题的提出受观测手段的限制,往往只能获得某一水文变量过程线上的一组有序的离散观测点,而无法(或难以)获得任意时刻的数值,因此,常常需要根据离散观测点来重构水文过程线,籍此获得任意时刻的水文变量数值。

分段三次H e r m i t e插值 Revised by Petrel at 2021摘要用函数来表示变量间的数量关系广泛应用于各学科领域，但是在实际问题中，往往是通过实验、观测以及计算等方法，得到的是函数在一些点上的函数值。

如何通过这些离散数据找到函数的一个满足精度要求且便于使用的近似表达式，是经常遇到的问题。

对于这类问题我们解决的方法为插值法，而最常用也最简单的插值方法就是多项式插值。

当然用插值法得到的近似表达式必须满足插值条件即假设给定了n+1个点的自变量的值以及函数值，近似函数必须要过这n+1个点。

多项式插值，从几何角度看，就是寻求n次代数曲线（x）通过n+1个点作为f（x）的近似。

y=Pn但是随着插值节点个数的增加，高次插值多项式的近似效果并不理想。

根据大量实验得出，在进行高次多项式插值时，会出现龙格现象。

因此，为了解决这样的一个问题，我们可以通过缩小插值区间的办法达到减小误差的目的。

但是当在每个小区间上用一次函数进行插值时，有很好的收敛性但是光滑度不够，因此本实验将用三次Hermite进行插值，做具体的讨论和学习。

关键词：龙格现象分段差值三次Hermite进行插值1、实验目的1)通过对分段三次Hermite插值算法程序的编写，提高自己编写程序的能力2)体会分段三次Hermite插值比分段线性插值优越在哪里3)用实验报告的形式展现，提高自己在写论文方面的能力2、算法流程分段线性插值多项式在插值区间上只能保证连续性，而不光滑。

要想得到在插值区间上光滑的分段线性插值多项式，可采用分段埃尔米特（Hermite）插值，这里我们考虑在整个上用分段三次埃尔米特插值多项式来逼近。

一般的将带有导数的插值多项式称为Hermite插值多项式。

如果已知函数在节点处的函数的值和导数值：则在小区间上有四个插值条件：故能构造一个三次多项式，并称为三次Hermite插值多项式。

这时在整个上可以用分段三次Hermite插值多项式来逼近。

摘要用函数来表示变量间的数量关系广泛应用于各学科领域，但是在实际问题中，往往是通过实验、观测以及计算等方法，得到的是函数在一些点上的函数值。

如何通过这些离散数据找到函数的一个满足精度要求且便于使用的近似表达式，是经常遇到的问题。

对于这类问题我们解决的方法为插值法，而最常用也最简单的插值方法就是多项式插值。

当然用插值法得到的近似表达式必须满足插值条件即假设给定了 n+1 个点的自变量的值以及函数值，近似函数必须要过这n+1 个点。

多项式插值，从几何角度看，就是寻求 n 次代数曲线y=Pn （x）通过 n+1 个点作为 f（x）的近似。

但是随着插值节点个数的增加，高次插值多项式的近似效果并不理想。

根据大量实验得出，在进行高次多项式插值时，会出现龙格现象。

因此，为了解决这样的一个问题，我们可以通过缩小插值区间的办法达到减小误差的目的。

但是当在每个小区间上用一次函数进行插值时，有很好的收敛性但是光滑度不够，因此本实验将用三次 Hermite 进行插值，做具体的讨论和学习。

关键词：龙格现象分段差值三次Hermite 进行插值i i ‒ 1 i ‒ 1 i iH 2(x ),x ∈ [x 1,x 2] ⋯⋯⋯⋯⋯⋯⋯ H n (x ),x ∈ [x n ‒ 1,x n ]1、实验目的1) 通过对分段三次 Hermite 插值算法程序的编写，提高自己编写程序的能力2) 体会分段三次 Hermite 插值比分段线性插值优越在哪里 3) 用实验报告的形式展现，提高自己在写论文方面的能力2、算法流程分段线性插值多项式S (x )在插值区间[a ,b ]上只能保证连续性，而不光滑。

要想得到在插值区间上光滑的分段线性插值多项式，可采用分段埃尔米特（Hermite ）插值，这里我们考虑在整个[a ,b ]上用分段三次埃尔米特插值多项式来逼近f (x )。

一般的将带有导数的插值多项式称为 Hermite 插值多项式。

如果已知函数y = f (x )在节点a = x 0 < x 1 < ⋯ < x n = b 处的函数的值 和导数值：y i = f (x i ),y ' = f '(x i ),i = 0,1,2,⋯,n则在小区间[x i ‒ 1,x i ]上有四个插值条件：y i ‒ 1 = f (x i ‒ 1),y i = f (x i )y ' = f '(x ),y ' = f '(x ) 故能构造一个三次多项式H i (x )，并称为三次 Hermite 插值多项式。