下载文档原格式
量⼦⼒学第⼀章习题答案第⼀章1.1 由⿊体辐射公式导出维恩位移定律：能量密度极⼤值所对应的波长λm 与温度T 成反⽐，即λm T = b （常量）；并近似计算b 的数值，准确到两位有效数字。
解：⿊体辐射的普朗克公式为：)1(833-=kT h e c h νννπρ∵ v=c/λ∴ dv/dλ= -c/λ2⼜∵ρv dv= -ρλdλ∴ρλ=-ρv dv/dλ=8πhc/[λ5(ehc/λkT-1)] 令x=hc/λkT ,则ρλ=8πhc(kT/hc)5x 5/(e x -1)求ρλ极⼤值，即令dρλ(x)/dx=0，得：5(e x -1)=xe x可得： x≈4.965∴ b=λm T=hc/kx≈6.626 *10-34*3*108/(4.965*1.381*10-23)≈2.9*10-3（m K ）1.2√. 在0 K 附近，钠的价电⼦能量约为3电⼦伏，求其德布罗意波长。
解： h = 6.626×10-34 J ·s , m e = 9.1×10-31 Kg,， 1 eV = 1.6×10-19 J故其德布罗意波长为：07.0727A λ=== 或λ= h/2mE = 6.626×10-34/(2×9.1×10-31×3×1.6×10-19)1/2 ≈ 7.08 ?1.3 √.氦原⼦的动能是E=32KT （K B 为波尔兹曼常数），求T=1 K 时，氦原⼦的德布罗意波长。
解：h = 6.626×10-34 J ·s , 氦原⼦的质量约为=-26-2711.993104=6.641012kg , 波尔兹曼常数K B =1.381×10-23 J/K故其德布罗意波长为：λ= 6.626×10-34/ (2×-276.6410?×1.5×1.381×10-23×1)1/2≈01.2706A或λ= ⽽KT E 23=601.270610A λ-==?1.4利⽤玻尔-索末菲量⼦化条件，求：a ）⼀维谐振⼦的能量：b ）在均匀磁场作圆周运动的电⼦轨道的可能半径。
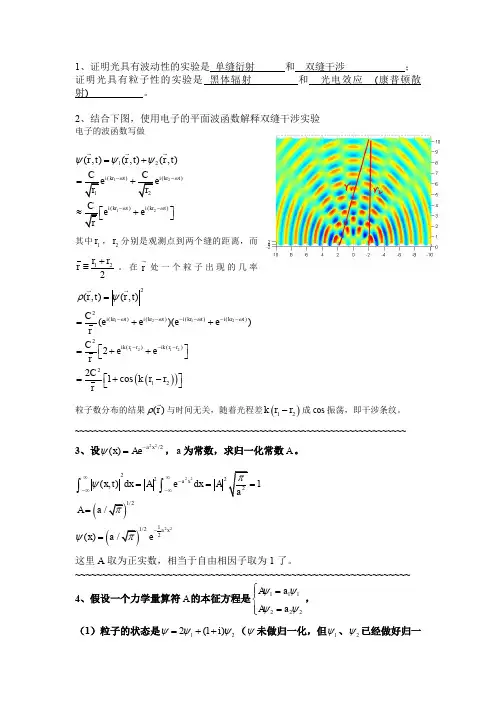
第一章 绪论1.1．由黑体辐射公式导出维恩位移定律：C m b b T m 03109.2 ,⋅⨯==-λ。
证明：由普朗克黑体辐射公式：ννπνρννd e c h d kTh 11833-=， 及λνc=、λλνd cd 2-=得1185-=kThc ehc λλλπρ，令kT hcx λ=，再由0=λρλd d ，得λ.所满足的超越方程为 15-=x xe xe用图解法求得97.4=x ，即得97.4=kThcm λ，将数据代入求得C m 109.2 ,03⋅⨯==-b b T m λ 1.2．在0K 附近，钠的价电子能量约为3eV,求de Broglie 波长.解：010A 7.09m 1009.72=⨯≈==-mEh p h λ #1.3. 氦原子的动能为kT E 23=，求K T 1=时氦原子的de Broglie 波长。
解：010A 63.12m 1063.1232=⨯≈===-mkTh mE h p h λ 其中kg 1066.1003.427-⨯⨯=m ，123K J 1038.1--⋅⨯=k#1.4利用玻尔—索末菲量子化条件，求： （1）一维谐振子的能量。
（2）在均匀磁场中作圆周运动的电子的轨道半径。
已知外磁场T 10=B ，玻尔磁子123T J 10923.0--⋅⨯=B μ，求动能的量子化间隔E ∆，并与K 4=T 及K 100=T 的热运动能量相比较。
解：（1）方法1：谐振子的能量222212q p E μωμ+=可以化为()12222222=⎪⎪⎭⎫ ⎝⎛+μωμE q Ep的平面运动，轨道为椭圆，两半轴分别为22,2μωμEb E a ==，相空间面积为,2,1,0,2=====⎰n nh EEab pdq νωππ所以，能量 ,2,1,0,==n nh E ν方法2：一维谐振子的运动方程为02=+''q q ω，其解为()ϕω+=t A q sin速度为 ()ϕωω+='t A q cos ，动量为()ϕωμωμ+='=t A q p cos ，则相积分为()()nh TA dt t A dt t A pdq T T==++=+=⎰⎰⎰2)cos 1(2cos 220220222μωϕωμωϕωμω， ,2,1,0=nνμωnh Tnh A E ===222， ,2,1,0=n（2）设磁场垂直于电子运动方向，受洛仑兹力作用作匀速圆周运动。
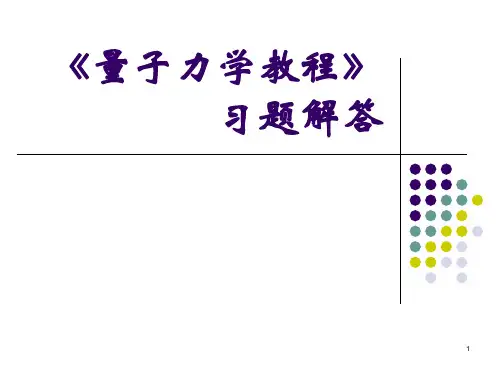
第一章 绪论1.1 由黑体辐射公式导出维思位移定律，能量密度极大值所对应的波长m λ与温度T 成反比，即 b T m =λ （常数），并近似计算b 的数值，准确到二位有效值。
[解]：由黑体辐射公式，频率在ν与ννd +之间的辐射能量密度为ννπνρννd ec hd kTh 11833-=由此可以求出波长在λ与λλd +之间的能量密度λλρd )( 由于 λν/c =,λλνd cd 2+=因而有： λλπλλρλd ehcd kT hc 118)(5-=令λkT hc x =所以有：11)(5-=xe Ax λρ （44558c h T k A π=常数） 由 0)(=λλρd d 有0)1(115)(254=⎥⎦⎤⎢⎣⎡---=λλλρd dxe e x e x A d d x x x于是，得： 1)51(=-x e x该方程的根为 965.4=x 因此，可以给出，k hcxk hc T m 2014.0==λ即 b T m =λ （常数）其中 k hcb 2014.0=2383410380546.110997925.21062559.62014.0--⨯⨯⨯⨯⨯=k m ⋅⨯=-310898.2[注]根据11833-=kTh ec h νννπρ 可求能量密度最大值的频率：令kT h x ν=113-=xe Ax νρ （23338h c T k A π=） 0]11[3=-=ννρνd dxe Ax dx d d d x因而可得 131=⎪⎭⎫ ⎝⎛-x e x此方程的解 821.2=xh kTh kTx 821.2max ==νb T Tb '=⇒'=-1max max νν其中34231062559.610380546.1821.2821.2--⨯⨯=='h k b 1910878.5-⋅︒⨯=s k这里求得m ax ν与前面求得的m ax λ换算成的m ν的表示不一致。
找了好久才找到的，希望能给大家带来帮助量子力学习题及解答第一章 量子理论基础1．1 由黑体辐射公式导出维恩位移定律：能量密度极大值所对应的波长m λ与温度T 成反比，即m λ T=b 〔常量〕；并近似计算b 的数值，准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ， 〔1〕以及 c v =λ， 〔2〕λρρd dv v v -=， 〔3〕有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
此题关注的是λ取何值时，λρ取得极大值，因此，就得要求λρ 对λ的一阶导数为零，由此可求得相应的λ的值，记作m λ。
但要注意的是，还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零，如果小于零，那么前面求得的m λ就是要求的，具体如下：01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kT hc e kT hc e hc λλλλλπρ ⇒ 0115=-⋅+--kT hce kThc λλ ⇒ kThce kT hc λλ=--)1(5 如果令x=kThcλ ，则上述方程为x e x =--)1(5第一章绪论这是一个超越方程。
首先，易知此方程有解：x=0，但经过验证，此解是平庸的；另外的一个解可以通过逐步近似法或者数值计算法获得：x=4.97，经过验证，此解正是所要求的，这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此，我们知识物体温度升高的话，辐射的能量分布的峰值向较短波长方面移动，这样便会根据热物体〔如遥远星体〕的发光颜色来判定温度的高低。
1．2 在0K 附近，钠的价电子能量约为3eV ，求其德布罗意波长。
量子力学课后习题详解 第二章波 函数和薛定谔方程2.1证明在定态中，几率流与时间无关。
证：对于定态，可令)]r ()r ()r ()r ([m 2i ]e )r (e )r (e )r (e )r ([m2i )(m2i J e )r ( )t (f )r ()t r (**Et iEt i **Et i Et i **Eti）（）（， 可见t J 与无关。
2.2 由下列定态波函数计算几率流密度：ikr ikr e re r1)2( 1)1(21 从所得结果说明1 表示向外传播的球面波，2 表示向内(即向原点) 传播的球面波。
解：分量只有和r J J 21在球坐标中sin r 1e r 1e r r 0r mrk r mr k r r ik r r r ik r r m i r e rr e r e r r e r m i mi J ikr ikr ikr ikr30202201*1*111 )]11(1)11(1[2 )]1(1)1(1[2 )(2 )1(r J 1与同向。
表示向外传播的球面波。
rmrk r mr k r )]r 1ik r 1(r 1)r 1ik r 1(r 1[m 2i r )]e r1(r e r 1)e r 1(r e r 1[m 2i )(m2i J )2(3020220ik r ik r ik r ik r *2*222可见，r J与2反向。
表示向内(即向原点) 传播的球面波。
补充：设ikx e x )( ，粒子的位置几率分布如何？这个波函数能否归一化？dx dx *∴波函数不能按1)(2dx x 方式归一化。
其相对位置几率分布函数为12表示粒子在空间各处出现的几率相同。
2.3 一粒子在一维势场a x a x x x U ，，，0 00)( 中运动，求粒子的能级和对应的波函数。
解：t x U 与)(无关，是定态问题。
其定态S —方程)()()()(2222x E x x U x dx d m 在各区域的具体形式为Ⅰ： )()()()(2 0111222x E x x U x dx d m x ①Ⅱ： )()(2 0 22222x E x dx d m a x②Ⅲ： )()()()(2 333222x E x x U x dxd m a x ③由于(1)、(3)方程中，由于 )(x U ，要等式成立，必须0)(1 x 0)(2 x即粒子不能运动到势阱以外的地方去。
量子力学课后习题详解第一章 量子理论基础1、1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b(常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv echv d kThv v v 11833-⋅=πρ, (1) 以及 λνc =, (2)||λνρρλd d v =, (3)有(),118)(|)(||52-⋅=⋅===kThc v v ehc cd c d d dvλνλλπλλρλλλρλρρ 这里的λρ的物理意义就是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的就是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的就是,还需要验证λρ对λ的二阶导数在m λ处的取值就是否小于零,如果小于零,那么前面求得的m λ就就是要求的,具体如下:01151186=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcd d λλλλλπλρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThcλλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这就是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解就是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4、97,经过验证,此解正就是所要求的,这样则有xkhc T m =λ把x 以及三个物理常量代入到上式便知K m T m ⋅⨯≈-3109.2λ这便就是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1、2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解:根据德布罗意波粒二象性的关系,可知λh P =。
所考虑的粒子就是非相对论性的电子(动能eV c m E e k 621051.0⨯=<<),满足ek m p E 22=, 因此利用非相对论性的电子的能量—动量关系式,有nmm mE c m hc E m h ph e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯====--λ在这里,利用了m eV hc ⋅⨯=-61024.1, eV c m e 621051.0⨯=。
最后,对 Em h e 2=λ作一点讨论,从上式可以瞧出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都就是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。
自然单位制: 在粒子物理学中,利用三个普适常数(光速c,约化普朗克常数h ,玻耳兹曼常数 k)来减少独立的基本物理量的个数,从而把独立的量纲减少到只有一种(能量量纲,常用单位eV)。
例:1nm=5、07/keV ,1fm=5、07/GeV ,电子质量m=0、51MeV 、 核子(氢原子)质量M=938MeV ,温度518.610K eV -=⨯、1、3 氦原子的动能就是kT E 23=(k 为玻耳兹曼常数),求T=1K 时,氦原子的德布罗意波长。
解:根据 eV K k 5106.81-⨯=⋅, 知本题的氦原子的动能为,1029.123234eV K k kT E -⨯=⋅==显然远远小于2c 核μ这样,便有Ec m hc He 22=λnmmm3.1103.11029.1107.321024.19496=⨯=⨯⨯⨯⨯⨯=---这里,利用了eV eV c m He 962107.3109384⨯≈⨯⨯=。
最后,再对德布罗意波长与温度的关系作一点讨论,由某种粒子构成的温度为T 的体系,其中粒子的平均动能的数量级为kT,这样,其相应的德布罗意波长就为mkTh mEh 22==λ据此可知,当体系的温度越低,相应的德布罗意波长就越长,这时这种粒子的波动性就越明显,特别就是当波长长到比粒子间的平均距离还长时,粒子间的相干性就尤为明显,因此这时就不能用经典的描述粒子统计分布的玻耳兹曼分布,而必须用量子的描述粒子的统计分布——玻色分布或费米公布。
1、4 利用玻尔——索末菲的量子化条件,求:(1)一维谐振子的能量; 解:玻尔—索末菲的量子化条件为:⎰=nh pdq其中q 就是微观粒子的一个广义坐标,p 就是与之相对应的广义动量,回路积分就是沿运动轨道积一圈,n 就是正整数。
(1)设一维谐振子的劲度常数为k,谐振子质量为m,于就是有22212kx m p E +=这样,便有 )21(22kx E m p -±=这里的正负号分别表示谐振子沿着正方向运动与沿着负方向运动,一正一负正好表示一个来回,运动了一圈。
此外,根据谐振子在最大位移±x 处p=0,221±=kx E 可解出 kEx 2±=±。
这样,根据玻尔——索末菲的量子化条件,有⎰⎰-++-=--+-x x x x nh dx kx E m dx kx E m )21(2)()21(222⇒nh dx kx E m dx kx E m x x x x =-+-⎰⎰+--+)21(2)21(222⇒2)21(22nh dx kx E m x x =-⎰+-为了积分上述方程的左边,作以下变量代换:θsin 2kEx =这样,便有2sin 2cos 2222nh k E d mE =⎪⎪⎭⎫⎝⎛⎰-θθππ⇒ 2cos 2222nh d k m E =⎰-θθππ ⇒2212cos 222nh d k m E =+⎰-θθππ⇒222nh k m E=π⇒ 2nh k m E =π⇒ m k n E η=。
能量间隔 mk E η=∆ 最后,对此解作一点讨论。
首先,注意到谐振子的能量被量子化了;其次,这量子化的能量就是等间隔分布的。
1、5 两个光子在一定条件下可以转化为正负电子对,如果两光子的能量相等,问要实现实种转化,光子的波长最大就是多少？解:关于两个光子转化为正负电子对的动力学过程,如两个光子以怎样的概率转化为正负电子对的问题,严格来说,需要用到相对性量子场论的知识去计算,修正当涉及到这个过程的运动学方面,如能量守恒,动量守恒等,我们不需要用那么高深的知识去计算,具体到本题,两个光子能量相等,因此当对心碰撞时,转化为正负电子对所需的能量最小,因而所对应的波长也就最长,而且,有2c m hv E e ==此外,还有 λhcpc E ==于就是,有 2cm hc e =λ612361.2410 2.410 2.4100.5110m m nm ---⨯==⨯=⨯⨯ 尽管这就是光子转化为电子的最大波长,但从数值上瞧,也就是相当小的,我们知道,电子就是自然界中最轻的有质量的粒子,如果就是光子转化为像正反质子对之类的更大质量的粒子,那么所对应的光子的最大波长将会更小,这从某种意义上告诉我们,当涉及到粒子的衰变,产生,转化等问题,一般所需的能量就是很大的。
能量越大,粒子间的转化等现象就越丰富,这样,也许就能发现新粒子,这便就是世界上在造越来越高能的加速器的原因:期待发现新现象,新粒子,新物理。
第二章波 函数与薛定谔方程2、1证明在定态中,几率流与时间无关。
证:对于定态,可令(,)()i Et r t r e ψ-ψ=hr r ,得******()2 [()()()()]2 [()()()()]2i i i i Et Et Et Et i J mi r e r e r e r e mi r r r r mψψψψψψψψ----=ψ∇ψ-ψ∇ψ=∇-∇=∇-∇h h h hr hh r r r r h r r r r （）（） 可见t J 与ρ无关。
2、2 由下列定态波函数计算几率流密度:ikr ikr e re r -==1)2( 1)1(21ψψ说明1ψ表示向外传播的球面波,2ψ表示向内(即向原点) 传播的球面波。
解:在球坐标中11sin r e e e r r r θφθθφ∂∂∂∇=++∂∂∂r r v 所以,12r J J e r r v和只有方向分量。
**111112223(1) ()21111 [()()]2111111 [()()]2 ikr ikr ikr ikr rrri J mi e e e e e m r r r r r ri ik ik e m r r r r r r k k e r mr mrψψψψ--=∇-∇∂∂=-∂∂=----+==r h h vh vh h rv r J 1ρρ与同向,表示向外传播的球面波。
**22222223(2) ()21111 [()()]2111111 [()()]2 ikr ikr ikr ikr rrr i J mi e e e e e m r r r r r r i ik ik e m r r r r r r k k e rmr mrψψψψ--=∇-∇∂∂=-∂∂=-+---=-=-r h h vh v h h rvr J ρρ与2反向,表示向内(即向原点) 传播的球面波。
2、3一粒子在一维势场⎪⎩⎪⎨⎧>∞≤≤<∞=a x a x x x U ，，，0 00)( 中运动,求粒子的能级与对应的波函数。
补充:设已知t=0时刻波函数为2,0(,0)0,0,x x x a x a ax x a ππ<<ψ=<>⎩,求 (,)x t ψ。
解:t x U 与)(无关,就是定态问题。
其定态S —方程)()()()(2222x E x x U x dxd m ψψψ=+-η 在各区域的具体形式为Ⅰ: )()()()(2 0111222x E x x U x dx d m x ψψψ=+-<η① Ⅱ: )()(2 0 22222x E x dx d m a x ψψ=-≤≤η② Ⅲ: )()()()(2 333222x E x x U x dx d m a x ψψψ=+->η③ 由于(1)、(3)方程中,由于∞=)(x U ,要等式成立,必须0)(1=x ψ 3()0x ψ= 即粒子不能运动到势阱以外的地方去。
方程(2)可变为 0)(2)(22222=+x mEdx x d ψψη 令222ηmEk =,得 0)()(22222=+x k dx x d ψψ 其解为 kx B kx A x cos sin )(2+=ψ ④ 根据波函数的标准条件确定系数A 、B,由连续性条件,得 )0()0(12ψψ= ⑤)()(32a a ψψ= ⑥⑤0=⇒B⑥0sin =⇒ka A),3 ,2 ,1( 0sin 0ΛΘ==⇒=∴≠n n ka ka A π∴x an A x πψsin )(2= 由归一化条件1)(2=⎰dx x ψ得 1sin 022=⎰axdx an Aπ由三角函数正交性sinsin 2amn m n ax xdx a a ππδ*=⎰x an a x aA πψsin 2)(22=∴=⇒222ηΘmEk = ),3,2,1( 22222Λη==⇒n n ma E n π可见E 就是量子化的。
