奥数练习 稍复杂的鸡兔同笼问题
- 格式:docx
- 大小:10.83 KB
- 文档页数:2

第五课鸡兔同笼问题例:鸡兔同笼,上有40个头,下有100只足。
鸡兔各有多少只?1、极端假设解法一:假设40个头都是鸡,那么应有足2×40=80(只),比实际少100-80=20(只)。
这是把兔看作鸡的缘故。
而把一只兔看成一只鸡,足数就会少4-2=2(只)。
因此兔有20÷2=10(只),鸡有40-10=30(只)。
解法二:假设40个头都是兔,那么应有足4×40=160(只),比实际多160-100=60(只)。
这是把鸡看作兔的缘故。
而把一只鸡看成一只兔,足数就会多4-2=2(只)。
因此鸡有60÷2=30(只),兔有40-30=10(只)。
解法三:假设100只足都是鸡足,那么应有头100÷2=50(个),比实际多50-40=10(个)。
把兔足看作鸡足,兔的只数(头数)就会扩大4÷2倍,即兔的只数增加(4÷2-1)倍。
因此兔有10÷(4÷2-1)=10(只),鸡有40-10=30(只)。
解法四:假设100只足都是兔足,那么应有头100÷4=25(个),比实际少40-25=15(个)。
把鸡足看作兔足,鸡的只数(头数)就会缩小4÷2倍,即鸡的只数减少1-1÷(2÷4)=1/2。
因此鸡有15÷1/2=30(只),兔有40-30=10(只)。
2、任意假设解法五:假设40个头中,鸡有12个(0至40中的任意整数),则兔有40-12=28(个),那么它们一共有足2×12+4×28=136(只),比实际多136-100=36(只)。
这说明有一部分鸡看作兔了,而把一只鸡看成一只兔,足数就会多4-2=2(只),因此把鸡看成兔的只数是36÷2=18(只)。
那么鸡实际有12+18=30(只),兔实际有28-18=10(只)。
解法六:假设100只足中,有鸡足80只(0至100中的任意整数,最好是2的倍数),则兔足有100-80=20(只),那么它们一共有头80÷2+20÷4=45(个),比实际多45-40=5(个)。

鸡兔同笼问题1、鸡和兔共有8只,脚共28只,鸡和兔各几只?8×2=16(只)28-16=12(只)4-2=2(只)12÷2=6(只)8-6=2(只)答:鸡有6只,兔有2只。
解题思路:⑴把这8只动物都看做鸡,一只鸡有两只腿,8只动物一共应该有16只腿,可是现在一共有28只腿,少了12只。
为什么会少12只,是因为把兔子算成了鸡,如果有一只兔子那就少了2只腿。
那几只兔子才能少12只腿,就看12里面有几个2,就是有几只兔子。
⑵或者把这8只动物都看做兔,一只兔有四只腿,8只动物一共应该有32,可是现在一共有28只腿,多了4只。
为什么会多4只,因为把鸡算成了兔子,如果有一只鸡看成了兔子,就多算了两只腿。
多少只鸡才能多算4只腿呢,就看4 里面有几个2,就是有几只鸡。
8-2=6(只)兔子有6只。
(3)或者让鸡和兔都抬起一只腿,现在腿数就少了8只,28-8=20(只),再让它们都抬起一只腿,腿数又少了8只,20-8=12(只)。
现在地上就剩下兔子的腿,每只兔子两只腿。
剩下的这12只腿里有几个2,就是有几只兔。
做这样的题时候,尽量假设成腿少的动物。
2、小强是个汽车迷,他来到展厅,一看有大、小两种车,用14辆,数数车轮,大汽车6个轮子,小汽车4个轮子,14辆车数在一起一共64个轮子,请问:有几辆大汽车,几辆小汽车?14×4=56(个)64-56=8(个)6-4=2(个)8÷2=4(辆)14-4=10(辆)答:大汽车4辆,小汽车10辆。
解题思路:⑴把这14辆车都看成小汽车,应该有56个轮子。
可是现在一共有64个轮子,少了8个轮子。
为什么会少8个轮子,是因为把大汽车算成了小汽车,如果一辆大汽车算成小汽车就少算2个轮子。
那几辆大汽车才能少算8个轮子,就看8里面有几个2,就是有4辆大汽车,小汽车就有10辆。
⑵把这14辆车都看成大汽车,应该有84个轮子。
可是现在一共有64个轮子,多了20个轮子。
鸡兔同笼问题的四种题型(一)常规题例如:有鸡、兔共36只,它们共有脚100只,鸡、兔各是多少只?解一(100-2×36)÷(4-2)=14(只)………兔; 36-14=22(只)………鸡。
解二(4×36-100)÷(4-2)=22(只)………鸡; 36-22=14(只)………兔。
练习与提高:1、现有鸡和兔共35只,合计腿数共100只。
鸡和兔各有多少只?2、2、21枚5分和2分的硬币共6角,其中5分、2分硬币各几枚?3、某人购买1元、8角、4角的邮票20张,共计15元,其中1元与8角邮票的张数相等。
三种邮票各几张?(二)得失问题(鸡兔问题的推广题):例如:某小学举行一次数学竞赛,共15道题,每做对一题得8分,每做错一题倒扣4分,小明共得了72分。
他做对了几道题?解一(72+4×15)÷(8+4)=11(道)……对题数; 15-11=4(道)……………错题数。
解二(8×15-72)÷(8+4)=4(道)………错题数; 15-4=11(道)……………对题数。
练习与提高:1、一次智力测验有10道题,每答对一道得3分,每答错一道扣2分,小红答完了10道题,只得了20分。
她答对了几道题?2、南城区举行小学数学竞赛共15道题,每做对一题得8分,做错一题倒扣4分,李明共得84分,他做对了几道题?3、给商店运货,规定每件商品运费是4元,如果搬运时损坏商品,每损坏一件不但不给运费还要罚款5元。
结果运了100件商品,得运费220元。
问损坏了多少件商品?(三)巧用和倍解“头和腿差的问题“(总头数和鸡兔脚数的差):例如:鸡兔同笼,它们一共有100只,而鸡足比兔足多80只。
鸡兔各有多少只?解一:80÷2=40(只)(100-40)÷(2+1)=20(只)…………………………兔; 100-20=80(只)…………………………鸡。

鸡兔同笼最难的奥数题
这道题叫鸡兔同笼,又叫兔鸡同框,不管叫啥,其实都是一个数学题,
它考察数学的一些思路问题,具体来说:
问题是:一个笼子里有30只动物,其中有鸡和兔,他们合计有94只脚,问这笼子里有多少只鸡多少只兔?
这个问题在初中数学里面比较常见,只是有的时候可能物种、数量或者
脚都会稍有不同,不过解法却都是一样的。
首先,我们要基于一个数学等式来解答这个问题:
30只动物合计有94只脚其实就是说鸡+兔=30,鸡脚+兔脚=94。
使用这个等式,我们就可以确定,鸡脚数x,兔脚数y // x+y=94
再假定:鸡数c,兔数r // c+r=30
组合上面两个等式,再假定,每只鸡有2只脚,兔有4只脚
那么最终x=2c,y=4r,把它代入之前等式里,就得到一个二元一次方程组:
2c+4r=94
c+r=30
可以用带入/消元法来求解,比如从左边把第一个方程乘2,变为
4c+8r=188,再加上第二个方程它们就变成了5c+9r=218;
把右边减去第二个方程就变成了5c=188,即可求得c=37
再将c=37代入第二个方程就得到了r=30-37=-7,k小于0则没有解,而且动物不可能负数,也不可能是小数更何况有脚所以根据现实原理该方程也
不存在解
加法综上,我们可以得到正确答案:
笼子里有37只鸡,30只兔。
通过解题步骤,我们发现这道题不仅考察学生的数学思路,也是在考察学生的计算能力。
所以,做这道题,首先要了解问题,看懂实际情况,然后构造数学方程,再运用数学算法求解问题,最后做出正确的结论。

最难的鸡兔同笼类奥数题在进行讨论最难的鸡兔同笼类奥数题之前,我们先了解一下鸡兔同笼问题的基本概念。
鸡兔同笼问题是一种常见的数学问题,它是通过利用已知条件,求解未知变量的数学题目。
题目:有一笼子里关着一些鸡和兔,已知总共有n只头,而且总共有m只脚。
问这个笼子里到底有多少只鸡和兔?解答:这是一道经典的鸡兔同笼问题,也是较为难解的一类奥数题。
首先,我们先分析一下题目的已知条件和需要求解的未知变量。
已知条件:- 总共有n只头,代表着鸡和兔的总数量。
- 总共有m只脚,代表着鸡和兔的总脚数。
需要求解的未知变量:- 鸡的数量。
- 兔的数量。
接下来,我们通过建立方程来求解这道题。
假设鸡的数量为x,兔的数量为y。
根据已知条件可得:(1)x + y = n (鸡和兔的总数量等于总头数)(2)2x + 4y = m (鸡的脚数乘以2加上兔的脚数乘以4等于总脚数)我们可以通过解这个方程组来求解题目。
首先,用第一个方程解出一个变量,比如将x表示为 n-y。
将第一个方程带入第二个方程,得到:2(n-y) + 4y = m简化得到:2n - 2y + 4y = m2n + 2y = m整理得到:2y = m - 2ny = (m - 2n) / 2现在我们已经求得了兔的数量y,我们可以将其带入第一个方程,得到:x + (m - 2n) / 2 = n进一步整理得到:2x + m - 2n = 2n继续整理得到:2x = 4n - mx = (4n - m) / 2现在我们已经求得了鸡的数量x和兔的数量y,根据题目要求得出答案。
需要注意的是,由于题目要求鸡和兔的数量是正整数,所以我们需要对x和y进行约束条件的判断。
判断约束条件:1. x和y为正整数。
2. 鸡和兔的总数量等于总头数。
3. 鸡的脚数乘以2加上兔的脚数乘以4等于总脚数。
根据上述步骤,我们能得出最终的答案。
综上所述,这道题目虽然难度较大,但通过建立方程,代入已知条件和未知变量,再通过解方程组得出答案,我们可以很好地解决这个问题。

数学应用题1、鸡、兔共居一笼,已知鸡头和兔头共35个,鸡脚和兔脚共94只。
鸡、兔各有多少只?2、12张乒乓球台上共有34人在打球,问:正在进行单打和双打的台子各有几张?3、有鸡兔共20只,脚44只,鸡兔各几只?4、小红的储钱罐里有面值2元和5元的人民币共65张,总钱数为205元,两种面值的人民币各多少张?5、现有大小油桶50个,每个大桶可装油4千克,每个小桶可装油2千克,大桶比小桶共多装油20千克,问大小桶各多少个?6、有若干只鸡和兔子,它们共有88个头,244只脚,鸡和兔各有多少只?7、龟鹤共有100个头,350只脚。
龟、鹤各多少只?8、学校有象棋、跳棋共26副,恰好可供120个学生同时进行活动.象棋2人下一副棋,跳棋6人下一副.象棋和跳棋各有几副?9、有2分和5分的硬币,共值2.99元,其中2分硬币个数是5分硬币个数的4倍,问5分硬币有多少个?10、班主任张老师带五年级(7)班50名同学栽树,张老师栽5棵,男生每人栽3棵,女生每人栽2棵,总共栽树120棵,问几名男生,几名女生?11、小毛参加数学竞赛,共做20道题,得67分,已知做对一道得5分,不做得0分,错一题扣1分,又知道他做错的题和没做的同样多。
问小毛做对几道题?12、池塘里有青蛙和鸭子共50只,共有脚130只。
青蛙有几只?鸭子有几只?13、明明用6元钱买了2角和5角的邮票共18张。
2角的邮票几张?5角的呢?14、有2分和5分的硬币共78枚,总共2元6角4分。
2分的硬币有几枚?5分的硬币几枚?15、小容有2分、5分的硬币共35枚,一共是1元1角5分,2分的硬币有几枚?5分的硬币有几枚?16、王师傅到家具厂买了桌子和椅子共19件。
桌子每张35元,椅子每张20元,共付现金400元。
桌子和椅子各买了几张?17、长江家具厂有一种桌子每张32元,椅子每张24元。
花园小学买桌子和椅子共38件,共付款976元。
桌子和椅子各买了几张?19、操场上停放着39辆三轮车和自行车。

【奥数系列训练】(含答案)鸡兔同笼【奥数系列训练】(含答案)——鸡兔同笼请填入正确答案:【题目1】一个大笼子里关了一些鸡和兔子。
数它们的头,一共有36个;数它们的腿,共100条。
则鸡有多少只,兔有多少只?【题目2】王老师用40元钱买来20枚邮票,全是1元和5元的。
求这两种邮票分别买了多少枚和多少枚。
【题目3】兔妈妈上山采蘑菇,晴天,每天能採30个,雨天,每天能採12个.它从4月10号开始,到4月29号,中间没休息,一共採了510个蘑菇。
那么,晴天是多少天?雨天有多少天?【题目4】肖老师带51名学生去公园里划船。
他们一共租了44条船,其中有大船和小船,每条大船坐6人,小船4人。
每条都坐满了人。
他们租的大船有几条,小船有几条?【题目5】一辆汽车参加车赛,9天共行了5000公里。
已知它晴天每天行688公里,雨天平均每天行390公里。
在比赛期间,有几个晴天?有几个雨天?【题目6】有大小两种塑料桶共60只。
每个大桶装水5公斤,每个小桶只能装水2公斤。
又知大桶一共比小桶多装26公斤。
则大桶有多少只,小桶有多少只?【题目7】用单价为6元/公斤的两种水果糖,配制成单价为6元/公斤的混合型糖15公斤。
有的原来单价11元/公斤的糖取了几公斤?【题目8】一百个和尚吃一百个馒头,大和尚一人吃三个,小和尚三人吃一个。
大和尚有多少个?小和尚有多少个?【题目9】孙老师带领99名同学种100棵树,他先种了一棵示范后,安排男同学一人种两棵,女生每两人种一棵。
植树的男生有多少人?而女生有多少人?【题目10】某化工厂甲、乙两车间共110人,现在要求甲车间每8人选出一名代表,乙车间每6人选出一名代表。
两车间一共选出了16名代表。
则甲车间有多少名工人,乙车间有多少名工人?【参考答案】1.【解答】鸡22只,兔子14只。
可先假设这36个全是鸡,那么应该只有36×2=72条腿。
而实际上有100条腿,这是因为兔子有4条腿,比鸡多2条。

鸡兔同笼问题(4)超难级1.小华有1分、2分、5分的硬币共38枚,合计9角2分,已知1分与2分的硬币的枚数相等。
这三种硬币各有多少枚?2.100个馒头100个和尚吃,大和尚每人吃3个,小和尚3人吃一个,则大和尚有多少个?小和尚有多少个?3.100个馒头100个和尚吃,大和尚每人吃4个,小和尚4人吃一个,则大和尚有多少个?小和尚有多少个?4.大油瓶一瓶装4千克,小油瓶两瓶装1千克。
现在100千克油装了60个瓶。
求大,小油瓶各有多少个?5.在很久很久以前,传说有九头一尾的九头鸟和九尾一头的九尾鸟。
有一次这两种鸟栖息在树林里,一位猎人经过此地数了数,这两种鸟头共268个,尾332个,那么有九头鸟和九尾鸟各多少只?6.某校数学竞赛,共有20道填空题。
评分标准是:每做对1题得5分,做错1题倒扣3分,没做的一题得0分,小英的得分是69分,那么小英有几题没做?7.某校数学竞赛,共有20道填空题。
评分标准是:每做对1题得5分,做错1题倒扣3分,没做的一题得0分,小英的得分是72分,那么小英有几题没做?8.某次数学抢答比赛共20题,做对一题得5分,做错一题倒扣2分,不做倒扣1分.小华得了74分,问他做对几题?答错几题?没答的有几题?9.一件工程甲独做12天完成,乙独做18天完成,现在由甲先做若干天后,再由乙单独完成余下的任务,这样前后共用了16天,甲先做了多少天?10.一份稿件,甲单独打字需6小时完成.乙单独打字需10小时完成,现在甲单独打若干小时后,因有事由乙接着打完,共用了7小时.甲打字用了多少小时?11.鸡兔共有脚100只,若将鸡换成兔,兔换成鸡,则共有脚92只,则鸡兔各有多少只?12.鸡与兔共有220只脚,若原来所有的鸡都换成兔,所有的兔都换成鸡后,则脚只有212只,求原来鸡兔各有多少头?11.鸡与兔共有220只脚,若原来所有的鸡都换成兔,所有的兔都换成鸡后,则脚只有212只,求原来鸡兔各有多少头?12.甲乙两人射击比赛,每人各射10发。

奥数鸡兔同笼问题1、有若干只鸡和兔子,它们共有88个头,244只脚,鸡和兔各有多少只?解:我们设想,每只鸡都是“金鸡独立”,一只脚站着;而每只兔子都用两条后腿,像人一样用两只脚站着.现在,地面上出现脚的总数的一半,•也就是244 + 2=122 (只).在122这个数里,鸡的头数算了一次,兔子的头数相当于算了两次.因此从122减去总头数88,剩下的就是兔子头数122-88=34,有34只兔子.当然鸡就有54只.答:有兔子34只,鸡54只.上面的计算,可以归结为下面算式:总脚数+ 2-总头数二兔子数.2、红铅笔每支0.19元,蓝铅笔每支0.11元,两种铅笔共买了 16支,花了 2.80元.问红、蓝铅笔各买几支?解:以“分”作为钱的单位.我们设想,一种“鸡”有11只脚,一种“兔子”有19只脚,它们共有16个头,280只脚.现在已经把买铅笔问题,转化成“鸡兔同笼”问题了.利用上面算兔数公式,就有蓝笔数=(19x 16-280) + (19-11)=24 + 8=3 (支).红笔数=16-3=13 (支).答:买了13支红铅笔和3支蓝铅笔.3、一份稿件,甲单独打字需6小时完成.乙单独打字需10小时完成, 现在甲单独打若干小时后,因有事由乙接着打完,共用了7小时.甲打字用了多少小时?解:我们把这份稿件平均分成30份(30是6和10的最小公倍数),甲每小时打30 + 6=5 (份),乙每小时打30 + 10=3 (份).现在把甲打字的时间看成“兔”头数,乙打字的时间看成“鸡” 头数,总头数是7.“兔”的脚数是5,“鸡”的脚数是3,总脚数是30,就把问题转化成“鸡兔同笼”问题了.根据前面的公式“兔”数二(30-3X7)・(5-3)=4.5,“鸡”数=7-4.5=2.5,也就是甲打字用了 4.5小时,乙打字用了 2.5小时.答:甲打字用了 4小时30分.4.今年是1998年,父母年龄(整数)和是78岁,兄弟的年龄和是17岁.四年后(2002年)父的年龄是弟的年龄的4倍,母的年龄是兄的年龄的3倍.那么当父的年龄是兄的年龄的3倍时,是公元哪一年?解:4年后,两人年龄和都要加8.此时兄弟年龄之和是17+8=25,父母年龄之和是78+8=86.我们可以把兄的年龄看作“鸡”头数,弟的年龄看作“兔”头数.25是“总头数”.86是“总脚数”.根据公式,兄的年龄是(25X4-86) + (4-3) =14 (岁).1998年,兄年龄是14-4=10 (岁).父年龄是(25-14)X4-4=40 (岁).因此,当父的年龄是兄的年龄的3倍时,兄的年龄是(40-10) + (3-1) =15 (岁).这是2003年.答:公元2003年时,父年龄是兄年龄的3倍.5.蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀.现在这三种小虫共18只,有118条腿和20对翅膀.每种小虫各几只?解:因为蜻蜓和蝉都有6条腿,所以从腿的数目来考虑,可以把小虫分成“8条腿”与“6条腿”两种.利用公式就可以算出8条腿的蜘蛛数二(118-6X18)0(8-6)=5 (只).因此就知道6条腿的小虫共18-5=13 (只).也就是蜻蜓和蝉共有13只,它们共有20对翅膀.再利用一次公式蝉数二(13X2-20)0(2-1) =6 (只).因此蜻蜓数是13-6=7 (只).答:有5只蜘蛛,7只蜻蜓,6只蝉.6.某次数学考试考五道题,全班52人参加,共做对181道题,已知每人至少做对1道题,做对1道的有7人,5道全对的有6人,做对7道和3道的人数一样多,那么做对4道的人数有多少人?解:对2道、3道、4道题的人共有52-7-6=39 (人).他们共做对181Tx7-5X6=144 (道).由于对2道和3道题的人数一样多,我们就可以把他们看作是对2.5道题的人((2+3)+2=2.5).这样兔脚数=4,鸡脚数=2.5,总脚数=144,总头数=39.对4道题的有(144-2.5X39) + (4-1.5) =31 (人).答:做对4道题的有31人.7.买一些4分和8分的邮票,共花6元8角.已知8分的邮票比4分------------------------------------------------ 百度文库 ---------------------------------------------- 的邮票多40张,那么两种邮票各买了多少张?解一:如果拿出40张8分的邮票,余下的邮票中8分与4分的张数就一样多.(680-8X40) + (8+4) =30 (张),这就知道,余下的邮票中,8分和4分的各有30张.因此8分邮票有40+30=70 (张).答:买了 8分的邮票70张,4分的邮票30张.也可以用任意假设一个数的办法.解二:譬如,假设有20张4分,根据条件“8分比4分多40张”,那么应有60张8分.以“分”作为计算单位,此时邮票总值是4X20+8X60=560.比680少,因此还要增加邮票.为了保持“差”是40,每增加1 张4分,就要增加1张8分,每种要增加的张数是(680-4X20-8X60) + (4+8) =10 (张).因此4分有20+10=30 (张),8分有60+10=70 (张).------------------------------------------------ 百度文库 ----------------------------------------------- 8.一项工程,如果全是晴天,15天可以完成.倘若下雨,雨天一天工程要多少天才能完成?解:类似于例3,我们设工程的全部工作量是150份,晴天每天完成10份,雨天每天完成8份.用上一例题解一的方法,晴天有(150-8X3) + (10+8) = 7 (天).雨天是7+3=10天,总共7+10=17 (天).答:这项工程17天完成.。

暑期奥数练习鸡兔同笼问题奥数练习鸡兔同笼姓名__________2016/7/12例1、一笼中鸡和兔共有10只,共有脚32只,那么鸡和兔各有多少只?答:鸡有()只,兔有()只。
练习:1、鸡兔同笼,共50个头,160只脚,求鸡和兔各多少只?答:鸡有()只,兔有()只。
2、动物园里养了90梅花鹿和鸵鸟,共有脚240只,鸵鸟和梅花鹿各有多少只?答:鸵鸟()只,梅花鹿()只。
例2、张军买5角一支和2角一支的铅笔共18支,用了6元钱,张军买了5角的铅笔几支,买了2角的铅笔几支?答:张军买了5角的铅笔()支,买2角的铅笔()支。
练习:1、小敏用8元钱正好买了面值为20分和100分的邮票共16张,求两种邮票各有多少张?答:20分的邮票()张,100分的邮票()张。
例3、星期天46名学生去公园划船,一共乘坐10条船,其中大船坐6人,小船坐4人,问大船、小船各有多少条?答:需要租大船()条,小船()条。
练习1、王领队带领51名队员一同去划船,共租了11条船,每条大船坐6人,每条小船坐4人,那么需要租大船几条,小船几条?答:需要租大船()条,小船()条。
例4、一张试卷25题,答对一题得4分,答错一题或不答倒扣1分,小红得了60分,她答对了几题?答:她答对了()题。
练习:1、红星小学举行数学竞赛,共20道题,若做对一题得5分,做错或没做一题扣2分,李东得了79分,他作对了几道题?答:他作对了()道题。
2、实验小学四年级举行数学竞赛,一共出了10道题,答对一题得10分,答错一题反扣5分(没有不答的情况)。
张华得了70分,他答对了几道题?答:他答对了()道题。
例5、鸡兔同笼共100只,鸡的脚比兔的脚多80只,问鸡兔各多少只?答:鸡()只,兔()只。
练习1、已知鸡兔共有120只,鸡脚比兔脚多54只,问鸡兔各有多少只?答:鸡有()只,兔有()只。
2、已知鸡兔共有107只,兔脚比鸡脚多56只,问鸡兔各有多少只?答:鸡有()只,兔有()只。

小学六年级奥数鸡兔同笼问题专项强化训练题(高难度)例题1:把鸡和兔子一共放在一个笼子里,一共有20个头,64只脚。
问鸡和兔子各有多少只?解析:设鸡的数量为x,兔子的数量为y。
根据题意,可列出以下方程组:x + y = 20 (1)(鸡和兔子的总数为20)2x + 4y = 64 (2)(鸡和兔子的脚的总数为64)通过方程(1)将y表示为x的式子,代入方程(2)得:2x + 4(20 - x) = 642x + 80 - 4x = 64-2x = -16x = 8将x = 8代入方程(1)得:8 + y = 20y = 12所以,鸡有8只,兔子有12只。
专项练习题:1. 把鸡和兔子一共放在一个笼子里,一共有28个头,84只脚。
问鸡和兔子各有多少只?2. 把鸡和兔子一共放在一个笼子里,一共有16个头,40只脚。
问鸡和兔子各有多少只?4. 把鸡和兔子一共放在一个笼子里,一共有24个头,56只脚。
问鸡和兔子各有多少只?5. 把鸡和兔子一共放在一个笼子里,一共有10个头,28只脚。
问鸡和兔子各有多少只?6. 把鸡和兔子一共放在一个笼子里,一共有40个头,110只脚。
问鸡和兔子各有多少只?7. 把鸡和兔子一共放在一个笼子里,一共有18个头,50只脚。
问鸡和兔子各有多少只?8. 把鸡和兔子一共放在一个笼子里,一共有12个头,26只脚。
问鸡和兔子各有多少只?9. 把鸡和兔子一共放在一个笼子里,一共有14个头,44只脚。
问鸡和兔子各有多少只?10. 把鸡和兔子一共放在一个笼子里,一共有36个头,98只脚。
问鸡和兔子各有多少只?11. 把鸡和兔子一共放在一个笼子里,一共有20个头,52只脚。
问鸡和兔子各有多少只?12. 把鸡和兔子一共放在一个笼子里,一共有22个头,60只脚。
问鸡和兔子各有多少只?13. 把鸡和兔子一共放在一个笼子里,一共有26个头,68只脚。
问鸡和兔子各有多少只?14. 把鸡和兔子一共放在一个笼子里,一共有32个头,88只脚。
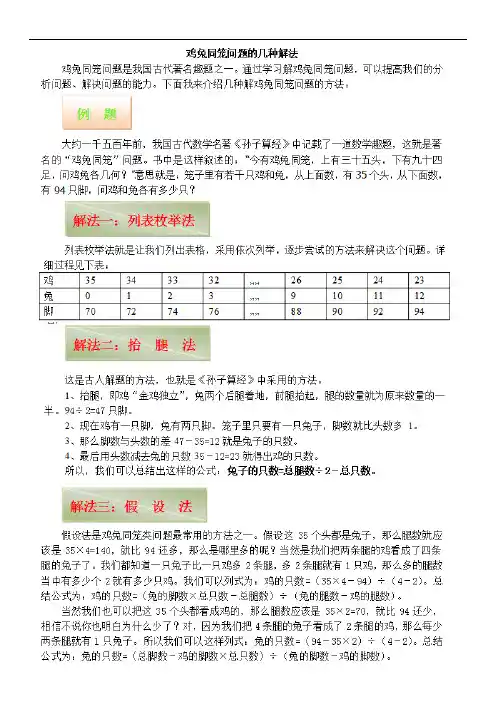
四年级鸡兔同笼奥数题及答案
鸡兔同笼的例题及答案【1】
鸡和兔共有100只脚,若将鸡换成兔,将兔换成鸡,则共有86只脚,则鸡有多少只?兔有多少只?
【分析】【解法一】:鸡兔互换后减少的腿数:100-86=14(条);
鸡比兔子少的只数:14÷(4-2)=7(只);
让鸡只数和兔只数相等后的脚数:100+7×2=114(条);
鸡的脚数:114÷(2+1)=38(条);
鸡的只数:38÷2=19(只);兔的.只数:19-7=12(只);
【解法二】鸡兔互换后减少的腿数:100-86=14(条);
鸡比兔子少的只数:14÷(4-2)=7(只);
让兔只数和鸡只数相等后的脚数:100-7×4=72(条);
鸡的脚数:72÷(2+1)=24(条);
兔(鸡)的只数:24÷2=12(只);鸡的只数:12+7=19(只);
【解法三】:方程法设鸡有x只,兔有y只;
解方程得:x=12;y=19;
鸡兔同笼的例题及答案【2】
鸡兔同笼,头共46,足共128,鸡兔各几只
【分析】假设只都是兔,一共应有4×46=184只脚,这和已知的128只脚相比多了184-128=56只脚,这是因为我们把鸡当成了兔子,如果把1只鸡当成1只兔,就要比实际多4-2=2(只)脚,那么56只脚是我们把56÷2=28只鸡当成了兔子,所以鸡的只数就是28,兔的只数是46-28=18(只).当然,这里我们也可以假设46只全是鸡,小朋友们,请你按此思路做做这道题目!。
1、某玩具店新购进飞机和汽车模型共30个,其中飞机模型每个有5个轮子,汽车模型每个有6个轮子,这些玩具模型共有160个轮子。
则新购进的飞机模型有多少个?A. 10个B. 15个C. 20个D. 25个(答案:C)2、小福奥数考试,一共15题,每题5分,错一题或者不答一题倒扣3分,小福一共得了51分,他对了多少题?A. 10题B. 11题C. 12题D. 13题(答案:B)3、动物园饲养的食肉动物分大型动物和小型动物两类,规定老虎、狮子一类的大动物每次喂肉每头三斤,狐狸、山猫一类小动物每三头喂一斤。
该动物园共有这两类动物100头,每次需喂肉100斤,问大、小动物各多少?A. 大动物20头,小动物80头B. 大动物25头,小动物75头C. 大动物30头,小动物70头D. 大动物35头,小动物65头(答案:B)4、自行车和三轮车共5辆,总共13个轮子,三轮车有:A. 2辆B. 3辆C. 4辆D. 5辆(答案:B)5、乐乐百货商店委托搬运站运送500只花瓶,双方商定每只运费0.24元,但如果发生损毁,那么每打破一只不仅不给运费,而且还要赔偿1.26元,结果搬运站共得运费115.5元。
问:搬运过程中共打破了几只花瓶?A. 5只B. 10只C. 15只D. 20只(答案:A)6、鸡兔同笼有23个头,有62条腿.兔有多少只?A. 10只B. 11只C. 12只D. 13只(答案:D)7、鸡比兔多13只,鸡腿比兔腿多16条,鸡和兔各有多少只?A. 鸡23只,兔10只B. 鸡20只,兔10只C. 鸡15只,兔10只D. 鸡25只,兔12只(答案:D)8、小福奥数考试,一共10题,每题2分,错一题或者不答一题倒扣1分,小福一共得了15分,他对了多少题?A. 8题B. 9题C. 10题D. 11题(答案:B)9、鸡兔同笼共有脚100只,若将鸡换成兔,兔换成鸡,则共有脚92只,则鸡有多少只.A. 10只B. 12只C. 14只D. 16只(答案:D)10、动物园饲养的食肉动物分大型动物和小型动物两类,规定老虎、狮子一类的大动物每次喂肉每头三斤,狐狸、山猫一类小动物每三头喂一斤。
1.小学生奥数鸡兔同笼问题1、鸡兔同笼,鸡兔共35个头,94条腿,问鸡兔各多少只?2、鸡兔同笼,鸡比兔多15只,鸡兔共有脚132只,问鸡兔各多少只?3、鸡兔同笼,鸡兔共40个头,鸡脚比兔脚共多32只,问鸡兔各多少只?4、鸡兔同笼,鸡比兔多10只,但脚却比兔子少60只,问鸡兔各多少只?5、鸡兔同笼,鸡比兔多10只,鸡脚比兔脚多10只,问鸡兔各多少只?6、在一个停车场内,汽车、摩托车共停了48辆,其中每辆汽车有4个轮子,每辆摩托车有3个轮子,这些车共有172个轮子,停车场内有汽车、摩托车各多少辆?7、张大妈养鸡兔共200只,鸡兔足数共560只,求鸡兔各有多少只?8、张大妈家养的鸡比兔多13只,兔足比鸡足少16只,求鸡兔各有多少只?9、鹤龟同池,鹤比龟多12只,鹤龟足共72只,求鹤龟各有多少只?10、小刚买回8分邮票和4分邮票共100张,共付出6.8元,问,小刚买回这两种邮票个多少张?各付出多少元?2.小学生奥数鸡兔同笼问题1、鸡兔同笼,共有头30个,足86只,求鸡兔各有多少只?2、有20张5元和10元的人民币,一共是175元,5元和10元的人民币各有多少张?3、王老师圆珠笔和钢笔共买了15枝,圆珠笔每枝1.5元,钢笔每枝4.5元,共花了49.5元,圆珠笔和钢笔各买了多少枝?4、鸡兔同笼,鸡兔共35个头,94条腿,问鸡兔各多少只?5、在一个停车场内,汽车、摩托车共停了48辆,其中每辆汽车有4个轮子,每辆摩托车有3个轮子,这些车共有172个轮子,停车场内有汽车摩托车各多少辆?6、小刚买回8分邮票和4分邮票共100张,共付出6.8元,问,小刚买回这两种邮票各多少张?7、在知识竞赛中,有10道判断题,评分规定:每答对一道题的两分,答错一道题要倒扣一分。
小明答了全部题目,但最后只得了14分,他答错几题?8、某运输队为超市运送暖瓶500箱,每箱装有6个暖瓶。
已知每10个暖瓶的运费为5元,损坏一个不但不给运费还要赔10元,运后结算时,运输队共得1350元的运费。
复杂的鸡兔同笼问题专题训练一、知识要点和基本方法1.鸡兔同笼的基本问题是:已知鸡、兔总头数和总脚数,求鸡、兔各有多少只.(1)解决鸡兔同笼问题的方法通常是用假设法,解题思路是:先假设笼子里装的全是鸡,根据鸡兔的总数就可以算出在假设下共有几只脚,把这样得到的脚数与题中给出的脚数相比较,看看差多少,每差2只脚就说明有1只兔,将所差的脚数除以2,就可以算出共有多少只兔.(2)解决鸡兔同笼问题的基本关系式是:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数).兔数=(总脚数-鸡脚数×总头数)÷(兔脚数-鸡脚数).注意,这两个基本关系式不必都用,用其中一个算出兔数或鸡数,又知总数,所以另一个也就知道了.2.鸡兔同笼问题的变型有两类:(1)将鸡、兔的总头数和总脚数中的“两数之和”变成“两数之差”,这样得到三种情况:已知鸡、兔头数之差和总脚数,求鸡兔各有多少只;已知鸡、兔脚数之差和总头数,求鸡兔各有多少只;已知鸡、兔头数之差和脚数之差,求鸡兔各有多少只.(2)将基本问题中同笼的是鸡、兔两种不同东西,还可以引伸到同笼中不同东西是三种,四种等等.注意:鸡兔同笼问题的两种变型均可转化成基本问题来解决.二、例题精讲例1、在同一个笼子中,有若干只鸡和兔,从笼子上看有40个头,从笼子下数有130只脚,那么这个笼子中装有兔、鸡各多少只?分析:题目中给出了鸡、兔共有40只,如果把兔子的两只前脚用绳子捆起来,看作是一只脚,两只后脚也捆起来,也看成是一只脚,那么兔子就成了2只脚(即把兔子都当成两只脚的鸡).鸡兔总的脚数是40×2=80(只)比题中所说的130只要少130-80=50(只).现在松开一只兔子脚上的绳子,总的脚数就会增加2,即80+2=82.再松开一只兔子脚上的绳子,总的脚数又增加2,即82+2=84,…一直继续下去,直至增加到50.因此,兔子数是50÷2=25(只).实际上,这就是上述基本关系式(2).解:(130-40×2)÷(4-2)=(130-80)÷2=50÷2=25(只).40-25=15(只).答:笼子中有兔子25只,有鸡15只.例2、蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀,现在这三种小虫共21只,有140条腿和24对翅膀,求每种小虫各几只?分析:此题中出现了3种昆虫,不仅有腿的比较,而且又出现了翅膀,显然比例1复杂了.解此题的关键就是将3种昆虫转化为2种昆虫,这样解起来就比较容易了.突破口在于:蝉和蜻蜓都有6条腿.解:因为蜻蜓和蝉都有6条腿,所以从腿的数目考虑,可以把昆虫分成“8条腿”和“6条腿”两种,利用基本关系式算出8条腿的蜘蛛数=(140-6×21)÷(8-6)=(140-126)÷2=14÷2=7(只).因此,知道了6条腿的昆虫共有21-7=14(只),也就是蜻蜓和蝉共有14只.因为蜻蜓和蝉共有24对翅膀,现在再用一次基本关系式,得蝉数=(14×2-24)÷(2-1)=(28-24)÷1=4(只).因此,蜻蜓数是14-4=10(只).答:有7只蜘蛛,4只蝉,10只蜻蜓.例3、鸡与兔共40只,鸡的脚数比兔的脚数少70,问鸡与兔各多少只?解:假设再补上70只鸡脚,也就是再有鸡70÷2=35(只),则鸡与兔的脚数就相等,兔的脚数是鸡的脚数4÷2=2(倍).于是鸡的只数是兔的只数的2倍.因此,兔的只数是(40+70÷2)÷(2+1)=25(只),鸡的只数是40-25=15(只).答:鸡15只,兔25只.例4、在一个停车场上,停放的车辆(汽车和三轮摩托车)数恰好是24.其中每辆汽车有四个轮子,每辆摩托车有三个轮子.这些车共有86个轮子.那么,三轮摩托车有多少辆?分析:我们可将汽车“看作兔子”,将三轮摩托车“看作鸡”,轮子“看作腿”,就可用鸡兔同笼的原理来解此题.解:24辆车如果都算作汽车,那么将有24×4=96(个)轮子.比现有的86个多10个轮子.每一辆三轮摩托车比每一辆汽车少一个轮子,故要有10辆三轮摩托车来抵消10个轮子.答:共有10辆三轮摩托车.公式套用:若用基本关系式,鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)“翻译”为摩托车车辆数计算公式(这里将摩托车看作“鸡”):摩托车数=(汽车轮子数×车辆总数-轮子总数)÷(汽车轮子数-摩托车轮子数),即有摩托车数:(4×24-86)÷(4-3)=10(辆).三、专题特训1.有一首民谣:“一队猎手一队狗,二队并着一起走,数头一共三百六,数腿一共八百九。
奥数练习稍复杂的鸡兔同笼问题LELE was finally revised on the morning of December 16, 2020奥数练习稍复杂的鸡兔同笼应用题2 姓名_______ 2016/7/14例1、蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀,现有蜘蛛、蜻蜓和蝉三种小虫16只,共有110条腿和14对翅膀,每种小虫各有几只?答:蜘蛛()只,蝉()只,蜻蜓()只。
练习:已知蜘蛛8条腿,蜻蜓6条腿,两对翅膀,蝉有6条腿,一对翅膀,现在有这三种动物47只,共有腿324条,翅膀37对,问这三种动物各有几只?答:蜘蛛()只,蝉()只,蜻蜓()只。
例2、大嫂家里养了一些鸡和兔,已知鸡比兔多48只,而鸡脚比兔脚多38只,那么大嫂家中养的鸡和兔各多少只?答:鸡()只,兔()只。
练习:鸡兔同笼,鸡比兔多25只,鸡脚比兔脚多20只,鸡、兔各有多少只?答:鸡()只,兔()只。
例3、鸡兔共有脚100只,若将鸡换成兔,兔换成鸡,则共有脚86只,鸡兔各有几只?答:鸡()只,兔()只。
练习:鸡兔同笼,共有脚106只,如果将鸡换成兔,兔换成鸡,则共有脚122只,鸡兔各有多少只?答:鸡()只,兔()只。
例4、传说中,九头鸟有9个头1个尾,五尾鸟有1个头5个尾。
如果共有头9999个,共有尾5555个,那么九头鸟有多少只?五尾鸟有多少只?答:九头鸟有()只?五尾鸟有()只练习:九尾狐(每只含1头9尾)和九头鸟(每只含9头1尾)共有头84个,尾116只,问狐和鸟各有多少只?答:狐()只,鸟()只。
例5、育才小学3名同学去参加数学竞赛,共10道题,答对一题得10分,答错一题扣3分,这3名同学都回答了所有的题,小勇得87分,小亮得74分,小明得9分,他们三人共答对了多少道题?答:他们三人共答对了()题。
练习1、甲、乙两人参加数学竞赛,每做对一题得20分,每做错一题倒扣12分,两人各做了10题,共得208分,其中甲比乙多得64分,甲、乙两人各做对几题答:甲做对()题,乙做对()题。
奥数练习稍复杂的鸡兔同笼应用题2 姓名_______ 2016/7/14
例1、蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀,现有蜘蛛、蜻蜓和蝉三种小虫16只,共有110条腿和14对翅膀,每种小虫各有几只
答:蜘蛛()只,蝉()只,蜻蜓()只。
练习:已知蜘蛛8条腿,蜻蜓6条腿,两对翅膀,蝉有6条腿,一对翅膀,现在有这三种动物47只,共有腿324条,翅膀37对,问这三种动物各有几只
答:蜘蛛()只,蝉()只,蜻蜓()只。
例2、大嫂家里养了一些鸡和兔,已知鸡比兔多48只,而鸡脚比兔脚多38只,那么大嫂家中养的鸡和兔各多少只
答:鸡()只,兔()只。
练习:鸡兔同笼,鸡比兔多25只,鸡脚比兔脚多20只,鸡、兔各有多少只
答:鸡()只,兔()只。
例3、鸡兔共有脚100只,若将鸡换成兔,兔换成鸡,则共有脚86只,鸡兔各有几只
答:鸡()只,兔()只。
练习:鸡兔同笼,共有脚106只,如果将鸡换成兔,兔换成鸡,则共有脚122只,鸡兔各有多少只
答:鸡()只,兔()只。
例4、传说中,九头鸟有9个头1个尾,五尾鸟有1个头5个尾。
如果共有头9999个,共有尾5555个,那么九头鸟有多少只五尾鸟有多少只
答:九头鸟有()只五尾鸟有()只练习:九尾狐(每只含1头9尾)和九头鸟(每只含9头1尾)共有头84个,尾116只,问狐和鸟各有多少只
答:狐()只,鸟()只。
例5、育才小学3名同学去参加数学竞赛,共10道题,答对一题得10分,答错一题扣3分,这3名同学都回答了所有的题,小勇得87分,小亮得74分,小明得9分,他们三人共答对了多少道题
答:他们三人共答对了()题。
练习1、甲、乙两人参加数学竞赛,每做对一题得20分,每做错一题倒扣12分,两人各做了10题,共得208分,其中甲比乙多得64分,甲、乙两人各做对几题?
答:甲做对()题,乙做对()题。
奥数综合练习姓名_______2016/7/14
1、某粮库,甲仓存粮比乙仓多18吨,要使乙仓存粮比甲仓多4吨,要从甲仓取出()吨粮食放入乙仓。
2、姐妹两人共有480元,如果姐给妹34元,则两人钱数相等,原来姐妹两人各有多少元
答:原来姐姐()元,妹妹()元3、大书架有书124本,小书架有书98本,应从小书架取出()本书放入大书架,才能使大书架上的书的本数是小书架的2倍
4、大小两数的和是136,大数是小数的3倍,求两数各是多少
答:大数(),小数()。
5、大数比小数多88,大数是小数的9倍,两数各是多少
答:大数(),小数()。
6、鸡兔同笼,共54个头,144只脚,求鸡和兔各多少只
答:鸡()只,兔()只。
7、一个饲养小组一共养鸡、兔55只,共有脚170只,求鸡兔各多少只
答:鸡()只,兔()只。
8、一张试卷25题,答对一题得4分,答错一题或不答倒扣4分,小红得了60分,她答对了
()题
9、甲乙两箱苹果共96千克,如果从甲箱取出16千克放入乙箱,那么乙箱的千克数是甲箱的3倍,两箱原来有苹果各是多少千克
答:甲箱原来有()千克,乙箱原来有()千克。
10、甲乙两筐梨,一共有120个,如果从乙筐取13个放入甲筐,则甲筐的个数是乙筐的2倍,求甲乙两筐原来有梨各多少个
答:甲筐原来()个,乙筐原来()个。
11、东水池有水3830立方米,西水池有水850立方米,如果东水池里的水每分钟以32立方米的速度流入西水池,求多少分钟后东水池中的水是西水池中的水的3倍
答:()分钟后东水池中的水是西水池中的水的3倍12、游泳馆里有大小两个水池,大水池里有水2800立方米,小水池里有水1000立方米,如果大水池以每分钟20立方米的速度流入小水池,那么,多少分钟后小水池中的水是大水池的4倍
答:()分钟后小水池中的水是大水池的4倍。
13、一个粮油店运来两桶油,大桶有油120千克,小桶有油90千克,两桶油卖出同样多后,大桶剩下的油刚好是小桶剩的油的4倍,两桶各剩多少千克油各卖出多少千克油
答:大桶剩下()千克,小桶剩下()千克。
各卖出()千克油。