高考数学中的29个问题_理科数学问题

注：尊敬的各位读者，本文是笔者教育资料系列文章的一篇，由于时间关系，如有相关问题，望各位雅正。

希望本文能对有需要的朋友有所帮助。

如果您需要其它类型的教育资料，可以关注笔者知识店铺。

由于部分内容来源网络，如有部分内容侵权请联系笔者。

专题三：高考数学不等式问题的题型与方法（理科）一、考点回顾1．高考中对不等式的要求是：理解不等式的性质及其证明；掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用；掌握分析法、综合法、比较法证明简单的不等式；掌握简单不等式的解法；理解不等式│a│-│b│≤│a+b│≤│a│+│b│。

2．不等式这部分内容在高考中通过两面考查，一是单方面考查不等式的性质，解法及证明；二是将不等式知识与集合、逻辑、函数、三角函数、数列、解析几何、立体几何、平面向量、导数等知识交汇起来进行考查，深化数学知识间的融汇贯通，从而提高学生数学素质及创新意识．3．在不等式的求解中，换元法和图解法是常用的技巧之一，通过换元，可将较复杂的不等式化归为较简单的或基本不等式，通过构造函数，将不等式的解化归为直观、形象的图象关系，对含有参数的不等式，运用图解法，可以使分类标准更加明晰．4．证明不等式的方法灵活多样，但比较法、综合法、分析法仍是证明不等式的最基本方法．要依据题设、题断的结构特点、内在联系，选择适当的证明方法，要熟悉各种证法中的推理思维，并掌握相应的步骤，技巧和语言特点．比较法的一般步骤是：作差(商)→变形→判断符号(值)．5．在近几年全国各省市的高考试卷中，不等式在各种题型中都有出现。

在解答题中，不等式与函数、数列与导数相结合，难度比较大，使用导数解决逐渐成为一般方法6．知识网络其中：指数不等式、对数不等式、无理不等式只要求了解基本形式，不做过高要求.二、 经典例题剖析 1．有关不等式的性质此类题经常出现在选择题中，一般与函数的值域，最值与比较大小等常结合在一起例1．（2006年江西卷）若a >0，b >0，则不等式－b <1x<a 等价于（ ） A ．1b －<x <0或0<x <1a B.－1a <x <1b C.x <-1a 或x >1b D.x <1b －或x >1a解析：－b <1x <a 等价于－b <1x <0或0<1x <a 等价于x <1b －或x >1a答案：D点评：注意不等式ba b a 11>⇔<和适用条件是0>ab 例2.（2007年北京卷）如果正数a b c d ，，，满足4a b cd +==，那么（ ）Ａ．ab c d +≤，且等号成立时a b c d ，，，的取值唯一 Ｂ．ab c d +≥，且等号成立时a b c d ，，，的取值唯一 Ｃ．ab c d +≤，且等号成立时a b c d ，，，的取值不唯一 Ｄ．ab c d +≥，且等号成立时a b c d ，，，的取值不唯一解析：正数a b c d ，，，满足4a b cd +==，∴ 4=a b +≥，即4ab ≤，当且仅当a =b =2时，“=”成立；又4=2()2c d cd +≤，∴ c+d ≥4，当且仅当c =d =2时，“=”成立；综上得ab c d +≤，且等号成立时a b c d ，，，的取值都为2 答案：A点评：本题主要考查基本不等式，命题人从定值这一信息给考生提供了思维，重要不等式可以完成和与积的转化，使得基本不等式运用成为现实。

2020年高考理科数学《数列》题型归纳与训练【题型归纳】等差数列、等比数列的基本运算题组一 等差数列基本量的计算例1 设S n 为等差数列{a n }的前n 项和，若a 1=1，公差d =2，S n ＋2−S n =36，则n = A ．5 B ．6 C ．7 D ．8【答案】D【解析】解法一：由题知()21(1)21n S na d n n n n n n ==+-=-+，S n ＋2=(n ＋2)2，由S n ＋2−S n =36得，(n ＋2)2−n 2=4n ＋4=36，所以n =8.解法二：S n ＋2−S n =a n ＋1＋a n ＋2=2a 1＋(2n ＋1)d =2＋2(2n ＋1)=36，解得n =8.所以选D ． 【易错点】对S n ＋2−S n =36，解析为a n ＋2，发生错误。

题组二 等比数列基本量的计算例2 在各项均为正数的等比数列{a n }中，若28641,2a a a a ==+，则a 6的值是________． 【答案】4【解析】设公比为q (q ≠0)，∵a 2=1，则由8642a a a =+得6422q q q =+，即4220q q --=，解得q 2=2，∴4624a a q ==.【易错点】忘了条件中的正数的等比数列. 【思维点拨】等差（比）数列基本量的计算是解决等差（比）数列题型时的基础方法，在高考中常有所体现，多以选择题或填空题的形式呈现，有时也会出现在解答题的第一问中，属基础题.等差(比)数列基本运算的解题思路：(1)设基本量a 1和公差d (公比q )．(2)列、解方程组：把条件转化为关于a 1和d (q )的方程(组)，然后求解，注意整体计算，以减少运算量．等差数列、等比数列的判定与证明题组一 等差数列的判定与证明例1设数列{a n }的各项都为正数，其前n 项和为S n ，已知对任意n ∈N *，S n 是a 2n 和a n 的等差中项． (1)证明：数列{a n }为等差数列；(2)若b n =−n ＋5，求{a n ·b n }的最大项的值并求出取最大值时n 的值． 【答案】(1)见解析；(2) 当n =2或n =3时，{a n ·b n }的最大项的值为6. 【解析】(1)由已知可得2S n =a 2n ＋a n ，且a n >0， 当n =1时，2a 1=a 21＋a 1，解得a 1=1； 当n ≥2时，有2S n −1=a 2n －1＋a n −1，所以2a n =2S n −2S n −1=a 2n −a 2n －1＋a n −a n −1，所以a 2n −a 2n －1=a n ＋a n −1，即(a n ＋a n −1)(a n −a n −1)=a n ＋a n −1，因为a n ＋a n −1>0， 所以a n −a n −1=1(n ≥2)．故数列{a n }是首项为1，公差为1的等差数列． (2)由(1)可知a n =n ，设c n =a n ·b n ，则c n =n (−n ＋5)=−n 2＋5n =−⎝⎛⎭⎫n －522＋254， 因为n ∈N *，所以当n =2或n =3时，{a n ·b n }的最大项的值为6.【易错点】S n 是a 2n 和a n 的等差中项，无法构建一个等式去求解出a n 。

专题十五 复数1.【20xx 高考新课标2，理2】若a 为实数且(2)(2)4ai a i i +-=-，则a =（ ）A ．1-B ．0C ．1D ．2【答案】B【解析】由已知得24(4)4a a i i +-=-，所以240,44a a =-=-，解得0a =，故选B ．【考点定位】复数的运算．【名师点睛】本题考查复数的运算，要利用复数相等列方程求解，属于基础题．2.【20xx 高考四川，理2】设i 是虚数单位，则复数32i i-( ) （A ）-i （B ）-3i （C ）i. （D ）3i【答案】C【解析】32222i i i i i i i i-=--=-+=，选C. 【考点定位】复数的基本运算.【名师点睛】复数的概念及运算也是高考的热点，几乎是每年必考内容，属于容易题.一般来说，掌握复数的基本概念及四则运算即可.3.【20xx 高考广东，理2】若复数()32z i i =- ( i 是虚数单位 )，则z =（ ）A ．32i -B ．32i +C ．23i +D ．23i -【答案】D ．【解析】因为()3223z i i i =-=+，所以z =23i -，故选D ．【考点定位】复数的基本运算，共轭复数的概念．【名师点睛】本题主要考查复数的乘法运算，共轭复数的概念和运算求解能力，属于容易题；复数的乘法运算应该是简单易解，但学生容易忘记和混淆共轭复数的概念，z a bi =+的共轭复数为z a bi =-．4.【20xx 高考新课标1，理1】设复数z 满足11z z+-=i ，则|z|=( )（A ）1 （B （C （D ）2【答案】A【解析】由11z i z +=-得，11i z i -+=+=(1)(1)(1)(1)i i i i -+-+-=i ，故|z|=1，故选A. 【考点定位】本题主要考查复数的运算和复数的模等.【名师点睛】本题将方程思想与复数的运算和复数的模结合起来考查，试题设计思路新颖，本题解题思路为利用方程思想和复数的运算法则求出复数z ，再利用复数的模公式求出|z|,本题属于基础题，注意运算的准确性.5.【20xx 高考北京，理1】复数()i 2i -=（ ）A ．12i +B ．12i -C ．12i -+D ．12i --【答案】A考点定位：本题考查复数运算，运用复数的乘法运算方法进行计算，注意21i =-.【名师点睛】本题考查复数的乘法运算，本题属于基础题，数的概念的扩充部分主要知识点有：复数的概念、分类，复数的几何意义、复数的运算，特别是复数的乘法与除法运算，运算时注意21i =-，注意运算的准确性,近几年高考主要考查复数的乘法、除法，求复数的模、复数的虚部、复数在复平面内对应的点的位置等.6.【20xx 高考湖北，理1】 i 为虚数单位，607i 的共轭复数．．．．为（ ） A ．i B ．i - C ．1 D ．1-【答案】A【解析】i i i i -=⋅=⨯31514607,所以607i 的共轭复数．．．．为i ，选A . 【考点定位】共轭复数.【名师点睛】复数中，i 是虚数单位,24142434111()n n n n i i i i i i i n +++=-==-=-=∈Z ；，，，7.【20xx 高考山东，理2】若复数z 满足1z i i=-，其中i 为虚数为单位，则z =（ ） （A ）1i - （B ）1i + （C ）1i -- （D ）1i -+【答案】A 【解析】因为1z i i=-，所以，()11z i i i =-=+ ，所以，1z i =- 故选：A. 【考点定位】复数的概念与运算.【名师点睛】本题考查复数的概念和运算，采用复数的乘法和共轭复数的概念进行化简求解. 本题属于基础题，注意运算的准确性.8.【20xx 高考安徽，理1】设i 是虚数单位，则复数21i i-在复平面内所对应的点位于（ ） （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限【答案】B 【解析】由题意22(1)2211(1)(1)2i i i i i i i i +-+===-+--+，其对应的点坐标为(1,1)-，位于第二象限，故选B.【考点定位】1.复数的运算；2.复数的几何意义.【名师点睛】复数的四则运算问题主要是要熟记各种运算法则，尤其是除法运算，要将复数分母实数化（分母乘以自己的共轭复数），这也历年考查的重点；另外，复数z a bi =+在复平面内一一对应的点为(,)Z a b .9.【20xx 高考重庆，理11】设复数a +bi （a ，b ∈R ），则（a +bi ）（a -bi ）=________.【答案】3【解析】由a +得=，即223a b +=，所以22()()3a bi a bi a b +-=+=.【考点定位】复数的运算.【名师点晴】复数的考查核心是代数形式的四则运算，即使是概念的考查也需要相应的运算支持．本题首先根据复数模的定义得a +，复数相乘可根据平方差公式求得()()a bi a bi +-22()a bi =-22a b =+，也可根据共轭复数的性质得()()a bi a bi +-22a b =+．10.【20xx 高考天津，理9】i 是虚数单位，若复数()()12i a i -+ 是纯虚数，则实数a 的值为 .【答案】2-【解析】()()()12212i a i a a i -+=++-是纯虚数，所以20a +=，即2a =-.【考点定位】复数相关概念与复数的运算.【名师点睛】本题主要考查复数相关概念与复数的运算.先进行复数的乘法运算，再利用纯虚数的概念可求结果，是容易题.11.【20xx 江苏高考，3】设复数z 满足234z i =+（i 是虚数单位），则z 的模为_______.【解析】22|||34|5||5||z i z z =+=⇒=⇒=【考点定位】复数的模【名师点晴】在处理复数相等的问题时，一般将问题中涉及的两个复数均化成一般形式，利用复数相等的充要条件“实部相等，虚部相等”进行求解.本题涉及复数的模，利用复数模的性质求解就比较简便：2211121222||||||||||||.||z z z z z z z z z z ==⋅=，， 12.【20xx 高考湖南，理1】已知()211i i z -=+（i 为虚数单位），则复数z =（ ） A.1i + B.1i - C.1i -+ D.1i --【答案】D.【考点定位】复数的计算.【名师点睛】本题主要考查了复数的概念与基本运算，属于容易题，意在考查学生对复数代数形式四则运算的掌握情况，基本思路就是复数的除法运算按“分母实数化”原则，结合复数的乘法进行计算，而复数的乘法则是按多项式的乘法法则进行处理.13.【20xx 高考上海，理2】若复数z 满足31z z i +=+，其中i 为虚数单位，则z = ．【答案】1142i +【解析】设(,)z a bi a b R =+∈，则113()1412142a bi a bi i a b z i ++-=+⇒==⇒=+且 【考点定位】复数相等，共轭复数【名师点睛】研究复数问题一般将其设为(,)z a bi a b R =+∈形式，利用复数相等充要条件：实部与实部，虚部与虚部分别对应相等，将复数相等问题转化为实数问题：解对应方程组问题.复数问题实数化转化过程中，需明确概念，如(,)z a bi a b R =+∈的共轭复数为(,)z a bi a b R =-∈，复数加法为实部与实部，虚部与虚部分别对应相加.【20xx 高考上海，理15】设1z ，2C z ∈，则“1z 、2z 中至少有一个数是虚数”是“12z z -是虚数”的（ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件【答案】B【解析】若1z 、2z 皆是实数，则12z z -一定不是虚数，因此当12z z -是虚数时，则“1z 、2z 中至少有一个数是虚数”成立，即必要性成立；当1z 、2z 中至少有一个数是虚数，12z z -不一定是虚数，如12z z i ==，即充分性不成立，选B.【考点定位】复数概念，充要关系【名师点睛】形如a ＋b i(a ，b ∈R )的数叫复数，其中a ，b 分别是它的实部和虚部．若b ＝0，则a ＋b i 为实数；若b ≠0，则a ＋b i 为虚数；若a ＝0且b ≠0，则a ＋b i 为纯虚数．判断概念必须从其定义出发，不可想当然.。

第8讲二项分布与正态分布一、选择题1．甲、乙两地都位于长江下游，根据天气预报的纪录知，一年中下雨天甲市占20%，乙市占18%，两市同时下雨占12%.则甲市为雨天，乙市也为雨天的概率为( )A．0.6 B．0.7C．0.8 D．0.66解析甲市为雨天记为事件A，乙市为雨天记为事件B，则P(A)＝0.2，P(B)＝0.18，P(AB)＝0.12，∴P(B|A)＝P ABP A＝0.120.2＝0.6.答案 A2．投掷一枚均匀硬币和一枚均匀骰子各一次，记“硬币正面向上”为事件A，“骰子向上的点数是3”为事件B，则事件A，B中至少有一件发生的概率是( )A.512B.12C.712D.34解析本题涉及古典概型概率的计算．本知识点在考纲中为B级要求．由题意得P(A)＝12，P(B)＝16，则事件A，B至少有一件发生的概率是1－P(A)·P(B)＝1－12×56＝712.答案 C3．在4次独立重复试验中，随机事件A恰好发生1次的概率不大于其恰好发生两次的概率，则事件A在一次试验中发生的概率p的取值范围是()．A．[0.4,1] B．(0,0.4]C．(0,0.6] D．[0.6,1]解析设事件A发生的概率为p，则C14p(1－p)3≤C24p2(1－p)2，解得p≥0.4，故选A.答案 A4．设随机变量X 服从正态分布N (2,9)，若P (X >c ＋1)＝P (X <c －1)，则c 等于( )． A ．1B ．2C ．3D ．4解析 ∵μ＝2，由正态分布的定义，知其函数图象关于x ＝2对称，于是c ＋1＋c －12＝2，∴c ＝2. 答案 B5．在正态分布N ⎝ ⎛⎭⎪⎫0，19中，数值前在(－∞，－1)∪(1，＋∞)内的概率为( )．A ．0.097B ．0.046C ．0.03D ．0.0026 解析 ∵μ＝0，σ＝13∴P (X ＜1或x ＞1)＝1－P (－1≤x ≤1)＝1－P (μ－3σ≤X ≤μ＋3σ)＝1－0.997 4＝0.002 6. 答案 D6．已知三个正态分布密度函数φi (x )＝12πσi·e －(x －μi )22σ2i (x ∈R ，i ＝1,2,3)的图象如图所示，则 ( )．A ．μ1＜μ2＝μ3，σ1＝σ2＞σ3B ．μ1＞μ2＝μ3，σ1＝σ2＜σ3C ．μ1＝μ2＜μ3，σ1＜σ2＝σ3D ．μ1＜μ2＝μ3，σ1＝σ2＜σ3解析 正态分布密度函数φ2(x )和φ3(x )的图象都是关于同一条直线对称，所以其平均数相同，故μ2＝μ3，又φ2(x )的对称轴的横坐标值比φ1(x )的对称轴的横坐标值大，故有μ1＜μ2＝μ3.又σ越大，曲线越“矮胖”，σ越小，曲线越“瘦高”，由图象可知，正态分布密度函数φ1(x )和φ2(x )的图象一样“瘦高”，φ3(x )明显“矮胖”，从而可知σ1＝σ2＜σ3. 答案 D 二、填空题7．三支球队中，甲队胜乙队的概率为0.4，乙队胜丙队的概率为0.5，丙队胜甲队的概率为0.6，比赛顺序是：第一局是甲队对乙队，第二局是第一局的胜者对丙队，第三局是第二局胜者对第一局的败者，第四局是第三局胜者对第二局败者，则乙队连胜四局的概率为________．解析设乙队连胜四局为事件A，有下列情况：第一局中乙胜甲(A1)，其概率为1－0.4＝0.6；第二局中乙胜丙(A2)，其概率为0.5；第三局中乙胜甲(A3)，其概率为0.6；第四局中乙胜丙(A4)，其概率为0.50，因各局比赛中的事件相互独立，故乙队连胜四局的概率为：P(A)＝P(A1A2A3A4)＝0.62×0.52＝0.09.答案 0.098．设随机变量X服从正态分布N(0,1)，如果P(X≤1)＝0.8413，则P(－1<X<0)＝________.解析∵P(X≤1)＝0.841 3，∴P(X>1)＝1－P(X≤1)＝1－0.841 3＝0.158 7.∵X～N(0,1)，∴μ＝0.∴P(X<－1)＝P(X>1)＝0.158 7，∴P(－1<X<1)＝1－P(X<－1)－P(X>1)＝0.682 6.∴P(－1<X<0)＝12P(－1<X<1)＝0.341 3.答案0.341 39．设随机变量ξ服从正态分布N(0,1)，记Ф(x)＝P(ξ＜x)，给出下列结论：①Φ(0)＝0.5；②Φ(x)＝1－Φ(－x)；③P(|ξ|＜2)＝2Φ(2)－1.则正确结论的序号是________．答案①②③10．商场经营的某种包装大米的质量(单位：kg)服从正态分布X～N(10,0.12)，任选一袋这种大米，质量在9.8～10.2 kg的概率是________．解析P(9.8<X<10.2)＝P(10－0.2<X<10＋0.2)＝0.954 4.答案0.954 4三、解答题11．设在一次数学考试中，某班学生的分数X～N(110,202)，且知试卷满分150分，这个班的学生共54人，求这个班在这次数学考试中及格(即90分以上)的人数和130分以上的人数．解由题意得μ＝110，σ＝20，P(X≥90)＝P(X－110≥－20)＝P(X－μ≥－σ)，∵P(X－μ<－σ)＋P(－σ≤X－μ≤σ)＋P(X－μ>σ)＝2P(X－μ<－σ)＋0.682 6＝1，∴P(X－μ<－σ)＝0.158 7，∴P(X≥90)＝1－P(X－μ<－σ)＝1－0.158 7＝0.841 3.∴54×0.841 3≈45(人)，即及格人数约为45人．∵P(X≥130)＝P(X－110≥20)＝P(X－μ≥σ)，∴P(X－μ≤－σ)＋P(－σ≤X－μ≤σ)＋P(X－μ>σ)＝0.682 6＋2P(X－μ≥σ)＝1，∴P(X－μ≥σ)＝0.158 7.∴54×0.158 7≈9(人)，即130分以上的人数约为9人．12．在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100)，已知成绩在90分以上的学生有13人．(1)求此次参加竞赛的学生总数共有多少人？(2)若计划奖励竞赛成绩排在前228名的学生，问受奖学生的分数线是多少？解设学生的得分情况为随机变量X，X～N(60,100)．则μ＝60，σ＝10.(1)P(30＜X≤90)＝P(60－3×10＜X≤60＋3×10)＝0.997 4.∴P(X＞90)＝12[1－P(30＜X≤90)]＝0.001 3∴学生总数为：130.001 3＝10 000(人)．(2)成绩排在前228名的学生数占总数的0.022 8. 设分数线为x.则P(X≥x0)＝0.022 8.∴P(120－x0＜x＜x0)＝1－2×0.022 8＝0.954 4. 又知P(60－2×10＜x＜60＋2×10)＝0.954 4.∴x0＝60＋2×10＝80(分)．13．某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.(1)确定x，y的值，并求顾客一次购物的结算时间X的分布列与数学期望；(2)若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2.5分钟的概率．(注：将频率视为概率)解(1)由已知得25＋y＋10＝55，x＋30＝45，所以x＝15，y＝20.该超市所有顾客一次购物的结算时间组成一个总体，所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本，将频率视为概率得P(X＝1)＝15100＝320，P(X＝1.5)＝30100＝310，P(X＝2)＝25100＝14，P(X＝2.5)＝20100＝15，P(X＝3)＝10100＝110.X的分布列为X的数学期望为E(X)＝1×320＋1.5×310＋2×14＋2.5×15＋3×110＝1.9.(2)记A为事件“该顾客结算前的等候时间不超过2.5分钟”，X i(i＝1,2)为该顾客前面第i位顾客的结算时间，则P(A)＝P(X1＝1且X2＝1)＋P(X1＝1且X2＝1.5)＋P(X1＝1.5且X2＝1)．由于各顾客的结算相互独立，且X1，X2的分布列都与X的分布列相同，所以P(A)＝P(X1＝1)×P(X2＝1)＋P(X1＝1)×P(X2＝1.5)＋P(X1＝1.5)×P(X2＝1)＝320×320＋320×310＋310×320＝980.故该顾客结算前的等候时间不超过2.5分钟的概率为980.14．现有甲、乙两个靶，某射手向甲靶射击一次，命中的概率为34，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为23，每命中一次得2分，没有命中得0分．该射手每次射击的结果相互独立．假设该射手完成以上三次射击．(1)求该射手恰好命中一次的概率；(2)求该射手的总得分X 的分布列及数学期望E (X )．解 (1)记：“该射手恰好命中一次”为事件A ，“该射手射击甲靶命中”为事件B ，“该射手第一次射击乙靶命中”为事件C ，“该射手第二次射击乙靶命中”为事件D .由题意，知P (B )＝34，P (C )＝P (D )＝23， 由于A ＝B C － D －＋B －C D －＋B － C －D ， 根据事件的独立性和互斥性，得 P (A )＝P (B C － D －＋B －C D －＋B － C －D ) ＝P (B C － D －)＋P (B －C D －)＋P (B － C －D )＝P (B )P (C －)P (D －)＋P (B －)P (C )P (D －)＋P (B －)P (C －)P (D )＝34×⎝ ⎛⎭⎪⎫1－23×⎝ ⎛⎭⎪⎫1－23＋⎝ ⎛⎭⎪⎫1－34×23×⎝ ⎛⎭⎪⎫1－23＋⎝ ⎛⎭⎪⎫1－34×⎝ ⎛⎭⎪⎫1－23×23＝736.(2)根据题意，知X 的所有可能取值为0,1,2,3,4,5.根据事件的独立性和互斥性，得P (X ＝0)＝P (B － C － D －) ＝[1－P (B )][1－P (C )][1－P (D )] ＝⎝ ⎛⎭⎪⎫1－34×⎝ ⎛⎭⎪⎫1－23×⎝ ⎛⎭⎪⎫1－23＝136； P (X ＝1)＝P (B C － D －)＝P (B )P (C －)P (D －)＝34×⎝ ⎛⎭⎪⎫1－23×⎝ ⎛⎭⎪⎫1－23＝112；P (X ＝2)＝P (B － C D －＋B － C － D )＝P (B － C D －)＋P (B － C －D ) ＝⎝ ⎛⎭⎪⎫1－34×23×⎝ ⎛⎭⎪⎫1－23＋⎝ ⎛⎭⎪⎫1－34×⎝ ⎛⎭⎪⎫1－23×23＝19； P (X ＝3)＝P (BC D －＋B C －D )＝P (BC D －)＋P (B C －D ) ＝34×23×⎝ ⎛⎭⎪⎫1－23＋34×⎝ ⎛⎭⎪⎫1－23×23＝13；P (X ＝4)＝P (B －CD )＝⎝ ⎛⎭⎪⎫1－34×23×23＝19，P (X ＝5)＝P (BCD )＝34×23×23＝13. 故X 的分布列为所以E (X )＝0×136＋1×112＋2×19＋3×13＋4×19＋5×13＝4112.。

形的面积为2π
√C.若点N到直线BB1与直线DC的距离相等，则点N的轨迹为抛物线 √D.若D1N与AB所成的角为 π3，则点N的轨迹为双曲线
如图所示，对于A， 根据正方体的性质可知，MD⊥平面ABCD， 所以∠MND为MN与平面ABCD所成的角， 所以∠MND＝4π，所以 DN＝DM＝12DD1＝12×4＝2， 所以点N的轨迹是以D为圆心，2为半径的圆，故A正确；
思维导图
内容索引
典型例题
热点突破
PART ONE
典型例题
考点一 动点的轨迹
典例1 (1)(多选)已知正方体ABCD－A1B1C1D1 的棱长为4，M为DD1的中点，N为四边形ABCD 所在平面上一动点，则下列命题正确的是
√A.若MN与平面ABCD所成的角为 π4，则点N的
轨迹为圆
B.若MN＝4，则MN的中点P的轨迹所围成图
当 B 是 AC 的中点时，AB＝BC＝ 6，
此时△SAB为等腰三角形，△ABC为等腰直角三角形，
将△SAB，△ABC沿AB展开至同一个平面，得到如
图2所示的平面图形，
取AB的中点D，连接SC，SD，CD，
则 SD＝
22－
262＝
210，
所以 sin ∠ABS＝SSDB＝ 410， 所以 cos∠CBS＝cos(90°＋∠ABS)＝－sin∠ABS＝－ 410，
此时点B与点Q重合，点P与点O1重合，故C正确；
对于D，当点P与点B1，点Q与点A重合时，
AP＋PQ＋QB1 的值为 3AP＝3 12＋22＝3 5>2 3＋ 5，故 D 错误.
考点二 折叠、展开问题
典例2 (多选)如图，在矩形ABCD中，M为BC的中点，将△ABM沿直线 AM翻折成△AB1M，连接B1D，N为B1D的中点，则在翻折过程中，下列 说法正确的是 A.存在某个位置，使得CN⊥AB1

高考数学四点共圆问题练习专项讲解一、解答题1．已知直线:l y x m +＝交抛物线2:4C y x =于,A B 两点． （1）设直线l 与x 轴的交点为T ．若=2AT TB ，求实数m 的值；（2）若点,M N 在抛物线C 上，且关于直线l 对称，求证：,,,A B M N 四点共圆． 【答案】（1）8m ＝－；（2）证明见解析． 【分析】（1）设()()1122,,,A x y B x y ，直线方程代入抛物线方程后由判别式得m 的范围，由韦达定理得1212,y y y y +，再由向量的数乘可得122y y +＝0，结合韦达定理可得12,,y y m 值；（2）设()()3344,,,M x y N x y ，由对称性得434y y =--，4342x m x =---．再由,M N 在抛物线上，代入变形得3y 与m 的关系，然后计算MA MB ⋅，得MA MB ⊥， 同理NA NB ⊥，得证四点共圆． 【详解】解：由24y x m y x=+⎧⎨=⎩得2440y y m −+=．设()()1122,,,A x y B x y ， 则12124,4y y y y m +==． 因为直线l 与C 相交， 所以16160,m ∆−>= 得1m <．（1）由2AT TB =，得1220y y +=， 所以240y +=，解得24,y =- 从而18y =， 因为124,y y m =所以432,m =-解得8m =-．（2）设()()3344,,,M x y N x y ， 因为,M N 两点关于直线y x m =+对称，则4343223443434=144y y y y y y x x y y −−==−+−解得434y y =--．又434322y y x x m ++=+ 于是3343422y y x x m −−++=+ 解得4342x m x =---． 又点N 在抛物线上，于是233()()4442y m x --=---． 因为2334,y x =所以23341640y y m =+++，于是13231323()()()()MA M x x x x y y y y B ⋅=--+--222233121323()()(-)(-)4444y y y y y y y y =−−()()()13231323()1616y y y y y y y y −−=−−+⎡⎤⎣⎦ ()()132********()1616y y y y y y y y y y −−⎡⎤=++++⎣⎦ ()()2231333404()1616y y y y y m y −−==+++ 因此MA MB ⊥， 同理,NA NB ⊥于是点,M N 在以AB 为直径的圆上， 即,,,A B M N 四点共圆．【点睛】方法点睛：本题考查直线与抛物线相交问题，解题方法是设而不求的思想方法，如设交点坐标为()()1122,,,A x y B x y ，直线方程代入抛物线方程后应用韦达定理可得1212,y y y y +，再利用向量的线性运算求得12,y y 关系，从而可求得12,,y y m 值．2．已知椭圆22:14x C y +=上三点A 、M 、B 与原点O 构成一个平行四边形AMBO ．（1）若点B 是椭圆C 的左顶点，求点M 的坐标； （2）若A 、M 、B 、O 四点共圆，求直线AB 的斜率．【答案】（1）1,2⎛⎫−± ⎪ ⎪⎝⎭；（2）2±． 【分析】（1）由已知可得()2,0B −，由//AM BO ，且AM BO =，设()00,M x y ， ()002,A x y +代入椭圆方程解方程即可得解；（2）因为A 、M 、B 、O 四点共圆，则平行四边形AMBO 是矩形且OA OB ⊥，设直线AB 的方程为y kx m =+，与椭圆方程联立，根据韦达定理代入 12120OA OB x x y y →→⋅=+=，化简计算求解即可.【详解】解析：（1）如图所示： 因为()2,0B−，四边形AMBO 为平行四边形，所以//AM BO ，且2AM BO ==． 设点()00,M x y ，则()002,A x y +因为点M 、A 在椭圆C 上，所以()2200202014214x y x y ⎧+=⎪⎪⎨+⎪+=⎪⎩，解得001x y =−⎧⎪⎨=⎪⎩，所以1,2M ⎛−± ⎝⎭．（2）因为直线AB 的斜率存在， 所以设直线AB 的方程为y kx m =+，()11,A x y ，()22,B x y ．由2214y kx m x y =+⎧⎪⎨+=⎪⎩消去y 得()222418440k x kmx m +++−=， 则有122814km x x k −+=+，21224414m x x k−=+．因为平行四边形AMBO ， 所以()1212,OM OA OB x x y y →→→=+=++．因为122814kmx x k −+=+，所以()12122282221414km my y k x x m k m k k −+=++=⋅+=++，所以2282,1414kmm M k k −⎛⎫ ⎪++⎝⎭． 因为点M 在椭圆C 上，所以将点M 的坐标代入椭圆C 的方程化得22441m k =+．① 因为A 、M 、B 、O 四点共圆，所以平行四边形AMBO 是矩形， 且OA OB ⊥，所以12120OA OB x x y y →→⋅=+=．因为()()()2222121212122414m k y y kx m kx m k x x km x x m k-=++=+++=+， 所以22212122244401414m m k x x y y k k−−+=+=++，化得22544m k =+．② 由①②解得2114k =，23m =，此时>0∆，因此2k =±． 所以所求直线AB的斜率为2±．【点睛】本题主要考查了联立直线与椭圆的方程利用韦达定理列式表达斜率以及垂直的方法进而代入求解的问题，考查计算能力和逻辑推理能力，属于难题. 3．已知抛物线P ：22y px =（0p >）上的点3,4a ⎛⎫⎪⎝⎭到其焦点的距离为1． （Ⅰ）求p 和a 的值；（Ⅱ）求直线l ：y x m =+交抛物线P 于两点A 、B ，线段AB 的垂直平分线交抛物线P 于两点C 、D ，求证：A 、B 、C 、D 四点共圆．【答案】（Ⅰ）12p =，2a =±；（Ⅱ）证明见解析. 【分析】（Ⅰ）根据抛物线的定义可得点3,4a ⎛⎫⎪⎝⎭到其焦点的距离等于该点到准线距离，即可求出p ，从而得到抛物线方程，再计算出参数a 的值；（Ⅱ）设()11,A x y ，()22,B x y ，联立直线与抛物线方程，消元、列出韦达定理，即可求出线段AB 的中点M 的坐标，因为直线CD 为线段AB 的垂直平分线，直线CD 的方程为1y x m =−+−，设()33,C x y ，()44,D x y ，求出线段CD 的中点坐标，再利用勾股定理计算可得；【详解】解：（Ⅰ）22y px =的准线为2px =−， 因为点3,4a ⎛⎫⎪⎝⎭到其焦点的距离等于该点到准线距离， 所以3124p +=， 故12p =，即2y x =， 又3,4a ⎛⎫⎪⎝⎭在2y x =上，所以2a =±；（Ⅱ）设()11,A x y ，()22,B x y ，联立2y x x x m⎧=⎨=+⎩，得20y y m −+=，则121y y +=，12y y m ⋅=， 且140m −>，即14m <，则12A y B =−=且线段AB 中点的纵坐标为12122y y +=，则12x m =−，所以线段AB 中点为11,22M m ⎛⎫−⎪⎝⎭，因为直线CD 为线段AB 的垂直平分线，直线CD 的方程为1y x m =−+−，联立21y xy x m⎧=⎨=−+−⎩，得210y y m ++−=，设()33,C x y ，()44,D x y ， 则341y y +=−，341y y m ⋅=−故34D y C =−= 线段CD 中点为31,22N m ⎛⎫−−⎪⎝⎭，因为()21154108242m CD m −⎛⎫=−= ⎪⎝⎭，22225422AN AM m MN −==+=+， 所以12AN CD =， 所以点A 在以CD 为直径的圆上， 同理点B 在以CD 为直径的圆上， 所以A 、B 、C 、D 四点共圆． 【点睛】(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系； (2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式．4．已知直线1:360l x y −−=与x 轴，y 轴分别交于A ，B ，线段AB 的中垂线2l 与抛物线()2:20E y px p =>有两个不同的交点C 、D ．（1）求p 的取值范围；（2）是否存在p ，使得A ，B ，C ，D 四点共圆，若存在，请求出p 的值，若不存在，请说明理由． 【答案】（1）16,9⎛⎫+∞ ⎪⎝⎭（2）存在，5p = 【分析】（1）求出,A B 两点坐标，得出其中垂线方程为380x y ++=，与抛物线方程联立根据0∆>即可得结果； （2）设()11,C x y ，()22,D x y ，线段CD 的中点为()00,M x y ，将（1）和韦达定理可得()98,3M p p −−，CD =2214MA CD =，代入两点间距离公式可解得p 的值. 【详解】（1）因为直线1:360l x y −−=与x 轴，y 轴分别交于A ，B . 所以()2,0A ，()0,6B −，所以线段AB 的中点为()1,3−，3AB k =， 所以线段AB 的中垂线2l 的方程为()1313y x +=−−，即380x y ++=. 将38x y =−−代入()2:20E y px p =>，得26160y py p ++=，因为2l 与E 有两个不同的交点C ，D . 所以2364160p p ∆=−⨯>， 又0p >，所以169p >，即p 的取值范围为16,9⎛⎫+∞ ⎪⎝⎭. （2）若A ，B ，C ，D 四点共圆，由对称性可知，圆心应为线段CD 的中点，设()11,C x y ，()22,D x y ，线段CD 的中点为()00,M x y ，则1212616y y py y p+=−⎧⎨=⎩，所以12032y y y p +==−，003898x y p =−−=−，CD ====若A ，B ，C ，D 四点共圆，则12MA CD =，即2214MA CD =， 所以()()2220012409164x y p p −+=⨯−. 所以()222910990160p p p p −+=−，解得5p =， 又5p =满足169p >，所以存在5p =，使得A ，B ，C ，D 四点共圆. 【点睛】本题主要考查了直线与抛物线的位置关系，圆内接四边形的特征，考查了学生的计算能力，属于中档题. 5．已知斜率为k 的直线交椭圆()2230x y λλ+=>于A ，B 两点，AB 的垂直平分线与椭圆交于C ，D 两点，点()01,N y 是线段AB 的中点.（1）若03y =，求直线AB 的方程以及λ的取值范围；（2）不管λ怎么变化，都有A ，B ，C ，D 四点共圆，求0y 的取值范围. 【答案】（1）40x y +−=，12λ>；（2）{}3,3−. 【分析】（1）将直线AB 的方程()13y k x =−+代入椭圆方程223x y λ+=，再利用根与系数的关系可得()1223123k k x x k −+==+，从而可求出k 的值，进而可得到直线AB 的方程，由判别式大于零可求出λ的取值范围；（2）设直线AB 的方程为()01y k x y =−+，代入椭圆方程中，利用根与系数的关系，再利用弦长公式表示出AB ,由于DC 是AB 的垂直平分线，所以同理可表示DC 的长，求出CD 中点P 的横坐标，则可求出点P 到AB 的距离d ，由A ，B ，C ，D 四点共圆22222CD AB d ⎛⎫⎛⎫⇔=+ ⎪ ⎪⎝⎭⎝⎭，将AB ，DC ，d 代入化简可得222211313k k k k++=++，从而可求出k 的值，进而可求得0y 【详解】设()11,A x y ，()22,B x y .（1）当03y =时，直线AB 的方程为()13y k x =−+， 将AB 方程代入223x y λ+=得：()()()22232330kx k k x k λ++−+−−=.①由()1223123k k x x k −+==+，解得1k =−，此时AB 的方程为40x y +−=. 将1k =−代入①，得248160x x λ−+−=. 由()6416160λ∆=−−>，解得12λ>. （2）设直线AB 的方程为()01y k x y =−+， 将方程代入223x y λ+=得：()()()22200320kxk y k x y k λ++−+−−=.②由题意()0122123k k y x x k−+==+，即03ky −=.12AB x =−===同理得CD ==，所以CD 中点P 的横坐标0032221112131313y ky k k x k k k⎛⎫−−− ⎪+−⎝⎭===+++，点P 到AB 的距离d1−=，由A ，B ，C ，D 四点共圆22222CD AB d ⎛⎫⎛⎫⇔=+ ⎪ ⎪⎝⎭⎝⎭，即()()2222222211912133313kk k k k k λλ⎛⎫++⎛⎫⎡⎤−++=−−+ ⎪ ⎪⎣⎦+⎝⎭⎝⎭+，③ 不管λ怎么变化，都有A ，B ，C ，D 四点共圆，即上式恒成立，所以222211313k k k k++=++，解得21k =， 此时③式成立.代入②，由0∆>得12λ>. 所以0y 的取值范围为{}3,3−. 【点睛】关键点点睛：此题考查直线与椭圆的位置关系，考查计算求解能力，解题的关键是由A ，B ，C ，D 四点共圆22222CD AB d ⎛⎫⎛⎫⇔=+ ⎪ ⎪⎝⎭⎝⎭，将AB ，DC ，d 代入化简可得222211313k k k k ++=++，从而可求出k 的值，进而可求得0y ，考查数学转化思想，属于较难题6．已知椭圆22221x y a b+=(0)a b >>的左，右焦点分别为1F ，2F ，且126F F ||=，直线y kx =与椭圆交于A ，B 两点．（Ⅰ）若△12AF F 的周长为16，求椭圆的标准方程；，且A ，B ， 1F ，2F 四点共圆，求椭圆离心率e 的值；（Ⅲ）在（Ⅱ）的条件下，设00(,)P x y 为椭圆上一点，且直线PA 的斜率1(2,1)k ∈−−，试求直线PB 的斜率2k 的取值范围．【答案】（Ⅱ）23=e ．【解析】试题解析：（Ⅰ）由题意得3c =， 根据2216a c +=，得5a =．结合222a b c =+，解得2225,16a b ==（Ⅱ）设1122(,),(,)A x y B x y由AB 、EF 互相平分且共圆，易知，22AF BF ⊥，因为211(3,)F A x y =−，222(3,)F B x y =−， 所以221(F A F B x ⋅=− 即 128x x =−，所以有结合229b a +=．解得212a =，所以离心率 （若设1111(,),(,)A x y B x y −−相应给分）（解法二）设）（11,y x A ，又AB 、EF 互相平分且共圆，所以AB 、EF 是圆的直径， 所以92121=+y x ，又由椭圆及直线方程综合可得：⎪⎪⎪⎩⎪⎪⎪⎨⎧=+==+1429221221112121b y a x x y y x 前两个方程解出1,82121==y x ，将其带入第三个方程并结合92222−=−=a c a b ，解得：122=a ，23=e ．…8分由题可设1111(,),(,)A x y B x y −−，又22012201222201013(1)3(1)112124x x y y x x x x −−−−==−−− ，由121k −<<−考点：1．椭圆的标准方程及其几何性质；2．直线与椭圆的位置关系．7．如图，在平面直角坐标系xOy 中，已知椭圆22221(0)x y a b a b+=>>的右焦点为F ，P 为右准线上一点．点Q 在椭圆上，且FQ FP ⊥．（1）若椭圆的离心率为12，短轴长为 （2）若在x 轴上方存在,P Q 两点，使,,,O F P Q 四点共圆，求椭圆离心率的取值范围．【答案】（1）22143x y +=； （21e <<. 【分析】（1）设椭圆的焦距为2c，由题意，可得222122c a b a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩，即可求得椭圆C 的标准方程；（2）设2(a P c，)t ，0(Q x ，0)y ，可得FPQ ∆的外接圆即为以PQ为直径的圆200()()()()0a x x x y t y y c−−+−−=，可得20a x c c =−，根据点P ，Q 均在x 轴上方，可得 210e e +−>，解得即可；【详解】解：（1）设椭圆的焦距为2c，由题意，可得222122c a b a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩，解得2a =，b =∴椭圆的方程为22143x y +=， （2）设2(a P c，)t ，0(Q x ，0)y ， FP FQ ⊥，则FPQ ∆的外接圆即为以PQ 为直径的圆200()()()()0a x x x y t y y c−−+−−=， 由题意，焦点F ，原点O 均在该圆上， ∴200200()()00a c c x ty c a x ty c⎧−−+=⎪⎪⎨⎪+=⎪⎩， 消去0ty 可得2200()()0a a c c x x c c −−−=， 20a x c c∴=−， 点P ，Q 均在x 轴上方，2a a c c c∴−<−<， 即220c ac a +−>，210e e ∴+−>，01e <<Q ，∴1e <<， 故e的范围为1,12⎛⎫⎪ ⎪⎝⎭．【点睛】本题考查椭圆的标准方程及简单几何性质，直线的圆锥曲线的位置关系，考查圆的方程及点到直线的距离公式，直线的斜率公式，考查计算能力，解题时要认真审题，属于中档题．8．已知抛物线2:4E y x =的焦点为F ，准线为l O ，为坐标原点，过F 的直线m 与抛物线E 交于A B 、两点，过F 且与直线m 垂直的直线n 与准线l 交于点M ．（1）若直线m ||||AF BF 的值； （2）设AB 的中点为N ，若O M N F 、、、四点共圆，求直线m 的方程．【答案】（1）||3||AF BF =或||1||3AF BF =；（2）1)y x =−． 【分析】（1）由抛物线的定义建立方程即可.（2）设直线m 的方程为1x ty =+，用t 表示,M N 坐标，再结合条件得到0OM ON ⋅=，建立关于t 的方程即可获解.【详解】（1）设||||AF BF λ=，当1λ>时，设||0BF k =>，则||AF k λ=，直线m ∴直线m 的倾斜角为60︒， 由抛物线的定义，有()()1cos60cos602AB AF BF k k k k λλ⋅︒=+⋅︒=+⨯=−， 112λλ+∴=−，解得：3λ=， 若01λ<<时，同理可得：13λ=， ||3||AF BF ∴=或||1||3AF BF =． （2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty −−=．设()()1122,,,A x y B x y ，则12124,4y y t y y +==−．由2211224,4y x y x ==， 得()22221212212122(4)2(4)424444y y y y y y t x x t +−−⨯−+=+===+， 所以()221,2N t t +．因为直线m 的斜率为1t，所以直线n 的斜率为t −，则直线n 的方程为(1)t y x −−=． 由1(1)x y t x =−⎧⎨=−−⎩，，解得(1,2)M t −． 若O M N F 、、、四点共圆，再结合FN FM ⊥，得OM ON ⊥，则()2212122210OM ON t t t t ⋅=−⨯++⋅=−=，解得t = 所以直线m的方程为1)y x =−．【点睛】（1）有些题目可以利用抛物线的定义结合几何关系建立方程获解；（2）直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系. 9．如图，已知椭圆C 的方程为22221(0)x y a b a b+=>>，c 为半焦距，椭圆C 的左、右焦点分别为12,F F ，椭圆C 的离心率为e ．（1）若椭圆过点(e ，两条准线之间的距离为4b ，求椭圆C 的标准方程； （2）设直线y kx =与椭圆C 相交于A ，B 两点，且12,,,A F B F 四点共圆，c ≤，试求2k 的最大值．【答案】（1）22142x y +=（2）13 【分析】(1)利用准线,以及222a b c =+求出离心率,又因为椭圆过点e ⎛ ⎝⎭,确定方程. (2)将直线方程代入椭圆方程, 根据中心对称性和12,,,F B F 四点共圆，所以22AF BF ⊥. 所以三角形2ABF 是直角三角形,()()22221 211e k e −=−+,根据2213e ≤<得出2k 取得最大值.【详解】 （1）因为两条准线之间的距离为4b ，所以224a b c=，又222a b c =+，故22b c =， 因为222b a c =−，所以222a c c −=，解得e =， 因为椭圆C过点e ⎛ ⎝⎭，所以222212b b⎝⎭⎝⎭+=， 故222b c ==，24a =，所以椭圆C 的标准方程为22142x y +=. （2）设()()1122,,,A x y B x y ， 由22221,,x y a b y kx ⎧+=⎪⎨⎪=⎩得()2222220b a k x a b +−=，解得12x x ==.由椭圆的中心对称性得，12AF B AF B ∠=∠，因为12,,,A F B F 四点共圆，所以12AF B AF B π∠+∠=， 所以22AF B π∠=，即22AF BF ⊥，所以三角形2ABF 是直角三角形，且22OF AB =，所以122|c x x =−，即22c =，故()()22222221c b a k k a b +=+，所以()()()2222222221c a c a k k a a c −+=+−，即()()()22222111e e k k e −+=+−， 分离k ，e 得，()()22221211e k e −=−+，c ≤，所以()22222222213b c a c c e ≤⇔−≤⇔≤<， 令21,t e =−则1,03t ⎡⎫∈−⎪⎢⎣⎭，所以2221t k t =+， 令()21(0)213t k t t t =−≤<+， 则()2211(0)21213t k t t t t t==−≤<++，易得当103t −≤<，()k t 单调递减， 所以13t =−时，()k t 取最大值，即2k 取得最大值为13． 【点睛】本题考查椭圆方程,直线与椭圆的位置关系,含参分式的最值,属于难题. 10．如图,在平面直角坐标系xOy 中,椭圆C ：22221x y a b +=(a ＞b ＞0)经过点(﹣2,0)和⎛ ⎝⎭,椭圆C 上三点A ,M ,B 与原点O 构成一个平行四边形AMBO .（1）求椭圆C 的方程；（2）若点B 是椭圆C 左顶点,求点M 的坐标；（3）若A ,M ,B ,O 四点共圆,求直线AB 的斜率.【答案】（1）24x ＋y 2＝1；（2）M (－；（3）±2【分析】(1)将点()2,0−和⎛ ⎝⎭代入椭圆22x a ＋22y b ＝1求解即可. (2)根据平行四边形AMBO 可知AM ∥BO ,且AM ＝BO ＝2.再设点M (x 0,y 0),则A (x 0＋2,y 0),代入椭圆C 求解即可.(3) 因为A ,M ,B ,O 四点共圆,所以平行四边形AMBO 是矩形,且OA ⊥OB ,再联立直线与椭圆的方程,结合韦达定理代入OA ·OB ＝x 1x 2＋y 1y 2＝0求解即可.【详解】（1）因为椭圆22x a ＋22y b ＝1(a ＞b ＞0)过点()2,0−和⎛ ⎝⎭, 所以a ＝2,21a ＋234b ＝1,解得b 2＝1,所以椭圆C 的方程为24x ＋y 2＝1. （2）因为B 为左顶点,所以B (－2,0).因为四边形AMBO 为平行四边形,所以AM ∥BO ,且AM ＝BO ＝2.设点M (x 0,y 0),则A (x 0＋2,y 0).因为点M ,A 在椭圆C 上,所以()2200202014214x y x y ⎧+=⎪⎪⎨+⎪+=⎪⎩解得001x y =−⎧⎪⎨=⎪⎩所以M (－). （3）因为直线AB 的斜率存在,所以设直线AB 的方程为y ＝kx ＋m ,A (x 1,y 1),B (x 2,y 2). 由2214y kx m x y =+⎧⎪⎨+=⎪⎩消去y ,得(4k 2＋1)x 2＋8kmx ＋4m 2－4＝0, 则有x 1＋x 2＝2814km k −+,x 1x 2＝224414m k−+. 因为平行四边形AMBO ,所以OM ＝OA ＋OB ＝(x 1＋x 2,y 1＋y 2).因为x 1＋x 2＝2814km k −+,所以y 1＋y 2＝k (x 1＋x 2)＋2m ＝k ·2814km k −+＋2m ＝2214m k +,所以M (2814km k −+,2214m k +). 因为点M 在椭圆C 上,所以将点M 的坐标代入椭圆C 的方程,化得4m 2＝4k 2＋1.①因为A ,M ,B ,O 四点共圆,所以平行四边形AMBO 是矩形,且OA ⊥OB ,所以OA ·OB ＝x 1x 2＋y 1y 2＝0.因为y 1y 2＝(kx 1＋m )(kx 1＋m )＝k 2x 1x 2＋km (x 1＋x 2)＋m 2＝222414m k k −+, 所以x 1x 2＋y 1y 2＝224414m k−+＋222414m k k −+＝0,化得5m 2＝4k 2＋4.②由①②解得k 2＝114,m 2＝3,此时△＞0,因此k ＝±2所以所求直线AB 的斜率为 【点睛】 本题主要考查了椭圆方程的基本求法,同时也考查了联立直线与椭圆的方程,利用韦达定理列式表达斜率以及垂直的方法,进而代入求解的问题.属于难题.11．如图，在平面直角坐标系xOy 中，已知P 为椭圆2222:1(0)x y C a b a b+=>>上异于长轴端点的一点，过P 与x 轴平行的直线交椭圆C 的两条准线于点1T ，2T ，直线11T F ，22T F 交于点Q .（1）若12PF F ∆与12QF F ∆的面积相等，求椭圆C 的离心率；（2）若126F F =，12503TT =. ①求椭圆C 的标准方程；②试判断点P ，1F ，Q ，2F 是否四点共圆，并说明理由.【答案】（1）2；（2）①2212516x y +=； ②P ，1F ，Q ，2F 四点共圆，理由见解析. 【分析】（1）设()()000,0P x y y ≠，210,a T y c ⎛⎫− ⎪⎝⎭，可表示出直线11T F 的方程，从而求得Q 点坐标；根据三角形面积相等可构造关于,a c 的齐次方程，进而求得离心率；（2）①根据126F F =，12503TT =和椭圆,,a b c 的关系，可求得,,a b c 的值，进而得到椭圆方程； ②设过点Q ，1F ，2F 三点的圆的方程为()2229x y s s +−=+，代入Q 点坐标可求得方程为2200982932y x y y y ⎛⎫+−−= ⎪⎝⎭；验证可知P 点坐标满足方程，由此得到四点共圆. 【详解】设()()000,0P x y y ≠，()1,0F c −，()2,0F c ，（1）由题意得：210,a T y c ⎛⎫− ⎪⎝⎭，220,a T y c ⎛⎫ ⎪⎝⎭. 直线11T F 的方程为：()02y y x c a c c=+−+，直线22T F 的方程为：()02y y x c a c c =−−， 将直线11T F 与22T F 联立可得：2020x c y y b =⎧⎪⎨=−⎪⎩，即点2020,c y Q b ⎛⎫− ⎪⎝⎭.12PF F ∆与12QF F ∆的面积相等， ()2000220c y y y c a ∴=−≠−， 2221c c a ∴=−−，2c e a ∴==，即椭圆C的离心率为2. （2）①126F F =，12503TT =，26c ∴=，25023a c ⋅=， 解得：3c =，225a =，22216b ac ∴=−=，∴以椭圆C 的标准方程为2212516x y +=. ②由①知：()13,0F −，()23,0F ，090,16y Q ⎛⎫− ⎪⎝⎭. 设过点Q ，1F ，2F 三点的圆的方程为()2229x y s s +−=+，即2229x y sy +−=. 将090,16y Q ⎛⎫− ⎪⎝⎭代入该方程得：009832y s y =−，∴过Q ，1F ，2F 三点的圆的方程为：2200982932y x y y y ⎛⎫+−−= ⎪⎝⎭，将()00,P x y 代入该方程左边，则220000098232y x y y y ⎛⎫+−− ⎪⎝⎭22000009825121632y y y y y ⎛⎫⎛⎫=−+−− ⎪ ⎪⎝⎭⎝⎭9=， ∴点P 也在过点Q ，1F ，2F 三点的圆上，从而点P ，1F ，Q ，2F 四点共圆.【点睛】本题考查直线与椭圆的综合应用问题，涉及到椭圆离心率和标准方程的求解、四点共圆问题的证明；证明四点共圆问题的关键是能够通过三点坐标确定三点所在圆的方程，进而代入第四个点的坐标，验证其满足方程即可.12．（题文）（题文）已知点F (p2,0)，直线l: x =−p2，点Μ是l 上的动点，过点Μ垂直于y 轴的直线与线段ΜF 的垂直平分线相交于点Ν． （1）求点Ν的轨迹方程；（2）若p =2，直线y =x 与点Ν的轨迹交于A 、B 两点，试问Ν的轨迹上是否存在两点C 、D ，使得A 、B 、C 、D 四点共圆？若存在，求出圆的方程；若不存在，请说明理由．【答案】（1）y 2=2px ；（2）存在a >72且a ≠4，a ≠8的无数个圆(x −a)2+(y +a −4)2=a 2+(−a +4)2满足条件. 【解析】试题分析：（1）借助点在线段ΜF 的中垂线上建立等式并化简即可；（2）依据题设条件建立方程,通过方程有无解的分析析作出推理和判断即可.试题解析：解: （1）设Ν(x,y)，依题意，|ΝF |=|ΝΜ|，即√(x −p2)2+y 2=|x +p2|． 化简整理得y 2=2px ．（2）把y =x 与y 2=4x 联立，解得Α(0,0)，Β(4,4)，则线段ΑΒ的垂直平分线方程y =−x +4 若存在C 、D 两点，使得Α、Β、C 、D 四点共圆，则圆心必在直线y =−x +4上， 设圆心坐标(a,−a +4)，则半径r =√a 2+(−a +4)2， ∴圆的方程为(x −a)2+(y +a −4)2=a 2+(−a +4)2， 将x =y 24代入并整理得y 4+(16−8a)y 2+32(a −4)y =0，则y(y −4)(y 2+4y +32−8a)=0，∴ y 1=0或y 2=4或y 2+4y +32−8a =0， ∴ y 2+4y +32−8a =0应有除y 1=0、y 2=4之外的两个根，∴ Δ>0，且32−8a ≠0，42+4×4+32−8a ≠0，解得a >72且a ≠4，a ≠8． ∴存在a >72且a ≠4，a ≠8的无数个圆(x −a)2+(y +a −4)2=a 2+(−a +4)2满足条件．考点：(1)轨迹方程与探求方法；(2)圆的方程及简单高次方程的求解等有关知识的运用. 13．从抛物线24y x =上各点向x 轴作垂线段，记垂线段中点的轨迹为曲线P ． （1）求曲线P 的方程，并说明曲线P 是什么曲线；（2）过点()2,0M 的直线l 交曲线P 于两点A 、B ，线段AB 的垂直平分线交曲线P 于两点C 、D ，探究是否存在直线l 使A 、B 、C 、D 四点共圆？若能，请求出圆的方程；若不能，请说明理由． 【答案】（1）曲线P 的方程为2y x =，曲线P 是焦点为1,04⎛⎫⎪⎝⎭的抛物线；（2）存在；圆N 的方程为227113222x y ⎛⎫⎛⎫−++= ⎪ ⎪⎝⎭⎝⎭或227113222x y ⎛⎫⎛⎫−+−= ⎪ ⎪⎝⎭⎝⎭．【分析】（1）设抛物线2y x =上的任意点为()00,S x y ，垂线段的中点为(),x y ，根据中点坐标公式得出002x x y y =⎧⎪⎨=⎪⎩，代入等式2004y x =化简可得出曲线P 的方程，进而可得出曲线P 的形状；（2）设直线l 的方程为2x ty =+，将直线l 的方程与曲线P 的方程联立，列出韦达定理，求出AB ，求出线段AB 的中点的坐标，进一步求出线段AB 的中垂线CD 的方程，求出CD ，根据四点共圆结合垂径定理可得出关于t 的等式，求出t 的值，进一步可求得圆的方程，由此可得出结论. 【详解】（1）设抛物线2y x =上的任意点为()00,S x y ，垂线段的中点为(),x y ，故002x x y y =⎧⎪⎨=⎪⎩，则002x x y y =⎧⎨=⎩，代入2004y x =得()224y x =，得曲线P 的方程为2y x =，所以曲线P 是焦点为1,04⎛⎫⎪⎝⎭的抛物线； （2）若直线l 与x 轴重合，则直线l 与曲线P 只有一个交点，不合乎题意. 设直线l 的方程为2x ty =+，根据题意知0t ≠，设()11,A x y 、()22,B x y ，联立22y x x ty ⎧=⎨=+⎩，得220y ty −−=，280t ∆=+>，则12y y t +=，122y y ⋅=−，则12A y y B =−==，且线段AB 中点的纵坐标为1222y y t +=，即2121222222x x y y t t ++=⋅+=+， 所以线段AB 中点为22,22t t M ⎛⎫+ ⎪⎝⎭，因为直线CD 为线段AB 的垂直平分线，可设直线CD 的方程为1x y m t=−+，则21222t t m t ⎛⎫+=−⨯+ ⎪⎝⎭，故252t m +=， 联立22152y x t x y t ⎧=⎪⎨+=−+⎪⎩，得()222250ty y t t +−+=， 设()33,C x y 、()44,D x y ，则341y y t +=−，()234152y y t ⋅=−+，故34y CD =−=，线段CD 中点为22151,222t N tt ⎛⎫++− ⎪⎝⎭， 假设A 、B 、C 、D 四点共圆，则弦AB 的中垂线与弦CD 中垂线的交点必为圆心， 因为CD 为线段AB 的中垂线，则可知弦CD 的中点N 必为圆心，则12AN CD =， 在Rt AMN △中，222AN AM MN =+，所以22212CD AM MN ⎛⎫=+ ⎪⎝⎭，则()()222222221111111121018442222t t t t t t tt ⎛⎫⎛⎫⎛⎫⎛⎫+++=++++++ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，故4228810t t t +−−=，即()()24264222198880t t t t t t t t −+++−−==， 解得21t =，即1t =±，所以存在直线l ，使A 、B 、C 、D 四点共圆，且圆心为弦CD 的中点N ，圆N 的方程为227113222x y ⎛⎫⎛⎫−++= ⎪ ⎪⎝⎭⎝⎭或227113222x y ⎛⎫⎛⎫−+−= ⎪ ⎪⎝⎭⎝⎭．【点睛】方法点睛：求动点的轨迹方程有如下几种方法：（1）直译法：直接将条件翻译成等式，整理化简后即得动点的轨迹方程；（2）定义法：如果能确定动点的轨迹满足某种已知曲线的定义，则可利用曲线的定义写出方程； （3）相关点法：用动点Q 的坐标x 、y 表示相关点P 的坐标0x 、0y ，然后代入点P 的坐标()00,x y 所满足的曲线方程，整理化简可得出动点Q 的轨迹方程；（4）参数法：当动点坐标x 、y 之间的直接关系难以找到时，往往先寻找x 、y 与某一参数t 得到方程，即为动点的轨迹方程；（5）交轨法：将两动曲线方程中的参数消去，得到不含参数的方程，即为两动曲线交点的轨迹方程. 14．在平面直角坐标系xOy 中，已知抛物线()2:20E y px p =>的焦点为F ，准线为l ，P 是抛物线上E上一点，且点P 的横坐标为2，3PF =.（1）求抛物线E 的方程；（2）过点F 的直线m 与抛物线E 交于A 、B 两点，过点F 且与直线m 垂直的直线n 与准线l 交于点M ，设AB 的中点为N ，若O 、M N 、F 四点共圆，求直线m 的方程.【答案】（1）24y x =（2）)1y x =− 【分析】（1）由抛物线的定义可得22pPF =+，即可求出p ，从而得到抛物线方程； （2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty −−=.设()11,A x y ，()22,B x y ，列出韦达定理，表示出中点N 的坐标，若O 、M 、N 、F 四点共圆，再结合FN FM ⊥，得OM ON ⊥，则0OM ON ⋅=即可求出参数t ，从而得解；【详解】解：（1）由抛物线定义，得232pPF =+=，解得2p =， 所以抛物线E 的方程为24y x =.（2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty −−=. 设()11,A x y ，()22,B x y ，则124y y t +=，124y y =−. 由2114y x =，2224y x =，得()()()22222121212122424424444y y y y t y y x x t +−−⨯−+=+===+， 所以()221,2N t t +.因为直线m 的斜率为1t，所以直线n 的斜率为t −，则直线n 的方程为()1y t x =−−.由()1,1,x y t x =−⎧⎨=−−⎩解得()1,2M t −.若O 、M 、N 、F 四点共圆，再结合FN FM ⊥，得OM ON ⊥，则()2212122210OM ON t t t t ⋅=−⨯++⋅=−=，解得t =所以直线m 的方程为)1y x =−. 【点睛】本题考查抛物线的定义及性质的应用，直线与抛物线综合问题，属于中档题.15．已知椭圆C ：22221(0)x y a b a b +=>>的左､右顶点分别为A ，B ，P 是C 上异于A ，B的动点.（1）证明：直线AP ，BP 的斜率之积为定值，并求出该定值.（2）设||AB =，直线AP ，BP 分别交直线l ：x =3于M ，N 两点，O 为坐标原点，试问：在x 轴上是否存在定点T ，使得O ，M ，N ，T 四点共圆？若存在，求出点T 的坐标；若不存在，请说明理由. 【答案】（1）证明见解析，定值13−；（2）存在，定点11,03T ⎛⎫⎪⎝⎭.【分析】（1）由题意知(,0),(,0)A a B a −，设P (x 0，y 0)，y 0≠0，则2200221x y a b+=，然后利用斜率公式求200022000y y y x a x a x a ⋅=+−−化简可得结果； （2）由题意先求出椭圆C 的方程为2213x y +=，设直线AP的方程为(y k x =+，则直线BP 的方程为1(3y x k =−，直线方程与椭圆方程联立可求出(3,3)M k，1N k ⎛⎫− ⎪⎝⎭，假设△MNO 的外接圆恒过定点T (t ，0)，t ≠0，然后求出线段MN 的垂直平分线所在直线的方程和线段OT 的垂直平分线所在直线的方程，从而可求出圆心2t E ⎛⎪⎪⎝⎭，再由|OE |=|ME |，可求出t 的值，进而得O ，M ，N ，T 四点共圆 【详解】（1）由题意知(,0),(,0)A a B a −，设P (x 0，y 0)，y 0≠0，则2200221x y a b+=，所以直线AP 与BP的斜率之积22022222200022222200001131x b a y y y b a c x a x a x a x a a a ⎛⎫− ⎪−⎝⎭⋅===−=−=−+−−⎭=−−⎝， 即直线AP ，BP 的斜率之积为定值13−. （2）存在.理由如下：由题意知2a =a =因为c a =，所以c =所以b 2=1，所以椭圆C 的方程为2213x y +=.设直线AP的方程为(y k x =，则直线BP的方程为1(3y x k=−.联立(3,y k x x ⎧=⎪⎨=⎪⎩可得(3,3)M k，同理可得1N k ⎛⎫− ⎪⎝⎭. 假设△MNO 的外接圆恒过定点T (t ，0)，t ≠0， 因为线段MN的垂直平分线所在直线的方程为y =，线段OT 的垂直平分线所在直线的方程为2t x =，所以圆心2t E ⎛⎪ ⎪⎝⎭. 又|OE |=|ME |解得t =113.所以存在定点11,03T ⎛⎫⎪⎝⎭，使得O ，M ，N ，T 四点共圆. 【点睛】此题考查直线与椭圆的位置关系，考查椭圆中的定点问题，考查计算能力，属于中档题16．在平面直角坐标系xOy 中，已知抛物线()2:20E y px p =>的焦点为F ，准线为l ，P 是抛物线E 上一点，且点P 的横坐标为2，3PF =. （1）求抛物线E 的方程；（2）过点F 的直线m 与抛物线E 交于A 、B 两点，过点F 且与直线m 垂直的直线n 与准线l 交于点M ，设AB 的中点为N ，若O 、M 、N 、F 四点共圆，求直线m 的方程. 【答案】（1）24y x =（2）)1y x =− 【分析】（1）首先根据抛物线的定义和题中条件求出抛物线的焦准距，即可得到抛物线的方程；（2）首先设直线m 的方程，然后与抛物线联立，利用韦达定理求出点N 坐标，然后设直线n 的方程求出点M 的坐标，最后利用O 、M 、N 、F 四点共圆即可求出直线m 的方程. 【详解】（1）由抛物线定义，得232pPF =+=，解得2p =， 所以抛物线F 的方程为24y x =；（2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty −−=， 设()11,A x y ，()22,B x y ，则124y y t +=，124y y =−， 由2114y x =，2224y x =，得()()()22222121212122424424444y y y y t y y x x t +−−⨯−+=+===+，所以()221,2N t t +，因为直线m 的斜率为1t，所以直线n 的斜率为t −， 则直线n 的方程为()1y t x =−−，由()11x y t x =−⎧⎨=−−⎩解得()1,2M t −，若O 、M 、N 、F 四点共圆，再结合FN FM ⊥，得OM ON ⊥， 则()2212122210OM ON t t t t ⋅=−⨯++⋅=−=，解得2t =±，所以直线m 的方程为)1y x =−. 【点睛】本题主要考查了抛物线的定理，直线与抛物线的交点问题，属于一般题.。

2023年高考-数学（理科）考试备考题库附带答案第1卷一.全考点押密题库(共50题)1.(单项选择题)(每题 5.00 分) 已知A，B 是球 O 的球面上两点，∠AOB = 90° ，C为该球面上的动点。

若三棱锥 O - ABC 体积的最大值为36，则球 O 的表面积为A. 36πB. 64πC. 144πD. 256π正确答案：C,2.(填空题)(每题 5.00 分) 已知圆锥的顶点为S，母线SA，SB所成角的余弦值为7/8,SA与圆锥底面所成角为45°.若△SAB的面积为5√15，则该圆锥的侧面积为.正确答案：40√2π，3.(单项选择题)(每题 5.00 分) 记SN.为等差数列αN}的前n项和.若3S3=S2+S4，α=2,则α5= {A. -12B. -10C. 10D. 12正确答案：B,4.(填空题)(每题5.00 分) 已知函数f(x)=2sinx+sin2x，则f(x)的最小值是_______?正确答案：-3√3/2，5.(单项选择题)(每题 5.00 分) 双曲线x2/α2-y2/b2=1(α>0,b>0)的离心率为√3，则其渐近线方程为A. y=±√2xB. y=±√3xC. y=±√2/2xD. y=±√3/2x正确答案：A,6.(单项选择题)(每题 5.00 分) 已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为A. 3√3/4B. 2√3/3C. 3√2/4D. √3/2正确答案：A,7.(单项选择题)(每题 5.00 分) 已知集合A=x∣x2-x-2>0}，则CRA={A. x∣-12}{D. {x∣x≦-1}∪{x∣x≧2}正确答案：B,8.(单项选择题)(每题 5.00 分) 在△ABC中，cos C/2=√5/5,BC=1,AC=5,则AB=A. 4√2B. √30C. √29D. 2√5正确答案：A,9.(填空题)(每题 5.00 分) 某髙科技企业生产产品 A 和产品 B 需要甲、乙两种新型材料。

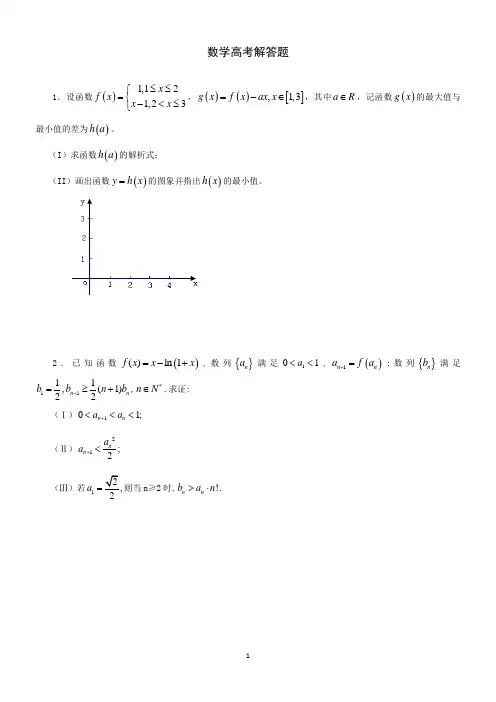
数学高考解答题1．设函数()1,121,23x f x x x ≤≤⎧=⎨-<≤⎩，()()[],1,3g x f x ax x =-∈，其中a R ∈，记函数()g x 的最大值与最小值的差为()h a 。

（I ）求函数()h a 的解析式；（II ）画出函数()y h x =的图象并指出()h x 的最小值。

2．已知函数()()ln 1f x x x =-+,数列{}n a 满足101a <<,()1n n a f a +=;数列{}n b 满足1111,(1)22n n b b n b +=≥+,*n N ∈.求证: （Ⅰ）101;n n a a +<<< （Ⅱ）21;2n n a a +<（Ⅲ）若12a =则当n ≥2时,!n n b a n >⋅.3．已知定义在R 上的函数f (x )同时满足：（1）21212122()()2()cos24sin f x x f x x f x x a x ++-=+（12,x x ∈R ，a 为常数）；（2）(0)()14f f π==； （3）当0,4x π∈［］时，()f x ≤2 求：（Ⅰ）函数()f x 的解析式；（Ⅱ）常数a 的取值范围．4．设)0(1),(),,(22222211>>=+b a bx x y y x B y x A 是椭圆上的两点，满足0),(),(2211=⋅a y b x a y b x ，椭圆的离心率,23=e 短轴长为2，0为坐标原点. （1）求椭圆的方程；（2）若直线AB 过椭圆的焦点F （0，c ），（c 为半焦距），求直线AB 的斜率k 的值；（3）试问：△AOB 的面积是否为定值？如果是，请给予证明；如果不是，请说明理由.个 个 5．已知数列{}n a 中各项为：12、1122、111222、……、111n ⋅⋅⋅⋅⋅⋅ 222n⋅⋅⋅⋅⋅⋅ …… （1）证明这个数列中的每一项都是两个相邻整数的积.（2）求这个数列前n 项之和S n .6．设1F 、2F 分别是椭圆22154x y +=的左、右焦点. （Ⅰ）若P 是该椭圆上的一个动点，求21PF PF ⋅的最大值和最小值；（Ⅱ）是否存在过点A （5，0）的直线l 与椭圆交于不同的两点C 、D ，使得|F 2C|=|F 2D|？若存在，求直线l 的方程；若不存在，请说明理由.7．已知动圆过定点P（1，0），且与定直线L:x=-1相切，点C在l上。

高考数学（理）真题专题汇编：集合与逻辑一、选择题1.【来源】2019年高考真题——数学（浙江卷） 若0,0ab >>，则“4a b +≤”是 “4ab ≤”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件2.【来源】2019年高考真题——数学（浙江卷）已知全集U={－1,0,1,2,3}，集合A={0,1,2}，B={－1,0,1}，则(C U A)∩B=（ ） A. {－1} B. {0,1} C. {－1,2,3}D. {－1,0,1,3}3.【来源】2019年高考真题——理科数学（北京卷）设点A ，B ，C 不共线，则“AB 与AC 的夹角为锐角”是“||||AB AC BC +>”的 A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件D. 既不充分也不必要条件4.【来源】2019年高考真题——理科数学（天津卷）设x R ∈，则“250x x -<”是“|1|1x -<”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.【来源】2019年高考真题——理科数学（天津卷）设集合A={－1,1,2,3,5}，B={2,3,4}，{|13}C x x =∈≤<R ，则()A C B =A.{2}B.{2,3}C.{－1,2,3}D.{1,2,3,4} 6.【来源】2019年高考真题——理科数学（全国卷Ⅱ） 设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线D ．α，β垂直于同一平面7.【来源】2019年高考真题——理科数学（全国卷Ⅱ） 设集合A={x|x 2-5x+6>0}，B={ x|x-1<0}，则A∩B= A ．(－∞，1) B ．(－2，1) C ．(－3，－1)D ．(3，+∞)8.【来源】2019年高考真题——理科数学（全国卷Ⅲ）已知集合A={－1,0,1,2}，B={x|x 2≤1}，则A∩B= A ．{－1,0,1}B ．{0,1}C ．{－1,1}D ．{0,1,2}9.【来源】2019年高考真题——理科数学（全国卷Ⅰ） 已知集合}242{60{}M x x N x x x =-<<=--<，，则M∩N=A ．}{43x x -<<B ．}42{x x -<<- C ．}{22x x -<< D ．}{23x x <<10.【来源】2018年高考真题——数学理（全国卷Ⅲ）已知集合A={x|x －1≥0}，B={0,1,2}，则A∩B= A ．{0}B ．{1}C.{1,2}D ．{0,1,2}11.【来源】2018年高考真题——理科数学（北京卷）设集合{(,)|1,4,2},A x y x y ax y x ay =-≥+>-≤则 （A ）对任意实数a ，(2,1)A ∈（B ）对任意实数a ，（2，1）A ∉（C ）当且仅当a<0时，（2，1）A ∉ （D ）当且仅当32a ≤时，（2，1）A ∉ 12.【来源】2018年高考真题——理科数学（北京卷）设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件13.【来源】2018年高考真题——理科数学（北京卷）（1）已知集合A={x||x|<2}，B={–2，0，1，2}，则A∩B = （A ）{0，1}（B ）{–1，0，1}（C ）{–2，0，1，2}（D ）{–1，0，1，2}14.【来源】2018年高考真题——理科数学（天津卷）设x ∈R ，则“11||22x -<”是“31x <”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件(D)既不充分也不必要条件15.【来源】2018年高考真题——理科数学（天津卷）设全集为R ，集合{02}A x x =<<，{1}B x x =≥，则()=R A B(A) {01}x x <≤ (B) {01}x x << (C){12}x x ≤<(D){02}x x <<16.【来源】2018年高考真题——理科数学（全国卷II ）已知集合(){}223A x y xy x y =+∈∈Z Z ，≤，，，则A 中元素的个数为 A ．9B ．8C ．5D ．417.【来源】2018年高考真题——理科数学（全国卷Ⅰ）已知集合A={x|x 2－x －2＞0}，则C R A= A.{ x|－1＜x ＜2} B. { x|－1≤x≤2}C. { x| x ＜－1}∪{ x|x ＞2}D. { x| x≤－1}∪{ x|x≥2} 18.【来源】2016年高考真题——理科数学（天津卷）设{a n }是首项为正数的等比数列，公比为q ，则“q<0”是“对任意的正整数n ，a 2n−1+a 2n <0”的（ ）（A ）充要条件 （B ）充分而不必要条件 （C ）必要而不充分条件 （D ）既不充分也不必要条件 19.【来源】2016年高考真题——理科数学（天津卷）已知集合{1,2,3,4},{|32},A B y y x x A ===-∈，则A B =（ ） （A ）{1}（B ）{4}（C ）{1,3}（D ）{1,4}20.【来源】2017年高考真题——理科数学（北京卷）设m,n 为非零向量，则“存在负数λ，使得λ=m n ”是“0<⋅m n ”的 （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件（D ）既不充分也不必要条件21.【来源】2017年高考真题——理科数学（北京卷）若集合A={x|–2＜x＜1}，B={x|x＜–1或x＞3}，则A∩B=（A）{x|–2＜x＜–1} （B）{x|–2＜x＜3}（C）{x|–1＜x＜1} （D）{x|1＜x＜3}22.【来源】2017年高考真题——数学（浙江卷）已知等差数列{a n}的公差为d，前n项和为S n，则“d>0”是“S4 + S6>2S5”的A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件23.【来源】2017年高考真题——数学（浙江卷）已知集合P={x|-1<x<1}，Q={x|0<x<2}，那么P∪Q=A． (-1,2) B. (0,1) C. (-1,0) D.(1,2)二、填空题24.【来源】2019年高考真题——数学（江苏卷）已知集合A={－1,0,1,6}，{}|0,B x x x R =>∈，则A∩B=_____. 25.【来源】2018年高考真题——理科数学（北京卷）能说明“若f （x ）>f （0）对任意的x ∈（0，2］都成立，则f （x ）在［0，2］上是增函数”为假命题的一个函数是__________．26.【来源】2018年高考真题——数学（江苏卷）已知集合*{|21,}A x x n n ==-∈N ，*{|2,}n B x x n ==∈N ．将A B 的所有元素从小到大依次排列构成一个数列{}n a ．记n S 为数列{}n a 的前n 项和，则使得112n n S a +>成立的n 的最小值为 ▲ ．27.【来源】2018年高考真题——数学（江苏卷）已知集合A={0,1,2,8}，B={－1,1,6,8}，那么A∩B = ▲ ． 28.【来源】2017年高考真题——理科数学（北京卷）能够说明“设a ，b ，c 是任意实数．若a ＞b ＞c ，则a+b ＞c”是假命题的一组整数a ，b ，c 的值依次为______________________________． 29.【来源】2017年高考真题——数学（江苏卷）已知集合A={1，2}，B={a ，a 2+3}，若A∩B={1}，则实数a 的值为________ 三、解答题（本题共1道小题,第1题0分,共0分） 30.【来源】2018年高考真题——理科数学（北京卷）（本小题14分）设n 为正整数，集合A=12{|(,,,),{0,1},1,2,,}n n t t t t k n αα=∈=．对于集合A 中的任意元素12(,,,)n x x x α=和12(,,,)n y y y β=，记M （αβ，）=111122221[(||)(||)(||)]2n n n n x y x y x y x y x y x y +--++--+++--．（Ⅰ）当n=3时，若(1,1,0)α=，(0,1,1)β=，求M （,αα）和M （,αβ）的值；（Ⅱ）当n=4时，设B 是A 的子集，且满足：对于B 中的任意元素,αβ，当,αβ相同时，M （αβ，）是奇数；当,αβ不同时，M （αβ，）是偶数．求集合B 中元素个数的最大值；（Ⅲ）给定不小于2的n ，设B 是A 的子集，且满足：对于B 中的任意两个不同的元素,αβ，M （αβ，）=0．写出一个集合B ，使其元素个数最多，并说明理由．试卷答案1.A 【分析】本题根据基本不等式，结合选项，判断得出充分性成立，利用“特殊值法”，通过特取,a b值，推出矛盾，确定必要性不成立.题目有一定难度，注重重要知识、基础知识、逻辑推理能力的考查.【详解】当0, 0a >b >时，a b +≥，则当4a b +≤时，有4a b ≤+≤，解得4ab ≤，充分性成立；当=1, =4a b 时，满足4ab ≤，但此时=5>4a+b ，必要性不成立，综上所述，“4a b +≤”是“4ab ≤”的充分不必要条件.【点睛】易出现的错误有，一是基本不等式掌握不熟，导致判断失误；二是不能灵活的应用“赋值法”，通过特取,a b 的值，从假设情况下推出合理结果或矛盾结果. 2. A【分析】本题借根据交集、补集的定义可得.容易题，注重了基础知识、基本计算能力的考查. 【详解】={1,3}U C A -，则(){1}U C A B =-【点睛】易于理解集补集的概念、交集概念有误. 3. C【分析】由题意结合向量的减法公式和向量的运算法则考查充分性和必要性是否成立即可. 【详解】∵A ､B ､C 三点不共线,∴|AB +AC |>|BC |⇔|AB +AC |>|AB -AC |⇔|AB +AC |2>|AB -AC |2AB ⇔•AC >0AB ⇔与AC的夹角为锐角.故“AB 与AC 的夹角为锐角”是“|AB +AC |>|BC |”的充分必要条件,故选C. 4. B化简不等式，可知 05x <<推不出11x -<； 由11x -<能推出05x <<，故“250x x -<”是“|1|1x -<”的必要不充分条件， 故选B. 5.因为{1,2}A C =， 所以(){1,2,3,4}A C B =.6. B根据面面平行的判定定理易得答案.选B. 7. A{2|<=x x A 或}3>x ，{}1|<=x x B ，∴）（1,∞-=⋂B A .8. A}11|{}1|{2≤≤-=≤=x x x x B ，所以}1,0,1{-=⋂B A .9. C由题意可知,}32|{<<-=x x N ,又因为}24|{<<-=x x M ,则}22|{<<-=x x N M ，故选C .10. C详解：由集合A 得 ,所以故答案选C. 11. D分析：求出 及 所对应的集合，利用集合之间的包含关系进行求解.详解：若，则且，即若，则 ，此命题的逆否命题为：若 ，则有，故选D.12. C分析：先对模平方，将 等价转化为0，再根据向量垂直时数量积为零得充要关系. 详解：，因为a ，b 均为单位向量，所以a ⊥b ，即“”是“a⊥b”的充分必要条件.选C.A分析：先解含绝对值不等式得集合A ，再根据数轴求集合交集. 详解：因此A∩B= ，选A.14. A分析：首先求解绝对值不等式，然后求解三次不等式即可确定两者之间的关系. 详解：绝对值不等式，由. 据此可知是的充分而不必要条件.本题选择A 选项. 15. B分析：由题意首先求得，然后进行交集运算即可求得最终结果.详解：由题意可得：，结合交集的定义可得：.本题选择B 选项. 16. A 详解： ，当 时， ； 当 时， ； 当时，；所以共有9个，选A. 17. B 解答：{|2A x x =>或1}x <-，则{|12}R C A x x =-≤≤.18. C试题分析：由题意得，22212(1)21210()0(1)0(,1)n n n n n a a a q q q q q ----+<⇔+<⇔+<⇔∈-∞-，故是必要不充分条件，故选C. 19.D试题分析：{1,4,7,10},A B {1,4}.B ==选D. 20. A若0λ∃<，使m n λ=，即两向量反向，夹角是180°，那么0cos1800m n m n m n ⋅==-<，反过来，若0m n ⋅<，那么两向量的夹角为（90°，180°]，并不一定反向，即不一定存在负数λ，使得λ=m n ，所以是充分不必要条件，故选A. 21. A{}21A B x x =-<<-，故选A.22.C试题分析：由46511210212(510)S S S a d a d d +-=+-+=，可知当0d >时，有46520S S S +->，即4652S S S +>，反之，若4652S S S +>，则0d >，所以“d>0”是“S 4 +S 6>2S 5”的充要条件，选C ．【名师点睛】本题考查等差数列的前n 项和公式，通过套入公式与简单运算，可知4652S S S d +-=， 结合充分必要性的判断，若p q ⇒，则p 是q 的充分条件，若p q ⇐，则p 是q 的必要条件，该题“0d >”⇔“46520S S S +->”，故互为充要条件． 23.A试题分析：利用数轴，取P 、Q 所有元素，得P ∪Q=(-1,2)【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理． 24. {1,6} 【分析】由题意利用交集的定义求解交集即可. 【详解】由题知，{1,6}AB =.【点睛】本题主要考查交集的运算，属于基础题. 25.y=sinx （答案不唯一）分析：举的反例要否定增函数，可以取一个分段函数，使得f （x ）>f （0）且（0，2］上是减函数.详解：令，则f （x ）>f （0）对任意的x ∈（0，2］都成立，但f （x ）在［0，2］上不是增函数. 又如，令f （x ）=sinx ，则f （0）=0，f （x ）>f （0）对任意的x ∈（0，2］都成立，但f （x ）在［0，2］上不是增函数.26.27分析：先根据等差数列以及等比数列的求和公式确定满足条件的项数的取值范围，再列不等式求满足条件的项数的最小值. 详解：设 ，则由得 所以只需研究是否有满足条件的解， 此时 ， ，m 为等差数列项数，且. 由得满足条件的n 最小值为27.27.{1，8} 分析：根据交集定义求结果. 详解：由题设和交集的定义可知：.28.1,2,3---（答案不唯一） 123,1(2)3->->--+-=-29.1由题意1B ∈，显然233a +≥，所以1a =，此时234a +=，满足题意，故答案为130.解：（Ⅰ）因为α=（1，1，0），β=（0，1，1），所以M(α，α)=12[(1+1−|1−1|)+(1+1−|1−1|)+(0+0−|0−0|)]=2， M(α，β）=12[(1+0–|1−0|)+(1+1–|1–1|)+(0+1–|0–1|)]=1．（Ⅱ）设α=（x1，x 2，x3，x4）∈B，则M(α，α）= x1+x2+x3+x4．由题意知x1，x 2，x3，x4∈{0，1}，且M(α，α)为奇数，所以x1，x 2，x3，x4中1的个数为1或3．所以B {(1，0，0，0），（0，1，0，0)，（0，0，1，0)，（0，0，0，1)，（0，1，1，1)，(1，0，1，1)，(1，1，0，1)，(1，1，1，0)}.将上述集合中的元素分成如下四组：（1，0，0，0)，(1，1，1，0)；（0，1，0，0)，(1，1，0，1)；（0，0，1，0)，（1，0，1，1)；（0，0，0，1)，（0，1，1，1).经验证，对于每组中两个元素α，β，均有M(α，β）=1.所以每组中的两个元素不可能同时是集合B的元素．所以集合B中元素的个数不超过4.又集合{（1，0，0，0），（0，1，0，0），（0，0，1，0），（0，0，0，1)}满足条件，所以集合B中元素个数的最大值为4.（Ⅲ）设S k=( x1，x 2，…，x n）|( x1，x 2，…，x n）∈A，x k =1，x1=x2=…=x k–1=0）（k=1，2，…，n)，S n+1={( x1，x 2，…，x n）| x1=x2=…=x n=0}，则A=S1∪S1∪…∪S n+1．对于S k（k=1，2，…，n–1）中的不同元素α，β，经验证，M(α，β)≥1.所以S k（k=1，2 ，…，n–1）中的两个元素不可能同时是集合B的元素．所以B中元素的个数不超过n+1.取e k=( x1，x 2，…，x n）∈S k且x k+1=…=x n=0（k=1，2，…，n–1）.令B=（e1，e2，…，e n–1）∪S n∪S n+1，则集合B的元素个数为n+1，且满足条件.故B是一个满足条件且元素个数最多的集合．。

高考数学精品复习资料2019.5第29练 完美破解立体几何证明题[内容精要] 立体几何中的题目最主要的两点就是证明和计算，其中证明主要是来证明空间中的点、线、面间的平行或垂直关系．本节就来探讨空间中的位置关系的证明问题．题型一 空间中的平行问题例1 在如图所示多面体ABCDE 中，AB ⊥平面ACD ，DE ⊥平面ACD ，且AC ＝AD ＝CD ＝DE ＝2，AB ＝1.(1)请在线段CE 上找到点F 的位置，使得恰有直线BF ∥平面ACD ，并证明．(2)求多面体ABCDE 的体积．破题切入点 (1)可先猜后证，可以利用线面平行的判定定理进行证明．(2)找到合适的底面．解 如图，(1)由已知AB ⊥平面ACD ，DE ⊥平面ACD ，所以AB ∥ED ，设F 为线段CE 的中点，H 是线段CD 的中点，连接FH ，AH ，则FH 綊12ED ， 所以FH 綊AB ，所以四边形ABFH 是平行四边形，所以BF ∥AH ，又因为BF ⊄平面ACD ，AH ⊂平面ACD ，所以BF ∥平面ACD .(2)取AD 中点G ，连接CG .因为AB ⊥平面ACD ，所以CG ⊥AB ，又CG ⊥AD ，AB ∩AD ＝A ，所以CG ⊥平面ABED ，即CG 为四棱锥C －ABED 的高，求得CG ＝3，所以V C －ABED ＝13×(1＋2)2×2×3＝ 3. 题型二 空间中的垂直问题例2 如图，三棱柱ABC －A 1B 1C 1的侧面AA 1B 1B 为正方形，侧面BB 1C 1C为菱形，∠CBB 1＝60°，AB ⊥B 1C .(1)求证：平面AA 1B 1B ⊥平面BB 1C 1C .(2)若AB ＝2，求三棱柱ABC －A 1B 1C 1的体积．破题切入点 (1)考查面面垂直的判定定理．(2)注意利用棱柱体积和锥体体积公式间的关系．(1)证明 由侧面AA 1B 1B 为正方形，知AB ⊥BB 1.又AB ⊥B 1C ，BB 1∩B 1C ＝B 1，所以AB ⊥平面BB 1C 1C ，又AB ⊂平面AA 1B 1B ，所以平面AA 1B 1B ⊥平面BB 1C 1C .(2)解 由题意，CB ＝CB 1，设O 是BB 1的中点，连接CO ，则CO ⊥BB 1.由(1)知，CO ⊥平面AA 1B 1B ，且CO ＝32BC ＝32AB ＝ 3.连接AB 1，则VC －ABB 1＝13S △ABB 1·CO ＝16AB 2·CO ＝233.因为VB 1－ABC ＝VC －ABB 1＝13VABC －A 1B 1C 1＝233，所以VABC －A 1B 1C 1＝2 3.故三棱柱ABC －A 1B 1C 1的体积为＝2 3.题型三 空间中的平行、垂直综合问题例3 在如图所示的几何体中，四边形ABCD 是正方形，MA ⊥平面ABCD ，PD ∥MA ，E 、G 、F 分别为MB 、PB 、PC 的中点，且AD ＝PD＝2MA .(1)求证：平面EFG ∥平面PMA ；(2)求证：平面EFG ⊥平面PDC ；(3)求三棱锥P －MAB 与四棱锥P －ABCD 的体积之比．破题切入点 (1)证明EG 、FG 都平行于平面PMA . (2)证明GF ⊥平面PDC .(3)设MA 为1，从而其他边的长度都可表示，问题可求解．(1)证明 ∵E 、G 、F 分别为MB 、PB 、PC 的中点，∴EG ∥PM ，GF ∥BC .又∵四边形ABCD 是正方形，∴BC ∥AD ，∴GF ∥AD .∵EG 、GF 在平面PMA 外，PM 、AD 在平面PMA 内，∴EG ∥平面PMA ，GF ∥平面PMA .又∵EG 、GF 都在平面EFG 内且相交，∴平面EFG ∥平面PMA .(2)证明 由已知MA ⊥平面ABCD ，PD ∥MA ，∴PD ⊥平面ABCD .又BC ⊂平面ABCD ，∴PD ⊥BC .∵四边形ABCD 为正方形，∴BC ⊥DC .又PD ∩DC ＝D ，∴BC ⊥平面PDC .由(1)知GF ∥BC ，∴GF ⊥平面PDC .又GF ⊂平面EFG ，∴平面EFG ⊥平面PDC .(3)解 ∵PD ⊥平面ABCD ，四边形ABCD 为正方形，不妨设MA ＝1，则PD ＝AD ＝2. ∵DA ⊥平面MAB ，且PD ∥MA ，∴DA 即为点P 到平面MAB 的距离，∴V P －MAB ∶V P －ABCD ＝13S △MAB ·DA ∶13S 正方形ABCD ·PD ＝S △MAB ∶S 正方形ABCD ＝⎝⎛⎭⎫12×1×2∶(2×2)＝1∶4. 即三棱锥P －MAB 与四棱锥P －ABCD 的体积之比为1∶4.总结提高 1.证明平行关系的方法：(1)证明线线平行的常用方法：①利用平行公理，即证明两直线同时和第三条直线平行；②利用平行四边形进行转换；③利用三角形中位线定理证明；④利用线面平行、面面平行的性质定理证明．(2)证明线面平行的常用方法：①利用线面平行的判定定理，把证明线面平行转化为证明线线平行；②利用面面平行的性质定理，把证明线面平行转化为证明面面平行．(3)证明面面平行的方法：证明面面平行，依据判定定理，只要找到一个面内两条相交直线与另一个平面平行即可，从而将证明面面平行转化为证明线面平行，再转化为证明线线平行．2．证明空间中垂直关系的方法：(1)证明线线垂直的常用方法①利用特殊平面图形的性质，如利用直角三角形、矩形、菱形、等腰三角形等得到线线垂直；②利用勾股定理逆定理；③利用线面垂直的性质，即要证明线线垂直，只需证明一线垂直于另一线所在平面即可．(2)证明线面垂直的常用方法①利用线面垂直的判定定理，把线面垂直的判定转化为证明线线垂直；②利用面面垂直的性质定理，把证明线面垂直转化为证明面面垂直；③利用常见结论，如两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面等．(3)证明面面垂直的方法证明面面垂直常用面面垂直的判定定理，即证明一个面过另一个面的一条垂线，将证明面面垂直转化为证明线面垂直，一般先从现有直线中寻找，若图中不存在这样的直线，则借助中点、高线或添加辅助线解决．1．若平面α∥平面β，直线a⊂α，点B∈β，则在β内过点B的所有直线中()A．不一定存在与a平行的直线B．只有两条与a平行的直线C．存在无数条与a平行的直线D．存在唯一与a平行的直线答案 D解析由直线a与B确定的平面与β有唯一交线．故存在唯一与a平行的直线．2．在正方体ABCD—A1B1C1D1中，E是棱AB上的动点，则直线A1D与直线C1E所成的角等于()A．60°B．90°C．30°D．随点E的位置而变化答案 B解析在正方体中，显然有A1D⊥AB，A1D⊥AD1，所以A1D⊥面AD1C1B，又C1E⊂面AD1C1B，故A1D⊥C1E.故选B.3．已知α、β是两个不同的平面，给出下列四个条件：①存在一条直线a，a⊥α，a⊥β；②存在一个平面γ，γ⊥α，γ⊥β；③存在两条平行直线a、b，a⊂α，b⊂β，a∥β，b∥α；④存在两条异面直线a、b，a⊂α，b⊂β，a∥β，b∥α，可以推出α∥β的是()A．①③B．②④C．①④D．②③答案 C解析 对于②，平面α与β还可以相交；对于③，当a ∥b 时，不一定能推出α∥β，所以②③是错误的，易知①④正确，故选C.4.如图，在正方形ABCD 中，E 、F 分别是BC 、CD 的中点，AC ∩EF ＝G .现在沿AE 、EF 、F A 把这个正方形折成一个四面体，使B 、C 、D 三点重合，重合后的点记为P ，则在四面体P －AEF 中必有( )A ．AP ⊥△PEF 所在平面B ．AG ⊥△PEF 所在平面C ．EP ⊥△AEF 所在平面D ．PG ⊥△AEF 所在平面答案 A解析 在折叠过程中，AB ⊥BE ，AD ⊥DF 保持不变． ∴ ⎭⎪⎬⎪⎫AP ⊥PE AP ⊥PF PE ∩PF ＝P ⇒AP ⊥面PEF .5．如图所示，直线P A 垂直于⊙O 所在的平面，△ABC 内接于⊙O ，且AB为⊙O 的直径，点M 为线段PB 的中点．现有结论：①BC ⊥PC ；②OM ∥平面APC ；③点B 到平面P AC 的距离等于线段BC 的长．其中正确的是( )A ．①②B ．①②③C ．①D ．②③答案 B解析 对于①，∵P A ⊥平面ABC ，∴P A ⊥BC .∵AB 为⊙O 的直径，∴BC ⊥AC ，∴BC ⊥平面P AC ，又PC ⊂平面P AC ，∴BC ⊥PC ；对于②，∵点M 为线段PB 的中点，∴OM ∥P A ，∵P A ⊂平面P AC ，∴OM ∥平面P AC ；对于③，由①知BC ⊥平面P AC ，∴线段BC 的长即是点B 到平面P AC 的距离，故①②③都正确．6.如图，若Ω是长方体ABCD —A 1B 1C 1D 1被平面EFGH 截去几何体EB 1F －HC 1G 所得到的几何体，其中E 为线段A 1B 1上异于B 1的点，F 为线段BB 1上异于B 1的点，且EH ∥A 1D 1，则下列结论中不正确的是( )A ．EH ∥FGB ．四边形EFGH 是矩形C ．Ω是棱柱D ．Ω是棱台答案 D解析 A 中，∵EH ∥A 1D 1，∴EH ∥BC ，∴EH ∥平面BCC 1B 1.又过EH 的平面EFGH 与平面BCC 1B 1交于FG ，∴EH ∥FG .故A 成立．B 中，易得四边形EFGH 为平行四边形，∵BC ⊥平面ABB 1A 1，∴BC ⊥EF ，即FG ⊥EF .∴四边形EFGH 为矩形．故B 正确．C 中可将Ω看作以A 1EFBA 和D 1HC 1CD 为上、下底面，以AD 为高的棱柱．故C 正确．7.如图，在空间四边形ABCD 中，M ∈AB ，N ∈AD ，若AMMB ＝AN ND，则直线MN 与平面BDC 的位置关系是________．答案 平行解析 在平面ABD 中，AM MB ＝AN ND， ∴MN ∥BD .又MN ⊄平面BCD ，BD ⊂平面BCD ，∴MN ∥平面BCD .8．如图，正方体ABCD —A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F在CD 上．若EF ∥平面AB 1C ，则线段EF 的长度等于______．答案 2解析 由于在正方体ABCD —A 1B 1C 1D 1中，AB ＝2，∴AC ＝2 2.又E 为AD 的中点，EF ∥平面AB 1C ，EF ⊂平面ADC ，平面ADC ∩平面AB 1C ＝AC ，∴EF ∥AC ，∴F 为DC 的中点，∴EF ＝12AC ＝ 2.9.如图，已知六棱锥P －ABCDEF 的底面是正六边形，P A ⊥平面ABC ，P A＝2AB ，则下列结论中：①PB ⊥AE ；②平面ABC ⊥平面PBC ；③直线BC∥平面P AE ；④∠PDA ＝45°.其中正确的有________(把所有正确的序号都填上)．答案 ①④解析 由P A ⊥平面ABC ，AE ⊂平面ABC ，得P A ⊥AE ，又由正六边形的性质得AE ⊥AB ，P A ∩AB ＝A ，得AE ⊥平面P AB ，又PB⊂平面P AB，∴AE⊥PB，①正确；∵平面P AD⊥平面ABC，∴平面ABC⊥平面PBC不成立，②错；由正六边形的性质得BC∥AD，又AD⊂平面P AD，BC⊄平面P AD，∴BC∥平面P AD，∴直线BC∥平面P AE也不成立，③错；在Rt△P AD中，P A＝AD＝2AB，∴∠PDA＝45°，∴④正确．10．给出命题：①在空间中，垂直于同一平面的两个平面平行；②设l，m是不同的直线，α是一个平面，若l⊥α，l∥m，则m⊥α；③已知α，β表示两个不同平面，m为平面α内的一条直线，“α⊥β”是“m⊥β”的充要条件；④在三棱锥S－ABC中，SA⊥BC，SB⊥AC，则S在平面ABC内的射影是△ABC的垂心；⑤a，b是两条异面直线，P为空间一点，过P总可以作一个平面与a，b之一垂直，与另一条平行．其中，正确的命题是________．(只填序号)答案②④解析①错误，垂直于同一个平面的两个平面也可能相交；③错误，“α⊥β”是“m⊥β”的必要不充分条件；⑤错误，只有当异面直线a，b垂直时才可以作出满足要求的平面；易知②④正确．11．如图所示，M，N，K分别是正方体ABCD—A1B1C1D1的棱AB，CD，C1D1的中点．求证：(1)AN∥平面A1MK；(2)平面A1B1C⊥平面A1MK.证明(1)如图所示，连接NK.在正方体ABCD—A1B1C1D1中，∵四边形AA1D1D，DD1C1C都为正方形，∴AA1∥DD1，AA1＝DD1，C1D1∥CD，C1D1＝CD.∵N，K分别为CD，C1D1的中点，∴DN∥D1K，DN＝D1K，∴四边形DD1KN为平行四边形．∴KN ∥DD 1，KN ＝DD 1，∴AA 1∥KN ，AA 1＝KN .∴四边形AA 1KN 为平行四边形．∴AN ∥A 1K .∵A 1K ⊂平面A 1MK ，AN ⊄平面A 1MK ，∴AN ∥平面A 1MK .(2)如图所示，连接BC 1.在正方体ABCD —A 1B 1C 1D 1中，AB ∥C 1D 1，AB ＝C 1D 1.∵M ，K 分别为AB ，C 1D 1的中点，∴BM ∥C 1K ，BM ＝C 1K .∴四边形BC 1KM 为平行四边形．∴MK ∥BC 1.在正方体ABCD —A 1B 1C 1D 1中，A 1B 1⊥平面BB 1C 1C ，BC 1⊂平面BB 1C 1C ，∴A 1B 1⊥BC 1.∵MK ∥BC 1，∴A 1B 1⊥MK .∵四边形BB 1C 1C 为正方形，∴BC 1⊥B 1C .∴MK ⊥B 1C .∵A 1B 1⊂平面A 1B 1C ，B 1C ⊂平面A 1B 1C ，A 1B 1∩B 1C ＝B 1，∴MK ⊥平面A 1B 1C . 又∵MK ⊂平面A 1MK ，∴平面A 1B 1C ⊥平面A 1MK .12．(20xx·课标全国Ⅱ)如图，四棱锥P －ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ；(2)设二面角D －AE －C 为60°，AP ＝1，AD ＝3，求三棱锥E －ACD 的体积．(1)证明 连接BD 交AC 于点O ，连接EO .因为ABCD 为矩形，所以O 为BD 的中点．又E 为PD 的中点，所以EO ∥PB .因为EO ⊂平面AEC ，PB ⊄平面AEC ，所以PB ∥平面AEC .(2)解 因为P A ⊥平面ABCD ，ABCD 为矩形，所以AB ，AD ，AP 两两垂直．如图，以A 为坐标原点，AB →、AD →、AP →的方向分别为x 轴、y 轴、z 轴的正方向，|AP →|为单位长，建立空间直角坐标系A －xyz ，则D (0，3，0)，E (0，32，12)，AE →＝(0，32，12)． 设B (m,0,0)(m >0)，则C (m ，3，0)，AC →＝(m ，3，0)．设n 1＝(x ，y ，z )为平面ACE 的法向量，则⎩⎪⎨⎪⎧ n 1·AC →＝0，n 1·AE →＝0， 即⎩⎪⎨⎪⎧mx ＋3y ＝0，32y ＋12z ＝0， 可取n 1＝(3m ，－1，3)． 又n 2＝(1,0,0)为平面DAE 的法向量，由题设|cos 〈n 1，n 2〉|＝12， 即 33＋4m 2＝12， 解得m ＝32. 因为E 为PD 的中点， 所以三棱锥E －ACD 的高为12， 三棱锥E －ACD 的体积V ＝13×12×3×32×12＝38.。

高考理科数学题型全归纳题型1、集合的基本概念题型2、集合间的基本关系题型3、集合的运算题型4、四种命题及关系题型5、充分条件、必要条件、充要条件的判断与证明题型6、求解充分条件、必要条件、充要条件中的参数范围题型7、判断命题的真假题型8、含有一个量词的命题的否定题型9、结合命题真假求参数的范围题型10、映射与函数的概念题型11、同一函数的判断题型12、函数解析式的求法题型13、函数定义域的求解题型14、函数定义域的应用题型15、函数值域的求解题型16、函数的奇偶性题型17、函数的单调性(区间)题型18、函数的周期性题型19、函数性质的综合题型20、二次函数、一元二次方程、二次不等式的关系题型21、二次方程ax2+bx+c=0(a≠0)的实根分布及条件题型22、二次函数"动轴定区间"、"定轴动区间"问题题型23、指数运算及指数方程、指数不等式题型24、指数函数的图像及性质题型25、指数函数中的恒成立的问题题型26、对数运算及对数方程、对数不等式题型27、对数函数的图像与性质题型28、对数函数中的恒成立问题题型29、幂函数的定义及基本性质题型30、幂函数性质的综合应用题型31、判断函数的图像题型32、函数图像的应用题型33、求函数的零点或零点所在区间题型34、利用函数的零点确定参数的取值范围题型35、方程根的个数与函数零点的存在性问题题型36、函数与数列的综合题型37、函数与不等式的综合题型38、函数中的创新题题型39、导数的定义题型40、求函数的导数题型41、导数的几何意义题型42、利用原函数与导函数的关系判断图像题型43、利用导数求函数的单调区间题型44、含参函数的单调性(区间)题型45、已知含参函数在区间上单调或不单调或存在单调区间,求参数范围题型46、函数的极值与最值的求解题型47、方程解(函数零点)的个数问题题型48、不等式恒成立与存在性问题题型49、利用导数证明不等式题型50、导数在实际问题中的应用题型51、终边相同的角的集合的表示与识别题型52、等分角的象限问题题型53、弧长与扇形面积公式的计算题型54、三角函数定义题题型55、三角函数线及其应用题型56、象限符号与坐标轴角的三角函数值题型57、同角求值---条件中出现的角和结论中出现的角是相同的题型58、诱导求值与变形题型59、已知解析式确定函数性质题型60、根据条件确定解析式题型61、三角函数图像变换题型62、两角和与差公式的证明题型63、化简求值题型64、正弦定理的应用题型65、余弦定理的应用题型66、判断三角形的形状题型67、正余弦定理与向量的综合题型68、解三角形的实际应用题型69、共线向量的基本概念题型70、共线向量基本定理及应用题型71、平面向量的线性表示题型72、平面向量基本定理及应用题型73、向量与三角形的四心题型74、利用向量法解平面几何题型75、向量的坐标运算题型76、向量平行(共线)、垂直充要条件的坐标表示题型77、平面向量的数量积题型78、平面向量的应用题型79、等差、等比数列的通项及基本量的求解题型80、等差、等比数列的求和题型81、等差、等比数列的性质应用题型82、判断和证明数列是等差、等比数列题型83、等差数列与等比数列的综合题型84、数列通项公式的求解题型85、数列的求和题型86、数列与不等式的综合题型87、不等式的性质题型88、比较数(式)的大小与比较法证明不等式题型89、求取值范围题型90、均值不等式及其应用题型91、利用均值不等式求函数最值题型92、利用均值不等式证明不等式题型93、不等式的证明题型94、有理不等式的解法题型95、绝对值不等式的解法题型96、二元一次不等式组表示的平面区域题型97、平面区域的面积题型98、求解目标函数的最值题型99、求解目标函数中参数的取值范围题型100、简单线性规划问题的实际运用题型101、不等式恒成立问题中求参数的取值范围题型102、函数与不等式综合题型103、几何体的表面积与体积题型104、球的表面积、体积与球面距离题型105、几何体的外接球与内切球题型106、直观图与斜二测画法题型107、直观图?三视图题型108、三视图?直观图---简单几何体的基本量的计算题型109、三视图?直观图---简单组合体的基本量的计算题型110、部分三视图?其余三视图题型111、证明"点共面"、"线共面"或"点共线"及"线共点" 题型112、异面直线的判定题型113、证明空间中直线、平面的平行关系题型114、证明空间中直线、平面的垂直关系题型115、倾斜角与斜率的计算题型116、直线的方程题型117、两直线位置关系的判定题型118、有关距离的计算题型119、对称问题题型120、求圆的方程题型121、直线系方程和圆系方程题型122、与圆有关的轨迹问题题型123、圆的一般方程的充要条件题型124、点与圆的位置关系判断题型125、与圆有关的最值问题题型126、数形结合思想的应用题型127、直线与圆的相交关系题型128、直线与圆的相切关系题型129、直线与圆的相离关系题型130、圆与圆的位置关系题型131、椭圆的定义与标准方程题型132、离心率的值及取值范围题型133、焦点三角形题型134、双曲线的定义与标准方程题型135、双曲线的渐近线题型136、离心率的值及取值范围题型137、焦点三角形题型138、抛物线的定义与方程题型139、与抛物线有关的距离和最值问题题型140、抛物线中三角形、四边形的面积问题题型141、直线与圆锥曲线的位置关系题型142、中点弦问题题型143、弦长与面积问题题型144、平面向量在解析几何中的应用题型145、定点问题题型146、定值问题题型147、最值问题题型148、已知流程框图,求输出结果题型149、根据条件,填充不完整的流程图题型150、求输入参量以活活被整死；堂堂大元帅受辱骂；……这哪里还有什么尊重可言！3、用在设问句后。

高考数学（理）真题专题汇编：数列一、选择题1.【来源】2019年高考真题——数学（浙江卷）设,a b R ∈，数列{a n }中，21,n n n a a a a b +==+，b N *∈ ,则（ ）A. 当101,102b a => B. 当101,104b a => C. 当102,10b a =->D. 当104,10b a =->2.【来源】2019年高考真题——数学（浙江卷）已知,a b R ∈，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则（ ） A. 1,0a b <-< B. 1,0a b <-> C. 1,0a b >->D. 1,0a b >-<3.【来源】2019年高考真题——数学（浙江卷）设三棱锥V -ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P -AC -B 的平面角为γ，则（ ）A. ,βγαγ<<B. ,βαβγ<<C. ,βαγα<<D. ,αβγβ<<4.【来源】2019年高考真题——数学（浙江卷） 在同一直角坐标系中，函数11,log (02a x y y x a a ⎛⎫==+> ⎪⎝⎭且0)a ≠的图象可能是（ ） A. B.C. D.5.【来源】2019年高考真题——数学（浙江卷） 若0,0ab >>，则“4a b +≤”是 “4ab ≤”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件6.【来源】2019年高考真题——数学（浙江卷）祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V Sh =柱体，其中S 是柱体的底面积，h 是柱体的高，若某柱体的三视图如图所示，则该柱体的体积(cm 3)是（ ）A. 158B. 162C. 182D. 3247.【来源】2019年高考真题——数学（浙江卷）若实数x ，y 满足约束条件3403400x y x y x y -+≥⎧⎪--≤⎨⎪+≥⎩，则32z x y =+的最大值是（ ）A. －1B. 1C. 10D. 128.【来源】2019年高考真题——数学（浙江卷）渐近线方程为0x y ±=的双曲线的离心率是（ ）B. 1D. 29.【来源】2019年高考真题——数学（浙江卷）已知全集U ={－1,0,1,2,3}，集合A ={0,1,2}，B ={－1,0,1}，则(C U A )∩B =（ ） A. {－1} B. {0,1} C. {－1,2,3}D. {－1,0,1,3}二、填空题10.【来源】2019年高考真题——数学（浙江卷）已知正方形ABCD 的边长为1，当每个(1,2,3,4,5,6)i i λ=取遍±1时，123456||AB BC CD DA AC BD λλλλλλ+++++的最小值是________；最大值是_______.11.【来源】2019年高考真题——数学（浙江卷）已知a R ∈，函数3()f x ax x =-，若存在t R ∈，使得2|(2)()|3f t f t +-≤，则实数a 的最大值是____.12.【来源】2019年高考真题——数学（浙江卷）已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______. 13.【来源】2019年高考真题——数学（浙江卷）在△ABC 中，90ABC ∠=︒，4AB =，3BC =，点D 在线段AC 上，若45BDC ∠=︒，则BD =____；cos ABD ∠=________.14.【来源】2019年高考真题——数学（浙江卷）在二项式9)x 的展开式中，常数项是________；系数为有理数的项的个数是_______. 15.【来源】2019年高考真题——数学（浙江卷）已知圆C 的圆心坐标是(0,m )，半径长是r .若直线230x y -+=与圆C 相切于点(2,1)A --，则m =_____，r =______.16.【来源】2019年高考真题——数学（浙江卷） 复数11z i=+（i 为虚数单位），则||z =________. 17.【来源】2019年高考真题——理科数学（北京卷）李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x 元．每笔订单顾客网上支付成功后，李明会得到支付款的80%．①当x =10时，顾客一次购买草莓和西瓜各1盒，需要支付__________元；②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x 的最大值为__________．18.【来源】2019年高考真题——理科数学（北京卷）设函数f （x ）=e x +a e −x （a 为常数）．若f （x ）为奇函数，则a =________；若f （x ）是R 上的增函数，则a 的取值范围是___________．三、解答题19.【来源】2019年高考真题——数学（浙江卷）已知实数0a ≠，设函数()=ln 0.f x a x x +>（Ⅰ）当34a =-时，求函数f (x )的单调区间；（Ⅱ）对任意21[,)e x ∈+∞均有()f x ≤ 求a 的取值范围. 注：e=2.71828…为自然对数的底数.20.【来源】2019年高考真题——数学（浙江卷）如图，已知点F (1,0)为抛物线22(0)y px p =>，点F 为焦点，过点F 的直线交抛物线于A ，B 两点，点C 在抛物线上，使得△ABC 的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q在点F 右侧.记,AFG CQG △△的面积为12,S S .（I）求p的值及抛物线的标准方程；（Ⅱ）求12SS的最小值及此时点G的坐标.21.【来源】2019年高考真题——数学（浙江卷）设等差数列{a n}的前n项和为S n，34a=，43a S=，数列{b n}满足：对每个12,,,n n n n n nn S b S b S b*++∈+++N成等比数列.（Ⅰ）求数列{a n}，{b n}的通项公式；（Ⅱ）记,,2nnnac nb*=∈N证明：12+2,.nc c c n n*++<∈N22.【来源】2019年高考真题——数学（浙江卷）如图，已知三棱柱ABC-A1B1C1，平面A1AC1C⊥平面ABC,90ABC∠=︒，1130,,,BAC A A AC AC E F∠=︒==分别是AC，A1B1的中点.（I）证明：EF⊥BC；（Ⅱ）求直线EF与平面A1BC所成角的余弦值.23.【来源】2019年高考真题——数学（浙江卷）设函数()sin ,f x x x =∈R .（I ）已知[0,2),θ∈π函数()f x θ+是偶函数，求θ的值； （Ⅱ）求函数22[()][()]124y f x f x ππ=+++ 的值域. 24.【来源】2019年高考真题——数学（浙江卷）设01a <<，则随机变量X 的分布列是：则当a 在(0,1)内增大时（ ） A. D (X )增大 B. D (X )减小 C. D (X )先增大后减小D. D (X )先减小后增大25.【来源】2019年高考真题——理科数学（北京卷）已知数列{a n }，从中选取第i 1项、第i 2项、…、第i m 项(i 1<i 2<…<i m )，若12m i i i a a a <<⋅⋅⋅<，则称新数列12m i i i a a a ⋅⋅⋅，，，为{a n }的长度为m 的递增子列．规定：数列{a n }的任意一项都是{a n }的长度为1的递增子列．（Ⅰ）写出数列1，8，3，7，5，6，9的一个长度为4的递增子列；（Ⅱ）已知数列{a n }的长度为p 的递增子列的末项的最小值为0m a ，长度为q 的递增子列的末项的最小值为0n a .若p <q ，求证：0m a <0n a ；（Ⅲ）设无穷数列{a n }的各项均为正整数，且任意两项均不相等.若{a n }的长度为s 的递增子列末项的最小值为2s –1，且长度为s 末项为2s –1的递增子列恰有2s -1个（s =1，2，…），求数列{a n }的通项公式．26.【来源】2019年高考真题——理科数学（北京卷）已知函数321()4f x x x x =-+. （Ⅰ）求曲线()y f x =的斜率为1的切线方程；（Ⅱ）当[2,4]x ∈-时，求证：6()x f x x -≤≤；（Ⅲ）设()|()()|()F x f x x a a =-+∈R ，记F (x )在区间[－2,4]上的最大值为M （a ），当M （a ）最小时，求a 的值．27.【来源】2019年高考真题——理科数学（北京卷）已知抛物线C ：x 2=−2py 经过点（2，−1）． （Ⅰ）求抛物线C 的方程及其准线方程；（Ⅱ）设O 为原点，过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ，N ，直线y =−1分别交直线OM ，ON 于点A 和点B .求证：以AB 为直径的圆经过y 轴上的两个定点．28.【来源】2019年高考真题——理科数学（北京卷）改革开放以来，人们的支付方式发生了巨大转变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月A ，B 两种移动支付方式的使用情况，从全校学生中随机抽取了100人，发现样本中A ，B 两种支付方式都不使用的有5人，样本中仅使用A 和仅使用B 的学生的支付金额分布情况如下：（Ⅰ）从全校学生中随机抽取1人，估计该学生上个月A ，B 两种支付方式都使用的概率； （Ⅱ）从样本仅使用A 和仅使用B 的学生中各随机抽取1人，以X 表示这2人中上个月支付金额大于1000元的人数，求X 的分布列和数学期望；（Ⅲ）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用A 的学生中，随机抽查3人，发现他们本月的支付金额都大于2000元．根据抽查结果，能否认为样本仅使用A 的学生中本月支付金额大于2000元的人数有变化？说明理由． 29.【来源】2019年高考真题——理科数学（北京卷）如图，在四棱锥P –ABCD 中，PA ⊥平面ABCD ，AD ⊥CD ，AD ∥BC ，PA =AD =CD =2，BC =3．E 为PD 的中点，点F 在PC 上，且13PF PC =．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）求二面角F–AE–P的余弦值；（Ⅲ）设点G在PB上，且23PGPB=．判断直线AG是否在平面AEF内，说明理由．30.【来源】2019年高考真题——理科数学（北京卷）在△ABC中，a=3，b−c=2，cos B=12 -．（Ⅰ）求b，c的值；（Ⅱ）求sin（B–C）的值．试卷答案1. A 【分析】本题综合性较强，注重重要知识、基础知识、运算求解能力、分类讨论思想的考查.本题从确定不动点出发，通过研究选项得解.【详解】选项B ：不动点满足2211042x x x ⎛⎫-+=-= ⎪⎝⎭时，如图，若1110,,22n a a a ⎛⎫=∈< ⎪⎝⎭，排除如图，若a 为不动点12则12n a = 选项C ：不动点满足22192024x x x ⎛⎫--=--= ⎪⎝⎭，不动点为ax 12-，令2a =，则210n a =<，排除选项D ：不动点满足221174024x x x ⎛⎫--=--= ⎪⎝⎭，不动点为1712x =±，令1712a =，则171102n a =±<，排除. 选项A ：证明：当12b =时，2222132431113117,,12224216a a a a a a =+≥=+≥=+≥≥， 处理一：可依次迭代到10a ； 处理二：当4n ≥时，221112n n n a a a +=+≥≥，则117117171161616log 2log log 2n n n n a a a -++>⇒>则12117(4)16n na n -+⎛⎫≥≥ ⎪⎝⎭，则626410217164646311114710161616216a ⨯⎛⎫⎛⎫≥=+=++⨯+⋯⋯>++> ⎪ ⎪⎝⎭⎝⎭.故选A【点睛】遇到此类问题，不少考生会一筹莫展.利用函数方程思想，通过研究函数的不动点，进一步讨论a 的可能取值，利用“排除法”求解. 2. D 【分析】本题综合性较强，注重重要知识、基础知识、运算求解能力、分类讨论思想及数形结合思想的考查.研究函数方程的方法较为灵活，通常需要结合函数的图象加以分析. 【详解】原题可转化为()y f x =与y ax b =+，有三个交点.当BC AP λ=时，2()(1)()(1)f x x a x a x a x '=-++=--，且(0)0,(0)f f a ='=，则（1）当1a ≤-时，如图()y f x =与y ax b =+不可能有三个交点（实际上有一个），排除A ，B（2）当1a >-时，分三种情况，如图()y f x =与y ax b =+若有三个交点，则0b <，答案选D下面证明：1a >-时，BC AP λ=时3211()()(1)32F x f x ax b x a x b =--=-+-，2()(1)((1))F x x a x x x a '=-+=-+，则(0)0 ,(+1)<0F >F a ，才能保证至少有两个零点，即310(1)6b a >>-+，若另一零点在0<【点睛】遇到此类问题，不少考生会一筹莫展.由于方程中涉及,a b 两个参数，故按“一元化”想法，逐步分类讨论，这一过程中有可能分类不全面、不彻底.. 3. B 【分析】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半.【详解】方法1：如图G 为AC 中点，V 在底面ABC 的投影为O ，则P 在底面投影D 在线段AO 上，过D 作DE 垂直AE ，易得//PE VG ，过P 作//PF AC 交VG 于F ，过D 作//DH AC ，交BG 于H ，则,,BPF PBD PED α=∠β=∠γ=∠，则cos cos PF EG DH BD PB PB PB PB α===<=β，即αβ>，tan tan PD PDED BDγ=>=β，即γ>β，综上所述，答案为B.方法2：由最小角定理βα<，记V AB C --的平面角为γ'（显然γ'=γ） 由最大角定理β<γ'=γ，故选B.法2：（特殊位置）取V ABC -为正四面体，P 为VA 中点，易得333222cos sin sin α=⇒α=β=γ=B. 【点睛】常规解法下易出现的错误有，不能正确作图得出各种角.未能想到利用“特殊位置法”，寻求简便解法. 4. D【分析】本题通过讨论a 的不同取值情况，分别讨论本题指数函数、对数函数的图象和，结合选项，判断得出正确结论.题目不难，注重重要知识、基础知识、逻辑推理能力的考查.【详解】当01a <<时，函数xy a =过定点(0,1)且单调递减，则函数1xy a =过定点(0,1)且单调递增，函数1log 2a y x ⎛⎫=+ ⎪⎝⎭过定点1(,0)2且单调递减，D 选项符合；当1a >时，函数x y a =过定点(0,1)且单调递增，则函数1x y a=过定点(0,1)且单调递减，函数1log 2a y x ⎛⎫=+ ⎪⎝⎭过定点1(,02）且单调递增，各选项均不符合.综上，选D.【点睛】易出现的错误有，一是指数函数、对数函数的图象和性质掌握不熟，导致判断失误；二是不能通过讨论a 的不同取值范围，认识函数的单调性. 5.A 【分析】本题根据基本不等式，结合选项，判断得出充分性成立，利用“特殊值法”，通过特取,a b的值，推出矛盾，确定必要性不成立.题目有一定难度，注重重要知识、基础知识、逻辑推理能力的考查.【详解】当0, 0a >b >时，a b +≥，则当4a b +≤时，有4a b ≤+≤，解得4ab ≤，充分性成立；当=1, =4a b 时，满足4ab ≤，但此时=5>4a+b ，必要性不成立，综上所述，“4a b +≤”是“4ab ≤”的充分不必要条件.【点睛】易出现的错误有，一是基本不等式掌握不熟，导致判断失误；二是不能灵活的应用“赋值法”，通过特取,a b 的值，从假设情况下推出合理结果或矛盾结果. 6. B【分析】本题首先根据三视图，还原得到几何体—棱柱，根据题目给定的数据，计算几何体的体积.常规题目.难度不大，注重了基础知识、视图用图能力、基本计算能力的考查.【详解】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯=⎪⎝⎭. 【点睛】易错点有二，一是不能正确还原几何体；二是计算体积有误.为避免出错，应注重多观察、细心算.7. C 【分析】本题是简单线性规划问题的基本题型，根据“画、移、解”等步骤可得解.题目难度不大题，注重了基础知识、基本技能的考查.【详解】在平面直角坐标系内画出题中的不等式组表示的平面区域为以(-1,1),(1,-1),(2,2)为顶点的三角形区域（包含边界），由图易得当目标函数=3+2z x y 经过平面区域的点(2,2)时，=3+2z x y 取最大值max 322210z =⨯+⨯=.【点睛】解答此类问题，要求作图要准确，观察要仔细.往往由于由于作图欠准确而影响答案的准确程度，也有可能在解方程组的过程中出错. 8. C 【分析】本题根据双曲线的渐近线方程可求得1a b ==，进一步可得离心率.容易题，注重了双曲线基础知识、基本计算能力的考查.【详解】因为双曲线的渐近线为0x y ±=，所以==1a b ，则c ==的离心率ce a==【点睛】理解概念，准确计算，是解答此类问题的基本要求.部分考生易出现理解性错误. 9. A 【分析】本题借根据交集、补集的定义可得.容易题，注重了基础知识、基本计算能力的考查. 【详解】={1,3}U C A -，则(){1}U C A B =-【点睛】易于理解集补集的概念、交集概念有误. 10.0 【分析】本题主要考查平面向量的应用，题目难度较大.从引入“基向量”入手，简化模的表现形式，利用转化与化归思想将问题逐步简化. 【详解】()()12345613562456AB BC CD DA AC BD AB ADλ+λ+λ+λ+λ+λ=λ-λ+λ-λ+λ-λ+λ+λ要使123456AB BC CD DA AC BD λ+λ+λ+λ+λ+λ的最小，只需要135562460λ-λ+λ-λ=λ-λ+λ+λ=，此时只需要取1234561,1,1,1,1,1λ=λ=-λ=λ=λ=λ=此时123456min0AB BC CD DA AC BDλ+λ+λ+λ+λ+λ=等号成立当且仅当1356,,λ-λλ-λ均非负或者均非正，并且2456,,λ-λλ+λ均非负或者均非正。

专题29圆锥曲线的综合问题25线与椭圆直线与椭圆考点出现频率2021年预测考点98曲线与方程37次考1次命题角度：（1）定点、定值问题；（2）最值、范围问题；（3）证明、探究性问题．核心素养：数学运算、逻辑推理、直观想象考点99定点与定值问题37次考6次考点100最值与范围问题37次考5次考点101探索型与存在性问题37次考3次考点98曲线与方程1．（2020山东）已知曲线22:1C mx ny +=．（）A ．若m>n>0，则C 是椭圆，其焦点在y 轴上B ．若m=n>0，则CC ．若mn<0，则C 是双曲线，其渐近线方程为y =D ．若m=0，n>0，则C 是两条直线2．（2020天津）设双曲线C 的方程为22221(0,0)x y a b a b-=>>，过抛物线24y x =的焦点和点(0,)b 的直线为l ．若C 的一条渐近线与l 平行，另一条渐近线与l 垂直，则双曲线C 的方程为（）A ．22144x y -=B ．2214y x -=C ．2214x y -=D ．221x y -=3．【2019北京理】数学中有许多形状优美、寓意美好的曲线，曲线C ：221||x y x y +=+就是其中之一（如图）．给出下列三个结论：①曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C ；③曲线C 所围成的“心形”区域的面积小于3．其中，所有正确结论的序号是A ．①B ．②C ．①②D ．①②③4．（2020全国Ⅱ文19）已知椭圆22122:1(0)x y C a b a b+=>>的右焦点F 与抛物线2C 的焦点重合，1C 的中心与2C 的顶点重合．过F 且与x 轴垂直的直线交1C 于,A B 两点，交2C 于,C D 两点，且43CD AB =．（1）求1C 的离心率；（2）若1C 的四个顶点到2C 的准线距离之和为12，求1C 与2C 的标准方程．5．（2020全国Ⅱ理19）已知椭圆22122:1(0)x y C a b a b+=>>的右焦点F 与抛物线2C 的焦点重合，1C 的中心与2C 的顶点重合．过F 且与x 轴垂直的直线交1C 于,A B 两点，交2C 于,C D 两点，且43CD AB =．（1）求1C 的离心率；（2）设M 是1C 与2C 的公共点，若5=MF ，求1C 与2C 的标准方程．6．（2018江苏）如图，在平面直角坐标系xOy 中，椭圆C 过点12，焦点12(F F ，圆O 的直径为12F F ．(1)求椭圆C 及圆O 的方程；(2)设直线l 与圆O 相切于第一象限内的点P ．①若直线l 与椭圆C 有且只有一个公共点，求点P 的坐标；②直线l 与椭圆C 交于,A B 两点．若OAB △的面积为7，求直线l 的方程．7．（2017新课标Ⅱ）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足NP =．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．8．（2016全国Ⅲ文理）已知抛物线C ：22y x =的焦点为F ，平行于x 轴的两条直线12,l l 分别交C 于A B，两点，交C 的准线于P Q ，两点．（I ）若F 在线段AB 上，R 是PQ 的中点，证明AR FQ ；（II ）若PQF ∆的面积是ABF ∆的面积的两倍，求AB 中点的轨迹方程．9．（2015江苏理）如图，在平面直角坐标系xoy 中，已知椭圆()222210x y a b a b +=>>的离心率为22，且右焦点F 到左准线l 的距离为3．（1）求椭圆的标准方程；（2）过F 的直线与椭圆交于,A B 两点，线段AB 的垂直平分线分别交直线l 和AB 于点,P C ，若2PC AB =，求直线AB 的方程．10．（2014广东理）已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点为，离心率为3．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若动点00(,)P x y 为椭圆外一点，且点P 到椭圆C 的两条切线相互垂直，求点P 的轨迹方程．11．（2014辽宁理）圆224x y +=的切线与x 轴正半轴，y 轴正半轴围成一个三角形，当该三角形面积最小时，切点为P （如图），双曲线22122:1x y C a b-=过点P ．（1）求1C 的方程；（2）椭圆2C 过点P 且与1C 有相同的焦点，直线l 过2C 的右焦点且与2C 交于A ，B 两点，若以线段AB 为直径的圆心过点P ，求l 的方程．12．（2013四川理）已知椭圆C ：)0(12222>>=+b a by a x 的两个焦点分别为1(10)F -，，210F （，），且椭圆C 经过点），3134(P ．（Ⅰ）求椭圆C 的离心率（Ⅱ）设过点），（20A 的直线l 与椭圆C 交于M ，N 两点，点Q 是MN 上的点，且222112ANAMAQ+=，求点Q 的轨迹方程．13．（2011天津理）在平面直角坐标系xOy 中，点(,)P a b (0)a b >>为动点，12,F F 分别为椭圆22221x y a b+=的左右焦点．已知△12F PF 为等腰三角形．（Ⅰ）求椭圆的离心率e ；（Ⅱ）设直线2PF 与椭圆相交于,A B 两点，M 是直线2PF 上的点，满足2AM BM ⋅=-，求点M 的轨迹方程．考点99定点与定值问题14．【2020全国Ⅰ文21理20】已知,A B 分别为椭圆()222:11x E y a a+=>的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线6x =上的动点，PA 与E 的另一交点为,C PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点．15．【2020山东】已知椭圆2222:1(0)x y C a b a b+=>>的离心率为2，且过点()2,1A ．（1）求C 的方程；（2）点M ，N 在C 上，且AM AN ⊥，AD MN ⊥，D 为垂足．证明：存在定点Q ，使得DQ 为定值．16．【2019全国Ⅲ理】已知曲线C：y=22x，D为直线y=12-上的动点，过D作C的两条切线，切点分别为A，B．（1）证明：直线AB过定点：（2）若以E(0，52)为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE的面积．17．【2019北京理】已知抛物线C：x2=−2py经过点（2，−1）．（1）求抛物线C的方程及其准线方程；（2）设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=−1分别交直线OM，ON于点A和点B．求证：以AB为直径的圆经过y轴上的两个定点．18．【2019全国Ⅲ文】已知曲线C：y=22x，D为直线y=12-上的动点，过D作C的两条切线，切点分别为A，B．（1）证明：直线AB过定点；（2）若以E(0，52)为圆心的圆与直线AB相切，且切点为线段AB的中点，求该圆的方程．19．【2019北京文】已知椭圆2222:1x yCa b+=的右焦点为(1,0)，且经过点(0,1)A．（1）求椭圆C 的方程；（2）设O 为原点，直线:(1)l y kx t t =+≠±与椭圆C 交于两个不同点P ，Q ，直线AP 与x 轴交于点M ，直线AQ 与x 轴交于点N ，若|OM|·|ON|=2，求证：直线l 经过定点．20．【2018北京文20】（本小题14分）已知椭圆M ：22221x y a b+=(0)a b >>的离心率为3，焦距为k 的直线l 与椭圆M 有两个不同的焦点,A B （I ）求椭圆M 的方程；（II ）若1k =，求AB 的最大值；（III ）设()2,0P -，直线PA 与椭圆M 的另一个交点为C ，直线PB 与椭圆M 的另一个交点为D ，若,C D 和点71,44Q ⎛⎫- ⎪⎝⎭共线，求k ．21．【2018北京理19】（本小题14分）已知抛物线2:2C y px =经过点()1,2P ，过点()0,1Q 的直线l 与抛物线C 有两个不同的交点,A B ，且直线PA 交于y 轴与M ，直线PB 交y 轴与N ．（I ）求直线l 的斜率的取值范围．（II ）设O 为原点，,QM QO QN QO λμ== ，求证：11λμ+为定值．22．（2017新课标Ⅰ理）已知椭圆C ：22221(0)x y a b a b +=>>，四点1(1,1)P ，2(0,1)P ，33(1,2P =-，43(1,2P =中恰有三点在椭圆C 上．（1）求C 的方程；（2）设直线l 不经过2P 点且与C 相交于A ，B 两点．若直线2P A 与直线2P B 的斜率的和为1-，证明：l 过定点．23．（2017新课标Ⅱ文理）设O 为坐标原点，动点M 在椭圆C ：2212x y +=上，过M 做x 轴的垂线，垂足为N ，点P 满足NP =．（1）求点P 的轨迹方程；（2）设点Q 在直线3x =-上，且1OP PQ ⋅=．证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F ．24．（2017北京文）已知椭圆C 的两个顶点分别为(2,0)A -，(2,0)B ，焦点在x 轴上，离心率为2．（Ⅰ）求椭圆C 的方程；（Ⅱ）点D 为x 轴上一点，过D 作x 轴的垂线交椭圆C 于不同的两点M ，N ，过D 作AM 的垂线交BN 于点E ．求证：BDE ∆与BDN ∆的面积之比为4：5．25．（2016年全国I 理）设圆222150x y x ++-=的圆心为A ，直线l 过点(1,0)B 且与x 轴不重合，l 交圆A 于C ，D 两点，过B 作AC 的平行线交AD 于点E ．（I ）证明EA EB +为定值，并写出点E 的轨迹方程；（II ）设点E 的轨迹为曲线1C ，直线l 交1C 于M ，N 两点，过B 且与l 垂直的直线与圆A 交于P ，Q 两点，求四边形MPNQ 面积的取值范围．26．（2016年北京文）已知椭圆C ：22221x y a b+=过(2,0)A ，(0,1)B 两点．（Ⅰ）求椭圆C 的方程及离心率；（Ⅱ）设P 为第三象限内一点且在椭圆C 上，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，求证：四边形ABNM 的面积为定值．27．（2016年北京理）已知椭圆C ：22221(0)x y a b a b+=>>的离心率为2，(,0)A a ，(0,)B b ，(0,0)O ，ΔOAB 的面积为1．（Ⅰ）求椭圆C 的方程；（Ⅱ）设P 是椭圆C 上一点，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ．求证：||||AN BM ⋅为定值．28．（2016年山东文）已知椭圆C ：22221(0)x y a b a b+=>>的长轴长为4，焦距为2 ．（Ⅰ）求椭圆C 的方程；（Ⅱ）过动点M(0，m)(m>0)的直线交x 轴与点N ，交C 于点A ，P(P 在第一象限)，且M 是线段PN的中点．过点P 作x 轴的垂线交C 于另一点Q ，延长线QM 交C 于点B ．(i)设直线PM 、QM 的斜率分别为k 、k'，证明k k'为定值；(ii)求直线AB 的斜率的最小值．29．（2015新课标2文）已知椭圆C ：22221(0)x y a b a b+=>>的离心率为22，点在C 上．（Ⅰ）求C 的方程；（Ⅱ）直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点,A B ，线段AB 的中点为M ．证明：直线OM 的斜率与直线l 的斜率的乘积为定值．30．（2015新课标2理）已知椭圆C ：2229x y m +=（0m >），直线l 不过原点O 且不平行于坐标轴，l与C 有两个交点A ，B ，线段AB 的中点为M ．（Ⅰ）证明：直线OM 的斜率与l 的斜率的乘积为定值；（Ⅱ）若l 过点(,)3mm ，延长线段OM 与C 交于点P ，四边形OAPB 能否为平行四边行？若能，求此时l 的斜率；若不能，说明理由．31．（2015陕西文）如图，椭圆E ：22221x y a b+=（a >b >0）经过点(0,1)A -，且离心率为2．（Ⅰ）求椭圆E 的方程；（Ⅱ）经过点(1,1)，且斜率为k 的直线与椭圆E 交于不同的两点,P Q （均异于点A ），证明：直线AP与AQ 的斜率之和为2．32．（2014江西文理）如图，已知双曲线C ：2221x y a-=(0a >)的右焦点F ，点B A ,分别在C 的两条渐近线上，x AF ⊥轴，BF OB AB ,⊥∥OA (O 为坐标原点）．（1）求双曲线C 的方程；（2）过C 上一点)0)((00,0≠y y x P 的直线1:020=-y y a x x l 与直线AF 相交于点M ，与直线23=x 相交于点N ，证明：当点P 在C 上移动时，NFMF恒为定值，并求此定值．33．（2013山东文理）椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别是12,F F，离心率为2，过1F 且垂直于x 轴的直线被椭圆C 截得的线段长为l ．（Ⅰ）求椭圆C 的方程；（Ⅱ）点P 是椭圆C 上除长轴端点外的任一点，连接12,PF PF ．设12F PF ∠的角平分线PM 交C 的长轴于点(),0M m ，求m 的取值范围；（Ⅲ）在（Ⅱ）的条件下，过点P 作斜率为k 的直线l ，使得l 与椭圆C 有且只有一个公共点．设直线12,PF PF 的斜率分别为12,k k ，若0k ≠，试证明1211kk kk +为定值，并求出这个定值．34．（2012湖南理）在直角坐标系xoy 中，曲线1C 的点均在2C ：22(5)9x y -+=外，且对1C 上任意一点M ，M 到直线2x =-的距离等于该点与圆2C 上点的距离的最小值．（Ⅰ）求曲线1C 的方程；（Ⅱ）设00(,)P x y （3y ≠±）为圆2C 外一点，过P 作圆2C 的两条切线，分别与曲线1C 相交于点A ，B 和C ，D ．证明：当P 在直线4x =-上运动时，四点A ，B ，C ，D 的纵坐标之积为定值．考点100最值与范围问题35．【2020年江苏18】在平面直角坐标系xOy 中，已知椭圆22:143x y E +=的左、右焦点分别为1F 、2F ，点A 在椭圆E 上且在第一象限内，212AF F F ⊥，直线1AF 与椭圆E 相交于另一点B ．（1）求12AF F ∆的周长；（2）在x 轴上任取一点P ，直线AP 与椭圆E 的右准线相交于点Q ，求OP QP ⋅的最小值；（3）设点M 在椭圆E 上，记OAB ∆与MAB ∆的面积分别为12,S S ，若213S S =，求点M 的坐标．36．【2020浙江21】如图，已知椭圆221:12x C y +=，抛物线22:2(0)C y px p =>，点A 是椭圆1C 与抛物线2C 的交点，过点A 的直线l 交椭圆1C 于点B ，交抛物线2C 于M （B ，M 不同于A ）．（Ⅰ）若116=p ，求抛物线2C 的焦点坐标；（Ⅱ）若存在不过原点的直线l 使M 为线段AB 的中点，求p 的最大值．37．【2019全国Ⅱ理】已知点A(−2，0)，B(2，0)，动点M(x ，y)满足直线AM 与BM 的斜率之积为−12．记M 的轨迹为曲线C ．（1）求C 的方程，并说明C 是什么曲线；（2）过坐标原点的直线交C 于P ，Q 两点，点P 在第一象限，PE ⊥x 轴，垂足为E ，连结QE 并延长交C 于点G ．（i ）证明：PQG △是直角三角形；（ii ）求PQG △面积的最大值．38．【2019浙江】如图，已知点(10)F ，为抛物线22(0)y px p =>的焦点，过点F 的直线交抛物线于A 、B 两点，点C 在抛物线上，使得ABC △的重心G 在x 轴上，直线AC 交x 轴于点Q ，且Q 在点F 的右侧．记,AFG CQG △△的面积分别为12,S S ．（1）求p 的值及抛物线的准线方程；（2）求12S S 的最小值及此时点G的坐标．39．（2018浙江21）如图，已知点P 是y 轴左侧（不含y 轴）一点，抛物线2:4C y x =上存在不同的两点,A B 满足,PA PB 的中点均在C 上．（I ）设AB 中点为M ，证明：PM 垂直于y 轴；（II ）若P 是半椭圆221(0)4y x x +=<上的动点，求PAB △面积的取值范围．40．（2017浙江文理）如图，已知抛物线2x y =．点11(,24A -，39(,)24B ，抛物线上的点(,)P x y 13()22x -<<，过点B 作直线AP 的垂线，垂足为Q ．（Ⅰ）求直线AP 斜率的取值范围；（Ⅱ）求||||PA PQ ⋅的最大值．41．（2017山东文）在平面直角坐标系xOy 中，已知椭圆C ：22221x y a b+=(0)a b >>的离心率为22，椭圆C 截直线1y =所得线段的长度为(Ⅰ)求椭圆C 的方程；(Ⅱ)动直线l ：(0)y kx m m =+≠交椭圆C 于A ，B 两点，交y 轴于点M ．点N 是M 关于O 的对称点，N 的半径为||NO ．设D 为AB 的中点，DE ，DF 与N 分别相切于点E ，F ，求EDF ∠的最小值．42．（2017山东理）在平面直角坐标系xOy 中，椭圆E ：22221x y a b+=()0a b >>的离心率为2，焦距为2．（Ⅰ）求椭圆E 的方程；（Ⅱ）如图，动直线l ：1y k x =-E 于,A B 两点，C 是椭圆E 上一点，直线OC 的斜率为2k ，且124k k =，M 是线段OC 延长线上一点，且:2:3MC AB =，M 的半径为MC ，,OS OT 是M 的两条切线，切点分别为,S T ．求SOT ∠的最大值，并求取得最大值时直线l 的斜率．43．(2016全国II 理)已知椭圆:E 2213x y t +=的焦点在x 轴上，A 是E 的左顶点，斜率为(0)k k >的直线交E 于,A M 两点，点N 在E 上，MA NA ⊥．（Ⅰ）当4,||||t AM AN ==时，求AMN ∆的面积；（Ⅱ）当2AM AN =时，求k 的取值范围．44．(2016天津理)设椭圆13222=+y a x (3)a >的右焦点为F ，右顶点为A ，已知||3||1||1FA eOA OF =+，其中O 为原点，e 为椭圆的离心率．（Ⅰ）求椭圆的方程；（Ⅱ）设过点A 的直线l 与椭圆交于点B （B 不在x 轴上），垂直于l 的直线与l 交于点M ，与y 轴交于点H ，若HF BF⊥，且MOA MAO ∠∠≤，求直线l 的斜率的取值范围．45．（2016浙江文）如图，设抛物线22(0)y px p =>的焦点为F ，抛物线上的点A 到y 轴的距离等于||1AF -．（I ）求p 的值；（II ）若直线AF 交抛物线于另一点B ，过B 与x 轴平行的直线和过F 与AB 垂直的直线交于点N ，AN 与x 轴交于点M ．求M 的横坐标的取值范围．45．（2015重庆文）如图，椭圆22221x y a b+=（a >b >0）的左、右焦点分别为1F ，2F ，且过2F 的直线交椭圆于,P Q 两点，且PQ ⊥1PF ．（Ⅰ）若12PF =+，22PF =-|，求椭圆的标准方程；（Ⅱ）若|1PQ PF λ=，且3443λ≤≤，试确定椭圆离心率e 的取值范围．46．（2014新课标1文理）已知点A (0,2)-，椭圆E ：22221(0)x y a b a b+=>>的离心率为32，F 是椭圆E 的右焦点，直线AF 的斜率为233，O 为坐标原点．（Ⅰ)求E 的方程；（Ⅱ）设过点A 的动直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程．47．（2014浙江文理）如图，设椭圆(),01:2222>>=+b a by a x C 动直线l 与椭圆C 只有一个公共点P ，且点P 在第一象限．（Ⅰ）已知直线l 的斜率为k ，用k b a ,,表示点P 的坐标；（Ⅱ）若过原点O 的直线1l 与l 垂直，证明：点P 到直线1l 的距离的最大值为b a -．48．（2015山东理）平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b +=>>的离心率为32，左、右焦点分别是1F 、2F ．以1F 为圆心以3为半径的圆与以2F 为圆心以1为半径的圆相交，且交点在椭圆C 上．（Ⅰ）求椭圆C 的方程；（Ⅱ）设椭圆E ：2222144x y a b+=，P 为椭圆C 上任意一点，过点P 的直线=+y kx m 交椭圆E 于,A B 两点，射线PO 交椭圆E 于点Q ．（i ）求||||OQ OP 的值；（ii ）求△ABQ 面积的最大值．49．（2014山东文理）已知抛物线）＞0(2:2p px y C =的焦点为F ，A 为C 上异于原点的任意一点，过点A的直线l 交C 于另一点B ，交x 轴的正半轴于点D ，且有FA FD =，当点A 的横坐标为3时，ADF ∆为正三角形．（Ⅰ）求C 的方程；（Ⅱ）若直线l l //1，且1l 和C 有且只有一个公共点E ，（ⅰ）证明直线AE 过定点，并求出定点坐标；（ⅱ）ABE ∆的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．50．（2014山东理）在平面直角坐标系xOy 中，椭圆2222:1(0)x y C a b a b +=>>的离心率为2，直线y x=被椭圆C 截得的线段长为5．（Ｉ）求椭圆C 的方程；（Ⅱ）过原点的直线与椭圆C 交于A ，B 两点（A ，B 不是椭圆C 的顶点）．点D 在椭圆C 上，且AD AB ⊥，直线BD 与x 轴、y 轴分别交于M ，N 两点．（ⅰ）设直线BD ，AM 的斜率分别为12,k k ，证明存在常数λ使得12k k λ=，并求出λ的值；（ⅱ）求OMN ∆面积的最大值．51．（2014四川文理）已知椭圆C ：22221x y a b+=（0a b >>）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设F 为椭圆C 的左焦点，T 为直线3x =-上任意一点，过F 作TF 的垂线交椭圆C 于点P ，Q ．（i ）证明：OT 平分线段PQ （其中O 为坐标原点）；（ii ）当||||TF PQ 最小时，求点T 的坐标．52．（2013广东文理）已知抛物线C 的顶点为原点，其焦点()()0,0F c c >到直线:20l x y --=的距离为2．设P 为直线l 上的点，过点P 作抛物线C 的两条切线,PA PB ，其中,A B 为切点．（Ⅰ）求抛物线C 的方程；（Ⅱ）当点()00,P x y 为直线l 上的定点时，求直线AB 的方程；（Ⅲ）当点P 在直线l 上移动时，求AF BF ⋅的最小值．53．（2011新课标文理）在平面直角坐标系xoy 中，已知点(0,1)A -，B 点在直线3y =-上，M 点满足//MB OA ，MA AB MB BA =，M 点的轨迹为曲线C ．（Ⅰ）求C 的方程；（Ⅱ）P 为C 上动点，l 为C 在点P 处的切线，求O 点到l 距离的最小值．54．（2011广东文理）设圆C 与两圆2222(4,(4x y x y ++=+=中的一个内切，另一个外切．（1）求C 的圆心轨迹L 的方程；（2）已知点M (,55F ，且P 为L 上动点，求MP FP -的最大值及此时点P 的坐标．考点101探索型与存在性问题55．【2018上海20】（本题满分16分，第1小题满分4分，第2小题满分6分，第2小题满分6分，第3小题满分6分）设常数2t >，在平面直角坐标系xOy 中，已知点()20F ,，直线:l x t =，曲线()2:800y x x t y Γ=≤≤≥,．l 与x 轴交于点A ，与Γ交于点B P Q ,,分别是曲线Γ与线段AB 上的动点．（1）用t 为表示点B 到点F 的距离；（2）设,23t FQ ==，线段OQ 的中点在直线FP 上，求AQP △的面积；（3）设8t =，是否存在以FP FQ ,为邻边的矩形FPEQ ，使得点E 在Γ上？若存在，求点P 的坐标；若不存在，说明理由．56．（2016全国I 文）在直角坐标系xOy 中，直线l ：(0)y t t =≠交y 轴于点M ，交抛物线C ：22(0)y px p =>于点P ，M 关于点P 的对称点为N ，连结ON 并延长交C 于点H ．（I ）求||||OH ON ；（II ）除H 以外，直线MH 与C 是否有其它公共点？说明理由．57．（2015新课标1理）在直角坐标系xoy 中，曲线C ：24x y =与直线y kx a =+(0)a >交与M ，N 两点，（Ⅰ）当0k =时，分别求C 在点M 和N 处的切线方程；（Ⅱ）y 轴上是否存在点P ，使得当k 变动时，总有OPM OPN ∠=∠？说明理由．58．（2015北京理）已知椭圆C ：()222210x y a b a b+=>>的离心率为22，点()01P ，和点()A m n ，()0m ≠都在椭圆C 上，直线PA 交x 轴于点M ．（Ⅰ）求椭圆C 的方程，并求点M 的坐标（用m ，n 表示）；（Ⅱ）设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N ．问：y 轴上是否存在点Q ，使得OQM ONQ ∠=∠？若存在，求点Q 的坐标；若不存在，说明理由．59．（2015湖北理）一种作图工具如图1所示．O 是滑槽AB 的中点，短杆ON 可绕O 转动，长杆MN 通过N 处铰链与ON 连接，MN 上的栓子D 可沿滑槽AB 滑动，且1DN ON ==，3MN =．当栓子D 在滑槽AB 内作往复运动时，带动．．N 绕O 转动一周（D 不动时，N 也不动），M 处的笔尖画出的曲线记为C ．以O 为原点，AB 所在的直线为x 轴建立如图2所示的平面直角坐标系．（Ⅰ）求曲线C 的方程；（Ⅱ）设动直线l 与两定直线1:20l x y -=和2:20l x y +=分别交于,P Q 两点．若直线l 总与曲线C 有且只有一个公共点，试探究：△OPQ 的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．60．（2015四川理）如图，椭圆E：2222+1(0)x y a ba b=>>的离心率是22，过点(0,1)P的动直线l与椭圆相交于,A B两点，当直线l平行与x轴时，直线l被椭圆E截得的线段长为．（1）求椭圆E的方程；（2）在平面直角坐标系xOy中，是否存在与点P不同的定点Q，使得QA PAQB PB=恒成立？若存在，求出点Q的坐标；若不存在，请说明理由．61．（2015浙江理）已知椭圆2212x y+=上两个不同的点,A B关于直线12y mx=+对称．（Ⅰ）求实数m的取值范围；（Ⅱ）求AOB∆面积的最大值（O为坐标原点）．62．（2014湖南文理）如图5，O 为坐标原点，双曲线221112211:1(0,0)x y C a b a b -=>>和椭圆222222222:1(0)x y C a b a b +=>>均过点23(,1)3P ，且以1C 的两个顶点和2C 的两个焦点为顶点的四边形是面积为2的正方形．（Ｉ）求12,C C 的方程；（Ⅱ）是否存在直线l ，使得l 与1C 交于,A B 两点，与2C 只有一个公共点，且||||OA OB AB +=？证明你的结论．63．（2013安徽文理）已知椭圆2222:1(0)x y C a b a b+=>>的焦距为4，且过点P ．64．（2013湖北文理）如图，已知椭圆1C 与2C 的中心在坐标原点O ，长轴均为MN 且在x 轴上，短轴长分别为2m ，2()n m n >，过原点且不与x 轴重合的直线l 与1C ，2C 的四个交点按纵坐标从大到小依次为A ，B ，C ，D ．记mnλ=，△BDM 和△ABN 的面积分别为1S 和2S ．（Ⅰ）当直线l 与y 轴重合时，若12S S λ=，求λ的值；（Ⅱ）当λ变化时，是否存在与坐标轴不重合的直线l ，使得12S S λ=并说明理由．65．（2012广东文理）在平面直角坐标系xOy 中，已知椭圆C ：22221(0)x y a b a b+=>>的离心率e =，且椭圆C 上的点到(0,2)Q 的距离的最大值为3．（Ⅰ）求椭圆C 的方程；（Ⅱ）在椭圆C 上，是否存在点(,)M m n 使得直线l ：1mx ny +=与圆O ：221x y +=相交于不同的两点,A B ，且OAB ∆的面积最大？若存在，求出点M 的坐标及相对应的OAB ∆的面积；若不存在，请说明理由．66．（2011山东文理）在平面直角坐标系xOy 中，已知椭圆22:13x C y +=．如图所示，斜率为(0)k k ＞且不过原点的直线l交椭圆C于A，B两点，线段AB的中点为E，射线OE交椭圆C于点G，交直线3x=-于点(3,)D m-．（Ⅰ）求22m k+的最小值；（Ⅱ）若2OG OD=∙OE，（i）求证：直线l过定点；（ii）试问点B，G能否关于x轴对称？若能，求出此时ABG的外接圆方程；若不能，请说明理由．。

高考数学中的置换组合问题解决方法高考数学中，置换组合问题是一个经典的题型。

这类题目考察的是置换和组合数学的相关概念与运算，需要学生理解和掌握置换群的概念、行列式的运算等高阶数学知识。

本文将分析一些典型的置换组合问题，并给出解决方法。

一、置换群的基本概念置换群是指同一个元素集合上的一些可能存在的变换所形成的群。

其中，每个变换都称为一个置换，所有置换构成的集合称为置换群，通常用S_n表示，其中n为元素集合的元素数量。

例如，如果元素集合为{1,2,3}，那么S_3就是由这三个元素的所有置换所构成的群。

置换群的基本性质是它是封闭的、可逆的和结合的。

封闭性指的是对于S_n中的任意两个置换，它们的复合操作仍然属于S_n 中；可逆性指的是对于S_n中的任意置换，它都有一个逆置换存在，使得它们的复合操作等于单位置换；结合性指的是对于S_n中的任意三个置换，在任意复合顺序下它们的结果都是相同的。

二、置换组合问题的解决方法在高考数学中，置换组合问题一般形式为：有n个不同的数，对它们进行若干次置换后，求出有多少个置换不改变这n个数的相对位置。

下面以一个典型的置换组合问题为例进行说明。

例1：有6个独立的物体放在数据线上，现要对它们进行随机的交换和移动操作，问有多少种操作方式，才能把数据线变为原始状态？解：首先，我们需要求解6个元素的置换群S_6中，有多少个置换能够将6个物体变回原始状态。

设A为将6个物体变回原始状态的置换集合，那么|A|表示置换集合A中元素的数量。

由于A中的每一个置换操作都是可逆的，只需要找到其中一个操作，后面的操作就可以根据该操作的逆置换进行计算。

换句话说，假设存在一个合法操作将这6个物体变为原始状态，那么我们可以考虑该操作能够带来些什么变化，进而推导出其他合法操作的数量。

对于该操作，我们假设其将第1个物体移动到了第k个位置，然后根据k和其他物体的位置确定该置换。

不难发现，由于6个物体原来的位置已经确定，第1个物体此时只能被移到5个特定的位置上，也就是第2个物体到第6个物体所在的位置。

故 O1A
2 3
33 2
3 ，∴ O 到平面 ABC 的距离 OO1
R2 O1A2 1.
图 A10
【答案】C
11. （函数，同文 12）若 2x 2 y 3 x 3 y ，则
A. ln( y x 1) 0
B. ln( y x 1) 0
C. ln | x y | 0
D. ln | x y | 0
和
a5 a1
1(k
1)
，因此可推出 C(1)
C (4)
1 5
，
C(2) C(3) 0 ，故 C 选项符合题意.
解法三（答案验证法）：
按照题设的定义 C(k)
1 m
m i 1
aiaik (k
1, 2,...m 1) ，逐个验证答案，使用
排除法，即可得到正确选项. 如 A 选项，C(2) 1 (0 1 0 1 0)= 2 1 ，
A. 2,3
B. 2, 2, 3 C. 2, 1, 0,3 D. 2, 1, 0, 2, 3
【解析】∵ A B {1,0,1, 2}，∴ CU A B 2,3 .
【答案】A
2. （三角函数）若 为第四象限角，则
A. cos 2 0
B. cos 2 0
C. sin 2 0
D. sin 2 0
C.是偶函数，且在 (, 1) 单调递增 2
B.是奇函数，且在 ( 1 , 1) 单调递减 22
D.是奇函数，且在 (, 1) 单调递减 2
【解析】∵ f (x) ln | 2x 1| ln | 2x 1| ln | 2x 1| ln | 2x 1| f (x) ，
∴ f (x) 是奇函数，
2020 年高考理科数学（全国 2 卷）答案详解及试题

新高考数学一轮复习考点知识归类讲义第29讲解三角形应用举例及综合问题1.仰角和俯角在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线上方叫仰角，目标视线在水平视线下方叫俯角(如图1).2.方位角从正北方向起按顺时针转到目标方向线之间的水平夹角叫做方位角.如B点的方位角为α(如图2).3.方向角正北或正南方向线与目标方向线所成的锐角，如南偏东30°，北偏西45°等.4.坡度：坡面与水平面所成的二面角的正切值.➢考点1 解三角形应用举例[名师点睛]1.距离问题的类型及解法(1)类型：两点间既不可达也不可视，两点间可视但不可达，两点都不可达.(2)解法：选择合适的辅助测量点，构造三角形，将问题转化为求某个三角形的边长问题，从而利用正、余弦定理求解.2.高度问题的类型及解法（1）在测量高度时，要理解仰角、俯角的概念，仰角和俯角都是在同一铅垂面内，视线与水平线的夹角.（2）准确理解题意，分清已知条件与所求，画出示意图.（3）运用正、余弦定理，有序地解相关的三角形，逐步求解问题的答案，注意方程思想的运用.3.角度问题的类型及解法（1）测量角度问题的关键是在弄清题意的基础上，画出表示实际问题的图形，并在图形中标出有关的角和距离，再用正弦定理或余弦定理解三角形，最后将解得的结果转化为实际问题的解.（2）方向角是相对于某点而言的，因此在确定方向角时，必须先弄清楚是哪一个点的方向角.[典例]1.（2022·湖北·华中师大一附中模拟预测）为了测量一个不规则公园,C D 两点之间的距离，如图，在东西方向上选取相距1km 的,A B 两点，点B 在点A 的正东方向上，且,,,A B C D 四点在同一水平面上．从点A 处观测得点C 在它的东北方向上，点D 在它的西北方向上；从点B 处观测得点C 在它的北偏东15︒方向上，点D 在它的北偏西75方向上，则,C D 之间的距离为______km.【答案】2 【分析】由题意确定相应的各角的度数，在ABC 中，由正弦定理求得BC ,同理再求出DB ，解DBC △，求得答案.【详解】由题意可知，904545,9045135,9015105CAB DAB CBA ∠=-=∠=+=∠=+=,157590,15CDB DBA ∠=+=∠= ,故在ABC 中，1804510530ACB ∠=--=，故sin sin BD AB DAB ADB =∠∠ ，1sin 452sin 30BC ⨯==在ABD △中，1801513530ADB ∠=--=， 故sin sin BC AB CAB ACB =∠∠ ，1sin1352sin 30BD ⨯==， 所以在DBC △中，90CBD ∠=，则22222CD BC DB =+=+= ,故答案为：22. (2021·全国甲卷)2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位：m).三角高程测量法是珠峰高程测量方法之一，如图是三角高程测量法的一个示意图，现有A ，B ，C 三点，且A ，B ，C 在同一水平面上的投影A ′，B ′，C ′满足∠A ′C ′B ′＝45°，∠A ′B ′C ′＝60°.由C 点测得B 点的仰角为15°，BB ′与CC ′的差为100；由B 点测得A 点的仰角为45°，则A ，C 两点到水平面A ′B ′C ′的高度差AA ′－CC ′约为(3≈1.732)( )A.346B.373C.446D.473答案 B解析如图所示，根据题意过C 作CE ∥C ′B ′，交BB ′于E ，过B 作BD ∥A ′B ′，交AA ′于D ，则BE ＝100，C ′B ′＝CE ＝100tan 15°.在△A ′C ′B ′中，∠C ′A ′B ′＝180°－∠A ′C ′B ′－∠A ′B ′C ′＝75°，则BD ＝A ′B ′＝C ′B ′·sin 45°sin 75°，又在B 点处测得A 点的仰角为45°，所以AD ＝BD ＝C ′B ′·sin 45°sin 75°， 所以高度差AA ′－CC ′＝AD ＋BE＝C ′B ′·sin 45°sin 75°＋100＝100tan 15°·sin 45°sin 75°＋100＝100sin 45°sin 15°＋100＝100×2222×⎝ ⎛⎭⎪⎫32－12＋100＝100(3＋1)＋100≈373.3．（2022·全国·高三专题练习）公路北侧有一幢楼，高为60米，公路与楼脚底面在同一平面上.一人在公路上向东行走，在点A 处测得楼顶的仰角为45°，行走80米到点B 处，测得仰角为30°，再行走80米到点C 处，测得仰角为θ.则tan θ=______________.【答案】37777【解析】首先得到60,603OA OB ==，然后由余弦定理得：2222cos OA AB OB AB OB ABO =+-⋅∠，2222cos OC BC OB BC OB OBC =+-⋅∠，然后求出OC 即可【详解】如图，O 为楼脚，OP 为楼高，则60OP =，易得：60,603OA OB ==由余弦定理得：2222cos OA AB OB AB OB ABO =+-⋅∠，2222cos OC BC OB BC OB OBC =+-⋅∠，两式相加得：()22222230800OA OC AB OB OC +=+⇒=，则77OC =故377tan 2077θ=377[举一反三] 1．（2022·山东师范大学附中模拟预测）魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高．一个数学学习兴趣小组研究发现，书中提供的测量方法甚是巧妙，可以回避现代测量器械的应用．现该兴趣小组沿用古法测量一山体高度，如图点E 、H 、G 在水平线AC 上，DE 和FG 是两个垂直于水平面且等高的测量标杆的高度，记为h ，EG 为测量标杆问的距离，记为d ，GC 、EH 分别记为,a b ，则该山体的高AB =（ ）A ．hd h a b +-B ．hd h a b--C ．hd d a b +-D ．hd d a b -- 【答案】A【分析】根据所给数据，利用解直角三角形先求出BM ，即可得解.【详解】连接FD ，并延长交AB 于M 点，如图， 因为在Rt BMD △中tan h BDM b ∠=，所以||||||tan BM BM b MD BDM h ==∠；又因为在Rt BMF △中tan h BFM a∠=， 所以||||||tan BM BM a MF BFM h ==∠，所以||||||||BM a BM b MF MD d h h-=-=， 所以||hd BM a b =-，即||hd AB BM h h a b =+=+-， 故选：A ．2．（2022·江苏南通·高三期末）某校数学建模社团学生为了测量该校操场旗杆的高AB ，先在旗杆底端的正西方点C 处测得杆顶的仰角为45°，然后从点C 处沿南偏东30°方向前进20m 到达点D 处，在D 处测得杆顶的仰角为30°，则旗杆的高为（ ）A ．20mB ．10mC ．103mD ．1033m 【答案】B 【分析】根据条件确定相关各角的度数，表示出AB ，,AD AC 等边的长度，然后在ACD △中用余弦定理即可解得答案.【详解】如图示，AB 表示旗杆，由题意可知：45,0,630ACB ACD ADB ∠=∠=∠=︒︒︒，所以设AB x = ，则3,AD x AC x ==，在ACD △ 中，2222cos AD AC CD AC CD ACD =+-⨯⨯⨯∠ ,即2221(3)()(20)2202x x x =+-⨯⨯⨯ ，解得10x = ，（20x =-舍去），故选：B.3．（2022·辽宁·沈阳二中模拟预测）沈阳二中北校区坐落于风景优美的辉山景区，景区内的一泓碧水蜿蜒形成了一个“秀”字，故称“秀湖”．湖畔有秀湖阁()A 和临秀亭()B 两个标志性景点，如图．若为测量隔湖相望的A 、B 两地之间的距离，某同学任意选定了与A 、B 不共线的C 处，构成ABC ，以下是测量数据的不同方案： ①测量A ∠、AC 、BC ；②测量A ∠、B 、BC ；③测量C ∠、AC 、BC ；④测量A ∠、C ∠、B ．其中一定能唯一确定A 、B 两地之间的距离的所有方案的序号是_____________．【答案】②③【分析】利用正弦定理可判断①②，利用余弦定理可判断③，根据已知条件可判断④不满足条件.【详解】对于①，由正弦定理可得sin sin AC BC B A =，则sin sin AC A B BC =， 若AC BC >且A ∠为锐角，则sin sin sin AC A B A AB=>，此时B 有两解， 则C ∠也有两解，此时AB 也有两解；对于②，若已知A ∠、B ，则C ∠确定，由正弦定理sin sin BC AB A C=可知AB 唯一确定； 对于③，若已知C ∠、AC 、BC ，由余弦定理可得222cos AB AC BC AC BC C =+-⋅ 则AB 唯一确定；对于④，若已知A ∠、C ∠、B ，则AB 不确定.故答案为：②③.4．（2022·辽宁·大连市一0三中学模拟预测）如图所示，遥感卫星发现海面上有三个小岛，小岛 B 位于小岛A 北偏东75距离60海里处，小岛B 北偏东15距离330海里处有一个小岛 C .(1)求小岛A 到小岛C 的距离；(2)如果有游客想直接从小岛A 出发到小岛 C ，求游船航行的方向.解：(1)在ABC 中，6030330，==AB BC1807515120ABC ∠=-+=，根据余弦定理得：.2222cos AC AB BC AB BC ABC =+-⋅⋅∠2260(30330)260(30330)cos1205400=+-⨯⨯⋅=306=AC 所以小岛A 到小岛 C 的最短距离是306.(2)根据正弦定理得：sin sin AC AB ABC ACB =∠∠ 30660120sin ACB=∠ 解得2sin ACB ∠=在ABC ∆中，,<BC ACACB ∴∠为锐角45ACB ∴∠=1801204515CAB ∴∠=--=. 由751560-=得游船应该沿北偏东60的方向航行答:小岛A 到小岛 C 的最短距离是306;游船应该沿北偏东60的方向航行. 5．（2022·广东·高三开学考试）如图，测量河对岸的塔高AB 时，可以选取与塔底B 在同一水平面内的两个测量基点C 与D ．现测得30BCD ∠=︒，135BDC ∠=︒，50CD =米，在点C 测得塔顶A 的仰角为45°，求塔高AB ．【解】在BCD △中，1801803013515CBD BCD BDC ∠=︒-∠-∠=︒-︒-︒=︒，∵()sin sin15sin 4530CBD ∠=︒=︒-︒sin 45cos30cos45sin30=︒︒-︒︒62-=由正弦定理sin sin BC CD BDC CBD =∠∠得()sin 5031sin 62CD BDC BC CBD ⋅∠===∠-.在Rt ABC △中45ACB ∠=︒．∴)5031AB BC ==．所以塔高AB 为)5031米．➢考点2 求解平面几何问题[名师点睛]平面几何中解三角形问题的求解思路(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解；(2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果.1.(2021·新高考八省联考)在四边形ABCD 中，AB ∥CD ，AD ＝BD ＝CD ＝1.(1)若AB ＝32，求BC ； (2)若AB ＝2BC ，求cos ∠BDC . 解(1)如图所示，在△ABD 中，由余弦定理可知，cos ∠ABD ＝AB 2＋BD 2－AD 22AB ·BD ＝⎝ ⎛⎭⎪⎫322＋12－122×32×1＝34.∵AB ∥CD ，∴∠BDC ＝∠ABD ，即cos ∠BDC ＝cos ∠ABD ＝34. 在△BCD 中，由余弦定理可得，BC 2＝BD 2＋CD 2－2BD ·CD cos ∠BDC ＝12＋12－2×1×1×34，∴BC ＝22. (2)设BC ＝x ，则AB ＝2BC ＝2x .由余弦定理可知， cos ∠ABD ＝AB 2＋BD 2－AD 22AB ·BD ＝（2x ）2＋12－122×2x ×1＝x ，①cos ∠BDC ＝CD 2＋BD 2－BC 22CD ·BD ＝12＋12－x 22×1×1＝2－x 22.②∵AB ∥CD ，∴∠BDC ＝∠ABD ，即cos ∠BDC ＝cos ∠ABD .联立①②，可得2－x 22＝x ，整理得x 2＋2x －2＝0，解得x 1＝3－1，x 2＝－3－1(舍去).将x 1＝3－1代入②，解得cos ∠BDC ＝3－1.2.（2022·湖北·襄阳四中模拟预测）在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，角A 的平分线AD 交BC 边于点D . (1)证明：AB DBAC DC=，2AD AB AC DB DC =⋅-⋅；(2)若1AD =，23A π=，求DB DC ⋅的最小值. 解：(1)在ABD △和BCD △中，可得BAD CAD ∠=∠，ADB ADC π∠+∠=， 所以sin sin BAD CAD ∠=∠，sin sin ADB ADC ∠=∠， 由正弦定理，得sin sin AB BDADB BAD =∠∠，sin sin AC DC ADC CAD=∠∠，两式相除得AB DB AC DC =，可得ABBD BC AB AC=+，AC DC BC AB AC =+， 又由cos cos ABD ABC ∠=∠，根据余弦定理得22222222AB BD AD AB BC AC AB BD AB BC+-+-=⋅⋅ 所以()()22222222BD DC BDAD AB BD AB BC AC AB AC BD BC BD BC BC BC=+-+-=+-- 代入可得222AC AB AD AB AC BD DC AB AC AB AC=+-⋅++ABAC AB AC BD DC AB AC BD DC AB AC AB AC ⎛⎫=⋅+-⋅=⋅-⋅ ⎪++⎝⎭.(2)由1AD =，23A π=及ABD ACD ABC S S S +=△△△，可得b c bc += 根据基本不等式得2bc b c bc=+≥，解得4bc ≥，当且仅当2b c ==时等号成立，又由1AD =，2AD AB AC DB DC =⋅-⋅，可得13DB DC bc ⋅=-≥， 所以DB DC ⋅的最小值是3. [举一反三]1．（2022·山东·济南市历城第二中学模拟预测）如图，已知在ABC 中，M 为BC 上一点，2AB AC BC =≤，π0,2B ⎛⎫∈ ⎪⎝⎭且15sin 8B =．(1)若AM BM =，求ACAM的值； (2)若AM 为BAC ∠的平分线，且1AC =，求ACM △的面积．解：（1）因为15sin B =π0,2B ⎛⎫∈ ⎪⎝⎭,所以27cos 1sin 8B B -=，因为2AB AC =，所以由正弦定理知sin 2sin C ABB AC==，即sin 2sin C B =，因为AM BM =，所以2AMC B ∠=∠，sin sin 22sin cos AMC B B B ∠==，在AMC 中，sin 2sin cos 7cos sin 2sin 8AC AMC B B B AM C B ∠====． （2）由题意知22AB AC ==，设BC x =，由余弦定理得222217cos 48x B x +-==，解得2BC =或32BC =．因为2AC BC ≤，所以2BC =，因为AM 为BAC ∠的平分线，BAM CAM ∠=∠所以11sin 2211sin 22ABM ACMAB AM BAM BM hS SAC AM CAM CM h⋅∠⨯==⋅∠⨯（h 为底边BC 的高）所以2BM AB CMAC ==，故1233CM BC ==，而由（1）知sin 2sin C B ==112sin 1223ACM S AC CM C =⋅⋅=⨯⨯=△． 2．（2022·福建省福州第一中学三模）已知ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ，sinsin2A Bb c B +=. (1)求角C ；(2)若AB 边上的高线长为ABC 面积的最小值. 解：(1)由已知A B C π++=，所以sin sin cos 222A B C Cb b b π+-==， 所以cossin 2C b c B =，由正弦定理得sin cos sin sin 2CB C B =， 因为B 、()0,C π∈，则sin 0B >，022C π<<，cos 02C>，所以，cos sin 2C C =，则cos 2sin cos 222C C C =，所以1sin 22C =，所以26C π=，则3C π=.(2)由11sin 22ABCSc ab C =⋅=，得4ab c =， 由余弦定理222222cos 2c a b ab C a b ab ab ab ab =+-=+-≥-=， 即24c c ≥，因为0c >，则4c ≥，当且仅当4a b c ===取等号，此时ABC 面积的最小值为3．（2022·山东师范大学附中模拟预测）在①2sin cos sin b C B c B =+，②cos cos 2B bC a c=-两个条件中任选一个，补充在下面的问题中，并解答该问题.在ABC 中，内角A 、B 、C 所对的边分别是a 、b 、c ，且________. (1)求角B ；(2)若a c +=D 是AC 的中点，求线段BD 的取值范围.解：(1)选①，由2sin cos sin b C B c B =+及正弦定理可得2sin sin cos sin sin B C C B C B =+，所以，sin sin cos C B C B =，因为B 、()0,C π∈，所以，sin 0C >，则sin 0B B =>，所以，tan B =3B π∴=；选②，由cos cos 2B bC a c=-及正弦定理可得()sin cos 2sin sin cos B C A C B =-， 所以，()2sin cos sin cos cos sin sin sin A B B C B C B C A =+=+=，A 、()0,B π∈，sin 0A ∴>，所以，1cos 2B =，则3B π=.(2)因为a c +=0a <<由已知AD DC =，即BD BA BC BD -=-，所以，2BD BA BC =+， 所以，()222242BD BA BC BA BC BA BC =+=++⋅，即())22222242cos33BD c a ac c a ac a c ac aa π=++=++=+-=-22993,344a a ⎛⎡⎫=+=+∈ ⎪⎢ ⎣⎭⎝⎭，所以，34BD ≤<➢考点3 三角函数与解三角形的交汇问题（2022·浙江省新昌中学模拟预测）已知函数21()cos sin 2f x x x x ωωω=-+，其中0>ω，若实数12,x x 满足()()122f x f x -=时，12x x -的最小值为2π． (1)求ω的值及()f x 的对称中心；(2)在ABC 中，a ，b ，c 分别是角A ，B ，C的对边，若()1,f A a =-=ABC 周长的取值范围． 解：(1)211cos 21()cos sin 2222x f x x x x x ωωωωω-=-+=-+12cos 2sin 226x x x πωωω⎛⎫=+=+ ⎪⎝⎭， 显然()f x 的最大值为1，最小值为1-，则()()122f x f x -=时，12x x -的最小值等于2T，则22T π=，则22ππω=，1ω=；令2,6x k k ππ+=∈Z ，解得,122k x k ππ=-+∈Z ，则()f x 的对称中心为,0,122k k ππ⎛⎫-+∈ ⎪⎝⎭Z ； (2)()sin(2)16f A A π=+=-，22,62A k k πππ+=-+∈Z ，又()0,A π∈，则23A π=， 由正弦定理得2sin sin sina b cA B C====，则2sin ,2sin b B c C ==， 则周长为2sin 2sin 2sin 2sin 3a b c B C B B π⎛⎫++=+=+- ⎪⎝⎭3sin 3cos 32sin()3B B B π=++=++，又03B π<<，则2333B πππ<+<，则32sin()23B π<+≤，故周长的取值范围为(23,23⎤+⎦.[举一反三]1．（2022·浙江湖州·模拟预测）已知函数()sin(),0,0,02f x A x x R A πωϕωϕ⎛⎫=+∈>><< ⎪⎝⎭的部分图像如图所示．(1)求()f x 的解析式；(2)在锐角ABC 中，若边1BC =，且3212Af π⎛⎫-= ⎪⎝⎭，求ABC 周长的最大值．解：(1)由图得2A =，32ππ3π43124T ⎛⎫=--= ⎪⎝⎭，又2πT ω=，所以2ω=， 将点π,012⎛⎫- ⎪⎝⎭代入()2sin(2)f x x ϕ=+，得πsin 06ϕ⎛⎫-+= ⎪⎝⎭，即π,6k k Z ϕπ=+∈， 考虑到π02ϕ<<，故π6ϕ=，即()f x 的解析式为π()2sin 26f x x ⎛⎫=+ ⎪⎝⎭(2)由π3212A f ⎛⎫-= ⎪⎝⎭3sin A =及π0,2A ⎛⎫∈ ⎪⎝⎭，故π3A =，因为ABC 为锐角三角形，且π3A =，故ππ,62B ⎛⎫∈ ⎪⎝⎭由正弦定理，得sin sin sin a b c A B C ===所以2π1sin )1sin sin3a b c B C B B ⎤⎛⎫++=+=+- ⎪⎥⎝⎭⎦1π12sin cos 12sin 26B B B ⎛⎫⎛⎫=+⋅=++ ⎪ ⎪⎝⎭⎝⎭又ππ2π,633B ⎛⎫+∈ ⎪⎝⎭，故π2sin 6B ⎛⎫+∈ ⎪⎝⎭， 故ABC 周长的最大值为3.2.（2022·山东淄博·三模）已知函数21()cos cos (0)2f x x x x ωωωω=-+>，其图像上相(1)求函数()f x 的解析式；(2)记ABC 的内角,,A B C 的对边分别为,,a b c ，4a =，12bc =，()1f A =．若角A 的平分线AD交BC 于D ，求AD 的长．解：(1)因为()211cos cos 2cos 222f x x x x x x ωωωωω=-+=-πsin 26x ω⎛⎫=- ⎪⎝⎭，设函数()f x 的周期为T ，由题意222444πT ⎛⎫+=⎪+ ⎝⎭，即2224ππω⎛⎫= ⎪⎝⎭，解得1ω=，所以()πsin 26f x x ⎛⎫=- ⎪⎝⎭.(2)由()1f A =得：sin 216A π⎛⎫-= ⎪⎝⎭，即22,Z 62A k k πππ-=+∈，解得,Z 3A k k ππ=+∈，因为[0,]A π∈，所以π3A =， 因为A 的平分线AD 交BC 于D ，所以ABCABDACDSSS=+，即111sinsin sin 232626bc c AD b AD πππ=⋅⋅+⋅⋅，可得AD = 由余弦定理得：，()22222cos 3a b c bc A b c bc =+-=+-，而12bc =，得()252b c +=，因此AD ==。

普通高等学校招生全国统一考试数学（理工农医类）（福建卷及详解）一.选择题：本小题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.函数()sin cos f x x x =最小值是A ．-1 B.12-C.12D.12.已知全集U=R ，集合2{|20}A x x x =->，则C U A 等于A ．{x ∣0≤x ≤2}B {x ∣0<x<2}C ．{x ∣x<0或x>2}D {x ∣x ≤0或x ≤2}3.等差数列{}n a 的前n 项和为n S ，且3S =6，1a =4，则公差d 等于A ．1B53C.-2D 34.22(1cos )x dx ππ-+⎰等于A ．π B.2C.π-2D.π+25.下列函数()f x 中，满足“对任意1x ，2x ∈（0，+∞），当1x <2x 时，都有1()f x >2()f x 的是A ．()f x =1xB.()f x =2(1)x -C .()f x =xe D()ln(1)f x x =+6.阅读右图所示的程序框图，运行相应的程序，输出的结果是A ．2B .4C.8D .167.设m ，n 是平面α内的两条不同直线，1l ，2l 是平面β内的两条相交直线，则α//β的一个充分而不必要条件是A.m //β且l //α B.m //l 且n //l 2C.m//β且n //βD.m//β且n //l 28.已知某运动员每次投篮命中的概率低于40%。

现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，指定1，2，3，4表示命中，5，6，，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果。

经随机模拟产生了20组随机数：907966191925271932812458569683431257393027556488730113537989据此估计，该运动员三次投篮恰有两次命中的概率为A ．0.35B 0.25C 0.20D 0.159.设a ，b ，c 为同一平面内具有相同起点的任意三个非零向量，且满足a 与b 不共线，若a ⊥c 且∣a∣=∣c∣,则∣b •c∣的值一定等于A ．以a ，b 为两边的三角形面积B 以b ，c 为两边的三角形面积C ．以a ，b 为邻边的平行四边形的面积D 以b ，c 为邻边的平行四边形的面积10.函数()(0)f x ax bx c a =++≠的图象关于直线2bx a=-对称。